O documento contém exercícios para a aplicação de conceitos de funções reais, abordando tópicos como a definição de funções, classificação de relações e propriedades de funções (injutivas, sobrejetivas e bijetivas). Os exercícios incluem a verificação de diagramas, a identificação de domínio e contradomínio, e questões sobre a paridade de funções. O material é voltado para alunos da 12ª classe e visa reforçar o entendimento teórico e prático sobre o tema.


![Funções reais de variável real e natural |O grupo de disciplina Página 10
0
II. REVISÃO DO ESTUDO DE FUNÇÕES
1. Se x 3 e y 2 , do gráfico abaixo:
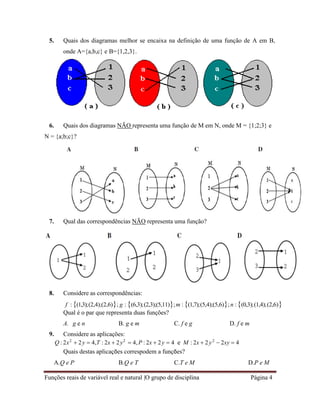
O ponto que representa localização (x;y) é:
A. P B. Q C. R D. S E. Origem do sistema cartesiano
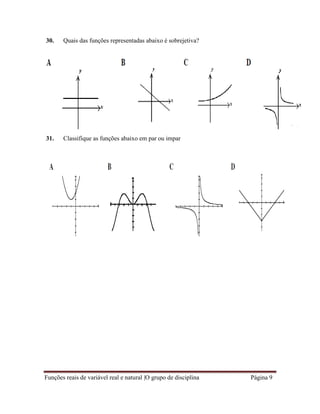
2. Qual é o domínio da função representada na figura?
A. [3;4] B.];04[ C.
D.
/{2}
3. Qual destas afirmações está correcta?
A. O gráfico de uma função quadrática e uma linha recta.
B. Qualquer função do primeiro grau e ímpar.
C. Qualquer função logaritmica tem assimptota horizontal.
D. As funções trigonométricas são periódicas.](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-10-320.jpg)
![Funções reais de variável real e natural |O grupo de disciplina Página 11
4. Observe a figura. Qual é o dominio da funçaõ?
A. R /{1;0} B. R /{1}] C. /{0} D.
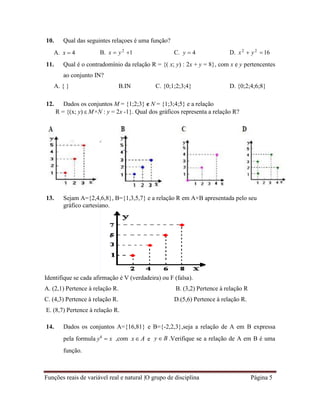
5. Observe a figura. Qual é o domínio da função?
A. B./{0} C. /{1} D. ];1[]0;[
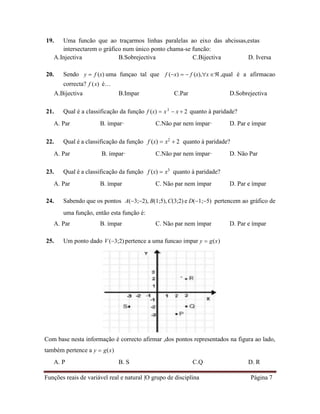
6. Qual é o gráfico que representa a função y = x + 2 com x; y 𝜖 IR ?
7. Se x1;x2
é ?
Df com x1 x2 tivermos f (x1) f (x2 ) diz-se que a função y f (x)
A. Bijectiva B. Crescente C. Decrescente D.Sobrejectiva](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-11-320.jpg)

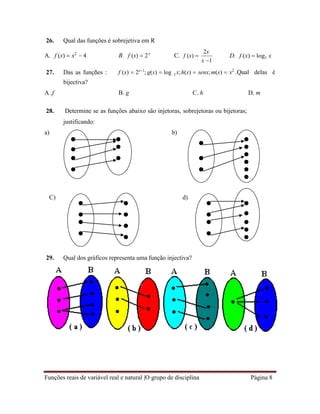
![Funções reais de variável real e natural |O grupo de disciplina Página 13
2 4
15. Qual é a expressão analítica da função cujo gráfico está representado na figura?
A. x2
2x 1 B. x2
2x 1 C. x2
2x 1 D. x2
2x 1
16. Em quantos pontos se intersectam os gráficos das funções
g(x) 3 ?
f (x) x2
4x e
A. 1 B.2 C.3 D. 4
17. Qual é a expressão analítica de uma função do segundo grau, cujo gráfico passa
pelo ponto P (0;-2) e tem como coordenadas de vértice V
3
;
1
?
A. f (x) x2
3x 2
B. f (x) x2
3x 2
C. f (x) x2
3x 2
D. f (x) x2
3x 2
18. O gráfico de uma função do primeiro grau passa pelo ponto (4;0) e pelo vértice da
parábola dada pela expressão
função do primeiro grau?
f (x) x2
2x. Qual é a expressão analítica dessa
A. y
1
x
4
B. y
1
x
4
C. y
1
x
4
D. y
1
x
4
3 3 3 3 3 3 3 3
19. Os gráficos das f (x) ax
e g(x) x2
1 interceptam – se num ponto de abcissa
3. Qual é o valor de a?
A. 1 B. 2 C. 3 D. 4
20. Qual é a abcissa do vértice do gráfico da função g(x) x2
2x?
A. 1 B. 2 C. 3 D. 4
21. Qual dos seguintes conjuntos é igual a Q {x R : x2
5x 6 0}?
A. [3;2] B. [3;2] C. ] ;3][2;[ D. ] ;3[] 2;[
22. Qual destas funções tem apenas como domínio
?
A. f (x) x2
B. f (x) 2x C. f (x)
1
x
D. f (x) log2 x](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-13-320.jpg)
![Funções reais de variável real e natural |O grupo de disciplina Página 14
23.Na figura abaixo está representa o gráfico da função f (x) = log b x:A
área da região sombreada é:
A. 2 B.2,2 C.2,8 D. 2,5 E. 3
24. O valor de sen12000
é:
A.
1
B.
3
C.
3
D.
1
2 2 2 2
25. Sabendo que é um ângulo do 1º quadrante. A que quadrante pertence o ângulo
?
A. IQ B. IIQ C. IIIQ D. IVQ
26. A expressão 1 senx* cos x *tgx é equivalente á?
A. sen2
x B. 1 senx C. cos2
x D. 1 tgx
27. Se Cos
1
2
e Sen 0 , qual é o valor de [0o
;360o
]?
A.60° B. 120° C. 240° D.300°
28. Qual é o valor do ângulo , para o qual Sen Cos , Sendo 180o
360o
?
A.270° B. 225° C. 210° D.180°
29. Qual é o contradomínio da função f (x) = 2+ cosx?
A. [3;1] B. [2;2] C. [1;1] D. [1;3]
30. Considere a função f (x) = senx com
h(x) f
x
?
x; . Qual é o domínio da função
A.
3
;
B.
;
3
C.
;
D.;
2 2 2 2 2 2
31. Seja
o perido da funcao
4
f (x) cos(2mx), com m
. Qual é o valor de m?
A.
1
B.
8
C. 4 D. 8
8
2](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-14-320.jpg)
![Funções reais de variável real e natural |O grupo de disciplina Página 15
3
3
2
3 2
4 2
2
4 4
32. O conjunto imagem (o contradomínio) da função f (x) (senx cosx)2
é:
A. [0;[ B. [1;1] C.[0;4] D.[0;2] E. ] ;[
33. O período da função f (x) 5sen
4x
é:
A.
B.
C.
D.
1
5 2 3 2
34. O período da função f (x) cos
2x
é:
A. 6
B. 4
C.3
D. 2
35. O período da função f (x) tgs
3x
é:
A.
B.
2
C.
2
D.
3 3 5
36. O período da função f (x) ctg
1
x
é:
A.
B.
3
C.2
2
D.3
37. Seja g(x) tgx .Qual é o conjunto que representa o domínio de g?
A. /
k
B. /
k
C.
D.
38. Determine o domínio das funções:
A. f (x) tgx 600
B. f (x) tg
x
C. f (x) ctg
x
D. f (x) ctg
2x
39. As declarações abaixo foram deduzidas por um estudante para a expressão:
g(x) 3 5sen2x 4
1.O domínio de g é ] ;[ 2.O domínio de g é [2;8]
3.O período de g é
4.
2
g(2) 3
Quais das afirmaçoes são correctas ?
A.1, 2 e 3 B.1,2 e 4 C.1, 3 e 4 D. 2,3 e 4](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-15-320.jpg)


![Funções reais de variável real e natural |O grupo de disciplina Página 18
19. Na figura, temos os esboços dos gráficos das funções f e g, sendo f(x) = a x
.
O valor de g(g (-1))+f(g (3)) é:
A.1 B. 2 C. 3 D. 3/2 E. 5/2
20. Seja y=f(x) uma função definida no intervalo [-3;6] conforme indicado no gráfico.
Deste modo, o valor de f(f(2)) é:
A. 3 B. 0 C.-3 D. -1/2 E. 1
21. Com respeito à função f:RR, cujo gráfico está representado abaixo:
É correcto afirmar:
A. (f o f) (-2) = 1 B. (f o f) (-1) = 2 C. (f o f) (-2) = -1
D. (f o f) (-1) = 0 E. f(-2) = 1
22. Duas funções, f e g , são tais que f(x)=3x-1 e f[g(x)]=2-6x. Nessas condições, o
valor de g(-1) é:
A. 3 B. 4 C. 5 D. 6](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-18-320.jpg)

![Funções reais de variável real e natural |O grupo de disciplina Página 20
29. Sendo g(x) = 3x + 1 e g(f(x)) =
3x
11, determine f(x). Sendo g(x) = 2x - 1 e
2
f(g(x)) = 2x – 5, determine f(x).
30. Sejam f e g funções de R em R, sendo R o conjunto dos números reais, dadas por:
f(x) = 2x - 3 e f(g(x)) = -4x + 1. Nestas condições, g(-1) é igual a:
A. -5 B. -4 C. 0 D. 4 E. 5
31. Considere a função f definida pela tabela seguinte:
Qual é o valor de f [f (4)]?
A. 4 B. 3 C. 2 D. 1
32. Na função
g[g(x)] 1 é:
g(x) representada no gráfico abaixo, o valor de x tal que
A. 2 B. -2 C. 1 D. -1](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-20-320.jpg)

![Funções reais de variável real e natural |O grupo de disciplina Página 24
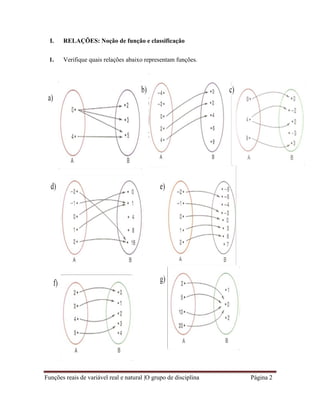
V. FUNÇÃO HOMÓGRAFA
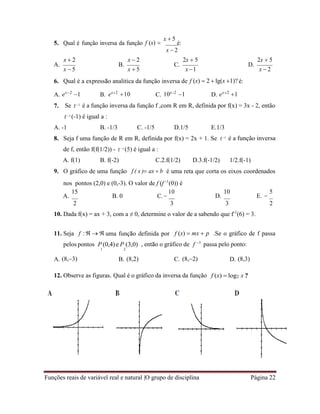
1. Diga qual das funções abaixo é homografa:
a) f (x)
2x 1
x 3
b) f (x)
2x 1
3
c) f (x)
1
x 3
d) f (x)
x2
x 3
e) f (x)
x
x2
3
f) f (x)
x
x 3
g) f (x)
2 x
x 1
e) f (x)
1
2x 5
2. Das funções homógrafas encontradas no exercício anterior, esboce o gráfico de cada
uma delas.
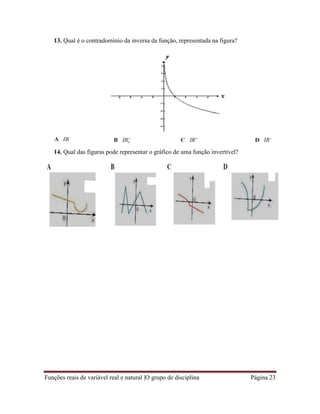
3. As assimptotas da função f (x)
x 1
são respectivamente:
x 3
A. x 1; y 3 B. x 3; y 1 C. x 1; y 3 D. x 3; y 1
4. As assimptotas da função f (x)
2x 1
são respectivamente:
x 1
A. x 2; y 1 B. x 1; y 2 C. x 1; y 1 D. x 1; y 1
5. As assimptotas da função f (x) 2
1
2x 1
são respectivamente:
A. x
1
; y 2
2
B. x
1
; y 2
2
C. x
1
; y 2
2
D. x 2; y
1
2
6. O contradominio da função f (x)
1
1 x
2 é:
A. R B. R/{1} C. R /{2} D.[3;[ E. ] ;2]
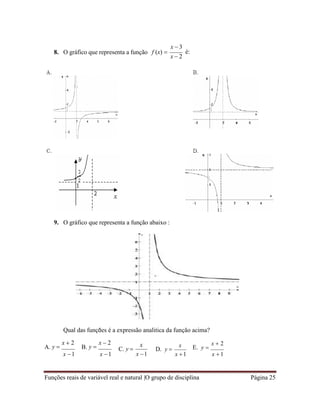
7. O gráfico que representa a função f (x)
x 1
é:
x 1](https://image.slidesharecdn.com/fichadeexerciciosiitrimestre-240830190012-a0067c31/85/Ficha-de-exemplos-e-exercicios-II-Trimestre-pdf-24-320.jpg)