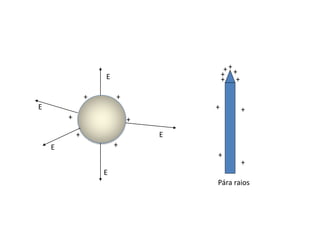
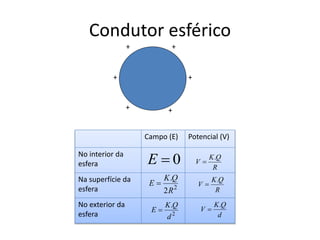
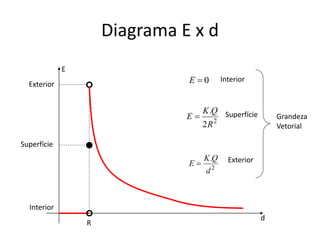
O documento descreve o equilíbrio eletrostático em condutores. Quando um condutor está em equilíbrio eletrostático, não há fluxo ordenado de elétrons livres em seu interior, as cargas distribuem-se na superfície externa e o campo elétrico e o potencial são nulos no interior.