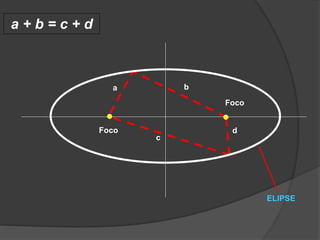
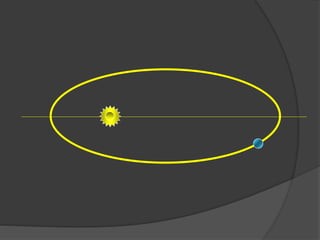
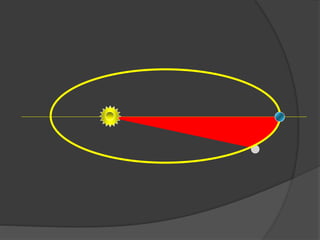
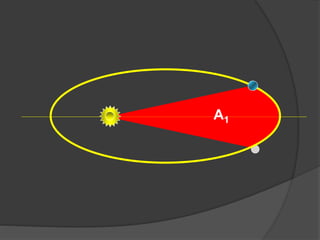
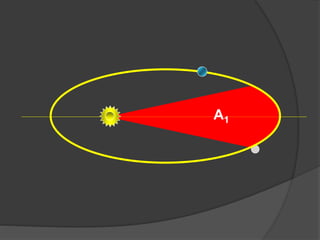
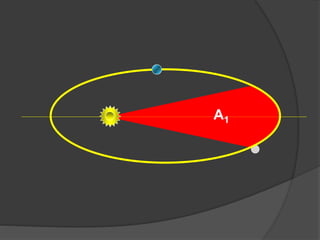
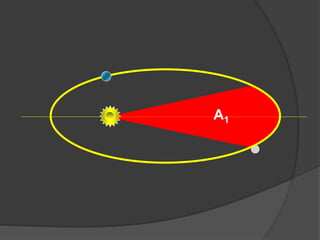
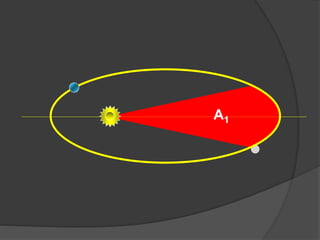
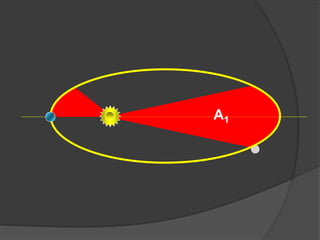
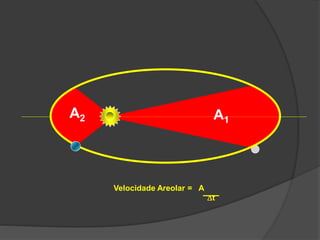
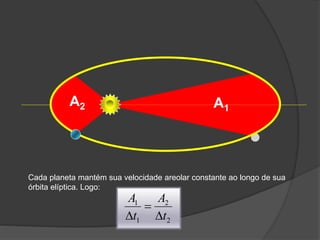
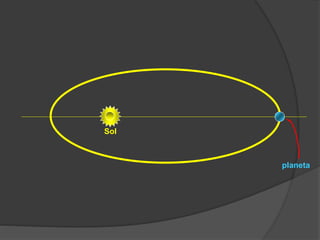
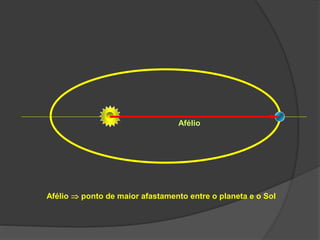
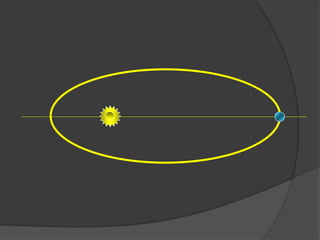
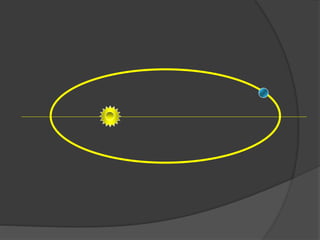
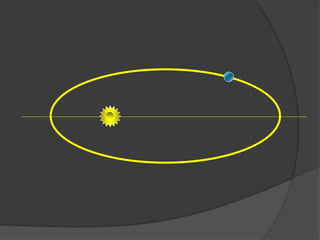
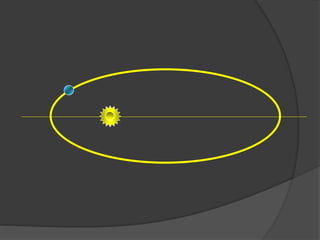
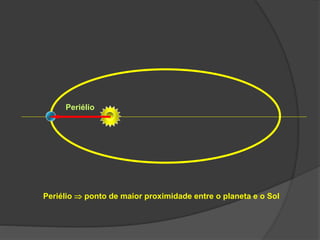
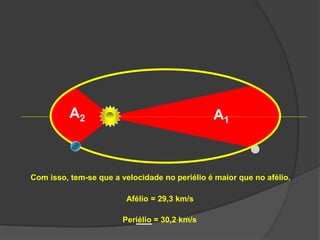
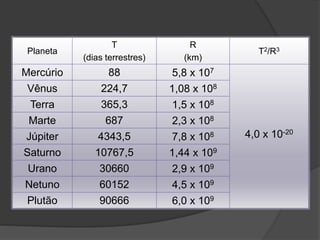
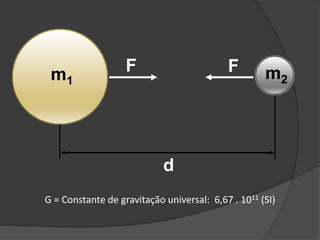
O documento descreve a evolução histórica dos modelos planetários, desde os gregos até Kepler e Newton. Kepler formulou três leis com base nas observações de Tycho Brahe, descrevendo os movimentos elípticos e periódicos dos planetas em torno do Sol. Newton explicou tais movimentos através da lei da gravitação universal.

2. Histórico
 Os primeiros a descreverem sistemas
planetários explicando os movimentos de
corpos celestes foram os gregos.
 O mais famoso sistema planetário grego
foi o de Cláudio Ptolomeu (100-170), que
considerava a Terra como o centro do
Universo (sistema geocêntrico).
 Segundo esse sistema, cada planeta
descrevia uma órbita circular cujo centro
descreveria outra órbita circular em torno
da Terra.

3.  Nicolau Copérnico (1473-1543), astrônomo
polonês, criou uma nova concepção de
Universo, considerando o Sol como seu
centro (sistema heliocêntrico).
 Segundo esse sistema, cada planeta,
inclusive a Terra, descrevia uma órbita
circular em torno do Sol.
 Entretanto, o modelo de Copérnico não foi
aceito pelo astrônomo dinamarquês Tycho
Brahe (1546-1601), segundo o qual o Sol
giraria em torno da Terra e os planetas em
torno do Sol.

4.  Ao morrer, Brahe cedeu suas observações a
seu discípulo Johannes Kepler (1571-1630),
que tentou, em vão, explicar o movimento
dos astros por meio das mais variadas
figuras geométricas.
 Baseado no heliocentrismo, em sua intuição
e após inúmeras tentativas, ele chegou à
conclusão de que os planetas seguiam uma
órbita elíptica em torno do Sol e, após anos
de estudo, enunciou três leis.

5. 1ª lei de Kepler
Numa elipse existem dois focos e a soma das
distâncias aos focos é constante.
“As órbitas dos planetas em torno do Sol
são elipses nas quais ele ocupa um dos
focos.”

6. Foco
Foco
a b
c
d
a + b = c + d
ELIPSE

7. 2ª lei de Kepler
Velocidade Areolar: velocidade com que as
áreas são descritas.
“A área descrita pelo raio vetor de um
planeta (linha imaginária que liga o planeta
ao Sol) é diretamente proporcional ao
tempo gasto para descrevê-la.”

10. A1

11. A1

12. A1

13. A1

14. A1

15. A1

16. A1
A2
Velocidade Areolar = A
t

17. A1
A2
Cada planeta mantém sua velocidade areolar constante ao longo de sua
órbita elíptica. Logo:
2
2
1
1
t
A
t
A




18. planeta
Sol

19. Afélio
Afélio  ponto de maior afastamento entre o planeta e o Sol

28. Periélio
Periélio  ponto de maior proximidade entre o planeta e o Sol

29. A1
A2
Com isso, tem-se que a velocidade no periélio é maior que no afélio.
Afélio = 29,3 km/s
Periélio = 30,2 km/s

30. 3ª lei de Kepler
(Lei dos períodos)
Raio Médio: média aritmética entre as distâncias
máxima e mínima do planeta ao Sol.
“O quadrado do período da revolução de um
planeta em torno do Sol é diretamente
proporcional ao cubo do raio médio de sua
elipse orbital.”
32
RKT 

31. Planeta
T
(dias terrestres)
R
(km)
T2/R3
Mercúrio 88 5,8 x 107
4,0 x 10-20
Vênus 224,7 1,08 x 108
Terra 365,3 1,5 x 108
Marte 687 2,3 x 108
Júpiter 4343,5 7,8 x 108
Saturno 10767,5 1,44 x 109
Urano 30660 2,9 x 109
Netuno 60152 4,5 x 109
Plutão 90666 6,0 x 109

32.  As Leis de Kepler dão uma visão
cinemática do sistema planetário.
 Do ponto de vista dinâmico, que tipo de
força o Sol exerce sobre os planetas,
obrigando-os a se moverem de acordo
com as leis que Kepler descobrira?
 A resposta foi dada por
Isaac Newton (1642-1727):
FORÇA GRAVITACIONAL!!!!

33. Lei da Gravitação Universal
“Dois pontos materiais se atraem mutuamente
com forças que têm a direção da reta que os
une e cujas intensidades são diretamente
proporcionais ao produto de suas massas e
inversamente proporcionais ao quadrado da
distância que os separa.”
2
d
mMG
F



34. d
m1 m2
F F
G = Constante de gravitação universal: 6,67 . 1011 (SI)

35.  Devido a sua enorme massa, o Sol
tende a atrair os planetas em sua
direção
 Quanto mais próximo do Sol, maior a
velocidade do planeta para que possa
escapar do campo de atração
gravitacional do Sol
 A densidade de um planeta influencia na
sua velocidade de rotação (quanto mais
denso, mais lento)
Ainda de acordo com as leis da
Gravitação Universal