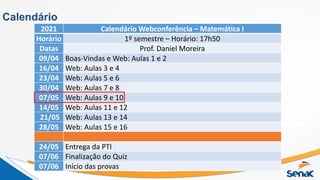
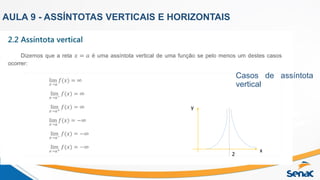
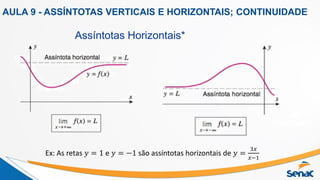
O documento apresenta o calendário das aulas 9 e 10 de Matemática I no primeiro semestre de 2021, ministradas pelo professor Daniel Moreira. Nas aulas serão abordados os tópicos de limites, assíntotas verticais e horizontais, introdução às derivadas, propriedades das derivadas e suas aplicações.













![𝑓´ 𝑥 = lim
ℎ→0
𝑓 𝑥 + ℎ − 𝑓(𝑥)
ℎ
𝑓 𝑥 = 𝑥2
− 12𝑥 − 5
𝑓´ 𝑥 = lim
ℎ→0
[(𝑥 + ℎ)2
−12 𝑥 + ℎ − 5] − [𝑥2
− 12𝑥 − 5)]
ℎ
𝑓´ 𝑥 = lim
ℎ→0
𝑥2
+ 2𝑥ℎ + ℎ2
− 12𝑥 − 12ℎ − 5 − 𝑥2
+ 12𝑥 + 5
ℎ
𝑓´ 𝑥 = lim
ℎ→0
2𝑥ℎ + ℎ2
− 12ℎ
ℎ
𝑓´ 𝑥 = lim
ℎ→0
ℎ(2𝑥 + ℎ − 12)
ℎ
𝑓´ 𝑥 = lim
ℎ→0
2𝑥 + ℎ − 12 = 2𝑥 − 12
Calculando derivada pela definição:
Aula 10: Derivadas: identificar como função](https://image.slidesharecdn.com/webconferncia07-05mati-240115013510-4aa60d7f/85/Webconferencia-07-05-Mat-I-pdf0098776421-17-320.jpg)
![𝑓 𝑥 = 𝑥3 𝑓´ 𝑥 = 3𝑥3−1 𝑓´ 𝑥 = 3𝑥2
𝑓 𝑥 =
3
𝑥2 podemos escrever como 𝑓 𝑥 = 𝑥
2
3
𝑓´ 𝑥 =
2
3
𝑥
−1
3
𝑓 𝑥 =
1
𝑥3 podemos escrever como 𝑓 𝑥 = 𝑥−3
Então 𝑓´ 𝑥 = −3𝑥−3−1= −3𝑥−4 =
−3
𝑥4
Regra da potência
𝑑
𝑑𝑥
𝑥𝑛
= 𝑛 ∙ [𝑥]𝑛−1
, onde n é um número qualquer.
Aula 10: Derivadas: identificar como função](https://image.slidesharecdn.com/webconferncia07-05mati-240115013510-4aa60d7f/85/Webconferencia-07-05-Mat-I-pdf0098776421-18-320.jpg)
![𝑓 𝑥 = 5𝑥3
Regra do múltiplo constante:
𝑑
𝑑𝑥
𝑘 ∙ 𝑓 𝑥 = 𝑘 ∙
𝑑
𝑑𝑥
[𝑓 𝑥 ], onde k é uma constante.
Regra da soma:
𝑑
𝑑𝑥
𝑓 𝑥 + 𝑔 𝑥 =
𝑑
𝑑𝑥
𝑓 𝑥 +
𝑑
𝑑𝑥
𝑔 𝑥 , onde f x e g x são funções contínuas.
𝑓 𝑥 = 5𝑥3
− 4𝑥 + 10
𝑓´ 𝑥 = 3.5𝑥2 = 15𝑥2
𝑓 ´ 𝑥 = 15𝑥2
− 4
Aula 10: Derivadas: identificar como função
𝑓 𝑥 = 3.5𝑥2 − 4 + 0](https://image.slidesharecdn.com/webconferncia07-05mati-240115013510-4aa60d7f/85/Webconferencia-07-05-Mat-I-pdf0098776421-19-320.jpg)
![Regra da potência geral
𝑓 𝑥 = (𝑥2
+ 4𝑥)3
𝑑
𝑑𝑥
𝑓 𝑥 𝑟 = 𝑟 ∙ [𝑓 𝑥 ]𝑟−1 ∙
𝑑
𝑑𝑥
[𝑓 𝑥 ], onde r é um número qualquer.
𝑓´ 𝑥 = 3. (𝑥2 + 4𝑥)2. (2𝑥 + 4)
Regra do produto
𝑑
𝑑𝑥
𝑓 𝑥 𝑔(𝑥) = 𝑓′(𝑥)𝑔 𝑥 + 𝑓 𝑥 𝑔′(𝑥)
𝑓 𝑥 = 𝑥6
. 5𝑥 − 4𝑥3 2
𝑓´ 𝑥 = 6𝑥5
. 5𝑥 − 4𝑥3 2
+ 𝑥6
. 2. (5𝑥 − 4𝑥3
) . (5 − 12𝑥2
)
Aula 10: Derivadas: identificar como função](https://image.slidesharecdn.com/webconferncia07-05mati-240115013510-4aa60d7f/85/Webconferencia-07-05-Mat-I-pdf0098776421-20-320.jpg)


