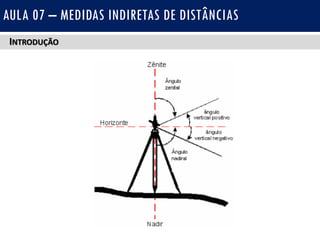
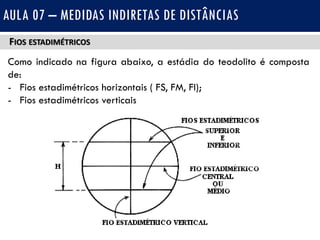
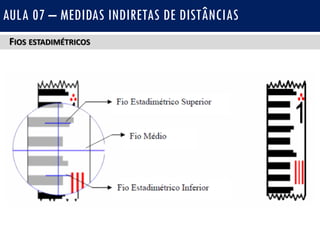
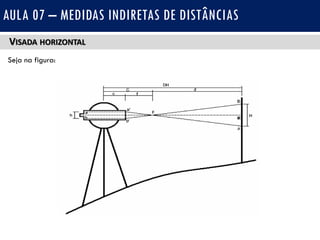
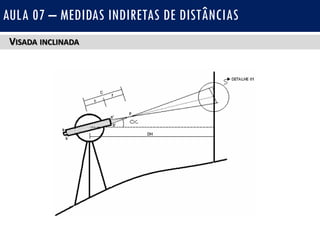
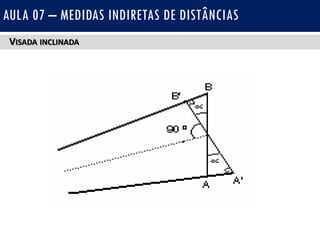
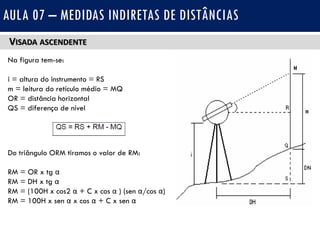
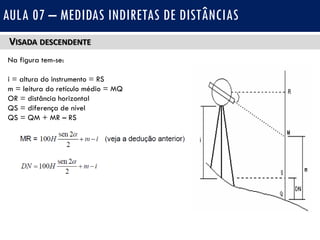
O documento discute medidas indiretas de distâncias em topografia, incluindo o uso de fios estadimétricos e teodolitos para medir distâncias horizontais e verticais. Explica as fórmulas para calcular distâncias horizontais em visadas horizontais e inclinadas, e distâncias verticais (diferenças de nível) em visadas ascendentes e descendentes. Também inclui exercícios e referências bibliográficas.