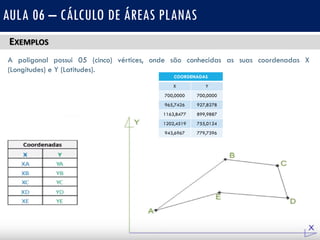
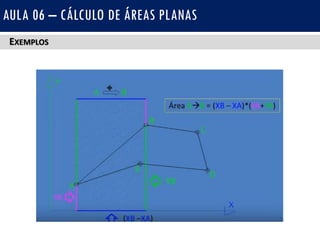
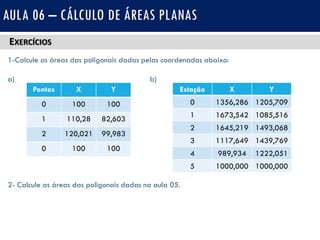
Este documento apresenta uma aula sobre o cálculo de áreas planas utilizando a fórmula de Gauss. Explica os métodos analíticos e geométricos para determinar áreas e se concentra no método analítico da fórmula de Gauss. Fornece exemplos passo a passo de cálculo de áreas de polígonos e exercícios para praticar a aplicação da fórmula.