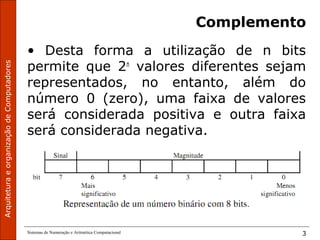
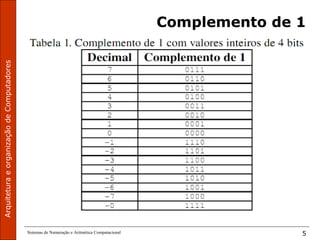
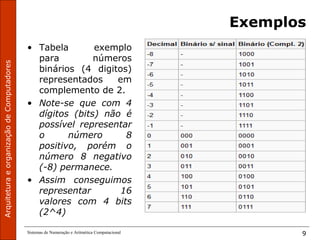
O documento discute sistemas de numeração e aritmética computacional, especificamente complemento de 1 e complemento de 2. Complemento de 1 é obtido pela negação de todos os bits de um número binário. Complemento de 2 representa números positivos diretamente e negativos como o complemento e mais um da representação binária invertida. Isso permite representar valores negativos de forma única usando a mesma regra de soma para positivos e negativos.

1. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 1
Arquitetura e Organização deArquitetura e Organização de
ComputadoresComputadores
Aritmética Computacional
(Complemento)

2. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 2
Complemento
• Dado um número binário A,
composto de n bits, tem-se que 1 bit
é usado para representar o sinal,
positivo ou negativo, e n-1 bits são
usados para representar o valor
numérico (magnitude) associada ao
número em questão.

3. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 3
Complemento
• Desta forma a utilização de n bits
permite que 2n
valores diferentes sejam
representados, no entanto, além do
número 0 (zero), uma faixa de valores
será considerada positiva e outra faixa
será considerada negativa.

4. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 4
Complemento de 1
• A representação em complemento de 1 de
um determinado número binário é obtido pela
negação de todos os seus bits. Ou seja, todo
bit 0 passa a ser bit 1 e, inversamente, todo o
bit 1 passa a ser bit 0.
• Cada bit deve ser negado, inclusive o bit de
sinal.
• Desta forma, ressalta-se que o número 0
(zero) tem duas representações: 0000
0000(+0) e 1111 1111(-0).
• A tabela seguinte apresenta os valores de
complemento de 1 para números com 4 bits de
precisão.

5. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 5
Complemento de 1

6. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 6
Complemento de 2
• Em computação, complemento para
dois ou complemento de dois é um tipo
de representação binária de números com
sinal amplamente usada nas arquiteturas
dos dispositivos computacionais
modernos.
• O dígito mais significativo (MSB) é o que
informa o sinal do número. Se este dígito
for 0 (zero) o número é positivo, e se for
1 (um) é negativo.
• MSB => Most Significant Bit (bit mais
significativo) é o bit mais à esquerda
do número binário.

7. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 7
Complemento de 2
• Os números são escritos da seguinte forma:
 Positivos: Sua magnitude é representada na
sua forma binária direta, e um bit de sinal
(0) é colocado no MSB.
– (bit 0) + o número em binário.
– Exemplos: 0001 (+1), 0100 (+4) e 0111 (+7)
 Negativos: Sua magnitude é representada na
forma de complemento de 2, e um bit de
sinal (1) é colocado no MSB.
– Pegamos o número em binário e "invertemos"
(0100 invertendo têm-se 1011) e
– Somamos um ao valor "invertido" (1011 + 0001 =
1100).

8. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 8
Complemento de 2
• Desta maneira, só existe uma
representação para o número zero
(000000).
• As vantagens do uso do complemento
de 2 é que existe somente um zero e
que as regras para soma e subtração
são as mesmas.
• A desvantagem é o fato de ser um
código assimétrico.

9. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 9
Exemplos
• Tabela exemplo
para números
binários (4 digitos)
representados em
complemento de 2.
• Note-se que com 4
dígitos (bits) não é
possível representar
o número 8
positivo, porém o
número 8 negativo
(-8) permanece.
• Assim conseguimos
representar 16
valores com 4 bits
(2^4)

10. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 10

11. ArquiteturaeorganizaçãodeComputadores
Sistemas de Numeração e Aritmética Computacional 11