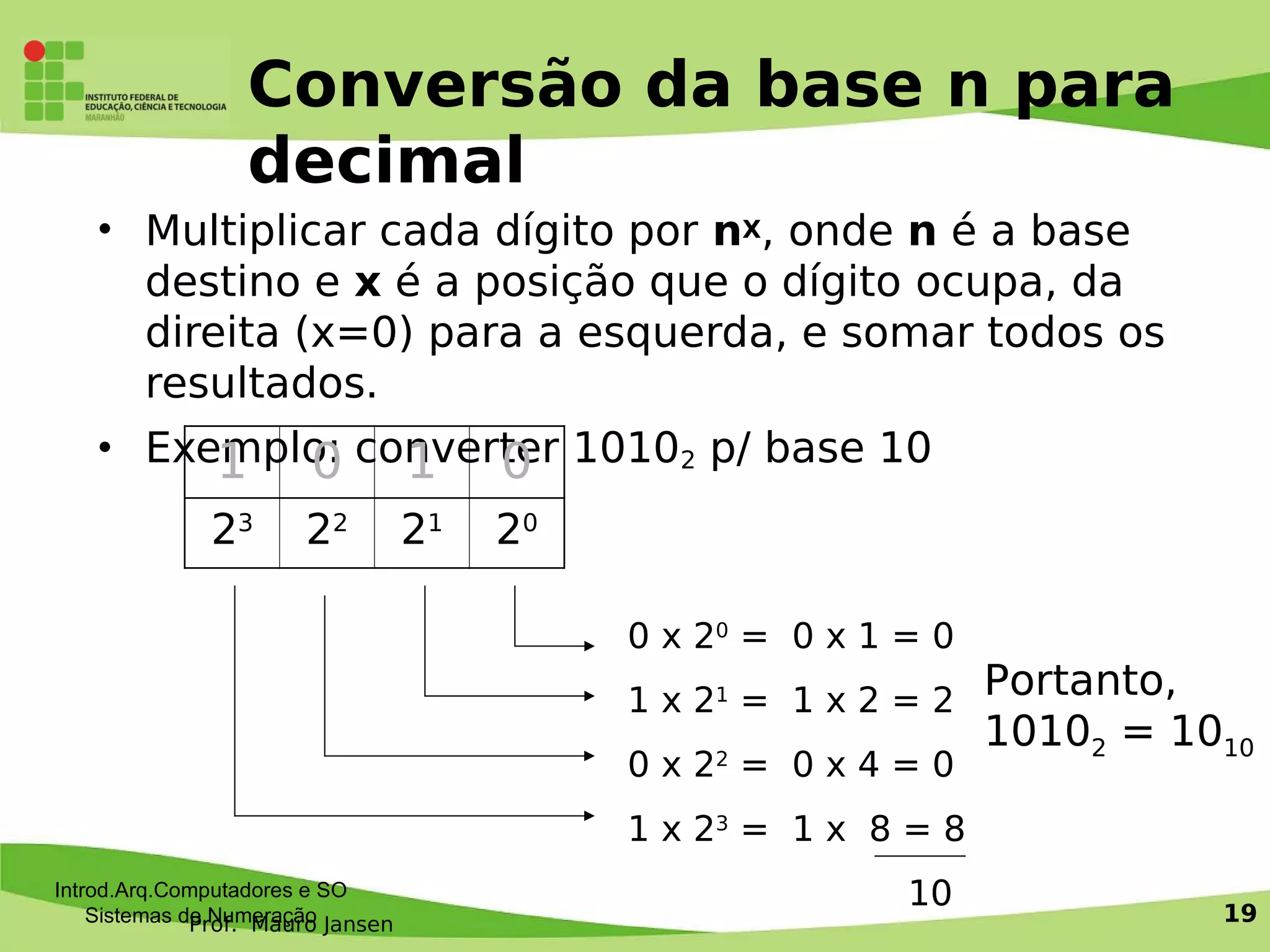
1) O documento apresenta os sistemas de numeração binário, decimal, octal e hexadecimal.
2) São explicados conceitos como bits, bytes, nibbles e as operações de conversão entre diferentes bases numéricas.
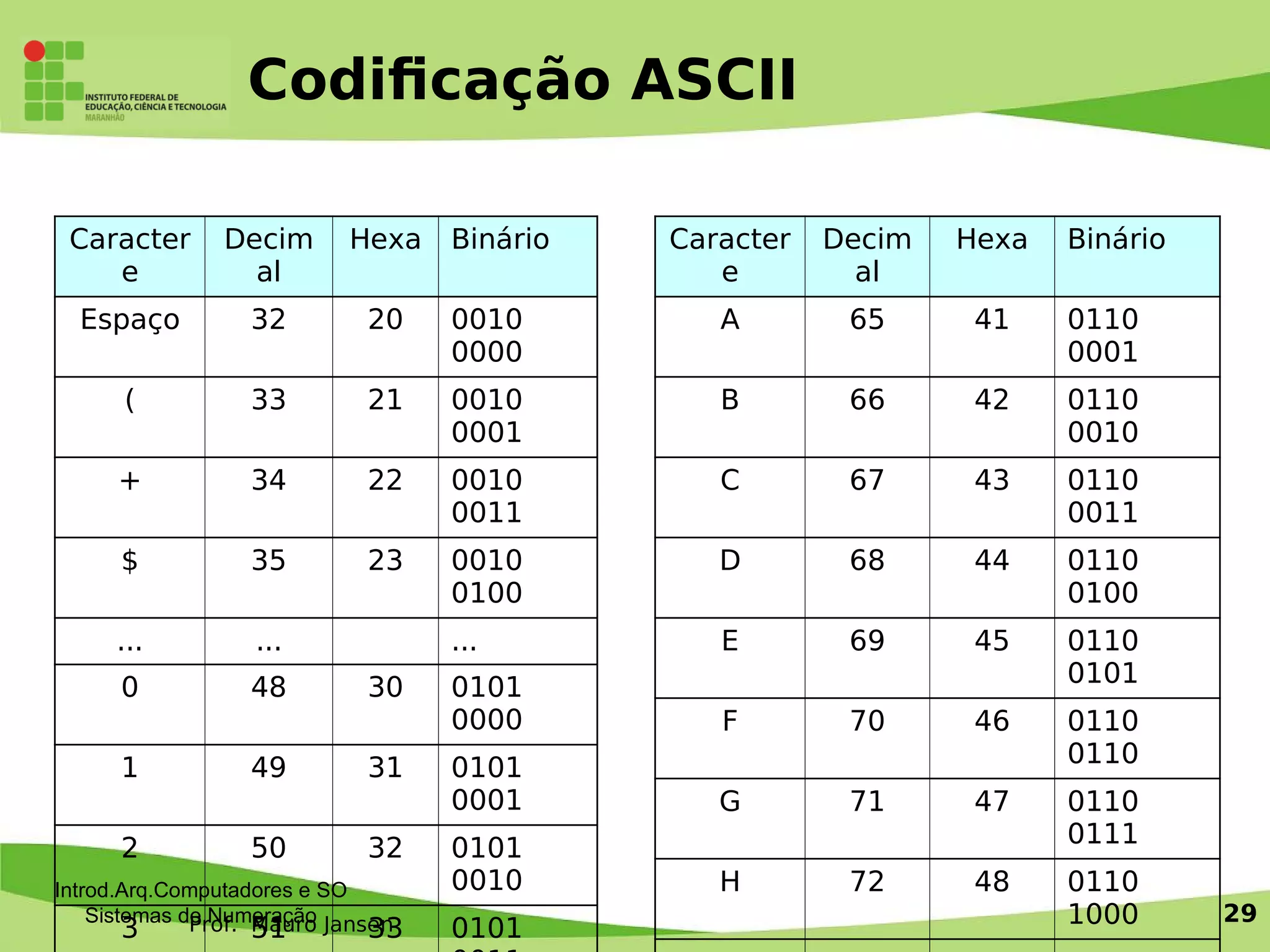
3) É detalhada a codificação ASCII utilizada pelo computador para representar caracteres alfabéticos e símbolos.