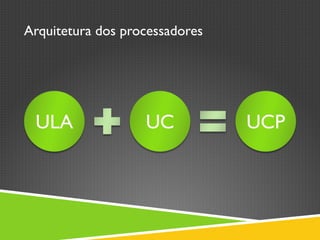
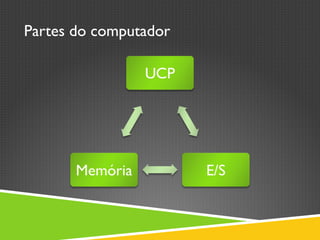
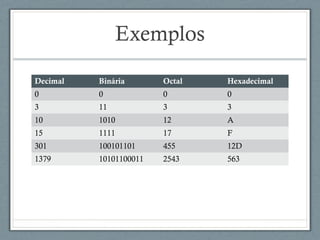
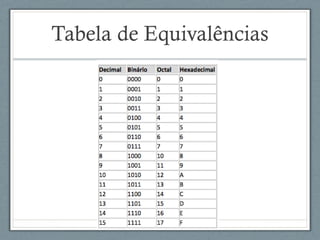
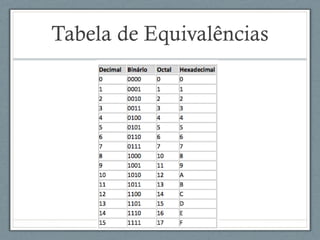
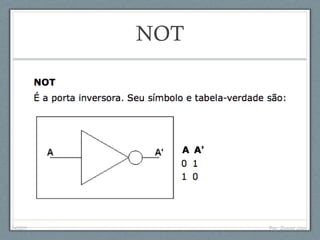
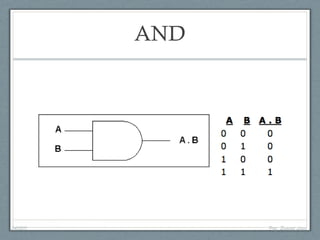
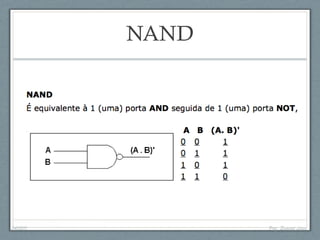
O documento descreve a história da arquitetura de computadores, começando com John von Neumann que formalizou o modelo de armazenamento de instruções na memória do computador. Em seguida, descreve as principais partes de um processador, incluindo a unidade lógica-aritmética, unidade de controle e memória. Por fim, discute as arquiteturas RISC e CISC e como os processadores modernos adotam uma abordagem híbrida.

1. Arquitetura e
Manutenção de
Computadores
Arquitetura de Processadores

2. John von neumann
 O matemático húngaro JohnVon Neumann (1903-1957) formalizou o
projeto lógico de um computador.
 Em sua proposta,Von Neumann sugeriu que as instruções fossem
armazenadas na memória do computador.Até então elas eram lidas de
cartões perfurados e executadas, uma a uma.
 A maioria dos computadores hoje em dia segue o modelo proposto
porVon Neumann.

3. Arquitetura dos processadores

4. Partes do computador

5. Unidade lógico-aritmética (ULA)
 A Unidade lógica e aritmética (ULA) ou em inglês Arithmetic Logic
Unit (ALU) é a unidade do processador (Central Processing Unit, ou
simplesmente CPU), que realmente executa as operações aritméticas e
lógicas referenciadas pelos opcodes.

6. Unidade de controle (UC)
 A unidade de controle executa três ações básicas intrínsecas e pré-
programadas pelo próprio fabricante do processador, são elas: busca
(fetch), decodificação e execução.
 Seu trabalho é ler instruções e dados da memória ou dos dispositivos
de entrada, decodificar as instruções, alimentar a ULA com as entradas
corretas de acordo com as instruções e enviar os resultados de volta à
memória ou aos dispositivos de saída.
 Desde a década de 1980, a ULA e a UC são inseridas em um único
circuito integrado: o microprocessador.

7. Memória
 A memória do computador pode ser vista como uma lista de células.
 Cada célula tem um "endereço" numerado que pode armazenar uma
quantidade fixa e pequena de informação.
 Essa informação pode ser ou uma instrução, que diz ao computador o
que fazer, ou dados, a informação que o computador deve processar
utilizando as instruções.

8. Dispositivos de e/s
 Os dispositivos de E/S definem como o computador recebe e devolve
informação do mundo exterior.

9. RISC x CISC
Qual a melhor?

10. RISC
 Reduction Instruction Set Computer – Computador com um conjunto
de instruções reduzidas;
 Mais simples e mais baratos;
 Operam em frequencias maiores;
 Trabalham em conjunto com softwares adequados;

11. CISC
 Complex Instruction Set Computer – Computador com um conjunto
complexo de instruções;
 Executa centenas de instruções complexas diferentes;
 Mais caros;
 Operam em velocidades menores;

12. Quem venceu?
Nenhum!

13. Atualmente
 Hoje temos processadores híbridos, onde internamente operam como
RISC, realizando operações simples e um circuito decodificador
converte as instruções mais complexas.

14. Instruções X86
 O conjunto básico de instruções usadas em micros PC é chamado de
conjunto x86.
 Este conjunto é composto por um total de 187 instruções, que são as
utilizadas por todos os programas.
 Além deste conjunto principal, alguns processadores trazem também
instruções alternativas, que permitem aos programas executar algumas
tarefas mais rapidamente do que seria possível usando as instruções
x86 padrão.

15. Conjuntos de Instruções alternativas
 MMX (Pentium MMX);
 3D-NOW! (AMD);
 SSE (Pentium III).

16. Processadores recentes

17. Arquitetura e
Manutenção de
Computadores
Conversão de Bases Numéricas
professor@emanoel.pro.br

18. Sistemas de Numeração
• Binário;
• Decimal;
• Octal;
• Hexadecimal.

19. Sistema Binário
• A base é o número 2, com utilização dos números 0
e 1;
• 0 é ausência de corrente e 1 a presença;

20. Sistema Octal
• A base do sistema octal é o número 8, com
utilização dos símbolos: 0 1 2 3 4 5 6 7

21. Sistema Hexadecimal
• A base do sistema é o número 16, utilizando os
símbolos: 0 1 2 3 4 5 6 7 8 9 A B C D E F.
• Os valores absolutos A, B, C, D, E e F são,
respectivamente, 10, 11, 12, 13, 14 e 15.

22. Exemplos
Decimal Binária Octal Hexadecimal
0 0 0 0
3 11 3 3
10 1010 12 A
15 1111 17 F
301 100101101 455 12D
1379 10101100011 2543 563

23. Teorema Fundamental de
Numeração - TFN
• …+ X2 x B2
+ X1 x B1
+ X0 x B0
+ X-1 x B-1
+…
Utilizado para conversões de outras bases em Decimal.
Ex: Binário  Decimal, Octal  Decimal,
Hexadecimal  Decimal.

24. Decimal para Base b qualquer
• Divisões sucessivas pela base desejada.
• Ex: (19)10 = (10011)2
• Ex: (500)10 = (764)8

25. Base b qualquer para Decimal
• Utilizar o TFN;
• Ex.: 1011012 = 1x25
+ 0x24
+ 1x23
+ 1x22
+ 0x21
+
1x20
= 32 + 0 + 8 + 4 + 0 + 1 = 4510, então
(1011012)2=(4510)10
• Converter 4F5H para a base 10 .Solução: Sabemos
que F16=1510. Então:4x162
+ 15x161
+ 5x160
= 4x256 +
15x16 + 5 = 1024 + 240 + 5 = 126910

26. Cuidado!
• Converter 38,38 para a base 10.Solução: Uma base
octal dispõe dos algarismos 0 a 7 e portanto o
algarismo 8 não existe nessa base. A representação
38,3 não existe na base 8.
• Converter 7G16 para a base 10.Solução: A base 16
dispõe dos algarismos 0 a F e portanto o símbolo G
não pertence à representação hexadecimal.

27. Tabela de Equivalências

28. Conversão entre binário e
octal
• Entre bases 2 e 8, temos que 23
= 8
• Ex: 101010012 = 10.101.0012utilizando a tabela
sabemos que:
0102 = 28; 1012 = 58 ; 0012 = 18 , então temos 2518

29. • Entre bases 2 e 16, temos que 24
= 16
• 110101011012 = 110.1010.11012
• Sabemos que 1102 = 616; 10102 = A16 ; 11012 = D16 ;
portanto 110101011012 = 6AD16
Entre binário e hexadecimal

30. Exercícios
• Entregue folha de exercícios em sala.

31. Arquitetura e
Manutenção de
Computadores
Aula 04 – 20.04.2011
Conversão de Bases Numéricas (cont.)
professor@emanoel.pro.br

32. Tabela de Equivalências

33. Conversão entre binário e
octal
• Entre bases 2 e 8, temos que 23
= 8
• Ex: 101010012 = 010.101.0012utilizando a tabela
sabemos que:
0102 = 28; 1012 = 58 ; 0012 = 18 , então temos 2518

34. • Entre bases 2 e 16, temos que 24
= 16
• 110101011012 = 0110.1010.11012
• Sabemos que 01102 = 616; 10102 = A16 ; 11012 = D16 ;
portanto 110101011012 = 6AD16
Entre binário e hexadecimal

35. Exercícios
• Entregue em sala na aula passada;
• Itens m até o final.

36. Aritmética binária
• Soma e subtração de números binários.

37. Adição binária
0
+0
0
+1
1
+0
1
+1
0 1 1 0 (vai um)

38. Subtração binária
0
- 0
1
- 1
1
- 0
0
- 1
0 0 1 1 e pede
emprestado

39. Exercícios
• Exercícios no quadro.

40. Arquitetura e
Manutenção de
Computadores
Álgebra Booleana
Circuitos Lógicos
professor@emanoel.pro.br
04/05/11 Prof. Emanoel Lopes

41. Objetivos da aula
• Conhecer as portas lógicas existentes.
04/05/11 Prof. Emanoel Lopes

42. Álgebra Booleana
• Em 1854, um matemático britânico chamado
George Boole publicou um sistema lógico que viria a
ser conhecido como álgebra booleana;
• Em 1937, Claude Shannon implementou Álgebra
booleana e aritmética binária utilizando circuitos
elétricos.
04/05/11 Prof. Emanoel Lopes

43. Portas e Circuitos Lógicos
• NOT
• AND
• NAND
• OR
• NOR
• XOR
• XNOR
04/05/11 Prof. Emanoel Lopes

44. NOT
04/05/11 Prof. Emanoel Lopes

45. AND
04/05/11 Prof. Emanoel Lopes

46. NAND
04/05/11 Prof. Emanoel Lopes

47. OR
04/05/11 Prof. Emanoel Lopes

48. NOR
04/05/11 Prof. Emanoel Lopes

49. XOR
04/05/11 Prof. Emanoel Lopes

50. XNOR
04/05/11 Prof. Emanoel Lopes

51. Na apostila…
04/05/11 Prof. Emanoel Lopes