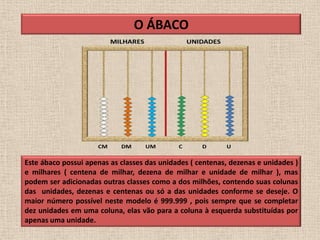
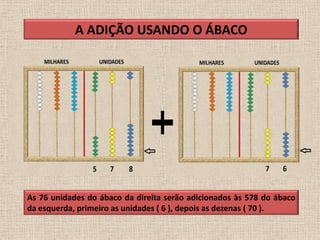
O documento descreve a história e o uso do ábaco, um dos primeiros instrumentos de cálculo. Foi inventado na China no século II d.C. e consiste em uma estrutura com hastes divididas em duas partes, onde contas deslizantes representam valores numéricos. Demonstra como realizar adições usando o ábaco, movendo as contas para cima e para baixo de acordo com os algarismos somados.

1. O ÁBACO
HISTÓRIA, LEITURA E ADIÇÃO DE NÚMEROS

2. HISTÓRIA
O ábaco foi o primeiro instrumento de auxílio ao cálculo, já que ele apenas
registra os resultados das operações realizadas pela mente do operador. Na forma
como o conhecemos foi inventado pelos chineses no século II d.C., mas existem
registros de instrumentos similares mais antigos originários da Mesopotâmia (
atual Iraque ), Egito, Grécia, Índia, Roma ( antigo império romano ) e também
entre os Incas, no continente sul-americano. Hoje existem versões melhoradas
chinesas, japonesas e coreanas que são muito utilizadas na educação das crianças.
Uma versão russa foi muito empregada na antiga União Soviética, mas após a
queda do regime, caiu em desuso. .

3. Criado na Antiguidade pelos romanos, era usado para calcular, e depois os
chineses e japoneses aperfeiçoaram-no.
Desde então vários tipos de ábacos foram reinventados ; o mais popular
utiliza uma combinação de dois números-base (2 e 5) para representar
números decimais.
A palavra ábaco resulta do Latim abax (tábua de cálculos)

4. O método normal de cálculo na Roma antiga, era mover bolas de
contagem numa tábua própria para o efeito. As bolas de contagem
originais denominavam-se calculi. Mais tarde, e na Europa medieval, os
jetons começaram a ser manufacturados. Linhas marcadas indicavam
unidades, meias dezenas, dezenas, etc., como na numeração romana. O
sistema de contagem contrária continuou até à queda de Roma, assim
como na Idade Média e até ao século XIX, embora já com uma utilização
mais limitada.
Nos sulcos menores, o sulco marcado I marca unidades, o X dezenas e
assim sucessivamente até aos milhões. As bolas nos sulcos menores
marcam os cincos - cinco unidades, cinco dezenas, etc. - essencialmente
baseado na numeração romana.

5. As duas últimas colunas de sulcos serviam para marcar as subdivisões da
unidade monetária. Temos de ter em conta que a unidade monetária se
subdividia em 12 partes, o que implica que o sulco longo marcado com o sinal
0(representando os múltiplos da onça ou duodécimos da unidade monetária)
comporte um máximo de 5 botões, valendo cada uma 1 onça, e que o botão
superior valha 6 onças. Os sulcos mais pequenos à direita são fracções da
onça romana sendo respectivamente, de cima para baixo, ½ onça, ¼ onça e ⅓
onça.

6. O ÁBACO
Este ábaco possui apenas as classes das unidades ( centenas, dezenas e unidades )
e milhares ( centena de milhar, dezena de milhar e unidade de milhar ), mas
podem ser adicionadas outras classes como a dos milhões, contendo suas colunas
das unidades, dezenas e centenas ou só a das unidades conforme se deseje. O
maior número possível neste modelo é 999.999 , pois sempre que se completar
dez unidades em uma coluna, elas vão para a coluna à esquerda substituídas por
apenas uma unidade.

7. Uma estrutura com hastes metálicas divididas em duas partes, das quais
uma tem duas contas e a outra, cinco contas, que deslizam nessas
hastes. Os ábacos orientais dispõem de varas verticais divididas em
dois, com as contas sobre a barra tendo o valor cinco vezes superior aos
das contas abaixo.

8. A LEITURA DE NÚMEROS
Os números são lidos na parte de baixo do ábaco
como indicado pela seta.
Leitura dos números:
1º) Seiscentos e oitenta e um mil, quatrocentos e
setenta e seis
2º) Cinquenta e um mil
3º) Três mil
4º) Duzentos

9. A ADIÇÃO USANDO O ÁBACO
As 76 unidades do ábaco da direita serão adicionados às 578 do ábaco
da esquerda, primeiro as unidades ( 6 ), depois as dezenas ( 70 ).

10. A ADIÇÃO DAS UNIDADES: 578 + 6
Fig. 1 Fig. 2 Fig. 3
Adicionando 2 unidades das 6, representadas por
duas contas azuis ( fig.1 ), completamos 10, que
são transferidas para a coluna das
dezenas, baixando uma conta amarela e subindo
as 10 contas azuis ( fig.2 e 3 ). Para adicionar as
outras 4 que faltam, baixamos 4 contas azuis (
fig. 4 ) encerrando o cálculo de adição das 6
unidades e obtendo o resultado de 584.
Fig. 4

11. A ADIÇÃO DAS DEZENAS: 584 + 70
Fig.1 Fig. 2 Fig. 3
Adicionando 2 dezenas das 7 ( fig.1 ), completamos 10
dezenas ( cem ), que devem ser transferidas para a
coluna das centenas. Baixa-se então uma conta
verde, totalizando 6, subindo as 10 contas amarelas (
fig.2 e 3 ). As 5 dezenas restantes são adicionadas
baixando 5 contas amarelas ( fig. 4 ), encerrando o
cálculo de adição das 7 dezenas ( 70 ). O resultado
Fig. 4 final, portanto, é 654.

12. O ÁBACO COM AS 76 UNIDADES
Fig. 1 Fig.2 Fig.3
Retiramos primeiro 2 unidades das 6 ( fig.1 ), subindo
duas contas azuis. Depois mais 4, subindo as contas
restantes e zerando as unidades ( fig.2 ). Nas dezenas
retiramos primeiro 2 das setes, subindo 2 contas
amarelas ( fig.3 ). A seguir subimos 5 contas amarelas
restantes, correspondendo as 5 dezenas, zerando o
número que foi adicionado ao 578 ( fig. 4 ). Os passos
realizados aqui estão de acordo com os realizados no
slide anterior ( adição ).
Fig. 4

14. Sabia que?
• Está provado que um utilizador de ábaco consegue calcular qualquer
número mais rápido que alguém com uma calculadora