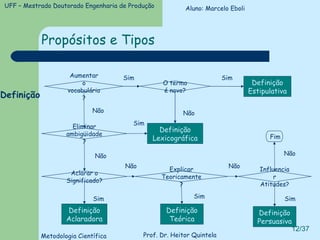
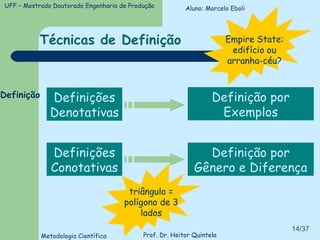
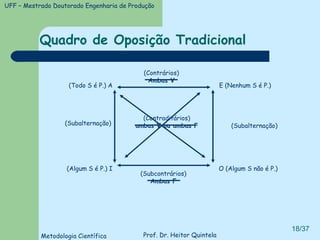
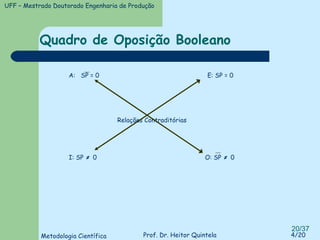
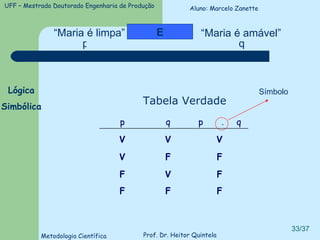
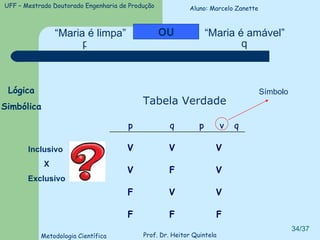
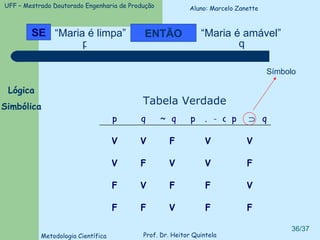
O documento introduz conceitos básicos de lógica, incluindo validade versus verdade, silogismos, dedução versus indução, e tipos de discurso. Exemplos ilustram conceitos como silogismos categóricos, termos distribuídos, e técnicas para traduzir argumentos da linguagem comum para a lógica formal.

1. INTRODUÇÃO À LÓGICA Professor Dr Heitor M Quintella Metodologia Científica Universidade Federal Fluminense

2. Seleção e articulação dos argumentos: Progressividade textual e consistência da argumentação: Introdução a Lógica Argumentação OBS: Verdade x Validade Todo cão é verde. Tudo que é verde é vegetal Todo cão é um vegetal. Se ganhasse na loto seria rico. Não ganhei na loto. Logo, Não sou rico. Introdução Exemplo: Toda Baleia é Mamífero Ora, nenhum mamífero é peixe. Logo, a baleia não é peixe.

3. Introdução Dedução Geral Particular Indução Particular Geral Introdução a Lógica Aluno: Lucas Euphrasio Exemplo Todo aluno do mestrado é estudioso. Lucas é aluno do mestrado. Logo, Lucas é estudioso. Exemplo Lucas é estudioso. Lucas representa os aluno do mestrado. Logo, todo aluno do mestrado é estudioso.

4. Silogismo Silogismo M – P S – M S - P M – P M – S S - P P – M M – S S - P P – M S – M S - P Aluno:Lucas Euphrasio

5. Funções Básicas da Linguagem Linguagem informativa, usada para afirmar ou negar proposições, tem caráter informativo Linguagem expressiva, caracterizada por expressar sentimentos e emoções Linguagem Diretiva, usada para expressar ordens e solicitações

6. Discursos servindo múltiplas funções “ Conto com o seu voto para Deputado, sou o candidato mais credenciado, fui autor das emendas xxx, yyy,....Além de tudo, sou o único que sei das dificuldades e dos sentimentos do povo brasileiro e tenho orgulho de ser honesto!

7. Formas de Discurso Orações declarativas, interrogativas, imperativas e exclamativas não têm relação direta com discursos informativos, diretivos e expressivos. Motorista, percebeste que estamos atrasados? Passei bons momentos em sua festa.

8. Palavras emotivas e Desacordos As palavras têm significados literais e emotivos (burocrata e servidor público) Desacordos de Convicções e de Atitudes. Trabalham científicos demandam discursos emotivamente neutros.

9. Falácias são aqueles argumentos que, embora incorretos, podem ser psicologicamente persuasivos. Falácia Falácias Falácia Erro no raciocínio ou na argumentação Aluna: Marcela Lomonaco

10. Falácias de Relevância Recurso à força Ofensivo Circunstancial Argumento pela Ignorância Apelo à Piedade Argumento ao Povo Falácia Apelo à Autoridade Acidente Acidente Convertido Falsa Causa Petição de Princípio Pergunta Complexa Conclusão Irrelevante Aluna: Marcela Lomonaco Premissas logicamente irrelevantes

11. Falácias de Ambigüidade Equívoco Anfibologia Ênfase Composição Divisão Falácia Aluna: Marcela Lomonaco Palavras ou frases ambíguas

12. Definição Propósitos e Tipos Aumentar o vocabulário? Sim O termo é novo? Definição Estipulativa Definição Lexicográfica Eliminar ambigüidade? Aclarar o Significado? Definição Aclaradora Explicar Teoricamente? Influenciar Atitudes? Definição Teórica Definição Persuasiva Fim Sim Sim Não Não Sim Não Sim Sim Não Não Não Aluno: Marcelo Eboli

13. Espécies de Significado Objetivo: extensão ou denotação Existente ou nula Propriedade comum a todos os objetivos: intensão ou conotação Subjetiva, objetiva ou convencional Definição Aluno: Marcelo Eboli

14. Técnicas de Definição Definição Definições Conotativas Definição por Gênero e Diferença Definições Denotativas Definição por Exemplos Aluno: Marcelo Eboli Empire State: edifício ou arranha-céu? triângulo = polígono de 3 lados

15. Definição por Gênero e Diferença Regra 1: Deve indicar os atributos essenciais da espécie Definição Regra 2: Não deve ser circular Regra 3: Não deve ser excessivamente ampla nem estreita Regra 4: N ão deve ser expressa em linguagem ambígua, obscura ou figurada Regra 5: Não deve ser negativa quando pode ser positiva Aluno: Marcelo Eboli

16. Proposições e Classes Categóricas Representam asserções sobre classes, afirmando ou negando que uma esteja incluída na outra; Exemplos de proposições categóricas: “Todos os políticos são mentirosos” ; “Alguns políticos são mentirosos”,... Todo S é P (PUP ou A), Nenhum S é P (PUN ou E), Algum S é P (PPP ou I) e Algum S não é P (PPN ou E).

17. Qualidade, Quantidade e Distribuição Qualidade : afirmativa ou negativa Quantidade: universal (Todos ou Nenhum), particular (Alguns) Quantificador (sujeito) cópula (predicado) Alguns cavalos são puro-sangues. Distribuição da Proposição A (Distribui o sujeito), E (Distribui sujeito e predicado), I (não distribui termo algum), O (Distribui o predicado*) *Alguns cavalos não são puro-sangues (asserção distribui alguns cavalos sobre a classe de todos os puro-sangues)

18. Quadro de Oposição Tradicional (Todo S é P.) A (Algum S é P.) I E (Nenhum S é P.) O (Algum S não é P.) (Contrários) Ambas V (Subcontrários) Ambas F (Contraditários) ambas V ou ambas F (Subalternação) (Subalternação)

19. O Contéudo Existencial (Todo S é P.) A (Algum S é P.) I E (Nenhum S é P.) O (Algum S não é P.) (Contrários) Ambas V (Subcontrários) Ambas F (Contraditários) ambas V ou ambas F (Subalternação) (Subalternação) Se Assumirmos que a classe S possa ser nula, temos que: X X X X Lógica Aristotélica ou Clássica, assume o pressuposta existencial, ou seja, Assume que S não pode ser nula.

20. Quadro de Oposição Booleano 4/20 A: SP = 0 E: SP = 0 Relações Contraditórias I: SP ≠ 0 O: SP ≠ 0

21. Argumentos em Linguagem Comum Argumento silogístico >> referência a qualquer raciocínio que é um silogismo categórico de forma típica. Os interesses combinados da simplicidade lógica e da adequação aos argumentos formulados em linguagem comum requerem que façamos duas coisas: testes simples para distinguir os silogismos categóricos, de forma típica, validos dos inválidos (conhecimento adquirido no Capitulo 6); compreender e dominar técnicas para traduzir silogismos categóricos de qualquer forma para forma típica. Estas são algumas das técnicas: Definição Aluno: Carlos Eduardo Siqueira

22. Argumentos em Linguagem Comum TECNICAS: Redução do número de termos num argumento silogístico >> tal tradução pode, com freqüência, ser realizada simplesmente pela eliminação dos sinônimos (exemplo 1). Ou também podem ser efetuadas, mediante interferências imediatas válidas: conversão, observação e contraposição (exemplo 2); A tradução das proposições categóricas para forma típica >> muitos argumentos silogísticos contem proposições em forma atípica. Para reduzir esses argumentos à forma típica é necessário traduzir suas proposições componentes. Estas são as 9 técnicas guias sugeridas pelo autor. Tradução Uniforme >> a introdução de parâmetros é freqüentemente necessária para este tipo de tradução das três preposições constituintes de um silogismo para a forma típica (exemplo 3); Aluno: Carlos Eduardo Siqueira

23. Argumentos em Linguagem Comum TECNICAS: Entidemas >> é o argumento que é enunciado de modo incompleto, parte do qual fica “subentendida” ou apenas “na idéia” (exemplo 4); Sorites >> ocorre em ocasiões em que um só silogismo categórico não será suficiente para extrair a conclusão deseja de um grupo de premissas (exemplo 5); Silogismo Disjuntivos e Hipotéticos >> a proposição disjuntiva, ou disjunção, contém duas proposições componentes que são os seus disjuntos. A disjunção não afirma categoricamente a verdade de um ou de outro de seus disjuntos, mas diz que, pelo menos, um deles é verdadeiro, admitindo a possibilidade de que ambos o sejam (exemplo 6); Dilema >> uma forma comum de argumento em linguagem corrente, é um legado de tempos mais antigos, quando a lógica e a retórica estavam mais estritamente ligadas do que são hoje. Mas, retoricamente, o dilema talvez seja o mais poderoso instrumento de persuasão até hoje utilizado. Na controvérsia, é uma arma devastadora (exemplo 7). Aluno: Carlos Eduardo Siqueira

24. Argumentos em Linguagem Comum Exemplo 1: Nenhum homem é vadio. Todos os advogados são homens ricos. ------------------------------------------------ Portanto, nenhum advogado é vagabundo. Realizando a eliminação dos sinônimos. Nenhum homem é vadio. Todos os advogados são homens ricos. ------------------------------------------------ Portanto, nenhum advogado é vadio. Aluno: Carlos Eduardo Siqueira

25. Argumentos em Linguagem Comum Exemplo 2: Nenhum não-residente é cidadão. Todos os não-cidadãos são não-eleitores. ------------------------------------------------ Portanto, todos os eleitores são residentes. Realizando as interferências válidas. Todos os cidadãos são residentes. Todos os eleitores são cidadãos. ------------------------------------------------ Portanto, todos os eleitores são residentes. Aluno: Carlos Eduardo Siqueira

26. Argumentos em Linguagem Comum 9 Técnicas Guias: Mencionar, primeiro, as proposições singulares; O primeiro grupo de proposições categóricas, é o formato por aquelas proposições que têm adjetivos ou frases adjetivas como predicados, em vez de substantivos ou termos de classe; Passemos agora às proposições categóricas nas quais os verbos principais são distintos da cópula de forma típica “ser”; Enunciados aonde estão presentes todos os ingredientes da forma típica, mas que não estão ordenados da maneira que é própria a essa forma; Enunciados que contem as palavras “cada” e “qualquer” podem ser facilmente traduzidos. Com também os termos “cada coisa” e “qualquer coisa”. Paralelas a estas, estão “cada um”, “qualquer um”, “quem quer que”, “todo aquele que”, “quem”, etc.; As proposições categóricas que envolvem as palavras “somente” ou “ninguém mais que” costumam ser designadas como proposições “exclusivas”, porque, em geral, afirmam que o predicado se aplica exclusivamente ao sujeito nomeado; Algumas proposições categóricas não contem palavra alguma para indicar quantidade; Algumas proposições que não se assemelham, em absoluto, às proposições categóricas de forma típica, mas que podem ser traduzidas em forma típica; Alguns quantifica dores quase-númericos ocorrem em argumentos que se prestam à analise silogística. Entre eles incluem-se “quase todos”, “nem todos”, “todos, salvo uns poucos”, “quase cada um”. Aluno: Carlos Eduardo Siqueira

27. Argumentos em Linguagem Comum Exemplo 3: Os pratos sujos, de papelão, só se encontram dispersos onde pessoas desleixadas fizeram um piquenique. Aqui há pratos sujos, de papelão, dispersos. ------------------------------------------------ Portanto, pessoas desleixadas devem ter feito, aqui, um piquenique. Realizando introdução de parâmetros. Todos os lugares onde estão dispersos pratos sujos, de papelão, são lugares onde pessoas desleixadas fizeram piquenique. Este lugar é um lugar onde estão dispersos pratos sujos, de papelão. ------------------------------------------------ Portanto, este lugar é um lugar onde pessoas desleixadas fizeram piquenique. Aluno: Carlos Eduardo Siqueira

28. Argumentos em Linguagem Comum Exemplo 4: Todos os estudantes se opõem ao novo regulamento, assim como todas as alunas se opõem a ele. ------------------------------------------------ Todas as alunas são estudantes. Aluno: Carlos Eduardo Siqueira

29. Argumentos em Linguagem Comum Exemplo 5: Todos os diplomatas são homens de tato. Alguns funcionários do governo são diplomatas. Todos os funcionários do governo são homens na vida pública, ------------------------------------------------ não se pode extrair a conclusão: “Alguns homens na vida publica são homens de tato”. Quando explicitamente enunciado. Todos os diplomatas são homens de tato. Alguns funcionários do governo são diplomatas. ------------------------------------------------ Portanto, alguns funcionários do governo são indivíduos de tato. Todos os funcionários do governo são homens na vida pública, ------------------------------------------------ Portanto, alguns homens na vida pública são homens de tato.. Aluno: Carlos Eduardo Siqueira

30. Argumentos em Linguagem Comum Exemplo 6: Fido escapou ou Fido foi Atropelado por um carro. Fido não escapou. ------------------------------------------------ Portanto, Fido foi atropelado por um carro. Aluno: Carlos Eduardo Siqueira

31. Argumentos em Linguagem Comum Exemplo 7: Se a tarifa proposta produz escassez, será prejudicial; e não produzindo escassez será inútil. Então, produzirá escassez ou não produzirá. Portanto, a tarifa proposta será prejudicial ou inútil. Aluno: Carlos Eduardo Siqueira

32. Por que a Lógica Simbólica? Quais os tipos enunciados? Como os enunciados se combinam? Lógica Simbólica Aluno: Marcelo Zanette

33. “ Maria é limpa” “ Maria é amável” E Tabela Verdade Símbolo p q Lógica Simbólica Aluno: Marcelo Zanette F F F F V F F F V V V V q  p q p

34. “ Maria é limpa” “ Maria é amável” OU Tabela Verdade Símbolo p q Inclusivo X Exclusivo Lógica Simbólica Aluno: Marcelo Zanette F F F V V F V F V V V V q v p q p

35. “ Maria é limpa” “ Maria é amável” NÃO Tabela Verdade Símbolo p q Lógica Simbólica Aluno: Marcelo Zanette F V V F p ~ p

36. “ Maria é limpa” “ Maria é amável” SE ENTÃO Tabela Verdade Símbolo p q Lógica Simbólica Aluno: Marcelo Zanette F F V F F V F F V F F V V F V V V F V V q  p q  . p q ~ q p

37. Princípio da Identidade – afirma que se qualquer enunciado é verdadeiro, então ele é verdadeiro; Princípio da Contradição – afirma que nenhum enunciado pode ser verdadeiro e falso; Princípio do Terceiro Excluido – afirma que um enunciado ou é verdadeiro, ou é falso. Lógica Simbólica Aluno: Marcelo Zanette