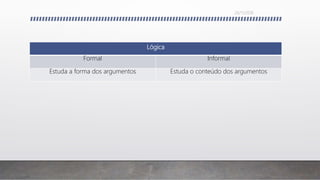
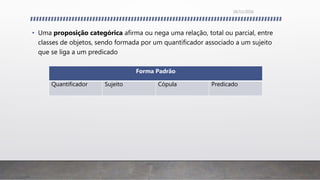
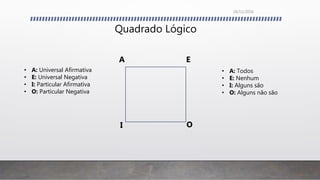
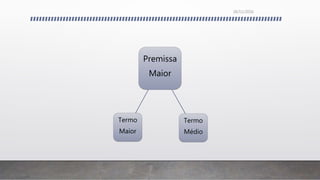
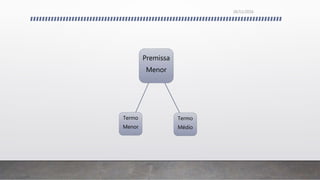
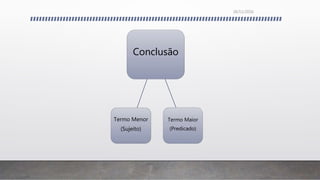
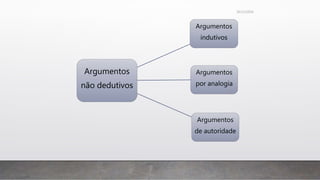
O documento discute os conceitos fundamentais da lógica formal e informal, incluindo: 1) a distinção entre argumentos dedutivos e indutivos; 2) as características dos argumentos dedutivos, indutivos, por analogia e de autoridade; 3) os elementos básicos da lógica silogística como proposições categóricas, termos e figuras de silogismos; 4) falácias formais e informais.