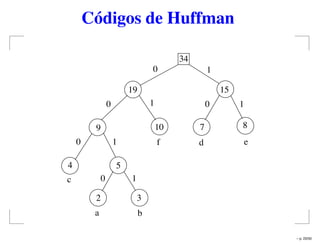
O documento analisa algoritmos gulosos aplicados a problemas de otimização, como as Árvores Geradoras de Custo Mínimo e os Códigos de Huffman. Os algoritmos de Kruskal e Huffman são discutidos em detalhes, incluindo suas implementações e complexidades, com ênfase na validade e correção de suas soluções. Também são apresentados exercícios para aprofundar a compreensão dos conceitos abordados.

1. An´alise de Algoritmos
Método Guloso
– p. 1/50

2. Método Guloso
Algumas características:
Aplicado a problemas de otimização, em que
queremos computar a melhor solução
– p. 2/50

3. Método Guloso
Algumas características:
Aplicado a problemas de otimização, em que
queremos computar a melhor solução
Em cada passo, o algoritmo sempre escolhe a
melhor opção local viável, sem se preocupar
com as consequências futuras
– p. 2/50

4. Método Guloso
Algumas características:
Aplicado a problemas de otimização, em que
queremos computar a melhor solução
Em cada passo, o algoritmo sempre escolhe a
melhor opção local viável, sem se preocupar
com as consequências futuras
Nem sempre produz a solução ótima, mas
muitas vezes sim.
– p. 2/50

5. M´etodo Guloso
Árvore geradora de custo mínimo
– p. 3/50

6. Árvore geradora de custo mínimo
Dado um grafo G = (V, E) com pesos nas arestas,
determinar um subgrafo gerador conexo de custo
mínimo, ou seja, uma árvore geradora de custo
mínimo.
– p. 4/50

7. Árvore geradora de custo mínimo
Dado um grafo G = (V, E) com pesos nas arestas,
determinar um subgrafo gerador conexo de custo
mínimo, ou seja, uma árvore geradora de custo
mínimo. O algoritmo que vamos estudar para
resolver este problema é de autoria de Kruskal
(1956).
– p. 4/50

8. Árvore geradora de custo mínimo
Dado um grafo G = (V, E) com pesos nas arestas,
determinar um subgrafo gerador conexo de custo
mínimo, ou seja, uma árvore geradora de custo
mínimo. O algoritmo que vamos estudar para
resolver este problema é de autoria de Kruskal
(1956).
Idéia do algoritmo:
Em cada passo, selecione a aresta de menor
custo e que não forma circuito.
– p. 4/50

9. Algoritmo de Kruskal
1. Dado um grafo G = (V, E), considere o grafo
T = (V (G), ∅)
2. S ← E(G)
– p. 5/50

10. Algoritmo de Kruskal
1. Dado um grafo G = (V, E), considere o grafo
T = (V (G), ∅)
2. S ← E(G)
3. Enquanto |T| < |V | − 1 faça
remova uma aresta e de peso mínimo de S
(Aqui está o guloso!!!)
Se e liga duas componentes distintas de T
então adicione e à T; Senão descarte e
– p. 5/50

11. Algoritmo de Kruskal
Qual é o tempo gasto por este algoritmo?
– p. 6/50

12. Algoritmo de Kruskal
Qual é o tempo gasto por este algoritmo?
Resp: O(m log n), onde
m é o número de arestas, e
n é o número de vértices do grafo.
– p. 6/50

13. Algoritmo de Kruskal
Qual é o tempo gasto por este algoritmo?
Resp: O(m log n), onde
m é o número de arestas, e
n é o número de vértices do grafo.
Sugestão de implementação: utilize heap e união
de conjuntos disjuntos.
– p. 6/50

14. Corretude do algoritmo de Kruskal
Teorema: O algoritmo de Kruskal determina
corretamente uma árvore geradora K de custo
mínimo em um grafo conexo com custos reais
associados às arestas.
– p. 7/50

15. Corretude do algoritmo de Kruskal
Teorema: O algoritmo de Kruskal determina
corretamente uma árvore geradora K de custo
mínimo em um grafo conexo com custos reais
associados às arestas.
Prova: Observe que uma árvore geradora de custo
mínimo pode não ser única.
Seja M uma árvore geradora de custo mínimo
mais próxima possível de K. Vamos mostrar que
M = K.
– p. 7/50

16. Corretude do algoritmo de Kruskal
Seja e1, e2, . . . , en−1 a sequência das arestas
incluídas em K.
– p. 8/50

17. Corretude do algoritmo de Kruskal
Seja e1, e2, . . . , en−1 a sequência das arestas
incluídas em K.
Suponha que M = K. Seja i o menor índice tal
que {e1, e2, . . . , ei} ⊆ E(M) e ei+1 /∈ E(M).
– p. 8/50

18. Corretude do algoritmo de Kruskal
Seja e1, e2, . . . , en−1 a sequência das arestas
incluídas em K.
Suponha que M = K. Seja i o menor índice tal
que {e1, e2, . . . , ei} ⊆ E(M) e ei+1 /∈ E(M).
A inclusão de ei+1 em M forma um único circuito.
Este circuito deve conter uma aresta x /∈ E(K),
senão teríamos um circuito em K.
– p. 8/50

19. Corretude do algoritmo de Kruskal
Como x, e1, e2, . . . , ei pertencem à M (que não
contém circuito), e como a algoritmo de Kruskal
consulta as arestas por ordem de custo,
concluímos que peso(x) ≥ peso(ei+1), senão x teria
sido escolhido no lugar de ei+1. Consideremos a
árvore geradora M = (M − {x}) ∪ {ei+1}.
– p. 9/50

20. Corretude do algoritmo de Kruskal
Se peso(x) > peso(ei+1), M é uma árvore
geradora de custo menor do que M, o que é
uma contradição.
– p. 10/50

21. Corretude do algoritmo de Kruskal
Se peso(x) > peso(ei+1), M é uma árvore
geradora de custo menor do que M, o que é
uma contradição.
Se peso(x) = peso(ei+1), M é uma árvore
geradora de custo mínimo, mas M contém as
arestas e1, e2, . . . , ei, ei+1, contradizendo a
escolha de M.
– p. 10/50

22. Corretude do algoritmo de Kruskal
Se peso(x) > peso(ei+1), M é uma árvore
geradora de custo menor do que M, o que é
uma contradição.
Se peso(x) = peso(ei+1), M é uma árvore
geradora de custo mínimo, mas M contém as
arestas e1, e2, . . . , ei, ei+1, contradizendo a
escolha de M.
Conclusão: M = K.
– p. 10/50

23. Exercícios
1. Estude e descreva o algoritmo de Prim. Faça
uma análise da complexidade e compare com o
algoritmo de Kruskal. (tem no Cormen!!!)
2. Para completar a prova da corretude do
algoritmo de Kruskal, mostre que se T é uma
árvore geradora de um grafo G então a inclusão
de uma nova aresta de G em T produz um
único circuito em T.
– p. 11/50

24. M´etodo Guloso
Códigos de Huffman
– p. 12/50

25. Códigos de Huffman
Suponha que temos um grande arquivo texto que
precisa ser compactado e transmitido para um
outro local. As hipóteses são:
– p. 13/50

26. Códigos de Huffman
Suponha que temos um grande arquivo texto que
precisa ser compactado e transmitido para um
outro local. As hipóteses são:
Sabemos a frequência de cada caracter, ou
seja, o números de vezes que cada caracter
aparece no texto;
– p. 13/50

27. Códigos de Huffman
Suponha que temos um grande arquivo texto que
precisa ser compactado e transmitido para um
outro local. As hipóteses são:
Sabemos a frequência de cada caracter, ou
seja, o números de vezes que cada caracter
aparece no texto;
No processo de compactação, queremos
atribuir um código binário para cada caracter.
– p. 13/50

28. Códigos de Huffman
Problema: Como atribuir códigos aos caracteres
de tal forma que o texto compactado seja o menor
possível?
– p. 14/50

29. Códigos de Huffman
Problema: Como atribuir códigos aos caracteres
de tal forma que o texto compactado seja o menor
possível?
Atenc¸ ˜ao: Para não ocorrer ambiguidade na
descompactação, é necessário que nenhum
código seja prefixo de outro.
– p. 14/50

30. Códigos de Huffman
Subproblema: Como atribuir códigos livres de
prefixos?
– p. 15/50

31. Códigos de Huffman
Subproblema: Como atribuir códigos livres de
prefixos? Sugest˜ao: Utilizando uma árvore binária.
– p. 15/50

32. Códigos de Huffman
Subproblema: Como atribuir códigos livres de
prefixos? Sugest˜ao: Utilizando uma árvore binária.
Exemplo: Se os caracteres são a, b, c, d, e, f,
podemos atribuir códigos da seguinte forma.
fa b
c d
e
0
0
0
0
0 11
1 1
1
– p. 15/50

33. Códigos de Huffman
Mas como atribuir códigos de forma que o texto
compactado seja o menor possível?
– p. 16/50

34. Códigos de Huffman
Mas como atribuir códigos de forma que o texto
compactado seja o menor possível?
Huffman propôs um algoritmo guloso para
atribuição dos códigos. Ilustraremos este algoritmo
através de um exemplo.
– p. 16/50

35. Códigos de Huffman
Vamos supor que as frequências dos caracteres
sejam: a = 2, b = 3, c = 4, d = 7, e = 8, f = 10.
– p. 17/50

36. Códigos de Huffman
Vamos supor que as frequências dos caracteres
sejam: a = 2, b = 3, c = 4, d = 7, e = 8, f = 10.
O passo geral do algoritmo é:
Escolha um par de valores mínimos f e f do
conjunto de frequências; (Aqui está o guloso!!!)
Substitua f e f por f + f no conjunto;
Repita este processo até que um único
elemento reste no conjunto.
– p. 17/50

37. Códigos de Huffman
Podemos ilustrar a execução deste algoritmo por
uma árvore binária da seguinte forma:
– p. 18/50

38. Códigos de Huffman
Podemos ilustrar a execução deste algoritmo por
uma árvore binária da seguinte forma:
101 2 3 4 7 8
– p. 18/50

39. Códigos de Huffman
Podemos ilustrar a execução deste algoritmo por
uma árvore binária da seguinte forma:
101 2 3 4 7 8
52 4 7 8 10
2 3
– p. 18/50

40. Códigos de Huffman
93 7 8 10
2 3
54
– p. 19/50

41. Códigos de Huffman
154 10
2 3
54
9
7 8
– p. 20/50

42. Códigos de Huffman
10
2 3
54
9
5
7 8
1519
– p. 21/50

43. Códigos de Huffman
6
7 8
1519
10
2 3
54
9
34
– p. 22/50

44. Códigos de Huffman
1
7 8
1519
10
2 3
54
9
34
a b
c
d ef
0
0
0
0
0
1
11
1
– p. 23/50

45. Códigos de Huffman
Qual o tempo gasto pelo algoritmo de Huffman?
– p. 24/50

46. Códigos de Huffman
Qual o tempo gasto pelo algoritmo de Huffman?
Lembre-se: O passo geral do algoritmo é:
Escolha um par de valores mínimos f e f do
conjunto de frequências;
Substitua f e f por f + f no conjunto;
Repita este processo até que um único
elemento reste no conjunto.
– p. 24/50

47. Códigos de Huffman
Qual o tempo gasto pelo algoritmo de Huffman?
Lembre-se: O passo geral do algoritmo é:
Escolha um par de valores mínimos f e f do
conjunto de frequências;
Substitua f e f por f + f no conjunto;
Repita este processo até que um único
elemento reste no conjunto.
O tempo gasto é O(n. log n) utilizando um heap.
– p. 24/50

48. Corretude do algoritmo de Huffman
Teorema: O algoritmo de Huffman atribui códigos
binários aos caracteres de forma ótima, ou seja, tal
que o texto compactado seja o menor possível.
– p. 25/50

49. Corretude do algoritmo de Huffman
Teorema: O algoritmo de Huffman atribui códigos
binários aos caracteres de forma ótima, ou seja, tal
que o texto compactado seja o menor possível.
Id´eia da prova: Observe primeiramente que toda
atribuição de códigos binários pode ser
representada por uma árvore binária.
– p. 25/50

50. Corretude do algoritmo de Huffman
Considere então uma atribuição binária ótima para
um dado texto e seja T a árvore binária que a
representa.
– p. 26/50

51. Corretude do algoritmo de Huffman
Considere então uma atribuição binária ótima para
um dado texto e seja T a árvore binária que a
representa.
Vamos mostrar que T pode ser transformada na
árvore de Huffman sem aumento do tamanho do
texto compactado.
– p. 26/50

52. Códigos de Huffman
Para isso, vamos considerar:
a e b dois caracteres “irmãos” de profundidade
máxima em T; (Vamos supor s.p.g. que
f(a) ≤ f(b))
x e y dois caracteres do texto que possuem as
menores frequências; (Vamos supor s.p.g. que
f(x) ≤ f(y))
– p. 27/50

53. Códigos de Huffman
Para isso, vamos considerar:
a e b dois caracteres “irmãos” de profundidade
máxima em T; (Vamos supor s.p.g. que
f(a) ≤ f(b))
x e y dois caracteres do texto que possuem as
menores frequências; (Vamos supor s.p.g. que
f(x) ≤ f(y))
Então f(x) ≤ f(a) e f(y) ≤ f(b).
– p. 27/50

54. Códigos de Huffman
Então f(x) ≤ f(a) e f(y) ≤ f(b).
T T T
xx
x
y
yy
aa
a
b
bb
– p. 28/50

55. Códigos de Huffman
Então f(x) ≤ f(a) e f(y) ≤ f(b).
T T T
xx
x
y
yy
aa
a
b
bb
Conclusão: uma prova por indução no número de
caracteres pode ser escrita.
– p. 28/50

56. Corretude do algoritmo de Huffman
A diferença no tamanho do texto compactado entre
T e T é:
C(T) − C(T ) = f(c).pT (c) − f(c).pT (c)
= f(x)pT (x) + f(a).pT (a)
−f(x).pT (x) − f(a).pT (a)
= f(x)pT (x) + f(a).pT (a)
−f(x).pT (a) − f(a).pT (x)
= (f(a) − f(x)).(pT (a) − pT (x))
≥ 0
– p. 29/50

57. Exercícios
1. Determine os códigos de Huffman para um texto com
os seguintes caracteres e frequências:
(a) a = 7, b = 5, c = 10, d = 21, e = 90, f = 11, g = 7 e
h = 2;
(b) a = 1, b = 1, c = 2, d = 3, e = 5, f = 8, g = 13 e
h = 21.
2. Descreva a árvore de Huffman quando as frequências
são os primeiros n números de Fibonacci.
3. Qual é um pior caso para o algoritmo de Huffman, ou
seja, um caso em que o texto compactado não é menor
do que o original?
4. Generalize o algoritmo de Huffman para códigos
ternários (isto é, códigos usando simbolos 0, 1 e 2).
– p. 30/50

58. Exercícios
5. Suponha que temos n listas ordenadas, com valores
inteiros, que precisam ser intercaladas 2 a 2 (como no
algoritmo mergesort) para produzir uma única lista
ordenada contendo os elementos de todas as listas.
Sabendo o número de elementos de cada lista, qual é
a sequência ótima de intercalação?
– p. 31/50

59. M´etodo Guloso
O problema do caminho mínimo
– p. 32/50

60. O problema do caminho mínimo
Seja G um grafo simples tal que a cada aresta e
associamos um custo c(e) ≥ 0. O problema do
caminho mínimo consiste em encontar um
caminho de menor custo entre dois vértices dados,
digamos u e v.
– p. 33/50

61. O problema do caminho mínimo
1
1 2
2
4
7
1
7
5
1
2
1
6
3
4
2
8
6
9
3
9 9
u v
– p. 34/50

62. O problema do caminho mínimo
Para resolver este problema, vamos estudar o
algoritmo de Dijkstra (1959). Como veremos, este
algoritmo não só encontra o caminho mínimo de u
a v, mas de u a qualquer outro vértice do grafo.
– p. 35/50

63. O problema do caminho mínimo
Para resolver este problema, vamos estudar o
algoritmo de Dijkstra (1959). Como veremos, este
algoritmo não só encontra o caminho mínimo de u
a v, mas de u a qualquer outro vértice do grafo.
O algoritmo de Dijkstra pode ser visto como uma
generalização da busca em largura.
Vamos assumir que c(x, y) = ∞ se (x, y) /∈ E(G).
– p. 35/50

64. Algoritmo de Dijkstra
1. d(u) ← 0; S ← {u};
2. Para cada v ∈ (V (G) − {u}) faça d(v) ← c(u, v)
– p. 36/50

65. Algoritmo de Dijkstra
1. d(u) ← 0; S ← {u};
2. Para cada v ∈ (V (G) − {u}) faça d(v) ← c(u, v)
3. Enquanto S = V (G) faça
Escolha v ∈ V (G) − S tal que d(v) seja
mínimo
S ← S ∪ {v}
Para cada w ∈ V (G) − S faça
d(w) ← min{d(w), d(v) + c(v, w)}
– p. 36/50

66. Algoritmo de Dijkstra
Qual é o tempo gasto por este algoritmo?
– p. 37/50

67. Algoritmo de Dijkstra
Qual é o tempo gasto por este algoritmo?
Resposta: O(n2
)
– p. 37/50

68. Corretude do algoritmo de Dijkstra
Teorema: O algoritmo de Dijkstra determina
corretamente as distâncias de u a cada vértice de
V (G).
– p. 38/50

69. Corretude do algoritmo de Dijkstra
Teorema: O algoritmo de Dijkstra determina
corretamente as distâncias de u a cada vértice de
V (G).
Prova: Suponha o contrário, ou seja, que existe um
vértice v tal que o valor d(v) calculado pelo
algoritmo não é a distância mínima de u a v.
Consideremos o primeiro vértice v nessa condição
durante a execução do algoritmo (ou seja, a
primeira vez que o algoritmo erra).
– p. 38/50

70. Corretude do algoritmo de Dijkstra
Então a distância de u a v é menor do que d(v), e
para todo vértice w ∈ S a distância de u a w está
correta, ou seja, é d(w).
– p. 39/50

71. Corretude do algoritmo de Dijkstra
Então a distância de u a v é menor do que d(v), e
para todo vértice w ∈ S a distância de u a w está
correta, ou seja, é d(w).
Considere um caminho P de u a v cujo custo é
menor do que d(v).
– p. 39/50

72. Corretude do algoritmo de Dijkstra
Então a distância de u a v é menor do que d(v), e
para todo vértice w ∈ S a distância de u a w está
correta, ou seja, é d(w).
Considere um caminho P de u a v cujo custo é
menor do que d(v). Então P contém um vértice
interno w fora de S (senão o algoritmo teria
escolhido P).
– p. 39/50

73. Corretude do algoritmo de Dijkstra
Logo, a distância de u a w é menor do que a
distância de u a v, pois os custos são todos não
negativos. Mas isto contradiz a escolha de v pelo
algoritmo (w deveria ter sido escolhido nesta
iteração). Portanto, o algoritmo está correto.
– p. 40/50

74. Exercícios
1. Determine o caminho mínimo entre os vértices u
e v.
1
1 2
2
4
7
1
7
5
1
2
1
6
3
4
2
8
6
9
3
9 9
u v
– p. 41/50

75. Exercícios
2. Determine o caminho mínimo entre os vértices u
e v.
3
5 5
5
9 2 9
1 6
9 2
3 4
1
5
2
6
u v
– p. 42/50

76. Exercícios
3. Determine o caminho mínimo entre os vértices u
e v.
9
7
1
5
4
8
2
6
7
2
6
4 1
2
8
10
6
1
3
5
5
8
3
2
4
u v
– p. 43/50

77. Exercícios
4. O algoritmo de Dijkstra funciona corretamente
se as arestas tiverem custos negativos?
– p. 44/50

78. M´etodo Guloso
Problema da Seleção de Atividades
(para estudar)
– p. 45/50

79. Seleção de atividades
Dada uma coleção de atividades
S = {a1, a2, . . . , an} para ser executada, onde cada
atividade ai tem um horário de início si e um
horário de término fi, determinar um subconjunto
sem sobreposição de horário (compatível) máximo
de atividades de S.
– p. 46/50

80. Exemplo
Conjunto de atividades S:
i 1 2 3 4 5 6 7 8 9 10 11
s[i] 1 3 0 5 3 5 6 8 8 2 12
f[i] 4 5 6 7 8 9 10 11 12 13 14
2 3 410 5 6 7 8 9 10 11 12 13 14
– p. 47/50

81. Exemplo
Conjunto de atividades S:
i 1 2 3 4 5 6 7 8 9 10 11
s[i] 1 3 0 5 3 5 6 8 8 2 12
f[i] 4 5 6 7 8 9 10 11 12 13 14
2 3 410 5 6 7 8 9 10 11 12 13 14
Um subconjunto compatível máximo de S: {a1, a4, a8, a11}
– p. 47/50

82. Seleção de atividades
O que pode ser uma estratégia gulosa para este problema?
– p. 48/50

83. Seleção de atividades
O que pode ser uma estratégia gulosa para este problema?
Ordene as atividades por ordem crescente de término;
A cada iteração, escolha uma atividade compatível e
que acaba mais cedo.
– p. 48/50

84. Seleção de atividades
O que pode ser uma estratégia gulosa para este problema?
Ordene as atividades por ordem crescente de término;
A cada iteração, escolha uma atividade compatível e
que acaba mais cedo.
Mais precisamente:
A ← {a1}; i ← 1;
Para j ← 2 até n faça
Se sj ≥ fi então {A ← A ∪ {aj}; i ← j}
– p. 48/50

85. Seleção de atividades
O que pode ser uma estratégia gulosa para este problema?
Ordene as atividades por ordem crescente de término;
A cada iteração, escolha uma atividade compatível e
que acaba mais cedo.
Mais precisamente:
A ← {a1}; i ← 1;
Para j ← 2 até n faça
Se sj ≥ fi então {A ← A ∪ {aj}; i ← j}
Qual o tempo gasto por este algoritmo?
– p. 48/50

86. Exercícios
1. Aplique o algoritmo acima para o conjunto de
atividades especificadas pelos seguintes pares de
horários inicial e final: S =
{(1, 2), (1, 3), (1, 4), (2, 5), (3, 7), (4, 9), (5, 6), (6, 8), (7, 9)}.
2. Argumente que este algoritmo realmente determina um
subconjunto compatível máximo de atividades.
3. Considere a seguinte estratégia para o problema da
seleção de atividades: A cada iteração, escolha uma
atividade compatível e que começa mais tarde. Será
que esta estratégia também produz uma solução
ótima?
4. O que voce acha da seguinte estratégia: A cada
iteração, escolha a atividade de menor duração.
– p. 49/50

87. Mais exercícios
1. Considere o problema de efetuar troco usando um
número mínimo de moedas.
(a) Descreva um algoritmo guloso para efetuar o troco
utilizando moedas de 1, 5, 10 e 25 centavos;
(b) Seu algoritmo produz a solução ótima?
(c) Seu algoritmo funciona corretamente para qualquer
conjunto de moedas?
2. Problema da mochila fracion´aria: Dados n objetos com
valor e peso associado a cada um deles, e uma
mochila que suporta peso máximo W, determinar um
subconjunto do conjunto de objetos de valor máximo e
cujo peso não excede W. Considere que é permitido
selecionar frações de quaisquer elementos.
– p. 50/50