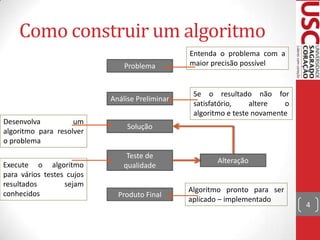
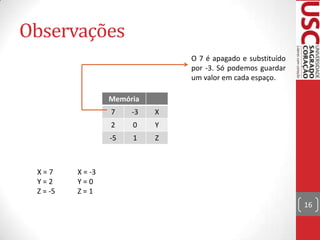
O documento discute lógica de programação, incluindo algoritmos, variáveis, tipos de dados, expressões aritméticas e lógicas. Explica que algoritmos são sequências ordenadas de passos para resolver problemas e fornece exemplos detalhados de algoritmos para trocar uma lâmpada.

1. LÓGICA DE
PROGRAMAÇÃO
Prof.ª Ms. Eng.ª Elaine Cecília Gatto
Algoritmos e Estruturas de Dados
Engenharia de Computação
Universidade Sagrado Coração

2. Lógica de programação
• Significa o uso correto das leis de pensamento, da “ordem
de razão” e de processos de raciocínio e simbolização
formais na programação de computadores, objetivando
racionalidade e o desenvolvimento de técnias que
cooperem para produção de soluções logicamente válidas e
coerentes, que resolvam com qualidade os problemas que
se deseja programar.
• Programação: é responsável pela instrução do computador
do que e de como um problema deve ser resolvido.
• Algoritmo: é uma sequencia ordenada e sem ambiguidade
de passos que visam atingir um objetivo bem definido e,
consequentemente levam à solução de um problema.
2

3. Lógica de programação
• Em um algoritmo, é importante salientarmos:
• Deve descrever exatamente quais são as instruções
que devem ser executadas e em que sequencia;
• Eficiente: resolve o problema com o mínimo de
recursos;
• Eficaz: consegue resolver o problema em qualquer
situação. Todas as situações de exceção, que possa
alterar o comportamento do algoritmo devem ser
especificados e tratados.
3

4. Como construir um algoritmo
Problema
Análise Preliminar
Desenvolva
um
algoritmo para resolver
o problema
Execute o algoritmo
para vários testes cujos
resultados
sejam
conhecidos
Entenda o problema com a
maior precisão possível
Se o resultado não for
satisfatório,
altere
o
algoritmo e teste novamente
Solução
Teste de
qualidade
Produto Final
Alteração
Algoritmo pronto para ser
aplicado – implementado
4

5. Exemplo
• Algoritmo para troca de uma lampada queimada.
1. Remova a lâmpada queimada
2. Coloque um a nova lâmpada
• Detalhando ou refinando os passos:
• Vamos trocar uma lâmpada de rosquear. Se a lâmpada está
queimada não é necessário fazer o teste se está ou não
funcionando. Temos uma lâmpada em casa igual àquela
que queimou – voltagem e potência. Temos uma lâmpada
para trocar pela outra. Temos uma escada para auxiliar na
troca.
• Sempre enumerar os passos a serem executados.
• Primeiro fazer a grosso modo e depois detalhar.
5

6. Exemplo
1.1. Coloque uma escada embaixo da lâmpada queimada.
1.2. Suba na escada até alcançar a lâmpada queimada.
1.3. Gire a lâmpada queimada no sentido anti-horário até que
ela se solte.
2.1. Escolha uma nova lâmpada da mesma potência/vontagem
da queimada.
2.2. Posicional a lâmpada nova no soquete.
2.3. Gire a lâmpada no sentido horário, até que ela se firme.
2.4. Desça da escada.
6

7. Exemplo
• Ordenando os passos:
1.1. Coloque uma escada embaixo da lâmpada
queimada.
2.1. Escolha uma nova lâmpada da mesma
potência/vontagem da queimada.
1.2. Suba na escada até alcançar a lâmpada queimada.
1.3. Gire a lâmpada queimada no sentido anti-horário
até que ela se solte.
2.2. Posicional a lâmpada nova no soquete.
2.3. Gire a lâmpada no sentido horário, até que ela se
firme.
2.4. Desça da escada.
7

8. Detalhando mais ainda os
passos – versão 1
1.
2.
3.
Coloque uma escada embaixo da lâmpada queimada.
Escolha uma lâmpada nova.
Enquanto a potência/voltagem não for a mesma da queimada.
• Descarte a lâmpada escolhida.
• Escolha outra lâmpada.
4. Suba um degrau da escada.
5. Enquanto não possa alcançar a lâmpada queimada
• Suba um degrau da escada.
6. Gire a lâmpada no sentido anti-horário.
7. Enquanto a lâmapda nao estiver livre do soquete
•
Gire a lâmpada no sentido anti-horário.
8. Posicione a nova lâmpada no soquete.
9. Gire a lâmpada no sentido horário.
10. Enquanto a lâmpada não estiver firme no soquete.
• Gire a lâmpada no sentido horário.
11. Desça da escada.
8

9. Detalhando mais ainda os
passos – versão 2
1.
2.
3.
Coloque uma escada embaixo da lâmpada queimada.
Escolha uma lâmpada nova.
Enquanto a potência/voltagem não for a mesma da queimada.
• Descarte a lâmpada escolhida.
• Escolha outra lâmpada.
4.
Suba um degrau da escada.
5.
Enquanto não possa alcançar a lâmpada queimada
• Suba um degrau da escada.
6. Gire a lâmpada no sentido anti-horário.
7.
Enquanto a lâmapda nao estiver livre do soquete
•
Gire a lâmpada no sentido anti-horário.
8.
Posicione a nova lâmpada no soquete.
9.
Gire a lâmpada no sentido horário.
10. Enquanto a lâmpada não estiver firme no soquete.
• Gire a lâmpada no sentido horário.
11. Desça um degrau da escada.
12. Enquanto não possa alcançar o chão.
• Desça um degrau da escada.
9

10. Estrutura condicional
Se condição
Então
Comandos 1
Senão
Comandos 2
10

11. Tipos de dados
• O objetivo principal de qualquer computador é a resolução de
problemas através da manipulação de dados, que podem ser de
vários tipos.
• Tipos primitivos: tipos de dados básicos utilizados na construção
de algoritmos.
• Inteiro: informação pertencente ao conjunto dos números
inteiros. Exemplo: -10, 0, 5, 100.
• Real: informação pertencente ao conjunto dos números reais.
Exemplo: 5.2 (tem que usar ponto e não vírgula), -3.93, 0.0, 7.
• Caracter: informação composta por um conjunto de caracteres
alfanuméricos. Exemplo: ‘a’, ‘ABC’, “F10B5’, ‘$?!5’.
• Lógico: informação que pode receber (assumir) apenas dois
valores possíveis: verdadeiro (V) ou falso (F).
11

12. Tipos de dados
• Constante: um dados é constante quando não se modifica
durante a execução do algoritmo (programa). Pode ser de
qualquer tipo primitivo.
• Variáveis: um dado é variável quando possui um conteúdo
(valor) que pode variar durante a execução de algoritmo
(programa).
• Embora a variável possa assumir diferentes valores, ela só
pode armazenar um valor a cada instante. Toda variável é
conhecida no algoritmo por um nome ou identificador. Ele é
formado por uma única letra ou então por uma letra seguida
de letras ou dígitos. Exemplo: X, Y, Z, salário, ano, etc.
12

13. Observações
• O cálculo – em computação – é feito com dados, geralmente
são números, porém podem ser caracteres. O computador faz
cálculos, o programa executa as instruções que damos. Dados
são jogados dentro da variável ou constante.
• Tipos primitivos são utilizados no algoritmo, porque já vem
definido na linguagem. A maioria das linguagens utilizam os
quatro tipos de dados.
• Tipo inteiro: números dos conjuntos dos números inteiros,
positivos, negativos e nulos.
• Números naturais: só números inteiros positivos.
• Tipo real: mais abrangentes, casas decimais. A casa decimal é
representada por ponto e não vírgula.
13

14. Observações
• Os números inteiros está contido no conjunto dos números
reais.
• O caracter tem que vir com apóstrofo – ou aspas simples –
‘ABC’ – cadeia de caracteres.
• Tipo lógico: ou é verdadeiro ou é falso. Por exemplo: x = 7 > 2,
então x = V.
• Tipo constante: espaço de memória onde o dado é jogado e
não muda o valor. Exemplo: pi = 3.14.
• Variável: espaço de memória do computador onde é guardado
um dado e pode ser alterado.
• Cada espaço tem um nome obrigatoriamente. Três espaços de
memória para três variáveis.
14

15. Observações
• Se chama variável porque os valores podem se alterar. Só
precisa saber o nome da variável.
• Geralmente a variável terá um nome parecido com o
programa – nome sugestivo.
• O DOS só reconhece 8 digítos – caracteres.
• O tamanho do espaço – ou seja, bytes de memória – vai variar
conforme o tipo das variáveis.
• O número máximo para os números inteiros são (faixa de
valores): -32.756 a 32.756.
15

16. Observações
O 7 é apagado e substituído
por -3. Só podemos guardar
um valor em cada espaço.
Memória
7
X
2
0
Y
-5
X=7
Y=2
Z = -5
-3
1
Z
X = -3
Y=0
Z=1
16

17. Expressões aritméticas
• São expressões em que os operadores são aritméticos e os
operandos são constantes e/ou variáveis numéricos.
Operadores Aritméticos
Operador
Função
Operadores Aritméticos
Operador
Função
+
Adição
pot(x,y)
Potenciação. Ex: pot(2,3) = 8
-
Subtração
rad(x,y)
Radiciação. Ex: rad(4) = 2
*
Multiplicação
sqrt(x)
sqrt(4)
/
Divisão
mod
div
sqr(x)
Resto da divisão. Ex: 9 mod 4 = 1
Quociente da divisão. Ex: 9 div 4 = 2
Quadrado de x. Ex: sqr(4) = 16
17

18. Prioridades
Parenteses mais internos
pot rad sqr
* / div mod
+Exemplo:
pot(5,2) – 4/2 + rad(1+3*5)/2
pot(5,2) – 4/2 + rad(1+15)/2
pot(5,2) – 4/2 + rad(16)/2
25 – 4/2 + rad(16)/2
25 – 2 + 4/2
25 – 2 + 2
23 + 2
25
18

19. Expressões lógicas
• São expressões cujos operadores são lógicos, ou relacionais e
cujos operandos são relações, constantes e/ou variáveis do
tipo lógico.
• Operadores relacionais: são utilizados para realizar
comparações entre dois valores do mesmo tipo. Estes valores
podem ser constantes, variáveis ou expressões aritméticas.
Operador
Função
=
Igual a
>
Maior que
<
Menor que
>=
Maior ou igual a
<=
Menor ou igual a
<>
Diferente
19

20. Expressões lógicas
• O resultado obtidode uma expressão realcional é sempre um
valor lógico – V ou F. Exemplo:
2 * 4 = 24 / 3
8=8
V
Operadores Lógicos:
Operador
Não ( ~ )
Função
Negação
E(^)
Conjunção
Ou ( v )
Disjunção
20

21. Tabelas verdade
• Sejam p e q proposições:
Negação
Conjunção
Disjunção
p
não p
p
q
peq
p
q
p ou q
V
F
F
F
F
F
F
F
F
V
F
V
F
F
V
V
V
F
F
V
F
V
V
V
V
V
V
V
O resultado de uma expressão lógica é sempre um valor lógico – V ou F.
Prioridades:
não
e ou
Prioridades entre todos os parênteses:
Parênteses mais internos
Operadores aritméticos
Operadores relacionais
Operadores lógicos
21

22. Exemplos
d = sqr(b) – 4 * a * c
2 < 5 e 15 / 3 = 5
2<5e5=5
VeV
V
22

23. Exemplos
não V ou pot(3,2) / 3 < 15 - 35 mod 7
não V ou 9 / 3 < 15 - 35 mod 7 (operadores atitméticos)
não V ou 3 < 15 - 35 mod 7 (operadores atitméticos)
não V ou 3 < 15 - 0 (operadores relacionais)
não V ou 3 < 15 (operadores relacionais)
não V ou V (operadores lógicos)
F ou V (operadores lógicos)
V
23

24. Exemplos
não ( 5 < > 10 / 2 ou V e 2 – 5 > 5 – 2 ou V )
não ( 5 < > 5 ou V e 3 > 3 ou V )
não ( F ou V e F ou V )
não ( V e F ou V )
não ( F ou V )
não ( V )
F
24

25. Exercícios
• Supondo A, B e C são variáveis do tipo inteiro, com valores
iguais a5, 10 e -8, respectivamente, e uma variável D de 1,5,
quais os resultados das expressões aritméticas a seguir?
a)
b)
c)
d)
e)
f)
2 * A mod 3 – C
rod( - 2 * C ) div 4
( ( 20 div 3 ) div 3 ) pot( 2, 8) / 2
( 30 mod 4 * pot (3,3) ) * ( -1 )
pot( - C, 2 ) + ( D * 10 ) / A
Rad( pot( A, B/A) ) + C * D
25