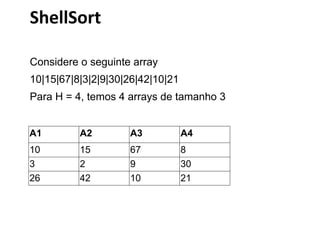
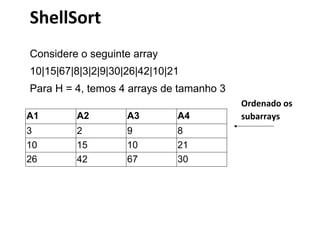
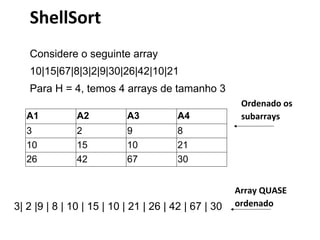
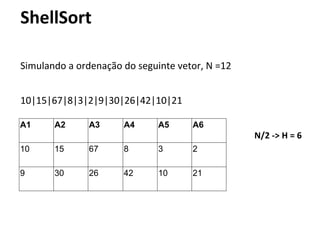
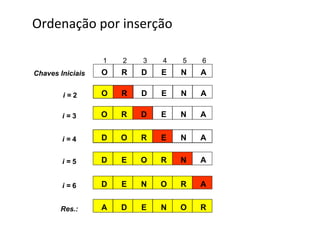
1) O documento apresenta uma introdução sobre ordenação em JQuery e AJAX, incluindo métodos de ordenação como seleção, inserção e bolha. 2) São descritos conceitos como ordenação interna, externa e local, além de análises de eficiência dos algoritmos. 3) Métodos simples como seleção, inserção e bolha são comparados a métodos eficientes como quicksort e mergesort.

1. Introdução ao
Ordenação
JQuery e AJAX
Prof: Sérgio Souza Costa

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
http://www.slideshare.net/skosta/presentations?order=popular
https://twitter.com/profsergiocosta
http://gplus.to/sergiosouzacosta

3. Introdução
Processo de organizar ítens em ordem (de)crescente, segundo algum critério.
Também chamado de classificaçao.
Aplicações que utilizam-se de dados classificados
● Teste de unicidade: verifica se todos os elementos de uma coleção são
distintos.
● Remoção de duplicatas: remove eventuais duplicatas de uma coleção.
● Busca: conforme foi visto, operações de busca são bastante facilitadas
quando os dados são ordenados.
● Encontrar o i-ésimo maior (ou menor) elemento de uma coleção
● Contagem de freqüência (moda): encontra o elemento que ocorre com
mais freqüência numa coleção.
● Encontrar a união ou a interseção de dois conjuntos.
Fonte: http://www.joinville.udesc.br/portal/professores/parra/materiais/cap9_classificacao.ppt

4. Introdução
Antes de prosseguimos, considere as seguintes definições.
Define-se um tabela de tamanho n como uma seqüência de n
itens:
r1, r2, ..., rn chamados de registros
Uma chave ki é associada com cada registro ri.
A chave é usualmente (mas nem sempre) um campo do registro.
struct Item{
int chave;
...
}

5. Principais características
Um método de ordenação é instável caso a ordem relativa dos
itens com chaves iguais é alterada durante o processo de
ordenação ou estável caso contrário.
Uma lista
ordenada
previamente pelo
horário
Agora a mesma
lista ordenada
por destino,
mantendo a
ordenação por
horários

6. Principais características
Ordenação interna o conjunto de registros cabe todo em na
memória principal, ou externa caso parte dos dados estejam em
memória auxiliar.
Classificação local: realização sobre a mesma área física onde se
encontram as chaves. Não usa memória adicional (in-loco)

7. ANÁLISE DE EFICIÊNCIA
A eficiência de tempo é calculada pelo número de operações
críticas efetuadas.
● comparação entre chaves;
● movimentação de registros ou de ponteiros para registros;
● troca de dois registros.
Para determinadas instâncias de um dado problema, alguns
algoritmos podem ser beneficiados em algumas dessas operações:
● Exemplo: menor número de trocas e mesmo número de
comparações.

8. Estratégias
Por troca: são baseados na troca de posição dos dados, se o segundo
elemento é menor do que o primeiro, de forma a ordená-los.
● Exemplos: BubbleSort (Bolha) e QuickSort
Por seleção: parte do princípio de realizar o isolamento de elementos
para posições ordenadas.
● Exemplos: selection sort e heap sort
Por inserção: baseiam-se no deslocamento de elementos da estrutura
frente a um elemento de busca.
Por intercalação, criar uma seqüência ordenada a partir de duas outras
também ordenadas. Esse método é conhecido também como mistura
ou merge em inglês.

9. Simples - Eficientes
Medidas de complexidade levam em conta:
● O número de comparação entre as chaves
● O número de trocas entre os itens
São classificados em dois tipos:
Métodos Simples: mais recomendados para conjuntos pequenos
de dados. Usam mais comparações, mas produzem códigos
menores e mais simples;
Métodos Eficientes ou Sofisticados: adequados para conjuntos
maiores de dados. Usam menos comparações, porém produzem
códigos mais complexos e com muitos detalhes.

10. Simples - Eficientes
Ordenação por Seleção (Selection Sort)
Ordenação por Inserção (Insertion Sort)
Métodos
Simples
Ordenação por Seleção e Troca (Bubble Sort)
Ordenação por Inserção através de incrementos
decrescentes (ShellSort)
Ordenação por Particionamento (QuickSort)
Ordenação de Árvores (HeapSort)
Métodos
Eficientes

11. Métodos Simples
Ordenação por Seleção (Selection Sort)
Ordenação por Inserção (Insertion Sort)
Ordenação por Seleção e Troca (Bubble Sort)

12. Ordenação por Seleção
A cada passo, seleciona o maior (ou menor), e colocálo na posição correta.

13. Ordenação por Seleção - Exemplo
1
2
3
4
5
6
Chaves Iniciais:
O
R
D
E
N
A
i=1:
A
R
D
E
N
O
i=2:
A
D
R
E
N
O
i=3:
A
D
E
R
N
O
i=4:
A
D
E
N
R
O
i=5:
A
D
E
N
O
R

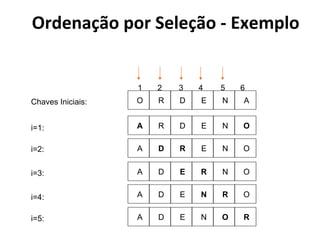
14. Ordenação por Seleção - Código
SelectionSort(A)
1 n <- tamanho[A]
2 para I <- 1 até N-1 faça
3 J <- indiceDoMenorValor (A,i,n)
4 troque A[i] com A[J]
5 // A[1..i] os menores números (1 até i) em ordem
6 fim para;
7 fim procedimento

15. Ordenação por Seleção Atividade
Suponha que se deseja classificar crescentemente o
vetor abaixo utilizando o método SelectionSort:
9 25 10 18 5 7 15 3
Simule as iterações necessárias para a classificação.
Quantas operações de comparações foram realizadas?

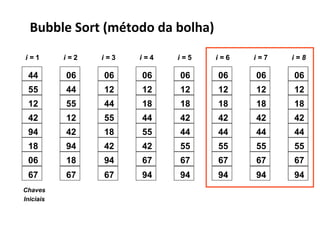
16. Bubble Sort (método da bolha)
Princípio:
● As chaves Item[1].Chave e Item[2].Chave são comparadas e
trocadas se estiverem fora de ordem;
● Repete-se o processo de comparação e troca com Item[2] e
Item[3], Item[3] e Item[4], ...
Por que Bolha?
Se o vetor a ser ordenado for colocado na vertical, com Item[n] em
cima e Item[1] embaixo, durante cada passo o menor elemento
“sobe” até encontrar um elemento maior ainda, como se uma
bolha subisse dentro de um tubo de acordo com sua densidade

17. Bubble Sort (método da bolha)
i=1
i=2
i=3
i=4
i=5
i=6
i=7
i=8
44
06
06
06
06
06
06
06
55
44
12
12
12
12
12
12
12
55
44
18
18
18
18
18
42
12
55
44
42
42
42
42
94
42
18
55
44
44
44
44
18
94
42
42
55
55
55
55
06
18
94
67
67
67
67
67
67
67
67
94
94
94
94
94
Chaves
Iniciais

18. Bubble Sort (método da bolha)
Note que no exemplo, as três últimas iterações não
afetam a ordem do vetor; assim o algoritmo pode ser
melhorado!
Técnica óbvia: manter uma indicação para saber se
houve ou não troca na última iteração: se não houve,
o vetor já está ordenado

19. Bubble Sort (método da bolha)
Existem várias variações de acordo com a ordem
desejada:
“Sobe” os menores valores em direção ao final do vetor
“Sobe” os maiores valores em direção ao final do vetor
“desce” os menores valores em direção ao inicio do vetor
“desce” os maiores valores em direção ao inicio do vetor

20. Bubble Sort (método da bolha)
BubbleSort(A)
1 n <- tamanho[A]
2 para I <- 1 até N faça
3 Para J <- N até i-1 faça {contador decrescente}
4 Se A[J] < A[J-1] então
5 troque A[i] com A[J]
6 fim se
7 fim para;
8 fim procedimento

21. Bubble Sort (método da bolha)
Suponha que se deseja classificar crescentemente o vetor
abaixo utilizando o método BubbleSort:
9 25 10 18 5 7 15 3
Simule as iterações necessárias para a classificação.
Quantas operações de comparações foram realizadas?

22. Ordenação por inserção
7
7
5 7
5/23/2011

23. Ordenação por inserção
3 5 7
3 5 7
8
3 5 6 7
8

24. Ordenação por inserção
Procedimento
Os elementos são divididos em uma seqüência de destino a1, ..., ai-1
e em uma seqüência fonte ai, ..., an.
Em cada passo, a partir de i =2, o i-ésimo item da seqüência fonte é
retirado e transferido para a seqüência destino sendo inserido na
posição adequada

25. Ordenação por inserção
1
2
3
4
5
6
O
R
D
E
N
A
i=2
O
R
D
E
N
A
i=3
O
R
D
E
N
A
i=4
D
O
O
R
E
N
A
i=5
D
E
O
R
N
A
i=6
D
E
N
O
R
A
Res.:
A
D
E
N
O
R
Chaves Iniciais

26. Ordenação por inserção
Suponha que se deseja classificar crescentemente o
vetor abaixo utilizando o método Insertion Sort:
9 25 10 18 5 7 15 3
Simule as iterações necessárias para a classificação.
Quantas operações de comparações foram
realizadas?

27. Métodos Eficiente
QuickSort
MergeSort
ShellSort

28. QuickSort
Baseia-se em um padrão de projeto fundamental para solução de
problemas conhecida como Divisão e Conquista (Divide-andConquer).
Segundo Goodrich, o padrão pode ser descrito, de maneira geral,
como sendo composto de 3 fases:
● Divisão: divide-se os dados de entrada em dois ou mais
conjuntos disjuntos (separados);
● Recursão: soluciona-se os problemas associados aos
subconjuntos recursivamente;
● Conquista: obtém-se as soluções dos subproblemas e junta-se
as mesmas em uma única solução.

29. QuickSort – Esquema conceitual
Inicialmente, o vetor de chaves C é particionado em três
segmentos S1, S2 e S3.
● S2 deverá conter apenas UMA chave denominada pivô.
● S1 deverá conter todas as chaves cujos valores são MENORES
ou IGUAIS ao pivô. Esse segmento está posicionado à esquerda
de S2.
● S3 deverá conter todas as chaves cujos valores são MAIORES do
que o pivô. Esse segmento está posicionado à direita de S2.

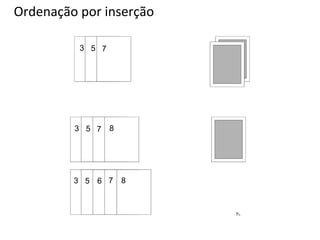
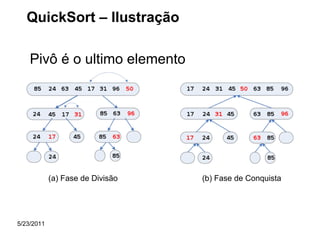
30. QuickSort – Esquema conceitual
Inicialmente, o vetor C é particionado em três segmentos S1, S2 e S3.
● S2 deverá conter apenas UMA chave denominada pivô.
● S1 deverá conter todas as chaves cujos valores são MENORES ou
IGUAIS ao pivô. Esse segmento está posicionado à esquerda de S2.
● S3 deverá conter todas as chaves cujos valores são MAIORES do que
o pivô. Esse segmento está posicionado à direita de S2.
Vetor Inicial : C [ 1 .. n ]
n
1
Vetor Particionado
1
k-1
S1
k
n
k+1
S2
onde: C [ i ] <= C [ k ] , para i = 1, … , k - 1
C [ i ] > C [ k ] , para i = k + 1 , … , n
S3

31. QuickSort – Ilustração
Pivô é o ultimo elemento
(a) Fase de Divisão
5/23/2011
(b) Fase de Conquista

32. QuickSort
O particionamento é reaplicado aos segmentos S1 e S3 e a todos os
segmentos correspondentes daí resultantes com quantidade de
chaves MAIOR que 1.
Quando não restarem segmentos a serem particionados, o vetor
estará ordenado.
Perguntas:
1. Qual é o pivô ideal ?
2. Como escolher este pivô ?
Fonte: Prof. Alexandre Parra Carneiro da Silva:http://www.joinville.udesc.
br/portal/professores/parra/materiais/cap10_quicksort.pp

33. QuickSort
O pivô ideal é aquele que produz segmentos S1 e S3 com tamanhos
(aproximadamente) iguais: chave de valor mediano.
A identificação do pivô ideal requer a varredura de todo o vetor (o
benefício não justifica o custo).
Deseja-se um critério de escolha simples e rápido.
Sem conhecimento prévio sobre a distribuição de valores das
chaves, supõe-se que qualquer uma possa ser o pivô e arbitra-se,
por exemplo, a primeira chave.
Caso o vetor já se encontre parcialmente ordenado, pode-se
utilizar o elemento médio.
Fonte: Prof. Alexandre Parra Carneiro da Silva:http://www.joinville.udesc.
br/portal/professores/parra/materiais/cap10_quicksort.pp

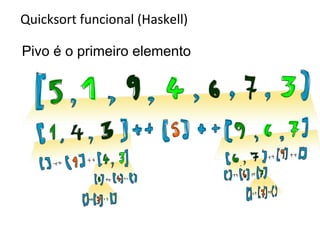
34. Quicksort funcional (Haskell)
qs [] = []
qs (x:xs) = qs [y | y <- xs, y < x]
++ [x]
++ qs [y | y <- xs, y >= x]
É o quicksort aplicado a
todos elemente menores
que o pivó X
Concatenada (++), com o
pivó X
Concatenado com o
quicksort aplicado a todos
elementos maiores que o
pivó X

35. Quicksort funcional (Haskell)
Pivo é o primeiro elemento

36. Quicksort - Imperativo
1) Escolha do pivô (p);
2) Processo de comparações:
Compara v[1], v[2], ... até encontrar um elemento v[a]>p, onde v é o vetor de chaves.
Compara, a partir do final do vetor, os elementos v[n-1],v[n-2], ... Até encontrar v[b]<=p.
3) Neste ponto, troca-se v[a] e v[b], e a busca continua, para cima a partir de v[a+1], e
para baixo, a partir de v[b-1];
4) A busca termina, quando os pontos (a e b) se cruzarem. Neste momento, a posição
definitiva de p foi encontrada, e os valores de p e v[b] são trocados;
5) O particionamento é realizado até os segmentos resultantes tiveram comprimento > 1.
Fonte: Prof. Alexandre Parra Carneiro da Silva:http://www.joinville.udesc.
br/portal/professores/parra/materiais/cap10_quicksort.pp

37. Quicksort - Imperativo
Fonte: Algoritimos - Teoria e Prática. Cormen

38. MergeSort
●
●
●
●
●
●
Algoritmo particular de ordenação.
Método “dividir para conquistar”.
Divide o array no meio.
Ordena cada metade com Mergesort novamente.
Junta (merge) as partes já ordenadas.
Problema: necessita de um espaço igual ao dobro do tamanho
da lista a ser ordenada.

39. MergeSort

40. MergeSort - Função (Merge)
11
70
72
82
Divisão da direita
10
25
36
44
Divisão da esquerda

41. MergeSort - Função (Merge)
11
70
72
82
Divisão da direita
10
10
25
36
44
Divisão da esquerda

42. MergeSort - Função (Merge)
11
70
72
82
Divisão da direita
10
11
10
25
36
44
Divisão da esquerda

43. MergeSort - Função (Merge)
11
70
72
82
10
11
36
44
Divisão da esquerda
Divisão da direita
10
25
25

44. MergeSort - Função (Merge)
11
70
72
82
10
11
36
44
Divisão da esquerda
Divisão da direita
10
25
25
36

45. MergeSort - Função (Merge)
11
70
72
82
10
11
36
44
Divisão da esquerda
Divisão da direita
10
25
25
36
44

46. MergeSort - Função (Merge)
11
70
72
82
10
11
36
44
Divisão da esquerda
Divisão da direita
10
25
25
36
44
70
72
82

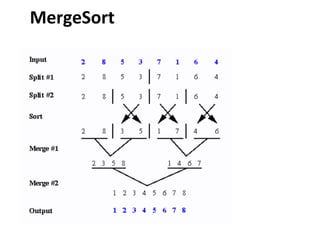
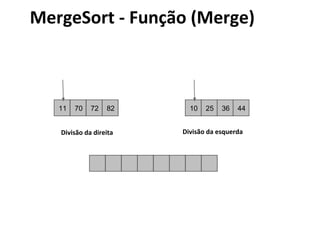
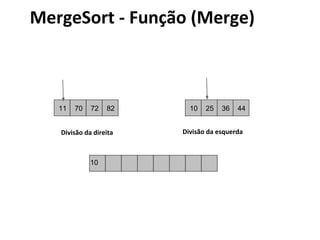
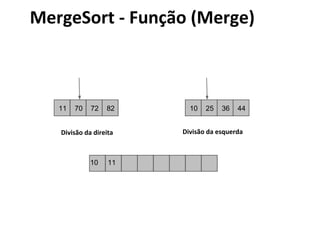
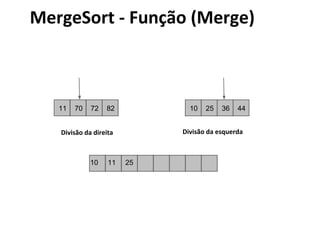
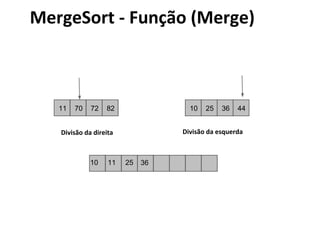
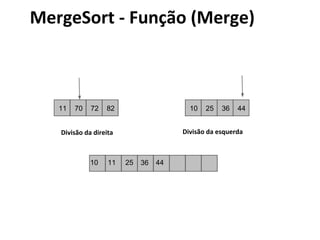
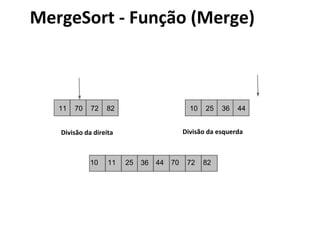
47. MergeSort - Algoritmo
void mergesort(int array[], int i, int f) {
if (i < f) {
int mid = (i+f)/2;
mergesort (array, i, mid);
mergesort (array, mid+1, f);
intercala (array, i, mid, f);
}

48. MergeSort - Atividade
Suponha que se deseja classificar crescentemente o
vetor abaixo utilizando o método Merge Sort:
9 25 10 18 5 7 15 3
Simule as iterações necessárias para a classificação.

49. ShellSort
A ideia básica
● O conceito pode ser usado com qualquer método de
ordenação
● Frequentemente, usamos o insertion sort
● Quando h é o gap entre os numeros a ser ordenados, caso
seja 1, temos um insertion sort
Divide o array em h subarrays
for (i =0 , i <= h, i ++)
Orderna subarray i
Ordena array

50. ShellSort
Considere o seguinte array
10|15|67|8|3|2|9|30|26|42|10|21
Para H = 4, temos 4 arrays de tamanho 3
A1
A2
A3
A4
10
3
26
15
2
42
67
9
10
8
30
21

51. ShellSort
Considere o seguinte array
10|15|67|8|3|2|9|30|26|42|10|21
Para H = 4, temos 4 arrays de tamanho 3
A1
A2
A3
A4
3
10
26
2
15
42
9
10
67
8
21
30
Ordenado os
subarrays

52. ShellSort
Considere o seguinte array
10|15|67|8|3|2|9|30|26|42|10|21
Para H = 4, temos 4 arrays de tamanho 3
A1
A2
A3
A4
3
10
26
2
15
42
9
10
67
Ordenado os
subarrays
8
21
30
3| 2 |9 | 8 | 10 | 15 | 10 | 21 | 26 | 42 | 67 | 30
Array QUASE
ordenado

53. ShellSort
Como calcular a sequência de H's ?
○ Uma forma simples é dividir o valor de N por dois a
cada iteração.
○ Exemplo, para N = 12 teremos
■ 12/ 2 → h = 6
■6 / 2 → h = 3
■3 / 2 → h = 1

54. ShellSort
Simulando a ordenação do seguinte vetor, N =12
10|15|67|8|3|2|9|30|26|42|10|21

55. ShellSort
Simulando a ordenação do seguinte vetor, N =12
10|15|67|8|3|2|9|30|26|42|10|21
A1
A2
A3
A4
A5
A6
N/2 -> H = 6
10
15
67
8
3
2
9
30
26
42
10
21

56. ShellSort
Simulando a ordenação do seguinte vetor, N =12
10|15|67|8|3|2|9|30|26|42|10|21
A1
A2
A3
A4
A5
A6
9
15
26
8
3
2
10
30
67
42
10
21
9|15|26|8|3|2|10|30|67|42|10|21
N/2 -> H = 6

57. ShellSort
Simulando a ordenação do seguinte vetor, N =12
9|15|26|8|3|2|10|30|67|42|10|21
A1
A2
A3
9
15
26
8
3
2
10
30
67
42
10
21
(N/2)/2 -> H = 3

58. ShellSort
Simulando a ordenação do seguinte vetor, N =12
9|15|26|8|3|2|10|30|67|42|10|21
A1
A2
A3
8
3
2
9
10
21
10
15
26
42
30
(N/2)/2 -> H = 3
67
8 |3 |2 |9 |10| 21| 10| 15| 26| 42| 30| 67

59. ShellSort
Simulando a ordenação do seguinte vetor, N =12
8 |3 |2 |9 |10| 21| 10| 15| 26| 42| 30| 67
2| 3| 8| 9| 10| 10| 15| 21| 26| 30| 42| 67
H=1

60. Referências
Estruturas de Dados e Algoritmos em Java
Por Michael T. Goodrich,Roberto Tamassia
Prof. Alexandre Parra Carneiro da Silva:http://www.
joinville.udesc.
br/portal/professores/parra/materiais/cap10_quicks
ort.pp