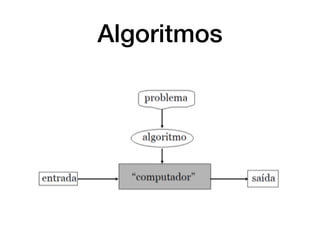
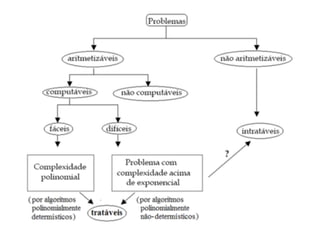
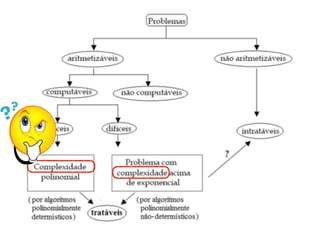
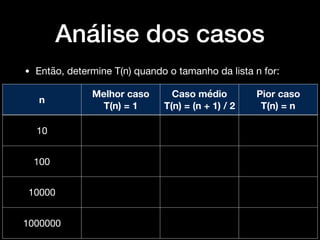
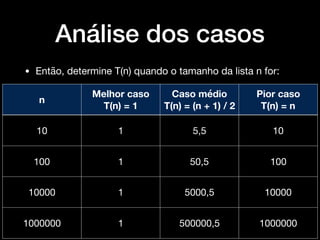
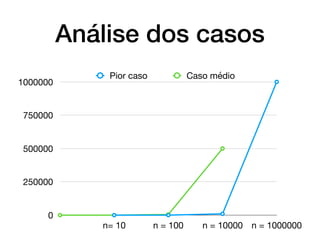
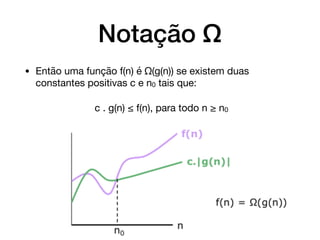
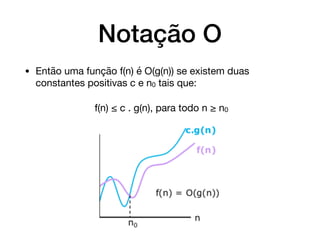
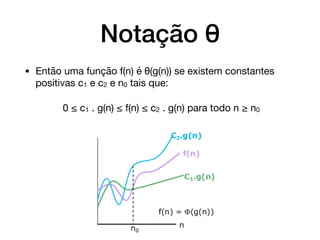
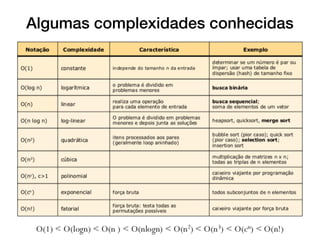
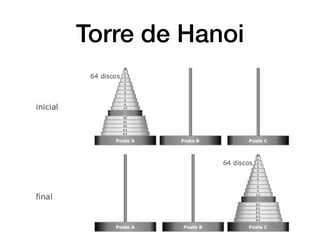
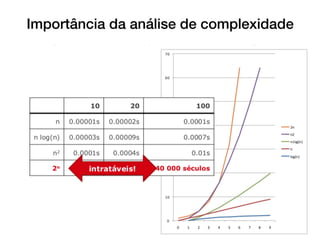
O documento introduz conceitos básicos sobre análise e complexidade de algoritmos. Aborda o que é um algoritmo, tipos importantes de problemas, estratégias de projeto de algoritmos e como calcular a complexidade temporal e espacial de um algoritmo, analisando os casos de melhor, pior e médio caso. Também apresenta a notação assintótica O, Ω e θ para definir limites do crescimento de funções.