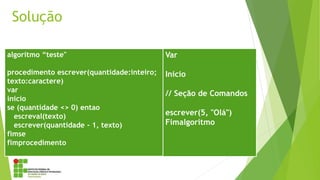
O documento discute algoritmos recursivos, definindo recursividade como um método de programação no qual uma função pode chamar a si mesma. Apresenta exemplos como o cálculo fatorial e de Fibonacci de forma recursiva e iterativa, destacando vantagens e desvantagens de cada abordagem.

1. Algoritmo Recursivo
Professor: Daniel Lobão
Estagiário: Carlos Rodrigo

2. Roteiro
Retomar conteúdo anterior;
Conceito de Recursão;
Objetivos da Função Recursiva;
Ligação com a Matemática;
Algoritmo Recursivo;
Como fazer um Algoritmo Recursivo;

3. Função e Procedimento
funcao <nome-de-função> [(<seqüência-de-
declarações-de-parâmetros>)]: <tipo-de-
dado>
// Seção de Declarações Internas
inicio
//precisa de um retorno
// Seção de Comandos
fimfuncao

4. Função e Procedimento
procedimento <nome-de-procedimento>
[(<seqüência-de-declarações-de-
parâmetros>)]
// Seção de Declarações Internas
inicio
// Seção de Comandos
fimprocedimento

5. O que é Recursão?
 É um método de programação no qual uma
função pode chamar a si mesma. O termo é
usado de maneira mais geral para descrever
o processo de repetição de um objeto de
um jeito similar ao que já fora mostrado.

6. Definição pelo dicionário
RECURSIVIDADE Qualidade do que é
recursivo.
RECURSIVO  Relativo a recursividade.

7. Objetivos da Função Recursiva
Ter uma condição de Parada;
Tornar o problema mais Simples;

8. Caso não tenha esses Objetivos?
Sem condição de Parada
Com Procedimento
enquanto (VERDADEIRO) faca
escreval("INFINITO")
fimenquanto
procedimento escrever(quantidade:inteiro;
texto:caractere)
var
inicio
escreval(texto)
escrever(quantidade - 1, texto)
fimprocedimento

9. Solução
algoritmo “teste"
procedimento escrever(quantidade:inteiro;
texto:caractere)
var
inicio
se (quantidade <> 0) entao
escreval(texto)
escrever(quantidade - 1, texto)
fimse
fimprocedimento
Var
Inicio
// Seção de Comandos
escrever(5, "Olá")
Fimalgoritmo

10. Fatorial
Representação n!;
n pertence ao conj. dos naturais;
n=0  0!=1;
n=5  5! = 5 x 4 x 3 x 2 x 1 = 120;

11. Fatorial
https://olamundo0.files.wordpress.com/2010/04/fatorial.jpg

12. No VisualG como seria a Função?
funcao fat (n:Inteiro):Inteiro
var i, resultado : inteiro
inicio
resultado <- 1
para i de n ate 1 passo -1 faca
resultado <- resultado * i
fimpara
retorne resultado
fimfuncao

13. No VisualG: Fatorial Recursivo
funcao fat (n:Inteiro):Inteiro
inicio
se n=0 entao
retorne 1
senao
retorne n * fat (n-1)
fimse
fimfuncao
Inicio
escreva("Digite um número: ")
leia (numero)
escreval("O fatorial de ",
numero, " é ", fat(numero))
fimalgoritmo

14. Atividade Prática
Criar um algoritmo recursivo que
digite um numero e faça a soma
dos números anteriores.

15. Resposta sem Recursividade
var
n, cont, soma, i: inteiro
inicio
escreval("Informe um número inteiro:")
leia(n)
se n <= 0 entao
repita
senao
cont <- 0
soma <- 0
para i de 1 ate n faca
soma <- soma + cont
cont <- cont + 1
fimpara
fimse
escreval ("Soma:", soma)

16. Somatório Recursivo
funcao somatorio (n:Inteiro):Inteiro
inicio
se n=1 entao
retorne 1
senao
retorne n + somatorio (n-1)
fimse
fimfuncao
Inicio
escreva("Digite um número: ")
leia (numero)
escreval("O Somatório de ",
numero, " é ",
somatorio(numero))
fimalgoritmo

17. Algoritmos Recursivos x Iterativos
Todo algoritmo recursivo possui um
algoritmo iterativo;
QUASE...

18. Vantagens
Simplifica a solução de alguns
problemas
Recursividades são mais compactas
para alguns tipos de algoritmo, mais
legíveis e mais fáceis de ser
compreendidas e implementadas.

19. Desvantagens
 Por usarem intensivamente a memória ou poder de
processamento, os algoritmos recursivos tendem a
ser mais lentos e a consumir mais memória que os
iterativos, porém pode valer a pena sacrificar a
eficiência em benefício da clareza.
 Erros de implementação podem levar a estouro de
pilha. Isto é, caso não seja indicada uma condição
de parada, ou se esta condição nunca for satisfeita,
entre outros.

20. Fibonacci

21. Fibonacci
funcao Iterativo(n : inteiro) : inteiro
var
fib, n1, n2, indice: inteiro
inicio
se (n = 0) ou (n = 1) entao
retorne n
senao
n1 <- 0
n2 <- 1
para indice de 2 ate n passo 1 faca
fib <- n2+n1
n1 <- n2
n2 <- fib
fimpara
retorne fib
fimse
fimfuncao

22. Fibonacci
funcao Recursivo(n : inteiro) :
inteiro
var
inicio
contadorRecursivo <-
contadorRecursivo + 1
se (n = 1) ou (n = 0) entao
retorne n
senao
retorne (Recursivo(n - 2) +
Recursivo(n - 1))
fimse
fimfuncao

23. Fibonacci
funcao RecursivoMemorizado(n :
inteiro) : inteiro
var
inicio
contadorRecursivoMemorizado <-
contadorRecursivoMemorizado +
1
se (n = 0) ou (n = 1) ou
(memorizado[n] <> 0) entao
retorne memorizado[n]
senao
memorizado[n] <-
(RecursivoMemorizado(n - 2) +
RecursivoMemorizado(n - 1))
retorne memorizado[n]
fimse
fimfuncao

24. Referências
 MEDINA, Marco; FERTIG, Cristina. Algoritmos e Programação - Teoria e
Prática. 2ª Edição. Editora Novatec, 2006.
 MAGALHÃES, Regis Pires. Lógica Algoritmo - Recursividade. 2009. Disponível
em: <http://pt.slideshare.net/regispires/logica-algoritmo-08-
recursividade-presentation>. Acesso em: 06 mar. 2015.
 RECURSIVIDADE. Disponível em:
<http://www.di.ufpe.br/~if096/recursao/sld001.htm>. Acesso em: 06 mar.
2015.