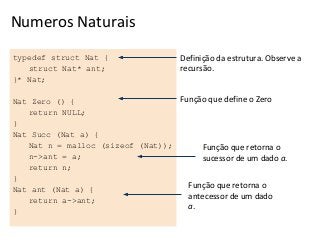
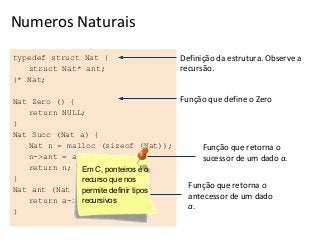
O documento discute recursividade e apresenta alguns conceitos e exemplos. Em três frases: A recursividade é uma forma de resolver problemas dividindo-os em subproblemas menores da mesma natureza até chegar a um caso trivial. Isso é ilustrado com exemplos como o cálculo fatorial e a multiplicação usando somas sucessivas. A implementação de funções recursivas no computador usa uma pilha de execução para gerenciar os chamados recursivos.

1. Recursividade
Prof. Sérgio Souza Costa

2. Recursividade
• Muitas estruturas de dados como listas e árvores são
recursivas, então é importante compreender
conceito de recursividade.
*

3. Recursividade
▪
A recursividade é uma forma de resolver problemas por meio da divisão
dos problemas em problemas menores de mesma natureza.
▪
Se a natureza dos subproblemas é a mesma do problema, o mesmo
método usado para reduzir o problema pode ser usado para reduzir os
subproblemas e assim por diante.
▪
Quando devemos parar? Quando alcançarmos um caso trivial que
conhecemos a solução.
*

4. Recursividade
• Exemplos de casos triviais:
–
–
–
–
–
Qual o fatorial de 0 ?
Quanto é um dado X multiplicado por 1 ?
Quanto é um dado X multiplicado por 0 ?
Quanto é um dado X elevado a 1 ?
Quantos elementos tem em uma lista vazia?

5. Recursividade
Assim, um processo recursivo para a solução de um
problema consiste em duas partes:
▪
▪
▪
▪
▪
O caso trivial, cuja solução é conhecida;
Um método geral que reduz o problema a um ou mais
problemas menores (subproblemas) de mesma
natureza.
Muitas funções podem ser definidas
recursivamente. Para isso, é preciso identificar as
duas partes acima.
Exemplo: fatorial de um número e o n-ésimo termo
da seqüência de Fibonacci.
*

6. Função fatorial
▪
A função fatorial de um inteiro não negativo pode
ser definida como:
▪
Esta definição estabelece um processo recursivo
para calcular o fatorial de um inteiro n.
Caso trivial: n=0.
Método geral: n x (n-1)!.
▪
▪
*

7. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! =
*

8. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
*

9. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)

10. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))

11. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * (1 * 0!)))

12. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * (1 * 0!)))
= 4 * (3 * (2 * (1 * 1)))

13. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * (1 * 0!)))
= 4 * (3 * (2 * (1 * 1)))
= 4 * (3 * (2 * 1))

14. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * (1 * 0!)))
= 4 * (3 * (2 * (1 * 1)))
= 4 * (3 * (2 * 1))
= 4 * (3 * 2)

15. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * (1 * 0!)))
= 4 * (3 * (2 * (1 * 1)))
= 4 * (3 * (2 * 1))
= 4 * (3 * 2)
=4*6

16. Função fatorial
▪
Assim, usando-se este processo recursivo, o cálculo
de 4!, por exemplo, é feito como a seguir:
4! = 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * (1 * 0!)))
= 4 * (3 * (2 * (1 * 1)))
= 4 * (3 * (2 * 1))
= 4 * (3 * 2)
=4*6
= 24
Mas como uma função recursiva
é de fato implementada no
computador?
Usando-se o mecanismo conhecido como
Pilha de Execução!
*

17. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Pilha de Execução
fatorial(4)
-> return 4*fatorial(3)
*

18. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Pilha de Execução
fatorial(3)
-> return 3*fatorial(2)
fatorial(4)
-> return 4*fatorial(3)
*

19. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Pilha de Execução
fatorial(2)
-> return 2*fatorial(1)
fatorial(3)
-> return 3*fatorial(2)
fatorial(4)
-> return 4*fatorial(3)
*

20. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Pilha de Execução
fatorial(1)
-> return 1*fatorial(0)
fatorial(2)
-> return 2*fatorial(1)
fatorial(3)
-> return 3*fatorial(2)
fatorial(4)
-> return 4*fatorial(3)
*

21. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Pilha de Execução
fatorial(0)
fatorial(1)
-> return 1 (caso trivial)
-> return 1*fatorial(0)
fatorial(2)
-> return 2*fatorial(1)
fatorial(3)
-> return 3*fatorial(2)
fatorial(4)
-> return 4*fatorial(3)
*

22. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Pilha de Execução
Desempilha fatorial(0)
fatorial(0)
fatorial(1)
-> return 1 (caso trivial)
-> return 1*fatorial(0)
fatorial(2)
-> return 2*fatorial(1)
fatorial(3)
-> return 3*fatorial(2)
fatorial(4)
-> return 4*fatorial(3)
*

23. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Desempilha fatorial(1)
fatorial(1)
-> return 1*1
fatorial(2)
-> return 2*fatorial(1)
fatorial(3)
fatorial(4)
-> return 3*fatorial(2)
-> return 4*fatorial(3)
*

24. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Desempilha fatorial(2)
fatorial(2)
-> return 2*1*1
fatorial(3)
-> return 3*fatorial(2)
fatorial(4)
-> return 4*fatorial(3)
*

25. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Desempilha fatorial(3)
fatorial(3)
-> return 3*2*1*1
fatorial(4)
-> return 4*fatorial(3)
*

26. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Desempilha fatorial(4)
fatorial(4)
-> return 4*3*2*1*1
*

27. Função fatorial
▪
Considere, novamente, o exemplo para 4!:
Resultado = 24
*

28. Recursividade
"Para fazer um procedimento recursivo é preciso ter fé.”
prof. Siang Wun Song
*

29. Recursividade
"Para fazer um procedimento recursivo é preciso ter fé.”
prof. Siang Wun Song
"Ao tentar resolver o problema, encontrei obstáculos dentro de obstáculos. Por
isso, adotei uma solução recursiva.” Aluno S.Y., 1998
*

30. Recursividade
"Para fazer um procedimento recursivo é preciso ter fé.”
prof. Siang Wun Song
"Ao tentar resolver o problema, encontrei obstáculos dentro de obstáculos. Por
isso, adotei uma solução recursiva.” Aluno S.Y., 1998
"To understand recursion, we must first understand recursion.” —anônimo
*

31. Funções recursivas
• Base do paradigma funcional.
– ○ Lisp, Haskell, Miranda, F#, Scheme, Erland
– Influenciou diversas: JavaScript, Python,Ruby, Lua
• Presente em praticamente todas as linguagens,
mesmo as imperativas, como
– C, Java, Pascal, ADA ...
*

32. Funções recursivas
• Muitos algoritmos complexos são resolvidos através
de soluções recursivas
– Quick-sort (ordenação rápida)
– Ordenação por intercalação (merge sort)
– Busca binária
• Muitas estruturas de dados são recursivas
– Listas encadeadas
– Árvores binárias, n-árias ...
• Tendem a gerar códigos menores
*

33. Recursividade - Natureza
*

34. Recursividade - Natureza
*

35. Vamos fazer mais um
exercício. Na atividade de
aprofundamento tem mais
exercícios. Tentem fazer e
postem suas dúvidas.

36. Exercício resolvido
• Codifiquem uma função que multiplica um dado
inteiro “a” por um inteiro “b”, usando somas
sucessivas. Exemplo:
• 4 * 3 = 3+ 3+ 3 +3 = 12

37. Exercício resolvido
int mult (int a, int b) {
}

38. Exercício resolvido
int mult (int a, int b) {
if (a == 0)
return
}

39. Exercício resolvido
int mult (int a, int b) {
if (a == 0)
return 0;
}

40. Exercício resolvido
int mult (int a, int b) {
if (a == 0)
return 0;
if (a == 1)
return
}

41. Exercício resolvido
int mult (int a, int b) {
if (a == 0)
return 0;
if (a == 1)
return b;
}

42. Exercício resolvido
int mult (int a, int b) {
if (a == 0)
return 0;
if (a == 1)
return b;
return b + mult (a-1,b);
}

43. Vamos testar ?

44. Vamos testar ?
mult (3,5)

45. Vamos testar ?
mult(3,5)=5+mult(2,5)

46. Vamos testar ?
mult(3,5)=5+mult(2,5)
=5+5+mult(1,5)

47. Vamos testar ?
mult(3,5)=5+mult(2,5)
=5+5+mult(1,5)
=5+5+5

48. Vamos testar ?
mult(3,5)=5+mult(2,5)
=5+5+mult(1,5)
=5+5+5
= 15

49. Exercícios
1. Faça uma função recursiva que calcula a divisão usando subtrações
sucessivas
int div (int a, int b);
2. Faça uma função recursiva que calcula o resto de uma divisão usando
subtrações sucessivas.
int mod (int a, int b);
3.Faça uma função recursiva que calcula a potencia de um numero usando
multiplicações sucessivas.
int pot (int base, int exp);
4. Faça uma função recursiva que calcula a quantidade de caracteres em uma
string.
int tamanho (char *str)
5. Fazer uma função recursiva que calcule o valor da série S descrita a seguir
para um valor n > 0 a ser fornecido como parâmetro para a mesma:
S = 1 + 1/2! + 1/3! + ... 1/n!

50. Tipos Recursivos
Um tipo recursivo é definido em termos de si.
Exemplos de tipos recursivos:
● listas
● árvores
A cardinalidade de tipos recursivos é infinita.
Os números naturais é outro exemplo de tipos recursivos

51. Axiomas de Peano
O matemático Giuseppe Peano (1858-1932) apresentou alguns axiomas sobre números
naturais, que ficaram posteriormente conhecidos como os Axiomas de Peano. Nele
precisamos admitir três conceitos primitivos. São eles: zero (denotado por 0), número
natural e a noção de sucessor de um número natural. Estes axiomas são listados abaixo:
(A1) 0 (zero) é um número natural e não é sucessor de
um número natural2.
(A2) Todo número natural tem um único sucessor,
que também é um número natural.
(A3) Se dois números naturais tem o mesmo sucessor,
então eles são iguais entre si.
(A4) Se um subconjunto S dos números naturais
possui o elemento zero e também o sucessor de todos
os elementos de S, então S é igual ao conjunto dos
números naturais.

52. Tipos Recursivos - Naturais
Exemplos:
0 -> Zero

53. Tipos Recursivos - Naturais
Exemplos:
0 -> Zero
1 -> Succ (Zero)

54. Tipos Recursivos - Naturais
Exemplos:
0 -> Zero
1 -> Succ (Zero)
2- > Succ ( Succ (Zero))

55. Tipos Recursivos - Naturais
Exemplos:
0 -> Zero
1 -> Succ (Zero)
2- > Succ ( Succ (Zero))
3- > Succ ( Succ ( Succ (Zero)))
...

56. Numeros Naturais
typedef struct Nat {
struct Nat* ant;
}* Nat;
Definição da estrutura. Observe a
recursão.
Função que define o Zero
Nat Zero () {
return NULL;
}
Nat Succ (Nat a) {
Nat n = malloc (sizeof (Nat));
Função que retorna o
n->ant = a;
sucessor de um dado a.
return n;
}
Função que retorna o
Nat ant (Nat a) {
antecessor de um dado
return a->ant;
a.
}

57. Numeros Naturais
typedef struct Nat {
struct Nat* ant;
}* Nat;
Definição da estrutura. Observe a
recursão.
Função que define o Zero
Nat Zero () {
return NULL;
}
Nat Succ (Nat a) {
Nat n = malloc (sizeof (Nat));
Função que retorna o
n->ant = a;
sucessor de um dado a.
return n; Em C, ponteiros é o
}
recurso que nos
Função que retorna o
Nat ant (Nat a) {
permite definir tipos
antecessor de um dado
return a->ant;
recursivos
a.
}

58. Numeros Naturais
Se b é o número 1, então a + b é definido como sucessor de a. Por
outro lado, se b fosse 2, a + b seria definido como sucessor de a + 1.
Ou seja, a + c é o sucessor de a + b, onde b é o antecessor de c. Isso
pode ser descrito na seguinte função:
Nat sum (Nat
if (c ==
return
else {
return
}
}
a, Nat c) {
Zero () )
a;
Succ ( sum
(a, ant(c)));

59. Numeros Naturais
A multiplicação pode ser definida em termos de soma
sucessivas.
Nat mult (Nat a, Nat b) {
if (a == Zero () )
return Zero ();
else
return sum (b, (mult (b, ant(a))));
}

60. Numeros Naturais
A multiplicação pode ser definida em termos de soma
sucessivas.
Nat mult (Nat a, Nat b) {
if (a == Zero () )
return Zero ();
else
return sum testem o
Baixem e (b, (mult (b, ant(a))));
}
código.

61. Atividade
1. Codifiquem a divisão inteira.
2. Codifiquem a função que retorna o resto de uma divisão
inteira, ou seja, equivalente ao operador %.