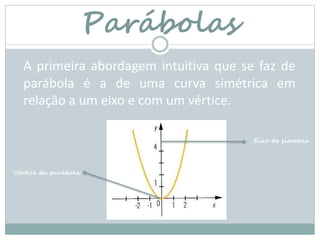
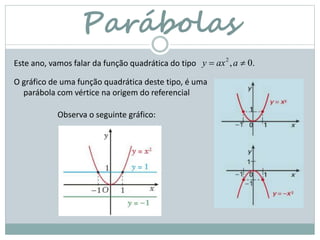
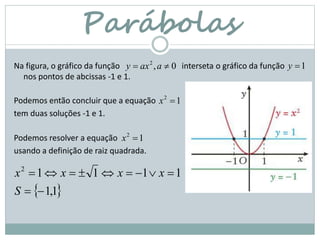
O documento discute funções quadráticas e parábolas. Explica que o gráfico de uma função quadrática é uma parábola e apresenta exemplos de parábolas na natureza, engenharia e arquitetura. Também aborda como resolver equações quadráticas e apresenta exercícios para a prática.

1. Escola Básica de Santa Catarina
Matemática
9º ano
Função
quadrática

2. Função quadrática
O gráfico da função quadrática é uma parábola.
2
( 0)y ax bx c a   
Uma função quadrática é uma função
com uma expressão algébrica do tipo

3. Há várias situações do dia-a-dia em que a
configuração de parábola está presente.
Natureza

4. Parábolas
Nas comunicações
Antena de Satélite

5. Parábolas
Na arquitectura
Forno Solar -
França
Murphy Center at Asphalt
Green - EUA

6. Parábolas
Ponte 25 de Abril
Ponte em betão
armado

7. Parábolas
A primeira abordagem intuitiva que se faz de
parábola é a de uma curva simétrica em
relação a um eixo e com um vértice.
Eixo de simetria
Vértice da parábola

8. Parábolas
Este ano, vamos falar da função quadrática do tipo .0,2
 aaxy
O gráfico de uma função quadrática deste tipo, é uma
parábola com vértice na origem do referencial
Observa o seguinte gráfico:

9. Parábolas
Na figura, o gráfico da função interseta o gráfico da função
nos pontos de abcissas -1 e 1.
Podemos então concluir que a equação
tem duas soluções -1 e 1.
0,2
 aaxy 1y
12
x
Podemos resolver a equação
usando a definição de raiz quadrada.
12
x
 1,1
11112


S
xxxx

10. Parábolas
81) 2
xa 812
x
Resolve cada uma das seguintes equações:
Exercíci
o
 9,999  Sxx81 x
1444) 2
xb 1444 2
x
4
1442
 x 362
 x 36 x 66  xx
 6,6S
0164) 2
xc 164 2
x
4
162
 x 42
 x 4 x
 S
Equação
impossível