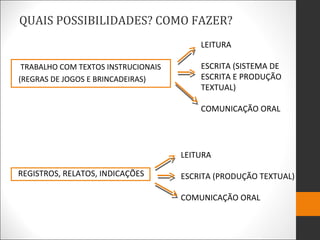
Este documento fornece orientações sobre a organização do trabalho pedagógico para a alfabetização matemática. Ele discute a importância de se pensar na sala de aula como um ambiente de aprendizagem que favoreça o diálogo e as interações entre os alunos. Também apresenta sugestões para a organização do espaço físico da sala de aula e da rotina de atividades, de modo a torná-la propícia para a aprendizagem da matemática.

1. PNAIC
Pacto Nacional para
Alfabetização na Idade Certa
2º Encontro com Professores Alfabetizadores
14/06/2014

2. Leitura de deleite
A pequenina luz azul
Sobre o autor...
M A L B A T A H A N
Nome: Júlio César de Mello e Souza (pseudônimo:
Malba Tahan )
vida: viveu 79 anos ( 1895 - 1974 ), a maior parte no
Rio de Janeiro
Formação:
Colégio D. Pedro II
Escola Normal do RJ
Escola Politécnica do RJ ( eng. civil )

3. VAMOS NOS CONHECER?
BREVE APRESENTAÇÃO/NOME/ ESCOLA QUE ATUA
FEZ PNAIC EM 2013?

4. O VASO

5. VOCÊ E A
MATEMÁTICA

7. Como você aprendeu matemática?
A matemática é vista por muitas pessoas como uma
disciplina difícil e destinada a poucos.
Tanto no Brasil, como em outros países, o Ensino da
Matemática passou por muitas modificações ao longo dos
anos.
Desta forma é interessante recordarmos nossa trajetória
pessoal sobre como aprendemos matemática em nossa
infância, adolescência e juventude.
Por este motivo gostaríamos que você nos relatasse quais
momentos foram mais marcantes em sua aprendizagem
matemática.

8. Como você aprendeu matemática?
Qual é a sua
percepção geral
sobre a
matemática?
Como eram as
aulas de
matemática
quando você
estudou?
Houve algum
professor de
matemática que
chamou sua atenção
por algum motivo?
Você se lembra de
alguma prática de sala
de aula marcante em
sua aprendizagem?

9. A formação dos professores de matemática
A formação inicial dos professores para a disciplina matemática ocorreu de
diversas maneiras no Brasil.
Alguns professores fizeram o antigo curso de Magistério (também conhecido
como curso Normal), cursos de Pedagogia (em Nível Superior) ou
licenciaturas em Matemática.
Além da formação inicial devemos levar em consideração outros tipos de
formação como cursos de capacitações, cursos de extensão e programas de
pós-graduação.
Devido a estes motivos a formação que os professores apresentam é
bastante heterogênea no que se refere aos conteúdos a serem
desenvolvidos na disciplina.
Portanto cabe-nos responder aos seguintes questionamentos:

10. A formação dos professores de matemática
Quais são as suas
expectativas em
relação a esta
formação?

11. A formação dos professores de matemática
Quais conteúdos
da matemática
você gostaria
que fossem
abordados?

12. Sistema
• Simec ( avaliação ) - NOTAS
• Datas
• Atenção aos Emails
• Tarefas
• Portfólio ( capa, breve currículo, perfil da turma, memórias,
expectativas, registro reflexivo e fotos do 1ºencontro, etc)
• Bolsa
• Cartão(banco)

13. CADERNO 1
Organização do Trabalho Pedagógico

14. Caderno 01 – Organização do Trabalho
Pedagógico
Quando iniciamos uma viagem, uma das
primeiras perguntas é para onde desejamos ir?
Tão importante quanto sabermos para onde
desejamos ir é conhecermos onde estamos.
Na área da Educação ocorre algo semelhante.
Lembrando que o objetivo do PNAIC é a
alfabetização plena de todas as crianças brasileiras
de 6 a 8 anos, o primeiro passo neste sentido é o
planejamento das ações que favorecerão tal
objetivo.

15. Iniciando a conversa
Pág
5
• As diferentes unidades que compõem o conjunto de
Cadernos de Formação de Alfabetização Matemática visam
proporcionar ao professor um repertório de saberes que
possibilitem desenvolver práticas de ensino de matemática
que favoreçam as aprendizagens dos alunos.
• A elaboração e execução dessas práticas requer que se pense
em modos de organização do trabalho pedagógico que
situem o aluno em um ambiente de atividade matemática,
possibilitando que ele aprenda, além de codificar e
decodificar os símbolos matemáticos, a realizar variadas
leituras de mundo, levantar conjecturas e validá-las,
argumentar e justificar procedimentos.

16. Iniciando a conversa (cont.)
Pág
5
• A sala de aula que vise à Alfabetização Matemática do aluno,
tal como concebida neste material, deve ser vista como um
ambiente de aprendizagem pautado no diálogo, nas
interações, na comunicação de ideias, na mediação do
professor e, principalmente, na intencionalidade pedagógica
para ensinar de forma a ampliar as possibilidades das
aprendizagens discentes e docentes. Tal intencionalidade
requer um planejamento consistente do professor, uma sala
de aula concebida como uma comunidade de aprendizagem e
uma avaliação processual e contínua do progresso dos
alunos, bem como dos vários fatores intervenientes no
processo como: a prática do professor, o material e a
metodologia utilizados, dentre outros.

17. Objetivos:
• caracterizar a comunidade de aprendizagem da sala de
aula com vistas à Alfabetização Matemática de todos os
alunos;
• destacar a intencionalidade pedagógica como elemento
essencial no processo de alfabetização;
• apontar possibilidades para a organização do trabalho
pedagógico
• compartilhar vivências de professores que buscam garantir
os Direitos de Aprendizagem de Matemática de todos os
alunos
Pág
5

18. Alguns questionamentos iniciais
Como o ambiente da sala de aula
deve ser entendido
para favorecer a aprendizagem da
matemática?
Qual é a intenção pedagógica que
deve permear o trabalho do professor
em sala de aula?
Quais sugestões podem auxiliar o
trabalho do professor na organização
das aulas de matemática?
Como o compartilhamento das ações
desenvolvidas por outros professores
podem nos auxiliar?

19. APROFUNDANDO O TEMA:
ORGANIZAÇÃO DO TRABALHO PEDAGÓGICO
PARA A ALFABETIZAÇÃO MATEMÁTICA
• No primeiro ciclo de alfabetização a sala de aula é
um ambiente formativo que ocupa uma posição
central no processo de alfabetização.
• A sala de aula deve se constituir como um espaço no
qual as crianças ficarão imersas no processo de
apropriação da leitura e da escrita, bem como da
linguagem matemática, com ampla exposição dos
alunos aos materiais impressos que nos envolvem
cotidianamente e possibilitam explicitar a função
social da escrita.
Pág
6

20. • As brincadeiras e as expressões culturais da infância
precisam estar presentes na sala de aula de modo a
tê-la como um ambiente formativo/alfabetizador
privilegiado e como um local em que ocorrem
interações e descobertas múltiplas, repletas de
significação.
• É importante que o professor, no momento de
organizar a sala como um espaço para a
Alfabetização Matemática, considere que brincar,
imaginar, expressar-se nas múltiplas linguagens são
direitos da criança, que contribuem para a
aprendizagem e para o desenvolvimento delas.
Pág
6

21. Organização da sala de aula:
fazendo a aula acontecer
• O que almejamos para os alunos no ciclo de
alfabetização se efetiva na realização do planejado.
• Para tanto, é preciso pensar nas diferentes formas de
organização tanto do espaço físico da sala de aula
quanto do movimento de problematização, discussão e
sistematização de conhecimentos matemáticos.
• O espaço físico da sala de aula, entendemos que este
necessite ser reconhecido como um espaço alfabetizador
em Matemática, com instrumentos, símbolos, objetos e
imagens pertencentes ao campo da Matemática escolar
e não escolar.
Pág
16

22. O espaço físico da sala de aula
• Portadores de textos com diferentes usos e representações
numéricas (reportagens de jornal com gráficos, tabelas de
pontuação de jogos e brincadeiras, rótulos de embalagens,
placas de carro).
Pág
16

23. O espaço físico da sala de aula
• Tabela numérica com números de 1 a 100.
Pág
16

24. O espaço físico da sala de aula
• Varal com os símbolos numéricos, construídos com os alunos.
Pág
16

25. O espaço físico da sala de aula
• Calendário para reconhecimento e contagem do tempo
(dia, mês).
Pág
16

26. O espaço físico da sala de aula
• Listas variadas (nomes dos alunos, datas de aniversário,
eventos da escola, brinquedos e brincadeiras preferidas).
• Régua para a medição de
altura dos alunos.
Pág
16

27. O espaço físico da sala de aula
• Balança que possibilite identificar o “peso”
(a massa corporal).
• Relógios para • Calculadoras
medição do tempo.
Pág
16

28. O espaço físico da sala de aula
Armários ( com jogos, materiais manipuláveis - ábacos,
material dourado, sólidos geométricos, materiais
confeccionados pelos alunos; livros de histórias infantis,
revistas para recorte, caixas, cordas , etc).
Pág
17
Estante com
materiais
manipuláveis

29. Rotina
• Com um ambiente físico preparado para o acolhimento dos
alunos e para que a aula de matemática aconteça, é
importante que o professor estabeleça uma orientação inicial
aos alunos, apresentando uma proposta de rotina de trabalho
no dia.
• O professor deve afixar na sala a rotina do que irá acontecer
naquele dia, listando e numerando cada atividade.
• Mesmo que os alunos ainda não saibam ler, o professor pode
ir fazendo a leitura e listando as atividades no canto da lousa
ou quadro, reduzindo a ansiedade e expectativa dos alunos
quanto ao trabalho do dia.
• Ao mesmo tempo, vai criando o hábito e identificando o
tempo que cada uma das atividades foi planejada e como as
diferentes disciplinas vão sendo contempladas na rotina do
dia e da semana.

30. Quadro de rotina

31. Organização da sala: as
carteiras• A organização das carteiras na sala de aula, também necessita
ser pensada com antecedência e executada em sala de aula.
• A decisão sobre como as carteiras são organizadas tem a ver
com a atividade planejada para aquele dia.
• As carteiras podem ser organizadas em duplas, (disposição
interessante para o coletivo das atividades em aulas de
Matemática, uma vez que propicia a troca, a negociação de
estratégias).
• Em grupos maiores (4 alunos) para atividades com jogos;
• Organizadas em “U” para momentos de discussão coletiva
e/ou socialização de registros e de resolução de atividades.
• As carteiras uma atrás da outra, como tradicionalmente as
salas de aula eram dispostas, pouco contribuem para que o
coletivo de alunos participe da aula.
Pág
17

32. O ambiente propício à
aprendizagem
• Cabe ao professor criar um ambiente problematizador que propicie
a aprendizagem matemática, uma comunidade de aprendizagem
compartilhada por professor e alunos, “os alunos podem formular
questões e planejar linhas de investigação de forma diversificada.
Eles podem participar do processo de investigação” (ALRO;
SKOVSMOSE, 2006, p. 55).
• Além disso, aprender Matemática em um ambiente colaborativo é
importante para a leitura e a escrita. Ler e escrever são ações não
somente restritas ao campo da linguagem e da alfabetização em
língua.
Pág
18

33. O ambiente propício à
aprendizagem
• Em muitas atividades relacionadas às práticas sociais dos alunos
os textos informativos, explicativos, narrativos, dentre outros,
apresentam escritas que são próprias da linguagem matemática:
porcentagens, tabelas, gráficos, algarismos romanos, números
na forma decimal, na forma fracionária, etc.
• A compreensão do texto, muitas vezes, perpassa o
reconhecimento dessa linguagem. Desse modo, a leitura
matemática necessita ser explorada no processo de
alfabetização para que o aluno se torne um leitor crítico desses
textos. O papel social da leitura em Matemática transcende essa
necessidade e assume também um papel político, como pontua
Fonseca (2013).
Pág
19

34. Os registros
• A escrita nas aulas de Matemática é necessária como forma
de registro e comunicação de ideias.
• O registro matemático é entendido como uma comunicação
sobre ideias, objetos e processos matemáticos.
• Pode ser realizado por meio de diferentes gêneros textuais,
assumindo sentidos diversos no contexto de aulas de
Matemática: registro reflexivo para os alunos , registro de
comunicação aos colegas e professor, registro do processo
para constituir memória, registro como forma de
sistematização, registro como apropriação de uma linguagem,
registro como forma de comunicação da resolução e/ou
formulação de um problema.
Pág
20

35. Registros
• A alfabetização acontece, na maioria das vezes, por meio de
desenhos, tabelas, gráficos, diagramas, relatório, registro de
uma estratégia de resolução, elaboração de textos de problema,
produção de cartas, produção de regras de jogo, produção de
tirinhas ou histórias em quadrinho, produção de cartazes,
produção de livros, relatórios de entrada múltipla, etc.
Pág
22

36. Registro: listas
Pág
24

37. Registro: tabela
Pág
24

38. • A produção de tais registros, principalmente no ciclo de
alfabetização, vem sempre acompanhada da oralidade.
• A comunicação oral possibilita uma maior interatividade entre
alunos e professor em sala de aula.
• É no momento da exposição oral de um raciocínio que o aluno
toma consciência sobre o seu modo de pensar, correto ou não.
• Captar os registros orais nem sempre é uma tarefa simples, o
professor precisa ter em mãos os recursos tecnológicos a fim de
facilitar a produção de registros( Câmeras de vídeo, gravadores,
câmeras fotográficas digitais ou um caderno de anotações para os
registros rápidos). O registro tecnológico pode ser uma forma de
envolver os alunos na ação e possibilitar que essas não “se
percam” aos olhos do professor.
• Todas as diferentes formas de registro aqui apresentadas
acontecem em meio a um ambiente de mediação pelo professor e
alunos quando esses se encontram em atividades de produção em
Matemática.
Pág
25

39. O fechamento da aula
• Todo o trabalho que foi planejado e desenvolvido em sala de
aula necessita de um fechamento.
• As formas de fazer esse fechamento precisam constar no
planejamento do professor.
Pág
27

40. Momento de socialização ou
entrega das produções
Momento de socialização
• As atividades desenvolvidas foram coletivas e em situações de
oralidade ou em um contexto de jogo ou de manipulação de
materiais.
• Se os alunos não estiver alfabetizados , o registro escrito fica
mais demorado. Nesse caso, o professor pode produzir,
coletivamente com os alunos, um texto síntese, discutindo
com eles as principais ideias que foram trabalhadas,
organizando-as num texto curto, escrito na lousa – o professor
como escriba – e copiado pelos alunos, dependendo do nível
de alfabetização das crianças.

41. As atividades desenvolvidas
individualmente
• Se a atividade tiver sido individual, os próprios alunos contam
aos demais colegas como pensaram na situação proposta.
• A cada exposição o professor registra na lousa as ideias
apresentadas.
• Não há necessidade de solicitar que todos os alunos da classe
apresentem e discutam suas estratégias de resolução.
• É importante também que os alunos adquiram o hábito de
ouvir o que o colega está dizendo. É importante evitar dizer se
está certo ou errado, mas solicitar a participação dos alunos
na discussão, problematizando as suas falas.

42. As atividades desenvolvidas
coletivamente
• A atividade foi realizada em grupo ou em dupla e durante a
realização das atividades o professor deve circular pelos grupos
e identificar as diferentes resoluções ou respostas dadas pelos
alunos.
• Ao acompanhar os grupos, seleciona três ou quatro duplas ou
grupos para fazer a exposição, procurando escolher respostas
ou estratégias diferenciadas, começando pelas menos
elaboradas, visto que estas é que gerarão maior discussão. O
grupo elege um relator do trabalho.
• É importante que a cada apresentação seja aberto um espaço
para debate e discussão das respostas apresentadas. Quando o
professor é problematizador em sala de aula, os alunos
também aprendem a formular boas perguntas aos colegas.

43. Entrega de produções escritas
• O professor poderá ainda optar por não socializar
coletivamente as respostas ou estratégias dos alunos, mas
recolher o registro produzido por eles. Nesse caso o retorno
que dará é fundamental.
• Se tiver solicitado a produção de um gênero textual, a
correção deve ser feita levando em consideração tanto as
ideias matemáticas registradas quanto a adequação do
gênero escolhido.
• Os diferentes registros produzidos pelos alunos precisam ser
anotados numa ficha de observação para que possa ser feito o
acompanhamento do progresso, diagnosticando os problemas
e avaliando se as intervenções estão contribuindo ou não para
o avanço das aprendizagens.

44. Síntese final do trabalho
• Após a etapa de socialização ou fechamento do trabalho do
aluno, é o momento que o professor precisa fazer a síntese da
aula.
• É preciso fazer a síntese das respostas dos alunos, explorando
as ideias que foram apresentadas e complementando as que
forem necessárias.
• Enfim, toda aula precisa ter um fechamento. Assim, o
planejamento precisa prever que a aula tenha início, meio e
fim.

45. A tarefa de casa
• Tarefas de retomada e/ou fixação do conteúdo trabalhado.
O professor poderá propor pequenas tarefas que possibilitem aos
alunos continuar pensando sobre o assunto tratado em aula.
• Tarefas que irão desencadear a próxima aula.
O professor poderá propor a resolução de uma situação pelos
alunos, na qual eles utilizarão diferentes formas de resolvê-la. No
dia seguinte essa tarefa desencadeará a aula.
• Tarefas que exigem coleta de material.
A tarefa pode ser a coleta de material em jornais ou revistas,
escolha de sucatas ou outros materiais que serão utilizados na
aula seguinte.

46. Avaliação, progressão e
continuidade das
aprendizagens• A avaliação vai ocorrendo ao longo do processo, seja pela
observação sistemática e intencional do professor, seja pelos
registros produzidos por alunos e professores. Espera-se que
esses momentos de avaliação tenham sido registrados e que
possibilitem replanejamentos ao longo do processo.
• Esse trabalho sistemático possibilitará que o professor
diagnostique as necessidades e avanços dos alunos em termos
da Alfabetização Matemática e possa dar continuidade ao
processo de ensino com vista à aprendizagem do aluno.
Entendemos que no ciclo de alfabetização não faz sentido
interromper o movimento de aprendizagem de sala de aula
para realização de uma prova formal pelo professor.

47. Atividade em grupo
Compartilhando
Pág
40

48. Proposta de Trabalho
Em grupos analise uma das
atividades da seção
“Compartilhando”. Em seguida
solicitamos, gentilmente, que cada
grupo apresente sua atividade.
Lembre-se que durante a análise da sua atividade seu grupo deve tentar
contemplar os objetivos do Caderno 01.

49. Compartilhando – Atividade 1
O texto “Diferentes Formas de Planejamento” destaca a importância do
planejamento anual e durante o período letivo. Divida com seus colegas os
encaminhamentos que planejou para este ano com relação à Alfabetização
Matemática. Informe e discuta o que houve de mudanças em relação ao que
fez no ano passado. O planejamento deste ano está considerando as ideias
presentes no texto?

50. Diferentes formas de planejamento
É realizado pelos
professores e
coordenação escolar. Seus
principais aspectos são
elencar os conhecimentos
que os alunos possuem e
selecionar os conteúdos
pertinentes à
aprendizagem
significativa.
É um momento onde pode-se
reconduzir o processo de
aprendizagem. Suas principais
características são a flexibilidade
e utilização da avaliação como
instrumento para nortear a ações
em sala de aula.
Neste instante o professor deve
prever ações pontuais para alcançar
com êxito os objetivos elencados
anteriormente. Tais ações
devem dar continuidade as
desenvolvidas anteriormente.

51. Compartilhando – Atividade 2
Leia a narrativa abaixo e discuta com seus colegas como tem sido a sua prática de
sala de aula com relação à Resolução de Problemas.
NEGOCIANDO SIGNIFICADOS NA LEITURA DE UM TEXTO DE PROBLEMA
Eliana Rossi EMEB Prof. Benno Carlos Claus Município de Itatiba, SP
ÚRSULA É UMA URSINHA. ELA PRECISA
APRENDER A ANDAR NA CORDA-BAMBA PARA
GANHAR UM EMPREGO NO CIRCO COMO
MALABARISTA. TODOS OS DIAS ÚRSULA
AUMENTA EM 5 CENTÍMETROS A ALTURA DO
ARAME EM QUE ELA TREINA. HOJE O ARAME
ESTAVA A QUINZE CENTÍMETROS DO SOLO.

52. Analisando a situação-problema
Quais as informações que traz
esse problema?
Qual é o problema dessa
situação?
Será que essa situação é para
resolver o problema de
desemprego da ursinha?
O que precisa ter em uma
situação-problema para ser
possível resolver?
Quantos dias ela treinou?
Quantos centímetros ela
aumentará
em uma semana?

53. Compartilhando – Atividade 3- A
Nas próximas narrativas, as professoras Selene e Ida apresentam trabalhos
relacionados à Educação Estatística. Após ler os relatos e os comentários
relacionados, discuta com seus colegas como tem sido o trabalho com esta
importante área na sua sala de aula. O que os alunos podem aprender com
atividades como esta, além de construir e ler gráficos?
EDUCAÇÃO ESTATÍSTICA: ALÉM DE GRÁFICOS E TABELAS
Selene Coletti EMEB Cel. Francisco Rodrigues Barbosa Município de Itatiba, SP
COMO VOCÊ VÊM PARA A ESCOLA
COMO VOCÊ VÊM PARA A ESCOLA
CARRO
A PÉ
ÔNIBUS
VAN

54. Analisando a 1ª proposta de Educação Estatística
OS ALUNOS DO 1º ANO B DA SELENE FIZERAM O CENSO ESCOLAR.
ENTREVISTARAM O 2º A E O 1º B TAMBÉM PARTICIPOU RESPONDENDO ÀS
PERGUNTAS.
O CENSO ESCOLAR TINHA 10 PERGUNTAS SOBRE A ESCOLA.
VINTE E SETE ALUNOS DA SELENE RESPONDERAM ÀS PERGUNTAS E VINTE E
QUATRO DA PROFESSORA CLAUDIA FORAM ENTREVISTADOS.
•TEM MAIS MENINOS;
•TEM MAIS PESSOAS QUE MORAM LONGE DA ESCOLA;
•TEM MAIS ALUNOS QUE VÊM A PÉ;
•SÃO MAIS AS MÃES QUE TRAZEM AS CRIANÇAS PARA A ESCOLA;
•TEM MAIS CRIANÇAS COM IRMÃOS ESTUDANDO NESTA ESCOLA;
•CINQUENTA ALUNOS GOSTAM DA ESCOLA E SÓ UM NÃO GOSTA;
•MUITAS PESSOAS ACHAM A ESCOLA LEGAL (44 PESSOAS);
•A QUADRA É O LUGAR QUE MAIS GOSTAM DA ESCOLA;
•TEM MAIS CRIANÇAS QUE GOSTAM DE INFORMÁTICA (40);
•AS CRIANÇAS DO 2º A E 1º B GOSTAM MAIS DOS AMIGUINHOS.
TEXTO PRODUZIDO PELOS ALUNOS DO 1º B

55. ATIVIDADE 3- B
PARTINDO DE UMA SITUAÇÃO DO LIVRO DIDÁTICO,
EXPLORANDO DIFERENTES FORMAS DE REGISTRO
Ida Maria Marassatto E.M.E.B. Professor Benno Carlos Claus Município de Itatiba, SP
O que é
aniversário?
1ª Passo
Coletando
dados
2ª Passo
Construindo
gráficos
3ª Passo
Gráfico de setores

56. ATIVIDADE
Analisando a 2ª proposta de Educação Estatística
Olha o tamanho
do pedaço é
grande se tiver
bastante criança
Março ficou
com
o maior pedaço
Formou um
pedaço com
pouca e bastante
pizza.
Conclusão
Enquanto professora, minhas expectativas foram além,
consegui manter um equilíbrio entre números e
operações, espaço e forma, medidas e educação
estatística, houve regularidade no passo a passo
envolvendo a resolução dos problemas que foram
ocorrendo, pois acredito que tais propostas permitem
ao aluno ampliar experiências de apropriação da
Matemática.

57. Compartilhando – Atividade 4
Quando trabalhamos com jogos, é fundamental vivenciar o jogo antes de levá-
lo à sala de aula. A partir desta vivência poderemos descobrir uma série de
conceitos que podem ser desenvolvidos com o jogo, além de imaginar
possibilidades de intervenção durante e após o momento do seu uso com as
crianças. Vamos iniciar jogando duas partidas do jogo “Travessia do Rio”:
Regras
1)Cada jogador coloca as suas fichas,
numa das margens do rio, da maneira que
quiser, podendo pôr mais do que uma na
mesma casa, deixando outras vazias.
2)Alternadamente, os jogadores lançam
dados e calcula a soma obtida.
3)Se a soma corresponder a uma casa
ondem estejam as suas fichas, na margem
respectiva, passar uma delas para o outro
lado do rio.
4)Ganha quem conseguir passar primeiro
todas as fichas para o outro lado.

58. Analisando o jogo “Travessia do Rio”
Discuta com seus colegas que conceitos podem ser desenvolvidos durante a
realização desse jogo e quais as dificuldades para o seu uso nas suas salas de
aula. Depois dessa discussão, leia a narrativa da professora Cidinéia, que
compartilha conosco sua experiência:
OS GÊNEROS ORAIS E ESCRITOS NAS AULAS DE MATEMÁTICA:
MOMENTOS DE REFLEXÕES E PROBLEMATIZAÇÕES
Cidinéia da Costa Luvison E. M. Professora Maria Losasso Sabella Município de Bragança Paulista, SP
Diário Isac [...] o jogo se joga assim pega os dois dados chacoalha
na mão e joga no tabuleiro e coloca a pecinha no número que
cair na tabela e assim continua até alguém completar as fileiras
quem terminar a fileira primeiro é o vencedor.
Diário Isac [...] Eu descobri que não dá 1 com 2 dados.
Diário Isac [...] os números que mais saem e o número são
essa 6, 7, 8 e 9 por causa que eu escolhi esses números eu
ganhei todas.

59. Compartilhando – Atividade 5
Consideramos o trabalho com resolução de problemas como um dos aspectos
centrais com a Educação Matemática já no início de escolarização. No entanto,
um trabalho com problemas sempre do mesmo tipo acaba por mecanizar
processos e rapidamente leva à pergunta clássica dos alunos: – Professora, é
de mais ou de menos? A narrativa da professora Daniela nos auxilia a repensar
este modelo. Depois de sua leitura, planeje uma intervenção em sua sala de
aula para compartilhar no próximo encontro.
FORMULAR PROBLEMAS FAVORECE A APRENDIZAGEM DE RESOLUÇÃO DE PROBLEMAS?
Daniela Aparecida de Souza EMEB Prof. Benno Carlos Claus Município de Itatiba, SP
Continuar um problema iniciado: o
aluno precisará fazer uma relação entre
o início dado dos problemas com as
informações que serão acrescentadas
por ele, finalizando o texto com uma
pergunta para solucionar a questão
contida no mesmo.
Elaborar um problema a partir de uma
operação: esse tipo de atividade tem
como finalidade desenvolver a relação
de uma determinada operação com sua
ideia textual, ou seja, se é de subtração
o sujeito precisa produzir uma situação
que esteja vinculada a esta operação.

60. Exemplos de produções elaboradas pelos alunos
Guilherme ficou com 95 figurinhas
47 + 13
Guilherme tinha 65 figurinhas e ganhou mais
31 figurinhas.
Com quantas figurinhas ele ficou?
Daniela tinha 47 reais e ganhou mais 13
reais de sua mãe.
Com quanto ela ficou?

61. Momentos Finais
Sabemos que, para que todas as crianças brasileiras de
6 a 8 anos de idade estejam plenamente alfabetizadas,
existe uma longa e árdua jornada.
Contudo esperamos que, durante este encontro,
tenhamos contribuído de maneira significativa para
que você desse o primeiro passo nesta caminhada.
Lembre-se que o nosso ambiente de formação é
inteiramente colaborativo e que suas reflexões e
contribuições são fundamentais para que todos
alcancemos nosso objetivo final.

63. Leitura de deleite
VÍDEO: THE POTTER

64. Tarefa
• Registro reflexivo do encontro .
• Preencher o Perfil da Turma em relação à Língua Portuguesa.
• Aplicar uma situação didática em sua sala de aula com foco em
um dos conteúdos abordados: Quantificação, Registro e
Agrupamentos. Fazer registro do planejamento, do
desenvolvimento e avaliação. Anexar fotos e atividades dos
alunos.
• Estudo do texto “Eixos Estruturantes e Objetivos dos Direitos de
Aprendizagem para a Alfabetização Matemática na Perspectiva
do Letramento” (p. 45 a 55). Fazer registro de seu estudo.
Próxima formação 26 julho

65. Sispacto 2014
• Avaliação - Frequência e atividades realizadas.
• Do dia 15 a 17: professor alfabetizador avalia orientador e
orientador avalia professor alfabetizador e coordenador local.
• Do dia 18 a 20: coordenador local avalia seus orientadores.
• Do dia 20 a 26: avaliação dos perfis da IES.
• Do dia 27 a 30: aprovação das avaliações pelo coordenador
adjunto e coordenador IES.
• Do dia 1 a 3: autorização de pagamento da bolsa do coordenador
geral da IES.

66. Datas da formação

67. CADERNO 2
Quantificação, Registros e Agrupamentos

68. Caderno 02 – Quantificação, Registros e
Agrupamentos
Frequentemente, durante o processo de
aprendizagem, nos deparamos com diversas
dúvidas sobre determinados conceitos.
Quando uma ideia não se encontra bem
definida em nossa mente, sentimos mais
dificuldade para desenvolvê-la perante nossos
alunos.
Desta forma convidamos você a repensar em
algumas questões abordadas no Caderno 02 do
PNAIC.

69. Iniciando a conversa
• O eixo Número e Operações será abordado em um conjunto de
três cadernos, sendo este o primeiro.
• O tema central deste caderno são os Números. Esses serão
observados, basicamente, a partir de duas perspectivas: a
primeira apresenta os números como resultantes de uma
operação de contagem que segue alguns princípios lógicos e
possui variadas formas de registro. A partir daí, estabelece-se a
relação entre a contagem, a quantificação, os sistemas de
registro e os sistemas de numeração.
• A segunda apresenta os números no âmbito das situações de
uso em contextos sociais. Ambas são abordadas
simultaneamente, de modo que os problemas que surgem num
lado encontram respostas no outro e geram novas questões
tanto para a matemática quanto para as práticas sociais.
Pág 5

70. Os objetivos:
• estabelecer relações de semelhança e de ordem, utilizando critérios
diversificados para classificar, seriar e ordenar coleções;
• identificar números em diferentes contextos e funções;
• quantificar elementos de uma coleção, utilizando diferentes
estratégias;
• comunicar as quantidades, utilizando a linguagem oral, os dedos da
mão ou materiais substitutivos aos da coleção;
• representar graficamente quantidades e compartilhar, confrontar,
validar e aprimorar seus registros nas atividades que envolvem a
quantificação;
• reproduzir sequências numéricas em escalas ascendentes e
descendentes a partir de qualquer número dado;
• elaborar, comparar, comunicar, confrontar e validar hipóteses sobre
as escritas e leituras numéricas, analisando a posição e a
quantidade de algarismos e estabelecendo relações entre a
linguagem escrita e a oral.
Pág 5

71. Jogo Pega Varetas
Número de jogadores
Grupo com 6 pessoas
Regras
As regras serão combinadas pelo grupo. O grupo deverá decidir:
•Como as varetas serão soltas;
•O que determinará a ordem dos jogadores;
•Se as varetas possuirão o mesmo valor ou qual valor terá cada cor;
•Quantas rodadas o grupo jogará;
•Como será decidido o vencedor.
Registro
O registro deverá ser feito de maneira espontânea utilizando folhas
sulfite e lápis de cor.
Pág 12

72. Jogo Pega Varetas
Como vocês
fizeram para
combinar as
regras?
Quais regras
vocês
combinaram?
É uma regra
que favorece
todos
participantes?
O que vocês
pensam sobre a
regra da
soltura das
varetas?
Teria alguma
forma de
modificar esta
regra para ficar
bom para todo
grupo?
Como vocês
contaram ou
registraram os
pontos?
Ocorreram
formas
diferentes de
registros?
Apresente os
registros feitos
pelo grupo.

73. QUESTÕES: Jogo Pega Varetas
O que podemos trabalhar com o Pega-varetas nos anos iniciais de acordo com
os conteúdos do Caderno 2?
Quais as principais dificuldades que as crianças teriam?
Como incentivar os registros espontâneos das crianças na contagem dos
pontos?
Como seria a proposta do grupo para trabalhar com os alunos o jogo Pega
Varetas?
Neste momento seu grupo apresentará a proposta elaborada de acordo com
tais problematizações.

74. Sistematização:
Integração das áreas de Língua
Portuguesa e Matemática.
INTERDISCIPLINARIDADE
O CAMINHO MAIS SEGURO PARA FAZER A RELAÇÃO ENTRE AS DISCIPLINAS É SE
BASEAR EM UMA SITUAÇÃO REAL. A ABORDAGEM INTERDISCIPLINAR PERMITE QUE
CONTEÚDOS QUE VOCÊ DARIA DE FORMA CONVENCIONAL, SEGUINDO O LIVRO
DIDÁTICO, SEJAM ENSINADOS E APLICADOS NA PRÁTICA ,O QUE DÁ SENTIDO AO
ESTUDO. PARA QUE A DINÂMICA DÊ CERTO, PLANEJAMENTO E SISTEMATIZAÇÃO SÃO
FUNDAMENTAIS.
No livro Globalização e Interdisciplinaridade, o educador espanhol Jurjo Torres
Santomé, da Universidade de La Coruña, afirma que a interdisciplinaridade dá
significado ao conteúdo escolar.
Fonte: http://revistaescola.abril.com.br/formacao/interdisciplinaridade-avanco-educacao-
426153.shtml

75. QUAIS POSSIBILIDADES? COMO FAZER?
TRABALHO COM TEXTOS INSTRUCIONAIS
(REGRAS DE JOGOS E BRINCADEIRAS)
REGISTROS, RELATOS, INDICAÇÕES
LEITURA
ESCRITA (SISTEMA DE
ESCRITA E PRODUÇÃO
TEXTUAL)
COMUNICAÇÃO ORAL
LEITURA
ESCRITA (PRODUÇÃO TEXTUAL)
COMUNICAÇÃO ORAL

76. • Facilita antecipações e permite que se coloque em
prática comportamento, procedimento e capacidade de
leitor com a finalidade de ler para fazer alguma coisa, um
dos importantes propósitos sociais de leitura que nossos
alunos precisam aprender.
• Abordagem significativa e contextualizada.
• Favorece aprendizagens relativas aos elementos e modo
de funcionamento da escrita, assim como da linguagem
escrita e seus propósitos comunicativos – análise e
reflexão sobre o sistema de escrita, produção textual,
leitura e oralidade.
TRABALHO COM TEXTOS INSTRUCIONAIS
(REGRAS DE JOGOS E BRINCADEIRAS)

77. REGISTROS, RELATOS,
INDICAÇÕES
• Leitura e análise desses gêneros.
• Desenvolvimento das operações de produção de
texto: contextualização – recuperar as
características da situação comunicativa;
elaboração e tratamento dos conteúdos temáticos;
planificação – organizar o texto parte a parte;
textualização – elaborar o texto, utilizando os
recursos da língua; revisão do texto em função da
situação comunicativa.
Kátia L. Bräkling

78. OBJETIVOS:
• Participar de situações de intercâmbio oral do cotidiano escolar (como, por
exemplo, situações de exposição oral e rodas em geral), ouvindo com atenção,
formulando perguntas, comentando e dando opinião sobre o tema tratado.
• Planejar sua fala, adequando-a a diferentes interlocutores em situações
comunicativas do cotidiano escolar (como situações de exposição oral e rodas em
geral) com maior e menor formalidade.
• Participar de situações de leitura de textos instrucionais mesmo antes de ser capaz
de ler convencionalmente.
• Ler – como apoio do professor ou colegas – textos de diferentes gêneros (como
contos, fábulas, lendas, mitos, textos instrucionais, de divulgação científica,
notícias, entre outros), com diferentes propósitos, apoiando-se em conhecimentos
sobre o tema do texto, as características do seu portador, do gênero e do sistema
de escrita.
• Participar de situações de produção de textos de autoria, realizadas de maneira
coletiva, em grupos, ou individualmente, ditando para o professor ou colegas, ou
escrevendo de próprio punho.
• No processo de produção de textos de autoria: planejar o que vai escrever
considerando o contexto de produção; reler o que está escrevendo, tanto para
controlar a progressão temática quanto para avançar nos aspectos discursivos e
textuais.
• Participar de situações de revisão coletiva de textos – ou realizadas em parceria
com colegas.
Programa Ler e Escrever – 2º ano.

79. Momentos Finais
Os momentos de atividades práticas são
aqueles momentos que mais envolvem os alunos e,
até mesmo, o professor. Porém a reflexão que
obtivemos sobre tais atividades é fundamental para
o (re)encaminhamento do processo de
aprendizagem.
Acreditamos que o uso da metodologia dos Jogos
Pedagógicos favorece no desenvolvimento de vários
conceitos matemáticos, especialmente nesta faixa
etária onde o brincar tem papel de destaque para o
indivíduo.