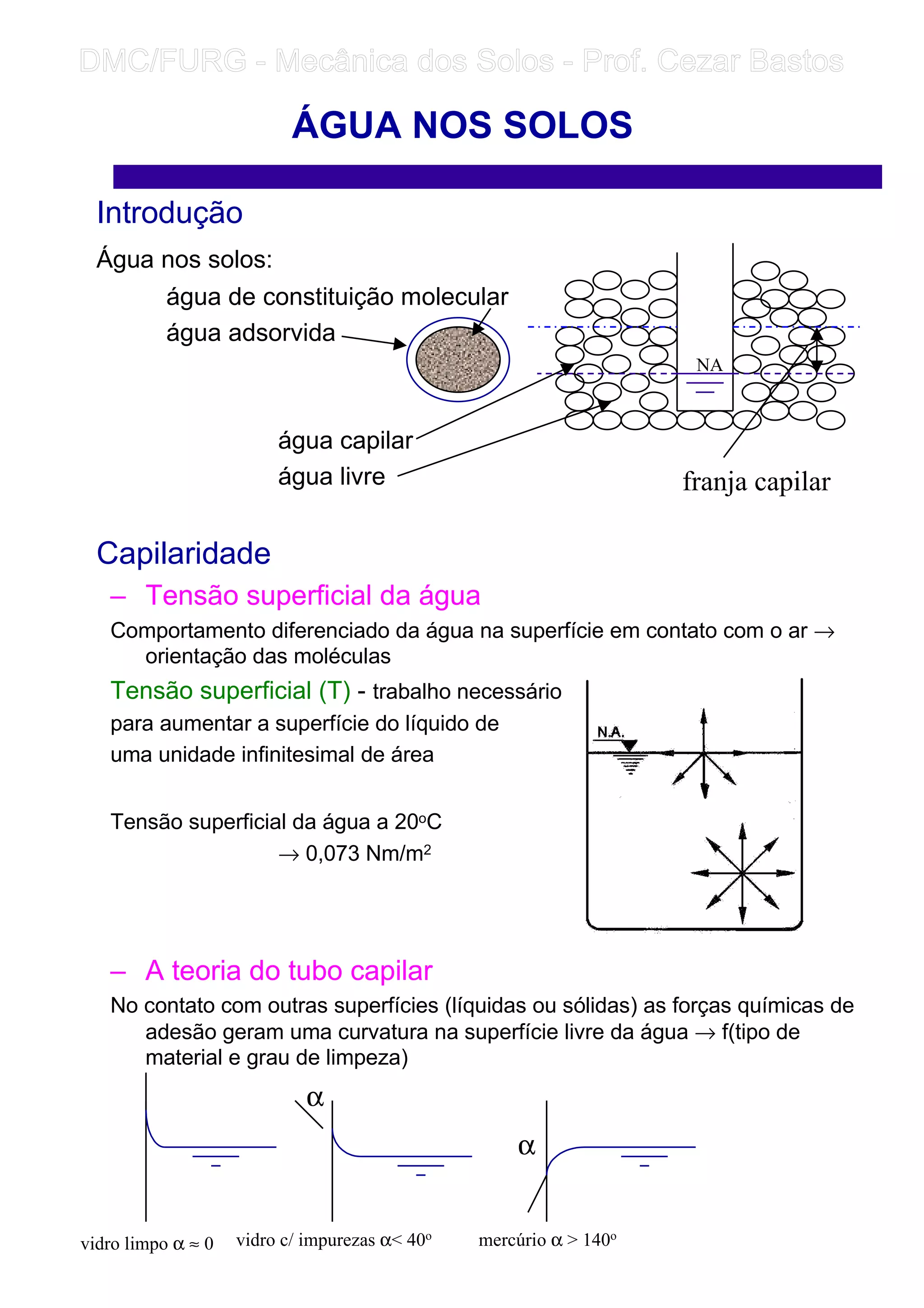
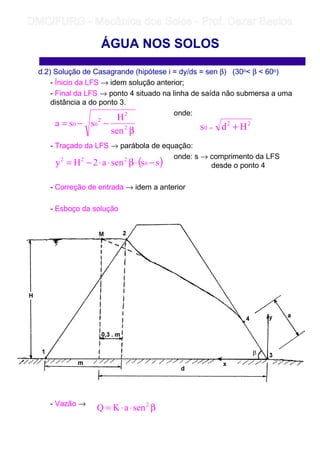
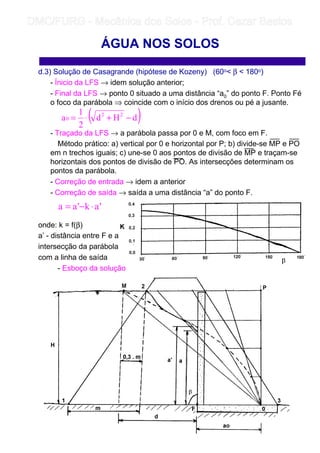
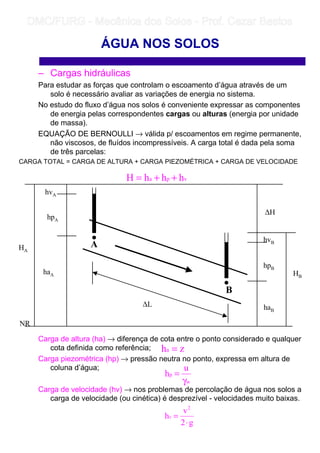
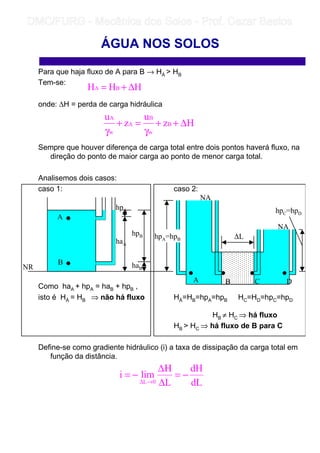
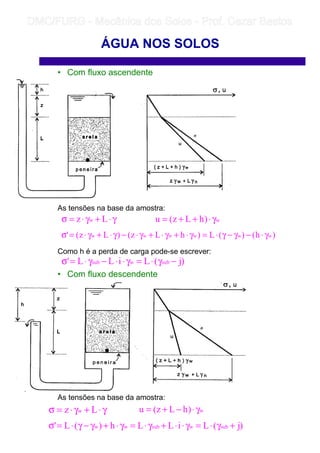
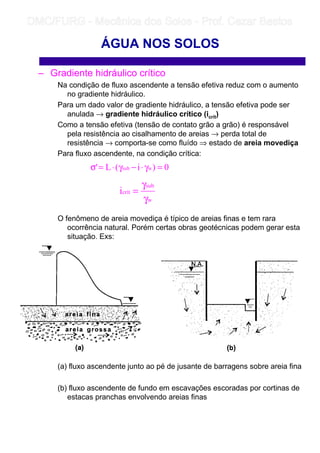
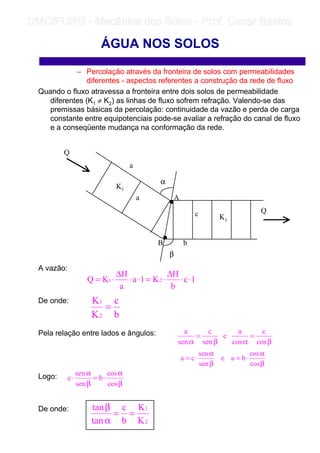
1) O documento discute a capilaridade da água nos solos, incluindo a tensão superficial, ascensão capilar em tubos e solos, e pressão negativa da água. 2) É explicado como a água sobe nos poros dos solos devido à capilaridade, variando de acordo com o tamanho dos grãos. 3) O fluxo da água nos solos depende de gradientes de carga hidráulica e é afetado pelas forças de percolação geradas pela perda de carga ao longo do caminho.

1. ÁGUA NOS SOLOS
Introdução
Água nos solos:
água de constituição molecular
água adsorvida
água capilar
água livre
Capilaridade
– Tensão superficial da água
Comportamento diferenciado da água na superfície em contato com o ar →
orientação das moléculas
Tensão superficial (T) - trabalho necessário
para aumentar a superfície do líquido de
uma unidade infinitesimal de área
Tensão superficial da água a 20oC
→ 0,073 Nm/m2
– A teoria do tubo capilar
No contato com outras superfícies (líquidas ou sólidas) as forças químicas de
adesão geram uma curvatura na superfície livre da água → f(tipo de
material e grau de limpeza)
NA
franja capilar
vidro limpo α ≈ 0
α
α
vidro c/ impurezas α< 40o mercúrio α > 140o

2. Em função da superfície curva, ocorre uma diferença nas pressões externa e
interna da superfície ar-água.
A diferença de tensões é equilibrada pela resultante da tensão superficial.
curvatura ↑ → diferença de pressões ↑ → T para equilíbrio ↑
• Comportamento da água em tubos capilares:
Quando um tubo capilar é colocado em contato com a superfície da água livre
forma-se uma superfície curva a partir do contato água-tubo. A curvatura é
função das propriedades do material do tubo. A água sobe pelo tubo
capilar até que seja estabelecido o equilíbrio das pressões interna e
externa à superfície → fenômeno de ascensão capilar
uA= uD = uF = atmosférica
uB = uC = atmosférica + γw z
uE = atmosférica - γw hc
ÁGUA NOS SOLOS
Fc
W

3. ÁGUA NOS SOLOS
A altura de ascensão capilar em um tubo de raio r pode ser calculada
igualando o peso da água no tubo acima do NA com a resultante da tensão
superficial responsável pelo equilíbrio.
Peso de água:
Resultante da tensão superficial ao longo do perímetro:
Para o equilíbrio W = Fc cos α:
Quando é atingido o equilíbrio (máxima ascensão) α → 0. Logo:
Ex: tubo de vidro com 1 mm de diâmetro → hc = 3 cm
• O comportamento da água capilar nos solos
Os vazios no solo são muito pequenos, comparáveis aos tubos capilares,
embora muito irregulares e interconectados.
A situação da água capilar no solo depende do histórico do NA.
wc
2
hrW γ⋅⋅⋅π=
Tr2Fc ⋅⋅π⋅=
α
γ⋅
⋅
= cos
r
T2
h
w
c
w
Cmáx
r
T2
h
γ⋅
⋅
=

4. ÁGUA NOS SOLOS
- Quando um solo seco é colocado em contato com água livre, esta sobe
por capilaridade até uma altura que é função do diâmetro dos vazios, este
relacionado como diâmetro das partículas. Como bolhas de ar ficam
enclausuradas, o solo mantém parcial e decrescente saturação até a altura
máxima de ascensão capilar.
- O mesmo fenômeno ocorre quando do rebaixamento do NA. O solo
mantém continuidade da água nos vazios até a máxima altura capilar.
Acima deste a coluna d’água se “rompe” e a água presente nos vazios é
isolada do lençol freático.
Interrompida a coluna d’água, a água pode manter-se isolada, aprisionada
entre os grãos por efeito dos meniscos capilares, desde que se
estabeleça o equilíbrio de forças
• Seqüência de fenômenos relacionados a capilaridade a partir
do umidecimento de um solo seco
1o) A água intersticial passa a incorporar a água adsorvida;
2o) A água vai sendo “armazenada” nos pontos de contato entre as
partículas. Formam-se os vasos capilares afunilados.
Em cada contato, em função da abertura do poro, tem-se certa
quantidade de água que pode ser mantida em suspensão;
3o) Adicionando mais água, chega-se a um ponto que não é mais
possível reter água por capilaridade. A água passa a ser livre
incorporando o lençol freático.
• Relações empíricas para a altura capilar
A altura de ascensão capilar está relacionada diretamente com os vazios
e diâmetro das partículas. Relações empíricas do tipo:
c - coeficiente de 0,1 a 0,5 cm2
situação
sem equilíbrio
situação de
possível equilíbrio
10
Cmáx
De
c
h
⋅
=

5. • Alturas capilares máximas atingíveis
– pedregulhos → alguns poucos centímetros;
– areias → um a dois metros;
– siltes → três a quatro metros;
– argilas → dezenas de metros.
• A pressão negativa na água do solo
A água capilar acima do NA assume poropressão negativa. Na realidade
assume valores menores que a pressão atmosférica (pressão de
referência = 100 kPa). A poropressão negativa da água nos solos devido
ao efeito da capilaridade é chamada de sucção matricial.
Esta “resistência a tração” da água se limita ao zero absoluto de pressão, isto
é, - 100 kPa, a partir do qual a água teoricamente entra em cavitação → o
ar dissolvido presente na água se instabiliza. Na prática, em condições
especiais (água desaerada e em volumes muito pequenos), consegue-se
atingir em laboratório pressões negativas na água inferiores a -100 kPa.
Em perfis de solos pouco saturados é possível medir pressões negativas na
água intersticial inferiores a -1000 kPa por meio de tensiômetros especiais.
Pelo conceito de tensão efetiva → para u (-) ⇒ σ’ σ. O acréscimo de tensão
efetiva por efeito da pressão neutra negativa representa um acréscimo na
força de contato entre os grãos e como conseqüência uma parcela
adicional de resistência ao cisalhamento dos solos não saturados chamada
de coesão aparente.
• Exemplos da importância no estudo da capilaridade
– Construção de aterros e pavimentos - a água que sobe por
capilaridade tende a comprometer a durabilidade de pavimentos
– Sifonamento capilar em barragens - a água pode, por
capilaridade, ultrapassar barreiras impermeáveis e gerar por
efeito de sifonamento percolação através do corpo da barragem
– Coesão aparente - parcela de resistência gerada pelos
meniscos capilares presentes em solos não saturados
ÁGUA NOS SOLOS

6. Permeabilidade e percolação
Os solos têm, com freqüência, a maior parte ou a totalidade de
seus poros ocupados por água, que, quando submetida a
uma diferença de potencial hidráulico, flui através dos poros
interconectados, fissuras e/ou outros caminhos preferenciais.
A facilidade com que a água flui através de um meio poroso,
como o solo, constitui uma importante propriedade
conhecida como permeabilidade. A permeabilidade de um
solo é quantificada pelo coeficiente de permeabilidade.
Um termo análogo a permeabilidade é condutividade
hidráulica, reservado ao fluxo em solos não saturados.
Chamamos de percolação o fluxo da água
através do solo.
O estudo do movimento da água no interior do solo é muito
importante para diferentes obras de engenharia.
Importância do estudo da permeabilidade dos solos. Exs:
– Determinação do fluxo e cálculo de vazões sob ou através de
barragens, na direção de escavações, cortinas ou poços de
rebaixamento;
– Determinação das forças de percolação exercidas sobre
estruturas hidráulicas;
– Análise da velocidade de recalques por adensamento,
associados a redução dos vazios a medida que a água dos
poros é expulsa;
– Nos estudos de estabilidade, uma vez que a tensão efetiva
(responsável pela resistência ao cisalhamento dos solos) é
função da pressão neutra, que por sua vez depende das
tensões provocadas pela percolação;
– No controle da erosão interna (“piping”) em solos finos.
ÁGUA NOS SOLOS

7. – Cargas hidráulicas
Para estudar as forças que controlam o escoamento d’água através de um
solo é necessário avaliar as variações de energia no sistema.
No estudo do fluxo d’água nos solos é conveniente expressar as componentes
de energia pelas correspondentes cargas ou alturas (energia por unidade
de massa).
EQUAÇÃO DE BERNOULLI → válida p/ escoamentos em regime permanente,
não viscosos, de fluídos incompressíveis. A carga total é dada pela soma
de três parcelas:
CARGA TOTAL = CARGA DE ALTURA + CARGA PIEZOMÉTRICA + CARGA DE VELOCIDADE
Carga de altura (ha) → diferença de cota entre o ponto considerado e qualquer
cota definida como referência;
Carga piezométrica (hp) → pressão neutra no ponto, expressa em altura de
coluna d’água;
Carga de velocidade (hv) → nos problemas de percolação de água nos solos a
carga de velocidade (ou cinética) é desprezível - velocidades muito baixas.
ÁGUA NOS SOLOS
vpa hhhH ++=
hvA
hvB
hpA
haA
hpB
haB
A
B
zha =
w
p
u
h
γ
=
g2
v
h
2
v
⋅
=
∆H
HA
HB
∆L
NR

8. hpA
Para que haja fluxo de A para B → HÁ HB
Tem-se:
onde: ∆H = perda de carga hidráulica
Sempre que houver diferença de carga total entre dois pontos haverá fluxo, na
direção do ponto de maior carga ao ponto de menor carga total.
Analisemos dois casos:
caso 1: caso 2:
Como haA + hpA = haB + hpB ,
isto é HÁ = HB ⇒ não há fluxo HÁ=HB=hpA=hpB HC=HD=hpC=hpD
HB ≠ HC ⇒ há fluxo
HB HC ⇒ há fluxo de B para C
Define-se como gradiente hidráulico (i) a taxa de dissipação da carga total em
função da distância.
ÁGUA NOS SOLOS
HHH BA ∆+=
A
B
haA
haB
hpB
NR
NA
NA
hpA=hpB
hpC=hpD
A B C D
dL
dH
L
limi
0L
−=
∆
∆Η
−=
→∆
∆L
Hz
u
z
u
B
w
B
A
w
A
∆++
γ
=+
γ

9. – Força de percolação
A perda de carga (∆H) é dissipada através de uma amostra de solo, de
seção (A) ao longo de uma distância (L), na forma de atrito viscoso. Este
atrito provoca um esforço de arraste das partículas na direção do
movimento. Esta chamada força de percolação (Fp) é dada por:
Esta força de percolação por unidade de volume (j) é:
– Tensões no solo submetido a percolação
Analisemos as tensões no solo em três condições: sem fluxo, fluxo
ascendente e fluxo descendente
• Sem fluxo
As tensões na base da amostra:
ÁGUA NOS SOLOS
AHFp w ⋅γ⋅∆=
ww
w
i
L
H
LA
AH
j γ⋅=γ⋅
∆
=
⋅
⋅γ⋅∆
=
γ⋅+γ⋅=σ Lz w w)Lz(u γ⋅+=
u' −σ=σ
LL)(' subw ⋅γ=⋅γ−γ=σ

10. • Com fluxo ascendente
As tensões na base da amostra:
Como h é a perda de carga pode-se escrever:
• Com fluxo descendente
As tensões na base da amostra:
ÁGUA NOS SOLOS
γ⋅+γ⋅=σ Lz w w)hLz(u γ⋅++=
)j(LiLL' subwsub −γ⋅=γ⋅⋅−γ⋅=σ
w)hLz(u γ⋅−+=γ⋅+γ⋅=σ Lz w
)j(LiLLh)(L' subwsubww +γ⋅=γ⋅⋅+γ⋅=γ⋅+γ−γ⋅=σ
)h()(L)hLz()Lz(' wwwwww γ⋅−γ−γ⋅=γ⋅+γ⋅+γ⋅−γ⋅+γ⋅=σ

11. – Gradiente hidráulico crítico
Na condição de fluxo ascendente a tensão efetiva reduz com o aumento
no gradiente hidráulico.
Para um dado valor de gradiente hidráulico, a tensão efetiva pode ser
anulada → gradiente hidráulico crítico (icrít)
Como a tensão efetiva (tensão de contato grão a grão) é responsável
pela resistência ao cisalhamento de areias → perda total de
resistência → comporta-se como fluído ⇒ estado de areia movediça
Para fluxo ascendente, na condição crítica:
O fenômeno de areia movediça é típico de areias finas e tem rara
ocorrência natural. Porém certas obras geotécnicas podem gerar esta
situação. Exs:
(a) fluxo ascendente junto ao pé de jusante de barragens sobre areia fina
(b) fluxo ascendente de fundo em escavações escoradas por cortinas de
estacas pranchas envolvendo areias finas
ÁGUA NOS SOLOS
0)i(L' wsub =γ⋅−γ⋅=σ
w
sub
críti
γ
γ
=

12. – Permeabilidade dos solos
• A Lei de Darcy (1850)
Experimentalmente Darcy verificou os fatores que influenciam o fluxo
de um fluído em um meio poroso e estabeleceu que a descarga (Q)
numa seção de área (A) é proporcional ao gradiente hidráulico (i) . A
equação que leva seu nome:
A constante de proporcionalidade é chamada de coeficiente de
permeabilidade (K), uma medida da propriedade do solo que
representa a facilidade do solo em permitir a percolação d’água pelos
seus interstícios.
A velocidade (v), razão entre a vazão e a área da seção de fluxo, é
assim representada pela Lei de Darcy:
Chama-se de velocidade de percolação (vp) a velocidade com que
a água escoa nos vazios do solo, considerando a área efetiva de
escoamento, isto é, a “área de vazios” (Av)
onde: n - porosidade do solo
– A validade da Lei de Darcy
A lei de Darcy á válida para fluxo laminar → no de Reynolds (R) 2000
v - velocidade
D - diâmetro da seção de escoamento
γ - peso específico do fluído
µ - viscosidade do fluído
g - aceleração da gravidade
ÁGUA NOS SOLOS
AiKQ ⋅⋅=
n
v
nA
Q
Av
Q
vp =
⋅
==
iK
A
Q
v ⋅==
g
Dv
R
⋅µ
γ⋅⋅
=
NA
NA
NR
HA
hpA
haA
A
B HB
hpB
haB
∆H
v
A
∆L

13. • Determinação do coeficiente de permeabilidade
– Ensaios de laboratório
A determinação do coeficiente de permeabilidade em laboratório é
realizada principalmente em ensaios com permeâmetros. O valor de K
pode também ser obtido em células triaxiais ou indiretamente em ensaios
oedométricos de adensamento.
• Ensaios em permeâmetro de carga constante
A carga hidráulica é mantida constante durante todo o ensaio.
Empregado principalmente para solos granulares.
Procedimento: Após garantida a constância de vazão, mede-se o volume
d’água (V) que percola pela amostra de comprimento (L) em
intervalos de tempo (t).
Pela Lei de Darcy:
• Ensaios em permeâmetro de carga variável
A carga hidráulica varia durante o ensaio. Usado para solos de baixa
permeabilidade. As vazões de ensaio são pequenas.
Procedimento: Após garantida a constância da vazão, faz-se leituras das
alturas inicial e final na bureta e o tempo decorrente.
Na bureta: Na amostra:
Pela equação da continuidade:
integrando entre hi e hf e entre ti e tf:
ÁGUA NOS SOLOS
A
L
h
KAiKQ ⋅⋅=⋅⋅=
t
V
Q =
thA
LV
K
⋅⋅
⋅
=
dt
dha
dQ
⋅
−= A
L
h
KdQ ⋅⋅=
h
dh
dt
aL
AK
dt
dha
A
L
h
K =⋅
⋅
⋅
⇒
⋅
−=⋅⋅
( )
hf
hi
lnhflnhilntitf
aL
AK
h
dh
dt
aL
AK
hf
hi
tf
ti
=−=−⋅
⋅
⋅
⇒−=⋅
⋅
⋅
∫∫
hf
hi
ln
)titf(A
aL
K ⋅
−⋅
⋅
=

14. – Ensaios de campo
Realizados em poços ou furos de sondagem.
• Ensaio de bombeamento
Ensaio realizado a partir de um poço filtrante e uma série de poços
testemunhos. Empregado principalmente na determinação da
permeabilidade de camadas arenosas e pedregulhosas abaixo do NA,
sujeitas ao rebaixamento do lençol freático.
Hipóteses: massa de solo homogênea e isotrópica e permeabilidade
média em todo o meio.
A partir do momento em que se tem fluxo estacionário (válida a Lei de
Darcy):
Integrando:
• Ensaios de infiltração - ensaio de tubo aberto
Mede-se a velocidade com que a água escoa por um tubo e infiltra no
terreno segundo superfícies esféricas concêntricas. Empregado em
terrenos permeáveis.
Integrando:
Pela eq. da continuidade:
Igualando:
ÁGUA NOS SOLOS
NAinicial
y2
y1
x1
x2
2r
Q NT
x
y
curva de
rebaixamento
dx
dy
yx2
dx
dy
KAiKQ ⋅⋅π⋅⋅⋅=⋅⋅=
dyy
Q
2K
x
dx
⋅⋅
π⋅⋅
=
∫∫ ⋅⋅
π⋅⋅
=
2
1
2
1
y
y
x
x
dyy
Q
2K
x
dx
( )2
1
2
2
1
2
yy
x
x
logQ3,2
K
−⋅π
⋅⋅
=
h
ho
h1
2R
r
r + dr
t=0
t
dh
NA
NT
A
Q
iKv =⋅=
dr
dh
K
r4
Q
2
⋅−=
⋅π⋅
2
r
dr
K4
Q
dh ⋅
⋅π⋅
=−
∫∫
∞
⋅
⋅π⋅
=−
R
2
h
h
r
dr
K4
Q
dh
0
1
R
1
K4
Q
hhh 01 ⋅
⋅π⋅
==−
RhK4Q ⋅⋅⋅π⋅=
dt
dhR
Q
2
⋅⋅π
=
dt
dh
h4
R
K ⋅
⋅
=

15. • Fatores que influenciam o coeficiente permeabilidade
Segundo a Lei de Poisseville para fluxo d’água em tubos circulares de
pequeno diâmetro:
R - raio do tubo
µ - viscosidade do fluído
Para tubos de qualquer forma:
Cs - fator de forma
RH - raio hidráulico
a = seção de passagem
Particularizando para o fluxo através do solo:
A - área da seção transversal
Substituindo:
Pela Lei de Darcy:
Sendo Ds o diâmetro de uma esfera equivalente ao tamanho médio dos
grãos do solo:
Equação de Kozeny-Carman
(válida para areias e pedregulhos)
Equação empírica de Hazen
(válida para areias uniformes) D10 em cm
ÁGUA NOS SOLOS
µ⋅
⋅⋅γ
=
8
iR
v
2
w
ai
RC
Q
2
Hws
⋅⋅
µ
⋅γ
=
⋅
molhadoperímetro
molhadaseçãodaárea
RH =
ASna ⋅⋅=
s
s
s
w
H
A
SVe
A
V
Lp
La
águaacomcontatodeárea
fluxoparadisponívelvolume
R
⋅⋅
==
⋅
⋅
==
( ) AiS
e1
e
A
VC
ASni
A
SVeC
Q 3
3
2
s
2
sws
2
s
sws
⋅⋅⋅
+
⋅⋅
µ
γ⋅
=⋅⋅⋅⋅




 ⋅⋅
⋅
µ
γ⋅
=
AiS
e1
e
A
VC
AiK 3
3
2
s
2
sws
⋅⋅⋅
+
⋅⋅
µ
γ⋅
=⋅⋅
3
3
2
s
2
sws
S
e1
e
A
VC
K ⋅
+
⋅⋅
µ
γ⋅
=
6
D
D
D
6
1
A
V s
2
s
3
s
s
s
=
⋅π
⋅π⋅
=
3
2
s
3
ws
S
36
D
e1
eC
K ⋅⋅
+
⋅
µ
γ⋅
=
2
10D100K ⋅=

16. – Fatores devido ao permeante
• peso específico do fluído;
• viscosidade do fluído;
• temperatura →influencia as duas propriedades anteriores
(principalmente a viscosidade). Convenciona-se tomar
como referência o coeficiente de permeabilidade a 20oC
– Fatores devido ao solo
• granulometria → K ∝ D2
• compacidade → (para areias)
log K ∝ e (para solos argilosos)
• composição
- minerais de argila - caulinitas (1:1) apresentam
permeabilidades 100 x maiores que montmorilonitas (2:1)
• estrutura
- solos argilosos → estrutura floculada determina maior
permeabilidade que a dispersa;
- solos compactados → pelo mesmo efeito, solos
compactados no ramo seco são mais permeáveis que
quando compactados no ramo úmido, mesmo com o
mesmo índice de vazios;
- solos residuais → maiores permeabilidades em virtude
dos macroporos (vazios entre os agregados de partículas)
• anisotropia
O solo geralmente não é isotrópico quanto a
permeabilidade → principalmente solos sedimentares,
solos residuais de rochas sedimentares e metamórficas
xistosas ou bandeadas e solos compactados.
Kh 5, 10 ou 15 x Kv → bastante comum nestes solos.
• grau de saturação
Como a percolação de água não remove todo o ar
existente no solo, bolhas de ar são obstáculos ao fluxo
d’água → K ∝ S3
ÁGUA NOS SOLOS
20
20 KK
µ
µ
⋅=
e1
e
K
3
+
∝

17. • Valores típicos para o coeficiente de permeabilidade
Ordem de grandeza do coeficiente de permeabilidade de solos
sedimentares
K (cm/s)
pedregulhos 10-1
areias grossas 10-1
areias médias 10-2
areias finas 10-3
areias siltosas 10-4
areias argilosas 10-5
siltes 10-4 a 10-5
argilas siltosas 10-5 a 10-7
argilas 10-7
Para pedregulhos e mesmo em algumas areias grossas a velocidade de
fluxo é muito elevada e pode se ter fluxo turbulento → não é mais
válida a Lei de Darcy.
Solos residuais e solos de evolução pedogenética → elevada
permeabilidade devido aos macroporos.
Ex: solo laterítico arenoso fino poroso (SP)
- estado natural → K ≈ 10-3 cm/s
- desagregado e recolocado no mesmo índice de vazios → K ≈ 10-5 cm/s
- compactado → K ≈ de 10-6 a 10-7 cm/s
ÁGUA NOS SOLOS

18. – Percolação d’água através do solos
• Equação diferencial do fluxo d’água nos solos
Seja um elemento de massa de solo submetido a um fluxo d’água.
– Equação da continuidade:
igualando:
ÁGUA NOS SOLOS
dx
dz
dy
x
z
y
vx
vz
vy
vx+ ∂vx/∂x
vz+ ∂vz/∂z
vy+ ∂vy/∂y
dydxvdzdxvdzdyvQ zyx)entra( ⋅⋅+⋅⋅+⋅⋅=
dydxdz
z
v
vdzdxdy
y
v
vdzdydx
x
v
vQ
z
z
y
y
x
x)sai( ⋅⋅





⋅
∂
∂
++⋅⋅





⋅
∂
∂
++⋅⋅





⋅
∂
∂
+=
dydxdz
z
v
dzdxdy
y
v
dzdydx
x
v
Q
zyx
⋅⋅⋅
∂
∂
+⋅⋅⋅
∂
∂
+⋅⋅⋅
∂
∂
=∆
)entra()sai( QQQ −=∆
t
V
Q
w
∂
∂
=∆
sw VSeV ⋅⋅=
te
s cV =
( )






∂
∂
⋅+
∂
∂
⋅⋅
+
=





∂
∂
⋅+
∂
∂
⋅⋅=
∂
⋅∂
⋅=
∂
∂
t
e
S
t
S
e
e1
V
t
e
S
t
S
eV
t
eS
V
t
V
ss
w






∂
∂
⋅+
∂
∂
⋅⋅
+
⋅⋅
=
∂
∂
=∆
t
e
S
t
S
e
e1
dzdydx
t
V
Q
w






∂
∂
⋅+
∂
∂
⋅⋅
+
=





∂
∂
+
∂
∂
+
∂
∂
t
e
S
t
S
e
e1
1
z
v
y
v
x
v zyx
(1)

19. – Lei de Darcy
derivando a velocidade
substituindo (2) em (1)
– Considerações sobre o fluxo
• Fluxo estacionário (regime permanente)
Q(entra) = Q(sai) ⇒ e e S → constantes
Se o meio é isotrópico:
Kx = Ky = Kz = K
• Fluxo transiente Q(entra) ≠ Q(sai)
e = constante S variável ⇒ S↑ - embebição
S↓ - drenagem
S = constante e variável ⇒ e ↑ - expansão
e ↓ - adensamento
e e S variáveis ⇒ equação mais genérica (solução mais complexa)
ÁGUA NOS SOLOS
x
H
KiKv xxx
∂
∂
⋅=⋅=
y
H
KiKv yyy
∂
∂
⋅=⋅=
z
H
KiKv zzz
∂
∂
⋅=⋅=
2
2
z
z
z
H
K
z
v
∂
∂
⋅=
∂
∂
2
2
x
x
x
H
K
x
v
∂
∂
⋅=
∂
∂
2
2
y
y
y
H
K
y
v
∂
∂
⋅=
∂
∂
2
2
z
2
2
y
2
2
x
zyx
z
H
K
y
H
K
x
H
K
z
v
y
v
x
v
∂
∂
⋅+
∂
∂
⋅+
∂
∂
⋅=
∂
∂
+
∂
∂
+
∂
∂
(2)






∂
∂
⋅+
∂
∂
⋅⋅
+
=
∂
∂
⋅+
∂
∂
⋅+
∂
∂
⋅
t
e
S
t
S
e
e1
1
z
H
K
y
H
K
x
H
K 2
2
z
2
2
y
2
2
x
Equação geral do fluxo d’água nos solos
0
t
e
=
∂
∂
0
t
S
=
∂
∂
0
z
H
K
y
H
K
x
H
K 2
2
z
2
2
y
2
2
x =
∂
∂
⋅+
∂
∂
⋅+
∂
∂
⋅
Equação do fluxo d’água estacionário nos solos
0
z
H
y
H
x
H
2
2
2
2
2
2
=
∂
∂
+
∂
∂
+
∂
∂
Equação do fluxo d’água estacionário em solos isotrópicos

20. • Fluxo bidimensional estacionário
A partir da situação mais genérica, se o fluxo ao longo de uma das
direções pode ser desconsiderado, a análise passa a ser
bidimensional. Em relação ao fluxo unidirecional, o escoamento se dá
ao longo de uma trajetória curva.
É regido pela seguinte equação:
– Métodos de solução
• Método analítico
Solução analítica da equação diferencial. Simples apenas
quando particularizada para fluxo unidirecional. Ex:
Equação do fluxo estacionário:
Solução:
onde C e D são constantes
Condições de contorno:
z = 0 → H = 150 e z = 50 → H = 100
Substituindo na solução tem-se:
D = 150 e C = -1
Logo:
• Método gráfico
A solução analítica da Equação de Laplace → duas famílias
de curvas ortogonais entre si → rede de fluxo.
LINHAS DE FLUXO → curvas na direção do fluxo
LINHAS EQUIPOTENCIAIS → curvas de igual carga total
• Métodos numéricos
Diferenças Finitas (MDF) e Elementos Finitos (MEF)
• Métodos analógicos
Analogias → fluxo viscoso, fluxo elétrico e fluxo de calor
• Modelos reduzidos
ÁGUA NOS SOLOS
Equação do fluxo d’água estacionário
bidimensional em solos isotrópicos -
Equação de Laplace
0
y
H
x
H
2
2
2
2
=
∂
∂
+
∂
∂
z
150
100
50
0
NA 0
z
H
2
2
=
∂
∂
DzCH +⋅=
z150H −=

21. – Rede de fluxo
Um dos métodos mais tradicionais na resolução de problemas de
fluxo bidimensional → traçado da REDE DE FLUXO ⇒
representação gráfica da solução para a equação diferencial
do fluxo d’água bidimensional estacionário dos solos.
Seja um fluxo bidimensional através de uma camada de solo
A família de curvas na direção do fluxo → LINHAS DE FLUXO
A família de curvas que une pontos de mesma carga hidráulica →
LINHAS EQUIPOTENCIAS
O canal formado por duas linhas de fluxo adjacentes → CANAL DE FLUXO
A diferença de carga entre duas equipotenciais → ∆Hi. A perda de carga ao
longo de L é ∆H = Σ ∆Hi
ÁGUA NOS SOLOS
FLUXO
LINHAS DE FLUXO
LINHAS EQUIPOTENCIAIS
NR
L
zA
hpA
zB=zC
hpB
∆HAB
hpC
zC’
hpC’
∆HBC
A
B C
C’
CANAIS DE
FLUXO

22. Dado um elemento da rede de fluxo:
A área da seção do canal de fluxo
(considerando largura unitária):
A área total:
onde nf = no de canais de fluxo
O comprimento L pode ser representado por:
onde nd = no de quedas de potencial
A vazão é dada por:
Se a rede de fluxo for traçada com malha quadrada (a = b):
• Passos na obtenção da rede de fluxo
(Método gráfico de Forchheimer)
a) Definir as fronteiras do fluxo (condições de contorno);
b) Traçar certo número de linhas de fluxo;
c) Traçar equipotenciais formando elementos retangulares na relação a/b, em
número compatível com o número de linhas de fluxo e interceptando estas
a 90o. Preferencialmente busca-se malha quadrada (a/b = 1).
• Recomendações úteis no traçado das rede de fluxo
- Usar poucos canais de fluxo, mantendo seções quadradas (em geral 4 a 6
canais de fluxo são suficientes);
- Verificar sempre a ortogonalidade entre as curvas e a constância na relação
de lados;
- A rede deve ser analisada por inteiro. Não se deve deter em pequenos
detalhes enquanto a rede não está refinada;
- Usar propriedades de simetria quando possível;
- As transições entre trechos retilíneos e curvos devem ser suaves.
ÁGUA NOS SOLOS
a
b
1aA ⋅=
AnA ftotal ⋅=
bnL d ⋅=
1-iaisequipotencdenn o
d =
1-fluxodelinhasdenn o
f =
A
L
H
KAiKQ ⋅
∆
⋅=⋅⋅=
bn
an
HKan
bn
H
KQ
d
f
f
d ⋅
⋅
⋅∆⋅=⋅⋅
⋅
∆
⋅=
d
f
n
n
HKQ ⋅∆⋅=

23. • Exemplos de redes de fluxo
ÁGUA NOS SOLOS

24. • Exemplos no traçado e interpretação de redes de fluxo
a) Permeâmetro curvo
Linhas de fluxo → face interna do permeâmetro - arco AC ⇒ i = 6/12
face externa do permeâmetro - arco BD ⇒ i = 6/24
as outras linhas de fluxo são círculos concêntricos -
comprimento de arco diferentes ⇒ gradientes diferentes → como
K = constante, pela Lei de Darcy as velocidades variam em cada canal
de fluxo. Como se procura que os canais tenham igual vazão ⇒ as áreas
de fluxo devem ser maiores da face interna a externa.
Linhas equipotenciais → ∆H = 6cm que dissipa linearmente ao longo de cada
linha de fluxo. Escolhida a análise da perda de carga em 12 intervalos de
0,5cm, ao longo da face interna distam 1cm e ao longo da face interna 2cm
→ as linhas euipotenciais são portanto retas convergentes que por
construção interceptam as linhas de fluxo a 90o
Definição da rede de fluxo → Busca-se na construção atender os critérios de
constância na relação de lados da malha (preferencialmente quadrada -
a/b = 1) e ortogonalidade entre LF e LE. Por força de construção
podemos ter canais de fluxo “incompletos” ou com fluxo “excedente”. No
exemplo o canal 6 tem 70% do fluxo pelos outros canais.
Vazão → K = 10-2cm/s; ∆H = 6cm; nf = 5,7; nd = 12
Q = 2,63.10-2 cm3/s/cm
ÁGUA NOS SOLOS
d
f
n
n
HKQ ⋅∆⋅=
K = 1 . 10-2 cm/s

25. b) Percolação sob pranchada (cortina de estacas-prancha) penetrante numa
camada de areia sendo o NA num dos lados rebaixado por bombeamento -
Análise
Linhas de fluxo → o contorno da pranchada e a superfície inferior impermeável
são linhas de fluxo definidas pela geometria do problema. Entre estas são
traçadas outras linhas de fluxo. A espessuras dos canais de fluxo variam
ao longo da distância → a seção de passagem da água sob a pranchada é
bem menor que a seção de entrada no terreno → como a vazão mantém-
se constante, a velocidade varia ao longo de um mesmo canal de fluxo.
Linhas equipotenciais → pela Lei de Darcy, se v varia e K = constante, o
gradiente i varia → como a perda de carga entre cada LE é constante, logo
varia a distância entre cada equipotencial. As superfícies livres do terreno
são equipotencias definidas pela geometria do problema.
Definição da rede de fluxo → As duas condições básicas das redes de fluxo
devem ser mantidas: as LF e as LE se interceptam perpendicularmente e,
em cada elemento da rede, a relação entre a distância média entre as LE e
a distância média entre as LF deve ser constante.
ÁGUA NOS SOLOS

26. c) Percolação pelo solo de fundação de uma barragem de concreto - Análise e
cálculos
Linhas de fluxo → o contorno submerso da barragem e a superfície inferior
impermeável são linhas de fluxo. Entre estas são traçadas outras LF.
Linhas equipotenciais → As superfícies livres do terreno são equipotencias.
Entre estas são traçadas outras LE.
Definição da rede de fluxo → As duas condições básicas das redes de fluxo
devem ser atendidas: as LF e as LE se interceptam perpendicularmente e,
em cada elemento da rede, a relação entre a distância média entre as LE e
a distância média entre as LF deve ser constante (de preferência igual a 1)
Vazão → K = 10-4 m/s; ∆H = 15,4m; nf = 5 e nd = 14
Q = 5,5.10-4 m3/s/m de barragem
Gradientes → a diferença de carga entre LE consecutivas (∆Hi )
∆∆∆∆Hi = 15,4/14 = 1,1m
O valor de ∆Hi dividido pela distância entre LE é o gradiente no elemento
da rede (ii ) No ponto A - lA= 6m ⇒ iA = 1,1/6 = 0,18
O gradiente é maior nos menores elementos (próximos a superfície da
barragem). Deve ser verificada a condição de gradiente crítico junto ao pé
de jusante (fluxo ascendente sob gradiente mais elevado).
Cargas e pressões → estabelecido um NR, para cada ponto temos a carga
altimétrica e a carga total (descontando da carga inicial o somatório de ∆Hi
até o ponto). A carga piezométrica é a diferença entre cargas total e
altimétrica. A pressão neutra é carga piezométrica em termos
de pressão: Ponto A: zA = 35m; HÁ = 55,4 - (8 . 1,1) = 48,8m;
hpA = 48,8 - 35 = 13,8m uA = 13,8 . 10 = 138 kPa
ÁGUA NOS SOLOS
d
f
n
n
HKQ ⋅∆⋅=
d
i
n
H
H
∆
=∆
i
i
i
l
H
i
∆
=
zHhp −=
wphu γ⋅=
K = 10-4 m/s
NR

27. d) Percolação pelo interior de barragens de terra - Análise
Neste caso tem-se uma condição de contorno indefinida → a linha de fluxo
superior não é previamente conhecida. O problema é indeterminado.
O primeiro passo é a estimativa da linha de fluxo superior - LFS (ou também
chamada linha freática superior). Existem na literatura vários métodos para
esta estimativa → função principalmente da geometria do talude de jusante
e da presença ou não de filtros.
Na análise deste caso consideram-se válidas as hipóteses de Dupuit:
- Para pequenas inclinações da LFS as linhas de fluxo podem ser
consideradas horizontais e as equipotenciais verticais;
- O gradiente hidráulico é a inclinação da LFS no ponto considerado.
O traçado do restante da rede de fluxo e os cálculos decorrentes seguem os
mesmos procedimentos e recomendações dos casos anteriores.
ÁGUA NOS SOLOS

28. Determinação da linha de fluxo superior (LFS) - soluções gráficas
d.1) Solução de Schaffernak e Van Iterson (β 30o)
- Ínicio da LFS → ponto M situado no NA a montante e distante 0,3 . m do
ponto 2. “m” é a projeção horizontal da superfície submersa do talude de
montante (linha equipotencial de entrada);
- Final da LFS → ponto 4 situado no talude de jusante (linha de saída não
submersa) a uma distância “a” do ponto 3.
onde:
d : distância da projeção horizontal de
M até 3;
H : altura d’água a montante
- Traçado da LFS → parábola de equação:
traçada de jusante a montante.
- Correção de entrada → a LFS tem entrada no ponto 2 e deve ser
perpendicular a linha equipotencial de entrada (1 2). O ajuste a parábola é
feito a mão livre.
- Esboço da solução:
- Vazão →
ÁGUA NOS SOLOS
β
−
β
−
β
= 2
2
2
2
sen
H
cos
d
cos
d
a
d
cos
sen
a2Hx
cos
sen
a2y
2
2
2
2
⋅
β
β
⋅⋅−+⋅
β
β
⋅⋅=
β⋅β⋅⋅= tansenaKQ

29. d.2) Solução de Casagrande (hipótese i = dy/ds = sen β) (30o β 60o)
- Ínicio da LFS → idem solução anterior;
- Final da LFS → ponto 4 situado na linha de saída não submersa a uma
distância a do ponto 3.
onde:
- Traçado da LFS → parábola de equação:
onde: s → comprimento da LFS
desde o ponto 4
- Correção de entrada → idem a anterior
- Esboço da solução
- Vazão →
ÁGUA NOS SOLOS
β
−−= 2
2
2
00
sen
H
ssa 22
0 Hds +=
( )sssena2Hy 0
222
−⋅β⋅⋅−=
β⋅⋅= 2
senaKQ

30. d.3) Solução de Casagrande (hipótese de Kozeny) (60o β 180o)
- Ínicio da LFS → idem solução anterior;
- Final da LFS → ponto 0 situado a uma distância “a0” do ponto F. Ponto Fé
o foco da parábola ⇒ coincide com o início dos drenos ou pé a jusante.
- Traçado da LFS → a parábola passa por 0 e M, com foco em F.
Método prático: a) vertical por 0 e horizontal por P; b) divide-se MP e PO
em n trechos iguais; c) une-se 0 aos pontos de divisão de MP e traçam-se
horizontais dos pontos de divisão de PO. As intersecções determinam os
pontos da parábola.
- Correção de entrada → idem a anterior
- Correção de saída → saída a uma distância “a” do ponto F.
onde: k = f(β)
a’ - distância entre F e a
intersecção da parábola
com a linha de saída
- Esboço da solução
ÁGUA NOS SOLOS
( )dHd
2
1
a 22
0 −+⋅=
'ak'aa ⋅−=

31. d.4) Solução de Kozeny (hipótese de Kozeny - parábolas confocais) (β = 180o)
- Ínicio da LFS → idem solução anterior;
- Final da LFS → ponto 0 situado a uma distância “a0” do início do dreno -
o foco da parábola
- Traçado da LFS → a parábola passa por 0 e M, com foco em F e também
pelo ponto situado a uma altura “y0” do início do dreno.
O traçado segue o método prático apresentado na solução anterior.
- Correção de entrada → idem a anterior
- Esboço da solução
- Vazão →
ÁGUA NOS SOLOS
( )dHd
2
1
a 22
0 −+⋅=
00 a2y ⋅=
0aK2Q ⋅⋅=

32. d.5) Condições de entrada e saída da LFS
ENTRADA:
SAÍDA :
ÁGUA NOS SOLOS
NA
α 90o
NA
α = 90o
NA
α 90o
NA
β 90o
NA
β = 90o
NA
β 90o

33. – Percolação em meios anisotrópicos - condição anisotrópica de
permeabilidade
Com freqüência o coeficiente de permeabilidade não é igual em todas as
direções → solos compactados (Kh Kv) , solos residuais de rochas
sedimentares e metamórficas (K é maior na direção da estratificação,
xistosidade ou bandeamento) e solos sedimentares.
Em geral: Kh Kv
Neste caso a equação para o fluxo d’água bidimensional estacionário nos
solos fica:
A equação do fluxo deixa de ser expressa por uma equação de Laplace. Como
resultado, na solução gráfica as linhas de fluxo deixam de ser
perpendiculares às equipotenciais:
• Artifício para solução:
Realizar uma transformação de coordenadas de forma a ter como equação
novamente um Laplaciano:
onde:
Feita a transformação de coordenadas, traça-se a rede de fluxo como em meio
isotrópico, utilizando para cálculo da vazão um coeficiente de
permeabilidade equivalente (Keq):
A vazão é dada por:
ÁGUA NOS SOLOS
0
z
H
x
H
2
2
2
T
2
=
∂
∂
+
∂
∂
0
z
H
K
x
H
K 2
2
z
2
2
x =
∂
∂
⋅+
∂
∂
⋅
x
z
T
K
K
xx ⋅=
zxeq KKK ⋅=
H
n
n
KQ
d
f
eq ∆⋅⋅=

34. • Exemplo de rede de fluxo com condição de anisotropia e
aplicação do artifício de transformação de coordenadas
• Observações:
- A transformação de coordenadas consiste, em geral, numa redução nas
distâncias horizontais, pois na maioria dos casos a permeabilidade
horizontal é menor que a vertical (Kh Kv);
- Para o cálculo do gradientes hidráulicos deve se considerar as distâncias
segundo a configuração original. Logo, após traçada a rede de fluxo na
seção transformada, se deve representa-la na seção natural, voltando ao
sistema de coordenadas original.
ÁGUA NOS SOLOS

35. – Percolação através de meios estratificados
É comum a análise de situações de fluxo ao longo de meios estratificados,
como depósitos de solos sedimentares. É conveniente transformar o perfil
estratificado em uma massa de solo homogênea equivalente com uma
espessura L e coeficiente de permeabilidade equivalente Keq.
Analogia → circuito elétrico ⇒ as camadas de solo correspondem a resistores
em série ou em paralelo.
• Fluxo vertical (perpendicular às camadas) resist. em série
As perdas de carga em cada camada:
Por outro lado:
onde:
∆H = Σ ∆Hi e L = Σ ∆li
Logo:
• Fluxo horizontal (paralelo às camadas) resist. em paralelo
Logo:
ÁGUA NOS SOLOS
∆l1
∆l3
∆l2
∆l4
L
m
1
Qv
Qh
∆H1
∆H2
∆H3
∆H4
K1
K2
K3
K4
A
l
H
KA
l
H
KA
l
H
KA
l
H
KAiKQ
4
4
4
3
3
3
2
2
2
1
1
1veqv ⋅
∆
∆
⋅=⋅
∆
∆
⋅=⋅
∆
∆
⋅=⋅
∆
∆
⋅=⋅⋅=
AK
l
QH
AK
l
QH
4
4
v4
1
1
v1
⋅
∆
⋅=∆⋅⋅⋅
⋅
∆
⋅=∆
A
L
H
KQ veqv ⋅
∆
⋅=
AH
LQ
K
v
veq
⋅∆
⋅
=
4
4
3
3
2
2
1
1
veq
K
l
K
l
K
l
K
l
L
K
∆
+
∆
+
∆
+
∆
=
)1l(iKAiKQ iiheqh ⋅∆⋅⋅∑=⋅⋅=
m
H
i
∆
=
44332211heq lKlKlKlK(
L
1
K ∆⋅+∆⋅+∆⋅+∆⋅⋅=

36. – Percolação através da fronteira de solos com permeabilidades
diferentes - aspectos referentes a construção da rede de fluxo
Quando o fluxo atravessa a fronteira entre dois solos de permeabilidade
diferentes (K1 ≠ K2) as linhas de fluxo sofrem refração. Valendo-se das
premissas básicas da percolação: continuidade da vazão e perda de carga
constante entre equipotenciais pode-se avaliar a refração do canal de fluxo
e a conseqüente mudança na conformação da rede.
A vazão:
De onde:
Pela relação entre lados e ângulos:
Logo:
De onde:
ÁGUA NOS SOLOS
a
a
K1
K1
c
b
β
α
Q
Q
A
B
1c
b
H
K1a
a
H
KQ 21 ⋅⋅
∆
⋅=⋅⋅
∆
⋅=
b
c
K
K
2
1
=
β
=
αβ
=
α cos
c
cos
a
e
sen
c
sen
a
β
α
⋅=
β
α
⋅=
cos
cos
bae
sen
sen
ca
β
α
⋅=
β
α
⋅
cos
cos
b
sen
sen
c
2
1
K
K
b
c
tan
tan
==
α
β

37. • Filtros de proteção
– Emprego
Filtros de proteção são empregados em obras hidráulicas de terra onde
se deseja reduzir o gradiente hidráulico com o uso de um material
que ofereça menor perda de carga (mais permeável).
A redução no gradiente é necessária para se evitar o fenômeno de
areia movediça em circunstâncias de fluxo ascendente e para reduzir
as forças de percolação responsáveis pelo arraste de partículas e
capazes de gerar processos de erosão interna (“piping’).
erosão interna → as forças de percolação superam a força de ligação
entre as partículas, deslocando os grãos através do maciço de solo.
O fenômeno é progressivo iniciando com o carreamento de finos e
chegando a formação de canais internos de grande diâmetro.
Materiais grosseiros (areias grossas e pedregulhos) determinam menor
perda de carga, entretanto tem vazios muito abertos que não
oferecem barreira física a erosão interna → devem ser seguidos
critérios de seleção granulométrica dos materiais.
Na prática os filtros são construídos em camadas de granulometria
crescente.
Filtros de proteção são empregados principalmente em zonas de
percolação onde há transição de materiais muito diferentes (p.ex.
argila compactada e enrocamento).
– Condições para material de filtro
a) Deve ser suficientemente fino para evitar a passagem das partículas do
solo adjacente pelos seus vazios e
b) Deve ser suficientemente grosso de modo a reduzir a perda de carga.
Terzaghi propôs critérios para projetos de filtro ainda hoje muito aceitos:
1. D15 (filtro) 4 a 5 x D85 (solo) → para evitar a erosão interna
2. D15 (filtro) 4 a 5 x D15 (solo) → para garantir menor perda de carga
Outra recomendação devido ao U.S. Corps of Engineers para garantir
redução de perda de carga:
D50 (filtro) 25 x D50 (solo)
ÁGUA NOS SOLOS

38. – Critério de seleção de material para filtro (Terzaghi)
ÁGUA NOS SOLOS