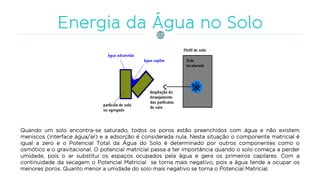
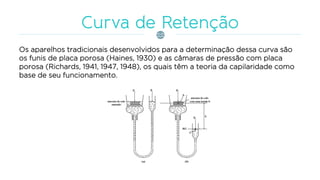
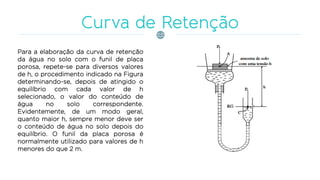
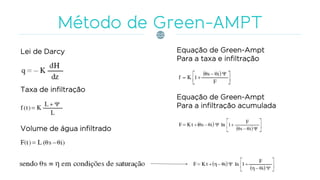
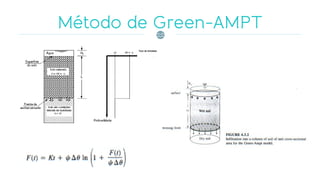
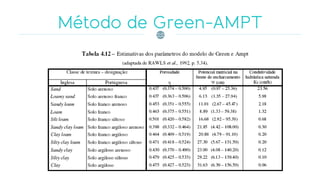
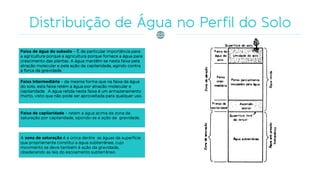
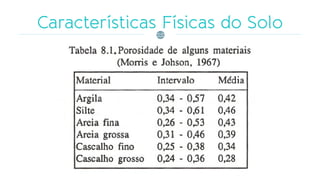
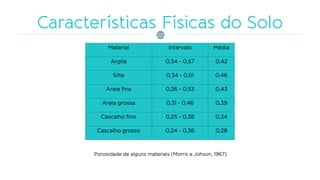
O documento discute os processos de infiltração e escoamento de água no solo, definindo termos como capacidade de infiltração, zona de saturação e não saturação. Apresenta equações empíricas e físicas para modelar a infiltração e fatores que a afetam, como tipo de solo, umidade, vegetação e compactação.

2.  Contexto na disciplina;
 Ocorrência da água na superfície e características do solo;
 Definição de infiltração e fatores que condicionam o processo;
 Medições: infiltração e umidade do solo;
 Fundamentos do escoamento subterrâneo: solo saturado e não saturado;
 Equações de infiltração: empíricas e físicas;
 Abstrações hidrológicas.

4. Escoamento Subsuperficial
Escoamento Subterrâneo
- Escoamento de Base
Aquíferos
- Não confinado -- Freático
- Confinado -- Artesiano

5. A camada superior onde os poros
estão parcialmente cheios d’água
é designada zona de aeração.
Imediatamente abaixo onde os
interstícios estão repletos d’água,
esta é a zona de saturação.

6. Faixa de água do subsolo – É de particular importância para
a agricultura porque a agricultura porque fornece a água para
crescimento das plantas. A água mantêm-se nesta faixa pela
atração molecular e pela ação da capilaridade, agindo contra
a força da gravidade.
Faixa intermediária – da mesma forma que na faixa de água
do solo, esta faixa retém a água por atração molecular e
capilaridade. A água retida nesta faixa é um armazenamento
morto, visto que não pode ser aproveitada para qualquer uso.
Faixa intermediária – da mesma forma que na faixa de água
do solo, esta faixa retém a água por atração molecular e
capilaridade. A água retida nesta faixa é um armazenamento
morto, visto que não pode ser aproveitada para qualquer uso.
Faixa de água do subsolo – É de particular importância para
a agricultura porque a agricultura porque fornece a água para
crescimento das plantas. A água mantêm-se nesta faixa pela
atração molecular e pela ação da capilaridade, agindo contra
a força da gravidade.
Faixa de capilaridade – retém a água acima da zona de
saturação por capilaridade, opondo-se a ação da gravidade.
A zona de saturação é a única dentre as águas da superfície
que propriamente constitui a água subterrânea, cujo
movimento se deve também à ação da gravidade,
obedecendo as leis do escoamento subterrâneo.

7. Densidade atual:
Densidade das partículas:
Densidade do solo (indicador do grau de
compactação do solo):
Porosidade - N (adimensional):
Ou ainda:
Volume dos poros:
Volume total:
Massa total do solo:
Onde os subescritos correspondem às fases gasosa, líquida e
sólida (massa do solo seco em estufa, 105 a 110ºC)

9. Material Intervalo Média
Argila 0,34 - 0,57 0,42
Silte 0,34 - 0,61 0,46
Areia fina 0,26 - 0,53 0,43
Areia grossa 0,31 - 0,46 0,39
Cascalho fino 0,25 - 0,38 0,34
Cascalho grosso 0,24 - 0,36 0,28
Porosidade de alguns materiais (Morris e Johson, 1967)

10. Teor da água no solo com base em massa (adimensional - %):
Teor de água no solo com base em volume (adimensional - %):
Obs: quando o solo está saturado, temos que
Conteúdo de água no solo (lâmina d'água) (são dados em 'mm' e L em 'm'):
Obs: representa a profundidade efetiva do sistema radicular.

11. Triângulo Textural da USDAClassificação dos Solos ABNT
Classificação Diâmetro dos grãos
Argila menor que 0,002 mm
Silte entre 0,06 e 0,002 mm
Areia entre 2,0 e 0,06 mm
Pedregulho entre 60,0 e 2,0 mm

13.  Infiltração é o processo hidrológico que trata da penetração da água no solo;
 Taxa de infiltração (f) é o volume infiltrado por unidade de tempo;
 Infiltração acumulada (F) é o volume total infiltrado em determinado espaço
de tempo.
Infiltração acumulada Taxa acumulada

14.  É a taxa máxima que um solo é capaz de absorver água, sob uma dada
condição. Geralmente é expressa em mm/h.
 A intensidade da chuva (i) afeta a quantidade de água que se infiltra no solo e
a que escoa superficialmente. Se a taxa real de infiltração é fa, então a
capacidade de infiltração fp representa o máximo valor de fa:
fa  fp
e, como i > fp  fa = i
i  fp  fa = fp

15.  Tipo de solo – A capacidade de infiltração varia diretamente com a porosidade
e com o tamanho das partículas do solo.
 Umidade do solo – Quando a água é aplicada em um solo seco, não há
movimento descendente dessa água até que as partículas do solo estejam
envolvidas por uma fina película d’água. As forças de atração molecular e
capilar fazem com que a capacidade de infiltração (fp) inicial de um solo seco
seja muito alta.

16.  Vegetação – Uma cobertura vegetal densa como grama ou floresta tende a
promover maiores valores de fp, devido ao sistema radicular que proporciona
a formação de pequenos túneis e que retira umidade do solo através da
transpiração, e à cobertura vegetal que previne a compactação do solo.
Capacidade de infiltração para um mesmo solo com:
cobertura vegetal e solo nu.
(Fonte: RAUDIKIVI, 1979).

17.  Compactação – solos nus podem se tornar parcialmente impermeáveis pela
ação compactadora das grandes gotas de chuva (que também preenchem os
vazios do solo com material fino), e pela ação do tráfego constante de
homens, veículos ou animais.
 Altura da retenção superficial e espessura da camada saturada – a água
penetra no solo sob a ação da gravidade, escoando nos canalículos formados
pelos interstícios das partículas.

19. Os infiltrômetros são aparelhos para determinação direta da capacidade de
infiltração do solo. Consistem de tubos ou qualquer outro limite projetado para
isolar uma seção do solo.

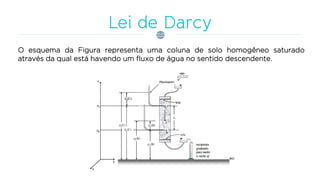
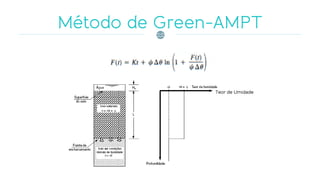
21. Se for desenvolvido um experimento com o arranjo experimental da Figura
para diferentes valores de:
L (comprimento de solo entre os pontos C e B),
A (área da secção transversal da coluna)
Diferença de potencial total t(C) - t(B), em que t(C) é o potencial total no ponto de
cima e t(B) é o potencial total no ponto de baixo,
obtém-se as seguintes conclusões:
1a. A vazão Q, isto é, o volume de água que atravessa a coluna por unidade de tempo é
proporcional a A, isto é, em símbolos:
Q α A.
2a. A vazão Q é proporcional à diferença de potencial total t(C) - t(B) através do solo:
Q α [ (C) - (B)] .
3a. A vazão Q é inversamente proporcional ao comprimento L de solo:
Q α 1/L.

22. O esquema da Figura representa uma coluna de solo homogêneo saturado
através da qual está havendo um fluxo de água no sentido descendente.

23. Para Solos Saturados como no experimento tem-se:
Como a velocidade dos escoamentos são muito pequenas, o termo cinético é
desprezado ficando os termos do potencial piezométrico
g
VP
h
2
2
t 




P
h t

24. Onde K é a condutividade hidráulica
   
L
B-C
AKQ tt
o



25.    
L
B-C
K
A
Q
q tt
oo


O parâmetro pode ser deduzido a partir do escoamento em um feixe de capilares,
Onde é a porosidade do meio (adimensional); é o diâmetro do poro (L); é a
massa específica da água (ML-3
); a aceleração da gravidade (LT-2
); a viscosidade
dinâmica (ML-1
T-1
) e representa a tortuosidade.

26.    
BC
tt
oo
z-z
B-C
Kq


Colocou-se o sinal negativo na equação para que um valor positivo de qo
indique fluxo na direção positiva de z (de zB para zC: para cima) e um valor
negativo de qo indique fluxo na direção negativa de z (de zC para zB: para
baixo).
Refinando um pouco mais o tratamento matemático da lei de Darcy pode-se escrever
sua equação na forma diferencial a partir da equação 08, ou seja
ds
d
Kq t
oo



27. Solos Não Saturados
A equação de Darcy pode ser generaliza modificando-se o potencial de água no
solo.
ds
dψ
Kq t
oo 

28. Solos Não Saturados
Componentes do potencial da água no solo:
Onde os índices indicam o potencial total da água no solo, pressão (1), matricial
(2), osmótico (3) e gravitacional (4), respectivamente.
Obs.: (1) pressão hidrostática provocada pela coluna do líquido e/ou a massa de
ar comprimido; (2) relativo à interação água/matriz solo, ou seja, devido às
forças de adorção e capilaridade; (3) relativo à presença de solutos e (4) estado
de referência.

29. Solos Não Saturados
Unidades (energia por unidade de peso):

30. Solos Não Saturados
Condutividade hidráulida em solos não saturados:
Curva de Retenção

32. Assumindo-se que K e D são constantes independentes do conteúdo de
umidade do solo
onde:
fp é a capacidade de infiltração no tempo t.
fc é a capacidade de infiltração final.
fo é a capacidade de infiltração inicial.
k é uma constante.

33. TI = a(S - I)n+ fc
 Onde:
 m do solo e da sua cobertura;
• S é o armazenamento potencial do solo acima da camada impermeável;
• I é a infiltração acumulada e
• fc é a infiltração na condição de regime estacionário.

34. Infiltração da água no solo -
Equações empíricas:
1. Equação de Kostiakov
Onde I é a infiltração acumulada (mm) e t é o tempo de inilftração (h).
Obs.: Os parâmetros k e a são determinados estatisticamente.

35. Obs.: Embora empírica, este modelo bons resultados se aplicando a períodos de
tempo não extensos
Derivando em relação a t temos a taxa de infiltração:

36. Obs.: TIB é a taxa de infiltração básica. Nesta equação, nota-se que quando
(1) Equação de Kostiakov-Lewis

37. (1) Equação de Richards para movimento vertical
Equações Físicas
Onde é a função capacidade hídrica, obtida da curva característica
do solo; é o potencial matricial da água no solo; z é a distância abaixo
da superfície; t é o tempo e é a função da condutividade hidráulica.

38. (1) Equação de Philip
Onde s é um parâmetro do solo denominado sortividade que indica a
capacidade de um solo homogêneo absorver água, em relação ao seu teor
de água inicial; é a condutividade hidráulica do solo saturado
são parâmetros de ajuste que dependem das propriedades do solo (LT¹) e
t é o tempo.
Obs.: Trata-se de uma solução analítica da equação de Richards, obtida através de algumas simplificações
(profundidade do solo e o teor de água uniforme ao longo do perfil do solo).

39. Como t  , f(t) tende a K.

40. Teor de Umidade

44. • Capacidade de Campo;
• Ponto de Murcha Permanente;
• Disponibilidade Total de Água no Solo.

45. DTA =1,000(θcc-θpm)
Sendo θcc e θpm o teor de água na capacidade de campo (umidade do solo após
drenagem) e no ponto de murcha permanente (teor de água onde a planta fica
impossibilitada de suprir a demanda atmosférica), respectivamente.

47. Problema na quantificação da relação precipitação-vazão.
Runoff = Precipitação Total – “Perdas”
- Tipos de Abstrações (Perdas):
(A) Interceptação;
(B) Aramzenamento em Depressões;
(C) Evaporação;
(D) Transpiração;
(E) Evapotranspiração;
(F) Infiltração (pode não ser uma abstração).

48. SI = Precipitação total – Atravessa a vegetação – escoa pelo tronco
Equação de Horton
r
tot
vegSP
VI t
A
A
EeSS V
 
)1( /
Onde:
SI é a Interceptação
Sv é a capacidade de armazenamento da vegetação
E é a evaporação
Aveg é a área da cobertura vegetal
Atot é a área total
tr é a duração do evento
Equação de Meriam
r
tot
veg
VI t
A
A
ESS 
Introduziu a precipitação (P) na equação de Horton
n
I bPaS 
Equações Empíricas

49. Linsley et al (1949)
 ekP
dd eSV 
 1
Onde
Vd é o volume retido
Sd é a capacidade máxima
Pe é a precipitação efetiva

52. • Método clássico;
• Amostras em vários locais e profundidades do solo;
• Deformadas ou indeformadas.

53. • Constante dielétrica global do solo
• Água em torno de 81 graus;
• 1 para o ar;
• 3-5 para os minerais do solo.
 Guias de onda ou sona:
monitoramento até 1,5m de
profundidade

54. • Vantagens:
• Não apresenta riscos para a saúde;
• Não necessita de calibração para a maioria dos solos;
• É altamente sensível às variações do teor de água no solo;
• Permite a coleta automática dos dados.

55. • Desvantagens:
• Custo relativamente elevado;
• Requer instalação de guias de ondas em trincheira para profundidades
maiores.

56. • Oscilador gera um campo de corrente alternada.
• Detecta mudanças nas propriedades dielétricas do solo.
• Sensores do tipo capacitivo
- Consistem em um par de eletrodos formando um capacitor com o solo.
- Mudanças nos teores de água – mudança de frequência na operação.

57. • Vantagens:
- Permitem maior liberdade de escolha da geometria do eletrodo e frequência
de operação;
- A maioria opera em baixa frequência e pode determinar a água retida nas
partículas finas do solo;
• pode constituir mais que 10% do teor de água no solo.

58. • Desvantagens:
- As leituras são bastante influenciadas pelo teor de água e lacunas de ar
junto aos eletrodos;
• É crucial ter um bom contato sensor-tubo-solo.
- Sistemas que operam a baixa frequência são mais suscetíveis a erro
decorrentes da salinidade do solo;
- Existe menos informação detalhada em comparação ao TDR.

59. Intrumentos dotados de uma fonte de material radioativo
- Amerício e Berilo
 Ao ser excitada , a fonte emite nêutrons rápidos que reduzem sua velocidade
(ou são termalizados) ao chocarem-se com o núcleo de hidrogênio da água;
 Existe uma correlação direta entre o número de nêutrons termalizados e o
teor de água no solo;
 Equação obtida pela calibração da sonda para cada tipo de solo e tubos de
acesso empregados.

60. • Vantagens:
- Um dos melhores instrumentos
• Desvantagens:
- Aplicabilidade limitada
• possível em apenas um ponto do
• perfil do solo.
- Fonte radioativa

62. Relações

63. Note que, quando se expressa potencial (o total ou qualquer componente) em
unidade de energia/volume, verifica-se, imediatamente que esta é idêntica à
unidade de pressão porque, dimensionalmente,
Pascal
m
N
m
Nm
m
J
233


64. Portanto, os valores de todos os potenciais da água no solo, tanto o total como
qualquer um dos seus componentes, podem ser considerados como idênticos
ao valor de uma diferença de pressão, isto é, diferença entre uma pressão cujo
valor é idêntico ao valor de ϵ e uma pressão cujo valor é idêntico ao valor de ϵo.

66. Condutividade Hidráulica em Meio Não Saturado
(1) Gardner (1958):

67. Condutividade Hidráulica em Meio Não Saturado
(2) Genuchten (1980) (modelo estatístico de distribuião dos poros em termos
dos parâmetros da curva de retenção - modelo VG para m=1-1/n);

68. Condutividade Hidráulica em Meio Não Saturado
Em termos de potencial matricial:
Onde é a Saturação Efetiva

69. Curva de retenção (relação funcional entre teor de água no
solo e o potencial matricial):
(1) Modelo VG
Onde é a relação funcional entre teor e água em base volume , e o
potencial matricial é o teor de água do solo na saturação; é o teor
de água residual; é um parâmetro de dimensão igual ao inverso da dimensão
do potencial e n, m, são parâmetros adimensionais

70. (1) Modelo BC
Onde é a pressão de borbulhamento (m) e é o índice de distribuição do
tamanho dos poros (adimensional). A pressão de borbulhamento é definida
como o menor valor de sucção a ser aplicado a um solo saturado para remover
a água 'retida' nos maiores poros.

71. Três formas principais: energia cinética, energia potencial e energia interna.
É importante esclarecer que em todo estudo com quaisquer destas formas de
energia, sempre se trabalha com uma diferença de energia entre duas
situações, uma tomada como referência.
A água no solo será aqui estudada, do ponto de vista energético, segundo um
modelo no qual se considera sempre duas situações com ela em equilíbrio.
• a água no solo propriamente dita, isto é, dentro do solo.
• a mesma água (com a mesma energia interna que a água no solo), mas fora
do solo, denominada água padrão e definida como água livre.

72. Energia potencial A
Energia potencial B
Com EA>EB
Haverá um movimento de A para B
Aqui o nosso corpo será a água no solo mas, nesse caso, é mais conveniente
utilizar a energia potencial total da água por unidade de massa ou volume de
água ou energia potencial total específica da água.

73. A água do solo esta sujeita a um número de forças no campo, as quais causam
a mudança de seu potencial em relação ao estado padrão.
O potencial da água do solo pode ser considerado como a soma das
contribuições separadas destas várias forças:
t = g + p + o + ......
onde:
t  Potencial total da água do solo;
g  Potencial gravitacional;
p  Potencial de Pressão (pressão +) ou Mátrico m (pressão -);
o  Potencial osmótico;
Equação 01

74. Potencial total da água no solo
Considere ϵ como sendo a energia potencial total específica da água num solo e ϵo a
energia potencial total específica da água padrão, a diferença ϵ – ϵo é o potencial total da
água no solo t, isto é,
t =ϵ - ϵo [energia/massa ou volume de água]. (Equação 02)
Considerando, agora, dois pontos A e B no perfil do solo, nos quais,
t(A) =ϵA −ϵo
e
t(B)= ϵB −ϵo
então,
t(A)- t(B)= (ϵA −ϵo)- (ϵB −ϵo)= ϵA −ϵB
Note que obtivemos o valor da diferença ϵA - ϵB por meio da diferença t(A) - t(B), sem a
necessidade de se conhecer individualmente ϵA e ϵB. Desse modo, se num determinado
momento t(A) > t(B), o movimento da água é de A para B porque ϵA >ϵB e se t(B) >
t(A), de B para A porque ϵB >ϵA. Quando t(A) = t(B), tem-se, evidentemente, uma
condição em que não há movimento entre A e B, porque ϵA = ϵB (equilíbrio).

75. Potencial gravitacional da água do solo
A água no solo, estando dentro do campo gravitacional terrestre possui,
evidentemente, esta energia, cuja equação, dado a necessidade de incluir neste
contexto a água padrão anteriormente definida, pode ser escrita como:
ΔE = ma g (r1 - ro)
ma = massa da água no solo;
g = aceleração da gravidade;
r1 = distância do centro da Terra ao ponto considerado no perfil do solo;
ro = distância do centro da Terra a um ponto arbitrário onde se deve imaginar
localizada a superfície plana da água padrão e que será denominada
simplesmente referência gravitacional.
O potencial gravitacional g o qual é dado por
  gZρ
V
rrgm
V
ΔE
ψ a
a
01a
a
g
g 

 Equação 03

76. em que
ρa = ma/Va = densidade da água no solo, considerada constante.
Z é o valor da distância vertical do ponto considerado à posição da referência gravitacional, de,
isto é, Z = r1 − ro.
Sendo que o sinal de Z e, portanto de g dependerá da posição do ponto considerado em
relação à referência gravitacional, isto é, o sinal será positivo se o ponto estiver acima da
referência gravitacional (r1 > ro), negativo se estiver abaixo (r1 < ro) e nulo se for coincidente com
ela (r1 = ro).
Dividindo-se o valor de g, expresso na unidade energia/volume, calculado a partir da equação
03, pela quantidade gρa, obtém-se o valor de g na unidade altura de água ou carga hidráulica:
g = ±Z [altura de água] , (Equação 04)
Portanto, para se obter o valor de g num determinado ponto no solo, precisa-se apenas de uma
régua para medir a distância vertical deste ponto à posição tomada como referência
gravitacional, que a unidade do resultado obtido será em altura de água.

77. Potencial pressão da água do solo
O potencial de pressão é a porção do potencial da água que resulta de um
pressão total diferente da pressão de referência.
A água do solo quando está a uma pressão hidrostática maior do que a
atmosférica, seu potencial de pressão é considerado positivo. Quando sua
pressão hidrostática é menor do que a atmosférica (uma sub pressão,
comumente conhecida como tensão ou sucção) o potencial de pressão é
considerado negativo. Desta forma, a água situada a um nível abaixo da
superfície livre possui potencial de pressão positivo, a água na superfície tem
potencial de pressão igual a zero e a água acima da superfície é caracterizada
por possuir potencial de pressão negativo.

78. Note, então, que a única diferença entre os dois pontos é a pressão de água Pa = ρagh que
atua no ponto da esquerda. Pelo fato de a única diferença entre a água padrão e a água
no ponto considerado ser a pressão de líquido no ponto considerado, tem-se que:
No ponto B, em equilíbrio no recipiente do lado direito desta figura, tem-se água padrão
pois a interface plana, coincidente com a referência gravitacional (RG) onde ele se localiza,
estão atuando a pressão atmosférica (Po) e a pressão interna (P’). Por outro lado, o ponto
A, em equilíbrio no recipiente do lado esquerdo da figura, é diferente do primeiro apenas
por nele atuar também a pressão da altura de água h.
p = ρagh[energia/volume] , (Equação 05)
sendo p = potencial de pressão.
De modo idêntico ao que vimos no caso do
potencial gravitacional, em termos de carga
hidráulica,
p = h [altura de água] .

79. Estas diferenças podem ser melhor observadas através do seguinte esquema:
Os potenciais de pressão da água nos pontos A, B e C são bastante diferentes e podem ser calculados
pela seguinte fórmula, tendo como referência a pressão atmosférica:
p  água . g . h , onde:
h - altura em relação à superfície de água livre (chamada de altura piezomérica);
água - densidade da água;
g - aceleração da gravidade;
p - potencial de pressão.

80. No ponto B, nível de referencia, a pressão da água é igual à pressão
atmosférica, convencionada como sendo igual a zero. Desta forma o potencial
de pressão no ponto B é, de acordo com a formula:
p  água . g . h
tal que
p = 1 g/cm3 . 981cm/s2. 0 = 0

81. No ponto C, na base do reservatório, uma volume de água faz uma pressão positiva
equivalente à profundidade do ponto C. Neste caso, considerando-se uma profundidade
de 30 cm (H1 = 30cm), o potencial de pressão no ponto C será o seguinte:
p  água . g . h
tal que
p = 1 g/cm3 . 981cm/s2. (+30 cm) = 29430 bária
tal que p = 0,029 atm = 30 cm H2O

82. No ponto A, acima do reservatório, o potencial de pressão é menor do que a pressão
atmosférica (referência 0), resultando em um pressão negativa. Assim o potencial de
pressão no ponto A, considerando uma altura igual a 30 cm, será:
p  água . g . h
tal que
p = 1 g/cm3 . 981cm/s2. (-30 cm)  - 29430 bária
tal que p = - 0,029 atm = - 30 cm H2O

84. Potencial mátrico da água do solo
Este potencial de pressão negativo é denominado de Potencial Mátrico e na verdade
refere-se a uma possibilidade de valor de pressão pertencente ao componente potencial de
pressão da água do solo. A diferença entre Potencial de Pressão e Potencial Mátrico do
Solo esta relacionada ao causador da pressão, o potencial mátrico ocorre devido à matrix
coloidal do solo, enquanto que o potencial de pressão é resultado da carga de um
determinado volume de água. Por definição Potencial Mátrico é a porção do potencial da
água do solo atribuível ao efeito da matrix coloidal do solo.
Distinguem-se dois tipos de força mátrica:
a) as forças capilares, responsáveis pela retenção da água nos microporos dos agregados;
b) as forças de adsorção, responsáveis pela retenção da água nas superfícies das partículas
do solo.
No slide seguinte é representado como funciona no solo o efeito do Potencial Mátrico.

85. Quando um solo encontra-se saturado, todos os poros estão preenchidos com água e não existem
meniscos (interface água/ar) e a adsorção é considerada nula. Nesta situação o componente matricial é
igual a zero e o Potencial Total da Água do Solo é determinado por outros componentes como o
osmótico e o gravitacional. O potencial matricial passa a ter importância quando o solo começa a perder
umidade, pois o ar substitui os espaços ocupados pela água e gera os primeiros capilares. Com a
continuidade da secagem o Potencial Matricial se torna mais negativo, pois a água tende a ocupar os
menores poros. Quanto menor a umidade do solo mais negativo se torna o Potencial Matricial.

86. Potencial osmótico da água do solo
O Potencial Osmótico do Solo é a porção do potencial da água que resulta do efeito combinado de todas
espécies de solutos presentes no solo.
A presença de solutos na água do solo afeta sua propriedade termodinâmica e baixa seu potencial
energético. Em particular, solutos diminuem a pressão de vapor da água do solo. Como este fenômeno
pode não afetar o fluxo de massa líquida significativamente, este não é considerado. O potencial osmótico
somente desempenha importante função sobre o fluxo de água do solo quando existe uma membrana
seletiva ou barreira de difusão, a qual transporta água mais rapidamente que do que sais. Por isso o efeito
osmótico é importante na interação entre raízes e solo, bem como em processos envolvendo difusão de
vapor.
Uma forma aproximada de se calcular o Potencial Osmótico é através da equação de van’t Hoff:
o = - RTC, onde:
o  Potencial Osmótico;
R  constante universal dos gases (0,082 atm);
T  temperatura absoluta (K);
C  concentração do soluto em mol/litro.

87. Equação psicométrica
Onde é o potencial matricial-osmótico (kPa); T é a temperatura (K); e é a
pressão de vapor e a pressão de vapor d'água no ar saturado.
Obs.: Muitas vezes não é possível separar os efeitos matricial e osmótico e medi-
los com um único aparelho. O psicrômetro é muito usado na medição do
potencial matricial em solos secos de baixa concentração de solutos, uma vez
que se torna desprezível o efeito osmótico! Na prática, tem sido usado
principalmente em pesquisas, em ambiente controlado.

88. Potencial osmótico
Onde o termo é definido como a condutividade elétrica da solução do solo
logo após a adição de uma quantidade suficiente de água destilada para elevar
o teor de água no solo àquele correspondente à saturação.

90. Como acabamos de ver, o potencial mátrico pode ser avaliado pelo trabalho
que se deve realizar à unidade de volume de água retida num solo não
saturado pelas forças mátricas, para torná-la livre como a água padrão.
Devido à heterogeneidade dos poros dos solos, com formas e tamanhos muito
variáveis de um solo para outro, não é possível se obter uma equação teórica
para o potencial mátrico como no caso dos potenciais gravitacional e de
pressão.

91. Entretanto, como este potencial varia com o conteúdo de água no solo, sendo
tanto menor quanto mais seco estiver o solo, foram desenvolvidos aparelhos
por meio dos quais se pudesse buscar uma correlação entre ele e o conteúdo
de água no solo. A curva resultante dessa correlação recebeu o nome de curva
de retenção da água no solo ou simplesmente curva de retenção.

92. Os aparelhos tradicionais desenvolvidos para a determinação dessa curva são
os funis de placa porosa (Haines, 1930) e as câmaras de pressão com placa
porosa (Richards, 1941, 1947, 1948), os quais têm a teoria da capilaridade como
base de seu funcionamento.

93. Considere-se a amostra de solo (ponto A) e a água padrão (ponto C) da
Figura. Quando para o gotejamento, a amostra de solo torna-se não saturada,
portanto com um determinado m. Como no equilíbrio,
t(A)= t(C) e, pela Figura ao lado,
t(A)= m(A)+ g(A)= m+h
t(C)= m(C)+ g(C)=0+0, então, m= -h

94. Para a elaboração da curva de retenção
da água no solo com o funil de placa
porosa, repete-se para diversos valores
de h, o procedimento indicado na Figura
determinando-se, depois de atingido o
equilíbrio com cada valor de h
selecionado, o valor do conteúdo de
água no solo correspondente.
Evidentemente, de um modo geral,
quanto maior h, sempre menor deve ser
o conteúdo de água no solo depois do
equilíbrio. O funil da placa porosa é
normalmente utilizado para valores de h
menores do que 2 m.

97. Velocidade de Darcy
dt
dh
.Kv 
Altura de sucção .
Permeabilidade (K)
D é a difusão
Lei de Darcy

100. Lei de Darcy
Taxa de infiltração
Volume de água infiltrado
Equação de Green-Ampt
Para a taxa e infiltração
Equação de Green-Ampt
Para a infiltração acumulada

101. Teor de Umidade