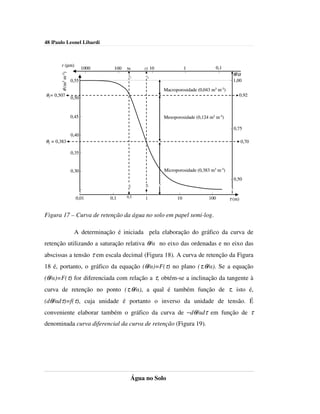
1) O documento descreve os aspectos básicos da retenção da água no solo, incluindo a teoria da capilaridade e o potencial mátrico. Ele também define índices para quantificar a água no solo e discute a energia da água e os modelos de fluxo de água no solo. 2) A retenção da água no solo ocorre através da capilaridade nos poros do solo e da adsorção nas superfícies dos sólidos do solo. 3) A tensão superficial causa a capilaridade, levando a água a

1. ÁGUA NO SOLO
Paulo Leonel Libardi
Descreve-se inicialmente os aspectos básicos da retenção da água no
solo, notadamente a teoria da capilaridade, visando principalmente a conceituação
do potencial mátrico e da curva de retenção da água no solo. Índices para
quantificar a água no solo, em especial a armazenagem da água, são definidos em
seguida. A energia da água, bem como o modelo dos potenciais e, então, as
equações de fluxo da água no solo, são tratados com certo detalhe. O texto termina
com uma discussão resumida a respeito do balanço de água no solo.
1 RETENÇÃO DA ÁGUA NO SOLO
Nesse estudo, o solo será considerado simplesmente como um
conjunto de partículas sólidas de diversas formas e tamanhos, entremeadas por
poros, também de diversas formas e tamanhos, e interconectados. Pode-se dizer,
portanto, que o solo é composto, basicamente, de duas partes: uma sólida, também
chamada de sólidos do solo ou matriz do solo e a parte não ocupada pelos sólidos,
denominada espaço poroso ou poros do solo.
Normalmente o espaço poroso do solo no campo é ocupado por
quantidades variáveis de uma solução aquosa denominada água no solo e de uma
solução gasosa denominada ar no solo; o solo nesta situação é dito estar não
saturado. Quando o espaço poroso do solo estiver totalmente cheio de água, o solo
é dito estar saturado.

2. 2 |Paulo Leonel Libardi
Dois são os processos que explicam a retenção da água num solo não-
saturado. No primeiro deles, a retenção ocorre nos chamados poros capilares do
solo e pode ser ilustrada, por isso, pelo fenômeno da capilaridade, o qual está
sempre associado a uma interface curva água-ar. No segundo processo, a retenção
ocorre nas superfícies dos sólidos do solo como filmes presos a ela, pelo fenômeno
da adsorção.
Desses dois fenômenos, o mais relevante é o da capilaridade daí ser
devotado a ele um item especial, a seguir, sob o título tensão superficial e
capilaridade.
Com relação ao processo de adsorção da água sobre as superfícies
sólidas, três são os mecanismos principais propostos para explicá-lo, a saber:
1. A superfície dos minerais de argila é coberta com átomos de oxigênio e grupos
oxidrilas negativamente carregados devido à substituição isomorfa de cátions.
Desse modo, cria-se ao redor das partículas desses minerais um campo elétrico
cuja intensidade decresce com a distância da superfície da partícula. Devido à
natureza dipolar das moléculas de água, elas se orientam neste campo elétrico e
experimentam uma força na direção da superfície da partícula, a qual decresce
gradualmente com a distância desta superfície até se tornar nula num ponto em
que não há mais influência do campo.
2. Os pares de elétrons não compartilhados do átomo de oxigênio das moléculas
de água podem ser eletricamente atraídos a cátions trocáveis que podem estar
adsorvidos sobre a superfície da argila, ou seja, os cátions que são retidos à
superfície negativamente carregada de argila (a concentração iônica é crescente
Água no Solo

3. Paulo Leonel Libardi| 3
na direção da superfície sólida) ocasionam também a adsorção das moléculas de
água.
3. Finalmente, as moléculas de água podem ainda ser atraídas às superfícies
sólidas pelas forças de London-van der Waals, que são forças de curto alcance e
decrescem rapidamente com a distância da superfície, de modo que uma
camada muito fina é adsorvida dessa maneira ao redor das partículas de solo.
É importante reforçar que essa película de água adsorvida às
superfícies dos sólidos do solo possui, como resultado destas forças de adsorção,
uma energia potencial extra, uma vez que, se afastarmos uma determinada porção
dessa película a uma distância dentro do raio de ação destas forças e a
abandonarmos, ela volta à posição original realizando um trabalho.
1.1 Tensão superficial e capilaridade
Ao se colocar uma das extremidades de um tubo capilar de vidro
dentro de um recipiente com água, observa-se que a água sobe no tubo e entra em
repouso a uma determinada altura acima da superfície da água no recipiente. Se
em vez de água for utilizado mercúrio, observa-se que o nível de mercúrio dentro
do tubo capilar se estabiliza a uma distância abaixo do seu nível no recipiente. No
primeiro caso, diz-se ter ocorrido uma ascensão capilar e no segundo uma
depressão capilar. A explicação destes fenômenos capilares é feita com base numa
propriedade associada com a superfície livre de qualquer líquido, denominada
tensão superficial.
Água no Solo

4. 4 |Paulo Leonel Libardi
A tensão superficial resulta da existência de forças de atração de curto
alcance entre as moléculas do líquido chamadas forças moleculares de London-
van der Waals de coesão, forças moleculares de coesão ou simplesmente forças
de coesão. A distância limite de atuação dessas forças, isto é, a distância máxima
que uma molécula consegue exercer atração sobre as outras, delimita uma esfera
de raio r conhecida pelo nome de esfera de ação das forças moleculares ou
simplesmente esfera de ação molecular. Para a água, r não excede 0,05 µm.
Nestas condições, moléculas como M1 ou M2 (Figura 1), cujas esferas
de ação molecular se encontram totalmente dentro do líquido, atraem e são
atraídas simetricamente por todas as moléculas vizinhas e a resultante sobre elas é
nula. Entretanto, em qualquer molécula, cuja esfera de ação não esteja
inteiramente no interior do líquido, como M3 por exemplo, as forças sobre ela não
se equilibram. Isso porque a calota inferior da esfera de ação (área hachurada,
Figura 1) está cheia de moléculas que atraem tal molécula, mas a calota
correspondente superior, caindo fora do líquido, não está cheia de moléculas
como a inferior para atraí-la. Como consequência, esta molécula é atraída para o
interior do líquido pela resultante dessas forças de coesão não equilibradas.
Esta resultante é então nula nas moléculas localizadas a partir de uma
distância r da superfície do líquido para baixo e aumenta nas localizadas a partir
desta distância para cima, atingindo um máximo nas moléculas da superfície
(molécula M4, Figura 1).
Água no Solo

5. Paulo Leonel Libardi| 5
esfera de ação
r molecular
interface líquido-gás M4
r
camada
ativa { r
M2
M3
F2 = 0
F4 F3
r
M1
F1 = 0
Figura 1 - Forças intermoleculares.
Em todas as moléculas situadas na camada superficial de espessura r
ou “camada ativa” de um líquido, atuam, portanto, forças que tendem a puxá-las
para o interior do líquido causando, com isso, uma enorme pressão, dirigida para o
interior do líquido, chamada pressão interna P'. Assim, todo líquido, além da
pressão atmosférica, que atua externamente sobre sua superfície, está sujeito
também à pressão interna P' oriunda das forças moleculares de coesão não
equilibradas da camada ativa. Para a água, P' ≅ 1700 MPa.
Além disso, pela ação dessas forças, a superfície do líquido se contrai,
minimizando sua área, e adquire uma energia potencial extra que se opõe a
qualquer tentativa de distendê-la, ou seja, ocorrendo uma distensão, a tendência da
superfície é sempre voltar a posição original. Em outras palavras, devido a essas
forças, a superfície do líquido se torna contrátil. A essa energia potencial extra
Água no Solo

6. 6 |Paulo Leonel Libardi
adquirida pela superfície do líquido, devido às forças moleculares de coesão não
equilibradas da camada ativa, dá-se o nome de energia potencial superficial.
Esse fato mostra que a superfície de qualquer líquido está num estado
de constante tensão pelo que, se traçarmos uma linha arbitrária de comprimento L
sobre a superfície de um líquido, a superfície de cada lado da linha puxa a
superfície do lado oposto com uma força igual a F perpendicular à linha e paralela
à superfície (Figura 2). A razão F/L é definida como tensão superficial (σ) do
líquido, isto é:
F
σ= (1)
L
A dimensão da tensão superficial é, portanto, força por unidade de
comprimento (N/m).
Superfície livre
de um líquido
L
F F
Linha arbitrária
de comprimento L
Figura 2 - Definição da tensão superficial de um líquido.
Água no Solo

7. Paulo Leonel Libardi| 7
Uma consequência importante dessa tensão superficial dos líquidos e
que é básica para o entendimento dos fenômenos capilares, é o fato de que se a
superfície de um líquido deixar de ser plana, surge uma nova pressão p que pode
atuar no mesmo sentido que a pressão P' que é o que ocorre numa superfície
convexa, ou opostamente a P' como numa superfície côncava. A primeira situação
(superfície convexa) está ilustrada na Figura 3 na qual: ABCD é uma pequena
porção (infinitesimal) da superfície; R1 e R2 seus dois raios principais de
curvatura*; σdl1, duas forças de tensão superficial (ver equação 1), que atuam nos
arcos opostos e iguais AB e DC, de comprimento infinitesimal dl1; e σdl2, duas
forças de tensão superficial que atuam nos arcos opostos e iguais AD e BC, de
comprimento infinitesimal dl2.
Como se pode ver, devido única e exclusivamente à curvatura da
superfície, estas quatro forças, resultantes da tensão exercida pelo restante da
superfície ABCD nos arcos AB, DC, AD e BC, adquirem uma resultante
infinitesimal dF = dF1 + dF2 (Figura 3) que é, portanto, a causa do surgimento da
pressão p. Com base nessas informações, pode-se deduzir (Libardi, 2005) que:
 1 1 
p =σ  +
 R R ,
 (2)
 1 2 
isto é, a nova pressão p, causada pela curvatura da superfície, está relacionada com
a tensão superficial do líquido e os raios de curvatura da superfície curva.
* Qualquer superfície curva pequena é caracterizada por dois raios principais de curvatura.
Água no Solo

8. 8 |Paulo Leonel Libardi
N
N
N
AR B AR
σdl1
AR
σdl1 σdl2 σdl2 σdl2
H I σdl1 H G E G
dF2 dF1
LÍQUIDO σdl2 σdl2
σdl1 σdl1 O LÍQUIDO
A C
E I R1
dF
R2 LÍQUIDO
σdl2 R1 σdl1
D
R2 O1
O1
O2
O2
(a) (b)
AB=DC=EG=dl1
AD=BC=HI=dl2
Figura 3 - Porção infinitesimal de uma superfície curva.
A superfície da Figura 3, a qual tem ambos os raios de curvatura de um
mesmo lado, é chamada de superfície sinclástica e a pressão extra causada pela
curvatura da superfície é, como se acabou de mostrar, dada pela equação (2). Note-
se ainda que, pelo fato de a superfície ser convexa, portanto, com os dois raios no
lado do líquido, a resultante dF e, conseqüentemente p, atua a favor de P'. Com
isso, pode-se dizer que a pressão interna que atua numa superfície convexa de um
líquido é igual a P' + p (Figura 4b). Considerando a mesma superfície ABCD da
Figura 3 mas que ao invés de convexa seja côncava, chega-se ao mesmo resultado
para p (equação 2) porque esta superfície também é sinclástica; no entanto, neste
caso, pelo fato de os dois raios ficarem no lado do ar, verifica-se que a resultante
dF e, conseqüentemente, p, atua contra a pressão P' pelo que a pressão interna
Água no Solo

9. Paulo Leonel Libardi| 9
numa superfície côncava de um líquido é igual a P' - p (Figura 4c). Evidentemente,
se a superfície for plana dF = 0 e p = 0 e, portanto, a pressão interna é igual a P'
(Figura 4a).
p
p
...
...
...
...
...
...
...
P' - p
P' P' P'
P' + p
(a) (b) (c)
interface interface interface
plana convexa côncava
Figura 4 - Pressão interna numa superfície: plana (a), convexa (b) e côncava (c).
Quando a superfície curva tem seus raios de curvatura em lados
opostos, isto é, um estendendo-se para o líquido e o outro para o ar (Figura 5), por
raciocínio semelhante chega-se à fórmula
 1 1 
p =σ −
R R  ,
 (3)
 1 2 
na qual, R1 < R2 e, portanto, dF1 > dF2 e o sentido da força dF1 é o inverso do
sentido da força dF2. Esta superfície é conhecida pelo nome de superfície
Água no Solo

10. 10 |Paulo Leonel Libardi
anticlástica e nela p pode atuar tanto contra como a favor de P' ou mesmo até ser
nula dependendo das magnitudes de dF1 e dF2.
Para uma superfície esférica, R1 = R2 = R e, como ela é
obrigatoriamente sinclástica,
2σ
p= . (4)
R
As equações (2) ou (3) ou (4) são chamadas de equação de Laplace da
capilaridade.
AR
R2
dF2
dF1
LÍQUIDO
R1
Figura 5 - Superfície anticlástica.
Após estas considerações a respeito das superfícies curvas dos
líquidos, surge, de imediato, a pergunta. Quais são as situações em que a superfície
livre de um líquido deixa de ser plana? Quando se coloca água pura num copo de
Água no Solo

11. Paulo Leonel Libardi| 11
vidro limpo, nota-se que próximo da sua parede a superfície da água se encurva
para cima. No caso de colocar-se mercúrio no copo observa-se que a curvatura da
superfície é voltada para baixo. Observa-se também que, no caso da água, a
superfície se adere ao vidro ao passo que no caso do mercúrio existe uma
tendência para sua superfície se afastar do vidro. Estes fatos mostram que quando
se tem um líquido adjacente a uma parede sólida, não somente as forças
moleculares de London-van der Waals de atração coesiva entre as moléculas do
líquido são importantes, senão também as forças moleculares de London-van der
Waals de atração adesiva entre as moléculas do sólido e as do líquido.
Evidentemente, no caso da água em vidro as forças adesivas são dominantes
enquanto que no caso de mercúrio em vidro dominam as forças de coesão do
líquido.
Pode-se, agora, explicar os fenômenos da capilaridade. Será visto o
caso da ascensão capilar, de maior interesse; no caso da depressão capilar o
raciocínio é o mesmo. Imagine-se, então, que um tubo capilar de vidro é colocado
verticalmente dentro de uma vasilha com água (Figura 6). Assim que o tubo toca
na superfície da água, as moléculas de sua parede interna atraem as moléculas da
superfície da água fazendo com que ela se curve para cima num menisco côncavo.
(Figura 6a). Esta curvatura para cima faz com que, de acordo com a fórmula de
Laplace, a pressão interna no menisco (côncavo) no tubo capilar se torne menor
do que a pressão interna na interface água-ar plana na vasilha.
Água no Solo

12. 12 |Paulo Leonel Libardi
P0
...
P'-p
h
P0 P0 P0 P0 P0
...
z P'-p z
...
...
P' P'
...
A B A B
(a) (b)
Figura 6 - Ascensão da água num tubo capilar: (a) formação do menisco
côncavo, (b) ascensão.
Sejam considerados dois pontos na água dentro da vasilha da Figura 6,
um abaixo do menisco côncavo recém formado no tubo capilar (ponto A) e outro
no mesmo plano horizontal do ponto A, mas abaixo da superfície plana (ponto B).
Percebe-se que, na situação da Figura 6a, o líquido não se encontra em equilíbrio
porque a pressão em B é maior do que em A e isso faz com que a água seja
empurrada para cima no tubo capilar até uma altura h (Figura 6b) quando a pressão
em A se iguala à pressão em B e o líquido atinge a situação de equilíbrio da Figura
6b. Portanto, na condição de equilíbrio da Figura 6b:
Água no Solo

13. Paulo Leonel Libardi| 13
Po + P'+ ρ a gz = Po + ( P'− p) + ρ a gh + ρ a gz
ou
p = ρ a gh , (5)
donde
p
h= , (6)
ρa g
sendo, evidentemente, h a altura da ascensão capilar da água, ρa a densidade da
água e g a aceleração da gravidade.
No caso em que a superfície côncava é esférica e de raio R (Figura 7),
resulta, pela substituição da equação (4) na equação (6), que
2σ
h= . (7)
ρ a gR
Por outro lado, da Figura 7:
r
R= , (8)
cos α
em que r é o raio do tubo capilar e α o ângulo de contato, o qual, como se pode
ver, é o ângulo formado no líquido entre o plano tangente à superfície do líquido
na linha de contato e a parede do tubo. Linha de contato é a linha composta pelos
pontos comuns às três fases: sólida (vidro), líquida (água) e gasosa (ar) que em
corte define o ponto de contato P mostrado na Figura 7.
Substituindo a equação (8) na equação (7):
Água no Solo

14. 14 |Paulo Leonel Libardi
2σ cos α
h= . (9)
ρ a gr
As equações 6, 7 e 9 são chamadas indistintamente de equação de
Kelvin da capilaridade.
r
R
α
P
α
Figura 7 - Detalhe da superfície líquida no capilar com o ângulo de contato α.
Maiores detalhes deste assunto podem ser encontrados, por exemplo,
em Kirkham & Powers (1972) e Libardi (2005).
Além dos mecanismos de retenção é também importante conhecer os
índices que são utilizados para quantificar a água no solo.
Água no Solo

15. Paulo Leonel Libardi| 15
1.2 Quantificação da água no solo
Seja uma amostra de solo não-saturado cujo volume V é,
evidentemente, igual à soma do seu volume de sólidos Vs e o seu volume de poros
Vp, isto é,
V = Vs + V p . (10)
Chamando de Va e Var os volumes de água (solução) e de ar, respectivamente,
presentes no interior do espaço poroso desta amostra, num determinado momento,
então
V p = Va + Var (11)
e, portanto,
V = Vs + Va + Var . (12)
Para solos de estrutura rígida (não-expansíveis), sempre Vp = Va + Var = constante
e, portanto, quando Va aumenta (ou diminui), Var diminui (ou aumenta) do mesmo
valor, ou seja, V e Vp não variam com Va. Para solos expansíveis, entretanto, Vp e,
portanto, também V variam com Va, ou seja, aumentam com o aumento de Va e
diminuem com a diminuição de Va; conseqüentemente, para estes solos, as
equações (10), (11) e (12) continuam válidas, mas sempre para um determinado
valor de Va.
Igualmente, se for chamada de m a massa desta amostra de solo não-
saturado num dado momento, de ms a massa de seus sólidos e, no mesmo
momento, de ma e mar as massas de água e de ar presentes no interior do seu
espaço poroso, evidentemente,
Água no Solo

16. 16 |Paulo Leonel Libardi
m = ms + ma + mar . (13)
Entretanto, em comparação com a magnitude de ms e ma, mar pode ser considerada
sempre desprezível, pelo que
m ≅ ms + ma . (14)
A partir dessas informações pode-se, agora, definir os índices que
quantificam a água no solo:
- Conteúdo de água no solo à base de massa U
É, por definição, o quociente da massa de água presente numa amostra
de solo num determinado instante e a massa de sólidos da amostra:
ma
U=
ms
[
→ kg kg −1 ] (15)
ou, tendo em vista a equação (14),
m − ms
U=
ms
[
→ kg kg −1 . ] (16)
É importante esclarecer que, pelo fato de U não ser uma fração (parte
de uma unidade), não deveria ser expressa em porcentagem, muito embora isso
seja muito comum! Observe-se, também, que não há necessidade de qualquer
informação adicional quando se utiliza U para quantificar a água de solos
expansíveis.
Água no Solo

17. Paulo Leonel Libardi| 17
- Conteúdo de água no solo à base de volume θ
É o quociente do volume de água presente numa amostra de solo, num
determinado instante, e o volume da amostra, ou seja,
Va
θ=
V
[
→ m 3 m −3 ] (17)
ou, lembrando que a densidade da água ρa = ma/Va e tendo em vista a equação
(14),
m − ms
θ=
ρ aV
[
→ m 3 m −3 . ] (18)
Como θ é uma fração (parte de uma unidade), isto é, mostra quanto de V é Va
num determinado instante, pode perfeitamente ser expressa também em
porcentagem, bastando para isso multiplicar por 100 o resultado obtido pelas
equações (17) ou (18).
O conteúdo de água θ pode ser calculado a partir da determinação do
conteúdo de água U e da densidade do solo ρ. Como, por definição, densidade de
um corpo é a razão da massa pelo volume desse corpo, então, no caso, para nosso
corpo poroso solo = sólidos + poros de massa ms e volume V,
ms
ρ=
V
[
→ kg m −3 . ] (19)
Assim, dividindo a equação (17) pela equação (15) verifica-se facilmente que
ρ
θ= U . (20)
ρa
Normalmente se assume para a densidade da água ρa o valor 1000 kg m-3.
Água no Solo

18. 18 |Paulo Leonel Libardi
É importante observar que, para solos expansivos, o valor de θ deve
sempre vir acompanhado do valor de ρ e o valor de ρ sempre acompanhado do
valor do conteúdo de água, no momento de amostragem.
Dividindo ambos os membros da equação (11) por V,
Vp Va Var
= + , (21)
V V V
verifica-se que a quantidade Vp/V é uma fração que mostra quanto do volume da
amostra de solo é volume de poros, sendo, por isso, denominada porosidade do
solo α:
Vp
α=
V
[
→ m 3 m −3 ] (22)
e que a quantidade Var/V é uma fração que mostra quanto do volume da amostra de
solo é volume de ar, num dado instante, sendo denominada, por esse motivo,
porosidade de aeração αar:
Var
α ar =
V
[
→ m 3 m −3 . ] (23)
A substituição das equações (17), (22) e (23) na equação (21) mostra que
α = θ + α ar . (24)
Por esta expressão (24) vê-se claramente que a) quando θ = 0, α = αar
(numericamente): solo completamente seco e b) quando αar = 0, α = θs
(numericamente), sendo θs = conteúdo de água à base de volume no solo saturado.
Água no Solo

19. Paulo Leonel Libardi| 19
Explicitando Vp da equação (10) e dividindo ambos os membros da
equação resultante por V, obtém-se
Vs
α = 1− . (25)
V
Sendo
ms
ρs =
Vs
[
→ kg m −3 , ] (26)
a densidade dos sólidos do solo, também chamada densidade das partículas do
solo, percebe-se, facilmente, que, pela substituição das equações (19) e (26) na
equação (25),
ρ
α = 1− . (27)
ρs
Será mostrado, a seguir, um outro modo de quantificar a água no solo
também muito utilizado quando se estuda água no solo.
- Armazenagem ou altura de água no solo
Imagine-se um perfil de solo no campo e que, num determinado
momento, ao longo de sua profundidade Z, sejam obtidos valores de θ a distâncias
tão próximas entre si quanto possível de tal maneira que, num gráfico de θ em
função de Z, o conjunto dos pontos obtidos resulte numa curva contínua
representando uma dada função θ = θ (Z). Tal gráfico recebe o nome de perfil de
conteúdo de água no solo à base de volume (Figura 8).
Água no Solo

20. 20 |Paulo Leonel Libardi
θi*
zo = 0 θ(m3 m-3)
A z1
*
z1
z2
*
L ∆ zi
zi-1
zi*
(Z i
*
, θ i* )
zi
zn = L
Z(m)
Figura 8 – Perfil do conteúdo de água solo à base de volume.
Pode-se obter a área aproximada sob a curva deste gráfico no intervalo
0 a L, dividindo-a em pequenos retângulos como mostra a Figura 8, tal que,
evidentemente,
n
Área aproximada = ∑ θ (Z
i =1
i
*
i )∆Z i , (28)
sendo θ i ( Z i* ) e ∆Z i = Z i − Z i −1 , os conteúdos de água à base de volume e os
incrementos de profundidade i, respectivamente. Se n tender para o infinito (n →
∞) e o ∆Zi máximo tender para zero [(∆Zi)m → 0], obtém-se a área exata sob a
curva θ = θ (Z) de 0 a L,
Água no Solo

21. Paulo Leonel Libardi| 21
n
Área exata = lim
n →∞
∑θ (Z )∆Z
*
i i (29)
( ∆Z i ) m →0 i =1
ou, com uma notação mais compacta,
L
Área exata = ∫ θ ( Z )dZ
0
(30)
e lê-se integral de θ(Z) com relação a Z de 0 a L.
Pela definição de conteúdo de água à base de volume θ (equação 17),
pode-se escrever o integrando da equação (30) como
dVa dVa dV
θ (Z )dZ = dZ = dZ = a = dh .
dV AdZ A
Nesta expressão, A é uma área de solo arbitrária representativa do
perfil de conteúdo de água (Figura 8), dVa é o elemento de volume de água
existente no elemento de volume de solo dV = AdZ e dh é a altura de água
representada por dVa (dentro de dV) por unidade de área de solo (A). Portanto,
voltando à equação (30), verifica-se que
L
hL = ∫ θ (Z )dZ → [m água] . (31)
0
Foi colocado o subíndice L em h para indicar que se trata do valor de h para a
camada 0 – L do perfil de solo.
A quantidade hL, dada pela expressão (31), representa, portanto,
exatamente a área sob a curva do gráfico do conteúdo de água θ em função da
profundidade do solo Z e é igual a altura de água que a camada 0 – L m do perfil
Água no Solo

22. 22 |Paulo Leonel Libardi
de solo armazena, no momento de medida dos valores de θ para obtenção da
função θ(Z), sendo, por isso, denominada armazenagem ou altura de água no solo.
Um aspecto importante a respeito da armazenagem de água é o que
será mostrado a seguir.
Referindo-se novamente ao gráfico da Figura 8, pode-se obter o valor
médio aproximado de θ = θ (Z) no intervalo 0 a L, tirando a média dos valores
θ (Z 1* ), θ (Z 2 ), ... , θ (Z n ) de θ (Z):
* *
θ (Z 1* ) + θ (Z 2 ) + ... + θ (Z n )
* *
θ ≅ . (32)
n
Evidentemente, a aproximação (≅) será tanto melhor quanto maior o número de
pontos n tomados para tirar a média. Fazendo com que os pontos Z0, Z1, ..., Zn
distem um do outro de ∆Zi = ∆Z = constante e multiplicando o numerador e o
denominador do segundo membro da equação (32) por esse valor (∆Z), obtém-se:
θ ≅
( ) ( ) *
( )
[θ Z 1* + θ Z 2 + .... + θ Z n ]∆Z
*
. (33)
n∆Z
O denominador da equação (33), n ∆Z = L – 0 = L, é o comprimento do intervalo
(= camada de solo) ao longo do qual é tirada a média, independentemente do valor
de ∆Z e do número de pontos n. Se, agora, n → ∞ e ∆Z → 0, o numerador da
expressão (33) torna-se igual à integral da equação (30) e o sinal de aproximação
da equação (33) torna-se sinal de igualdade, ou seja,
L
∫ θ (Z )dZ
0
θ = (34)
L
Água no Solo

23. Paulo Leonel Libardi| 23
ou, tendo em conta a equação (31),
hL = θ L . (35)
Evidentemente, se medirmos hL em dois instantes diferentes, temos
que a variação de armazenagem da água no solo, ∆hL , é obtida por
∆hL = (θ f − θi ) L (36)
sendo θ f o conteúdo de água no solo à base de volume médio no instante final e
θ i o conteúdo de água no solo à base de volume médio no instante inicial, ambos
dados pela equação (34).
2 ENERGIA DA ÁGUA NO SOLO
Todo corpo na natureza possui uma energia a qual é normalmente
subdividida em três formas principais: energia cinética, resultante da velocidade
instantânea do corpo em relação a algum referencial externo a ele, energia
potencial, resultante da posição instantânea do corpo em relação a campos de força
(gravitacional, elétrica, eletromagnética, etc) também externos a ele, e energia
interna, associada ao movimento e posição das moléculas, átomos, elétrons, etc. de
que se constitui a matéria do corpo, incluindo diversas formas como a energia
térmica, a energia química, a energia nuclear, etc.. É importante esclarecer que em
todo estudo com quaisquer destas formas de energia, nunca se trabalha com seu
valor absoluto (porque é praticamente impossível conhecê-lo), mas sempre com
uma diferença de energia entre duas situações, uma tomada como referência.
Água no Solo

24. 24 |Paulo Leonel Libardi
A água no solo será aqui estudada, do ponto de vista energético,
segundo um modelo no qual se considera sempre duas situações com ela em
equilíbrio. Umas das situações é a água no solo propriamente dita, isto é, dentro do
solo. A outra situação é a mesma água (com a mesma energia interna que a água
no solo), mas fora do solo, denominada água padrão e definida como água livre,
de mesma energia interna que a água no solo e em cuja superfície plana,
coincidente com a referência gravitacional, atua a pressão atmosférica do local
onde a medida é feita. Portanto, em ambas as situações, assume-se que a energia
interna da água é a mesma, isto é, mesma temperatura, mesma concentração salina,
enfim tudo é igual no que diz respeito às condições energéticas internas da água.
De acordo com este modelo, portanto, a única diferença que existe entre as águas
nas duas situações de equilíbrio (no solo e padrão), são os campos de força
externos a elas. Como podem atuar concomitantemente mais de um campo de
força externo, resultando, portanto, em mais de um tipo de energia potencial, será
aqui utilizado o termo energia potencial total para indicar a soma dos diversos
tipos ou componentes de energia potencial atuantes.
Se a energia potencial total de um corpo (com energia interna
constante) em equilíbrio for diferente em dois pontos de um determinado meio,
este corpo vai sempre se movimentar, se o meio permitir, do ponto onde sua
energia potencial total é maior para o ponto onde ela é menor. O raciocínio é o
mesmo quando o corpo é a água no solo mas, nesse caso, é mais conveniente
utilizar a energia potencial total da água por unidade de massa ou volume de água
ou energia potencial total específica da água como veremos no item a seguir.
Água no Solo

25. Paulo Leonel Libardi| 25
2.1 Potencial total da água no solo
Referindo-se ao modelo descrito no item anterior, o conceito de
potencial total da água foi introduzido com o intuito de estabelecer o sentido do
movimento da água entre dois pontos de um meio poroso, sem conhecer os valores
individuais da energia potencial total específica em cada ponto. Assim, por
exemplo, sendo ε a energia potencial total específica da água (em equilíbrio) num
solo e εo a energia potencial total específica da água (em equilíbrio) padrão, a
diferença ε – εo é, por definição, o potencial total da água no solo φt, isto é,
φt = ε − ε o [energia / massa ou volume de água] . (37)
Considerando, agora, dois pontos A e B no perfil do solo, nos quais,
evidentemente,
φ t ( A) = ε A − ε o
e
φt (B ) = ε B − ε o
então,
φt ( A) − φt (B ) = (ε A − ε o ) − (ε B − ε o ) = ε A − ε B .
Ou seja, como a energia potencial total específica da água padrão deve ser a
mesma para os dois pontos, medindo-se o potencial total nesses dois pontos
obtém-se o valor da diferença εA - εB por meio da diferença φt (A) - φt (B), sem a
Água no Solo

26. 26 |Paulo Leonel Libardi
necessidade de se conhecer individualmente εA e εB. Desse modo, se num
determinado momento φt(A) > φt(B), o movimento da água é de A para B porque
ε A > ε B e se φt (B) > φt (A), de B para A porque ε B > ε A . Quando φt (A) = φt (B),
tem-se, evidentemente, uma condição em que não há movimento entre A e B,
porque εA = εB (equilíbrio).
Evidentemente, cada tipo (ou componente) de energia potencial que
estiver atuando na água dentro do solo, dá origem a um potencial componente do
potencial total da água no solo.
Por outro lado, quando se expressa potencial (o total ou qualquer
componente) em unidade de energia/volume, verifica-se, imediatamente que esta é
idêntica à unidade de pressão porque, dimensionalmente,
J Nm N
3
= 3 = 2 = Pa (Pascal).
m m m
(Será considerado nesse estudo a energia potencial específica preferencialmente
como energia por unidade de volume; por unidade de massa o raciocínio é o
mesmo, muda apenas a unidade).
Portanto, os valores de todos os potenciais da água no solo, tanto o
total como qualquer um dos seus componentes, podem ser considerados como
idênticos ao valor de uma diferença de pressão, isto é, diferença entre uma pressão
cujo valor é idêntico ao valor de ε e uma pressão cujo valor é idêntico ao valor de
εo.
Água no Solo

27. Paulo Leonel Libardi| 27
A seguir, serão estudados os potenciais componentes do potencial total
da água no solo.
2.2 Potencial gravitacional da água no solo
Sabe-se da Mecânica que qualquer corpo num campo gravitacional
possui uma energia potencial gravitacional (Eg). A água no solo, estando dentro
do campo gravitacional terrestre possui, evidentemente, esta energia, cuja equação,
dado a necessidade de incluir neste contexto a água padrão anteriormente definida,
pode ser escrita como:
∆E g = ma g (r1 − ro ) , (38)
sendo ma = massa da água no solo; g = aceleração da gravidade; r1 = distância do
centro da Terra ao ponto considerado no perfil do solo e ro = distância do centro da
Terra a um ponto arbitrário onde se deve imaginar localizada a superfície plana da
água padrão e que será denominada simplesmente referência gravitacional. ∆Eg,
evidentemente, é o incremento de energia potencial gravitacional que a água
adquire quando de seu deslocamento da posição r1 para a posição ro contra ou a
favor a força da gravidade.
Considerando a existência apenas do campo gravitacional terrestre, o
potencial total, definido pela equação (37), torna-se apenas o potencial
gravitacional φg o qual, tendo em conta a equação (38), é dado por
∆E g
φg = ε − ε o = = ρ a g (r1 − r0 ) , (39)
Va
Água no Solo

28. 28 |Paulo Leonel Libardi
em que ρa = ma/Va = densidade da água no solo, considerada constante.
Chamando, então, o valor da distância vertical do ponto considerado à
posição da referência gravitacional, de Z, isto é,
Z = r1 − ro , (40)
reescreve-se a equação (39) como:
φ g = ± ρ a gZ [energia / volume] , (41)
sendo que o sinal de Z e, portanto de φg dependerá da posição do ponto
considerado em relação à referência gravitacional, isto é, o sinal será positivo se o
ponto estiver acima da referência gravitacional (r1 > r0), negativo se estiver abaixo
(r1 < r0) e nulo se for coincidente com ela (r1 = r0).
Com base no que foi afirmado no item anterior, pode-se considerar
também o valor da energia/volume como idêntico ao valor da pressão de uma
coluna de água causada pelo campo gravitacional terrestre. Tal pressão é dada por:
Pa = ρ a gh ,
em que Pa = pressão de água (N/m2, Pa), ρa = densidade da água (kg/m3),
g = aceleração da gravidade (m/s2) e h = altura da coluna de água (m).
Desta maneira, a partir das equações (39) a (41):
φ g = ρ a g(r1 − r0 ) ≡ ρ a g(h1 − h0 )
ou
Água no Solo

29. Paulo Leonel Libardi| 29
φ g = ± ρ a gZ ≡ ± ρ a gh [energia / volume] , (42)
sendo h = h1 − h0 , de modo que ρ a gh1 = valor da pressão de uma coluna de água
de altura h1 idêntico ao valor de ε da água no solo e ρ a gh0 = valor da pressão de
uma coluna de água de altura ho idêntico ao valor de εo da água padrão.
Dividindo ambos os membros da equação (42) por ρa g:
φ g = ± Z ≡ ± h [altura de água] , (43)
isto é, dividindo-se o valor de φg, expresso na unidade energia/volume, calculado a
partir da equação (41), pela quantidade ρ a g , obtém-se o valor de φg na unidade
altura de água ou carga hidráulica.
Portanto, para se obter o valor de φg num determinado ponto no solo,
precisa-se apenas de uma régua para medir a distância vertical deste ponto à
posição tomada como referência gravitacional, que a unidade do resultado obtido
será em altura de água, ou seja, se a distância medida for, por exemplo, 1 m, o
valor de φg será 1 m de água se o ponto estiver acima da referência gravitacional e
-1 m de água, se o ponto estiver abaixo da referência gravitacional.
2.3 Potencial de pressão da água no solo
Num solo com estrutura rígida, este componente do potencial total só
se manifesta sob a condição de saturação. Para defini-lo, considere-se o esquema
da Figura 9.
Água no Solo

30. 30 |Paulo Leonel Libardi
Po
Po
P’
h
A BB RG
P’
Água com energia potencial
Água com energia potencial
total específica ε no ponto
total ε (ponto considerado A,
considerado A
sob a pressão Po+P’+ρa gh.)
Água padrão com energia potencial total
Á
Água padrão com energia potencial
total ífica o (pontoεo (ponto B)
ε
total específica sob
espec
específica εo (ponto B,B) a pressão Po+P’).
Figura 9 - Definição do potencial de pressão.
No ponto B, em equilíbrio no recipiente do lado direito desta
figura, tem-se água padrão (com energia potencial total específica εo) porque na
interface plana, coincidente com a referência gravitacional (RG) onde ele se
localiza, estão atuando a pressão atmosférica (Po) e a pressão interna (P’). Por
outro lado, o ponto A, em equilíbrio no recipiente do lado esquerdo da figura, é
diferente do primeiro apenas por nele atuar também a pressão da altura de água h.
Note, então, que a única diferença entre os dois pontos é a pressão de água Pa = ρa
Água no Solo

31. Paulo Leonel Libardi| 31
gh que atua no ponto da esquerda. Conseqüentemente, esta pressão Pa torna a
energia potencial total específica ε no ponto à esquerda (considerado) maior do
que a energia potencial total específica εo no ponto à direita (água padrão): se for
permitida uma comunicação entre os dois pontos, a água, por ação desta pressão,
flui em direção à água padrão indicando que ε > εo.
Pela definição de potencial (equação 37) e, no caso, pelo fato de a
única diferença entre a água padrão e a água no ponto considerado ser a pressão de
líquido no ponto considerado, tem-se que:
φ p = ε − ε o = ρ a gh → [energia / volume] , (44)
sendo φ p = potencial de pressão.
De modo idêntico ao que vimos no caso do potencial gravitacional, em
termos de carga hidráulica,
φ p = h [altura de água] . (45)
Note-se, no entanto, que, no caso deste potencial de pressão, h é uma carga
hidráulica real que atua no ponto considerado.
Como se pode ver pela equação (45), φp pode ser determinado
medindo o comprimento h da coluna de líquido que atua acima do ponto de
medida. No campo, isto é feito inserindo um piezômetro no solo, adjacente ao
ponto onde se deseja conhecer φp, e mede-se a profundidade h do ponto abaixo da
superfície livre de água no piezômetro (Figura 10). Portanto, o valor do potencial
de pressão é sempre positivo ou no mínimo igual a zero. Esta última situação (φp=
0) ocorre quando o ponto se localiza na superfície livre de água.
Água no Solo

32. 32 |Paulo Leonel Libardi
piezômetro
superfície do solo
lençol freático
h
ponto em
questão
Figura 10 - Ilustração da medida de φp num determinado ponto no solo abaixo de
um lençol de água, por meio de um piezômetro.
2.4 Potencial mátrico da água no solo
Seja um determinado volume, um torrão, de solo não saturado. É fácil
verificar que para retirar a quantidade de água nele em equilíbrio, é necessário
realizar trabalho sobre ela, o qual é tanto maior quanto mais seco estiver o solo.
Isso nos leva a concluir que o solo retém a água no seu espaço poroso com forças
cujas intensidades aumentam conforme o seu conteúdo de água diminui. Essas
forças, por se manifestarem devido à presença da matriz do solo, são denominadas
Água no Solo

33. Paulo Leonel Libardi| 33
forças mátricas, relacionadas aos já mencionados fenômenos de capilaridade e
adsorção.
Distinguem-se, assim, dois tipos de força mátrica: a) as forças
capilares, responsáveis pela retenção da água nos poros capilares dos agregados e
b) as forças de adsorção, responsáveis pela retenção da água nas superfícies das
partículas do solo. Quantificar a contribuição de cada um desses tipos de força no
potencial mátrico é praticamente impossível na faixa do conteúdo de água no solo
que as plantas normalmente se desenvolvem. O que se pode dizer, em termos
qualitativos, é que logo após a drenagem livre de um solo saturado no campo, as
forças capilares são dominantes e que, à medida que o solo seca a partir daí, a
adsorção vai adquirindo maior importância.
Estes dois mecanismos de retenção da água no solo pelas forças
capilares e de adsorção reduzem a energia potencial total específica da água livre.
A veracidade desta afirmação pode ser demonstrada tanto pelo fato de se ter que
realizar trabalho sobre a água para retirá-la de um solo não-saturado, como
também pelo fato de que ao se colocar água livre (padrão) em contato com um
solo não saturado, num mesmo plano horizontal, a água flui naturalmente para o
solo, ou seja, de um local com maior para um local com menor energia potencial
total específica.
Nesse caso, portanto, como a única causa da diferença entre a energia
potencial total específica da água no solo não-saturado ε (ponto A) e a energia
potencial total específica da água padrão εo (ponto B) é a existência das forças
mátricas que atuam para reter a água no solo não saturado (Figura 11), o potencial
Água no Solo

34. 34 |Paulo Leonel Libardi
total definido pela equação (37) torna-se apenas o potencial mátrico φm, o qual
pode ser interpretado como uma medida do trabalho realizado por um agente
externo para tornar livre a unidade de volume de água retida num solo não
saturado, isto é, ε + W/Va = εo ou
W
φm = ε − ε o = − . (46)
Va
Po Po
W
A BB RG
V
a
P’
Água com energia potencial total Água padrão com energia
específica ε (ponto considerado A potencial total específica εo (ponto B)
do solo não saturado.
saturado).
Figura 11 - Definição do potencial mátrico.
Pela equação (46), percebe-se que, a não ser no caso particular de uma
interface água-ar plana como num lençol freático na qual ε = εo e então φm = 0, o
potencial mátrico é sempre uma quantidade negativa (ε < εo), sendo, por isso,
Água no Solo

35. Paulo Leonel Libardi| 35
comum a utilização do termo tensão da água no solo τ para eliminar o sinal
negativo, isto é, em vez de se dizer, por exemplo, que o potencial mátrico da água
no solo φm = -30 kPa, diz-se que a tensão da água no solo τ = 30 kPa.
3 CURVA DE RETENÇÃO
Como acabamos de ver, o potencial mátrico pode ser avaliado pelo
trabalho que se deve realizar à unidade de volume de água retida num solo não-
saturado pelas forças mátricas, para torná-la livre como a água padrão.
Devido à heterogeneidade dos poros dos solos, com formas e
tamanhos muito variáveis de um solo para outro, não é possível se obter uma
equação teórica para o potencial mátrico como no caso dos potenciais
gravitacional e de pressão. Entretanto, como este potencial varia com o conteúdo
de água no solo, sendo tanto menor quanto mais seco estiver o solo, foram
desenvolvidos aparelhos por meio dos quais se pudesse buscar uma correlação
entre ele e o conteúdo de água no solo. A curva resultante dessa correlação
recebeu o nome de curva de retenção da água no solo ou simplesmente curva de
retenção.
Os aparelhos tradicionais desenvolvidos para a determinação dessa
curva são os funis de placa porosa (Haines, 1930) e as câmaras de pressão com
placa porosa (Richards, 1941, 1947, 1948), os quais têm a teoria da capilaridade
como base de seu funcionamento.
Água no Solo

36. 36 |Paulo Leonel Libardi
3.1 Funil de placa porosa
A Figura 12 representa o experimento tradicional de demonstração da
ascensão capilar com tubos de diversas formas. Assim, enquanto no tubo A desta
figura, capilar em todo o seu comprimento, o desnível h se forma naturalmente,
nos tubos B e C isso não é possível por causa das suas partes não capilares. No
entanto, se forem preenchidas as partes não capilares destes tubos, elevando o
nível da superfície da água na cuba até a altura h', isto é, até que a porção capilar
seja atinjida, o menisco é formado e a coluna é mantida em h, sem a necessidade
de que o nível permaneça em h' o qual pode, então, ser rebaixado à posição
original esgotando-se a água através da torneira T (Figura 12). Imagine-se, no
entanto, que o nível da superfície da água na cuba da Figura 12 seja mantido a
altura h' . Pela equação de Kelvin, o valor da ascensão é h, mas, como há um
comprimento de tubo igual a H-h', menor do que h, acima da superfície da água na
cuba, evidentemente, a água sobe até o fim deste comprimento e adquire um
menisco mais plano, cujo raio de curvatura deve ser exatamente igual a h/(H-h')
vezes aquele que ela adquiriria normalmente, isto é, se houvesse um comprimento
mínimo h de capilar acima da superfície plana da água na cuba. Por exemplo, se
H-h'=h/2, o valor do raio de curvatura do menisco na extremidade do tubo A será o
dobro do valor normal. Este fato é depreendido facilmente da equação (7) de
Kelvin pela qual, uma vez que 2σ/ρag é constante, o fator de diminuição de h é
igual ao fator de aumento de R.
Analisando, agora, o tubo C da Figura 12, observa-se que há cinco
pequenos tubos capilares. Ao invés de cinco, poderiam haver dez, vinte, cem, ou
muito mais. Uma maneira prática de obter o maior número possível de capilares
Água no Solo

37. Paulo Leonel Libardi| 37
como no tubo C, consiste em utilizar uma placa porosa (de cerâmica, por exemplo)
conforme o tubo D da figura. Evidentemente, no caso da placa porosa, os
diâmetros dos seus capilares não são todos iguais e nem uniformes como no tubo
C, mas sendo pequena a espessura da placa (da ordem de 5 mm) e considerando
que o valor de h deve ser sempre menor do que o valor máximo calculado pela
equação (47) a seguir, pode-se dizer que os meniscos nos capilares da placa se
localizam, praticamente, na sua superfície para qualquer valor de h (Figura 12).
Placa porosa
h h
h' H
T
A B C D
Figura 12 - Tubos capilares com diferentes volumes de água.
O tubo D da Figura 12 pode ser confeccionado de tal maneira a se
tornar um funil de haste prolongada e flexível por meio da qual se pode aumentar
ou diminuir h pelo abaixamento ou elevação do nível de água mantido constante
em sua extremidade por um dispositivo simples (Figura 13).
Água no Solo

38. 38 |Paulo Leonel Libardi
Por ser um funil munido de uma placa porosa na parte inferior do seu
corpo, recebe a denominação de funil de placa porosa.
Po Po Po
placa porosa
funil de
placa
porosa
Po h
tubo
flexível
dispositivo para
manter o nível de
(a) (b) água constante
Figura 13 - Funil de placa porosa adaptado com uma haste flexível: (a) placa
porosa com a superfície dos meniscos nos seus poros, plana e (b)
placa porosa com a superfície dos meniscos nos seus poros, côncava,
com p = ρagh.
Como já se viu, o aumento de h faz com que os raios de curvatura dos
meniscos nos capilares da placa porosa decresçam, isto é, suas interfaces sejam
Água no Solo

39. Paulo Leonel Libardi| 39
“puxadas” para baixo. Isto, entretanto, acontece até o limite máximo quando o raio
de curvatura do menisco no maior poro da placa se torna igual ao raio r’ deste
poro. Nessa situação limite, a equação de Kelvin se torna, portanto,
2σ
hmax = . (47)
ρgr '
Um valor maior do que o hmax da placa, resultará em rompimento do
menisco e passagem de ar através da placa. Portanto, quanto menor r’ maior hmax,
que também é denominado valor de entrada de ar da placa porosa. Entretanto,
praticamente, o valor máximo de h que se consegue é ≅ 8,5 m, mesmo que o valor
de r’ permita um hmax maior, devido ao fenômeno da cavitação. Resumidamente,
este fenômeno consiste no seguinte: à medida que se aumenta a altura h, a pressão
interna no menisco diminui (lembre-se que a pressão interna no menisco é P’ - p e
p = ρagh = incremento da pressão interna devido à curvatura da superfície); esta
diminuição da pressão interna faz com que ar e vapor de água saiam do líquido ou
passem através das paredes da tubulação usada e concentre-se sob a placa,
quebrando a continuidade da coluna de água que então se desprende da placa,
normalmente quando h ≅ 8,5 m.
Considerando qualquer um dos poros da placa porosa do funil da
Figura 13 tem-se, como ilustra a Figura 14, (a) à esquerda (correspondente a
situação da Figura 13a) a água padrão com sua interface plana e (b) à direita
(correspondente a situação da Figura 13b) a água no mesmo poro capilar com sua
interface côncava (ponto considerado).
Água no Solo

40. 40 |Paulo Leonel Libardi
Note-se que a única diferença entre as duas situações é a curvatura
côncava da interface água-ar no ponto considerado causada pela matriz (= placa
porosa) ao se abaixar, de h, o dispositivo de manutenção do nível da água. Pode-se
observar que, devido a esta curvatura causada pela matriz, a energia potencial total
específica da água retida pela placa (ponto A, logo abaixo da camada ativa) é
menor do que a energia potencial total específica da água padrão (ponto B,
também logo abaixo da camada ativa), porque a pressão que atua em A (interface
côncava) é Po+ P' - p e a pressão que atua em B (interface plana da água padrão) é
Po+ P' (Figura 14). Logo, a semelhança do que vimos para o φp:
φ m = ε − ε o = − p → [energia/volume] (48)
Po Po
RG
B A
...
(a) (b)
...
P'-p
P'
Água padrão com energia Água com energia
potencial total específica εo potencial total específica ε
(ponto B) no ponto considerado A.
Figura 14 - Medida do potencial mátrico
ou, tendo em conta o valor de p = ρagh:
Água no Solo

41. Paulo Leonel Libardi| 41
φ m = − ρ g h → [energia / volume] (49)
ou ainda
φm = −h → [altura de água] (50)
Considere-se, agora, a colocação de uma amostra de solo na superfície
da placa porosa do funil, que ela seja saturada elevando o nível de água no tubo
flexível até torná-lo coincidente com o seu topo (Figura 15a) e, depois de um certo
tempo, quando se tem certeza que foi bem saturada, seja abaixado o nível de água
no tubo flexível a uma altura h (Figura 15b). Ao se fazer isso, os poros da amostra
de solo de raio maior do que o calculado pela equação
2σ
r= (51)
ρ a gh
são esvaziados, o que pode ser observado pelo gotejamento de água através da
pequena saída do dispositivo que mantém o nível de água constante na
extremidade do tubo flexível. Note-se que a equação (51) é a equação (9) com o r
explicitado, para α=0. Atingido o equilíbrio, isto é, assim que o gotejamento parar,
a situação da Figura 15 é idêntica à da Figura 13, com a diferença de que se tem
uma amostra de solo (ponto considerado A) em perfeito contato com a placa
porosa. Logo, as mesmas equações (48, 49 e 50) se aplicam, ou seja, a altura de
água h (agora a distância do centro da amostra de solo ao nível de água mantido
constante na extremidade da haste do funil), com o sinal trocado, representa o
potencial mátrico da água no solo após o equilíbrio.
Água no Solo

42. 42 |Paulo Leonel Libardi
Po Po Po
A
amostra de solo
amostra de solo com uma tensão h
saturado
h
Po
RG
C
(a) (b)
Figura 15 - Procedimento para medida de φm com o funil de placa porosa:
(a) saturação do solo, (b) aplicação da tensão h, com consequente
dessaturação da amostra de solo.
A equação (50) pode ser obtida de outra maneira. Considere-se a
amostra de solo (ponto A) e a água padrão (ponto C) da Figura 15b. Quando pára
o gotejamento, a amostra de solo torna-se não saturada, portanto com um
determinado φm. Como no equilíbrio, φt(A)=φt(C) e, pela Figura 15b,
φt(A)=φm(A)+φg(A)=φm+h m água e φt(C)=φm(C)+φg(C)=0+0, então, φm= -h m
água.
Para a elaboração da curva de retenção da água no solo com o funil de
placa porosa, repete-se para diversos valores de h, o procedimento indicado na
Água no Solo

43. Paulo Leonel Libardi| 43
Figura 15 determinando-se, depois de atingido o equilíbrio com cada valor de h
selecionado, o valor do conteúdo de água no solo correspondente. Evidentemente,
de um modo geral, quanto maior h (ou menor φm), sempre menor deve ser o
conteúdo de água no solo depois do equilíbrio.
O funil da placa porosa é normalmente utilizado para valores de h
menores do que 2 m.
3.2 Câmaras de Pressão
Para valores de φm menores do que ≅ -2,0 m de água até o limite de -
150 m de água, pode-se completar a curva de retenção no laboratório, utilizando
câmaras de ar comprimido munidas de placa porosa (Figura 16). Como se pode ver
por esta figura, a placa porosa separa a água no solo (ponto A) da água padrão
(ponto B). Estando a amostra de solo saturada, ao se aplicar uma pressão P na
câmara, toda unidade de volume de água retida no solo com uma energia menor do
que a pressão P aplicada, é dele retirada e goteja no tubo de saída. Portanto,
enquanto o tubo de saída estiver gotejando, o valor do potencial mátrico estará
diminuindo, uma vez que o solo estará sendo dessaturado. Quando parar de gotejar
(equilíbrio), o valor de φm é tal que compensa a pressão aplicada, ou seja,
ε + P = ε o e então
φm = ε − ε o = − P . (52)
Resumidamente, o procedimento de utilização da câmara consiste em
saturar a amostra de solo, aplicar a pressão de interesse P e, após o equilíbrio,
quando o tubo de saída parar de gotejar, medir o valor do conteúdo de água com
Água no Solo

44. 44 |Paulo Leonel Libardi
que ficou a amostra; repete-se o procedimento para vários valores de P e elabora-
se a curva.
medidor de
pressão
câmara de pressão de ar P
Po + P
Po + P
amostra compressor
Po de solo de ar
A RG
B
placa porosa
P’ P’- p água
tubo de saída
de água
Figura 16 - Câmara de pressão de ar com placa porosa para elaboração da curva
de retenção.
A explicação do porquê φm = -P com a câmara de pressão pode
também ser dada de outra maneira como a seguir. A amostra de solo, depois que
pára o gotejamento através do tubo de saída, torna-se não-saturada e, portanto,
com determinado φm; mas fica sujeita também à pressão de ar P, portanto com um
potencial de pressão φp = P que, neste caso, por tratar-se de pressão de ar, alguns
autores chamam de potencial pneumático. Portanto (ver Figura 16) na amostra
(ponto A),
Água no Solo

45. Paulo Leonel Libardi| 45
φ t ( A) = φ m + P
e na água padrão (ponto B)
φt (B ) = 0
Como no equilíbrio φt ( A) = φt (B ) , resulta imediatamente que
φm = − P → [energia/volume] (53)
Um ponto importante a ser considerado é que, com a aplicação da
pressão P, cria-se nos capilares não esvasiados da amostra de solo (ponto A), e nos
capilares da placa, um menisco côncavo no qual atua a pressão Po+P+P’-p e,
como no ponto B atua a pressão Po+P’, então, no equilíbrio, Po+P+P’-p = Po+P’,
resultando que P = p . Assumindo que o menisco côncavo seja esférico, tem-se,
com base nas equações (4) e (8) e no resultado acima (P=p), que
2σ cos α
r= (54)
P
e, à semelhança do que ocorre com o funil de placa porosa, quando se aplica a
pressão P, pode-se dizer que, de acordo com a teoria da capilaridade, todos os
poros da amostra de solo cujos raios são maiores do que o raio r calculado pela
equação
2σ
r= (55)
P
Água no Solo

46. 46 |Paulo Leonel Libardi
são esvaziados. Note-se aqui também que a equação (55) é a equação (54), para
α=0. Comparando as equações (51) e (55), pode-se verificar que são idênticas na
forma, visto que P = p = ρ a gh ; o que muda é a maneira de retirar a água do solo.
Como no caso do funil para a aplicação de h, o que limita o valor de P a ser
aplicado é a porosidade da placa. Placas com poros pequenos, evidentemente,
suportam uma pressão maior P sem rompimento do menisco nos seus poros
capilares. O valor máximo de pressão que a placa suporta é denominada de pressão
de borbulhamento da placa porosa e o valor do raio correspondente a esta pressão
pode ser calculado pela equção (55).
No comércio, encontram-se placas porosas com pressão de
borbulhamento de 100, 300, 500 e 1500 kPa. Para valores de pressão de 10 a 400
kPa, utiliza-se uma câmara de pressão também conhecida pelo nome popular de
“panela de pressão”, pela semelhança na forma com a panela de uso doméstico.
Para valores de pressão de 500 a 2000 kPa, utiliza-se uma outra câmara, de
constituição mais robusta e forma mais achatada para suportar estes altos valores
de pressão.
Também no caso das câmaras de pressão, o bom contato entre a placa
porosa e a amostra de solo é primordial, a fim de que o contato hidráulico entre
ambas seja sempre mantido.
Foi mostrado, portanto, que o potencial mátrico (φm) ou a tensão (τ) da
água no solo se relaciona com a curvatura das interfaces água-ar no solo não
saturado. Isto foi feito assumindo que estas interfaces na amostra de solo, tanto no
funil como na câmara de pressão, se acomodavam num capilar de secção
Água no Solo

47. Paulo Leonel Libardi| 47
transversal circular de raio r sob uma tensão de água h (equação 9), no caso dos
funis de placa porosa, ou P (equação 54), no caso das câmaras de pressão. O solo,
como sabemos, não é um simples tubo capilar, mas uma composição irregular de
poros e canais formados por seus sólidos. Conseqüentemente, é claro que as
interfaces não são iguais em todos os pontos do solo mas, como vimos, as
curvaturas estão todas com o mesmo valor de tensão h ou P, no equilíbrio. Isso nos
leva a concluir que o valor de r que se obtém pelas equações da capilaridade só
pode ser considerado com um “raio equivalente” sem qualquer tentativa de
quantificação do raio real do poro. De qualquer maneira, o cálculo do raio r por
meio das equações (51) e (55) para as diversas tensões, depois de determinada a
curva de retenção de um solo (Figura 17), não deixa de ser uma maneira válida
para avaliar o tamanho dos poros do solo e sua distribuição, como mostraremos a
seguir. Outra maneira válida para isso, mas que exige a visualização do poro é a)
pelo raio da maior esfera inscrita no poro, se o tamanho dos tres eixos principais
deste poro for comparável ou b) pelo raio do círculo inscrito, se a forma do poro
for tubular (Kutílek e Nielsen, 1994).
Será, agora, visto como se pode determinar a distribuição do tamanho
dos poros do solo com base na curva de retenção, pelo cálculo do “raio
equivalente” a cada tensão, pela teoria da capilaridade. Na abordagem, será
considerada a determinação da curva de retenção por secagem. Na determinação
por molhagem, a abordagem é a mesma apenas invertendo-se o sentido do
processo de determinação, isto é, enquanto na curva por secagem os poros são
esvaziados por aumento de tensão, na por molhagem os poros são preenchidos
com água por diminuição de tensão.
Água no Solo

48. 48 |Paulo Leonel Libardi
r (µm)
1000 100 50 15 10 1 0,1
θ/α
θ (m3 m-3)
r1 r2
0,55 1,00
Macroporosidade (0,043 m3 m-3)
θ1= 0,507 0,92
0,50
0,45 Mesoporosidade (0,124 m3 m-3)
0,75
0,40
θ2 = 0,383 0,70
0,35
0,30 Microporosidade (0,383 m3 m-3)
0,50
τ1 τ2
0,01 0,1 0,3 1 10 100 τ (m)
Figura 17 – Curva de retenção da água no solo em papel semi-log.
A determinação é iniciada pela elaboração do gráfico da curva de
retenção utilizando a saturação relativa θ/α no eixo das ordenadas e no eixo das
abscissas a tensão τ em escala decimal (Figura 18). A curva de retenção da Figura
18 é, portanto, o gráfico da equação (θ/α)=F(τ) no plano (τ,θ/α). Se a equação
(θ/α)=F(τ) for diferenciada com relação a τ, obtém-se a inclinação da tangente à
curva de retenção no ponto (τ,θ/α), a qual é também função de τ, isto é,
(dθ/αdτ)=f(τ), cuja unidade é portanto o inverso da unidade de tensão. É
conveniente elaborar também o gráfico da curva de −dθ/αdτ em função de τ
denominada curva diferencial da curva de retenção (Figura 19).
Água no Solo

49. Paulo Leonel Libardi| 49
θ/α
1,0
Macroporos (8%)
θ1/α = 0,92 dτ
θ 
0,9 d 
α 
dτ Mesoporos (22%)
0,8
θ 
θ2/α = 0,7 d 
α 
dτ
Microporos (70%)
0,6
τ1 τ2
0,300,360,5 1,0 1,5 2,0 τ (m)
r1 = 50 µm r2 = 15 µm
41 µm
Figura 18 – Curva de retenção da água no solo (θ/α em função deτ).
0,4
- dθ/αdτ (m-1)
0,3
0,2
τ2
− ∫τ 1
f (τ )dτ = 0,22
0,1
τ*
τ1τmax τ2
− ∫τ 2
f (τ )dτ = 0,7
0,0 0,30 0,36
0,5 1,0 1,5 2,0 τ (m)
τ1 r = 50 µm
− ∫
0
f (τ )dτ = 0,08 1 rmax = 41 µm r2 = 15 µm
Figura 19 – Curva diferencial da curva de retenção da Figura 18.
Água no Solo

50. 50 |Paulo Leonel Libardi
Observe-se que, enquanto na Figura 17 o eixo das abscissas está em
escala logarítmica (gráfico semi-log), nas Figuras 18 e 19 está em escala decimal.
Isso foi feito porque, como se pode notar pela Figura 17, para tensões acima de
aproximadamente 2 m água o conteúdo de água θ é sempre decrescente e já
tendendo para um valor constante e para algumas explicações no presente estudo é
didaticamente mais conveniente trabalhar em escala decimal.
Lembrando que θ = (Va / V) e α = (Vp / V), é fácil verificar que (θ /α)
= (Va / Vp), isto é, a saturação relativa é um índice que mede a fração cheia de água
do volume de poros de uma amostra de solo. No entanto, como ordenada da curva
de retenção, ela está vinculada à tensão τ e como tal representa, em associação
com a teoria da capilaridade, a fração do volume de poros de uma amostra de solo
correspondente aos poros (cheios de água) de raio menor do que r=2σ/ρagτ.
Observe ainda que, teoricamente, para τ =0, θ/α=1 (todos os poros cheios de água)
e, para uma τ =τ* muito alta, θ/α=0 (nenhum poro com água), pelo que a fração
θ/α também pode ser expressa em porcentagem, bastando para isso multiplicá-la
por 100.
Por outro lado, do Cálculo, se
dF (τ )
f (τ ) = ,
dτ
então
τ2 F (τ 2 )
∫
τ1
f (τ ) dτ = ∫ dF (τ ) = F (τ
F (τ 1 )
2 ) − F (τ 1 ).
Água no Solo

51. Paulo Leonel Libardi| 51
Como F(τ1)=(θ1/α) e F(τ2)=(θ2/α) (Figura 18), resulta que
τ2
θ1 θ 2
− ∫ f (τ ) dτ = − . (56)
τ1
α α
O primeiro membro da equação (56) está representado pela área hachurada da
Figura 19. Com relação ao segundo membro desta equação, percebe-se que
θ1 θ 2 θ1 − θ 2 ∆Va δVP
− = = ≡ (57)
α α α VP VP
em que ∆Va é a diferença entre o volume de água existente na amostra de solo
com conteúdo de água θ1 e o volume de água existente na amostra com conteúdo
de água θ2, portanto, igual ao volume de água liberado da amostra quando o seu
conteúdo de água decresce de θ1 para θ2 pelo aumento da tensão τ de τ1 a τ2. Tal
volume, evidentemente, é idêntico ao volume de poros esvaziados δVP quando do
aumento da tensão de τ1 a τ2.
Logo, a fração δVP/VP, medida por (θ1/α)−(θ2/α) (equação 57),
representa a fração do volume de poros da amostra correspondente aos poros de
raio menor do que r1 e maior do que r2 que são esvaziados quando se aumenta a
tensão de τ1 para τ2, visto que, pelo modelo em estudo, quando se aumenta a
tensão de 0 a τ1 são esvaziados os poros de raio maior do que r1 e quando se
aumenta a tensão de 0 a τ2 são esvaziados os poros de raio maior do que r2.
Água no Solo

52. 52 |Paulo Leonel Libardi
Exemplificando, para σ =0,072 N m-1, ρa=1000 kg m-3 e g=9,8 m s-2
na equação 51 ou 55, tem-se, para a tensão τ1= 0,3 m água (r1=50µm), que
(θ1/α)=0,92 (Figura 17 ou 18), significando que o volume de poros correspondente
aos poros de raio menor do que 50 µm é igual a 0,92 vezes o volume de poros da
amostra. Para a tensão τ2= 1,0 m água (r2=15 µm), o valor de θ2/α é
evidentemente menor, no caso 0,70 (Figura 17 ou 18), significando que 0,70 vezes
o volume de poros da amostra é igual ao volume dos poros de raio menor do que
15 µm. Como para τ0=0 m água, (θs/α)=1 e para τ =τ* m água, (θ0/α)=0, sendo θs
o conteúdo de água no solo saturado e θ0 o conteúdo de água no solo
completamente seco, então a) (θs/α)-(θ1/α)=1,00-0,92=0,08 é a fração do volume
de poros da amostra correspondente aos poros de raio maior do que r1=50 µm
(área sob a curva da Figura 19 à esquerda da área hachurada), b) (θ1/α)-
(θ2/α)=0,92-0,70=0,22 é a fração do volume de poros da amostra correspondente
aos poros de raio menor do que r1=50 µm e maior do que r2=15 µm (área
hachurada sob a curva da Figura 19) e c) (θ2/α)-(θ0/α)=0,70-0,00=0,70 é a fração
do volume de poros da amostra correspondente aos poros de raio menor do que
r2= 15µm (área sob a curva da Figura 19 à direita da área hachurada).
Empiricamente, os poros do solo têm sido classificados por meio dos
seus raios em, por exemplo (Koorevaar et al, 1983), a) macroporos: poros de raio
maior do que 50 µm, cuja principal função é a aeração do solo e a condução de
água durante o processo de infiltração, b) mesoporos: poros de raio entre 15 e
50 µm, com a função principal de conduzir a água durante o processo de
Água no Solo

53. Paulo Leonel Libardi| 53
redistribuição, isto é, após o esvaziamento dos macroporos e c) microporos: poros
de raio menor do que 15 µm que atuam, principalmente, na armazenagem da água.
Assim, pode-se dizer que, pelo modelo da capilaridade associado à
curva de retenção, 8% dos poros do solo do exemplo em estudo são macroporos,
22% são mesoporos e 70% são microporos (Figura 17, 18 ou 19). Além disso,
sendo θs = 0,55 m3m-3, θ1 = 0,507 m3m-3 e θ2 = 0,383 m3m-3 (Figura 17), pode-se
dizer também que a macroporosidade deste solo é 0,550-0,507=0,043 m3m-3, sua
mesoporosidade é 0,507-0,383=0,124 m3m-3 e sua microporosidade é 0,383-
0,000=0,383 m3m-3.
Observe-se ainda que, como para a tensão de 0,36 m água (ou o raio de
41 µm) o valor de dθ/αdτ é máximo neste solo (Figura 19), então para um dado
valor de dτ, o valor de dθ/α também é máximo à tensão de 0,36 m água (Figura
18). Consequentemente, os poros em maior porcentagem neste solo são aqueles
cujos raios estão em torno do valor de 41 µm.
Finalmente, não é demais lembrar que a colocação do eixo dos raios na
Figura 17 em comparação ao eixo das tensões, só pode ser feita quando se utiliza a
escala logarítmica nestes eixos, porque log r varia inversamente mas também
linearmente com log τ. Se fosse utilizada a escala decimal, o eixo dos raios não
poderia ser colocado em comparação ao eixo das tensões na figura, porque nessa
escala r varia inversamente mas não linearmente com τ.
Água no Solo

54. 54 |Paulo Leonel Libardi
3.3 O tensiômetro
O princípio de funcionamento do tensiômetro é muito semelhante ao
do funil de placa porosa, residindo a diferença fundamental no fato de que, no caso
do tensiômetro, ao invés de se trazer a amostra de solo para junto da placa porosa,
leva-se a placa porosa para junto da amostra, uma vez que o objetivo principal do
tensiômetro, ao contrário do funil, não é a elaboração da curva de retenção e, sim,
a medida de φm no local de interesse. Como o material poroso deve ser introduzido
no solo, é confeccionado, por esse motivo, numa forma cilíndrica, conhecida como
cápsula porosa.
O procedimento com o funil de placa porosa de se trazer o solo á
saturação e depois colocá-lo à tensão de interesse não se faz no caso do
tensiômetro. O importante, no caso do tensiômetro, é que o solo esteja o mais
úmido possível, quando da sua instalação, a fim de que haja o bom contato
necessário entre a cápsula porosa e o solo ou, em outras palavras, para que, através
dos poros da parede da cápsula, a água no tensiômetro entre em contato e se
equilibre com a água no solo. Após o estabelecimento deste equilíbrio, atinge-se,
teoricamente, a mesma situação da Figura 15b, como se pode ver na Figura 20,
que mostra um tensiômetro com manômetro de água instalado no campo medindo
a tensão τ = h m água ou o potencial mátrico φ m = -h m água no ponto C
adjacente à cápsula (note-se a semelhança entre as Figuras 15b e 20).
Evidentemente, numa condição de saturação, com o nível de um lençol de água
passando pelo ponto C, o nível da água no manômetro será coincidente com o
nível do lençol e localizar-se-á, portanto, em A (Figura 20), pelo que φ m = 0 m de
água, como na Figura 15a. Se o lençol subir para cima do ponto C, o tensiômetro
Água no Solo

55. Paulo Leonel Libardi| 55
passará a funcionar como um piezômetro de modo que, como na Figura 10, a
altura de água acima de A representará o potencial de pressão no ponto C.
Superfície do solo
z
A
C
h cápsula
porosa
água
Figura 20 - Tensiômetro com manômetro de água instalado no campo.
Devido à impraticabilidade de utilização do tensiômetro com
manômetro de água mostrado na Figura 20, principalmente sob condições de
campo, pelo fato de se ter que abrir uma trincheira para que a leitura possa ser
feita, substitui-se o manômetro de água por um manômetro de mercúrio, colocado
acima do nível do solo, conforme a Figura 21.
Evidentemente, para que o manômetro de mercúrio possa funcionar, o
tensiômetro precisa ficar com todas suas partes cheias de água, o que é feito com a
retirada da rolha de borracha, colocação de água sob pressão para eliminação de
todo o ar e recolocação da rolha à sua posição original. Assim, toda vez que sair
água do tensiômetro (aumento de h por secagem do solo ), aumenta o valor da
Água no Solo

56. 56 |Paulo Leonel Libardi
altura de mercúrio H. Evidentemente, uma diminuição de H indica diminuição da
tensão da água no solo τ = h. Há, portanto, uma dependência direta entre a leitura
do tensiômetro com manômetro de mercúrio H e a tensão da água h. A equação
que mostra como se obtém essa dependência será agora deduzida.
Sabemos que no tensiômetro da Figura 21, só haverá equilíbrio quando
a pressão líquida ∆PA, que atua na superfície do mercúrio na cuba empurrando-o
para dentro do tubo de leitura, for igual à pressão líquida ∆PB, que atua na
superfície da água no solo empurrando-a para dentro do tensiômetro através dos
poros da cápsula porosa, e que, como será esclarecido mais adiante, esse equilíbrio
só ocorre para valores da quantidade ρ Hg gH + ρ a gh2 até um máximo igual a Po.
Pelo balanço das pressões atuantes e fazendo P′ = PP = pressão interna na
interface plana e P′− p =PC = pressão interna na interface côncava, percebe-se que
(Figura 21):
∆PA = Po − (ρ Hg gH + ρ a gh2 − PP )
e
∆PB = (Po + PC ) − ρ a gh1 .
Água no Solo

57. Paulo Leonel Libardi| 57
h2
P’
H’
'
Pm
Po H
Rolha de h1
borracha
hc
'
Pm
Mercúrio Superfície do solo
Z
Parede da
cápsula Água
Po P’ - p
Partícula de Cápsula porosa
solo h
Po
P’
Figura 21 – Tensiômetro com manômetro de mercúrio instalado no campo, sendo
Po = pressão atmosférica do local, P´= pressão interna na água
numa interface plana água-ar e numa interface plana água-mercúrio
´
e Pm = pressão interna no mercúrio, numa interface plana mercúrio-
ar e numa interface plana mercúrio-água.
Água no Solo

58. 58 |Paulo Leonel Libardi
'
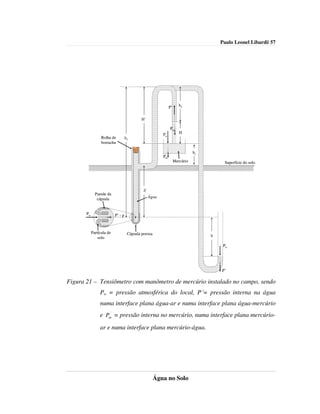
Observe-se que a pressão interna Pm na interface mercúrio-ar na cuba
'
de mercúrio se cancela com Pm na interface mercúrio-água no tubo de leitura
(Figura 21).
Conseqüentemente, no equilíbrio, ∆PA = ∆PB, porquanto,
Po − (ρ gH + ρ gh2 − PP ) = (Po + PC ) − ρ a gh1 . (58)
144Hg 424a4443 1442443
44 4 4 4
∆PA ∆PB
Explicitando PP − PC = p da equação (58) obtém-se:
p = ρ Hg gH − ρ a g (h1 − h2 ) .
Como p = ρagh e h1 – h2 = H + hc + Z (Figura 21), então,
ρ a h = ρ Hg H − ρ a H − ρ a (hc + Z ) .
Dividindo ambos os membros da equação acima por ρa, resulta que
 ρ Hg − ρ a 
h=
 ρ  H − hc − Z .
 (59)
 a 
Assumindo que ρHg = 13600 kg m-3 e ρa = 1000 kg m-3 e lembrando que φm = -h,
tem-se que
φ m = −12,6 H + hc + Z → [m água] (60)
Água no Solo

59. Paulo Leonel Libardi| 59
em que H = leitura do tensiômetro, em m Hg, hc = distância vertical do nível de
mercúrio na cuba à superfície do solo no momento da leitura, em m água e Z =
profundidade de instalação da cápsula porosa, em m água.
Um ponto importante a esclarecer a respeito do tensiômetro mostrado
na Figura 21 diz respeito a sua limitação em medir valores de tensão até um
máximo de aproximadamente 100 kPa (o valor de Po na figura). Partindo de uma
situação de equilíbrio, portanto ∆PA = ∆PB (equação 58), se o solo seca, p
aumenta, PC diminui e portanto ∆PB também diminui, com o que ∆PA tornando-se
maior do que ∆PB empurra o mercúrio para cima no tubo de leitura com
consequente aumento de H, diminuição de h2 e estabelecimento de um novo
equilíbrio. Evidentemente, a continuar o processo de secagem do solo, vai chegar
um momento em que ρHggH + ρagh2 se torna igual a Po, quando, então, a equação
(58) se torna
PP = (P + PC ) − ρ a gh1 . (61)
{ 1o4424434 4
∆PA ∆PB
Com a diminuição de PC = P′− p devido ao aumento de p a partir desse ponto, a
pressão atmosférica Po deixa de atuar para o aumento de H (empurrar o mercúrio
para dentro do tubo de leitura) e o tensiômetro não mais funciona. Isso porque,
pela equação (61), a diminuição de ∆PB = ( P0 + PC ) − ρ a gh1 por diminuição de PC
faz com que ∆PA = PP =P′ na interface água-mercúrio no tubo de leitura, tornando-
se maior do que ∆PB, tente puxar para cima a água no tubo de leitura e nesse
Água no Solo

60. 60 |Paulo Leonel Libardi
processo rompe a coluna na interface, devido a fraca adesão da água com o
mercúrio. Quando ocorre esse rompimento, que na prática se diz que o
“tensiômetro estourou”, é comum, se h2 for muito pequeno nesse momento, um
pouco de mercúrio ser impulsionado para dentro da cápsula. Portanto, o
tensiômetro funciona até o valor de PP−PC = p explicitado da equação (61):
p = Po − ρ a gh1 → [energia/volume] (62)
ou, como p = ρagh e Po = ρagHo,
h = H o − h1 → [m água]. (63)
É também conveniente incluir na equação (63) o comprimento do tubo
manométrico H’ = h1 - (hc + Z) (Figura 21), com o que:
h = H o − ( H '+ hc + Z ) (64)
Por exemplo, num local onde a pressão atmosférica (em m água) é Ho = 10 m
água, um tensiômetro com H’ = 0,8 m, hc = 0,2 m e Z = 0,5 m, funciona, de
acordo com a equação (64), até um máximo de τ = h = 8,5 m água ou a um φm
mínimo de -8,5 m água que corresponde à uma leitura máxima de H, de acordo
com a equação (60), de 0,73 m Hg.
Água no Solo

61. Paulo Leonel Libardi| 61
No caso de solos expansivos, o ponto de medida no perfil pode sofrer
a ação de uma sobrecarga (“overburden”) causada pelo material sólido acima dele,
resultando em um potencial de pressão. Quando for esse o caso, o primeiro
membro da equação (60) torna-se φm + φp e não apenas φm.
4 POTENCIAIS DO COMPONENTE ÁGUA NO SOLO
Como esclarecido no item 1 do presente texto, o que se chamou de
água no solo é na realidade uma solução aquosa que foi analisada como um todo,
sem qualquer consideração dos seus solutos dissolvidos.
O potencial de soluto surge quando estes solutos precisam ser
considerados e, para isso, a análise é feita com base no componente água da
solução no solo, utilizando o mesmo raciocínio empregado na análise da água ou
solução no solo.
Dessa forma, defini-se o potencial total do componente água no solo
ψ t , pela diferença entre a energia potencial total específica do componente água
no solo (ponto considerado), ε ca , e a energia potencial total específica do
o
componente água padrão (água pura), ε ca , ou seja, ψ t = ε ca − ε ca . A definição do
o
componente água padrão é idêntica a da água padrão: água pura e livre de mesma
energia interna que o componente água no solo e em cuja superfície plana,
coincidente com a referência gravitacional, atua a pressão atmosférica local.
Assim, igualmente ao caso da água ou solução no solo, no caso do
componente água, quando entre dois pontos num meio ∆ψ t = 0 , tem-se uma
Água no Solo

62. 62 |Paulo Leonel Libardi
condição de equilíbrio e, quando entre estes pontos ∆ψ t ≠ 0, há movimento do
componente água do ponto com maior ψ t para o ponto com menor ψ t , desde que
haja uma parede permeável somente ao componente água separando os dois
pontos. Tal parede recebe o nome de membrana semipermeável. É fácil perceber
que, na ausência de tal membrana, o movimento é da solução porque os solutos
dissolvidos estão presos às moléculas de água e movem-se sempre com elas.
À semelhança da matriz do solo, os solutos dissolvidos também
diminuem a energia potencial total específica da água pura, portanto, o potencial
de soluto do componente água no solo, ψs, é também interpretado como uma
medida do trabalho que se tem que dispender para liberar, da influência dos
solutos, a unidade de volume do componente água da solução, tornando-a livre
como o componente água padrão ou, quando a única causa da diferença entre εca e
o o
ε ca for a presença de solutos no ponto considerado, ψ s = ε ca − ε ca = − W Vca
(energia/volume de água pura). Fica, portanto claro que, para se medir ψs, há
necessidade de se ter a solução fora dos poros do solo.
Considere-se, então, uma solução extraída de um determinado solo.
Coloque-se esta solução em contato com água pura, por meio de uma membrana
semipermeável, num recipiente, de tal maneira que a membrana se posicione
verticalmente no centro, a água pura, sob pressão atmosférica, ocupe o volume à
esquerda e a solução, também sob pressão atmosférica, ocupe o volume (igual) à
direita do recipiente. Segue-se, pela teoria dos potenciais, que, como o potencial
total do componente água na água pura, ψt (água pura), é maior do que o potencial
total do componente água na solução, ψt (solução), vai ocorrer movimento de água
Água no Solo

63. Paulo Leonel Libardi| 63
pura em direção ao volume à direita (com solução) do recipiente, até que oψt
(solução) se iguale ao ψt (água pura). A esse fenômeno dá-se o nome de osmose.
Para se evitar o fenômeno da osmose no experimento acima, uma
pressão maior do que a pressão atmosférica, Po+π, deve ser aplicada à solução
para elevar o potencial total do componente água nesta solução e torná-lo igual ao
potencial total do componente água na água pura. Nessa condição de equilíbrio,
portanto, ψt (água pura)=ψt (solução) e, como ψt (água pura)=0 eψt
(solução)=ψs+π, resulta que ψs=-π (energia/volume de água pura).
A pressão π que deve ser aplicada à solução para evitar a osmose do
componente água para ela, é chamada de pressão osmótica da solução, daí ψ s ser
também chamado de potencial osmótico do componente água, pelo fato de ser
igual à pressão osmótica da solução com o sinal trocado.
A definição do potencial de pressão do componente água no solo
saturado, ψ p , é idêntica à definição de φ p , substituindo “água no solo” por
“componente água no solo”. Isto porque, sendo a concentração de solutos da água
no solo idêntica a da água padrão, os solutos não exercem qualquer influência na
definição de φ p . O que muda em ψ p em relação a φ p é sua referência ao
componente água: energia/massa ou volume de água pura.
Com relação aos potenciais gravitacional ψ g e mátrico ψ m do
componente água no solo, a definição é também a mesma que φ g e φ m da solução
no solo, mudando apenas a referência que é feita com relação ao componente água
Água no Solo

64. 64 |Paulo Leonel Libardi
no solo. Lembre-se que, no caso de φ m , as placas porosas dos funis de Haines e
das câmaras de Richards são permeáveis aos solutos pelo que, no equilíbrio, a
influência do soluto não é detectada. Evidentemente, se a placa porosa nestes
instrumentos fosse substituída por uma membrana semipermeável, no equilíbrio, o
valor de h (nos funis) e o de P (nas câmaras), com o sinal trocado, iriam
representar, teoricamente, a soma ψ m + ψ s .
5 MOVIMENTO DA ÁGUA NO SOLO
A quantificação do movimento da água no solo é feita pelas chamadas
equações de fluxo da água no solo. Estas equações são definidas para duas
situações, uma na qual as características do fluxo não variam com o tempo mas
podem variar com a posição e a outra na qual as características do fluxo variam
com o tempo e a posição. As equações desenvolvidas para o primeiro tipo de
situação são denominadas de equações para fluxo em regime estacionário e as
desenvolvidas para o segundo tipo de situação, de equações para fluxo em regime
não estacionário ou transiente.
5.1 Fluxo da água no solo em regime estacionário
O esquema da Figura 22 representa uma coluna de solo homogêneo
saturado através da qual está havendo um fluxo de água no sentido descendente.
Como se pode verificar por esta figura, há dois piezômetros instalados nesta
coluna: um no ponto C (ponto de cima) e um no ponto B (ponto de baixo). Além
Água no Solo

65. Paulo Leonel Libardi| 65
disso, está-se mantendo, durante o movimento, uma carga hidráulica constante
(representada pelo pequeno triângulo com um de seus vértices tocando a superfície
livre de água) nas duas extremidades da coluna. Com esse arranjo experimental,
depois de um certo tempo, atinge-se uma condição de equilíbrio dinâmico ou de
regime estacionário, isto é, uma situação em que os valores da vazão Q e do
potencial total φt não variam mais com o tempo. Observe que o potencial total
(soma do potencial de pressão pressão φp com o potencial gravitacional φg) é lido
diretamente no manômetro como sendo a distância vertical da referência
gravitacional (RG) à superfície de água no tubo manométrico.
Se for desenvolvido um experimento com o arranjo experimental da
Figura 22 para diferentes valores de L (comprimento de solo entre os pontos C e
B), diferentes valores de A (área da secção transversal da coluna) e diferentes
valores da diferença de potencial total φt (C) - φt (B), em que φt (C) é o potencial
total no ponto de cima (dai a letra C) e φt (B) é o potencial total no ponto de baixo
(daí a letra B), obtem-se as seguintes conclusões:
1a. A vazão Q, isto é, o volume de água que atravessa a coluna por unidade de
tempo é proporcional a A, isto é, em símbolos:
Qα A . (65)
2a. A vazão Q é proporcional à diferença de potencial total φt (C) - φt (B) através
do solo:
Água no Solo

66. 66 |Paulo Leonel Libardi
Qα [φt (C ) − φt ( B)] . (66)
3a. A vazão Q é inversamente proporcional ao comprimento L de solo:
1
Qα . (67)
L
Ora, quando uma grandeza é simultaneamente proporcional a várias
outras, é também proporcional ao produto delas. Assim, a combinação destas três
conclusões resulta em:
φt (C ) − φt (B )
Qα A . (68)
L
Substituindo, então, o símbolo de proporcionalidade por uma constante de
proporcionalidade Ko obtém-se:
φt (C ) − φt (B )
Q = Ko A . (69)
L
Este tipo de experimento que levou à obtenção da equação (69) foi
desenvolvido pela primeira vez em 1856 pela engenheiro hidráulico Henry Darcy,
daí a equação (69) ser conhecida pelo nome de Lei de Darcy. Na época, o que hoje
estamos chamando de potencial total (φt), Darcy chamava de carga piezométrica.
Água no Solo

67. Paulo Leonel Libardi| 67
Depreende da equação (69) que a constante de proporcionalidade Ko é
uma constante que diz respeito à transmissão da água através do solo na condição
de saturação, ou seja, é uma propriedade do solo que traduz quão rápido ou
devagar a água atravessa o solo, quando saturado. Por esse motivo, Ko é
denominada condutividade hidráulica do solo saturado.
Se ambos os membros da equação (69) forem divididos por A,
transforma-se seu membro da esquerda numa vazão por unidade de área, isto é,
num volume de água que passa verticalmente para baixo [se φt (C) > φt (B)] ou
para cima [se φt (C) < φt (B)] através da unidade de área da secção transversal da
coluna, por unidade de tempo. Assim:
Q φ (C ) − φt (B )
qo = = Ko t , (70)
A L
sendo qo, de valor igual a Q/A, denominado densidade de fluxo de água no solo
saturado.
A mesma coluna de solo que na Figura 22 está em pé (na vertical)
também pode ser colocada deitada (na horizontal) ou mesmo inclinada. Também
nestes casos a Lei de Darcy é válida. O importante é não esquecer que, em
qualquer caso (vertical, horizontal ou inclinada), L representa sempre o
comprimento de solo ao longo da direção do movimento da água.
Água no Solo

68. 68 |Paulo Leonel Libardi
z Piezômetro
φp(C)
tela
zC
C
L
φt(C) φp(B)
zB φg(C)
B
tela
φt(B)
φg(B) recipiente
graduado
para medir
a vazão Q
RG
y
x
Figura 22 - Fluxo da água em solo saturado: diagrama do arranjo experimental
para comprovação da lei de Darcy.
Para dar um tratamento matemático à Lei de Darcy, é necessária a
utilização de um sistema de coordenadas cartesianas x, y, z, como mostrado na
Figura 22. Com isso, pode-se substituir L por zC – zB e reescrever a equação (70)
como
Água no Solo

69. Paulo Leonel Libardi| 69
φt (C ) − φt ( B)
qo = − K o . (71)
zC − z B
Colocou-se o sinal negativo na equação para que um valor positivo de qo indique
fluxo na direção positiva de z (de zB para zc: para cima) e um valor negativo de qo
indique fluxo na direção negativa de z (de zc para zB: para baixo).
Na direção-x (horizontal), idêntico para a direção-y, a lei de Darcy
seria escrita como
φt ( D) − φt ( E )
qo = − K o (72)
xD − xE
sendo φt (D), o potencial total no ponto da direita da coluna (daí a letra D) e φt (E),
o potencial total no ponto da esquerda da coluna (daí a letra E). Dessa maneira,
quando qo > 0, o fluxo é na direção positiva de x (para a direita, de xE para xD) e
quando qo < 0, o fluxo é para a esquerda (de xD para xE).
Numa direção-s qualquer, coluna inclinada, tem-se
φt (C ) − φt ( B)
qo = − K o , (73)
sC − s B
em que φt (C) é o potencial total no ponto C, ponto de cima da coluna inclinada, e
φt (B) é o potencial total no ponto B, ponto de baixo da coluna inclinada, mantendo
a convenção de que quando qo > 0 o fluxo é na direção positiva de s (de sB para sC:
subindo a coluna inclinada) e quando qo < 0, na direção negativa de s (de sC para
sB: descendo a coluna inclinada).
Água no Solo

70. 70 |Paulo Leonel Libardi
Refinando um pouco mais o tratamento matemático da lei de Darcy
pode-se escrever sua equação na forma diferencial a partir da equação (73), ou
seja,
dφt
qo = − K o . (74)
ds
Nessa forma, pode-se ainda dar um tratamento vetorial à lei de Darcy, visto que qo
possui direção e sentido, o mesmo ocorrendo com o termo dφt/ds que, sendo a
variação de um escalar com a distância ao longo de uma direção entre duas
superfícies equipotenciais do escalar, é o que em Análise Vetorial define-se como
vetor gradiente de um escalar, no caso, vetor gradiente de potencial total, cujo
módulo é dφt/ds, cuja direção é a da reta s, perpendicular às superfícies
equipotenciais, e cujo sentido é o dos φt crescentes. Na notação vetorial, portanto,
a equação (74) é reescrita como
r dφ
ˆ
qo = − K o t s , (75)
ds
ˆ
sendo s o vetor unitário na direção-s. Pela equação (75) está-se assumindo que Ko
é uma propriedade isotrópica, ou seja, seu valor não depende da direção dentro do
r
meio, é um escalar, pelo que se pode dizer que q o possui o mesmo módulo, a
ˆ
mesma direção, mas sentido oposto do vetor Ko (dφt/ds) s , justificando,
vetorialmente, o sinal negativo da equação.
Água no Solo

71. Paulo Leonel Libardi| 71
Pela análise vetorial, pode-se decompor a equação (75) nas três
direções x, y e z perpendiculares entre si:
r ∂φ ˆ
qox = − K o t i , (76)
∂x
r ∂φ
q oy = − K o t ˆ
j (77)
∂y
e
r ∂φ ˆ
q oz = − K o t k , (78)
∂z
ˆ
sendo iˆ , ˆ e k , os vetores unitários nas direções x, y e z, respectivamente, Nas
j
expressões acima utilizou-se derivada parcial para indicar, em cada uma delas, que
φt varia com apenas uma das coordenadas de posição, as outras duas sendo
mantidas constantes.
Portanto, vetorialmente, para solos isotrópicos com relação a Ko,
r dφ  ∂φ ˆ ∂φ ∂φ ˆ
qo = − K o t s = − K o  t i + t ˆ + t
ˆ  ∂x j k.
 (79)
ds  ∂y ∂z 
A equação (79) que, como visto, se aplica para o fluxo da água em solo
saturado foi generalizada mais tarde, principalmente por Buckingham (1907) e
Richards (1928), para o fluxo da água em solo não saturado, como:
Água no Solo

72. 72 |Paulo Leonel Libardi
r dφ
q = − K (θ ) t s ,
ˆ (80)
ds
numa direção-s qualquer e, igualmente, considerando o sistema de coordenadas x,
y, z, como
r ∂φ ˆ
q x = − K (θ ) t i , (81)
∂x
na direção-x,
r ∂φ
q y = − K (θ ) t ˆ ,
j (82)
∂y
na direção-y, e
r ∂φ ˆ
q z = − K (θ ) t k , (83)
∂z
na direção-z, tal que
r ∂φ  ∂φ ˆ ∂φ ∂φ ˆ
q = − K (θ ) t s = − K (θ ) t i + t ˆ + t
ˆ  ∂x j k.
 (84)
∂s  ∂y ∂z 
Nesta equação (84), K(θ) é a condutividade hidráulica como função do conteúdo
de água θ e φt = φm (θ)+φg, sendo φm (θ) o potencial mátrico como função θ. Foi
Buckingham (1907) quem introduziu na Ciência do Solo as funções φm = φm (θ) e
K = K(θ). A equação (84) é denominada equação de Darcy-Buckingham, para
solos isotrópicos com relação a K(θ).
Água no Solo

73. Paulo Leonel Libardi| 73
À semelhança da equação (79), verifica-se facilmente que a
interpretação física dos parâmetros da equação (84) é idêntica a dos parâmetros da
equação (79), com a diferença de que, agora, o solo é não saturado. A propósito,
observe-se a semelhança entre as equações (79) e (84). Na realidade a equação
(79) é um caso particular da equação (84), visto que, quando o movimento da água
é sob condição saturada, θ = θs (conteúdo de água de saturação), K(θs) = Ko
(condutividade hidráulica do solo saturado), φt = φp + φz e a equação (84) se torna
idêntica à equação (79).
Na forma finita, a equação de Darcy-Buckingham na direção vertical
(83) pode, então, ser escrita, à semelhança da equação de Darcy (71), como
φt (C ) − φt ( B)
q = − K (θ ) , (85)
zC − z B
ou seja, idêntica à equação (71), evidentemente, com as diferenças já apontadas no
que diz respeito às funções K(θ) e φm(θ).
Assim, na montagem de um arranjo experimental para o estudo do
movimento da água em solo homogêneo sob condições de não-saturação, os
piezômetros da Figura 22 devem ser, portanto, substituidos por tensiômetros
(Figura 23), com o que, em regime de fluxo estacionário, a equação que quantifica
o movimento da água é a equação (85), do mesmo modo que a equação (71)
quantifica o movimento da água sob a condição de saturação.
Água no Solo

74. 74 |Paulo Leonel Libardi
z
coluna de solo
perfurada
placa porosa
tensiômetro com
manômetro de água
zC
C
−φm(C)
L
cápsula porosa
zB
φg(C) −φm(B)
B
φt(C) placa porosa
φg(B) Recipiente graduado
φt(B) para medir a vazão Q
y RG
x
Figura 23 - Fluxo da água em solo não saturado: diagrama do arranjo
experimental para comprovação da equação de Darcy-Buckingham.
Verifica-se que neste caso, o potencial total é também lido diretamente
no manômetro, agora do tensiômetro, como sendo a distância vertical da
referência gravitacional (RG) à superfície de água no tubo manométrico.
As placas porosas nos extremos da coluna da Figura 23 são necessárias
para que, com a utilização das tensões desejadas através delas, provoque-se a
dessaturação do solo. A coluna deve também ser perfurada para que o ar possa
Água no Solo

75. Paulo Leonel Libardi| 75
nela entrar e substituir a água quando deste processo de dessaturação.
Evidentemente, quanto maior o valor da tensão utilizada, mais seco o solo se torna.
Um ponto importante a esclarecer é que a condutividade hidráulica só
vai ser a mesma em todos os pontos ao longo da distância entre os pontos C e B da
Figura 23, se as tensões nestes pontos forem iguais (as leituras dos tensiômetros C
e B forem iguais) na condição de fluxo estacionário. No caso de as tensões não
serem iguais, θ e, conseqüentemente K, serão diferentes ao longo da coluna mas,
pela estacionaridade, não variarão com o tempo. Nesta situação, o gradiente de φt,
calculado por
[φt (C ) − φt ( B)] /( z C − z B )] ,
será uma aproximação da tangente à curva de φt em função de z, no ponto central
entre os pontos C e D, ou seja, o K da equação (85) refere-se ao K neste ponto
central, quando φm(C) for diferente de φm(B).
5.2 Fluxo da água em regime transiente
Para descrever uma situação transiente ou não-estacionária, tem-se que
lançar mão da equação da continuidade. Matematicamente, a equação da
continuidade estabelece que não pode haver nem criação nem destruição de massa,
isto é, é a equação da conservação de massa.
Água no Solo

76. 76 |Paulo Leonel Libardi
Para se obter a equação da continuidade para a densidade de fluxo da
água no solo, seja um elemento de volume dV retangular de solo ABCDEFGH,
localizado pelo seu vértice D num sistema de coordenadas cartesianas x, y, z, tal
que AD = BC = EH = FG = dx, AE = BF = DH = CG = dy, AB = CD = EF =
HG = dz e dx dy dz = dV (Figura 24).
z
C G
z
F
B
dz
^
qy j q'y ^
j
H
D
dx
E
A
dy
y
y
x
x
Figura 24 - Elemento de volume de solo, através do qual solução está fluindo.
Água no Solo

77. Paulo Leonel Libardi| 77
Nestas condições, chamando de qy a densidade de fluxo da água na
direção-y, então, o elemento de volume de água por unidade de tempo entrando
através da face ABCD de área dxdz, ∂Va, entra, y/∂ t, é dado por:
∂Va ,entra , y
= q y dxdz . (86)
∂t
Igualmente, o elemento de volume de água por unidade de tempo saindo através da
face EFGH, também de área dxdz, ∂Va, sai, y/∂ t, será
∂Va , sai , y
= q 'y dxdz (87)
∂t
ou
∂Va, sai, y  ∂q y 
= qy +
 dy dxdz .
 (88)
∂t  ∂y 
Consequentemente, subtraindo a equação (88) da equação (86), obtém-se a
diferença entre o elemento de volume de água que entra através da face ABCD e o
elemento de volume de água que sai através da face EFGH por unidade de tempo,
ou seja,
∂Va ,entra , y ∂Va ,sai , y ∂q y
− =− dxdydz (89)
∂t ∂t ∂y
ou, como dx dy dz = dV (Figura 24),
Água no Solo

78. 78 |Paulo Leonel Libardi
∂Va,entra, y ∂Va,sai, y ∂q y
− =− dV . (90)
∂t ∂t ∂y
Utilizou-se o símbolo ∂ nas equações (86) a (90) para indicar que se trata apenas
da direção-y.
De maneira idêntica à direção-y, tem-se que, para a direção-x,
∂V a ,entra , x ∂Va , sai , x ∂q x
− =− dV (91)
∂t ∂t ∂x
e, para a direção-z, que
∂V a ,entra , z ∂V a , sai , z ∂q z
− =− dV . (92)
∂t ∂t ∂z
A soma membro a membro das equações (90), (91) e (92) vai
representar, evidentemente, a diferença entre o elemento de volume de água que
entra através das faces DCGH, ABCD, e ADHE e o elemento de volume de água
que sai através das faces ABFE, EFGH e BCGF, respectivamente, do elemento de
volume dV, no intervalo de tempo ∂ t:
dVa ,entra − dVa ,sai  ∂q ∂q y ∂q z 
= − x +
 ∂x + dV , (93)
∂t  ∂y ∂z 
Água no Solo

79. Paulo Leonel Libardi| 79
em que, portanto, dVa ,entra = ∂Va ,entra , x + ∂Va ,entra , y + ∂Va ,entra , z e
dV a , sai = ∂V a , sai , x + ∂V a , sai , y + ∂Va , sai , z .
Como θ = dVa / dV , resulta, ao dividir ambos os membros da equação (93)
por dV, que
∂θ  ∂q ∂q y ∂q z 
= − x +
 ∂x + , (94)
∂t  ∂y ∂z 
em que ∂θ = θ t +∂t − θ t é idêntico a (dVa,entra - dVa,sai)/dV, sendo θt + ∂t o conteúdo de
água à base de volume no elemento de volume de solo dV, no tempo t + ∂ t, e θt o
conteúdo de água à base de volume no elemento, no tempo t.
A equação (94) é denominada equação da continuidade para a
densidade de fluxo da água no solo e nela utilizou-se diferencial parcial de θ com
relação a t, porque o elemento de volume e, portanto, as coordenadas x, y e z,
permanecem fixas no espaço enquanto t varia.
Para melhor compreender a equação da continuidade para o
movimento da água, considere-se que o movimento se dê em uma coluna de solo
de comprimento S posicionada numa direção qualquer s no espaço (figura 25).
Nestas condições, a equação da continuidade (equação 94) seria escrita como:
∂θ dq
=− (95)
∂t ds
Água no Solo

80. 80 |Paulo Leonel Libardi
ou, de forma finita, para uma fatia i de solo (Figura 25),
δθ qi − qi −1
=−
∆t si − si −1 , (96)
em que δθ = θ ( final) − θ (inicial) , sendo θ ( final ) = conteúdo de água no tempo t +
∆t e θ (inicial ) = conteúdo de água no tempo t. Como si – si - 1 = ∆si, então
δθ qi −1 − qi
= (97)
∆t ∆si
ou ainda
δθ∆s i
= q i −1 − q i . (98)
∆t
Pela definição de variação de armazenagem, pode-se escrever a equação (98)
também como:
δhi
= qi −1 − qi , (99)
∆t
sendo
δ hi = variação da armazenagem de água numa fatia i de solo de comprimento
∆si,entre os tempos t+ ∆t e t.
Água no Solo

81. Paulo Leonel Libardi| 81
qi-1 = densidade de fluxo de água que entra na fatia i durante o intervalo de tempo
∆t
qi = densidade de fluxo de água que sai da fatia i durante o intervalo de tempo ∆
t.
No intervalo de tempo ∆ t mas para o comprimento de solo S, tem-se:
∆h s 1 n n
∆t
= ∑
∆t i =1
δhi = ∑ (q i −1 − q i ) ,
i =1
(100)
sendo ∆hs, portanto, a variação da armazenagem de água no comprimento S de solo
entre os tempos t + ∆ t e t.
Como
n
∑ (q
i =1
i −1 − qi ) = qo − q n , (101)
então,
∆hs
= qo − q n , (102)
∆t
sendo n, evidentemente, o número de fatias que somam o comprimento S de solo,
qo a densidade de fluxo de água que entra no comprimento S de solo, durante o
Água no Solo

82. 82 |Paulo Leonel Libardi
intervalo de tempo ∆ t e qn a densidade de fluxo de água que sai do comprimento
S, durante o mesmo intervalo de tempo ∆ t (figura 25).
s
n=n
... qn
n=i
...
qi ∆sn
qi - 1
n=2
∆si
n=1
S si
q1
si - 1 ∆si = si – si -1
∆s2
qo ∆s1
Figura 25 – Coluna de solo de comprimento S subdividida em n fatias de
comprimentos ∆s1, ∆s2, ... , ∆si, ... , ∆sn.
Portanto, de maneira prática, pode-se concluir que a equação da
continuidade (equação 102) diz que “a variação da armazenagem de água num
determinado comprimento de solo, num certo intervalo de tempo, pode ser
determinada pela diferença entre a densidade de fluxo de água que entra numa das
extremidades deste comprimento e a densidade de fluxo de água que sai na outra
extremidade no intervalo de tempo considerado” ou, de maneira inversa, que “a
diferença entre a densidade de fluxo de água que entra numa das extremidades de
um determinado comprimento de solo e a densidade de fluxo de água que sai na
Água no Solo

83. Paulo Leonel Libardi| 83
outra extremidade, num um certo intervalo de tempo, pode ser determinada pela
variação da armazenagem de água neste comprimento de solo, no intervalo de
tempo considerado”.
A combinação da equação de Darcy-Buckingham (equação 84) com a
equação da continuidade (equação 94) fornece a equação diferencial geral que rege
o movimento da água no solo, também conhecida como equação de Richards, ou
seja,
a) na direção-x (horizontal), idêntico para a direção-y:
∂θ ∂ ∂φ
= [ K (θ ) m ] (103)
∂t ∂x ∂x
uma vez que ∂φ g / ∂x = 0 .
e
b) na direção-z (vertical):
∂θ ∂ ∂φ
= [ K (θ ) t ] (104)
∂t ∂z ∂z
ou, quando se expressa os potenciais em altura de água,
∂θ ∂   ∂φ 
=  K (θ ) m + 1 (105)
∂t ∂z   ∂z 
visto que ∂φ g / ∂z = 1 quando se expressa φg em altura de água.
Água no Solo

84. 84 |Paulo Leonel Libardi
6 BALANÇO DE ÁGUA NO SOLO
A diferença entre a quantidade de água que entra e a quantidade de
água que sai através das faces de um volume de solo, durante um certo intervalo de
tempo, é denominada de balanço de água no referido volume de solo. Expressando
estas quantidades em altura de água, este balanço representa a variação de
armazenagem de água no volume de solo considerado, no intervalo de tempo
selecionado.
Numa situação em que se deseja avaliar o balanço de água num solo
com uma cultura agrícola, no campo, o volume de solo considerado vai depender
da cultura em estudo, pois deve englobar o sistema radicular desta cultura. Assim,
considera-se como limite superior deste volume, a interface solo-atmosfera ou
superfície do solo e, como limite inferior, uma superfície paralela à primeira na
profundidade do sistema radicular da cultura. Neste caso, as quantidades de água
que entram e que saem são representadas pelos processos: precipitação pluvial P,
irrigação I, deflúvio superficial (de entrada Re e de saída Rs), deflúvio
subsuperficial (de entrada Re' e de saída R s' ), drenagem interna D, ascensão
capilar AC e evapotranspiração real ET (Figura 26). Com isso, obtém-se a seguinte
equação para o balanço ou variação de armazenagem ∆h :
∆h = P + I + R e + Re' + R s + R s' + AC + D + ET . (106)
Nessa equação, os valores dos processos de entrada são positivos e os de saída,
negativos.
Água no Solo

85. Paulo Leonel Libardi| 85
ET
P I E+T
Re
Z=0 Rs
R´
e
R´
sistema s
radicular hL
AC
Z=L
D
Figura 26 – Balanço de água no solo com uma cultura agrícola.
A drenagem interna representa a perda de água para fora da zona
radicular através do limite inferior do volume de solo considerado. Porém,
dependendo das condições, ao invés de sair, a água pode entrar através desse
limite. À essa entrada de água através da superfície inferior do volume de controle
de solo tem sido dado o nome de ascensão capilar (AC). O deflúvio superficial e o
deflúvio sub-superficial, dependendo da posição da área escolhida para o balanço
no relevo do terreno e das condições físicas do perfil de solo, também podem se
constituir de incrementos de água positivos ou negativos, isto é, entrando e saindo
lateralmente sobre e sob a superfície do solo, respectivamente (Figura 26).
Evidentemente, P e I são processos de entrada e ET processo de saída de água, no
volume de solo considerado.
Água no Solo

86. 86 |Paulo Leonel Libardi
É evidente que os termos da equação (106), também chamados de
componentes do balanço de água, podem, individualmente, estar mais ligados a
uma determinada área do conhecimento na qual são estudados com maior
profundidade. No âmbito da Física do solo, a variação de armazenagem, a
drenagem interna e a ascensão capilar são os componentes que se revestem de
maior importância e os tópicos anteriores desse texto fornecem a base para a sua
determinação. Numa situação na qual se tenha segurança de que os fluxos laterais,
de difícil determinação, podem ser desprezados, pode-se simplificar a equação do
balanço para
∆h = P + I + AC + D + ET . (107)
Na equação (107), tanto o componente precipitação pluvial P como o componente
irrigação I são de medida relativamente fácil. A precipitação é avaliada por meio
de pluviômetros e a irrigação, quando for o caso, deve ser eficientemente
controlada. Por outro lado, a variação de armazenagem é calculada a partir de
perfis de conteúdo de água e a drenagem interna e a ascensão capilar, no limite
inferior do volume de controle, são estimadas por meio da equação de Darcy-
Buckingham. Sobra a evapotranspiração real que é então estimada considerando-a
como a incógnita da equação (107). Essa maneira de estimar ET é conhecida como
método do balanço de água no solo para estimativa de ET.
Alguns exemplos sobre o estudo dos componentes do balanço de água
no solo podem ser vistos, por exemplo em Reichardt et al (1979), Libardi e Saad
(1994) e Cruz et al (2005).
Água no Solo

87. Paulo Leonel Libardi| 87
7 REFERÊNCIAS BIBLIOGRÁFICAS
BUCKINGHAM, . Studies of the movement of soil moisture.USDA Bur.,Soil
Bull. 38, 1907.
CRUZ, A.C.R., LIBARDI, P.L.,ROCHA, G.C. & CARVALHO, L.A.
Evapotranspiração real de uma cultura de laranja em produção num latossolo
vermelho-amarelo. R. Bras. Ci. Solo, 29: 659-668, 2005.
HAINES, W. B. Studies in the physical properties of soil: V. The hysteresis effect
in capillary properties and the modes of moisture associated therewith. J. Agr.
Sci. 20: 97-116, 1930.
KIRKHAM , D. & POWERS, W.L. Advanced Soil Physics. New York, Wiley-
Iterscience, a division of John Wiley & Sons, 533p, 1972.
KOOREVAAR, P., MENELIK, G. & DIRKSEN, C. Elements of Soil Physics.
Development in Soil Science, Amsterdam, Elsevier, 13, 228p,1983.
LIBARDI, P.L. Dinâmica da Água no Solo. São Paulo, Editora da Universidade de
São Paulo (EDUSP), 344p, 2005.
LIBARDI, P.L. & SAAD, A.M. Balanço hídrico em uma cultura de feijão irrigado
por pivot-central em latossolo roxo. R. Bras. Ci. Solo, 18; 529-532,1994.
REICHARDT, K., LIBARDI, P.L., SAUNDERS, L.C.U. & CADIMA, Z.A.
Dinâmica da água em solo cultivado com milho. R. Bras. Ci. Solo, 3: 1-5,1979.
RICHARDS, L. A. The usefulness of capillary potential of soil moisture and plant
investigation. J. Agr. Res. 37:719-742, 1928.
RICHARDS, L. A. A pressure membrane extractor apparatus of soil solution. Soil
Sci. 51: 377-386, 1941.
RICHARDS, L. A. A pressure membrane apparatus – construction and use. Agr.
Eng. 28: 451-454, 1947.
RICHARDS, L. A. Methods of measuring soil moisture tension. Soil Sci. 68: 95-
112, 1949.
Água no Solo