Operações com vetores
•Transferir como PPTX, PDF•
3 gostaram•1,126 visualizações
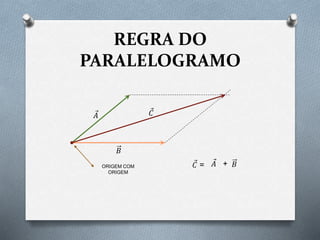
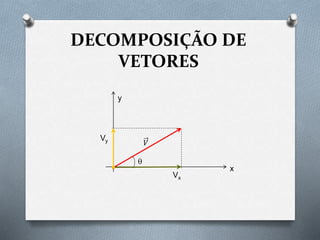
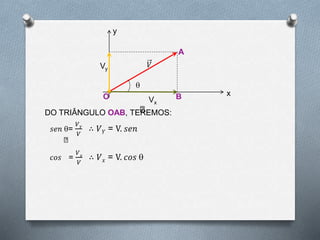
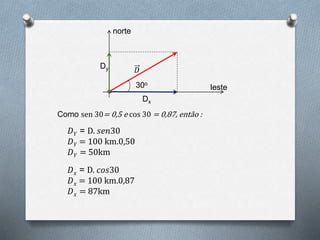
1) A soma de vetores ou vetor resultante consiste em representar dois ou mais vetores em um único vetor de acordo com as regras do paralelogramo ou poligono. 2) As componentes retangulares de um vetor podem ser calculadas usando as relações trigonométricas de senos e cossenos em um triângulo retângulo. 3) Um exemplo mostra como calcular as componentes leste-oeste e norte-sul de um deslocamento que forma um ângulo de 30° com a direção leste.
Denunciar
Compartilhar
Denunciar
Compartilhar
Recomendados
Cinemática introdução
O documento discute conceitos básicos de cinemática, incluindo: (1) movimento e repouso definidos em relação à variação da posição de um corpo em relação a um referencial com o tempo; (2) deslocamento e distância percorrida; e (3) velocidade média calculada pela razão entre deslocamento e intervalo de tempo. Exemplos ilustram como calcular essas grandezas cinemáticas.
MRU / MRUV - Slide de física.
O documento discute conceitos fundamentais de física como movimento retilíneo uniforme, movimento retilíneo uniformemente variado, funções de posição, velocidade e aceleração para diferentes tipos de movimento. Ele fornece exemplos como o movimento de um rapaz em movimento uniforme e de um paraquedista em queda livre para ilustrar esses conceitos.
Aula de unidades de medidas
O documento descreve o Sistema Métrico Decimal, incluindo a unidade de comprimento metro e seus múltiplos e submúltiplos. Explica como converter entre unidades como quilômetros, metros, decâmetros, decímetros e centímetros. Fornece exemplos de conversões e exercícios para praticar.
Porcentagem 2016
O documento explica o conceito de porcentagem e como calcular valores após aumentos ou descontos percentuais. É apresentado que porcentagem é uma razão especial e como transformar porcentagens em frações decimais. Exemplos demonstram cálculos de preços com acréscimos e reduções percentuais usando fatores de aumento e redução.
Introdução à ondulatória
O documento introduz conceitos fundamentais sobre ondas, classificando-as segundo sua natureza (mecânicas ou eletromagnéticas), direção de propagação (unidimensionais, bidimensionais ou tridimensionais) e direção de vibração (transversais ou longitudinais). Também define grandezas como frequência, período, comprimento de onda e velocidade, e apresenta exemplos de interferência, reflexão e refração de ondas em cordas.
TERMOLOGIA
1) A termologia estuda os fenômenos relacionados ao aquecimento e resfriamento dos corpos.
2) A temperatura está associada ao nível de agitação das partículas de um corpo, sendo maior quanto maior a temperatura.
3) As principais escalas termométricas são Celsius, Fahrenheit e Kelvin, cada uma definindo pontos fixos como o gelo fundente e a ebulição da água.
Medidas e sistema de unidades
O documento discute o histórico e os sistemas de medidas, incluindo o Sistema Métrico Decimal e o Sistema Internacional de Unidades (SI). O SI define sete unidades básicas e derivadas, como o metro e o quilograma. O documento também explica a notação científica e prefixos usados para expressar grandezas físicas.
Recomendados
Cinemática introdução
O documento discute conceitos básicos de cinemática, incluindo: (1) movimento e repouso definidos em relação à variação da posição de um corpo em relação a um referencial com o tempo; (2) deslocamento e distância percorrida; e (3) velocidade média calculada pela razão entre deslocamento e intervalo de tempo. Exemplos ilustram como calcular essas grandezas cinemáticas.
MRU / MRUV - Slide de física.
O documento discute conceitos fundamentais de física como movimento retilíneo uniforme, movimento retilíneo uniformemente variado, funções de posição, velocidade e aceleração para diferentes tipos de movimento. Ele fornece exemplos como o movimento de um rapaz em movimento uniforme e de um paraquedista em queda livre para ilustrar esses conceitos.
Aula de unidades de medidas
O documento descreve o Sistema Métrico Decimal, incluindo a unidade de comprimento metro e seus múltiplos e submúltiplos. Explica como converter entre unidades como quilômetros, metros, decâmetros, decímetros e centímetros. Fornece exemplos de conversões e exercícios para praticar.
Porcentagem 2016
O documento explica o conceito de porcentagem e como calcular valores após aumentos ou descontos percentuais. É apresentado que porcentagem é uma razão especial e como transformar porcentagens em frações decimais. Exemplos demonstram cálculos de preços com acréscimos e reduções percentuais usando fatores de aumento e redução.
Introdução à ondulatória
O documento introduz conceitos fundamentais sobre ondas, classificando-as segundo sua natureza (mecânicas ou eletromagnéticas), direção de propagação (unidimensionais, bidimensionais ou tridimensionais) e direção de vibração (transversais ou longitudinais). Também define grandezas como frequência, período, comprimento de onda e velocidade, e apresenta exemplos de interferência, reflexão e refração de ondas em cordas.
TERMOLOGIA
1) A termologia estuda os fenômenos relacionados ao aquecimento e resfriamento dos corpos.
2) A temperatura está associada ao nível de agitação das partículas de um corpo, sendo maior quanto maior a temperatura.
3) As principais escalas termométricas são Celsius, Fahrenheit e Kelvin, cada uma definindo pontos fixos como o gelo fundente e a ebulição da água.
Medidas e sistema de unidades
O documento discute o histórico e os sistemas de medidas, incluindo o Sistema Métrico Decimal e o Sistema Internacional de Unidades (SI). O SI define sete unidades básicas e derivadas, como o metro e o quilograma. O documento também explica a notação científica e prefixos usados para expressar grandezas físicas.
Lançamento horizontal
O documento descreve dois tipos de movimento: horizontal (constante) e vertical (variável devido à gravidade). Fornece as equações para calcular distância, tempo e velocidade vertical para cada movimento. Explica como determinar qual objeto atingirá o solo primeiro considerando suas velocidades iniciais horizontais e verticais.
Lançamento oblíquo
1) O lançamento oblíquo é composto por dois movimentos: movimento horizontal uniforme e movimento vertical uniformemente variado devido à gravidade.
2) Cada movimento ocorre independentemente de acordo com o princípio da independência dos movimentos.
3) O ângulo de lançamento de 45° resulta no maior alcance possível com a mesma velocidade inicial, enquanto ângulos complementares possuem o mesmo alcance.
Movimento Circular Uniforme
O documento discute o movimento circular uniforme (MCU), definindo-o como o movimento em que a trajetória é uma circunferência e a velocidade permanece constante no tempo. Apresenta as definições de frequência, período, velocidade angular e linear, e relaciona essas grandezas no contexto do MCU. Fornece também exemplos do MCU no cotidiano e exercícios sobre o tema.
Velocidade Escalar Média
O documento descreve conceitos básicos de cinemática, incluindo deslocamento escalar, distância percorrida e velocidade escalar média. Explica a diferença entre deslocamento e distância percorrida e fornece exemplos para ilustrar esses conceitos. Também discute a unidade de velocidade e lista alguns dos animais mais rápidos, como o guepardo, o agulhão-vela e o falcão-peregrino.
M.R.U.V.
Segundo a física, movimento é a variação de posição espacial de um objeto ou ponto material no decorrer do tempo. A área da Física que estuda o movimento é a Mecânica. Ela se preocupa tanto com o movimento em si quanto com o agente que o faz iniciar ou parar.
Física - Ondas
1) Uma onda é um movimento causado por uma perturbação que se propaga através de um meio.
2) As ondas podem ser mecânicas ou eletromagnéticas, transversais ou longitudinais, e se propagar em uma, duas ou três dimensões.
3) Propriedades como velocidade, comprimento de onda, frequência, reflexão, refração, difração e interferência destrutiva ou construtiva afetam como as ondas se comportam.
Movimento retilíneo uniforme - MRU
O documento descreve o movimento retilíneo uniforme (MRU), caracterizado por uma velocidade constante e aceleração nula. Apresenta as equações para calcular a posição em função do tempo e os gráficos de velocidade versus tempo e posição versus tempo para movimentos progressivos e retrógrados. Por fim, exemplifica o cálculo da posição inicial, velocidade e posição final a partir de uma equação horária dada.
Funções
Conceito de Função. Domínio, Contra-Domínio e Imagem. Notação f(x)=y. Diagramas e Gráficos de uma Função. Função Crescente, Decrescente e Constante. Exemplos Práticos.
Vetores
O documento discute vetores físicos, definindo-os como grandezas que requerem direção e sentido além de valor e unidade. Explica como representar vetores graficamente e suas características como módulo, direção e sentido. Também aborda operações com vetores como soma, subtração, decomposição e produto escalar.
Velocidade média, instantânea e aceleração escalar
O documento discute conceitos fundamentais de velocidade média, velocidade instantânea e aceleração escalar. A velocidade média é definida como a variação da posição dividida pelo intervalo de tempo. A velocidade instantânea se refere à velocidade em um instante de tempo específico. A aceleração escalar média é a taxa de variação da velocidade com o tempo.
Dinâmica
O documento discute as leis de Newton e os conceitos fundamentais de força. Em três frases:
1) Força é o resultado da interação entre dois corpos e pode ser classificada em força de contato ou de campo.
2) A segunda lei de Newton estabelece que a resultante das forças sobre um corpo é igual à massa desse corpo multiplicada por sua aceleração.
3) Exemplos de forças de campo incluem a força gravitacional, magnética e elétrica, enquanto a força de atrito e força elást
Aula de fração
O documento discute conceitos básicos de frações, incluindo: (1) exemplos do uso de frações no dia-a-dia, como dividir pizza ou bolo; (2) os termos numerador e denominador; (3) tipos de frações como própria, imprópria e aparente; (4) frações equivalentes; (5) número misto; (6) simplificação de frações; e (7) operações com frações como adição, subtração, multiplicação e divisão.
Física (calorimetria)
Calorimetria estuda as trocas de energia entre corpos na forma de calor. As partículas que constituem os corpos possuem energia térmica devido à agitação. Calor é transferido espontaneamente do corpo mais quente para o mais frio até o equilíbrio. Capacidade térmica e calor específico medem a quantidade de calor necessária para alterar a temperatura de um corpo.
Mru movimento retilineo uniforme
O documento discute conceitos fundamentais de cinemática, como movimento, repouso, velocidade e deslocamento. Apresenta exemplos de movimento retilíneo uniforme e exercícios resolvidos sobre o tema.
Física cinemática - aula - 11
O documento discute conceitos fundamentais de física como movimento, repouso, velocidade, deslocamento e movimento retilíneo uniforme. Explica que movimento e repouso são relativos e dependem do referencial, e define cada um dos conceitos apresentados, ilustrando-os com exemplos.
Plano Inclinado
O plano inclinado nada mais é do que um plano que se encontra em um desnível, ou seja, o seu ponto de início se encontra em uma altura diferente em relação ao seu ponto final.
Análise combinatória
1) A análise combinatória trata de problemas de contagem e utiliza o Princípio Fundamental da Contagem para calcular o número total de possibilidades quando um evento pode ocorrer de diferentes maneiras.
2) O documento apresenta fórmulas para calcular permutações, arranjos e outros conceitos combinatórios como fatorial e utiliza exemplos numéricos para ilustrar cada tópico.
3) As propriedades e aplicações dos principais conceitos da análise combinatória como permutações, arranjos e fatorial são detal
Medidas de comprimento e área
O documento discute medidas de comprimento e como calcular áreas e perímetros de figuras geométricas. Ele lista as principais unidades de medida de comprimento como quilômetro, metro e centímetro. Explica como calcular o perímetro de polígonos somando os comprimentos dos lados e como decompor figuras complexas em formas geométricas básicas para calcular suas áreas totais.
Introdução a Física
O documento apresenta uma introdução à física, definindo-a como a ciência que estuda os fenômenos da natureza, especialmente os físicos. Descreve o método científico e diferencia fenômenos físicos de químicos. Apresenta exemplos de cada um e explica a importância da física. Finalmente, descreve os principais ramos da física como mecânica, calor, movimento ondulatório, óptica, eletricidade e física moderna.
Polígonos regulares
O documento discute polígonos regulares, definindo-os como polígonos equiláteros e equiângulos. Ele explica que polígonos regulares podem ser inscritos ou circunscritos em uma circunferência e fornece fórmulas para calcular o lado e a apótema de polígonos regulares como quadrados, hexágonos e triângulos equiláteros em termos do raio da circunferência.
Riscos elétricos
O documento discute a eletricidade como um fenômeno natural que o homem aprendeu a usar de diferentes formas. A eletricidade pode ser útil ou perigosa dependendo de como é utilizada, e hoje é usada quase em todos os lugares, como em casas, indústrias e hospitais. Os acidentes com eletricidade podem ocorrer quando há contato com condutores energizados ou falhas na isolação elétrica.
Corrente elétrica, halliday, cap. 26
O documento descreve os conceitos fundamentais de corrente elétrica, incluindo que é o movimento ordenado de elétrons em um condutor quando submetido a um campo elétrico, e que a intensidade de corrente é definida como o fluxo de cargas por unidade de tempo atravessando uma seção do condutor. Também apresenta a lei de Ohm, relacionando corrente, tensão e resistência.
Mais conteúdo relacionado
Mais procurados
Lançamento horizontal
O documento descreve dois tipos de movimento: horizontal (constante) e vertical (variável devido à gravidade). Fornece as equações para calcular distância, tempo e velocidade vertical para cada movimento. Explica como determinar qual objeto atingirá o solo primeiro considerando suas velocidades iniciais horizontais e verticais.
Lançamento oblíquo
1) O lançamento oblíquo é composto por dois movimentos: movimento horizontal uniforme e movimento vertical uniformemente variado devido à gravidade.
2) Cada movimento ocorre independentemente de acordo com o princípio da independência dos movimentos.
3) O ângulo de lançamento de 45° resulta no maior alcance possível com a mesma velocidade inicial, enquanto ângulos complementares possuem o mesmo alcance.
Movimento Circular Uniforme
O documento discute o movimento circular uniforme (MCU), definindo-o como o movimento em que a trajetória é uma circunferência e a velocidade permanece constante no tempo. Apresenta as definições de frequência, período, velocidade angular e linear, e relaciona essas grandezas no contexto do MCU. Fornece também exemplos do MCU no cotidiano e exercícios sobre o tema.
Velocidade Escalar Média
O documento descreve conceitos básicos de cinemática, incluindo deslocamento escalar, distância percorrida e velocidade escalar média. Explica a diferença entre deslocamento e distância percorrida e fornece exemplos para ilustrar esses conceitos. Também discute a unidade de velocidade e lista alguns dos animais mais rápidos, como o guepardo, o agulhão-vela e o falcão-peregrino.
M.R.U.V.
Segundo a física, movimento é a variação de posição espacial de um objeto ou ponto material no decorrer do tempo. A área da Física que estuda o movimento é a Mecânica. Ela se preocupa tanto com o movimento em si quanto com o agente que o faz iniciar ou parar.
Física - Ondas
1) Uma onda é um movimento causado por uma perturbação que se propaga através de um meio.
2) As ondas podem ser mecânicas ou eletromagnéticas, transversais ou longitudinais, e se propagar em uma, duas ou três dimensões.
3) Propriedades como velocidade, comprimento de onda, frequência, reflexão, refração, difração e interferência destrutiva ou construtiva afetam como as ondas se comportam.
Movimento retilíneo uniforme - MRU
O documento descreve o movimento retilíneo uniforme (MRU), caracterizado por uma velocidade constante e aceleração nula. Apresenta as equações para calcular a posição em função do tempo e os gráficos de velocidade versus tempo e posição versus tempo para movimentos progressivos e retrógrados. Por fim, exemplifica o cálculo da posição inicial, velocidade e posição final a partir de uma equação horária dada.
Funções
Conceito de Função. Domínio, Contra-Domínio e Imagem. Notação f(x)=y. Diagramas e Gráficos de uma Função. Função Crescente, Decrescente e Constante. Exemplos Práticos.
Vetores
O documento discute vetores físicos, definindo-os como grandezas que requerem direção e sentido além de valor e unidade. Explica como representar vetores graficamente e suas características como módulo, direção e sentido. Também aborda operações com vetores como soma, subtração, decomposição e produto escalar.
Velocidade média, instantânea e aceleração escalar
O documento discute conceitos fundamentais de velocidade média, velocidade instantânea e aceleração escalar. A velocidade média é definida como a variação da posição dividida pelo intervalo de tempo. A velocidade instantânea se refere à velocidade em um instante de tempo específico. A aceleração escalar média é a taxa de variação da velocidade com o tempo.
Dinâmica
O documento discute as leis de Newton e os conceitos fundamentais de força. Em três frases:
1) Força é o resultado da interação entre dois corpos e pode ser classificada em força de contato ou de campo.
2) A segunda lei de Newton estabelece que a resultante das forças sobre um corpo é igual à massa desse corpo multiplicada por sua aceleração.
3) Exemplos de forças de campo incluem a força gravitacional, magnética e elétrica, enquanto a força de atrito e força elást
Aula de fração
O documento discute conceitos básicos de frações, incluindo: (1) exemplos do uso de frações no dia-a-dia, como dividir pizza ou bolo; (2) os termos numerador e denominador; (3) tipos de frações como própria, imprópria e aparente; (4) frações equivalentes; (5) número misto; (6) simplificação de frações; e (7) operações com frações como adição, subtração, multiplicação e divisão.
Física (calorimetria)
Calorimetria estuda as trocas de energia entre corpos na forma de calor. As partículas que constituem os corpos possuem energia térmica devido à agitação. Calor é transferido espontaneamente do corpo mais quente para o mais frio até o equilíbrio. Capacidade térmica e calor específico medem a quantidade de calor necessária para alterar a temperatura de um corpo.
Mru movimento retilineo uniforme
O documento discute conceitos fundamentais de cinemática, como movimento, repouso, velocidade e deslocamento. Apresenta exemplos de movimento retilíneo uniforme e exercícios resolvidos sobre o tema.
Física cinemática - aula - 11
O documento discute conceitos fundamentais de física como movimento, repouso, velocidade, deslocamento e movimento retilíneo uniforme. Explica que movimento e repouso são relativos e dependem do referencial, e define cada um dos conceitos apresentados, ilustrando-os com exemplos.
Plano Inclinado
O plano inclinado nada mais é do que um plano que se encontra em um desnível, ou seja, o seu ponto de início se encontra em uma altura diferente em relação ao seu ponto final.
Análise combinatória
1) A análise combinatória trata de problemas de contagem e utiliza o Princípio Fundamental da Contagem para calcular o número total de possibilidades quando um evento pode ocorrer de diferentes maneiras.
2) O documento apresenta fórmulas para calcular permutações, arranjos e outros conceitos combinatórios como fatorial e utiliza exemplos numéricos para ilustrar cada tópico.
3) As propriedades e aplicações dos principais conceitos da análise combinatória como permutações, arranjos e fatorial são detal
Medidas de comprimento e área
O documento discute medidas de comprimento e como calcular áreas e perímetros de figuras geométricas. Ele lista as principais unidades de medida de comprimento como quilômetro, metro e centímetro. Explica como calcular o perímetro de polígonos somando os comprimentos dos lados e como decompor figuras complexas em formas geométricas básicas para calcular suas áreas totais.
Introdução a Física
O documento apresenta uma introdução à física, definindo-a como a ciência que estuda os fenômenos da natureza, especialmente os físicos. Descreve o método científico e diferencia fenômenos físicos de químicos. Apresenta exemplos de cada um e explica a importância da física. Finalmente, descreve os principais ramos da física como mecânica, calor, movimento ondulatório, óptica, eletricidade e física moderna.
Polígonos regulares
O documento discute polígonos regulares, definindo-os como polígonos equiláteros e equiângulos. Ele explica que polígonos regulares podem ser inscritos ou circunscritos em uma circunferência e fornece fórmulas para calcular o lado e a apótema de polígonos regulares como quadrados, hexágonos e triângulos equiláteros em termos do raio da circunferência.
Mais procurados (20)
Velocidade média, instantânea e aceleração escalar
Velocidade média, instantânea e aceleração escalar
Destaque
Riscos elétricos
O documento discute a eletricidade como um fenômeno natural que o homem aprendeu a usar de diferentes formas. A eletricidade pode ser útil ou perigosa dependendo de como é utilizada, e hoje é usada quase em todos os lugares, como em casas, indústrias e hospitais. Os acidentes com eletricidade podem ocorrer quando há contato com condutores energizados ou falhas na isolação elétrica.
Corrente elétrica, halliday, cap. 26
O documento descreve os conceitos fundamentais de corrente elétrica, incluindo que é o movimento ordenado de elétrons em um condutor quando submetido a um campo elétrico, e que a intensidade de corrente é definida como o fluxo de cargas por unidade de tempo atravessando uma seção do condutor. Também apresenta a lei de Ohm, relacionando corrente, tensão e resistência.
Potêncial elétrico, halliday, cap. 24
1) O documento discute energia potencial elétrica e como ela varia quando uma partícula carregada se movimenta verticalmente em um campo elétrico;
2) Fornece os cálculos para determinar a variação na energia potencial de um elétron que se movimenta 520m para cima na atmosfera terrestre, encontrando uma redução de 1,2×10-14 J;
3) Explica que a variação de energia é igual ao trabalho feito pelo campo elétrico na partícula.
Vetores
O documento apresenta os conceitos de produto escalar entre vetores no espaço R3. São definidos o produto escalar, suas propriedades e expressão cartesiana. Também são apresentadas as interpretações geométricas do módulo do produto escalar como a projeção de um vetor na direção de outro e a determinação do ângulo entre dois vetores a partir do produto escalar. Exemplos ilustram o cálculo do produto escalar e a determinação de ângulos e projeções entre vetores.
Lei de gauss, halliday, cap. 23
O documento apresenta um cilindro oco com eixo paralelo a um campo elétrico uniforme. Calcula-se o fluxo do campo elétrico através do cilindro integrando o produto escalar E.dA em três partes do cilindro, resultando em um fluxo igual a E×A.
Vetores
O documento apresenta conceitos fundamentais sobre vetores no plano e no espaço, incluindo definição de vetor, operações com vetores, módulo de vetor, produto escalar e representação de vetores em função de uma base.
Campo elétrico 2016
O documento descreve o campo elétrico, incluindo suas propriedades, como vetor campo elétrico, linhas de força, campo elétrico gerado por cargas pontuais e múltiplas cargas. Exemplos ilustram como calcular o campo elétrico em diferentes situações e a força sobre cargas colocadas nesse campo.
132formulasdefisicarc 140501111333-phpapp02
Este documento resume os principais tópicos de física, incluindo cinemática, dinâmica, gravitação, fluidos, termodinâmica, óptica, ondulatória, eletrostática, eletrodinâmica e magnetismo. Ele lista as grandezas básicas, fórmulas e unidades de cada tópico, além de constantes físicas importantes.
Aterramento
O documento discute os tipos de aterramento elétrico, explicando conceitos como terra, neutro e massa. Apresenta as três principais funções do aterramento e descreve os sistemas TT, TN e IT de acordo com a norma NBR 5410.
Aula 4 vetores
O documento discute conceitos fundamentais de vetores, incluindo: (1) grandezas escalares e vetoriais, (2) representação gráfica e simbólica de vetores, (3) propriedades como módulo, direção e sentido, (4) comparação entre vetores iguais e opostos, e (5) operações como soma e diferença utilizando as regras do paralelogramo e polígono.
Física vetores
O documento descreve as propriedades de grandezas físicas escalares e vetoriais, incluindo a representação gráfica e operações com vetores, como adição, subtração, multiplicação e divisão. Grandezas escalares são expressas por valor e unidade, enquanto vetoriais requerem módulo, direção e sentido.
1ª lei de newton
A 1a Lei de Newton estabelece que um corpo permanece no estado de repouso ou movimento uniforme a menos que uma força externa atue sobre ele. Isso significa que um corpo em repouso permanecerá em repouso a menos que uma força o mova, e um corpo em movimento retilíneo uniforme continuará com a mesma velocidade e direção a menos que uma força altere isso. A inércia de um corpo está relacionada à sua massa, de modo que quanto maior a massa, maior a resistência a mud
Potencial elétrico
O documento discute descargas atmosféricas, explicando que elas ocorrem quando o campo elétrico produzido por uma tempestade excede a capacidade isolante do ar, iniciando o movimento de elétrons. Descargas podem ocorrer entre nuvens, do solo para a nuvem, ou vice-versa, sendo as internuvens as mais comuns devido à diminuição da capacidade isolante do ar com a altitude. Raios transferem carga da nuvem para o solo, aquecendo o ar e gerando trovões, e ajudam a criar a cam
Aula 1 resultante de um sistema de forças
O documento introduz conceitos básicos de mecânica geral e resultante de sistemas de forças. Discute definições de mecânica, forças escalares e vetoriais, leis de paralelogramo, triângulo e senos, e como determinar a resultante e momentos de sistemas de forças. Exemplos e exercícios são fornecidos para ilustrar os conceitos.
Leis De Newton
1) As leis de Newton descrevem o movimento e as forças que atuam sobre os objetos, incluindo a inércia, a segunda lei do movimento e a ação e reação.
2) A primeira lei estabelece que um corpo permanece em repouso ou movimento uniforme a menos que uma força externa atue sobre ele.
3) A segunda lei relaciona a força aplicada a um objeto com sua aceleração, sendo diretamente proporcional à força e inversamente proporcional à massa.
Sistema de Aterramento e SPDA
O documento descreve os sistemas de aterramento e proteção contra descargas atmosféricas (SPDA). Apresenta conceitos como objetivo do aterramento, partes constituintes, valores de resistência, tipos de sistemas de aterramento e componentes de um SPDA como captação, descida e aterramento. Explica também níveis de proteção de SPDA e a eficiência de cada nível.
Mecanica exercicios resolvidos
O documento apresenta os conceitos fundamentais da disciplina de Mecânica Técnica. É introduzido o curso, o professor, as unidades do Sistema Internacional e os principais tópicos a serem abordados, incluindo definição de mecânica, grandezas físicas, equilíbrio de corpos rígidos e bibliografia recomendada.
Destaque (18)
Último
Estrutura Pedagógica - Laboratório de Educação a Distância.ppt
Teorias da Aprendizagem
A.D.D.I.E
EAD
Educação a Distância
Aula história , caracteristicas e esteriótipos em relação a DANÇA DE SALAO.pptx
Educação física fundamental 1
Atividade letra da música - Espalhe Amor, Anavitória.
A música 'Espalhe Amor', interpretada pela cantora Anavitória é uma celebração do amor e de sua capacidade de transformar e conectar as pessoas. A letra sugere uma reflexão sobre como o amor, quando verdadeiramente compartilhado, pode ultrapassar barreiras alcançando outros corações e provocando mudanças positivas.
UFCD_10145_Enquadramento do setor farmacêutico_indice.pdf
Manual da UFCD_10145_Enquadramento do setor farmacêutico_pronto para envio, via email, formato editável.
email: formacaomanuaisplus@gmail.com
Sistema de Bibliotecas UCS - Chronica do emperador Clarimundo, donde os reis ...
A biblioteca abriga, em seu acervo de coleções especiais o terceiro volume da obra editada em Lisboa, em 1843. Sua exibe
detalhes dourados e vermelhos. A obra narra um romance de cavalaria, relatando a
vida e façanhas do cavaleiro Clarimundo,
que se torna Rei da Hungria e Imperador
de Constantinopla.
Introdução à Sociologia: caça-palavras na escola
Atividade de Sociologia para o Ensino Médio na forma de uma caça-palavras.
UFCD_3546_Prevenção e primeiros socorros_geriatria.pdf
Manual da UFCD_3546_Prevenção e primeiros socorros_geriatria_pronto para envio, via email e formato editável.
Email: formacaomanuaisplus@gmail.com
Slides Lição 11, Central Gospel, Os Mortos Em CRISTO, 2Tr24.pptx
Slideshare Lição 11, Central Gospel, Os Mortos Em Cristo, 1Tr24, Pr Henrique, EBD NA TV, Revista ano 11, nº 1, Revista Estudo Bíblico Jovens E Adultos, Central Gospel, 2º Trimestre de 2024, Professor, Tema, Os Grandes Temas Do Fim, Comentarista, Pr. Joá Caitano, estudantes, professores, Ervália, MG, Imperatriz, MA, Cajamar, SP, estudos bíblicos, gospel, DEUS, ESPÍRITO SANTO, JESUS CRISTO, Com. Extra Pr. Luiz Henrique, 99-99152-0454, Canal YouTube, Henriquelhas, @PrHenrique
Sinais de pontuação
Os sinais de pontuação são fundamentais para a organização dos diferentes tipos de texto, contribuindo para clareza daquilo que se escreve.
Último (20)
759-fortaleza-resultado-definitivo-prova-objetiva-2024-05-28.pdf
759-fortaleza-resultado-definitivo-prova-objetiva-2024-05-28.pdf
Estrutura Pedagógica - Laboratório de Educação a Distância.ppt
Estrutura Pedagógica - Laboratório de Educação a Distância.ppt
Aula história , caracteristicas e esteriótipos em relação a DANÇA DE SALAO.pptx
Aula história , caracteristicas e esteriótipos em relação a DANÇA DE SALAO.pptx
Atividade letra da música - Espalhe Amor, Anavitória.
Atividade letra da música - Espalhe Amor, Anavitória.
UFCD_10145_Enquadramento do setor farmacêutico_indice.pdf
UFCD_10145_Enquadramento do setor farmacêutico_indice.pdf
Sistema de Bibliotecas UCS - Chronica do emperador Clarimundo, donde os reis ...
Sistema de Bibliotecas UCS - Chronica do emperador Clarimundo, donde os reis ...
UFCD_3546_Prevenção e primeiros socorros_geriatria.pdf
UFCD_3546_Prevenção e primeiros socorros_geriatria.pdf
Slides Lição 11, Central Gospel, Os Mortos Em CRISTO, 2Tr24.pptx
Slides Lição 11, Central Gospel, Os Mortos Em CRISTO, 2Tr24.pptx
A QUESTÃO ANTROPOLÓGICA: O QUE SOMOS OU QUEM SOMOS.pdf
A QUESTÃO ANTROPOLÓGICA: O QUE SOMOS OU QUEM SOMOS.pdf
Operações com vetores
- 2. VETOR RESULTANTE SOMA DE VETORES OU RESULTANTE CONSISTE EM REPRESENTAR EM UM ÚNICO VETOR DOIS OU MAIS VETORES.
- 4. REGRA DO POLÍGONO 𝐴 𝐵 𝐶 ORIGEM COM EXTREMIDADE 𝐶 = 𝐴 + 𝐵
- 6. VETOR RESULTANTE 𝑅 = 𝑎 + 𝑏 + 𝑐 + 𝑑 + 𝑒
- 7. DOIS VETORES MESMA DIREÇÃO E MESMO SENTIDO 𝐴 𝐵 REGRA DO POLÍGONO 𝐴 𝐵 𝐶 = 𝐴 + 𝐵 ALGEBRICAMENTE C = A + B
- 8. DOIS VETORES MESMA DIREÇÃO E SENTIDOS OPOSTOS𝐴 𝐷 REGRA DO POLÍGONO 𝐴𝐷 𝐶 = 𝐴 + 𝐷 ALGEBRICAMENTE C = D - A
- 9. DOIS VETORES PERPENDICULARES ENTRE SI 𝐴 𝐸 𝐴 𝐸 𝐶 𝐴 + 𝐸 ALGEBRICAMENTE C² = A² + E² (TEOREMA DE PITÁGORAS) 𝐶 = REGRA DO POLÍGONO
- 11. COMPONENTES RETANGULARES DE UM VETOR PARA CALCULAR MATEMATICAMENTE OS VALORES DESSAS COMPOMENTES , PRECISAMOS RECORRER AS RELAÇÕES TRIGOMOMÉTRICAS DE UM TRIÂNGULO RETÂNGULO. b c a 𝑠𝑒𝑛= 𝑐𝑎𝑡𝑒𝑡𝑜 𝑜𝑝𝑜𝑠𝑡𝑜 𝑎 𝜃 ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 𝑐𝑜𝑠= 𝑐𝑎𝑡𝑒𝑡𝑜 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒 𝑎 𝜃 ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎
- 12. Vx y x 𝑉Vy O A B DO TRIÂNGULO OAB, TEREMOS: 𝑠𝑒𝑛 = 𝑉 𝑌 𝑉 ∴ 𝑉 𝑌 = V. 𝑠𝑒𝑛 𝑐𝑜𝑠 = 𝑉 𝑥 𝑉 ∴ 𝑉 𝑥 = V. 𝑐𝑜𝑠
- 13. Exemplo OConsidere um objeto que sofre um deslocamento, ,de 100 km, formando um ângulo de 30º com a direção oeste-leste, como mostra a figura. Considerando o eixo OX dirigido par leste e o eixo OU dirigido para norte, calcule as componentes Dx e Dy desse deslocamento. 𝐃
- 14. leste30o 𝐷 Dy Dx norte 𝐷 𝑌 = D. 𝑠𝑒𝑛30 𝐷 𝑌 = 100 km.0,50 𝐷 𝑌 = 50km Como sen 30= 0,5 e cos 30 = 0,87, então : 𝐷 𝑥 = D. 𝑐𝑜𝑠30 𝐷 𝑥 = 100 km.0,87 𝐷 𝑥 = 87km