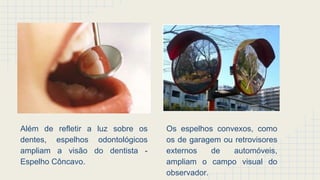
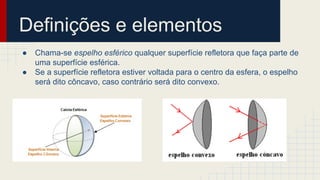
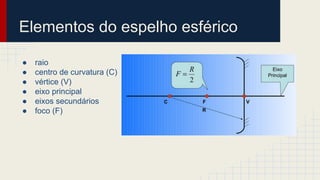
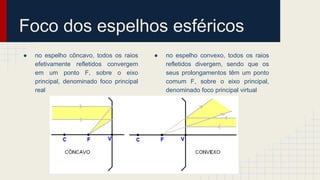
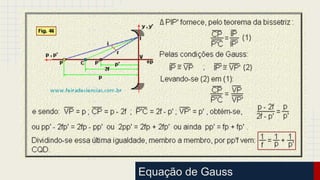
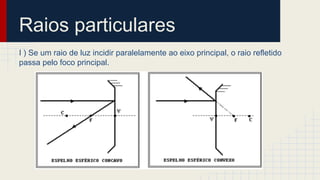
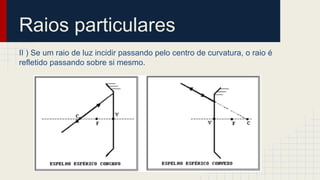
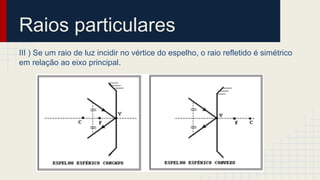
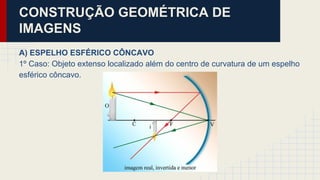
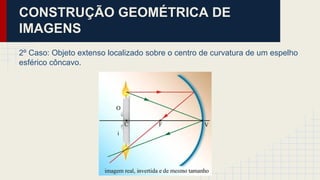
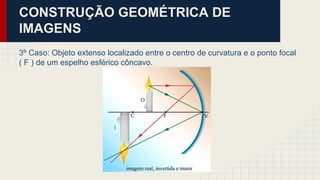
O documento discute as propriedades dos espelhos esféricos convexos e côncavos, incluindo sua definição, elementos, leis da reflexão, foco, construção geométrica de imagens e exercícios de aplicação. É explicado que espelhos côncavos formam imagens reais ampliadas enquanto espelhos convexos formam imagens virtuais reduzidas. Diferentes casos de posicionamento de objetos em relação aos espelhos são apresentados.

1. Reflexão da Luz em
Espelhos Esféricos
Camila Ferreira Aguiar

2. Auto retrato sobre esfera - Escher

3. Além de refletir a luz sobre os
dentes, espelhos odontológicos
ampliam a visão do dentista -
Espelho Côncavo.
Os espelhos convexos, como
os de garagem ou retrovisores
externos de automóveis,
ampliam o campo visual do
observador.

4. Definições e elementos
● Chama-se espelho esférico qualquer superfície refletora que faça parte de
uma superfície esférica.
● Se a superfície refletora estiver voltada para o centro da esfera, o espelho
será dito côncavo, caso contrário será dito convexo.

5. Elementos do espelho esférico
● raio
● centro de curvatura (C)
● vértice (V)
● eixo principal
● eixos secundários
● foco (F)

6. Centro de curvatura e raio
● O centro de curvatura C do espelho, coincide com o centro de curvatura
da calota.
● O raio R do espelho é o próprio raio de curvatura da esfera à qual
pertence a calota.
● O vértice V do espelho, é o vértice (pólo) da calota. Qual quer reta que
passa pelo centro de curvatura do espelho constitui um eixo. Se a reta
passa pelo vértice do espelho, o eixo será principal, caso contrário será
dito secundário

7. Reflexão da luz
● Assim como para espelhos planos, as duas leis da reflexão também são
obedecidas nos espelhos esféricos, ou seja, os ângulos de incidência e
reflexão são iguais, e os raios incididos, refletidos e a reta normal ao ponto
incidido.

8. Condições da nitidez de Gauss
O físico e matemático Carl Friedrich Gauss (1777-1885) verificou as condições
sob as quais os espelhos devem conjugar imagens nítidas, as quais ficaram
conhecidas como condições da nitidez de Gauss. São três:
1. o ângulo de abertura do espelho deve ser pequeno (α≤ 10º);
2. os raios incidentes devem ser paralelos ou pouco inclinados em relação
ao eixo principal;
3. os raios incidentes devem estar próximos ao eixo principal.

9. Condições da nitidez de Gauss
Sistema estigmático:
atribuir a cada ponto objeto
apenas um ponto imagem,
originando uma imagem
nítida.
Sistema astigmático:
conjuga infinitos pontos
imagem, formando uma
mancha luminosa.

10. Foco dos espelhos esféricos
● no espelho côncavo, todos os raios
efetivamente refletidos convergem
em um ponto F, sobre o eixo
principal, denominado foco principal
real
● no espelho convexo, todos os raios
refletidos divergem, sendo que os
seus prolongamentos têm um ponto
comum F, sobre o eixo principal,
denominado foco principal virtual

11. Espelho convexo

12. Espelho côncavo

13. Relação entre curvatura e distância focal
O triângulo CFI é isósceles, donde: FC = FI (eq.1)
Por tratar de um espelho de Gauss, o ponto de incidência I se localiza nas
proximidades de V, assim, pode-se escrever: FI ~= FV (eq.2)
Comparando (eq.1) e (eq.2) temos FC = FV e, portanto, o ponto F é
aproximadamente ponto médio do segmento CV, ou seja: f = R/2

14. Equação de Gauss
Equação de Gauss

15. Aumento linear transversal
A ampliação ou aumento da
imagem é dada por:
Convenção de sinais
● f > 0 → R > 0 → espelho
côncavo;
● f < 0 → R < 0 → espelho
convexo;
● p > 0 → objeto real;
● p < 0 → objeto virtual;
● p’ > 0 → imagem real;
● p’ < 0 → imagem virtual;
● o > 0 → objeto para cima;
● o < 0 → objeto para baixo;
● i > 0 → imagem para cima;
● i < 0 → imagem para baixo;
● A > 0 → imagem direita em relação
ao objeto;
● A < 0 → imagem invertida em
relação ao objeto;
● |A| = 1 → imagem do mesmo
tamanho que o objeto;
● |A| > 1 → imagem maior do que o
objeto;
● |A| < 1 → imagem menor do que o
objeto;

16. Raios particulares
I ) Se um raio de luz incidir paralelamente ao eixo principal, o raio refletido
passa pelo foco principal.

17. Raios particulares
II ) Se um raio de luz incidir passando pelo centro de curvatura, o raio é
refletido passando sobre si mesmo.

18. Raios particulares
III ) Se um raio de luz incidir no vértice do espelho, o raio refletido é simétrico
em relação ao eixo principal.

19. CONSTRUÇÃO GEOMÉTRICA DE
IMAGENS
A) ESPELHO ESFÉRICO CÔNCAVO
1º Caso: Objeto extenso localizado além do centro de curvatura de um espelho
esférico côncavo.

20. CONSTRUÇÃO GEOMÉTRICA DE
IMAGENS
2º Caso: Objeto extenso localizado sobre o centro de curvatura de um espelho
esférico côncavo.

21. CONSTRUÇÃO GEOMÉTRICA DE
IMAGENS
3º Caso: Objeto extenso localizado entre o centro de curvatura e o ponto focal
( F ) de um espelho esférico côncavo.

22. CONSTRUÇÃO GEOMÉTRICA DE
IMAGENS
4º Caso: Objeto extenso localizado sobre o ponto focal ( F ) de um espelho
esférico côncavo.

23. CONSTRUÇÃO GEOMÉTRICA DE
IMAGENS
5º Caso: Objeto extenso localizado entre o ponto focal ( F ) e o vértice de um
espelho esférico côncavo.

24. CONSTRUÇÃO GEOMÉTRICA DE
IMAGENS
B) ESPELHO ESFÉRICO CONVEXO: Objeto extenso localizado em frente a
um espelho esférico convexo.

25. Exercícios

26. Exercícios

27. Exercícios
1- Num anteparo a 30cm de um espelho esférico forma-se a imagem de um
objeto real situado a 10cm do espelho. Determine:
a)A natureza do espelho:
Imagem em um anteparo, logo é uma imagem real. O espelho é côncavo, pois
espelhos convexos só formam imagens virtuais
b)O raio de curvatura do espelho e a distância focal.
f=7,5cm
R=15cm

28. Exercícios
2-Um observador, estando a 20cm de distância de um espelho esférico, vê sua
imagem direita e ampliada três vezes. Determine:
a)o tipo do espelho:
Como a imagem é direita ela é virtual. Somente em espelho côncavo a imagem
virtual é maior que o objeto.
b)sua distância focal
f=30cm

29. Exercícios
3- Um espelho esférico conjuga, de um objeto situado a 30cm dele, uma
imagem direita e três vezes menor que o objeto. Determine:
a) tipo do espelho:
Convexo, pois a imagem é direita e menor, logo virtual.
b)sua distância focal:
Como a imagem é virtual p’<0. f=-15cm

30. Exercício
4- A distância entre um objeto e a imagem que um espelho esférico lhe
conjuga mede 30cm, sendo ambos reais, com o objeto apresentando altura
quatro vezes superior à da imagem. Determine:
a)o raio de curvatura do espelho:
A imagem sendo real e menor, é o espelho côncavo, logo a imagem também é
invertida. Deve estar entre o centro e o foco. O objeto quatro vezes maior A=-
4, então p’=4p.
R=16cm