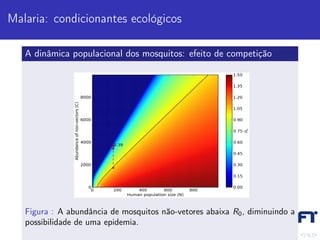
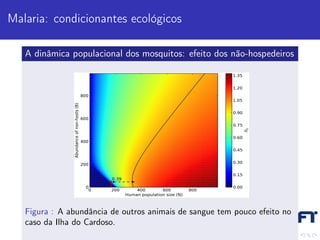
Este documento discute modelos matemáticos para epidemias. Primeiro, apresenta exemplos históricos como a Peste de Atenas e a Gripe Espanhola. Em seguida, descreve o modelo SIR básico e como ele pode prever se uma epidemia ocorrerá. Por fim, discute modelos para doenças transmitidas por vetores, como a malária, levando em conta a dinâmica dos vetores.

1. Modelos Matemáticos para Epidemias
Roberto André Kraenkel, IFT-UNESP
http://www.ift.unesp.br/users/kraenkel
São Paulo, 11 de Abril de 2013
IFUSP

2. Outline
1 Um pouco de história
A peste de Atenas
Peste
A pandemia de influenza de 1918 - gripe espanhola
2 Modelos
O modelo SIR
3 Modelos para doenças transmitidas por vetores
Malária
Modelo de Ross-MacDonald
4 Contribuições Recentes
Condicionantes Ecológicos da Malária
5 Comentários Finais

3. Epidemias históricas
A Peste de Atenas
A Peste de Atenas foi uma epidemia
que atingiu Atenas ∼ 430 AC,
durante a guerra do Peloponeso.
Foi descrita pro Tucídides: calores na
cabeça, tosse forte, bile, espasmos
violentos, ...
1/3 da população morreu, inclusive
Péricles.
Nem os médicos eram capazes de enfren- Não se sabe ao certo que doença
tar a doença, já que de início tinham de provocou esta epidemia. Pesquisas
tratá-la sem lhe conhecer a natureza e que
a mortalidade entre eles era maior por es-
recente apontam para tifo
tarem mais expostos a ela, nem qualquer epidêmico, cujo agente infeccioso é
outro recurso humano era da menor valia. uma bactéria ( Rickettsia prowazekii)
As preces feitas nos santuários, ou os ape- transmitida por piolhos.
los aos oráculos e atitudes semelhantes,
foram todas inúteis e afinal a população Sabe-se que sua origem foi africana.
desistiu delas, vencida pelo flagelo.

4. Epidemias históricas
Cito, longe, tarde.
Peste
A peste é uma doença infecciosa causada
pela bactéia Yersinia pestis. Há várias formas
de peste:
peumônica, afeta os pulmões e é transmissível
de humano para humano diretamente.
bubônica, ataca os gânglios linfáticos e é
transmitida pela pulga Xenopsylla cheopis (a
pulga do rato). A pulga adquire a bactéria ao
picar um rato.
septicêmica, passa à corrente sanguínea e
infecta diversos orgãos.
Se não tratada, a peste induz alta
mortalidade. Antibióticos são eficientes.
Se aplicados em algumas horas!

5. Histórias da Peste.
Tamanho medo e pensamentos fantasiosos tomavam conta das pessoas que todos recorriam à mesma
atitude, que era de evitar totalmente os doentes e as suas posses. Assim fazendo, pensavam que
poderiam salvar a sua vida (Bocaccio, Decameron).
A Peste.
Três pandemias ;
Peste de Justiniano, (541 DC,), Espalhou-se
a partir de Constantinopla e provocou a
morte de 25 % da população do
Mediterrâneo. No entanto, pouco se
propagou para dentro do continente.
A Peste Negra, (1347), entrando na Europa
pela Sicília, matou 1/3 da população
européia.
A terceira pandemia, começando na China
em 1855 matou 12 milhões de pessoas na
China e na Índia
Paul Louis Simond; "Naquele dia de 2 de
junho de 1898, experimentei uma emoção
inexprimível ao pensar que havia acabado de
desvendar um segredo que angustiava a
humanidade desde a aparição da peste no
mundo".
A peste ainda existe em níveis muito baixos hoje,
sobretudo nas regiões áridas dos EUA. Usualmente
não leva à morte, devido ao uso de antiobióticos.

6. Epidemics: history
Aqueles dias, ninguém que os tenha vivido poderá jamais esquecê-los. (Pedro
Dantas)
A pandemia de influenza de 1918
A pandemia de influenza de 1918 foi devida a uma
forma particularmente severa do virus influenza A.
Durou de 1918 a 1919.
Atingiu praticamente todas as regiões do mundo.
Aproximadamente 50 milhões de pessoas morreram
devido à doença. 500 milhões (quase 1/3 da
população mundial) de pessoas foram atingidas.
É transmitida diretamente de pessoa à pessoa.
Em São Paulo, a primeira morte aconteceu em 21 de
outubro de 1918. No fim de novembro, a epidemia
havia passado..

7. Modelos Matemáticos
As bases da epidemiologia matemática
Comecemos com algumas simplificações.
A população é "bem-misturada",
E espacialmente homogênea,
O que define implicitamente as escalas de tempo e espaço da
validade dos modelos.,
Vamos classificar indivíduos em três classes:
S susceptíveis;
I infectantes ( ou infecciosos, ou ainda, infectados);
R recuperados (pode incluir imunes e mortos)

8. Modelos Matemáticos
Modelo mais simples
Não estamos interessados na dinâmica da população em si.
Queremos saber a dinâmica da passagem entre as classes S,I,R.
Queremos sobretudo caracterizar uma possível epidemia:
condições para que ocorra, sua prevalência, se chegará a um
fim ou não.
Vamos supor que o tamanho da população é constante, N.
É va’lida essa aproximação para doenças cujo tempo
característico de infecção é pequeno. Isso vale para muitas
doençaa: gripe, rubéola, sarampo, ....

9. Kermack & McKendrick (1927)
A taxa per capita de variação no número de susceptíveis é
propocional ao número de infectados:
dS
= −rSI
dt
onde r é a taxa de infecção e pode depender de N.

10. Kermack & McKendrick (1927)
A taxa per capita de variação do número de infectados é
propocional ao número de susceptíveis menos um fator
representando a passagem para a classe dos removidos
dS
= −rSI
dt
dI
= rSI − aI
dt

11. Kermack & McKendrick (1927)
A taxa de variação dos recuperados é proporcional ao número de
infectados .
dS
= rSI
dt
dI
= rSI − aI
dt
dR
= aI
dt

12. Kermack & McKendrick (1927)
Três equações, três variáveis. Ótimo!:
dS
= −rSI
dt
dI
= rSI − aI
dt
dR
= aI
dt
Vamos agora tirar algumas conclusões a partir destas equações

13. Modelo SIR
dS dI dR
dt
= −rSI dt
= rSI − aI dt
= aI
Vamos ser mais precisos sobre qual pergunta queremos
responder:
Digamos que em t = 0, temos: S(0) = S0 , I (0) = I0 and
R(0) = 0 .
Ou seja, temos um certo número de infectados (I0 ) e de
susceptíveis (S0 ).
Dados r , a, S0 e I0 , queremos saber se haverá ou não uma
epidemia. Caracterizamos uma epidemia por I (t) > I0 durante
algum tempo.

14. Modelo: resultados
dS dI dR
dt
= −rSI dt
= rSI − aI dt
= aI
Se S0 > a/r teremos uma epidemia, e se S0 < a/r , não
teremos.
Ou:
S0 r
R0 ≡ >1
a
é a condição para que haja uma epidemia
R0 é chamado de razão reprodutiva básica.
Mesmo em modelos mais complexos define-se essa quantidade
.

15. Modelo SIR
Gráficos
Vamos olhar para dinâmica no espaço de fase.
Como temos três variáveis, mas S + I + R = N, o espaço de fase é
na prática bi-dimensional.
Note que todas as trajetórias
terminam em I = 0 quando
t → ∞. A epidemia cessa
por si mesma.
Veja que S(t → ∞) = 0.
Nem todo mundo adquiriu a
doença.

16. Modelos para doenças transmitidas por vetores
Malária
Muitas doenças não são transmitidas diretamente de pessoa a pessoa. Há
um agente transmissor, que é chamdo de vetor da doença.
Mosquitos, carrapatos, pulgas...
Para muitas situações é preciso levar em conta a dinâmica do vetor.
São inúmeras doenças deste tipo: malária, dengue, febre amarela, doença
de Lyme, leishmaniose, doença do sono.
A doença mais bem estudada neste caso é a malária.
Fatos sobre a malária
A malária é causada por um protozoário chamado Plasmodium.
Plasmodium é transmitido por mosquitos do genus Anopheles.

17. Modelo de Ross-MacDonald
Humanos e mosquitos!
Agora consideramos uma população contante de humanos, uma população
constante de mosquitos, ambos divididos em duas classes, S e I, sem imunidade.

18. Modelo de Ross-MacDonald
Medidas de Saúde Pública
O modelo de Ross-MacDonald também tem um limiar
epidêmico caracterizado por uma razão reprodutiva básica R0 .
É uma expressão grande que omitimos aqui.
Do modelo se conclui que:
Diminuir pela metade o número de mosquitos, diminue R0 pela
metade;
Diminuir pela metade a taxa de picadas, diminue R0 por um
fator 4.!
Para dimunir o número de mosquitos usam-se larvicidas.
Para diminuiro o número de picadas, usam-se redes de
proteção sobre as camas.

19. Malaria: condicionantes ecológicos
Malária na Mata Atlântica
Os casos de malária na Mata Atlântica são raros.
Porém, uma espécie de Anopheles é bastante abundante, A.
cruzii. E ele é um vetor da malária.
Por que não há malaria na Mata Atlântica?
A Ilha do Cardoso
Estudamos um caso concreto: a Ilha do Cardoso.
Não há caso de malária há 30 anos.
Usamos dados de coletas de campo sobre abundância de
mosquitos.
O modelo de Ross-MacDonald prevê um R0 > 1.
Por que não há malaria na Ilha do Cardoso?

20. Malaria: condicionantes ecológicos
A dinâmica populacional dos mosquitos
Construímos um novo modelo que leva em conta
a competição de Anopheles com outros mosquitos,
a existência de outros animais de sangue quente na mata.
Os efeitos disso são:
a competição diminui a taxa de picadas infectantes,
a presença de outros animais, por um lado, aumenta a taxa de
reprodução do mosquito, por outro lado, elimina Plasmodium
do sistema (o ciclo do patógeno só se completa em humanos).
O modelo usa parâmetros reais, medidos ou inferidos de
coletas.

21. Modelo epidemiológico para malária
Laporta, G.Z. et alli, PLoS Neglected Tropical Diseases 7(3) e2139 (2013).

22. Malaria: condicionantes ecológicos
A dinâmica populacional dos mosquitos: efeito de competição
Figura : A abundância de mosquitos não-vetores abaixa R0 , diminuindo a
possibilidade de uma epidemia.

23. Malaria: condicionantes ecológicos
A dinâmica populacional dos mosquitos: efeito dos não-hospedeiros
Figura : A abundância de outros animais de sangue tem pouco efeito no
caso da Ilha do Cardoso.

24. Comentários finais
Modelos matemáticos simples podem levar ao entendimento
de diversas características de epidemias:
Existe um limiar para que uma epidemia possa acontecer;
Epidemias se esgotam por si mesmas
Nem todas a pessoas são afetadas
Quais parâmetros são mais importantes para que haja uma
epidemia
Para modelos em casos reais é necessário um maior
refinamento dos modelos básicos.
Condicionantes ecológicos e/ou ambientais
Sazonalidade
Estrutura de contactos entre pessoas
Períodos de incubação
....

25. Muito obrigado pela atenção
kraenkel@ift.unesp.br