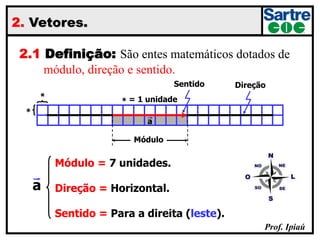
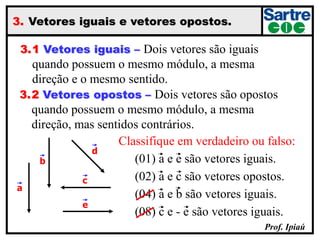
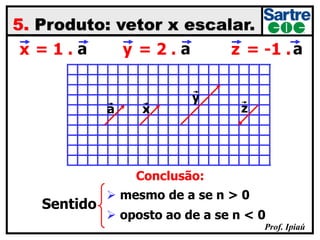
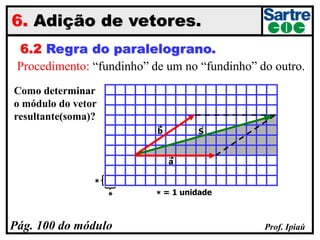
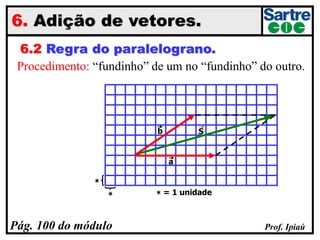
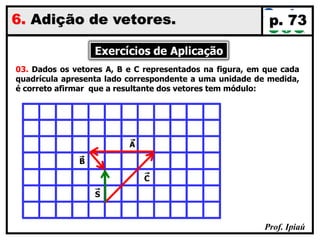
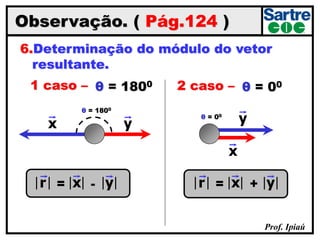
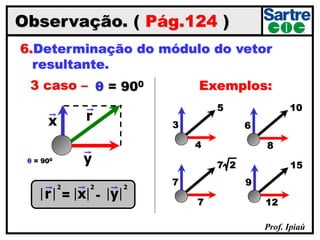
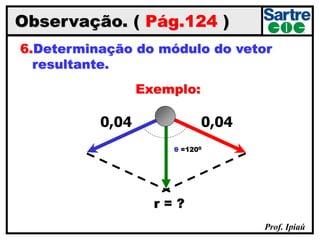
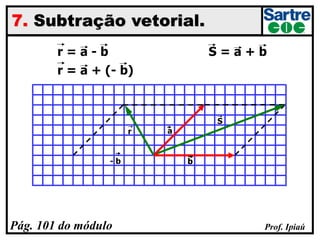
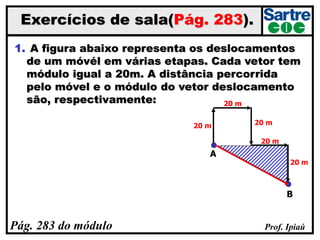
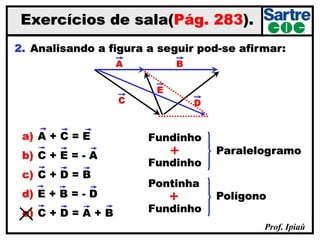
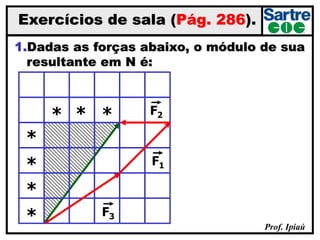
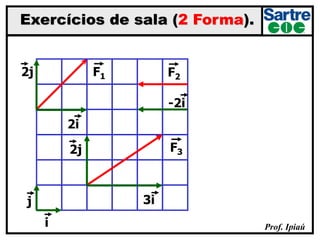
O documento discute grandezas escalares e vetoriais, definindo-as e dando exemplos de cada tipo. Também aborda conceitos como módulo, direção e sentido de vetores, além de igualdade, oposição e adição de vetores. Há exercícios sobre determinação do módulo do vetor resultante e adição/subtração vetorial.

1. Prof. Ipiaú
1. Grandezas escalares e vetoriais.
1.1 Grandezas escalares: São aquelas que ficam
….perfeitamente definidas com intensidade e unidade.
1.2 Grandezas vetoriais: São aquelas que ficam
….perfeitamente definidas apenas quando acompanhadas
….de intensidade, direção, sentido e unidade.
Exemplos:
Exemplos:
massa,
Massa
força,
Força
tempo,
, tempo
gravidade,
, gravidade
peso,
, peso.
temperatura.
, temperatura.
Amor ?

2. Prof. Ipiaú
2. Vetores.
*
*
* = 1 unidade
a
Módulo
Sentido Direção
2.1 Definição: São entes matemáticos dotados de
…módulo, direção e sentido.
a
Módulo =
Sentido =
Direção =
Módulo = 7 unidades.
Sentido = Para a direita (leste).
Direção = Horizontal.

3. Prof. Ipiaú
3. Vetores iguais e vetores opostos.
3.1 Vetores iguais – Dois vetores são iguais
quando possuem o mesmo módulo, a mesma
direção e o mesmo sentido.
3.2 Vetores opostos – Dois vetores são opostos
quando possuem o mesmo módulo, a mesma
direção, mas sentidos contrários.
a
b
e
c
d
Classifique em verdadeiro ou falso:
(01) a e e são vetores iguais.
(02) a e c são vetores opostos.
(04) a e b são vetores iguais.
(08) c e - e são vetores iguais.

4. Prof. Ipiaú
5. Produto: vetor x escalar.
ax = 1 . ay = 2 . = -1 .az
a x
y
z
Conclusão:
Sentido
 mesmo de a se n > 0
 oposto ao de a se n < 0

5. Prof. Ipiaú
6. Adição de vetores.
Vetor resultante – É o vetor que sozinho produz o
mesmo efeito que os demais em conjunto.
Jean Debret

6. Prof. Ipiaú
6. Adição de vetores.
6.2 Regra do paralelograno.
Procedimento: “fundinho” de um no “fundinho” do outro.
*
*
* = 1 unidade
Pág. 100 do módulo
S
a
b
Como determinar
o módulo do vetor
resultante(soma)?

7. Prof. Ipiaú
6. Adição de vetores.
6.2 Regra do paralelograno.
Procedimento: “fundinho” de um no “fundinho” do outro.
*
*
* = 1 unidade
Pág. 100 do módulo
S
a
b

8. Prof. Ipiaú
p. 736. Adição de vetores.
03. Dados os vetores A, B e C representados na figura, em que cada
quadrícula apresenta lado correspondente a uma unidade de medida,
é correto afirmar que a resultante dos vetores tem módulo:
A
B
C
S

9. Prof. Ipiaú
Observação. ( Pág.124 )
6.Determinação do módulo do vetor
resultante.
1 caso – θ = 1800
x y
θ = 1800
x yr = -
2 caso – θ = 00
x
yθ = 00
x yr = +

10. Prof. Ipiaú
6.Determinação do módulo do vetor
resultante.
105
Observação. ( Pág.124 )
3 caso – θ = 900
θ = 900
x
y
r
x yr = -
2 2 2
3
4
6
8
7
7
15
12
9
Exemplos:
7 2

11. Prof. Ipiaú
6.Determinação do módulo do vetor
resultante.
Observação. ( Pág.124 )
4 caso – θ ≠ 00 ≠ 900 ≠ 1800
r2 = a2 + b2 + 2ab.cosθ
a
b
r

12. Prof. Ipiaú
6.Determinação do módulo do vetor
resultante.
Observação. ( Pág.124 )
Exemplo:
0,04 0,04
θ =1200
r = ?

13. Prof. Ipiaú
θ
a
6. Adição de vetores (Pág101).
6.3 Método dos componentes vetoriais.
Pág. 101 do módulo
x
y
ax
ay
ay
Sen θ =
Cos θ =
Cop
Hip
Cad
Hip
ax = a . cosθ ay = a . senθ

14. Prof. Ipiaú
7. Subtração vetorial.
Pág. 101 do módulo
S
b
a
r = a - b S = a + b
r = a + (- b)
- b b
r

15. Prof. Ipiaú
1. A figura abaixo representa os deslocamentos
de um móvél em várias etapas. Cada vetor tem
módulo igual a 20m. A distância percorrida
pelo móvel e o módulo do vetor deslocamento
são, respectivamente:
Pág. 283 do módulo
Exercícios de sala(Pág. 283).
A
B
20 m
20 m
20 m
20 m
20 m
20 m

16. Prof. Ipiaú
Fundinho
Fundinho
+
2. Analisando a figura a seguir pod-se afirmar:
Exercícios de sala(Pág. 283).
A
C
B
D
E
a) A + C = E
b) C + E = - A
c) C + D = B
d) E + B = - D
e) C + D = A + B
Pontinha
Fundinho
+
Paralelogramo
Polígono

17. Prof. Ipiaú
1.Dadas as forças abaixo, o módulo de sua
resultante em N é:
Exercícios de sala (Pág. 286).
F1
F3
F2***
*
*
*
*

18. Prof. Ipiaú
Exercícios de sala (2 Forma).
F1
F3
F2
-2i
i
j
2i
2j
2j
3i

19. Prof. Ipiaú
1. Grandezas escalares e vetoriais.
1.São conjuntos de grandezas escalares e
vetoriais respectivamente:
a) (pressão, força, aceleração) e (tempo, densidade, temperatura)
b) (carga, temperatura, massa) e (empuxo, velocidade, aceleração)
c) (deslocamento, volume e massa) e (campo magnético, campo
elétrico, campo gravitaçional)
d) (massa, tempo, energia) e (peso, pressão, carga elétrica)
e) (densidade, volume e massa) e (empuxo, força, trabalho)