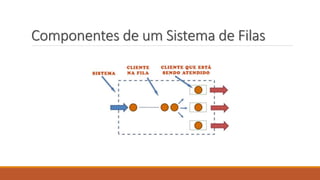
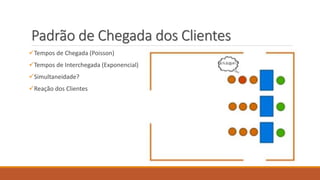
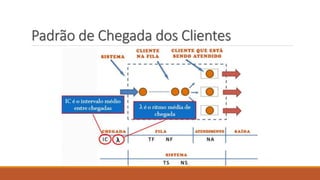
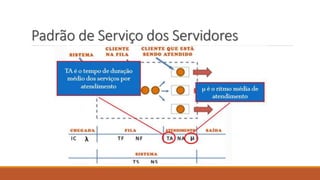
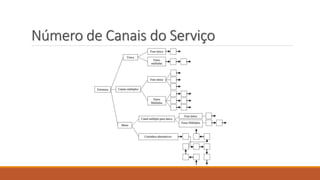
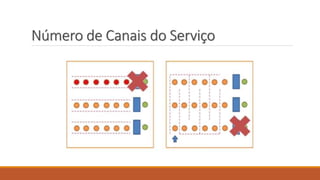
O documento aborda a teoria das filas, definindo conceitos como cliente, atendimento e servidor. Discute características das filas, notação de Kendall, e apresenta aplicações práticas com exemplos de probabilidade e estatística. Referências acadêmicas e materiais complementares são também citados para aprofundamento no tema.

1. Teoria das Filas
EDUARDO ARAÚJO, JULIANO FLORES E LUÍS JAEGER

2. Agenda
O que é fila
Teoria das Filas
Principais Características de uma Fila
Notação e Terminologia
Probabilidade e Estatística para Filas
Exemplo de Aplicação
Referências

3. O que é fila
Cliente
Atendimento
Servidor
Demanda > Capacidade

4. Teoria das Filas
Agner Erlang (1909)
Tráfego de Telefonia
Teoria das Probabilidades
Processos Estocásticos
Pesquisa Operacional
Ponto de Equilíbrio

5. Componentes de um Sistema de Filas

6. Principais Características de uma Fila
Padrão de Chegada dos Clientes
Padrão de Serviço dos Servidores
Disciplina de Filas
Capacidade do Sistema
Número de Canais do Serviço

7. Padrão de Chegada dos Clientes
Tempos de Chegada (Poisson)
Tempos de Interchegada (Exponencial)
Simultaneidade?
Reação dos Clientes

8. Padrão de Chegada dos Clientes

9. Padrão de Serviço dos Servidores

10. Disciplina de Filas
FCFS
LCFS
SIRO
PRI
Prempetiva
Não Premptiva

11. Capacidade do Sistema
Finita
Infinita

12. Número de Canais do Serviço

13. Número de Canais do Serviço

14. Notação e Terminologia
Notação de Kendall
Criada pelo professor D. G. Kendall em 1953
FormatoA/B/c:K/m/Z
Algumas notações omitem o “m”

15. Notação e Terminologia
Notação de Kendall  A/B/c : K/m/Z ou A/B/c : Z/m/K
A: distribuição dos intervalos entre chegadas
B: distribuição do tempo de serviço
c: o número de servidores ou quantidade de atendentes
K: a capacidade da fila de espera (alguns autores definem K como capacidade total de usuários no sistema)
m: tamanho da população que fornece clientes
Z a disciplina de atendimento.

16. Notação e Terminologia
Notação de Kendall  Valores para A e B
M: Distribuição Exponencial (processo Poisson, M de Markov)
Ek: Distribuição de Erlang-k
D: Distribuição Determinística ou degenerada
U: Distribuição Uniforme
G: Distribuição Geral (não especificada)

17. Notação e Terminologia
Notação de Kendall
Caso K, m e Z sejam omitidos
Disciplina FIFO (First In First Out)
População Infinita
Capacidade Infinita

18. Outras notações e terminologias
Estado do Sistema: Número de clientes no sistema de fila
Comprimento de Fila: Número de clientes esperando um serviço ou estado do sistema menos o
número de clientes sendo servido
N(t): Número de clientes no sistema de fila no tempo t (t maior ou igual a 0)
Pn(t): Probabilidade de que exatamente n clientes estejam no sistema de fila no tempo t, dado o
número no tempo 0
S: Número de servidores (canais de serviços paralelos) no sistema de fila

19. Outras notações e terminologias
λn: Taxa média de chegada de novos clientes quando n clientes estão no sistema.
μn: Taxa média de serviço para todo o sistema quando n clientes estão no sistema.
Quando a taxa média de serviço por servo ocupado é constante para todo n >= 1, está constante
é representada por μ
ρ = λ/(sμ) é a taxa de utilização do sistema: fração de tempo esperada dos servos em que eles
estão ocupados

20. Outras notações e terminologias

21. Probabilidade e Estatística para Filas
Processo de Poisson

22. Exemplo 1:
Em uma barbearia de um único barbeiro, os clientes chegam, com uma duração média
de 20 minutos entre cada chegada. O barbeiro gasta em média 15 minutos com cada
cliente.
a) Qual a probabilidade de um cliente não ter que esperar para ser atendido?
b) Qual o número esperado de clientes no salão do barbeiro? Na fila?
c) Quanto tempo, em média, um cliente permanece no salão?
d) Quanto tempo, em média, um cliente espera na fila?

23. Exemplo 2:
Supondo-se que a chegada de um navio ao berço portuário siga a distribuição de Poisson, com uma
taxa de 6 navios por dia. A duração média de atendimento dos navios é de 3 horas, seguindo-se a
distribuição exponencial.
a) Qual a probabilidade de um navio chegar ao porto e não esperar para atracar?
b) Qual é a quantidade média de navios na fila do porto?
c) Qual é a quantidade média de navios no sistema portuário?
d) Qual é a quantidade média de navios utilizando o porto?
e) Qual é o tempo médio de um navio na fila?
f) Qual deve ser a taxa de chegada de um navio para que o tempo médio na fila seja de 3 horas?
g) Qual é a probabilidade do berço portuário estar um uso?

24. Exemplo 3:
Uma filial de grande empresa contábil recebe semanalmente em média 200 processos para
cálculo dos encargos trabalhistas, estes processos são verificados e calculados por 3
funcionários contábeis em uma média de 1 processo a cada 45 minutos para cada
funcionário. Esta empresa enfrenta um problema de acúmulo de trabalho, o que por fim
torna necessário o envio dos processos para cálculo na matriz.
a) Qual seria a probabilidade de não existir nenhum documento na fila?
b) Qual a média de processos na fila?
c) Qual o tempo médio de um processo na fila?

25. Referências
CARDELLINI, Valeria; Colajanni, Michele; Yu, Philip S. Dynamic Load Balancing on Web-Server
Systems. IEEE Internet Computing 3, 3, 28-39. Maio 2009.
COSTA, Luciano Cajado. Teoria das Filas. Universidade Federal do Maranhão. Setembro 2010.
FILHO, Virgílio José Martins Ferreira. Processos Estocásticos e Teoria de Filas. Universidade
Federal do Rio de Janeiro. 2009.
TEORIA DAS FILAS. Teoria das Filas. Disponível em <
http://www.youtube.com/watch?v=ybZe4spMFfk>. Acesso em 21/09/2014.
YNOGUTI, Carlos Alberto. Probabilidade, Estatística e Processos Estocásticos. Universidade
Federal do Paraná. Janeiro 2011.

26. Perguntas?

27. Obrigado!