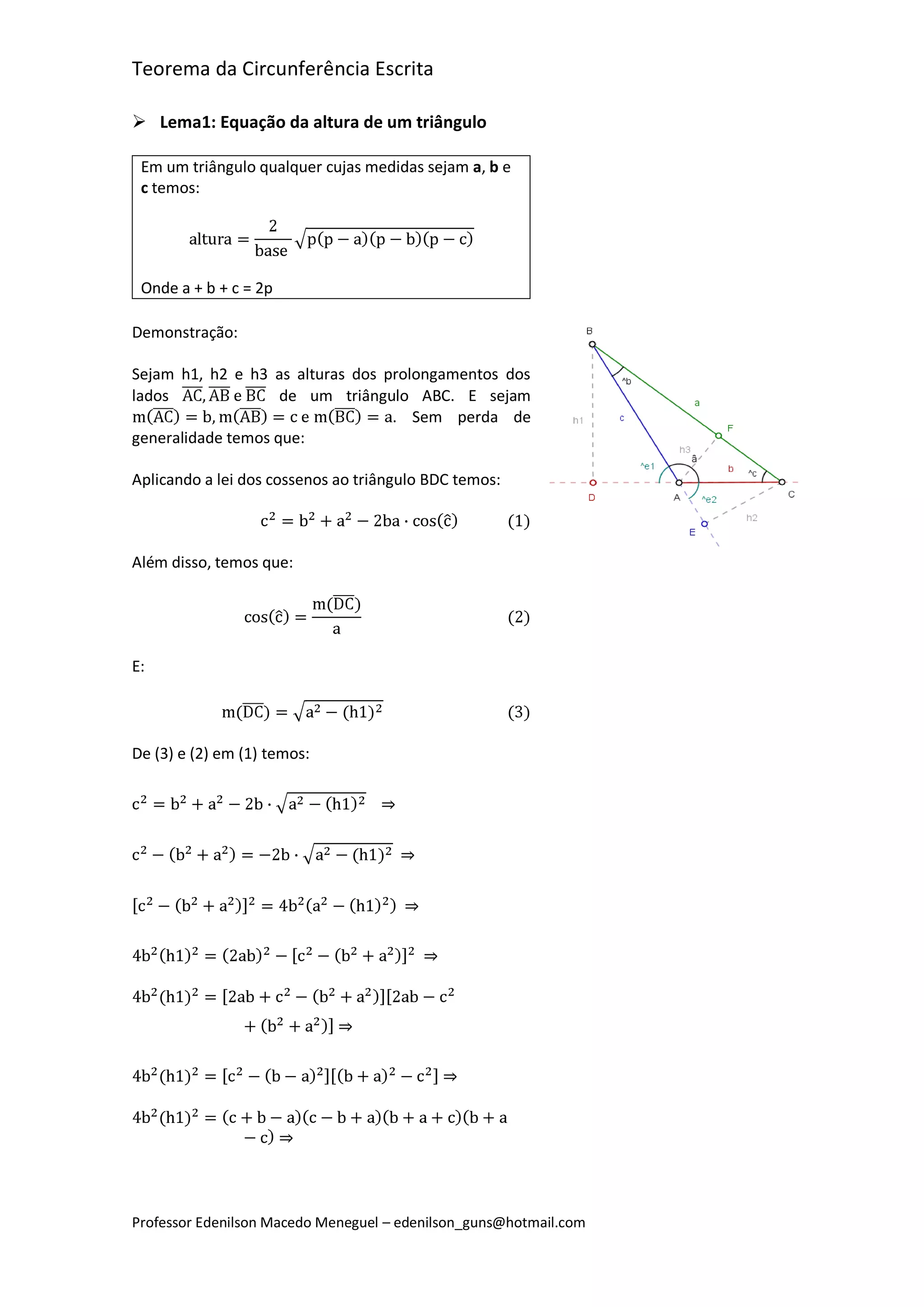
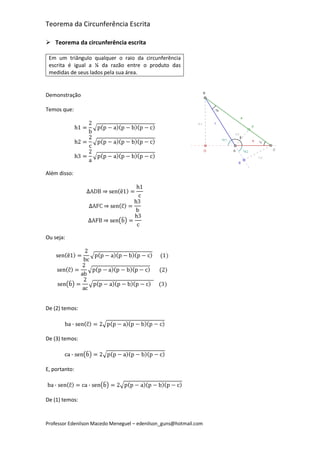
O documento apresenta o Teorema da Circunferência Escrita, demonstrando-o em três etapas: 1) Apresenta o Lema 1 sobre a altura de um triângulo e o Teorema de Heron sobre a área de um triângulo; 2) Apresenta a Lei dos Senos; 3) Chega ao Teorema da Circunferência Escrita, que afirma que o raio da circunferência inscrita é igual a um quarto da razão entre o produto das medidas dos lados do triângulo pela sua área.

1. Teorema da Circunferência Escrita
 Lema1: Equação da altura de um triângulo
Em um triângulo qualquer cujas medidas sejam a, b e
c temos:
Onde a + b + c = 2p
Demonstração:
Sejam h1, h2 e h3 as alturas dos prolongamentos dos
lados de um triângulo ABC. E sejam
. Sem perda de
generalidade temos que:
Aplicando a lei dos cossenos ao triângulo BDC temos:
Além disso, temos que:
E:
De (3) e (2) em (1) temos:
Professor Edenilson Macedo Meneguel – edenilson_guns@hotmail.com

2. Teorema da Circunferência Escrita
Logo, genericamente temos:
Onde 2p = a + b + c
 Teorema de Heron
Em um triângulo qualquer cujas medidas sejam a, b e
c sua área é dada pela formula
, onde a + b + c = 2p.
Demonstração
Pelo lema 1 , temos que:
Portanto:
Professor Edenilson Macedo Meneguel – edenilson_guns@hotmail.com

3. Teorema da Circunferência Escrita
 Lei dos senos
Em um triângulo qualquer cujas medidas sejam a, b e
c temos:
Onde r é o raio da circunferência escrita.
Demonstração
Para demonstrar a lei dos senos, tomamos um triângulo
ABC qualquer inscrito em uma circunferência de raio r. A
partir do ponto B pode-se encontrar um ponto
diametralmente oposto D, e, ligando D a C, formamos
um novo triângulo BCD retângulo em C. Da figura,
pelo teorema do ângulo inscrito podemos chegar a
conclusão que , porque determinam na
circunferência uma mesma corda . Desta forma,
podemos relacionar:
Fazendo todo este mesmo processo para os ângulos
e , teremos as relações:
Em que b é a medida do lado , oposto a , c é a
medida do lado , oposto a , e 2r é uma constante.
Logo, podemos concluir que:
Professor Edenilson Macedo Meneguel – edenilson_guns@hotmail.com

4. Teorema da Circunferência Escrita
 Teorema da circunferência escrita
Em um triângulo qualquer o raio da circunferência
escrita é igual a ¼ da razão entre o produto das
medidas de seus lados pela sua área.
Demonstração
Temos que:
Além disso:
Ou seja:
De (2) temos:
De (3) temos:
E, portanto:
De (1) temos:
Professor Edenilson Macedo Meneguel – edenilson_guns@hotmail.com

5. Teorema da Circunferência Escrita
Logo:
Donde temos:
Pelo teorema de Heron temos:
Ou seja, o raio da circunferência escrita é igual a ¼ da razão entre o produto da medida dos
lados do triângulo pela sua área.
Professor Edenilson Macedo Meneguel – edenilson_guns@hotmail.com