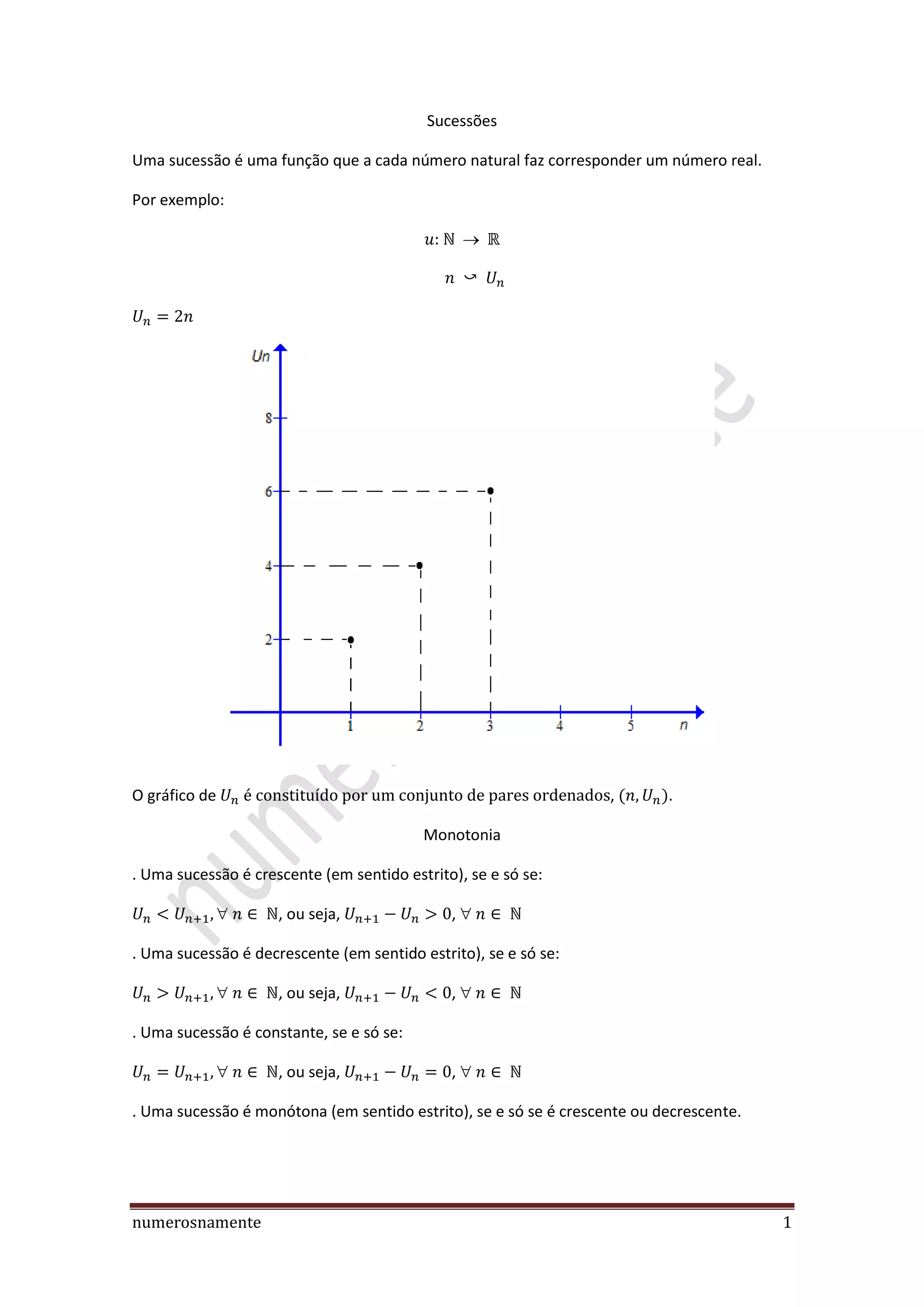
1) O documento discute conceitos sobre sucessões numéricas, incluindo definições de monotonia, sucessão limitada, limites de sucessões, progressão aritmética e progressão geométrica. 2) São apresentadas fórmulas e exemplos para calcular termos gerais, somas e limites de sucessões. 3) Os principais tipos de sucessões estudados são sucessões constantes, crescentes, decrescentes, limitadas e infinitamente grandes ou pequenas.

1. numerosnamente 1
Sucessões
Uma sucessão é uma função que a cada número natural faz corresponder um número real.
Por exemplo:
O gráfico de , .
Monotonia
. Uma sucessão é crescente (em sentido estrito), se e só se:
, ou seja, ,
. Uma sucessão é decrescente (em sentido estrito), se e só se:
, ou seja, ,
. Uma sucessão é constante, se e só se:
, ou seja, ,
. Uma sucessão é monótona (em sentido estrito), se e só se é crescente ou decrescente.

2. numerosnamente 2
. Uma sucessão é monótona crescente em sentido lato, se e só se:
,
. Uma sucessão é monótona decrescente em sentido lato, se e só se:
,
exemplos:
1- Estude a monotonia de
Resolução:
A sucessão .
2- Estude a monotonia de
Resolução:
Assim o sinal de ) depende do valor de .
Se ,
Se ,
,
Conclui-se que é uma sucessão não monótona.
3- Estude a monotonia de
Resolução:
Se é par em  que é decrescente
Se é impar em  que é crescente
A sucessão

3. numerosnamente 3
Sucessão Limitada
Uma sucessão se o conjunto dos seus termos é majorado e minorado.
,
Ou | |  definição de sucessão limitada
Se uma sucessão só for majorada, então não é limitada pois não tem minorante.
Se uma sucessão só é minorada, então não é limitada, pois não tem majorante.
Exemplos:
1- Verifique se é limitada.
Resolução:
Como
Minorante ); Majorante
A sucessão é limitada.
2- Considere a sucessão { . Verifique se é limitada.
Resolução:
Para termos de ordem impar:
Como
Para o conjunto de termos da sucessão que têm ordem impar, 3 é o minorante e 5 é o
majorante.
Para termos de ordem par:

4. numerosnamente 4
, que é um valor constante. O majorante é igual ao minorante.
Considere-se:
- Maior dos majorantes
-Menos dos minorantes
Temos então que a sucessão é limitada.
3- Considere a sucessão . Verifique se é limitada.
Resolução:
Se é par  . Então todos os termos pares são
Se é impar  . Então todos os termos ímpares são
 A sucessão é limitada.
4- Considere a sucessão . Verifique se é limitada.
Resolução:
Se é par 
Como
Para os termos de ordem par, é o minorante e é o majorante.
Se é par 
Como
Para os termos de ordem impar, é o minorante e o majorante.
Considere-se então:
-Maior dos majorantes
-Menos dos minorantes
 A sucessão é limitada.

5. numerosnamente 5
Limites de sucessões
Definição de infinitamente grande positivo :
Uma sucessão diz-se um infinitamente grande positivo, se para todo o número real que
se considere, existe uma ordem a partir da qual todos os termos da sucessão são maiores
que .
.

Demonstração:
Considere a sucessão
Fixado um número real , pretende-se determinar uma ordem a partir da qual se tenha
.Se , neste caso se (ordem 1), verifica-se que .
.Se , , pode-se concluir a ordem que vai satisfazer a condição
.
Se existe sempre um nº , que satisfaz esta condição .
Assim (infinitamente grande positivo).
Teorema: Se uma sucessão é um infinitamente grande positivo e se, a partir de uma
ordem , , então a sucessão é um infinitamente grande positivo.
Hipótese: e existe uma ordem , tal que, se , então .
Tese:
Demonstração:
Qualquer número real , sabe-se que existe uma certa ordem , tal que se , então
.
Também se sabe que a partir de uma ordem , tem-se que .
Sendo o maior dos números , então a partir da ordem se tem
Assim temos , permitindo concluir que : (infinitamente grande
positivo)
Exemplo:
Mostre que a sucessão √ é um infinitamente grande positivo.

6. numerosnamente 6
Por comparação temos:
√ √ ,
Como √ conclui-se que √
Definição de infinitamente grande negativo:
Um a sucessão é um infinitamente grande negativo, se e só se a sucessão for um
infinitamente grande positivo.
.

Exemplo:
Mostre que a sucessão é um infinitamente grande negativo.
Teremos que:
se e só se
Assim:
, então a partir
da ordem 1 se tem que e
Se  (c.q.d)
Definição de infinitamente grande (ou infinitamente grande em módulo):
Uma sucessão é um infinitamente grande em módulo, se e só se a sucessão | | é um
infinitamente grande positivo, isto é, | | .
 | |
Exemplo:
Considere a sucessão . Verifique que a sucessão é um infinitamente grande em
módulo.
{
A sucessão tem termos alternados:

7. numerosnamente 7
Para os pares = 4,16,36,….
Para os ímpares = -1, -9,-25,….
Assim á medida que vai aumentando, o valor absoluto dos termos vai também aumentando,
o que faz com que | | = seja um infinitamente grande positivo. Logo se a condição
anterior se verifica, então é um infinitamente grande em módulo.
Definição de infinitésimo:
Uma sucessão diz-se um infinitésimo, se e só se para todo o número real positivo ,
existe uma ordem a partir da qual todos os termos satisfazem a condição | | .
.
 | |
Exemplo:
Seja . Mostre que a sucessão é um infinitésimo.
Temos que
, temos:
; Como a sucessão é um infinitésimo, conclui-se que é um
infinitésimo.
Exemplo:
Mostre que é um infinitésimo.
Seja | | | | , se
Comparando | | com os termos do infinitésimo , temos:
 | | e como a sucessão é um infinitésimo, conclui-se
que é um infinitésimo.

8. numerosnamente 8
Definição de limite:
Uma sucessão converge para um número real se qualquer que seja o número real
positivo , existe uma ordem a partir da qual se tem | |
.
 | |
Uma sucessão é convergente se tiver como limite um número finito (real) e este limite é único.
Uma sucessão que seja monótona e limitada é então convergente.
A notação lê vizinhança de centro e raio .
| |
Exemplo:
Mostre que
Temos:
 | | | | | |
, como existe uma ordem que é igual ou
superior ao maior número natural que não satisfaz a condição . Por exemplo
, , assim neste caso . Fica provado que .
Operações com limites:
Se e
1-
2-
3-
4- ( ) ,
Indeterminações:
1-
2-
3- 0

9. numerosnamente 9
Exemplo:
Considere as sucessões ; √ ; . Determine os
limites.
(ind)
√
(√ ) (ind) ---Aplicar a regra do conjugado
(√ ) (
√
√
)
√
(ind)
√ √
( )
( )
( )
Generalizando, sejam
Sucessões Sucessão soma
O comportamento da sucessão depende
das sucessões consideradas.
Sucessões Sucessão Produto
Sucessões Sucessão quociente
O comportamento da sucessão , Vn
Depende das sucessões consideradas

10. numerosnamente 10
Por exemplo:
Seja e ;
e
Sucessões do tipo ,
1- Se , então é um infinitamente grande positivo.
2- Se | | , então é um infinitésimo.
3- Se , então é um infinitamente grande em módulo.
4- Se , então é uma sucessão constante com todos os termos iguais a 1.
5- Se , então é uma sucessão de termos alternadamente iguais a 1 ou a -1.
Por exemplo:
Seja e . Para a base é 1,2 >1 , assim estamos na presença de
um infinitamente grande positivo.
Para a base é <1 , estamos na presença de um infinitésimo.
Progressão Aritmética
Uma sucssão é uma progressão aritmética se e só se existe um número real (razão)
tal que ,
A monotonia de uma progressão aritmética é estudada atravéz de
- Se , a progressão (sucessão) é crescente (estritamente).
- Se , a progressão (sucessão) é decrescente (estritamente).
- Se , a progressão (sucessão) é constante.
O termo geral é
A soma de primeiros termos é
O número de termos da soma é . Na determinação da soma, temos de atender
qual o termo a ser considerado na soma. Assim sempre que se diz que é a partir de…, o
termo a considerar é o termo posterior ao referido. Se for mencionado a palavra inclusivé,
então considera-se o termo referido no inclusivé.
Por exemplo:
Sabe-se que numa progressão aritmética o e .
Escreva o seu termo geral.

11. numerosnamente 11
Calcule a soma de 20 termos consecutivos a partir do 3º termo inclusivé.
Calcule a soma de 5 termos consecutivos a partir do 10 termo.
Resolução:
12
3 2
de 20 termos consecutivos a começar em
; Nº de termos = 20 = n-p+1 , com p=3 então n=22 é o termo
onde termina a soma.
=
Soma de 5 termos consecutivos a partir o 10 termo.
Considera-se que começa no 11 termo.
Nº de termos = 5 =n-p+1 , com p=11 então n=15 o termo onde termina a soma.
=
Porgressão Geométrica
Uma sucessão é uma progressão geométrica se e só se existe um número real
(razão) talque:
, ou
Quanto à monotonia, temos que fazer o estudo do sinal do 1º termo e da razão.
- Se A progressão geométrica é crescente (não limitada)
- Se A progressão geométrica é decrescente (não limitada)
- Se A progressão geométrica é crescente (limitada)
- Se A progressão geométrica é decrescente (limitada)

12. numerosnamente 12
- Se A progressão geométrica é constante (limitada)
- Se A progressão geométrica é não monotona (limi2tada)
- Se A progressão geométrica é não monotona (limitada)
- Se A progressão geométrica é não monotona (não limitada)
O termo geral é ,
A soma de n primeiros termos é , ,
Muitas vezes calcula-se o limite da soma de n termos e então temos de atender ao valor
de
-Se
- Se
Por exemplo:
Considere a sucessão . Mostre que é uma progressão geométrica e calcule a soma
de 10 termos consecutivos a partir do 5º.
e é progressão geometrica crescente.
;
21824