O documento aborda problemas de sucessões e suas aplicações, incluindo o cálculo do número máximo de pessoas que podem sentar em mesas dispostas de maneira específica e a determinação de termos em várias sequências matemáticas. Ele apresenta exercícios que envolvem a continuidade de sucessões numéricas, suas características e propriedades, como monotonicidade e termos gerais. As soluções são fornecidas com justificativas detalhadas para cada questão.

1. 243
Generalidades
acerca de sucessões
8
U
NIDADE
TAREFAS E AVALIAR CONHECIMENTOS
8.1 Sucessões numéricas
Tarefa 1
Um grupo de amigos vai jantar a um restaurante onde as mesas existentes,
dispostas individualmente, permitem sentar confortavelmente quatro pessoas.
As figuras seguintes ilustram a disposição que as cadeiras devem ter, à volta
das mesas, juntando duas mesas, três mesas, etc., de forma a sentar o número
máximo de pessoas, confortavelmente.
1.1
Qual é o número máximo de amigos que se podem sentar confortavelmente
se juntarem 10 mesas? E 20 mesas?
1.2
Qual é o número mínimo de mesas necessárias para sentar confortavelmente
100 amigos?
1.3
Na inauguração da ponte Vasco da Gama
foi servida uma feijoada em cima
da ponte. Admitindo que foram usadas
11 000 mesas como estas, colocadas
juntas ao longo da ponte, indique
o número máximo de pessoas que
se sentaram à mesa confortavelmente.
1.4
Determine o número máximo, N , de amigos que é possível sentar
confortavelmente em função do número, n , de mesas juntas.
1.1
Para 10 mesas tem-se 2 × 10 + 2 = 22 pessoas e para 20 mesas
são 2 × 20 + 2 = 42 pessoas.
1.2 Como
2
100 2
-
= 49 , então, são necessárias 49 mesas.
1.3 Para 11 000 mesas tem-se 2 × 11 000 + 2 = 22 002 pessoas.
1.4
N = 2n + 2
u3p8h1 u3p8h2 u3p8h3
000707 243-251 U8.indd 243 01/07/16 12:35

2. 244
Generalidades acerca de sucessões
1
Nas figuras seguintes estão representados o 1.o
, o 2.o
e o 3.o
termos de uma
sucessão.
1.1
Represente o 4.º e o 5.º termos desta sucessão.
1.2 Sendo n a ordem da figura, indique, em função de n :
a)
o número de quadradinhos brancos.
b)
o número total de quadradinhos.
1.1
1.2 a) 2n(n - 1) + n = 2n2
- n
b) (2n + 1)n = 2n2
+ n
2
Nas figuras seguintes estão os três primeiros termos de uma sucessão
de quadrados construídos com fósforos.
1
u3p8h5
2
u3p8h6
4
u3p8h7
u3p9h2
u3p9h3
u3p9h4
u3p184hs1
u3p184hs2
4.o
termo 5.o
termo
Supondo que o processo de construção de cada quadrado se mantém, determine:
a)
o número de fósforos necessários para construir a figura de ordem 20 .
b)
um termo geral da sucessão do número total de fósforos.
a)
Contando separadamente os fósforos verticais e horizontais, obtém-se
21 × 20 + 20 × 21 = 2 × 20 × 21 = 840 fósforos.
b) 2n(n + 1) = 2n2
+ 2n
000707 243-251 U8.indd 244 01/07/16 12:35

3. 245
8
U
NIDADE
Domínio 3 SUCESSÕES
3
Indique um termo geral da sucessão cujos primeiros termos são:
a)
0, 3, 8, 15, 24, … b)
1, 4, 7, 10, …
a)
n2
- 1 b) 3n - 2
4
Calcule o 2.o
e o 10.o
termos da sucessão de termo geral:
a)
un =
n
n
1 2
2 3
-
+
b) vn = (-1)2n + 1
n
3
a)
u2 =
1 2 2
2 2 3
#
#
-
+
= -
3
7
e u10 =
1 2 10
2 10 3
#
#
-
+
= -
19
23
b)
v2 = (-1)2 × 2 + 1
2
3
= -
2
3
e v10 = (-1)2 × 10 + 1
10
3
= -
10
3
5
Averigue se -2 é termo de alguma das sucessões seguintes, e, se o for,
indique a sua ordem.
a)
an =
n
n
3
3 1
+
-
b) bn =
n
n
3
3 5
2
-
+
c)
cn = n2
- 2n - 2
d)
dn = n 3
+ - 4
e)
en = -6 + 2 n 1
+
a) an = -2 +
n
n
3
3 1
+
-
= -2 + 3n - 1 = -2n - 6 + n = -1 IN
Logo, -2 não é termo de (an) .
b) bn = -2 +
n
n
3
3 5
2
-
+
= -2 + 3 + 5n = -2n2
+ 6 +
+ 2n2
+ 5n - 3 = 0 + n =
( )
2 2
5 25 4 2 3
#
! # #
- - -
+
+ n =
4
5 7
!
-
+ n = -3 0 n =
2
1
Como -3,
2
1
IN , -2 não é termo de (bn) .
c) cn = -2 + n2
- 2n - 2 = -2 + n(n - 2) = 0 + n = 0 0 n = 2
Como 2 ! IN , -2 é termo de (cn) , de ordem 2 .
d) dn = -2 + qn + 3u - 4 = -2 + qn + 3u = 2 +
+ n + 3 = 2 0 n + 3 = -2 + n = -1 0 n = -5
Como -1 , -5 IN , -2 não é termo de (dn) .
e) en = -2 + -6 + 2 n 1
+ = -2 + n 1
+ = 2 n + 1 = 4 +
+ n = 3 ! IN
Como 3 é solução da equação, pois -6 + 2 3 1
+ = -2 ,
-2 é termo de (en) de ordem 3 .
000707 243-251 U8.indd 245 01/07/16 12:35

4. 246
Generalidades acerca de sucessões
Tarefa 2
Considere a sequência de figuras seguinte.
N.º da figura 1 2 3 4
Figura
u3p10h1
u3p10h2 u3p10h3 u3p10h4
Seja (un) a sucessão que ao número de triângulos de cada figura faz corresponder
o número de segmentos de reta representados na figura.
2.1
Justifique que um termo geral da sucessão (un) pode ser:
un = 3 + 2(n - 1)
2.2
Determine o número de segmentos da 49.a
figura.
2.3
Averigue, justificando, se existe alguma figura com 150 segmentos.
2.1
Em cada figura são adicionados 2 segmentos. Assim, a figura n
tem mais 2(n - 1) segmentos do que os 3 do triângulo inicial, ou seja:
un = 3 + 2(n - 1)
2.2 u49 = 3 + 2 × 48 = 99
2.3 3 + 2(n - 1) = 150 + n = 74,5 IN
Portanto, não existe nenhuma figura com 150 segmentos.
8.2 Sucessões monótonas
6
Considere a sucessão de termo geral:
an = n
n
3 2
-
6.1
Represente graficamente os cinco primeiros termos da sucessão.
6.2
Averigue se 3 é termo da sucessão.
6.3 Prove que:
6n ! IN, an 3
6.4 Calcule an + 1 e a2n .
6.1 Como a1 = 1 , a2 = 2 , a3 =
3
7
, a4 =
2
5
e a5 =
5
13
, tem-se:
3
2,5
2
1,5
1
0,5
an
n
0 1 2 3 4 5
000707 243-251 U8.indd 246 01/07/16 12:35

5. 247
8
U
NIDADE
Domínio 3 SUCESSÕES
6.2
an = 3 + n
n
3 2
-
= 3 + 3n - 2 = 3n + -2 = 0
Equação impossível; logo, 3 não é termo da sucessão.
6.3
Tem-se que n
n
3 2
-
= n
n
3
- n
2
= 3 - n
2
.
Como n
2
0, 6n ! IN , então, an 3 .
6.4 an + 1 =
( )
n
n
1
3 1 2
+
+ -
=
n
n
1
3 1
+
+
a2n =
( )
n
n
2
3 2 2
-
=
n
n
2
6 2
-
= n
n
3 1
-
Tarefa 3
Na figura seguinte está representada uma sequência de figuras constituídas
por semicircunferências, em que o 1.o
termo desta sequência é uma
semicircunferência de diâmetro igual a 2 cm , e, como sugere a figura,
cada um dos outros termos é constituído pelo dobro das semicircunferências
do termo anterior, tendo cada uma delas diâmetro igual a metade do diâmetro
de cada semicircunferência do termo anterior.
u3p12h2
2 cm
u3p12h3
2 cm
u3p12h4
2 cm
Seja (cn) a sucessão dos comprimentos de cada termo.
3.1
Calcule os três primeiros termos de (cn) .
3.2
Escreva um termo geral de (cn) .
3.3
Como classifica (cn) quanto à monotonia?
3.1
c1 = r , c2 = 2 ×
2
r
= r e c3 = 4 ×
4
r
= r
3.2 cn = n × n
r
= r
3.3
Sucessão monótona em sentido lato.
7
Mostre que as sucessões seguintes são monótonas e indique o tipo de monotonia.
a)
un =
n
n
1
2
+
b)
vn = 5 - 4n
c)
wn = n2
+ 1
d)
xn = 2 - sin(nr)
000707 243-251 U8.indd 247 01/07/16 12:35

6. 248
Generalidades acerca de sucessões
a) un + 1 - un =
( )
n
n
n
n
2
2 1
1
2
+
+
-
+
=
( )( )
( ) ( )
n n
n n n
2 1
2 1 2 2
2
+ +
+ - +
=
=
( )( )
n n
n n n n
2 1
2 4 2 2 4
2 2
+ +
+ + - -
=
( )( )
n n
2 1
2
+ +
0, 6n ! IN
Logo, (un) é monótona crescente.
b)
vn + 1 - vn = ^5 - 4(n + 1)h - (5 - 4n) = 5 - 4n - 4 - 5 + 4n =
= -4 0, 6n ! IN
Logo, (vn) é monótona decrescente.
c)
wn + 1 - wn = ^(n + 1)2
+ 1h - (n2
+ 1) =
= n2
+ 2n + 1 + 1 - n2
- 1 = 2n + 1 0, 6n ! IN
Logo, (wn) é monótona crescente.
d)
xn + 1 - xn = _2 - sin^(n + 1)rhi - ^2 - sin(nr)h =
= 2 - 2 = 0, 6n ! IN
Logo, (xn) é constante.
8
Classifique quanto à monotonia as sucessões de termo geral:
a) an = 4n2
- 1
b) bn = (5 - n)2
c) cn =
n
n
2
3
-
d) dn = n 6
-
e)
en =
n
n
2 se par
3 se ímpar
*
a)
an + 1 - an = ^4(n + 1)2
- 1) - (4n2
- 1) =
= 4n2
+ 8n + 4 - 1 - 4n2
+ 1 = 8n + 4 0, 6n ! IN
Logo, (an) é monótona crescente.
b)
bn + 1 - bn = ^5 - (n + 1)h2
- (5 - n)2
=
= 16 - 8n + n2
- 25 + 10n - n2
= 2n - 9
2n - 9 0 para n H 5 mas 2n - 9 0 para n 5 ; logo,
(bn) não é monótona.
c)
cn + 1 - cn =
( )
( )
n
n
n
n
2 1
1 3
2
3
+
+ -
-
-
=
( )( )
n n
n n n n
2 2
2 3 1
2
2
+
- - - +
=
=
n n
n n n n n
2 2
2 3 3
2
2 2
+
- - - + +
=
n n
2 2
3
2
+
0, 6n ! IN
Logo, (cn) é monótona crescente.
d)
dn + 1 - dn = q(n + 1) - 6u - qn - 6u = qn - 5u - qn - 6u
Para n = 1 obtém-se qn - 5u - qn - 6u = -1 e para n = 7
obtém-se qn - 5u - qn - 6u = 1 ; logo, (dn) não é monótona.
e)
e1 = 3 e2 = 2 e e2 = 2 e3 = 3 ; logo, (en) não é monótona.
000707 243-251 U8.indd 248 01/07/16 12:35

7. 249
8
U
NIDADE
Domínio 3 SUCESSÕES
9
Considere as sucessões de termo geral: un = kn + 2, k ! IR .
Indique os valores de k para os quais (un) é:
a) crescente. b)
decrescente em sentido lato. c)
constante.
un + 1 - un = ^k(n + 1) + 2h - (kn + 2) = kn + k + 2 - kn - 2 = k
a) (un) é crescente, se k 0 , ou seja, se k ! ]0, +3[ .
b) (un) é decrescente em sentido lato, se k G 0 , ou seja, se k ! ]-3, 0].
c) (un) é constante, se k = 0 .
10
Sejam (un) e (vn) duas sucessões tais que, para todo n ! IN :
un + 1 - un = 4
vn + 1 - vn = 4 - n
10.1 Sabendo que u1 = 5 , determine os cinco primeiros termos de (un) .
10.2
Classifique, justificando, cada uma das sucessões quanto à monotonia.
10.1
u1 = 5 ; u2 - u1 = 4 + u2 = 9 ; u3 - u2 = 4 + u3 = 13 ;
u4 - u3 = 4 + u4 = 17 e u5 - u4 = 4 + u5 = 21
10.2 Como un+1 - un = 4 0 , (un) é crescente.
Como para n = 1 , 4 - n = 3 e para n = 5 , 4 - n = -1 ,
(vn) não é monótona.
8.3 Sucessões limitadas
11
Considere os seguintes subconjuntos de números reais:
A = ]-3, 5] B = ]-1, 4] , {7} C = {0, 1}
11.1
Quais dos conjuntos dados são minorados? E limitados?
11.2
Indique o conjunto dos majorantes de cada um dos conjuntos apresentados.
11.1
Tem-se que 6a ! A, a G 5 mas bm ! IR: a H m .
Logo, A é apenas majorado e, por isso, não é limitado.
Tem-se que 6b ! B, -1 G b G 7 .
Logo, B é minorado e majorado, sendo, por isso, limitado.
Tem-se que 6c ! C, 0 G c G 1 .
Logo, C é minorado e majorado, sendo, por isso, limitado.
11.2
Majorantes de A : [5, +3[
Majorantes de B : [7, +3[
Majorantes de C : [1, +3[
000707 243-251 U8.indd 249 01/07/16 12:35

8. 250
Generalidades acerca de sucessões
12
Dê um exemplo de um subconjunto de números reais:
a) limitado.
b)
majorado e não limitado.
c) não limitado.
a) ]2, 4[ b) ]-3, 4[ c) ]-3, 4[
13
Prove que são limitadas as sucessões com os termos gerais seguintes,
indicando um majorante e um minorante para cada.
a) an =
n
2 1
3
-
b) bn = -7 c) cn = n
n
5 1
-
a)
Tem-se que 2n - 1 H 1 ; logo, 0
n
2 1
3
-
G 3, 6n ! IN .
Assim, (an) é limitada; 0 é um minorante e 3 é um majorante.
b)
Tem-se que (bn) é constante; logo, (bn) é limitada; -7 é simultaneamente
um minorante e um majorante.
c)
Tem-se que n
n
5 1
-
= 5 - n
1
e 0 n
1
G 1 , ou seja, -1 G - n
1
0 .
Portanto, -1 G - n
1
0 + 4 G 5 - n
1
5, 6n ! IN .
Assim, (cn) é limitada; 4 é um minorante e 5 é um majorante.
14
Uma sucessão (wn) de termos positivos é tal que, para todo o número natural
n , w
3
n
H 4 .
Justifique que a sucessão é limitada.
Caderno de Apoio do 11.º ano
w
3
n
H 4 +
w
3 4
1
n
G + wn G
4
3
, 6n ! IN
Como (wn) é uma sucessão de termos positivos, tem-se wn H 0 .
Logo, 0 G wn G
4
3
, ou seja, (wn) é limitada.
15
Considere a sucessão de termo geral:
wn = n2
- 15n
15.1
Mostre que (wn) é não monótona.
15.2
Indique, caso exista, o mínimo do conjunto dos termos da sucessão.
000707 243-251 U8.indd 250 01/07/16 12:35

9. 251
8
U
NIDADE
Domínio 3 SUCESSÕES
15.1 wn + 1 - wn = ^(n + 1)2
- 15(n + 1)h - (n2
- 15n) =
= n2
+ 2n + 1 - 15n - 15 - n2
+ 15n = 2n - 14
Para n = 1 , 2n - 14 = -12 , e, para n = 8 , 2n - 14 = 2 ;
logo, (wn) não é monótona.
15.2
n2
- 15n = 0 + n = 0 0 n = 15
Logo, se considerarmos a parábola dada por x2
- 15x , o seu vértice
tem de abcissa 7,5 . Assim, o mínimo desta sucessão será atingido
na ordem 7 ou 8 .
Como w7 = 72
- 15 × 7 = -56 e w8 = 82
- 15 × 8 = -56 ,
o mínimo é -56 .
16
De uma sucessão (an) sabe-se que:
• a1 = 1
• 6n ! IN, an + 1 an
• 6n ! IN, an G 4
Em nenhuma das figuras seguintes estão representados graficamente os dez
primeiros termos de (an) .
Indique, para cada representação, uma razão que justifique a afirmação
anterior.
(I) (III)
0 1
1
4
2 3 4 5 6 7 8 9 10 n
u3p16h1
y
0 1
1
4
2 3 4 5 6 7 8 9 10 n
u3p16h3
y
Na figura (I), tem-se a1 = 4 ! 1 ; na figura (II), a sucessão não é estritamente
crescente; e, na figura (III), há termos superiores a 4 .
(II)
0 1
1
4
2 3 4 5 6 7 8 9 10 n
u3p16h2
y
000707 243-251 U8.indd 251 01/07/16 12:35

10. 252
Princípio de indução
matemática
9
U
NIDADE
TAREFAS E AVALIAR CONHECIMENTOS
9.1
Princípio de indução matemática
1
Se estiver vivo num dia, também estarei no dia seguinte.
Justifique que está garantida a vida eterna a quem formular
este pedido ao génio da lâmpada e este o conceder.
Obviamente que a pessoa está viva no dia em que faz o pedido; logo, também
estará viva no dia seguinte e no seguinte e no seguinte, e assim por diante,
nunca podendo morrer.
2
Prove, por indução matemática, que é verdadeira a seguinte propriedade:
6n ! IN,
i
n
1
=
/(6i - 3) = 3n2
Considere-se a condição P(n):
i
n
1
=
/(6i - 3) = 3n2
.
A proposição P(1) é 6 × 1 - 3 = 3 × 1 , que é verdade.
Hipótese: Para um certo n ! IN ,
i
n
1
=
/(6i - 3) = 3n2
.
Tese:
i
n
1
1
=
+
/ (6i - 3) = 3(n + 1)2
Demonstração:
i
n
1
1
=
+
/ (6i - 3) =
i
n
1
=
/(6i - 3) + ^6(n + 1) - 3h
Usando a hipótese de indução, obtém-se:
i
n
1
1
=
+
/ (6i - 3) = 3n2
+ ^6(n + 1) - 3h = 3n2
+ 6n + 3 =
= 3(n2
+ 2n + 1) = 3(n + 1)2
Portanto, pelo princípio de indução matemática, a proposição
6n ! IN,
i
n
1
=
/(6i - 3) = 3n2
é verdadeira.
000707 252-267 U9.indd 252 01/07/16 12:36

11. 253
9
U
NIDADE
Domínio 3 SUCESSÕES
3
Prove, por indução matemática, que são verdadeiras as seguintes propriedades:
a)
6n ! IN2, 3n
2n + 1
b)
6n ! IN,
k
n
1
=
/(k + 1) =
( )
n n
2
3
+
c)
6n ! IN, n3
+ 5n é divisível por 3
d)
6n ! IN4, 2n
3n
a)
Considere-se a condição P(n): 3n
2n + 1
.
A proposição P(2) é 32
22 + 1
, que é verdade, pois 9 8 .
Hipótese: Para um certo n ! IN2 , 3n
2n + 1
.
Tese: 3n + 1
2n + 2
Demonstração:
3n + 1
= 3n
× 3
Usando a hipótese de indução, obtém-se:
3n + 1
2n + 1
× 3 2n + 1
× 2 = 2n + 2
Portanto, pelo princípio de indução matemática, a proposição
6n ! IN2, 3n 2n + 1
é verdadeira.
b)
Considere-se a condição P(n):
k
n
1
=
/ (k + 1) =
( )
n n
2
3
+
.
A proposição P(1) é 1 + 1 =
( )
2
1 1 3
+
, que é verdade.
Hipótese: Para um certo n ! IN,
k
n
1
=
/ (k + 1) =
( )
n n
2
3
+
.
Tese:
k
n
1
1
=
+
/ (k + 1) =
( )( )
n n
2
1 4
+ +
Demonstração:
k
n
1
1
=
+
/ (k + 1) =
k
n
1
=
/ (k + 1) + (n + 1 + 1)
Usando a hipótese de indução, obtém-se:
k
n
1
1
=
+
/ (k + 1) =
( )
n n
2
3
+
+ (n + 1 + 1) =
=
( ) ( )
n n n
2
3 2 2
+ + +
=
n n n
2
3 2 4
2
+ + +
=
=
n n n
2
4 4
2
+ + +
=
( )
n n n
2
4 4
+ + +
=
( )( )
n n
2
1 4
+ +
Portanto, pelo princípio de indução matemática, a proposição
6n ! IN,
k
n
1
=
/ (k + 1) =
( )
n n
2
3
+
é verdadeira.
000707 252-267 U9.indd 253 01/07/16 12:36

12. 254
Princípio de indução matemática
1 2 3 4
c)
Considere-se a condição P(n): « n3
+ 5n é divisível por 3 » .
A proposição P(1) é « 13
+ 5 é divisível por 3 » , que é verdade.
Hipótese: Para um certo n ! IN , « n3
+ 5n é divisível por 3 » .
Tese: « (n + 1)3
+ 5(n + 1) é divisível por 3 »
Demonstração:
(n + 1)3
+ 5(n + 1) = (n + 1)(n2
+ 2n + 1) + 5n + 5 =
= n3
+ 2n2
+ n + n2
+ 2n + 1 + 5n + 5 =
= (n3
+ 5n) + 3n2
+ 3n + 6 = (n3
+ 5n) + 3(n2
+ n + 2)
Tem-se que (n + 1)3
+ 5(n + 1) é a soma de dois múltiplos de 3
^ n3
+ 5n que por hipótese de indução é múltiplo de 3 e 3(n2
+ n + 2) h .
Logo, (n + 1)3
+ 5(n + 1) é divisível por 3 .
Portanto, pelo princípio de indução matemática, a proposição
« n3
+ 5n é divisível por 3 » é verdadeira.
d)
Considere-se a condição P(n): 2n
3n .
A proposição P(4) é 24
3 × 4 , o que é verdade, pois 16 12 .
Hipótese: Para um certo n ! IN4 , 2n
3n .
Tese: 2n + 1
3(n + 1)
Demonstração:
2n + 1
= 2n
× 2
Usando a hipótese de indução, obtém-se:
2n + 1
3n × 2 3n + 3 = 3(n + 1)
Portanto, pelo princípio de indução matemática, a proposição
6n ! IN4, 2n
3n
é verdadeira.
Em alternativa:
Considere-se a condição P(n): 3n × 2 = 3n + 3n 3n + 3 .
Como 6n 3n + 3 + n 1 , obtém-se uma condição universal em IN4 .
Tarefa 1
Na figura seguinte estão representados os quatro primeiros números triangulares,
construídos com seixos.
000707 252-267 U9.indd 254 01/07/16 12:36

13. 255
9
U
NIDADE
Domínio 3 SUCESSÕES
1.1
Construa o 5.º e o 6.º números triangulares e indique o número necessário
de seixos para construir cada um deles.
1.2
Indique, dado o número triangular de ordem n , o processo de obter
o número triangular de ordem n + 1 e, considerando (tn) a sucessão
dos números triangulares, escreva tn + 1 em função de tn .
1.3
Prove, utilizando o princípio de indução matemática, que a sucessão
de números triangulares pode ser definida pelo termo geral:
tn =
n n
2
2
+
1.4
Averigue se 160 é um número triangular.
1.1
O 5.º número triangular tem 15 seixos e o 6.º tem 21 .
1.2
O número triangular de ordem n + 1 obtém-se acrescentando uma fila
com n + 1 seixos ao número triangular de ordem n .
tn + 1 = tn + (n + 1), 6n ! IN
1.3 Para n = 1 , tem-se t1 = 1 , que é verdade.
Hipótese: Para um certo n ! IN , tn =
n n
2
2
+
.
Tese: tn + 1 =
( )
n n
2
1 1
2
+ + +
=
n n
2
3 2
2
+ +
Demonstração:
tn + 1 = tn + n + 1
Por hipótese, obtém-se:
tn + 1 =
n n
2
2
+
+ n + 1 =
n n
2
3 2
2
+ +
Portanto, pelo princípio de indução, a proposição 6n ! IN, tn =
n n
2
2
+
é verdadeira.
1.4
tn = 160 +
n n
2
2
+
= 160 + n2
+ n - 320 = 0 +
+ n =
2
1 1 4 320
! #
- +
IN
Logo, 160 não é um número triangular.
000707 252-267 U9.indd 255 01/07/16 12:36

14. 256
Princípio de indução matemática
4
Seja P(n) a seguinte condição:
k
k
n
1
=
/ =
( )( )
n n
2
1 2
- +
4.1
Prove que a proposição 6n ! IN, P(n) P(n + 1) é verdadeira.
4.2
Pode-se concluir que 6n ! IN, P(n) é verdadeira? Justifique a sua resposta.
4.1
Suponha-se que P(n) se verifica, ou seja, que para n ! IN se tem:
k
n
1
=
/ k =
( )( )
n n
2
1 2
- +
Tese:
k
n
1
1
=
+
/ k =
( )
n n
2
3
+
Tem-se que
k
n
1
1
=
+
/ k =
k
n
1
=
/ k + (n + 1) ; logo, usando a hipótese:
k
n
1
1
=
+
/ k =
( )( )
n n
2
1 2
- +
+ (n + 1) =
( )( )
n n n
2
1 2 2 2
- + + +
=
=
n n n n
2
2 2 2 2
2
+ - - + +
=
n n
2
3
2
+
=
( )
n n
2
3
+
Portanto, P(n + 1) também se verifica.
4.2
Não, porque P(1) é falsa:
k 1
1
=
/ k = 1 ! 0 =
( )( )
2
1 1 1 2
- +
.
9.2
Sucessões definidas por recorrência
5
Considere a sucessão (un) definida por:
u
u u
4
3
n n
1
1
=
= -
+
*
, 6n ! IN
5.1
Determine os cinco primeiros termos de (un) .
5.2
Prove que (un) é monótona decrescente.
5.1
u1 = 4 ; u2 = u1 - 3 = 1 ; u3 = u2 - 3 = -2 ;
u4 = u3 - 3 = -5 ; u5 = u4 - 3 = -8
5.2
un + 1 - un = un - 3 - un = -3 0, 6n ! IN
Logo, a sucessão é estritamente decrescente.
6
Na figura estão representados os três primeiros
termos de uma sucessão de figuras constituídas
por quadrados. 1
u3p22h2
2 3
000707 252-267 U9.indd 256 01/07/16 12:36

15. 257
9
U
NIDADE
Domínio 3 SUCESSÕES
6.1
Indique o número de quadrados que constituem o 7.º e o 8.º termos.
6.2
Seja (qn) a sucessão do número de quadrados em cada termo.
Defina a sucessão (qn) por recorrência.
6.3
Mostre, por indução matemática, que um termo geral de (qn) é:
qn = 2n - 1
6.1
O 7.º termo tem 13 quadrados e o 8.º tem 15 quadrados, pois o número
de quadrados aumenta duas unidades de um termo para o termo seguinte.
6.2
q
q q
1
2
n n
1
1
=
= +
+
*
, 6n ! IN
6.3 Para n = 1 , tem-se q1 = 2 - 1 = 1 , que é verdade.
Hipótese: Para um certo n ! IN , qn = 2n - 1 .
Tese: qn + 1 = 2(n + 1) - 1
Demonstração:
qn + 1 = qn + 2
Por hipótese, obtém-se:
qn + 1 = 2n - 1 + 2 = 2(n + 1) - 1
Portanto, pelo princípio de indução, a proposição 6n ! IN , qn = 2n - 1
é verdadeira.
7
Seja (un) a sucessão definida por:
u
u
u
5
2
1
n
n
1
1
=
=
+
+
*
,6n ! IN
7.1
Mostre, por indução, que 6n ! IN, un 1 .
7.2
Deduza da alínea anterior que (un) é decrescente.
Caderno de Apoio do 11.º ano
7.1 Para n = 1 , tem-se u1 = 5 1 , que é verdade.
Hipótese: Para um certo n ! IN , un 1 .
Tese: un + 1 1
Demonstração:
un + 1 =
u
2
1 n
+
=
2
1
+
u
2
n
Por hipótese, un 1 ; logo,
u
2
n
2
1
e, portanto, un + 1 1 .
Portanto, pelo princípio de indução, a proposição 6n ! IN, un 1 é verdadeira.
7.2
un + 1 - un =
u
2
1 n
+
- un =
u
2
1 n
-
Como un 1 ,
u
2
1 n
-
0, 6n ! IN ; logo, (un) é decrescente.
000707 252-267 U9.indd 257 01/07/16 12:36

16. 258
Princípio de indução matemática
8
Seja (an) a sucessão definida por:
a
a
a
a
2
1
1
n
n
n
1
1
=
=
+
+
*
,6n ! IN
Prove, por indução matemática, que
6n ! IN, 0 G an G 1
Para n = 1 , tem-se 0 G a1 =
2
1
G 1 , que é verdade.
Hipótese: Para um certo n ! IN , 0 G an G 1 .
Tese: 0 G an + 1 G 1
Demonstração:
an + 1 =
a
a
1
n
n
+
Por hipótese, an H 0 ; logo,
a
a
1
n
n
+
H 0 e
a
a
1
n
n
+
an G 1 .
Portanto, pelo princípio de indução, a proposição 6n!IN, 0Gan G1 é verdadeira.
9
Seja (un) a sucessão definida por:
u
u
u
u
1
1 2
n
n
n
1
1
=-
=
-
+
* ,6n ! IN
9.1
Mostre, por indução, que um termo geral de (un) é un =
n
1 2
1
-
.
9.2
Mostre que (un) é monótona e limitada.
9.1 Para n = 1 , tem-se u1 =
1 2
1
-
= -1 , que é verdade.
Hipótese: Para um certo n ! IN , un =
n
1 2
1
-
.
Tese: un + 1 =
( )
n
1 2 1
1
- +
Demonstração:
un + 1 =
u
u
1 2 n
n
-
Usando a hipótese de indução, obtém-se:
un + 1 =
n
n
1 2
1 2
1
1 2
1
-
-
-
=
n
n
n
1 2
1 2 2
1 2
1
-
- -
-
=
( )
n
n
1 2 2
1 2
- -
-
=
( )
n
1 2 1
1
- +
Portanto, pelo princípio de indução, a proposição 6n ! IN, un =
n
1 2
1
-
é verdadeira.
000707 252-267 U9.indd 258 01/07/16 12:36

17. 259
9
U
NIDADE
Domínio 3 SUCESSÕES
9.2
un + 1 - un =
( )
n
1 2 1
1
- +
-
n
1 2
1
-
=
=
( )( )
n n
n n
1 2 1 2
1 2 1 2
- - -
- + +
=
n
1 4
2
2
- +
0, 6n ! IN
Logo, (un) é crescente.
Tem-se que
n
1 2
1
-
0, 6n ! IN ; logo, (un) é majorada.
Como (un) é crescente, tem de ser limitada.
AVALIAR CONHECIMENTOS
ESCOLHA MÚLTIPLA
Para cada uma das questões desta secção, selecione a opção correta de entre
as alternativas que lhe são apresentadas.
1
O termo geral de uma sucessão cujos cinco primeiros termos são -1 , -
2
1
,
-
1
5
, 0 e
1
7
pode ser:
(A)
-n (B)
n
n
2 2
4
+
-
(C)
n
n
2
4
+
-
(D)
n
n
2
3
-
A opção (A) não pode ser, pois o 2.º termo desta sucessão é igual a -2 .
A opção (B) não pode ser, pois o 2.º termo desta sucessão é igual a
3
4
-
.
A opção (C) não pode ser, pois o 2.º termo desta sucessão é igual a
4
1
-
.
A opção correta é a (C).
2
Seja T1 um triângulo equilátero. Construa-se T2 unindo os pontos médios dos lados
de T1 e pintando de azul o triângulo central. Considere-se que Tn + 1 é construído
a partir de Tn aplicando o processo anterior a cada triângulo branco de Tn .
u3p25h1
T1 T2 T3 T4
2.1 O número de triângulos brancos em T5 é:
(A) 40 (B) 54 (C) 81 (D) 243
2.2
Um termo geral da sucessão (An) das razões entre as áreas a branco
e a área total em cada figura pode ser:
(A)
An =
4
3 n
c m
(B)
An =
4
3 n 1
-
c m
(C)
An =
4
1 n
c m
(D)
An = 3n
000707 252-267 U9.indd 259 01/07/16 12:36

18. 260
Princípio de indução matemática
2.1
De um termo para o termo seguinte, cada triângulo branco é dividido
em três triângulos brancos. Como T4 tem 27 triângulos brancos,
T5 tem 27 × 3 = 81 triângulos brancos.
A opção correta é a (C).
2.2 Sejam Ab a área a branco, AT a área total e a , b e c os valores
das áreas de cada um dos triângulos em que se encontra dividido T1 ,
respetivamente, em T2 , T3 e T4 . Então:
T1 :
A
A
T
b
= 1 , pois Ab = AT
T2 :
A
A
T
b
=
a
a
4
3
=
4
3
T3 :
A
A
T
b
=
b
b
16
9
=
4
3 2
c m
T4 :
A
A
T
b
=
c
c
64
27
=
4
3 3
c m
A opção correta é a (B).
3
Considere a sucessão de termo geral vn = (-1)n
$ n . Indique qual das seguintes
afirmações é verdadeira.
(A) (vn) é monótona e limitada.
(B) (vn) é monótona e não limitada.
(C) (vn) é limitada e não monótona.
(D) (vn) é não monótona e não limitada.
Se n for par, vn = n 0 , mas se n for ímpar, vn = -n 0 ; portanto,
(vn) não é monótona. As sucessões de termos gerais n e -n não são
limitadas; logo, vn também não é limitada.
A opção correta é a (D).
4
De uma sucessão (un) sabe-se que:
•
(un) é estritamente monótona; • 6n ! IN, un G 10
Qual das seguintes afirmações é necessariamente verdadeira?
(A)
Se (un) for crescente, então, é limitada.
(B)
u1 = 10
(C)
6n ! IN, u1 G un G 10
(D)
Se (un) for decrescente, então, é limitada.
Contraexemplos:
(B) un = (-1)n
× 10 G 10 , mas u1 = -10
(C) un = n
10
; 0 un G 10 e u1 = 10
(D) un = n
10
-n
A opção correta é a (A).
000707 252-267 U9.indd 260 01/07/16 12:36

19. 261
9
U
NIDADE
Domínio 3 SUCESSÕES
5
Seja a um número real. Considere a sucessão (un) definida por
u a
u u
3 2
n n
1
1
=
=- +
+
)
, 6n ! IN
Qual é o 3.º termo desta sucessão?
(A) 6a + 4
(B) 9a - 4
(C) 6a - 4
(D) 9a + 4
Exame Nacional do 12.º ano, 2015
u2 = -3a + 2
u3 = -3(-3a + 2) + 2 = 9a - 6 + 2 = 9a - 4
A opção correta é a (B).
RESPOSTA ABERTA
Nas questões desta secção, apresente o seu raciocínio de forma clara, indicando todos
os cálculos que tiver de efetuar e as justificações necessárias.
6
Nas listagens seguintes estão os quatro primeiros termos de sucessões
de números reais. Sugira um termo geral para cada uma delas.
a)
10
1
,
1
11
,
1
12
,
1
13
, …
b)
3 , 9 , 27 , 81 , …
c)
3 , -9 , 27 , -81 , …
d)
2 ,
2
3
,
3
4
,
5
4
, …
a)
n 9
1
+
b) 3n
c) (-1)n + 1
3n
d) n
n 1
+
7
Considere a sucessão (un) de termo geral un =
n
n
3 1
2 3
-
+
.
7.1 Determine u5 e u20 .
7.2
Classifique, justificando, (un) quanto à monotonia.
7.3
Mostre que 6n ! IN, un
3
2
.
7.4
Justifique que (un) é limitada.
7.5
Mostre que existe um número real positivo L , tal que 6n ! IN, un G L .
000707 252-267 U9.indd 261 01/07/16 12:36

20. 262
Princípio de indução matemática
7.1
u5 =
3 5 1
2 5 3
#
#
-
+
=
14
13
e u20 =
3 20 1
2 20 3
#
#
-
+
=
59
43
7.2 un + 1 - un =
( )
( )
n
n
3 1 1
2 1 3
+ -
+ +
-
n
n
3 1
2 3
-
+
=
n
n
3 2
2 5
+
+
-
n
n
3 1
2 3
-
+
=
=
( )( )
( )( ) ( )( )
n n
n n n n
3 2 3 1
2 5 3 1 2 3 3 2
+ -
+ - - + +
=
=
( )( )
n n
n n n n n n
3 2 3 1
6 2 15 5 6 4 9 6
2 2
+ -
- + - - - - -
=
( )( )
n n
3 2 3 1
11
+ -
-
Como (3n + 2)(3n - 1) 0 ,
( )( )
n n
3 2 3 1
11
+ -
-
0
Logo, (un) é decrescente.
7.3
n
n
3 1
2 3
-
+
3
2
+ 6n + 9 6n - 2 + 9 -2 (Proposição verdadeira)
Logo, un
3
2
, 6n ! IN .
7.4 Como (un) é decrescente, é majorada por u1 =
2
5
. Pela alínea anterior,
3
2
é um minorante de (un) ; logo, (un) é limitada.
7.5 Seja L =
2
5
. Tem-se que
n
n
3 1
2 3
-
+
0, 6n ! IN ; logo,
qunu = un G
2
5
= L .
8
Na figura seguinte estão representados os três primeiros termos da sucessão (qn)
que conta os quadrados das figuras.
u3p26h1
3
2
1
Tal como a figura sugere, q1 = 5 , q2 = 13 e q3 = 25 .
8.1
Indique os valores de q4 e q5 .
8.2
Defina a sucessão (qn) por recorrência e utilize essa definição para justificar
que (qn) é monótona crescente.
8.1 q4 = 25 + 4 × 4 = 41 e q5 = 41 + 4 × 5 = 61
8.2
q
q q n
5
4
n n
1
1
=
= +
+
*
,6n ! IN
Tem-se que qn + 1 - qn = qn + 4n - qn = 4n 0, 6n ! IN ;
logo, (qn) é crescente.
000707 252-267 U9.indd 262 01/07/16 12:36

21. 263
9
U
NIDADE
Domínio 3 SUCESSÕES
9
Seja (cn) uma sucessão crescente e limitada.
Prove que:
a) (-cn) é decrescente e limitada.
b) (3cn - 4) é limitada.
a) Como (cn) é crescente, então, cn + 1 - cn 0 . Assim:
-cn + 1 + cn = -cn + 1 - (-cn) 0, 6n ! IN
Logo, (-cn) é decrescente.
Como (cn) é limitada, 7L 0: 6n ! IN, cn L .
Tem-se que cn
- = cn ; logo, (-cn) é limitada.
b)
Como (cn) é limitada, tem um majorante e um minorante.
Seja m um minorante de (cn) e M um majorante.
Tem-se que 3cn - 4 3cn 3M (porque M é majorante de (cn) ) .
Logo, 3M é majorante de (3cn - 4) .
Do mesmo modo, 3cn - 4 3cn - 5 3m - 5 (porque m é minorante
de (cn) ) .
Logo, 3m - 5 é minorante de (3cn - 4) . Portanto, (3cn - 4) é limitada.
10
Justifique que uma sucessão decrescente (wn) de termos positivos é limitada.
Como (wn) é decrescente, tem como majorante w1 , e como é positiva,
tem como minorante o 0 . Logo, (wn) é limitada.
11
Considere as seguintes sucessões:
un = 1 - 4n , vn = (-1)2n
, wn = 4 - n
1
,
xn =
n
n n
2
1
se é par
se é ímpar
* e yn = nsin
n
2
r
c m
Indique, justificando, quais destas sucessões são:
a)
monótonas e limitadas.
b)
monótonas e não limitadas.
c)
não monótonas e limitadas.
d)
não monótonas e não limitadas.
000707 252-267 U9.indd 263 01/07/16 12:36

22. 264
Princípio de indução matemática
un + 1 - un = ^1 - 4(n + 1)h - (1 - 4n) =
= 1 - 4n - 4 - 1 + 4n = -4 0, 6n ! IN
Logo, (un) é decrescente.
Seja a ! Z-
. Tem-se u-a = 1 + 4a a ; logo, (un) não tem minorantes
e, por isso, é não limitada.
vn = (-1)2n
= ^(-1)2
hn
= 1n
Logo, (vn) é constante, pelo que é monótona e limitada.
wn + 1 - wn =
n
4
1
1
-
+
d n - n
4
1
-
c m = -
n 1
1
+
+ n
1
=
=
( )
n n
n n
1
1
+
- + +
=
( )
n n 1
1
+
0, 6n ! IN
Logo, (wn) é crescente.
Tem-se que 6n ! IN , 4 - n
1
4 e 4 - n
1
0 ; logo, (wn) é limitada.
Como x1 = 1 , x2 = 2 e x3 =
3
1
, (xn) é não monótona.
Tem-se que 6n ! IN , xn G 2 e xn 0 ; logo, (xn) é limitada.
Como y1 = 1 , y2 = 0 , y3 = -3 e y4 = 0 , (yn) é não monótona.
Seja a ! IN , com a par. qya + 1u = ( )
( )
sin
a
a
1
2
1 r
+
+
d n = qa + 1u a ;
logo, (yn) é não limitada.
Assim:
a) (vn) e (wn)
b) (un)
c) (xn)
d) (yn)
12
Mostre, utilizando o princípio de indução matemática, que as proposições
seguintes são verdadeiras.
a) 6n ! IN,
i
n
1
=
/ i2
=
( )( )
n n n
6
1 2 1
+ +
b)
6n ! IN5, 2n
n2
c)
6n ! IN, 2n
- (-1)n
é múltiplo de 3
000707 252-267 U9.indd 264 01/07/16 12:36

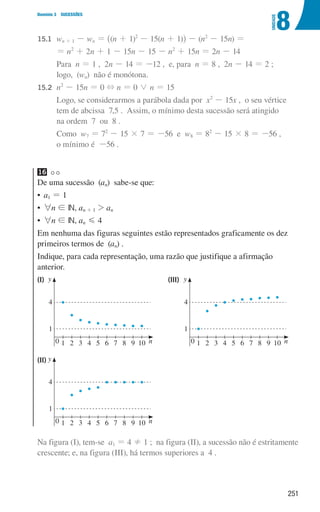
23. 265
9
U
NIDADE
Domínio 3 SUCESSÕES
a) Para n = 1 , tem-se 12
= 1 =
( )( )
6
1 1 1 2 1
+ +
, que é verdade.
Hipótese: Para um certo n ! IN ,
i
n
1
=
/ i2
=
( )( )
n n n
6
1 2 1
+ +
.
Tese:
i
n
1
1
=
+
/ i2
=
( )( ) ( )
n n n
6
1 2 2 1 1
+ + + +
_ i
Demonstração:
i
n
1
1
=
+
/ i2
=
i
n
1
=
/ i2
+ (n + 1)2
Por hipótese, obtém-se:
i
n
1
1
=
+
/ i2
=
( )( )
n n n
6
1 2 1
+ +
+ (n + 1)2
=
( )( ) ( )
n n n n
6
1 2 1 6 1 2
+ + + +
=
=
( ) ( ) ( )
n n n n
6
1 2 1 6 1
+ + + +
7 A
=
( )[ ]
n n n n
6
1 2 6 6
2
+ + + +
=
=
( )[ ]
n n n n
6
1 2 3 4 6
2
+ + + +
=
( )( )( )
n n n
6
1 2 2 3
+ + +
=
=
( )( ) ( )
n n n
6
1 2 2 1 1
+ + + +
_ i
Portanto, pelo princípio de indução, a proposição
6n ! IN,
i
n
1
=
/ i2
=
( )( )
n n n
6
1 2 1
+ +
é verdadeira.
b) Para n = 5 , tem-se 25
= 32 25 = 52
, que é verdade.
Hipótese: Para um certo n ! IN5 , 2n
n2
.
Tese: 2n + 1
(n + 1)2
Demonstração:
2n + 1
= 2n
× 2
Por hipótese, obtém-se:
2n + 1
n2
× 2 = n2
+ n2
( )
1
n2
+ (2n + 1) = (n + 1)2
Portanto, pelo princípio de indução, tem-se 6n ! IN5, 2n
n2
.
(1) Para n = 5 , tem-se 52
= 25 11 = 2 × 5 + 1 , que é verdade.
Hipótese: Para um certo n ! IN5 , n2
2n + 1 .
Tese: (n + 1)2
2(n + 1) + 1
Demonstração:
(n + 1)2
= n2
+ 2n + 1
Por hipótese, obtém-se:
(n + 1)2
(2n + 1) + 2n + 1 = 2n + 2 + 2n =
= 2(n + 1) + 2n 2(n + 1) + 1
Pelo princípio de indução, tem-se 6n ! IN5, n2
2n + 1 .
000707 252-267 U9.indd 265 01/07/16 12:36

24. 266
Princípio de indução matemática
Em alternativa, para evitar duas induções, pode-se ter a seguinte demonstração:
( )
n
n 1
2
2
+
=
n
n n
2 1
2
2
+ +
= 1 + n
2
+
n
1
2
Se n 4 , tem-se n
2
2
1
e
n
1
2
2
1
; logo,
( )
n
n 1
2
2
+
= 1 + n
2
+
n
1
2
2 .
Portanto, usando a hipótese de indução:
2n + 1
= 2n
× 2 2n2
( )
n
n 1
2
2
+
n2
= (n + 1)2
c) Para n = 1 , tem-se 21
- (-1)1
= 3 que é múltiplo de 3 .
Hipótese: Para um certo n ! IN , 2n
- (-1)n
é múltiplo de 3 .
Tese: 2n + 1
- (-1)n + 1
é múltiplo de 3
Demonstração:
2n + 1
- (-1)n + 1
= 2n
× 2 - (-1)n
× (-1) =
= 3 × 2n
- 2n
- (-1)n
× (-1) = 3 × 2n
- ^2n
- (-1)n
h
^2n
- (-1)n
h é múltiplo de 3 por hipótese de indução e 3 × 2n
também
é múltiplo de 3 ; logo, 2n + 1
- (-1)n + 1
é múltiplo de 3 .
Portanto, pelo princípio de indução, a proposição 6n ! IN, 2n
- (-1)n
é múltiplo de 3 é verdadeira.
13
Considere a sucessão (pn) dos números pentagonais cujos quatro primeiros
termos estão representados na figura seguinte.
13.1 Calcule p6 , p7 e p8 .
13.2
Defina (pn) por recorrência.
13.3
Prove, por indução matemática, que um termo geral de (pn) é:
pn =
n n
2
3 2
-
13.4
Averigue se 477 é um número pentagonal e, em caso afirmativo,
indique a sua ordem.
13.1
p5 = 35 ; p6 = 35 + 2 × 6 + 4 = 51 ; p7 = 51 + 2 × 7 + 5 = 70 ;
p8 = 70 + 2 × 8 + 6 = 92
13.2
( ) ( )
p
p p n n
1
2 1 1
n n
1
1
=
= + + + -
+
*
, 6n ! IN
+
+
p
p p n
1
3 1
n n
1
1
=
= + +
+
*
, 6n ! IN
u3p27h1
000707 252-267 U9.indd 266 01/07/16 12:37

25. 267
9
U
NIDADE
Domínio 3 SUCESSÕES
13.3 Para n = 1 , tem-se p1 =
2
3 1
-
= 1 , que é verdade.
Hipótese: Para um certo n ! IN , pn =
n n
2
3 2
-
.
Tese: pn + 1 =
( ) ( )
n n
3 1 1
2
2
+ - +
Demonstração: pn + 1 = pn + 3n + 1
Por hipótese, obtém-se:
pn + 1 =
n n
2
3 2
-
+ 3n + 1 =
=
n n n
2
3 2
6
2
- + +
=
( )
n n n
2
3 6 3 1
2
+ + - +
=
=
( ) ( )
n n n
2
3 2 1 1
2
+ + - +
=
( ) ( )
n n
2
3 1 1
2
+ - +
Portanto, pelo princípio de indução, tem-se 6n ! IN, pn =
n n
2
3 2
-
.
13.4
pn = 477 +
n n
2
3 2
-
= 477 + 3n2
- n - 954 = 0 +
+ n =
6
1 1 4 3 954
! # #
+
=
6
1 107
!
+ n = 18 0 n = -
6
106
Logo, 477 é um número pentagonal de ordem 18 .
14
Considere a sucessão (an) definida por recorrência:
a
a a
1
4
1
n n
1
1
=
= -
+
*
, 6n ! IN
14.1 Determine a6 - a5 .
14.2
Mostre que (an) é monótona.
14.3
Prove, por indução matemática, que um termo geral de (an) é an =
n
4
5-
.
14.1
a6 - a5 = a5 -
4
1
- a5 = -
4
1
14.2 an + 1 - an = an -
4
1
- an = -
4
1
0, 6n ! IN
Logo, (an) é decrescente.
14.3 Para n = 1 , tem-se a1 =
4
5 1
-
= 1 , que é verdade.
Hipótese: Para um certo n ! IN , an =
n
4
5 -
.
Tese: an + 1 =
( )
n
4
5 1
- +
Demonstração: an + 1 = an -
4
1
Por hipótese, obtém-se:
an + 1 =
n
4
5 -
-
4
1
=
n
4
5 1
- -
=
( )
n
4
5 1
- +
Portanto, pelo princípio de indução, tem-se 6n ! IN, an =
n
4
5 -
.
000707 252-267 U9.indd 267 01/07/16 12:37

26. 268
Progressões
aritméticas
e Progressões
geométricas
10
UNIDADE
TAREFAS E AVALIAR CONHECIMENTOS
10.1 Progressões aritméticas
Tarefa 1
No dia em que a Joana ingressou no 10.º ano
do Ensino Secundário, em meados de setembro,
os seus pais decidiram iniciar uma poupança
destinada a juntar dinheiro para que a filha
pudesse fazer uma viagem no final do 12.º ano.
Colocaram 20 euros num mealheiro e, todos
os meses, no início de cada mês, a partir desse dia,
juntaram na poupança mais 5 euros do que
no mês anterior.
1.1
Quanto dinheiro foi colocado no mealheiro no início de janeiro do ano
seguinte? E um ano depois do início da poupança?
1.2
Deduza uma expressão, por recorrência, que permita saber
a quantia colocada no mealheiro num determinado mês.
1.1
Os termos da sucessão são:
20 , 25 , 30 , 35 , 40 , …
No início de janeiro do ano seguinte, o valor colocado na poupança
corresponderá ao termo de ordem 5 , isto é, a 40 euros.
Um ano depois, corresponderá ao termo de ordem 13 , isto é,
a 20 + 12 × 5 = 80 euros.
1.2
Representando o plano de poupança por uma sucessão (pn) ,
esta é dada por:
p
p p
20
5
n n
1
1
=
= +
+
*
, 6n ! IN
Em que p1 representa o valor poupado no primeiro mês e 5 , o valor
(constante) a acrescentar em cada mês.
000707 268-295 U10.indd 268 01/07/16 12:38

27. 269
Domínio 3 SUCESSÕES
10
UNIDADE
1
Considere a sucessão (vn) definida por recorrência:
v
v v
2
3
n n
1
1
=-
= +
+
*
, 6n ! IN
1.1
Calcule os quatro primeiros termos de (vn) .
1.2
Justifique que (vn) é uma progressão aritmética.
1.3
Mostre, utilizando o princípio de indução matemática, que:
vn = 3n - 5, 6n ! IN
1.4 Calcule v100 .
1.1
v1 = -2 ; v2 = -2 + 3 = 1 ; v3 = 1 + 3 = 4 ; v4 = 4 + 3 = 7
1.2 (vn) é uma progressão aritmética porque cada termo se obtém, a partir
do anterior, somando sempre a mesma constante ( 3 ) .
1.3 Para n = 1 , tem-se v1 = 3 - 5 = -2 , que é verdade.
Hipótese: Para um certo n ! IN , vn = 3n - 5 .
Tese: vn + 1 = 3(n + 1) - 5
Demonstração:
vn + 1 = vn + 3
Por hipótese, obtém-se:
vn + 1 = 3n - 5 + 3 = 3(n + 1) - 5
Portanto, pelo princípio de indução, tem-se 6n ! IN, vn = 3n - 5 .
1.4
v100 = 3 × 100 - 5 = 295
2
Mostre que dados dois valores reais quaisquer a e b , os termos a ,
a b
2
+
e b
são termos consecutivos de uma progressão aritmética.
Seja (vn) a sucessão em questão, em que vp = a , vp + 1 =
a b
2
+
e vp + 2 = b .
Então, tem-se:
vp + 1 - vp =
a b
2
+
- a =
b a
2
-
vp + 2 - vp + 1 = b -
a b
2
+
=
b a
2
-
Como a diferença entre dois termos consecutivos é igual e constante, tem-se
que os termos dados são termos de uma progressão aritmética de razão
b a
2
-
.
Em alternativa:
Considere-se a sucessão (vn) definida por recorrência:
v a
v v
b a
2
n n
1
1
=
= +
-
+
*
Como
b a
2
-
é constante, (vn) é uma progressão aritmética. Tem-se que:
v1 = a ; v2 = a +
b a
2
-
=
a b a
2
2 + -
=
a b
2
+
;
v3 =
a b
2
+
+
b a
2
-
=
a b b a
2
+ + -
=
b
2
2
= b
000707 268-295 U10.indd 269 01/07/16 12:39

28. 270
Progressões aritméticas e Progressões geométricas
Tarefa 2
Dados c, d ! IR , justifique que (un) definida por un = cn + d
é uma progressão aritmética de razão c .
A sucessão un = cn + d é uma progressão aritmética de razão c , pois:
un + 1 - un = c(n + 1) + d - (cn + d) =
= cn + c + d - cn - d = c, 6n ! IN
3
Verifique se são progressões aritméticas as sucessões de termo geral:
a) an =
n
2
1
- 5
b) bn =
n
2
- 5
c) cn = 1 +
n
2
5
-
d) dn = 2 × (-1)n
+ 5
a) an + 1 - an =
( )
n
2 1
1
5
+
-
d n -
n
2
1
5
-
c m =
=
( )
n n
n n
2 2 1
2 2 2
# +
- -
=
( )
n n
2 1
1
-
+
Não é uma progressão aritmética, pois a diferença an + 1 - an não é constante.
b)
bn + 1 - bn =
n
2
1
5
+
-
d n -
n
2
5
-
c m =
n n
2
1
+ -
=
2
1
É uma progressão aritmética de razão
2
1
.
c)
cn + 1 - cn =
n
1
2
1 5
+
+ -
d n -
n
1
2
5
+
-
d n =
=
n n
2
4 5
- - +
=
2
1
É uma progressão aritmética de razão
2
1
.
d)
dn + 1 - dn = ^2 × (-1)n + 1
+ 5h - ^2 × (-1)n
+ 5) =
= 2 × (-1)n + 1
+ (-1) × 2 × (-1)n
= 4 × (-1)n + 1
Não é uma progressão aritmética.
4
Considere a sucessão (vn) , em que se sabe que:
• v1 = -
2
5
• vn + 1 = vn +
2
1
, 6n ! IN
4.1
Justifique que (vn) é uma progressão aritmética e indique a sua razão.
4.2 Determine v8 .
000707 268-295 U10.indd 270 01/07/16 12:39

29. 271
Domínio 3 SUCESSÕES
10
UNIDADE
4.1 (vn) é uma progressão aritmética de razão
2
1
porque cada termo se obtém
a partir do anterior, somando
2
1
.
4.2
v8 = -
2
5
+ 7 ×
2
1
= 1
5
Os comprimentos dos lados de um triângulo
retângulo são três termos consecutivos de uma
progressão aritmética de razão 3 .
Determine a área desse triângulo.
Seja x = AC . Então, x + 3 = AB e x + 6 = BC .
Pelo teorema de Pitágoras:
(x + 6)2
= (x + 3)2
+ x2
+
+ x2
+ 12x + 36 = x2
+ 6x + 9 + x2
+
+ -x2
+ 6x + 27 = 0 + x =
2
6 36 4 27
! #
-
- +
+
+x =
2
6 12
!
-
-
+ x = 9 0 x = -3
Logo, AC = 9 , AB = 12 e BC = 15 .
Assim, A[ABC] =
AB AC
2
#
= 54 u. a.
6
Três termos consecutivos de uma progressão aritmética são dados, para um
determinado valor de x , respetivamente, por:
x - 1 , x2
e x + 5
Determine esses três termos.
Adaptado do Caderno de Apoio do 11.º ano
Seja r a razão da progressão aritmética. Então:
x x r
x x r
1
5
2
2
= - +
+ = +
* +
r x x
x x x x
1
5 1
2
2 2
= - +
+ = + - +
* +
r x x
x x
1
2 2 4 0
2
2
= - +
- - =
* +
+
r x x
x
1
2
1 1 8
2
!
= - +
=
+
* +
r x x
x x
1
2 1
2
0
= - +
= =-
*
Se x = -1 , r = 12
+ 1 + 1 = 3 e os termos são: -2 , 1 e 4 .
Se x = 2 , r = 22
- 2 + 1 = 3 e os termos são: 1 , 4 e 7 .
u3p29h1
A B
C
000707 268-295 U10.indd 271 01/07/16 12:39

30. 272
Progressões aritméticas e Progressões geométricas
Tarefa 3
Demonstre, aplicando o princípio de indução matemática, que dada uma
progressão aritmética (un) de razão r e de 1.o
termo a , se tem:
un = a + (n - 1)r,6n ! IN
Considere-se a condição P(n) dada por un = a + (n - 1)r .
A proposição P(1) é u1 = a + (1 - 1)r = a , que é verdade.
Considere-se, por hipótese, que para um certo n ! IN , un = a + (n - 1)r .
Pretende-se provar que un + 1 = a + nr .
Por definição de progressão aritmética, tem-se que un + 1 = un + r .
Por hipótese, obtém-se:
un + r = a + (n - 1)r + r = a + nr
Portanto, un + 1 = a + nr .
Conclui-se, assim, pelo princípio de indução matemática, que a proposição
un = a + (n - 1)r, 6n ! IN é verdadeira.
7
Considere a progressão aritmética (un) de razão -2 e u2 = 10 .
7.1
Defina (un) por recorrência.
7.2
Determine um termo geral de (un) .
7.1 Tem-se u1 = u2 - (-2) = 10 + 2 = 12 ; logo,
u
u u
12
2
n n
1
1
=
= -
+
* .
7.2
un = 12 - 2(n - 1) = 12 - 2n + 2 = 14 + 2n
8
Seja (un) uma progressão aritmética de razão r .
Sendo k ! IN , mostre que o termo geral de (un) pode ser dado por:
un = uk + (n - k)r
Tem-se que un = u1 + (n - 1)r e uk = u1 + (k - 1)r . Então:
un - uk = 6u1 + (n - 1)r@ - [u1 + (k - 1)r] +
+ un - uk = (n - 1)r - (k - 1)r + un - uk = (n - 1 - k + 1)r +
+ un = uk + (n - k)r
c.q.d.
9
Determine o termo geral de uma progressão aritmética (an) em que:
a)
a1 = 2 e r = -
2
1
b)
a1 = -4 e a9 = 20 c)
a5 = 7 e a15 = 22
000707 268-295 U10.indd 272 01/07/16 12:39

31. 273
Domínio 3 SUCESSÕES
10
UNIDADE
a) an = 2 -
2
1
(n - 1) =
2
5
-
n
2
b) an = -4 +
( )
8
20 4
- -
(n - 1) = -4 + 3(n - 1) = 3n - 7
c) an = 7 +
10
22 7
-
(n - 5) = 7 +
2
3
(n - 5) =
2
3
n -
2
1
10
A Sandra é uma atleta que decidiu implementar
o seguinte esquema de treino:
•
correr 12 km no 1.º dia;
•
correr mais 1,5 km em cada novo dia de treino.
Em que dia a Sandra corre 36 km ?
Seja (an) a sucessão do número de quilómetros que a Sandra corre em cada dia.
Então, an = 12 +
2
3
(n - 1) ; logo:
an = 36 + 12 +
2
3
(n - 1) = 36 +
2
3
(n - 1) = 24 + n = 17
A Sandra corre 36 km ao 17.º dia.
11
Classifique quanto à monotonia e escreva um termo geral das progressões
aritméticas em que:
a) b1 = -1 e r =
3
2
b) b4 = 5 e b10 = 2
a) Como r 0 , (bn) é monótona crescente. Um termo geral pode ser:
bn = -1 +
3
2
(n - 1) =
3
2
n -
3
5
b)
Como r =
b b
4 10
4 10
-
-
=
6
5 2
-
-
= -
2
1
0 , (bn) é monótona decrescente.
Um termo geral pode ser (pelo exercício 8):
5 -
2
1
(n - 4) = 7 -
n
2
12
Determine a progressão arimética de comprimento 4 , em que:
a) un = 10 - n
b) un =
n
2
5 2
+
000707 268-295 U10.indd 273 01/07/16 12:39

32. 274
Progressões aritméticas e Progressões geométricas
a) u1 = 10 - 1 = 9 ; u2 = 10 - 2 = 8 ; u3 = 10 - 3 = 7 ; u4 = 10 - 4 = 6
Logo, tem-se (9, 8, 7, 6) .
b)
u1 =
2
5 1 2
# +
=
2
7 2
; u2 =
2
5 2 2
# +
= 6 2 ;
u3 =
2
5 2
3
# +
=
2
2
17
; u4 =
2
5 2
4
# +
= 11 2
Logo, tem-se , , ,
2
7 2
6 2
2
17 2
11 2
e o .
13
Sabendo que a soma dos três primeiros termos de uma progressão aritmética
é 15 e que o seu produto é 120 , determine a progressão arimética
de comprimento 4 .
Sejam a = u1 e r a razão desta progressão. Tem-se que:
( )( )
a a r a r
a a r a r
2 15
2 120
+ + + + =
+ + =
* +
( )( )( )
a r
r r r r r
5
5 5 5 2 120
= -
- - + - + =
* +
+
a r
r
5
5 5 0
2
= -
- + =
) +
a r
r r
5
1 1
0
= -
= =-
)
Se r = 1 , a = 4 e a progressão é (4, 5, 6, 7) ; se r = -1 , a = 6
e a progressão é (6, 5, 4, 3) .
14
Determine a soma dos elementos da sequência correspondente aos 100 primeiros
números naturais.
Calcule-se a soma
S = 1 + 2 + 3 + … + 97 + 98 + 99 + 100
escrevendo as parcelas de forma inversa:
1 2 3 … 98 99 100 S
100 99 98 … 3 2 1 S
101 101 101 101 101 101 101 2S
Assim:
2S = 101 × 100 + S =
2
10 100
= 5050
000707 268-295 U10.indd 274 01/07/16 12:39

33. 275
Domínio 3 SUCESSÕES
10
UNIDADE
15
Demonstre, aplicando o princípio de indução matemática, que, dada uma
progressão aritmética (un) de razão r e dado N ! IN , a soma dos termos
de (un) de comprimento N , (u1, u2, …, uN) , é dada por:
i
N
1
=
/ui =
u u
2
N
1+
× N
Para N = 1 , tem-se
i 1
1
=
/ui = u1 =
u u
2
1 1
+
× 1 , que é verdade.
Hipótese: Para um certo N ! IN ,
i
N
1
=
/ui =
u u
2
N
1 +
× N .
Tese:
i
N
1
1
=
+
/ ui =
u u
2
N
1 1
+ +
× (N + 1)
Demonstração:
i
N
1
1
=
+
/ ui =
i
N
1
=
/ui + uN + 1
Por hipótese, obtém-se:
i
N
1
1
=
+
/ ui =
u u
2
N
1 +
× N + uN + 1 =
Nu Nu u
2
2
N N
1 1
+ + +
Mas, como (un) é uma progressão aritmética, uN + 1 = u1 + Nr . Logo:
i
N
1
1
=
+
/ ui =
Nu Nu u u Nr
2
N N
1 1 1
+ + + +
+
=
=
( ) [ ]
N u Nu Nr u
2
1 N N
1 1
+ + + + +
=
=
( )
N u Nu u
2
1 N N
1 1 1
+ + +
+ +
=
=
( ) ( )
N u N u
2
1 1 N
1 1
+ + + +
=
u u
2
N
1 1
+ +
× (N + 1)
Portanto, pelo princípio de indução, 6N ! IN,
i
N
1
=
/ ui =
u u
2
N
1 +
× N .
16
Calcule a soma dos 20 primeiros múltiplos de 3 .
Considere-se a sucessão dos múltiplos de 3 , de termo geral un = 3n .
Então:
S20 =
u u
2
1 20
+
× 20 =
2
3 60
+
× 20 = 630
000707 268-295 U10.indd 275 01/07/16 12:39

34. 276
Progressões aritméticas e Progressões geométricas
17
Seja (un) uma progressão aritmética definida por:
un =
n
3
2 5
-
Determine a soma:
a)
dos 15 primeiros termos de (un) .
b)
do 11.º ao 34.º termo, inclusive, de (un) .
a)
S15 =
u u
2
1 15
+
× 15 =
2
3
2 5
3
2 15 5
#
-
+
-
× 15 =
=
2
1
3
25
- +
× 15 =
3
165
= 55
b)
S =
i 11
34
=
/ ui =
u u
2
11 34
+
× 24 =
2
3
2 11 5
3
2 34 5
# #
-
+
-
× 24 =
=
2
3
17
3
63
+
× 24 =
3
40
× 24 = 320
18
A Joana gosta muito de nozes e, durante 10 dias consecutivos, comeu 175 .
Sabendo que a Joana aumentou o consumo de nozes
de forma constante de dia para dia e que no último dia
comeu 31, quantas nozes comeu no 1.º dia?
Seja (un) a sucessão do número de nozes que a Joana comeu em cada dia.
S10 =
u u
2
1 10
+
× 10 + 175 =
u
2
31
1 +
× 10 + 35 = u1 + 31 + u1 = 4
A Joana comeu 4 nozes no 1.º dia.
19
O Ricardo é ciclista e durante uma competição
de ciclismo percorreu com a sua bicicleta 1500 km .
Sabendo que, de dia para dia, aumentava 10 km
a distância a percorrer e que no 6.º dia percorreu
80 km , quantos dias demorou a competição?
Seja (un) a sucessão do número de quilómetros percorridos em cada dia
da competição. Então:
Sn =
u u
2
n
1 +
× n + 1500 =
( )
u u n r
2
1
1 1
+ + -
× n +
+ 1500 =
( )
u n
2
2 10 1
1 + -
× n
000707 268-295 U10.indd 276 01/07/16 12:39

35. 277
Domínio 3 SUCESSÕES
10
UNIDADE
Por outro lado, u6 = u1 + 5r + 80 = u1 + 50 + u1 = 30 .
Logo:
1500 =
( )
n
2
2 30 10 1
# + -
× n + 300 = 6n + (n2
- n) +
+ n2
+ 5n - 300 = 0 + n =
2
5 25 4 300
! #
- +
+
+ n =
2
5 35
!
-
+ n = -20 0 n = 15
Portanto, a competição durou 15 dias.
Tarefa 4
Um caracol inicia uma viagem.
No 1.o
minuto percorre uma determinada distância,
em centímetros, e depois, em cada minuto, percorre
sempre 1,2 cm a mais do que no minuto anterior.
Sabe-se ainda que no 10.º minuto de viagem percorreu 15,8 cm .
4.1
Mostre que o caracol percorreu 5 cm no 1.º minuto.
4.2
Determine a distância total percorrida pelo caracol no 15.o
minuto.
4.3
Sabendo que o caracol parou após ter percorrido 5,2 metros, durante
quanto tempo esteve o caracol a rastejar?
4.1
Seja (dn) a distância percorrida pelo caracol no n-ésimo minuto.
Tem-se que:
d10 = d1 + 9r + 15,8 = d1 + 9 × 1,2 + d1 = 5
Conclui-se, assim, que a distância percorrida pelo caracol no 1.º minuto
foi de 5 cm .
4.2
d15 = d1 + 14r + d15 = 5 + 14 × 1,2 + d15 = 21,8
4.3
A distância percorrida pelo caracol ao fim de n minutos é dada por:
S =
d d
2
n
1 +
× n
Como o caracol percorreu 5,2 metros, ou seja, 520 centímetros,
tem-se que:
d d
2
n
1 +
× n = 520 +
( ) ,
n
2
5 5 1 1 2
#
+ + -
× n = 520 +
+
, , n
2
8 8 1 2
+
× n = 520 + 1,2n2
+ 8,8n - 1040 = 0 +
+ n = 26 0 n = -
3
100
Conclui-se, assim, que o caracol rastejou durante 26 minutos.
000707 268-295 U10.indd 277 01/07/16 12:39

36. 278
Progressões aritméticas e Progressões geométricas
10.2 Progressões geométricas
Tarefa 5
Num lago, sem quaisquer plantas, foram colocados
três nenúfares (ano 1 ) de uma espécie em que
cada exemplar dá origem a outro exemplar a cada
ano que passa.
5.1
Determine o número de nenúfares existentes no ano 5 .
5.2
Defina, por um termo geral, o número de nenúfares existentes no ano n .
5.1
O número de nenúfares em cada ano é dado por: 3, 6, 12, 24, 48, …
Assim sendo, no 5.º ano existem 48 nenúfares.
5.2 Seja Pn o número de nenúfares existentes no n-ésimo ano.
Então:
P1 = 3 ; P2 = 3 × 2 ; P3 = 3 × 22
; P4 = 3 × 23
Logo, Pn = 3 × 2n - 1
.
20
Considere a sucessão (an) definida por recorrência:
a
a a
6
3
n n
1
1 #
=
=
+
*
, 6n ! IN
20.1
Calcule os quatro primeiros termos de (an) .
20.2
Justifique que (an) é uma progressão geométrica.
20.3
Mostre, utilizando o princípio de indução matemática, que:
an = 2 × 3n
, 6n ! IN
20.1
a1 = 6 ; a2 = 6 × 3 = 18 ; a3 = 18 × 3 = 54 ; a4 = 54 × 3 = 162
20.2 (an) é uma progressão geométrica porque cada termo se obtém
multiplicando o anterior por 3 (constante).
20.3 Para n = 1 , tem-se a1 = 2 × 31
= 6 , que é verdade.
Hipótese: Para um certo n ! IN , an = 2 × 3n
.
Tese: an + 1 = 2 × 3n + 1
Demonstração:
an + 1 = an × 3
Por hipótese, obtém-se:
an + 1 = 2 × 3n
× 3 = 2 × 3n + 1
Portanto, pelo princípio de indução, 6n ! IN, an = 2 × 3n
.
000707 268-295 U10.indd 278 01/07/16 12:39

37. 279
Domínio 3 SUCESSÕES
10
UNIDADE
21
Escreva os quatro primeiros termos de uma progressão geométrica (un)
e defina-a por recorrência, sabendo que:
a)
u1 = 64 e r =
4
1
b)
u1 = -3 e r = -2 c)
u1 = -2 e u2 = 4
a)
u1 = 64 , u2 = 64 ×
4
1
= 16 , u3 = 16 ×
4
1
= 4 e u4 = 4 ×
4
1
= 1 ;
,
u
u u
64
4
1
n n
1
1 #
=
=
+
*
6n ! IN
b)
u1 = -3 , u2 = -3 × (-2) = 6 , u3 = 6 × (-2) = -12 e
u4 = -12 × (-2) = 24 ;
u
u u
3
2
n n
1
1
=-
=-
+
*
, 6n ! IN
c)
r =
2
4
-
= -2 ; u1 = -2 , u2 = 4 , u3 = 4 × (-2) = -8 e
u4 = -8 × (-2) = 16 ;
u
u u
2
2
n n
1
1
=-
=-
+
*
, 6n ! IN
22
Averigue quais das sucessões seguintes são progressões geométricas:
a) an = -3 × 2n
b) bn =
n
3
2
c) cn = 31 - 2n
d) dn = 3 - 2n
a) a
a
3 2
3 2
n
n
n
n
1
1
#
#
=
-
-
+
+
= 2
É uma progressão geométrica, pois o quociente a
a
n
n 1
+
é constante.
b)
( )
( )
b
b
n
n
n
n
n
n
2
3
2 1
3
2 1
2
1
n
n 1
=
+
=
+
=
+
+
Não é uma progressão geométrica.
c) c
c
3
3
3
1
9
1
( )
n
n
n
n
1
1 2
1 2 1
2
= = =
+
-
- +
É uma progressão geométrica.
d)
d
d
3 2
3 2
n
n
n
n
1
1
=
-
-
+
+
Para n = 1 , obtém-se
3 2
3 22
-
-
= -1 ; e para n = 2 , obtém-se
3 2
3 2
2
3
-
-
= 5 .
Logo, não é uma progressão geométrica.
000707 268-295 U10.indd 279 01/07/16 12:39

38. 280
Progressões aritméticas e Progressões geométricas
23
Uma cultura de bactérias aumenta 12 % a cada dia que passa.
Qual é o quociente entre o número de bactérias num determinado dia
e no dia anterior?
Seja a o número de bactérias no 1.o
dia e seja b o número de bactérias no 2.o
dia. Então, b = a + 0,12a = 1,12a .
Logo, a
b
=
,
a
a
1 12
= 1,12 .
24
O valor comercial de uma máquina industrial é dado, em euros, em cada ano,
pela progressão geométrica (vn) . Sabendo que a sua razão é 0,96 ,
qual é a percentagem de desvalorização a cada ano que passa?
Tem-se que vn + 1 = vn × 0,96 , então:
vn + 1 - vn = vn × 0,96 - vn = -0,04vn
Portanto, a percentagem de desvalorização é de 4 % .
25
Para x ! IR-
, sejam
2
1
, x e
8
9
os três primeiros termos de uma
progressão geométrica (un) .
25.1
Determine o valor de x .
25.2
Determine a razão e u5 .
25.1
x
x
2
1
9
8
= + x2
=
16
9
IR
x
! -
x = -
4
3
25.2
r =
2
1
4
3
-
= -
2
3
e u5 =
8
9
2
3
2
3
32
81
# #
- - =
c c
m m
26
Considere as sucessões (un) e (vn) , em que se sabe que:
•
(un) é uma progressão aritmética de razão r ;
•
vn = u
1 n
r -
Mostre que a sucessão (vn) é uma progressão geométrica de razão
1
r
r
.
Como un + 1 = un + r , tem-se:
v
v
n
n
u
u r
1
1
1
n
n
r
r
=
+
-
- -
= r-r
=
1
r
r
000707 268-295 U10.indd 280 01/07/16 12:39

39. 281
Domínio 3 SUCESSÕES
10
UNIDADE
Tarefa 6
Demonstre, aplicando o princípio de indução matemática, que, dada uma
progressão geométrica (un) de razão r e de 1.o
termo a , se tem:
un = arn-1
,6n ! IN
Considere-se a condição P(n) dada por un = arn - 1
.
A proposição P(1) é u1 = ar1 - 1
= a , o que é verdade.
Considere-se, por hipótese, que para um certo n ! IN , un = arn - 1
.
Pretende-se provar que un + 1 = arn
.
Por definição de progressão geométrica, tem-se que un + 1 = un × r .
Por hipótese, obtém-se:
un × r = arn - 1
× r = arn
Portanto, un + 1 = arn
.
Conclui-se, assim, pelo princípio de indução matemática, que a proposição
un = arn - 1
, 6n ! IN é verdadeira.
27
Justifique se os números representados em cada alínea podem ser os primeiros
termos de uma progressão geométrica e, em caso afirmativo, escreva uma
expressão para o seu termo geral:
a)
2 ,
3
4
,
9
8
,
27
16
, …
b) 2 , 5 , 8 , 11 , …
c) 3 , 1 ,
3
3
,
3
1
, …
a)
Sim, porque
2
3
4
3
4
9
8
9
8
27
16
3
2
= = = .
O termo geral pode ser dado por un = 2 ×
3
2
n 1
-
d n .
b)
Não, porque
2
5
5
8
! .
c)
Sim, porque
3
1
1
3
3
3
3
3
1
3
3
= = = .
O termo geral pode ser dado por un = 3
3
3
n
e o .
000707 268-295 U10.indd 281 01/07/16 12:39

40. 282
Progressões aritméticas e Progressões geométricas
28
Determine um termo geral da progressão geométrica (un) e o valor de u7 ,
em que se sabe:
a) u1 = 10 e r = 5 b) u1 = 14 e u5 = 112 c) u4 = 27 e u11 =
81
128
a)
un = 10 × 5n - 1
e u7 = 10 × 57 - 1
= 156 250
b)
u5 = 14 × r4
+
14
112
= r4
+ r = ! 8
4
un = 14 × 8
n
4 1
-
` j ou un = 14 × 8
n
4 1
-
-
` j
u7 = 14 × 8
4 7 1
-
` j = 224 2
c)
u11 = 27 × r7
+
27
81
128
= r7
+ r =
10287
128
7
+ r =
3
2
u4 = u1 × r3
+ 27 = u1 ×
3
2
3
d n + u1 =
27
8
27
+ u1 =
8
729
un =
8
729
×
3
2
n 1
-
d n e u7 =
8
729
×
3
2
7 1
-
d n =
8
729
×
729
64
= 8
29
A Mariana, desde o seu 15.º aniversário, recebe todos
os anos uma boneca russa (matriosca).
Em cada ano, a boneca que lhe oferecem tem um peso
20 % superior ao peso da boneca do ano anterior.
Sabendo que a boneca que lhe ofereceram quando
fez 18 anos pesava 345,6 g , determine o peso
da boneca que lhe ofereceram no 24.º aniversário.
Apresente o resultado em gramas, com aproximação às unidades.
Seja (un) a sucessão do peso das bonecas em gramas. Então, u4 = 345,6 ,
pretendendo obter-se o valor de u10 .
Portanto, u10 = u4 × 1,2010 - 4
= 345,6 × 1,206
á 1032 g .
30
Um barco foi comprado novo por 30 000
euros. Por cada ano, após a sua compra,
sofrerá uma desvalorização de 8 % .
Determine o valor do barco 15 anos após
a sua compra.
Apresente o valor em euros, arredondado à centésima.
Seja (un) a sucessão do valor, em euros, do barco.
Assim, u15 = u1 × 0,9214
á 30 000 × 0,3112 á 9335,78 €
000707 268-295 U10.indd 282 01/07/16 12:39

41. 283
Domínio 3 SUCESSÕES
10
UNIDADE
31
Classifique quanto à monotonia as progressões geométricas (un) definidas por:
a) rn
b) 3 ×
3
2
n
-
d n
c)
u
u u
5
2
n n
1
1
=-
=
+
*
, 6n ! IN
d)
6
2
n
n 2
+
a)
Monótona crescente, pois r = r 1 e u1 0 .
b)
Não monótona, pois r = -
3
2
0 .
c)
Monótona decrescente, pois r = 2 1 e u1 = -5 0 .
d) Tem-se
6
2
2 3
2
3
4
n
n
n n
n
n
2 2
#
= =
+ +
= 4 ×
3
1
n
d n .
Monótona decrescente, pois 0 r =
3
1
1 e u1 =
3
4
0 .
32
Determine o termo geral da progressão geométrica (un) , monótona, sabendo que
u5 = 125 e u11 =
125
1
.
Caderno de Apoio do 11.º ano
u11 = u5 × r6
+
125
125
1
= r6
+ r = !
15 625
1
6
+ r = !
5
1
.
Como a sucessão é monótona, a sua razão é positiva, ou seja, r =
5
1
.
Por outro lado:
u5 = u1 × r4
+ 125 = u1 ×
5
1
4
d n + u1 =
625
1
125
+ u1 = 78 125
Assim, un = 78 125 ×
5
1
n 1
-
d n .
33
Determine uma expressão para o termo geral da progressão geométrica
de comprimento 3 :
a) (-18, -6, -2)
b) (-2, 4, -8)
a) Tem-se u1 = -18 e r =
18
6
-
-
=
3
1
; logo, un = -18 ×
1
3
n 1
-
d n .
b) Tem-se u1 =-2 e r=
2
4
-
=-2 ; logo, un =-2×(-2)n - 1
=(-2)n
.
000707 268-295 U10.indd 283 01/07/16 12:39

42. 284
Progressões aritméticas e Progressões geométricas
34
Determine:
S = 3 + 32
+ … + 38
+ 39
Efetuando:
S = 3 + 32
+ … + 38
+ 39
-3S = -32
- … - 38
- 39
- 310
S - 3S = 3 + 0 + … + 0 + 0 - 310
Obtém-se -25 = 3 - 310
, ou seja:
S =
2
3 310
- +
+ S = 29 523
35
Considere a progressão geométrica (un) em que u1 = -6 e r = 3 .
Determine:
a)
um termo geral de (un) .
b)
a soma dos 10 primeiros termos.
a)
un = -6 × 3n - 1
b)
S10 = -6 ×
1 3
1 310
-
-
= -6 ×
2
59048
-
-
= -177 144
36
Seja (an) a sucessão definida por an = 2
n
1
2
-
.
36.1
Mostre que (an) é uma progressão geométrica e determine a sua razão.
36.2 Calcule o valor exato:
a)
da soma dos 12 primeiros termos.
b) de a5 + a6 + … + a12 .
36.1 Como a
a
n
n 1
+
=
2
2
n
n
1
2
1
2
1
-
-
+
= 2 2
1
-
, (an) é uma progressão geométrica
de razão
2
2
.
36.2 a) S12 = a1 ×
1
2
2
1
2
2
12
-
-e o
= 2 ×
1
2
2
1
2
1 6
-
-c m
= 2 ×
2
2 2
64
63
-
=
= 2 ×
32 2 2
63
-
_ i
=
64 32 2
63 2
-
=
64 32 2 64 32 2
63 2 64 32 2
- +
+
_ _
_
i i
i
=
=
4096 2048
63 2 64 32 2
-
+
_ i
=
64
63 2 2 2
+
_ i
=
32
63 2 63
+
000707 268-295 U10.indd 284 01/07/16 12:39

43. 285
Domínio 3 SUCESSÕES
10
UNIDADE
b) a5 + a6 + … + a12 = S12 - S4 =
=
32
63 2 63
+
- 2 ×
1
2
2
1
2
2
4
-
-e o
=
=
32
63 2 63
2
2 2
4
3
2
+
-
-
=
=
32
63 2 63
4 2 2 4 2 2
3 2 4 2 2
+
-
- +
+
_ _
_
i i
i
=
=
32
63 2
16 8
3 2
63 4 2 2
-
-
+ +
_ i
=
=
32
63 2 63 3 2 2 2
8
4
+
-
+
_ i
=
=
32
63 2 63
32
48 2 48
+
-
+
=
32
15 2 15
+
37
A Andreia estacionou o seu carro num local
em que o placar informativo indica que
o estacionamento de qualquer viatura custa
na primeira hora 0,50 euros, aumentando
20 % em cada hora que passa.
Se a Andreia deixar o seu carro no local
durante 5 horas, quanto irá pagar no final?
Seja (un) a sucessão do valor, em euros, a pagar por hora. A sucessão (un)
é uma progressão geométrica de razão r = 1,20 e u1 = 0,50 .
Assim:
S5 = 0,50 ×
,
,
1 1 20
1 1 205
-
-
= 0,50 ×
,
,
1 1 20
1 2 48832
-
-
=
= 0,50 × 7,4416 = 3,7208
A Andreia irá pagar, aproximadamente, 3,72 € .
000707 268-295 U10.indd 285 01/07/16 12:39

44. 286
Progressões aritméticas e Progressões geométricas
38
Determine:
4
1
+
1
8
+
1
16
+ … +
1
1024
O termo geral da sucessão que tem como primeiros termos estes valores é:
un =
4
1
×
2
1 n 1
-
c m =
2
1
2
×
2
1
n 1
-
=
2
1
n 1
+
Tem-se que
1024
1
é o termo de ordem 9, pois 2n + 1
= 1024 , ou seja,
2n + 1
= 210
.
Assim:
S9 =
4
1
×
1
2
1
1
2
1 9
-
- c m
=
4
1
×
2
1
512
511
=
4
1
×
256
511
=
1024
511
Tarefa 7
O Sr. Moreira é dono de uma fábrica de calçado
para exportação e necessitou de uma máquina
industrial para fazer face ao volume de encomendas
que tinha.
Optou, então, por efetuar um contrato de aluguer, com a duração máxima
de 10 anos, em que tinha de pagar no 1.º ano 15 milhares de euros e a cada
ano que passasse teria uma redução de 5 % no aluguer devido à desvalorização
da máquina.
7.1
Deduza uma expressão que permita calcular, para cada ano,
o valor a pagar, em milhares de euros, pelo aluguer da máquina.
7.2
Determine o valor acumulado do aluguer se o contrato permanecer
durante a sua vigência máxima.
7.1
Atendendo ao contrato de aluguer, o custo da máquina, em milhares
de euros, no 1.º ano, c1 , é de 15 ; no 2.º ano, c2 , é de:
15 - 15 × 0,05 = 15 × (1 - 0,05) = 15 × 0,95 ;
no 3.º ano, c3 = 15 × 0,952
.
Tem-se, assim, que o custo da máquina, num determinado ano, é dado
por uma progressão geométrica de razão 0,95 ( cn + 1 = 0,95 × cn )
e de primeiro termo 15 e, portanto, a expressão pretendida é:
cn = 15 × 0,95n - 1
7.2
O custo acumulado da máquina ao longo dos 10 anos de contrato é dado por:
S = 15 ×
,
,
1 0 95
1 0 9510
-
-
á 120,37892
O valor máximo a pagar será de, aproximadamente, 120 378,92 euros.
000707 268-295 U10.indd 286 01/07/16 12:39

45. 287
Domínio 3 SUCESSÕES
10
UNIDADE
AVALIAR CONHECIMENTOS
ESCOLHA MÚLTIPLA
Para cada uma das questões desta secção, selecione a opção correta de entre
as alternativas que lhe são apresentadas.
1
De uma progressão aritmética (un) sabe-se que a soma dos dois primeiros
termos é 7 e a razão é -3 . O 6.º termo desta sucessão é:
(A) -8 (B) -10 (C) -12 (D) -14
u2 = u1 - 3 e u2 = 7 - u1 ; logo, u1 - 3 = 7 - u1 + u1 = 5 .
Assim, u6 = 5 + 5 × (-3) .
A opção correta é a (B).
2
Num jogo de snooker, o Diogo e o Mário pagam
2 euros pelo aluguer da mesa de jogo e a cada bloco
de 15 minutos que passa pagam mais 45 cêntimos.
Num determinado dia, o jogo entre os dois prolongou-se
um pouco mais e pagaram 5 euros e 15 cêntimos.
Qual foi a duração máxima do jogo?
(A) 1 h 30 min (B) 1 h 45 min (C) 2 h (D) 2 h 15 min
5,15 - 2 = 3,15 e
,
,
0 45
3 15
= 7
A duração máxima foi de 7 blocos de 15 minutos, ou seja, 1 h 45 min .
A opção correta é a (B).
3
Um atleta efetuou um treino de 12 dias em que todos
os dias correu sempre mais 800 metros do que havia
corrido no dia anterior. Sabendo que nos primeiros
11 dias correu um total de 88 quilómetros, quantos
quilómetros correu no 12.º, e último, dia de treino?
(A) 10,6 (B) 11,4 (C) 12,8 (D) 14,3
S11 =
u u
2
1 11
+
× 11 + 88 000 =
u u
2
10 800
1 1 #
+ +
× 11 +
+ 8000 = u1 + 4000 + u1 = 4000
u12 = u1 + 11 × 800 = 12 800 metros
A opção correta é a (C).
000707 268-295 U10.indd 287 01/07/16 12:39

46. 288
Progressões aritméticas e Progressões geométricas
4
Numa progressão geométrica de razão negativa, o 1.º termo é 2 e o 3.º termo
resulta da diferença entre 3 e a razão.
Nesta progressão, a razão é:
(A) -2 (B) -
3
2
(C) -1 (D) -
2
1
u3 = u1 × r2
+ 3 - r = 2 × r2
+ 2r2
+ r - 3 = 0 +
+ r =
4
1 1 4 2 3
! # #
- +
+ r =
4
1 5
!
-
+ r = -
2
3
0 r = 1
A opção correta é a (B).
5
Uma bomba de vácuo retira, em cada sucção,
3 % do gás existente num certo recipiente.
Depois de 40 sucções, quanto restará do gás
inicialmente existente?
(A) 30,5 %
(B) 29,6 %
(C) 28,7 %
(D) 27,8 %
0,9740
á 0,296
A opção correta é a (B).
6
Um caracol percorre o caminho desenhado
a azul na figura ao lado.
O lado de cada quadrado representado
na figura mede
4
3
do lado do quadrado
anterior (à esquerda deste).
Se o lado do primeiro quadrado medir 16 cm , a distância percorrida pelo
caracol é, arredondada ao centímetro:
(A) 167 (B) 170 (C) 173 (D) 174
S8 = u1 ×
1
4
3
1
4
3 8
-
- c m
= 16 × 3 ×
4
1
65 536
58 975
=
1024
176 925
á 172,77
A opção correta é a (C).
u3p40h4
000707 268-295 U10.indd 288 01/07/16 12:39

47. 289
Domínio 3 SUCESSÕES
10
UNIDADE
RESPOSTA ABERTA
Nas questões desta secção, apresente o seu raciocínio de forma clara, indicando todos
os cálculos que tiver de efetuar e as justificações necessárias.
7
Num hipermercado, colocou-se em exposição uma
pilha com um determinado número de embalagens.
Na primeira camada, colocaram-se 52 embalagens
e, em cada camada seguinte, menos duas
embalagens do que na anterior.
7.1
Calcule o número de embalagens na 18.a
camada.
7.2
Sabendo que existem 24 camadas, determine o número total de embalagens
existentes na pilha.
7.1
Seja (un) a sucessão do número de embalagens em cada camada.
u18 = 52 + 17 × (-2) = 18 embalagens
7.2
S24 =
u u
2
1 24
+
× 24 =
( )
2
52 52 23 2
#
+ + -
× 24 = 696 embalagens
8
Considere a progressão aritmética (an) , em que a2 + a4 = 15 e a5 + a6 = 25 .
8.1
Determine a razão da progressão e escreva o termo geral de (an) .
8.2
Sabendo que a soma dos n primeiros termos é 975 , calcule o valor de n .
8.1
Tem-se que:
a2 + a4 = 15 + a1 + r + a1 + 3r = 15 + a1 =
r
2
15 4
-
a5 + a6 = 25 + a1 + 4r + a1 + 5r = 25 + a1 =
r
2
25 9
-
Logo:
r
2
15 4
-
=
r
2
25 9
-
+ r = 2 e a1 =
r
2
25 9
-
=
2
7
Portanto, o termo geral da sucessão é an =
2
7
+ 2(n - 1) = 2n +
2
3
.
8.2
Sn =
u u
2
n
1 +
× n + 975 =
n
2
2
7
2
2
3
+ +
× n +
+ 1950 = (5 + 2n) × n + 5n + 2n2
- 1950 = 0 +
+ n =
4
5 25 4 2 1950
! # #
- +
+ n =
4
5 125
!
-
+
+ n = 30 0 n = -
2
65
O valor de n é 30 .
000707 268-295 U10.indd 289 01/07/16 12:39

48. 290
Progressões aritméticas e Progressões geométricas
9
A soma dos primeiros n termos de uma progressão geométrica (bn) é dada
por Sn = 3n+1
- 3 .
9.1
Determine o 1.o
termo desta sucessão.
9.2
Justifique que uma expressão do termo geral da progressão é:
bn = 6 × 3n-1
9.1
b1 = S1 = 32
- 3 = 6
9.2
S2 = 33
- 3 = 24 e b2 = 24 - 6 = 18 .
Assim, r =
b
b
1
2
=
6
18
= 3 .
Logo, a expressão do termo geral é dada por:
bn = b1 × rn - 1
= 6 × 3n - 1
10
A espiral representada ao lado é constituída por
semicircunferências.
A semicircunferência maior tem 3 cm de diâmetro
e o diâmetro de cada semicircunferência seguinte
mede menos 10 % do que o da anterior.
10.1
Determine o comprimento da 6.a
semicircunferência, aproximado
às centésimas.
10.2
Determine uma expressão em função do número n de semicircunferências
que represente o comprimento da espiral.
10.1
Seja (un) a sucessão do diâmetro, em centímetros, de cada
semicircunferência.
Tem-se:
u6 = 3 × 0,905
á 1,77 cm
Então, o comprimento da 6.a
semicircunferência é igual a:
,
2
1 77r
á 2,78 cm
10.2
Seja (vn) a sucessão do comprimento, em centímetros, de cada
semicircunferência.
vn =
,
u u
2 2
0 90
n
n
1
1
# # #
r r
=
-
= 1,5r × 0,90n - 1
Assim, S = v1 ×
,
,
1 0 90
1 0 90n
-
-
= 1,5r ×
,
,
1 0 90
1 0 90n
-
-
= 15r(1 - 0,9n
)
u3p41h2
000707 268-295 U10.indd 290 01/07/16 12:39

49. 291
Domínio 3 SUCESSÕES
10
UNIDADE
11
Considere as sucessões (an) e (bn) definidas por:
a
a a
3
5
n n
1
1
=
= +
+
*
, 6n ! IN
e bn = 2 × 3n-1
11.1
Mostre que (an) é uma progressão aritmética e determine uma expressão
do termo geral.
11.2 Determine n ! IN tal que bn + 2 = a98 .
11.3
Calcule a soma:
a) dos primeiros 10 termos de cada uma das sucessões (an) e (bn) .
b)
dos 8 termos de cada uma das sucessões (an) e (bn) a partir do 5.º,
inclusive.
11.1
an + 1 - an = an + 5 - an = 5 ; logo, (an) é uma progressão aritmética.
O termo geral é an = 3 + (n - 1) × 5 = 5n - 2 .
11.2 bn + 2 = a98 + bn + 2 = 5 × 98 - 2 + 2 × 3n - 1
= 486 +
+ 3n - 1
= 243
Como 35
= 243 , n = 6 .
11.3 a) Para (an) :
S10 =
a a
2
1 10
+
× 10 =
2
3 48
+
× 10 = 255
Para (bn) :
S10 = b1 ×
1 3
1 310
-
-
= 2 ×
2
1 310
-
-
= 59 048
b) Sa =
a a
2
5 8 4
+ +
× 8 =
2
5
5 2 5 12 2
# #
+
- -
× 8 = 324
Sb = b5 ×
1 3
1 38
-
-
= 2 × 34
×
2
1 38
-
-
= 531 360
12
Considere a sucessão (vn) definida por
v
v v
2
2 1
n n
1
1
=
= -
+
*
, 6n ! IN
.
12.1
Seja (wn) a sucessão definida por wn = vn - 1 . Mostre que (wn) é uma
progressão geométrica de razão 2 e determine o termo geral de (wn) .
12.2
Mostre, utilizando o principio de indução matemática, que a soma dos n
primeiros termos de (vn) é dada por S = 2n
+ n - 1, 6n ! IN .
12.1
w
w
v
v
v
v
1
1
1
2 1 1
n
n
n
n
n
n
1 1
=
-
-
=
-
- -
+
+
=
( )
v
v
1
2 1
n
n
-
-
= 2
Logo, (wn) é uma progressão geométrica de razão 2 e de 1.o
termo
w1 = v1 - 1 = 2 - 1 = 1 . Portanto, o termo geral é:
wn = 1 × 2n - 1
= 2n - 1
000707 268-295 U10.indd 291 01/07/16 12:39

50. 292
preparação para o teste 6
12.2 Para n = 1 , tem-se S1 = 21
+ 1 - 1 = 2 , que é verdade.
Hipótese: Para um certo n ! IN , Sn = 2n
+ n - 1 .
Tese: Sn + 1 = 2n + 1
+ n
Demonstração:
Sn + 1 = Sn + vn + 1
Por hipótese, obtém-se:
Sn + 1 = 2n
+ n - 1 + vn + 1 = 2n
+ n - 1 + 2vn - 1 =
= 2n
- 2 + 2vn + n
Tem-se que wn = vn - 1 + vn = wn + 1 + vn = 2n - 1
+ 1 .
Assim:
Sn + 1 = 2n
- 2 + 2(2n - 1
+ 1) + n =
= 2n
- 2 + 2n
+ 2 + n = 2 × 2n
+ n = 2n + 1
+ n
Portanto, pelo princípio de indução, 6n ! IN, Sn = 2n
+ n - 1 .
PREPARAÇÃO PARA O TESTE 6
I
Para cada uma das questões deste grupo, selecione a opção correta de entre
as alternativas que lhe são apresentadas.
1
Considere a sucessão (un) definida pelo termo geral:
un = arcsin n
1
-
c m
Indique a afirmação falsa:
(A) (un) é crescente.
(B) (un) é limitada.
(C) sin(u1) = -1
(D) cos(u2) = -
2
3
u2 = arcsin
2
1
-
c m = -
6
r
e cos
6
r
-
c m =
3
2
A opção correta é a (D).
2
As figuras representam os três primeiros termos de uma sucessão.
O número de círculos necessários
para representar os 10 primeiros
termos da sucessão é:
(A) 41
(B) 210
(C) 230
(D) 300
S10 =
u u
2
1 10
+
× 10 =
2
5 5 9 4
#
+ +
× 10 = 230
A opção correta é a (C).
u3p42h1
000707 268-295 U10.indd 292 01/07/16 12:39

51. 293
Domínio 3 SUCESSÕES
3
Considere a sucessão (vn) definida pelo termo geral:
vn = 3 × 4
n
2
1
-
Sabendo que (vn) é uma progressão geométrica, qual é a sua razão?
(A)
4
1
(B)
1
2
(C) 2 (D) 4
v
v
n
n 1
+
=
3 4
3 4
4
n
n
2
1
2
1
1
2
1
#
#
=
-
+
-
= 2
A opção correta é a (C).
4
O número de abelhas numa determinada
colmeia diminui a um ritmo mensal de 3 % .
Sabendo que existiam cerca de 2000 abelhas
no início de janeiro deste ano, qual o número
aproximado de abelhas se prevê que existam
no fim do mês de dezembro do corrente ano?
(A) 1475 (B) 1431 (C) 1388 (D) 1346
v12 = v1 × 0,9711
= 2000 × 0,9711
. 1431
A opção correta é a (B).
5
Para cada valor de n ! IN , considere, num referencial o.n. Oxyz , o ponto A
de coordenadas (n + 2, 3, 1 - n) .
Sabendo que o ponto A pertence ao plano que passa pela origem do referencial
e é perpendicular à reta r de equação:
(x, y, z) = (1, 2, -1) + k(-2, 1, -3) , k ! IR
Qual o valor de n ?
(A) 2 (B) 3 (C) 4 (D) 5
A equação do plano é -2x + y - 3z = 0 .
Assim:
-2(n + 2) + 3 - 3(1 - n) = 0 +
+ -2n - 4 + 3 - 3 + 3n = 0 + n = 4
A opção correta é a (C).
000707 268-295 U10.indd 293 01/07/16 12:40

52. 294
preparação para o teste 6
II
Nas questões seguintes, apresente o seu raciocínio de forma clara, indicando todos
os cálculos que tiver de efetuar e as justificações necessárias.
1
Considere as sucessões (un) , (vn) e (wn) definidas, respetivamente, por:
un =
n
n
2
2 1
+
+
;
v
v v
3
2
n n
1
1
=
= -
+
*
, 6n ! IN
e wn = 3v 2
n-
1.1
Prove que (un) é monótona e limitada.
1.2
Determine um termo geral de (vn) .
1.3 Calcule v5 + v6 + … + v20 .
1.4
Mostre que (wn) é uma progressão geométrica decrescente.
1.1
un + 1 - un =
( )
n
n
n
n
3
2 1 1
2
2 1
+
+ +
-
+
+
=
=
( )( )
( )( ) ( )( )
n n
n n n n
3 2
2 3 2 2 1 3
+ +
+ + - + +
=
=
( )( )
( )
n n
n n n n
3 2
2 7 6 2 7 3
2 2
+ +
+ + - + +
=
( )( )
n n
3 2
3
+ +
0
Logo, (un) é crescente.
Assim, u1 =
1 2
2 1
+
+
= 1 é um minorante de (un) .
Além disso, tem-se que
( )
n
n
n
n
n
n
2
2 1
2
2 4
2
2 2
1
+
+
+
+
=
+
+
= 2 .
Logo, 2 é um majorante de (un) e, portanto, (un) é limitada.
1.2 (vn) é uma progressão aritmética de razão -2 e de primeiro termo 3 .
Logo, vn = 3 - 2(n - 1) = 5 - 2n .
1.3
v5 + v6 + … + v20 =
v v
2
5 20
+
× 16 =
=
2
2 5 5 2 20
5 #
#
- + -
× 16 =
=
2
5 5
3
-
-
× 16 = -320
1.4 w
w
3
3
3
n
n
v
v
v v
1
2
2
n
n
n n
1
1
= =
+
-
-
-
+
+
= 3-2
=
9
1
Logo, (wn) é uma progressão geométrica de razão
9
1
e de primeiro
termo w1 = 3v 2
1 -
= 33 - 2
= 3 .
Assim, como a razão é inferior a 1 e o primeiro termo é positivo,
(wn) é decrescente.
000707 268-295 U10.indd 294 01/07/16 12:40

53. 295
Domínio 3 SUCESSÕES
2
O Sr. Madureira comprou uma televisão LED Smart TV 3D 55m a prestações.
O primeiro pagamento, um mês após a compra,
foi de 120 euros; o segundo, dois meses após a compra,
foi de 140 euros; o terceiro foi de 160 euros; e assim
sucessivamente até pagar a totalidade do valor da televisão.
2.1
Determine qual foi a prestação a pagar no 10.o
mês.
2.2
Sabendo que o Sr. Madureira pagou a televisão
em 12 meses, determine o valor total pago.
2.3
No momento em que o Sr. Madureira efetuou o crédito, foi-lhe proposto
comprar outro modelo de televisão, no valor de 2550 euros, a qual seria
paga da seguinte forma: 10 euros na 1.a
prestação; 20 euros na 2.a
; 40
euros na 3.a
; e assim sucessivamente até perfazer o valor total a pagar.
Nesta modalidade, quantos meses levaria a livrar-se das suas obrigações?
2.1
Seja (vn) a sucessão do valor, em euros, de cada prestação. Então,
(vn) é uma progressão aritmética de razão 20 e de primeiro termo 120 .
Assim, v10 = 120 + (10 - 1) × 20 = 300 € .
2.2
S =
v v
2
1 12
+
× 12 =
( )
2
120 120 12 1 20
+ + -
× 12 = 2760€
2.3
Seja (un) a sucessão do valor, em euros, de cada prestação. Então,
(un) é uma progressão geométrica de razão 2 e de primeiro termo 10 .
Assim:
S = 2550 + u1 ×
r
r
1
1 n
-
-
= 2550 + 10 ×
1 2
1 2n
-
-
= 2550 +
+ 1 - 2n
= -255 + 2n
= 256
Como 28
= 256 , n = 8 . Logo, levaria 8 meses a pagar a televisão.
3
No referencial o.n. xOy da figura estão representadas
a circunferência de centro C(3, -4) , e que passa pela origem
do referencial, e a reta t tangente à circunferência em O .
3.1
Mostre que a reta t pode ser definida por 3x - 4y = 0 .
3.2
Defina por uma condição a zona colorida, incluindo a fronteira.
3.1
Tem-se que o vetor OC(3, -4) é perpendicular à reta t ; logo, (4, 3)
é um vetor diretor da reta. Como t passa na origem do referencial, a sua
ordenada na origem é nula. Assim, a sua equação reduzida é do tipo
y = mx . Neste caso, obtém-se y =
4
3
x + 4y = 3x + 3x - 4y = 0 .
Em alternativa:
P é ponto da reta se, e só se, OP for perpendicular a OC . Portanto:
t: (x, y) $ (3, -4) = 0 + 3x - 4y = 0
3.2 0 G y G
4
3
x / (x - 3)2
+ (y + 4)2
H 25
u3p43h2
y
x
t
O
C(3, 24)
000707 268-295 U10.indd 295 01/07/16 12:40

54. 296
Limites
de sucessões
11
UNIDADE
TAREFAS E AVALIAR CONHECIMENTOS
11.1
Definição de limite
1
Relativamente ao exemplo 1, determine uma ordem p ! IN , a partir da qual
a área do triângulo [BCP] é inferior a:
a) 0,001 b) 10-5
a) Se a área do triângulo [BCP] for inferior a 0,001 , tem-se:
n
2 2
1
+
0,001 + 2n + 2 1000 + n 499
Portanto, basta escolher uma ordem superior a 499 , por exemplo 500 ,
uma vez que, para todo o natural n , n H 500 qan - 1u 0,001 .
b) Se a área do triângulo [BCP] for inferior a 10-5
, tem-se:
n
2 2
1
+
0,00001 + 2n + 2 100 000 + n 49 999
Portanto, basta escolher uma ordem superior a 49 999 , por exemplo 50 000 ,
uma vez que, para todo o natural n , n H 50 000 qan - 1u 10-5
.
2
Considere a sucessão de termo geral:
un = n
1
2.1 Calcule u1 , u10 , u500 e u10 000 .
2.2
Determine uma ordem a partir da qual:
a) un 0,0001 b) un 0,00003
2.3
Prove que un 0 .
2.1 u1 = 1 ; u10 =
1
10
; u500 =
0
1
50
; u10 000 =
1
1
0 000
2.2 a) un 0,0001 + n
1
0,0001 + n
1
0,0001 + n 10 000
A partir da ordem 10 000 , exclusive, ou 10 001 , inclusive.
b) un 0,00003 + n
1
0,00003 + n
1
0,00003 + n 33 333,(3)
A partir da ordem 33 334 , inclusive.
000707 296-327 U11.indd 296 01/07/16 12:48

55. 297
Domínio 3 SUCESSÕES
11
UNIDADE
2.3
Por definição un 0 se, e somente se, para todo o d 0 , existe uma
ordem p ! IN , tal que
6n ! IN, n H p u 0
n - d
Considerando um número real d 0 , a condição
un d
é equivalente a
n
1
d + n
1
d
Conclui-se, então, que a condição un d é possível em IN e tem como
conjunto solução
S = IN + ,
1
3
d
+
F
Assim, considerando p = min S , tem-se:
6n ! IN, n H p un d
Fica, assim, provado, por definição, que un 0 .
3
Considere a sucessão (un) definida por:
un = n
n
3 1
+
3.1
Determine uma ordem, p ! IN , a partir da qual todos os termos
da sucessão (un) verificam a condição:
u 3
n- 0,001
3.2
Prove, utilizando a definição, que un 3 .
3.3
Determine o conjunto solução da condição qun - 3,1u 0,001 e conclua
que 3,1 não é limite de (un) .
3.1 Tem-se que:
n
n
3 1
3
+
- = n
1
Como n
1
0,001 + n 1000 , basta escolher uma ordem superior
a 1000 , por exemplo, 1001 , para que isso aconteça, uma vez que,
para todo o natural n , n H 1001 qun - 3u 0,001 .
3.2
Por definição, un 3 se, e somente se, para todo o d 0 existe uma
ordem p ! IN , tal que 6n ! IN, n H p qun - 3u d .
Considerando um número real d 0 , a condição qun - 3u d
é equivalente a n
1
d , para todo o n ! IN .
Tem-se que n
1
d + n
1
d
.
000707 296-327 U11.indd 297 01/07/16 12:48

56. 298
Limites de sucessões
Conclui-se, então, que a condição qun - 3u d é possível em IN
e tem como conjunto solução S = IN + ,
1
3
d
+
F .
Assim, considerando p = minS , tem-se:
6n ! IN, n H p qun - 3u d
Fica, assim, provado, por definição, que un 3 .
3.3 ,
u 3 1
n - 0,001 + ,
n
n
3 1
3 1
+
- 0,001 +
, n
n
1 0 1
-
0,001 +
+ , n
1 0 1
- 0,001n + -0,001n 1 - 0,1n / 1 - 0,1n 0,001n +
+ -0,001n + 0,1n 1 / -0,1n - 0,001n -1 +
+ 0,099n 1 / -0,011n -1 + n 10,101 / n 90,91 (Impossível)
Conclui-se, assim, que não existe nenhuma ordem para a qual
,
u 3 1
n - 0,001 e, portanto, 3,1 não é limite da sucessão considerada.
4
Prove, por definição, que as sucessões definidas pelos termos gerais seguintes
tendem para -2 .
a) an = -2 - n
2
b) bn = n
n
1 2
-
a)
Por definição, an -2 se, e somente se, para todo o d 0 , existe
uma ordem p ! IN , tal que 6n ! IN, n H p qan + 2u d .
Considerando um número real d 0 , a condição qan + 2u d
é equivalente a n
2
- d , para todo o n ! IN .
Tem-se que n
2
d + n
2
d
.
Conclui-se, então, que a condição qan + 2u d é possível em IN e tem
como conjunto solução S = IN + ,
2
3
d
+
F .
Assim, considerando p = minS , tem-se:
6n ! IN, n H p qan + 2u d
Fica, assim, provado, por definição, que an -2 .
b)
Por definição, bn -2 se, e somente se, para todo o d 0 ,
existe uma ordem p ! IN , tal que 6n ! IN, n H p qbn + 2u d .
Considerando um número real d 0 , a condição qbn + 2u d
é equivalente a n
1
d , para todo o n ! IN .
Tem-se que n
1
d + n
1
d
.
000707 296-327 U11.indd 298 01/07/16 12:48

57. 299
Domínio 3 SUCESSÕES
11
UNIDADE
Conclui-se, então, que a condição qbn + 2u d é possível em IN e tem
como conjunto solução S = IN + ,
1
3
d
+
F .
Assim, considerando p = minS , tem-se:
6n ! IN, n H p qbn + 2u d
Fica, assim, provado, por definição, que bn -2 .
11.2
Convergência e limitação
5
Considere a sucessão (un) de termo geral:
un =
n
n
2
5 6
+
5.1
Mostre que un 3 .
5.2
Determine quantos termos de (un) não pertencem à vizinhança 0,2 de 3 .
5.3
Indique um majorante e um minorante de (un) .
5.1
Por definição, un 3 se, e somente se, para todo o d 0 ,
existe uma ordem p ! IN , tal que 6n ! IN, n H p qun - 3u d .
Considerando um número real d 0 , a condição qun - 3u d
é equivalente a
n
2
5
d , para todo o n ! IN .
Tem-se que
n
2
5
d + n
2
5
d
.
Conclui-se, então, que a condição qun - 3u d é possível em IN
e tem como conjunto solução S = IN + ,
2
5
3
d
+
F .
Assim, considerando p = minS , tem-se:
6n ! IN, n H p qun - 3u d
Fica, assim, provado, por definição, que un 3 .
5.2
qun - 3u H 0,2 +
n
n
2
5 6
3
+
- H 0,2 +
n
2
5
H 0,2 +
+
n
2
5
H 0,2 ++ n G
,
0 4
5
+ n G 12,5
Então, existem 12 termos de (un) que não pertencem à vizinhança 0,2 de 3 .
5.3
Tem-se que
n
n
2
5 6
+
= 3 +
n
2
5
, 6n ! IN .
Então:
6n ! IN, 0
n
2
5
G
2
5
+ 6n ! IN, 3 3 +
n
2
5
G
2
11
Conjunto dos minorantes: ]-3, 3]
Conjunto dos majorantes: ,
2
11
3
+
; ;
Logo, por exemplo, 3 é um minorante de (un) e
2
11
é um majorante de (un) .
000707 296-327 U11.indd 299 01/07/16 12:48

58. 300
Limites de sucessões
6
Mostre que a sucessão de termo geral
un = 3 +
( )
n
1 n
-
converge para 3 e não é monótona.
Por definição, un 3 se, e somente se, para todo o d 0 , existe uma ordem
p ! IN , tal que 6n ! IN, n H p qun - 3u d .
Considerando um número real d 0 , a condição qun - 3u d
é equivalente a
( )
n
1 n
-
d , para todo o n ! IN .
Para todos os termos, tem-se que
( )
n
1 n
-
d + n
1
d + n
1
d
.
Conclui-se, então, que a condição qun - 3u d é possível em IN e tem como
conjunto solução S = IN + ,
1
3
d
+
F .
Assim, considerando p = minS , tem-se:
6n ! IN, n H p qun - 3u d
Fica, assim, provado, por definição, que un 3 .
Monotonia:
u1 = 3 +
( )
1
1 1
-
= 2 ; u2 = 3 +
( )
2
1 2
-
=
2
7
; u3 = 3 +
( )
3
1 3
-
=
3
8
Como u1 u2 e u2 u3 , a sucessão não é monótona.
7
Considere uma sucessão (un) convergente e monótona, de limite l ! IR .
Mostre que (un) é limitada, exibindo um majorante e um minorante dessa sucessão.
Caderno de Apoio do 11.º ano
Dada uma sucessão (un) convergente de limite l , por definição, dado um
número real d 0 , existe um número finito, p - 1 , de termos que não
pertencem à vizinhança d de l , ou seja, que não pertencem ao intervalo
]l - d, l + d[ .
Então, sendo m e M , o mínimo e o máximo, respetivamente, do conjunto
{u1, u2, …, up - 1, l - d, l + d} , tem-se 6n ! IN, m G un G M , ou seja,
a sucessão (un) é limitada.
Se (un) for monótona crescente, então, u1 é um minorante e l é um majorante.
Se (un) for monótona decrescente, então, l é um minorante e u1 é um
majorante.
000707 296-327 U11.indd 300 01/07/16 12:48

59. 301
Domínio 3 SUCESSÕES
11
UNIDADE
8
Justifique que a sucessão (an) definida por an =
n
n
3 2
2
+
-
é convergente.
Como
an + 1 - an =
( )
( )
n
n
n
n
3 2 1
2 1
3 2
2
+ +
- +
-
+
-
=
( )( )
n n
2 5 2 3
7
+ +
0, 6n ! IN
(an) é monótona decrescente e, como tal, a1 =
5
1
é majorante.
n
n
n
n
n
n
n
n
3 2
2
2 3
2
2
2
3
2
2
3
2
1
1
+
-
=
+
- +
=
+
- +
=
+
- +
c m
2
1
- n + 1 n +
3
2
2
1
n +
4
3
2
1
-
4
7
Como an =
2
1
- +
n
2
3
4
7
+
, tem-se:
6n ! IN,
n
2
3
4
7
+
0 + 6n ! IN, an
2
1
-
Logo,
2
1
- é minorante de (an) .
Portanto, pelo teorema sobre sucessões monótonas e limitadas e convergência,
(an) é convergente.
9
Considere as sucessões definidas por:
un =
n 3
5
+
vn = cos2
(n + 1)
9.1
Mostre que un 0 .
9.2
Indique, justificando, lim(unvn) .
000707 296-327 U11.indd 301 01/07/16 12:48

60. 302
Limites de sucessões
9.1
Por definição, un 0 se, e somente se, para todo o d 0 , existe uma
ordem p ! IN , tal que 6n ! IN, n H p qun - 0u d .
Considerando um número real d 0 , a condição qun - 0u d
é equivalente a
n 3
5
+
d , para todo o n ! IN .
Tem-se que
n 3
5
+
d + n
5 3
d
d
-
.
Conclui-se, então, que a condição qun - 0u d é possível em IN e tem
como conjunto solução S = IN + ,
5 3
3
d
d
-
+
F .
Assim, considerando p = minS , tem-se:
6n ! IN, n H p qun - 0u d
Fica, assim, provado, por definição, que un 0 .
9.2 lim(un vn) = 0 , porque é o limite do produto de uma sucessão que tende
para zero, (un) , por uma sucessão limitada, (vn) .
Tarefa 1
Justifique o seguinte resultado:
Dadas duas sucessões, (un) e (vn) , convergentes, tais que limun = a
e limvn = 0 , então, lim(unvn) = 0 .
Atendendo a que (un) é convergente, então, é também limitada.
Como limvn = 0 , tem-se, por teorema, que lim(unvn) = 0 .
11.3 Limites infinitos
10
Considere a sucessão de termo geral:
an = 3n + 1
10.1
Determine a ordem a partir da qual todos os termos da sucessão são
maiores do que:
a) 100 b) 5000
10.2 Justifique que liman = +3 .
10.1 a)
Como 3n + 1 100 + 3n 99 + n 33 , basta escolher uma ordem
superior a 33 , uma vez que, para todo o natural n , n H 34 an 100 .
b)
Como 3n + 1 5000 + n
3
4999
, basta escolher uma ordem
superior a
3
4999
= 1666,(3) . Assim, para todo o natural n ,
n H 1667 an 5000 .
000707 296-327 U11.indd 302 01/07/16 12:48

61. 303
Domínio 3 SUCESSÕES
11
UNIDADE
10.2
Provar que lim(3n + 1) = +3 é o mesmo que provar que, para
qualquer número real L 0 , existe uma ordem p ! IN , tal que
6n ! IN, n H p 3n + 1 L
Como
3n + 1 L + n
L
3
1
-
,
basta, para cada L 0 , considerar p igual ou superior ao menor
natural que verifica a condição n
L
3
1
-
, para que a proposição
6n ! IN, n H p 3n + 1 L seja verdadeira.
Portanto, lim(3n + 1) = +3 .
Tarefa 2
Prove que un = 2n + (-1)n
n é não monótona e que limun = +3 .
Calculando os três primeiros termos, tem-se que u1 = 1 , u2 = 6 e u3 = 3 ;
logo, u1 u2 e u2 u3 e, sendo assim, (un) é não monótona.
Por definição, un +3 se, e somente se, para todo o L 0 existe uma
ordem p ! IN , tal que 6n ! IN, n H p un L .
Considerando um número real L 0 , a condição un L é equivalente a:
• para n ímpar, n L ;
• para n par, 3n L + n
L
3
.
Conclui-se, então, que a condição un L é possível em IN e tem como
conjunto solução:
S = IN + ]L, +3[ + ,
L
3
3
+ ;
E
Assim, considerando p = minS , tem-se:
6n ! IN, n H p un L
Fica, assim, provado, por definição, que un +3 , isto é, limun = +3 .
11
Prove, usando a definição, que:
a) lim(5n2
) = +3 b) lim_- ni = -3
a)
Para qualquer L 0 , como qualquer natural é positivo, tem-se
5n2
L + n
L
5
Então, considerando p igual ao menor natural superior a
L
5
, tem-se,
para todo o natural n , n H p 5n2
L .
Como L 0 pode ser qualquer, tem-se que lim5n2
= +3 .
000707 296-327 U11.indd 303 01/07/16 12:48

62. 304
Limites de sucessões
b)
Analogamente à alínea a), como - n -L + n L + n L2
,
basta, para cada L 0 , escolher p como sendo o menor natural
superior a L2
para que a proposição 6n ! IN, n H p - n -L
seja verdadeira.
Portanto, lim n
-
_ i = -3 .
12
Considere a sucessão de termo geral:
un =
n n
n n
3
3
se é par
se é ímpar
+
*
12.1
Estude a monotonia de (un) .
12.2
Mostre que:
un +3
12.1
Calculando o 8.º , o 9.º e o 10.º termos da sucessão, tem-se que
u8 = 11 , u9 = 27 e u10 = 13 ; logo, u8 u9 e u9 u10 e,
sendo assim, (un) é não monótona.
11.2
Provar que lim(un) = +3 é o mesmo que provar que para
qualquer número real L 0 existe uma ordem p ! IN ,
tal que 6n ! IN, n H p un L .
Para n par:
n + 3 L + n L - 3
Para n ímpar:
3n L + n
L
3
Portanto, basta, para cada L 0 , considerar p igual ou superior
ao menor natural que verifica simultaneamente as condições
n L - 3 e n
L
3
, que se sabe existir, para que a proposição
6n ! IN, n H p un L seja verdadeira.
Fica, assim, provado, por definição, que un +3 , isto é,
limun = +3 .
000707 296-327 U11.indd 304 01/07/16 12:49

63. 305
Domínio 3 SUCESSÕES
11
UNIDADE
11.4
Limites de sucessões que diferem num número finito de termos
13
Considere as sucessões (an) e (bn) definidas, respetivamente, por:
an =
n
n
1
2
+
e
bn = n
n
n
n n
1
2
20
4 20
se
se 2
G
+
*
13.1 Mostre que:
a) liman = 2
b) limbn = +3
13.2
As sucessões (an) e (bn) têm termos em comum. Explique por que razão
o resultado de 13.1 não contradiz a seguinte propriedade:
Duas sucessões (un) e (vn) que diferem apenas num número finito
de termos têm o mesmo limite (real ou infinito) ou não têm limite.
13.1 a) Dado um número real d 0 :
n
n
1
2
2
+
- d +
n
n n
1
2 2 2
+
- -
d +
n 1
2
+
d + n
2
d
- 1
Então, escolhendo p ! IN igual ou superior a
2
d
- 1 , tem-se,
para todo o natural n , n H p ,
n
n
1
2
2
+
- d .
E, como d 0 é qualquer, conclui-se o pretendido, ou seja,
liman = 2 .
b)
Provar que limbn = +3 é o mesmo que provar que, para qualquer
número real L 0 , existe uma ordem p ! IN , tal que:
6n ! IN, n H p bn L
Tome-se p1 igual ou superior ao menor natural que verifica a condição
n
L
4
.
Para n H 21 , bn = 4n ; então, para todo o L 0 , basta escolher
uma ordem p igual ou superior ao máximo entre 21 e p1
para que a proposição 6n ! IN, n H p bn L seja verdadeira.
Portanto, limbn = +3 .
13.2
Porque estas sucessões diferem uma da outra num número infinito
de termos.
000707 296-327 U11.indd 305 01/07/16 12:49

64. 306
Limites de sucessões
Tarefa 3
Considere uma sucessão (un) convergente, com limite l , e um número
real d 0 .
3.1
Justifique que existe p1 ! IN , tal que n H p1 qun -lu d .
3.2
Seja (vn) uma sucessão tal que vn = un , qualquer que seja n H p2
(isto é, (un) e (vn) diferem apenas num número finito de termos).
Conclua que, sendo p3 o máximo entre p1 e p2 , 6n ! IN, n H p3
qvn -lu d , ou seja, limvn = limun = l .
3.1
Por definição de limite, existe p1 ! IN: n H p1 qun -lu d .
3.2
Se diferem apenas num número finito de termos, existe
p3 ! IN: n H p3 vn ! ]l - d, l + d[ , ou seja, limvn = l .
11.5
Aplicação da definição de limite a casos particulares
14
Indique o limite das sucessões definidas por:
a) an = 5 + 3n
b) bn =
n
3
4-
a) liman = +3 , pois 3 0
b) limbn = lim
3
4
-
n
3
= -3 , pois -
3
1
0
15
Considere uma progressão aritmética crescente (an) . Indique, justificando,
o seu limite.
Como (an) é crescente, então, tem razão positiva, ou seja, an = an + b ,
com a 0 , e, como consequência, o seu limite é +3 .
16
Utilize a definição de limite para provar que:
a) lim2 = 2
b) lim
n 10
5
+
-
= 0
c) lim
n
n
3 1
6 7
- +
+
= -2
000707 296-327 U11.indd 306 01/07/16 12:49

65. 307
Domínio 3 SUCESSÕES
11
UNIDADE
a) Seja un = 2 . Tem-se, para qualquer real d 0 e para qualquer
n ! IN , n H p qun - 2u = q2 - 2u = 0 d .
Donde, lim2 = 2 .
b)
Dado um número real d 0 e n ! IN :
n 10
5
+
-
d +
n 10
5
+
d + n + 10
5
d
+ n
5
d
- 10
Então, escolhendo p ! IN , tal que p
5
d
- 10 , tem-se para todo
o natural n :
n H p
n 10
5
+
-
d
Como d 0 é qualquer, conclui-se o pretendido, ou seja, lim
n 10
5
+
-
= 0 .
c)
Dado um número real d 0 e n ! IN :
n
n
3 1
6 7
2
- +
+
+ d +
n
n n
3 1
6 7 6 2
- +
+ - +
d +
n
3 1
9
- +
d +
+
n
3 1
9
-
d + n
3
d
+
3
1
Então, escolhendo p ! IN superior a
3
d
+
3
1
, tem-se, para todo
o natural n , n H p :
n
n
3 1
6 7
2
- +
+
+ d
Como d 0 é qualquer, conclui-se o pretendido, ou seja,
lim
n
n
3 1
6 7
- +
+
= -2 .
Tarefa 4
Prove que, dados os números reais a , b , c e d , se
c ! 0 e 6n ! IN , cn + d ! 0 , então, lim
cn d
an b
+
+
= c
a
.
Seja d 0 qualquer. Então, u c
a
n - d +
c n dc
bc ad
2
+
-
d e, a partir
de certa ordem, tem-se c2
n + dc 0 , e a condição anterior verifica-se para
n
c
bc ad
c
d
2
d
-
- .
Assim, considerando p igual ao menor natural que verifica as condições,
tem-se o pretendido.
000707 296-327 U11.indd 307 01/07/16 12:49

66. 308
Limites de sucessões
11.6
Álgebra de limites de sucessões convergentes
17
Indique:
a) limn3
b) lim n
2
c) lim4
d) lim
n
n
1 2
3
+
-
e) lim
n
1
2
a) limn3
= +3 , pois r = 3 0 .
b) lim n
2
= 0
c) lim4 = 4
d) lim
n
n
1 2
3
+
-
= -
2
1
e) lim
n
1
2
= limn-2
= 0 , pois r = -2 0 .
18
Considere duas sucessões (un) e (vn) convergentes, tais que:
limun = -1 e limvn = 4
Calcule:
a) lim(un + vn)
b) lim(un - 2vn)
c) lim^un
2
h
d) lim v
u
n
1
n
n
+
e o
a) lim(un + vn) = limun + limvn = -1 + 4 = 3
b) lim(un - 2vn) = limun + lim(-2vn) = limun - 2limvn =
= -1 - 2 × 4 = -9
c) lim(un
2
) = lim(un × un) = limun × limun = (limun)2
= (-1)2
= 1
d) lim v
u
n
1
n
n
+
e o = lim v
u
n
n
c m + lim
n
1
e o = -
4
1
+ lim
n
1
2
1
f p =
= -
4
1
+ lim n 2
1
-
a k = -
4
1
+ 0 = -
4
1
000707 296-327 U11.indd 308 01/07/16 12:49

67. 309
Domínio 3 SUCESSÕES
11
UNIDADE
11.7
Álgebra de limites infinitos e indeterminações
19
Calcule:
a) lim n
2
3
+
c m b) lim
n
n
n
1
3 1
+
+ - -
c m c) lim
n
n
3
3
1
3
+
-
d n
a) lim n
2
3
+
c m = lim2 + lim n
3
= 2 + 0 = 2
b) lim
n
n
n
1
3 1
+
+ - -
c m = lim
n
n
1
+
c m + lim3 + lim(-n-1
) =
= 1 + 3 - 0 = 4
c) lim
n
n
3
3
1
3
+
-
d n = lim
n
n
3
10 1
3
-
d
f np =
3
10
3
d n =
27
1000
20
Calcule:
a) lim n n
1
2
+
c m b) lim
n
n
n
2
5 1
3+
+
-
-
d n
a) lim n n
1
2
+
c m = limn2
+ lim n
1
= limn2
+ limn-1
= +3 + 0 = +3
b) lim
n
n
n
3
2
5 1
+
+
-
-
d n = lim
n
n
n
3
2
5 1
+
-
- +
d n =
= lim(3 - n) + lim
n
n
2
5 1
+
-
d n = -3 + 5 = -3
21
Considere a sucessão de termo geral:
un = 2n2
- 3
Indique um termo geral de uma sucessão (vn) com limite -3 , tal que:
a) lim(un + vn) = 0
b) lim(un + vn) = +3
c) lim(un + vn) = -3
d) lim(un + vn) = 2
a)
Por exemplo, vn = 3 - 2n2
.
b)
Por exemplo, vn = -n2
.
c)
Por exemplo, vn = -3n2
.
d)
Por exemplo, vn = 5 - 2n2
.
000707 296-327 U11.indd 309 01/07/16 12:49

68. 310
Limites de sucessões
22
Considere as sucessões (un) , (vn) e (wn) , em que:
limun = -3 limvn = +3 limwn = -3
Indique, se possível:
a) lim(unvn)
b) lim(unwn)
c) lim(un + vn)
d) lim(wn - vn)
e) lim(2un - 3vn)
a) lim(unvn) = limun × limvn = -3 × (+3) = -3
b) lim(unwn) = limun × limwn = -3 × (-3) = +3
c) lim(un + vn) = limun + limvn = -3 + (+3) = +3
d) lim(wn - vn) = limwn - limvn = limwn + lim(-vn) =
= -3 + (-3) = -3
e) lim(2un - 3vn) = lim(2un) + lim(-3vn) = 2 × (-3) + (-3) × +3 =
= -6 + (-3) = -3
23
Considere as sucessões (un) , (vn) e (wn) , em que:
limun = 2 limvn = +3 limwn = -3
Indique, se possível:
a) lim(wnvn)
b) lim(unwn)
c) lim(un + wn)
d) lim(wn)2
a) lim(wnvn) = -3 × (+3) = -3
b) lim(unwn) = 2 × (-3) = -3
c) lim(un + wn) = 2 + (-3) = -3
d) lim(wn)2
= -3 × (-3) = +3
24
Considere as sucessões (un) e (vn) tais que:
•
6n ! IN, un 0
•
limun = +3
•
limvn = -3
Determine:
a) lim(un
3
vn)
b) lim(unvn)3
c) lim un
d) lim u v
n n
2
5
5
b l
000707 296-327 U11.indd 310 01/07/16 12:49

69. 311
Domínio 3 SUCESSÕES
11
UNIDADE
a) lim(un
3
vn) = limun
3
× limvn = +3 × (-3) = -3
b) lim(unvn)3
= ^lim(unvn)h3
= ^+3 × (-3)h3
= -3
c) lim un = limun
2
1
= ( )
lim un
2
1
= +3
d) lim u v
n n
2
5
5
b l = lim un
2
5
b l × lim(vn
5
) = ( )
lim un
2
5
× (limvn)5
=
= +3 × (-3) = -3
25
Considere a sucessão (un) de termo geral un =
n
5
2
.
Dê exemplo de uma sucessão (vn) , tal que limvn = +3 , e:
a) lim(unvn) = 0 b) lim(unvn) = +3 c) lim(unvn) = 1
a)
Por exemplo, vn = n .
b)
Por exemplo, vn = n3
.
c)
Por exemplo, vn =
n
5
2
.
26
Seja (un) uma progressão aritmética de razão e termos não nulos.
Justifique que:
lim u
1
n
= 0
Tem-se que limun = -3 ou limun = +3 .
Pelo teorema da inversa de uma sucessão de limite infinito, lim u
1
n
= 0 .
27
Justifique que
lim
n
n
6
3
+
= +3
começando por calcular
lim
n
n 6
3
+
lim
n
n 6
3
+
= lim
n n
n
1 6
2
#
+
c
e mo = lim
n
1
2
× lim n
n 6
+
=
= limn-2
× lim n
n 6
+
= 0 × 1 = 0+
(pois tem todos os termos positivos)
Como lim
n
n 6
3
+
= 0+
, então, lim
n
n 6
3
+
= lim
n
n 6
1
3
+
= +3 ,
pois
0
1
+
= +3 .
000707 296-327 U11.indd 311 01/07/16 12:49

70. 312
Limites de sucessões
28
Calcule:
a) lim 3
3
2
n
#d n
H
b) limvn , em que (vn) é definida por
v
v v
2
2
5
n n
1
1
=
=
+
*
, 6n ! IN
.
c) lim^2n
+ 3-n
h
a) lim 3
3
2
n
# d n
H = lim3 × lim
3
2
n
d n = 3 × 0 = 0
,
3
2
1
3
2
0
omo
C
n
1 d
f n p
b)
vn é uma progressão geométrica de razão
2
5
e, sendo assim, o termo geral
pode ser dado por vn = 2 ×
2
5
n 1
-
d n .
Então, limvn = lim 2
2
5
n 1
#
-
d n
H = lim2 × lim
2
5
n
d n × lim
2
5
1
-
d n =
= +3 ×
5
4
= +3
,
2
5
1
2
5
omo
C
n
3
2 +
d
f n p
c) lim(2n
+ 3-n
) = lim2n
+ lim
3
1
n = lim2n
+ lim
3
1
n
d n =
= +3 + 0 = +3
,
3
1
1 2 1
3
1
0 2
omo e e
C
n
n
3
1 2 +
d
f n p
Tarefa 5
Considere as sucessões (un) , (vn) , (wn) e (zn) de termos gerais,
respetivamente:
un = n2
+ n , vn = -2n , wn = n + 1 e zn = n3
5.1 Justifique que limun = +3 e que:
a) limvn = -3 e lim v
u
n
n
= -3
b) limwn = +3 e lim w
u
n
n
= +3
c) limzn = +3 e lim z
u
n
n
= 0
000707 296-327 U11.indd 312 01/07/16 12:49

71. 313
Domínio 3 SUCESSÕES
11
UNIDADE
5.2
Considere as sucessões (an) , (bn) e (cn) de termos gerais, respetivamente:
an = v
1
n
, bn = w
1
n
e cn = z
1
n
5.2.1 Justifique que liman = limbn = limcn = 0 .
5.2.2 Calcule:
a) lim c
a
n
n
b) lim
b
c
n
n
c) lim
b
a
n
n
5.1 limun = lim(n2
+ n) = limn2
+ limn = +3 + (+3 ) = +3
a) limvn = lim(-2n) = -2 × (+3) = -3
lim v
u
n
n
= lim
n
2 2
1
- -
c m = -3
b) limwn = lim(n + 1) = +3 + 1 = -3
lim w
u
n
n
= lim
( )
n
n n
1
1
+
+
= limn = +3
c) limzn = limn3
= (+3)3
= +3
lim z
u
n
n
= lim n n
1 1
2
+
d n = 0
5.2 5.2.1
As sucessões (an) , (bn) e (cn) são inversas de sucessões de limite
infinito; logo, têm todas limite zero.
5.2.2 a) lim c
a
n
n
= lim
n
2
2
-
d n = -3
b) lim
b
c
n
n
= lim
n
n 1
3
+
d n = lim
n n
1 1
2 3
+
d n = 0
c) lim
b
a
n
n
= lim
n
n
2
1
-
+
=
2
1
-
29
A figura apresenta os primeiros termos de uma
sucessão de triângulos equiláteros, alternadamente
brancos e azuis, em que os vértices de cada triângulo
são os pontos médios dos lados do triângulo anterior.
O 1.o
termo desta sucessão tem área 3 .
29.1
Seja (an) a sucessão das áreas dos triângulos.
Mostre que an =
4
3
n 1
-
.
29.2
Determine liman .
u3p66h1
000707 296-327 U11.indd 313 01/07/16 12:49

72. 314
Limites de sucessões
29.1
A sucessão (an) é uma progressão geométrica de razão
2
1
4
1
2
=
c m , pois
a razão de semelhança entre os lados de dois triângulos consecutivos é
2
1
;
logo, a razão de semelhança entre as áreas dos mesmos triângulos é
2
1 2
c m .
Então, o termo geral de (an) pode ser dado por:
an = 3 ×
4
1 n 1
-
c m =
4
3
n 1
-
29.2 lim
4
3
n 1
-
= lim 3 ×
4
1 n 1
-
c m = lim 3 × lim
4
1 n
c m × lim
4
1 1
-
c m =
= 4 3 × 0 = 0
,
4
1
1
4
1
0
omo
C
n
1 c
e m o
11.8
Levantamento algébrico de indeterminações
30
Considere as sucessões definidas por un = n3
e vn = n2
.
30.1 Complete a tabela:
n un vn un - vn
2 ? ? ?
10 ? ? ?
102
? ? 9,9 × 105
105
? ? ?
30.2
Mostre que lim(un - vn) .
30.1
n un vn un - vn
2 8 4 4
10 1000 100 900
102
106
104
9,9 × 105
105
1015
1010
9,9999 × 1014
30.2 lim(un - vn) = lim(n3
- n2
) = lim n n
1
1
3
-
c m
= G =
= limn3
× lim n
1
1
-
c m = +3 × 1 = +3
000707 296-327 U11.indd 314 01/07/16 12:49

73. 315
Domínio 3 SUCESSÕES
11
UNIDADE
31
Determine:
a) lim^-2n3
+ n4
h
b) lim(n5
- 4n)
c) lim^5n
- rn + 3
h
d) lim_n - n 1
2
+ i
a) lim(-2n3
+ n4
) = lim n n
2
1
4
- +
c m
= G = +3 × (0 + 1) = +3
b) lim(n5
- 4n) = lim n
n
1
4
5
4
-
d
f np = +3 × (1 - 0) = +3
c) lim(5n - rn + 3
) = lim 5 1
5
n
n
n 3
r
-
+
d n
H =
= lim5n × lim 1
5
n
3
#
r
r
- c
e m o = +3 × (1 - 0 × r3
) = +3
d) lim n n 1
2
- +
_ i = lim
n n
n n n n
1
1 1
2
2 2
+ +
- + +
+
_ _
i i
=
= lim
( )
n n
n n
1
1
2
2 2
+ +
- +
= lim
n n 1
1
2
+ +
-
=
1
3
+
-
= 0
32
Determine:
a) lim
n n
n n
5
2 3
2
3
+
+ -
b) lim
n n
n n
2
3 5
2
2
-
- + +
c) lim
n
n n
3
2
4
3
+
-
a) lim
n n
n n
5
2 3
2
3
+
+ -
= lim
n n
n
n n
1
5
1
2 3
2
3
2 3
+
+ -
c
d
m
n
= lim
n
n
n n
1
5
1
2 3
2 3
+
+ -
d n
=
=
( )
1 0
1 0 0
#
3
+
+ + -
= +3
b) lim
n n
n n
2
3 5
2
2
-
- + +
= lim
n
n
n
n n
2
2
1
1
3 1
3
1
3
5
2
2
2
- - +
- - -
c
d
m
n
=
= lim
n
n n
2
2
1
1
3 1
3
1
3
5
2
- +
- -
c
d
m
n
=
( )
( )
2 0 1
3 1 0 0
+
- -
=
2
3
c) lim
n
n n
3
4 2
3
+
-
= lim
n
n n
n 1
3
4
2
3
3
+
-
d
c
n
m
= lim
n
n
n
1
3
4
2
3
2
+
-
d n
=
2
3
+
-
= 0
000707 296-327 U11.indd 315 01/07/16 12:49

74. 316
Limites de sucessões
33
Seja (an) uma sucessão de termo geral:
an = 2n3
+ n2
- 10
Dê exemplo de uma sucessão (bn) tal que limbn = -3 , em que:
a) lim
b
a
n
n
= -3 b) lim
b
a
n
n
= 0 c) lim
b
a
n
n
= -
3
1
a)
Por exemplo, bn = -2n2
+ 1 .
b)
Por exemplo, bn = -n4
.
c)
Por exemplo, bn = -6n3
+ 1 .
34
Determine:
a) lim
4 3
4 1
n
n
2
+
+
+
b) lim ( )
5
2
3 1
n
n
-
d n
H c) lim
n
n
2
3
1
+
a) lim
4 3
4 1
n
n
2
+
+
+
= lim
4 4
4
3
4 1
4
1
n
n
n
n
2
+
+
d
d
n
n
= lim
4
4
3
1
4
1
n
n
2
+
+
=
16 0
1 0
+
+
=
16
1
b) lim ( )
5
2
3 1
n
n
-
d n
H = lim
5
6
5
2
n n
-
d d
n n
H = +3 - 0 = +3
c) lim
n
n
2
3
1
+
= lim
n
n
3
2
+
= lim
n
n n
3
1
2
# +
=
= lim
n
3
1
2
+
=
3
1
11.9
Limite de a
n
, com a 0
35
Prove, utilizando o princípio de indução matemática, que a proposição
6n ! IN, (1 + h)n
H 1 + nh (h 0)
é verdadeira.
000707 296-327 U11.indd 316 01/07/16 12:49

75. 317
Domínio 3 SUCESSÕES
11
UNIDADE
Para n = 1 , tem-se (1 + h)1
H 1 + h , que é verdade.
Hipótese: Para um certo n ! IN, (1 + h)n
H 1 + nh .
Tese: (1 + h)n + 1
H 1 + (n + 1)h
Demonstração:
(1 + h)n + 1
H (1 + h)n
(1 + h)
Por hipótese, obtém-se:
(1 + h)n
H 1 + nh (1 + h)n
(1 + h) H (1 + nh)(1 + h) +
+ (1 + h)n + 1
H 1 + nh + h + nh2
nh 0
2
H
H
1 + nh + h = 1 + (n + 1)h
Portanto, pelo princípio de indução, 6n ! IN, (1 + h)n
H 1 + nh é verdadeira.
36
Calcule:
a) lim
n
n
2
3 2
2 1
n
+
+
-
d n b) lim
n 2
7
n
+
a) lim
n
n
2
3 2
2 1
n
+
+
-
d n = lim 2
n
+ lim
n
n
n
n
3 1
3
2
2 1
2
1
+
-
d
c
n
m
=
= 1 + lim
n
n
3 1
3
2
2 1
2
1
+
-
d
c
n
m
= 1 +
( )
( )
3 1 0
2 1 0
+
-
=
3
5
b) lim
n 2
7
n
+
= lim
n n
7
1
2
n
+
=
( )
1 0
1
#
3
+ +
= 0
37
Considere a sucessão de triângulos retângulos
(a azul) em que o primeiro triângulo é obtido
a partir da diagonal de um quadrado de lado
2
1
,
e assim sucessivamente, como é sugerido na figura.
37.1
Justifique que a sucessão das áreas dos
triângulos é uma progressão geométrica
e determine um termo geral desta sucessão.
37.2
Determine o limite, quando n tende para +3 , da soma das áreas
dos n triângulos e interprete esse resultado geometricamente.
u3p71h1
000707 296-327 U11.indd 317 01/07/16 12:49

76. 318
Limites de sucessões
37.1
Dois triângulos sucessivos são semelhantes. A razão de semelhança
entre os lados é de
2
1
e, como tal, a razão de semelhança entre as áreas
é de
4
1
. Logo, o termo geral pode ser dado por An =
8
1
×
4
1 n 1
-
c m
ou An =
1
2
n
2 1
+
c m .
37.2
A soma dos primeiros n triângulos sucessivos é dada por:
S =
8
1
×
1
4
1
1
4
1 n
-
- c m
Assim, limS =
8
1
×
1
4
1
1
-
=
6
1
.
Geometricamente, tal significa que, à medida que o número de triângulos
assim formados tende para +3 , os triângulos preenchem
3
2
da área
do quadrado inicial.
Tarefa 6
Seja (un) a sucessão definida por recorrência:
u
u u
3
2 1
n n
1
1
=
= -
+
*
, 6n ! IN
6.1
Prove, utilizando o princípio de indução matemática, que 6n ! IN, un 1
e conclua que:
• (un) está bem definida;
• (un) é monótona decrescente.
6.2
Justifique que (un) é convergente e calcule o seu limite.
Adaptado do Caderno de Apoio do 11.º ano
6.1 Para n = 1 , u1 = 3 e 3 1 .
Hipótese: Para um certo n ! IN, un 1 .
Tese: un + 1 1
Demonstração:
Como un + 1 = u
2 1
n - , por hipótese de indução, tem-se:
un 1 2un 2 2un - 1 1 u
2 1
n - 1
Fica, assim, provado que 6n ! IN, un 1 .
000707 296-327 U11.indd 318 01/07/16 12:49

77. 319
Domínio 3 SUCESSÕES
11
UNIDADE
•
Como 2un 2 2un - 1 1, 6n ! IN, u
2 1
n - tem significado
para todo o n ! IN .
• un + 1 - un = u
2 1
n - - un =
( )
u u
u u
2 1
2 1
n n
n n
2
- +
- -
=
= -
( )
u u
u
2 1
1
n n
n
2
- +
-
0, 6n ! IN
Portanto, (un) é monótona decrescente.
6.2
Por 6.1 sabe-se que (un) é monótona decrescente e, como 6n ! IN, un 1 ,
(un) é minorada. Logo, (un) é convergente.
Seja limun = a . Logo, limun + 1 = a . Assim:
limun + 1 = lim u
2 1
n - + a = a
2 1
- a2
= 2a - 1 + a = 1
Como 1 = 2 1
- , limun = 1 .
AVALIAR CONHECIMENTOS
ESCOLHA MÚLTIPLA
Para cada uma das questões desta secção, selecione a opção correta de entre
as alternativas que lhe são apresentadas.
1
Considere a sucessão (an) de termo geral an = 1 + n
2
.
Indique o número de termos da sucessão que não pertencem à vizinhança
V0,1(1) .
(A) 19 (B) 20 (C) 21 (D) 22
(an - 1) H 0,1 + n
2
H 0,1 + n G 20
A opção correta é a (B).
2
Selecione a afirmação verdadeira:
(A) Uma sucessão convergente é monótona.
(B) Uma sucessão limitada é convergente.
(C) Uma sucessão convergente é limitada.
(D) Uma sucessão divergente não é limitada.
A opção correta é a (C).
000707 296-327 U11.indd 319 01/07/16 12:49

78. 320
Limites de sucessões
3
Considere a sucessão (un) definida por:
u
u u
3
3
n n
1
1
=-
= +
+
*
, 6n ! IN
Então:
(A) (un) é limitada.
(B) (un) é crescente e majorada.
(C) limun = +3
(D) limun = -3
A opção correta é a (C).
4
Seja (bn) a sucessão de termo geral bn = 4 × 3-n
.
Então:
(A) limbn = +3
(B) limbn = -3
(C) limbn = 0
(D) limbn = 4
limbn = lim 4
3
1
n
#d
f n p = 4 × 0 = 0
A opção correta é a (C).
5
Considere a sucessão (un) de termo geral un = n3
+ 4n .
Qual dos termos gerais seguintes define uma sucessão (vn) tal que
lim(un + vn) = -3 ?
(A) vn = -n3
- n
(B) vn = -n3
- 4n + 3
(C) vn = -n2
- 5n
(D) vn = -n5
+ 10n
lim(n3
+ 4n - n5
+ 10n) = lim(-n5
+ n3
+ 14n) =
= lim n
n n
1
1 14
5
2 4
- - -
d n
H = -3
A opção correta é a (D).
000707 296-327 U11.indd 320 01/07/16 12:49

79. 321
Domínio 3 SUCESSÕES
11
UNIDADE
6
Seja (an) uma sucessão de termos positivos em que liman = 0 .
Qual das seguintes afirmações é necessariamente verdadeira?
(A) lim a
1
n
= -3
(B) lim(n2
an) = 0
(C) lim
a
2 n
n
-
c m = 0
(D) lim a
1
n
= +3
A opção correta é a (D).
7
Considere a sucessão das
semicircunferências em que a primeira
semicircunferência tem de diâmetro 16 ,
a segunda semicircunferência resulta
de uma redução da primeira com razão igual a
3
2
, e assim sucessivamente.
Admitindo que o processo de construção desta linha não tem fim,
o seu comprimento é:
(A) 12r
(B) 18r
(C) 24r
(D) 27r
Seja (un) a sucessão do comprimento de cada semicircunferência.
Tem-se que un = 8r ×
3
2
n 1
-
d n .
A sucessão (un) é uma progressão geométrica; logo:
Sn = 8r ×
1
3
2
1
3
2
n
-
- d n
Assim:
limSn = lim 8
1
3
2
1
3
2
n
#
r
-
- d
f
n
p=
1
3
2
8r
-
lim 1
3
2
n
- d
f n p =
= 24r(1 - 0) = 24r
A opção correta é a (C).
u3p72h1
000707 296-327 U11.indd 321 01/07/16 12:49

80. 322
Limites de sucessões
RESPOSTA ABERTA
Nas questões desta secção, apresente o seu raciocínio de forma clara, indicando todos
os cálculos que tiver de efetuar e as justificações necessárias.
8
Considere a sucessão (un) definida por un =
n
n
3
1 2
+
-
.
8.1
Mostre que (un) é monótona.
8.2
Determine um majorante e um minorante de (un) e conclua que (un)
é limitada.
8.3
Determine quantos termos de (un) pertencem a V0,01(-2) .
8.4
Prove, recorrendo à definição de limite, que un -2 .
8.1
un + 1 - un =
( )
n
n
n
n
4
1 2 1
3
1 2
+
- +
-
+
-
=
=
( )( )
( )( ) ( )( )
n n
n n n n
4 3
2 1 3 1 2 4
+ +
- - + - - +
=
=
( )( )
( )
n n
n n n n n n
4 3
2 6 3 4 2 8
2 2
+ +
- - - - - + - -
=
=
( )( )
n n
4 3
7
+ +
-
0, 6n ! IN
Logo, (un) é decrescente.
8.2
Como (un) é decrescente, tem-se que
u1 =
1 3
1 2
+
-
= -
4
1
é um majorante de (un) .
Como
un =
n
n
1 2
3
-
+
=
n
n
3
2 1
+
- +
=
( )
n
n
3
2 3 7
+
- + +
= -2 +
n 3
7
0
+
2
,
tem-se 6n ! IN, un -2 , ou seja, -2 é um minorante de (un) .
Portanto, tem-se
6n ! IN, -2 un G -
1
4
,
ou seja, (un) é limitada.
8.3
qun + 2u 0,01 +
n
n
3
1 2
2
+
-
+ 0,01 +
+
n
n n
3
1 2 2 6
+
- + +
0,01 +
n 3
7
+
0,01 +
+ 7 0,01(n + 3) + 700 n + 3 + n 697
Logo, há infinitos termos de (un) que pertencem a esta vizinhança.
000707 296-327 U11.indd 322 01/07/16 12:49

81. 323
Domínio 3 SUCESSÕES
11
UNIDADE
8.4 Dado d 0 , qun + 2u d +
n
n
3
1 2
2
+
-
+ d +
+
n
n n
3
1 2 2 6
+
- + +
d +
n 3
7
+
d + 7 d(n + 3) +
+
7
d
n + 3 + n
7
d
- 3
Assim, basta tomar o primeiro natural superior a
7
d
- 3 , e tem-se que
todos os termos seguintes pertencem à vizinhança de -2 de raio d .
Conclui-se, assim, que un -2 .
9
Recorrendo à definição de limite, prove que:
a)
n
n
1
2
2
+
1 b)
n
n
2 1
3 1
2
3
+
-
- 0 c)
n
n n
2
2
-
+ 1 0
a) Dado d 0 ,
n
n
1
1
2
2
+
- d +
n
n n
1
2
2 2
+ -
d +
n
1
2
d +
+ 1 dn2
+
1
d
n2
.
Como n é positivo, obtém-se n
1
d
. Assim, basta tomar o primeiro
natural superior a
1
d
e tem-se que todos os termos seguintes pertencem
à vizinhança de 1 de raio d . Conclui-se, assim, que
n
n
1
2
2
+
1 .
b) Dado d 0 ,
n
n
2 1
3 1
2
3
0
+
-
- - d +
n
n n
4 2
6 2 6 3
+
- - -
d +
+
n
4 2
5
+
-
d + 5 d(4n + 2) +
5
d
4n + 2 + n
4
5 2
d
d
-
.
Assim, basta tomar o primeiro natural superior a
4
5 2
d
d
-
, e tem-se que
todos os termos seguintes pertencem à vizinhança de 0 de raio d .
Conclui-se, assim, que
n
n
2 1
3 1
2
3
+
-
- 0 .
c) Dado d 0 ,
n
n n
1 0
2
2
-
+ - d +
n
n n n
2
2 2
- +
d +
+
n
n
2
d + n
1
d + 1 dn + n
1
d
. Assim, basta tomar o primeiro
natural superior a
1
d
, e tem-se que todos os termos seguintes pertencem
à vizinhança de 0 de raio d . Conclui-se, assim, que
n
n n
2
2
-
+ 1 0 .
000707 296-327 U11.indd 323 01/07/16 12:49

82. 324
Limites de sucessões
10
Seja (vn) uma sucessão, com todos os termos positivos, em que se sabe que:
v
v
n
n 1
+
1, 6n ! IN
Justifique que:
a) (vn) é convergente.
b) wn 0 , sendo (wn) definida por wn = n
vn
.
a) v
v
n
n 1
+
1
v 0
n
+
2
vn + 1 vn + vn + 1 - vn 0, 6n ! IN
Logo, (vn) é decrescente. Então, como (vn) é uma sucessão com todos
os termos positivos, 0 é um minorante de (vn) . Como toda a sucessão
decrescente e minorada é convergente, (vn) é convergente.
b)
A sucessão (wn) é o produto de uma sucessão que tende para zero, n
1
,
por uma sucessão limitada, (vn) ; logo, wn 0 .
Alternativamente:
Dado d 0 , qwnu d + n
vn
d + n
vn
d + vn nd + n
vn
d
.
Como v1 é um majorante de (vn) , v1 vn, 6n ! IN . Assim, basta tomar
o primeiro natural superior a
v1
d
, e tem-se que todos os termos seguintes
pertencem à vizinhança de 0 de raio d . Conclui-se, assim, que wn 0 .
11
Considere as sucessões (an) e (bn) definidas, respetivamente, por:
an = n2
- 4 e bn = 2 - n
11.1
Determine a menor ordem p ! IN , tal que n H p an bn + 24 .
11.2
Prove, recorrendo à definição de limite, que:
a)
an +3 b)
a
b
n
n
0
11.1 an bn + 24 + n2
- 4 2 - n + 24 + n2
+ n - 30 0
n2
+ n - 30 = 0 + n =
2
1 1 4 30
! #
- +
+
+ n =
2
1 11
!
-
+ n = -6 0 n = 5
Logo:
n2
+ n - 30 0 + n -6 0 n 5 + n 5
Assim, p = 6 .
n ! IN
000707 296-327 U11.indd 324 01/07/16 12:49

83. 325
Domínio 3 SUCESSÕES
11
UNIDADE
11.2 a) Seja L 0 . Então, an L + n2
- 4 L + n2
L + 4 .
Assim, basta considerar p = L 4
+
7 A + 1 , e tem-se todos os termos
seguintes superiores a L . Conclui-se, assim, que an +3 .
b) Seja d 0 . Então:
a
b
n
n
d +
n
n
4
2
2
-
-
d +
( )( )
n n
n
2 2
2
- +
-
d +
+
n 2
1
+
-
d + 1 d(n + 2) + n
1
d
- 2
Assim, basta tomar o primeiro natural superior a
1
d
- 2 e tem-se que
todos os termos seguintes pertencem à vizinhança de 0 de raio d .
Conclui-se, assim, que a
b
n
n
0 .
12
Considere três sucessões (un) , (vn) e (wn) tais que:
• limun = -1
• limvn = +3
• limwn = 0-
Determine:
a) lim(3un - wn) b) lim(unvn) c) lim v
w
n
n
a) lim(3un - wn) = 3 limun - limwn = -3 - 0-
= -3
b) lim(unvn) = limun × limvn = -1 × (+3) = -3
c) lim v
w
n
n
=
lim
lim
v
w 0
n
n
3
=
+
-
= 0-
13
Calcule o limite das sucessões cujo termo geral se indica, identificando
as indeterminações encontradas:
a)
an =
n
n
3 1
2
+
+
b)
bn =
n
n
3
2
2
+
+
c)
cn =
n
n
5
1 4
4
+
-
d)
dn = n 2
+ - n
e)
en =
3 2
2 1
n
n 1
-
+
+
f)
fn = (3n
- 4) × 2-2n
000707 296-327 U11.indd 325 01/07/16 12:49

84. 326
Limites de sucessões
a) liman = lim
n
n
3 1
2
+
+
=
3
1
aIndeterminação 3
3 k
b) limbn = lim
n
n
3
2
2
+
+
= lim
n n
n
n
3
1
1
2
2
2
+
+
c
d
m
n
= lim n
n
n
1
3
1
2
2
+
+
H= +3
aIndeterminação 3
3 k
c) limcn = lim
n
n
5
1 4
4
+
-
= lim
n
n
n n
1
5
1
4
2
4
+
-
c m
=
= lim n
n
n
1
1
5
1
4
4
#
+
-
H= 0
aIndeterminação 3
3 k
d) limdn = lim n n
2
+ -
_ i = lim
n n
n n n n
2
2 2
+ +
+ - + +
_ _
i i
=
= lim
n
n n
n
2
2
+
+ -
+
=
2
3
+
= 0
^Indeterminação +3 + (-3) h
e) limen = lim
3 2
2 1
n
n 1
-
+
+
= lim
2
2
3
1
2 2
2
1
n
n
n
n
-
+
d
d
n
n
= lim
2
3
1
2
2
1
n
n
-
+
=
=
1
2
-
= -2
aIndeterminação 3
3 k
f) limfn = lim^(3n
- 4) × 2-2n
h = lim
2
3 4
n
n
2
-
= lim
4
3 4
n
n
-
=
= lim
4
1
4
3
3
n
n
n
-
d n
= lim
4
3 3
4
1
1
n n
#
-
c m
H= 0
aIndeterminação 3 × 0 k
000707 296-327 U11.indd 326 01/07/16 12:49

85. 327
Domínio 3 SUCESSÕES
11
UNIDADE
14
Dada a sucessão (vn) , definida por:
v
v
v
2
2
1
n
n
1
1
=
=
+
+
*
, 6n ! IN
14.1
Prove, recorrendo ao princípio de indução matemática, que (vn) é monótona
decrescente.
14.2
Justifique que todos os termos de (vn) são positivos e conclua que (vn)
é convergente.
14.3
Determine limvn .
14.1 Pretende-se provar que:
6n ! IN, vn + 1 vn
Para n = 1 , tem-se v2 =
v
2
1 1
+
=
2
3
2 = v1 , que é verdade.
Hipótese: Para um certo n ! IN, vn + 1 vn .
Tese: vn + 2 vn + 1
Demonstração:
vn + 2 =
v
2
1 n 1
+ +
Por hipótese, obtém-se:
vn + 2
v
2
1 n
+
= vn + 1
Assim, pelo princípio de indução matemática, 6n ! IN, vn + 1 vn ,
ou seja, (vn) é decrescente.
14.2
Cada termo de (vn) obtém-se a partir do anterior somando uma constante
positiva e dividindo por uma constante positiva.
Assim, como o primeiro termo de (vn) é positivo, todos os termos
de (vn) serão positivos. Então, 0 é um minorante de (vn) .
Como (vn) é decrescente e minorada, é também convergente.
14.3 limvn = lim
lim
v v
2
1
2
1
n n
1 1
+
=
+
- -
Mas limvn = limvn - 1 , que existe por 14.2.
Logo:
limvn =
lim v
2
1 n
+
+ 2 limvn = 1 + limvn + limvn = 1
000707 296-327 U11.indd 327 01/07/16 12:49

86. 328
Avaliação global de conhecimentos
AVALIAÇÃO GLOBAL DE CONHECIMENTOS
ESCOLHA MÚLTIPLA
Para cada uma das questões desta secção, selecione a opção correta de entre
as alternativas que lhe são apresentadas.
1
Considere a sucessão (un) em que se sabe os cinco primeiros termos:
3, 10, 17, 24, 31, …
Sabendo que se mantém a lei de formação, qual é o valor de u20 ?
(A) 129 (B) 136 (C) 139 (D) 143
un = 3 + 7(n - 1) e u20 = 3 + 19 × 7 = 136
A opção correta é a (B).
2
Considere as sucessões (an) , (bn) , (cn) e (dn) definidas, respetivamente, por:
an =
n
n
2 9
3
-
-
; bn = n2
- 5n + 5 ; cn =
( )
n
2 3
1 n
-
-
e dn = -4 ×
2
1 n
c m
2.1
Indique qual das sucessões não tem -1 como termo.
(A) (an) (B) (bn) (C) (cn) (D) (dn)
2.2 Qual das sucessões é monótona?
(A) (an) (B) (bn) (C) (cn) (D) (dn)
2.1
( )
n
2 3
1 n
-
-
= -1 + (-1)n
= -2n + 3
Se n for par, obtém-se 1 = -2n + 3 + n = 1 , que é um absurdo.
Se n for ímpar, obtém-se -1 = -2n + 3 + n = 2 , que é um absurdo.
A opção correta é a (C).
2.2 A opção correta é a (D).
3
Seja (xn) a sucessão em que se sabe que:
6n ! IN, xn + 1 - xn = (-1)n
O termo geral da sucessão (xn) pode ser dado por:
(A) n + 1 (B) -n + 2 (C)
( )
2
1 n 1
- +
+ 1 (D)
( )
2
1 n
-
+ 2
( )
2
1 n 2
- +
+ 1 -
( )
2
1
1
n 1
-
+
+
= G =
( ) ( )
2
1 1
n n
2 2
- + -
+ +
= (-1)n
A opção correta é a (C).
000707 328-351.indd 328 01/07/16 13:41

87. 329
Domínio 3 SUCESSÕES
4
Considere a sucessão (vn) definida por:
vn =
n n
n n
3 1
3 2
se par
se ímpar
+
-
*
Indique qual das seguintes afirmações é verdadeira.
(A) (vn) é monótona e limitada.
(B) (vn) é monótona e não limitada.
(C) (vn) é limitada e não monótona.
(D) (vn) é não monótona e não limitada.
A sucessão (vn) não é limitada, pois lim(3n + 1) = +3 e lim(3n - 2) = -3 .
Para verificar a monotonia:
• Se n for par, então, vn + 1 - vn = 3(n + 1) - 2 - (3n + 1) = 0 .
• Se n for ímpar, então, vn + 1 - vn = 3(n + 1) + 1 - (3n - 2) = 6 0 .
Portanto, (vn) é monótona crescente em sentido lato.
A opção correta é a (B).
5
A pilha de cartas da figura ao lado tem três andares.
Indique o número de cartas da base de uma pilha e o
número total de cartas utilizado na construção da pilha,
supondo que tem 6 andares e se mantém o mesmo
processo de empilhamento, respetivamente:
(A) 12 e 60
(B) 18 e 63
(C) 12 e 57
(D) 15 e 45
A sucessão do número de cartas da base tem termo geral an = 2n ,
em que n representa o número de cartas da pilha.
Assim, a6 = 12 é o número de cartas da base e o total de cartas é igual a
3 + 6 + 9 + 12 + 15 + 12 = 57 .
A opção correta é a (C).
6
Considere um triângulo em que os comprimentos dos seus lados estão
em progressão aritmética de razão 2 . Sabendo que o cosseno do maior
ângulo do triângulo é -
4
1
, qual é o perímetro desse triângulo?
(A) 12 (B) 15 (C) 18 (D) 21
000707 328-351.indd 329 01/07/16 13:41

88. 330
Avaliação global de conhecimentos
Sabe-se que o maior ângulo é oposto ao maior lado. Seja x o comprimento
de menor lado.
Pelo teorema de Carnot:
c2
= a2
+ b2
- 2ab cosC
W +
+ (x + 4)2
= (x + 2)2
+ x2
- 2(x + 2)x
4
1
-
c m +
+ x2
+ 8x + 16 = x2
+ 4x + 4 + x2
+
x x
2
2
2
+
+
+ 8x + 24 = 2x2
+ x2
+ 2x + -3x2
+ 6x + 24 = 0 +
+ x =
6
6 36 4 3 24
! # #
-
- +
+ x =
6
6 18
!
-
-
+
+ x = 4 0 x = -2
x 0
+
2
x = 4
Assim, P9 = x + x + 2 + x + 4 = 18 .
A opção correta é a (C).
7
Numa ilha isolada do Pacífico sul, foi efetuado
o registo parcial das distâncias percorridas por
uma tartaruga.
Verificou-se que esta percorreu 40 metros no
1.º dia de registo e a cada dia que passava percorria
mais 5 metros do que no dia anterior.
Ficou igualmente registado que a tartaruga percorreu 13 quilómetros durante
todo o tempo da experiência.
Quantos dias decorreram entre o 1.o
dia e o último dia de registo?
(A) 55 (B) 60 (C) 65 (D) 70
Seja (an) a sucessão que representa o número de metros percorridos no n-ésimo
dia. Então, (an) é uma progressão aritmética de razão 5 e de primeiro termo
40 e, por isso, o seu termo geral pode ser an = 40 + 5(n - 1) = 5n + 35 .
Assim:
Sn =
a a
2
n
1 +
× n + 13 000 =
n
2
40 5 35
+ +
× n +
+ 26 000 = 5n2
+ 75n + 5n2
+ 75n - 26 000 = 0 +
+ n2
+ 15n - 5200 = 0 +n =
2
15 225 4 5200
! #
- +
+
+ n =
2
15 21 025
!
-
+ n = 65
A opção correta é a (C).
n ! IN
000707 328-351.indd 330 01/07/16 13:41

89. 331
Domínio 3 SUCESSÕES
8
Seja (vn) a sucessão das áreas dos
quadrados representados na figura.
O primeiro quadrado tem lado 3
e o lado de cada quadrado seguinte é
metade do lado do quadrado anterior.
8.1 O termo geral da sucessão é:
(A)
n
2
9
(B)
n
3
(C)
2
9
n
2 2
-
(D)
2
9
n 2
-
8.2 A soma das áreas dos dez primeiros quadrados é:
(A)
4
9
9
(B) 6 -
2
3
9
(C) 12 -
4
3
9
(D) 18 -
9
29
8.1
A sucessão (vn) é uma progressão geométrica com v1 = 9 e razão
4
1
;
logo, vn = 9 ×
4
1 n 1
-
c m =
4
9
n 1
-
= n 1
-
( )
2
9
2
=
9
2 n
2 2
-
.
A opção correta é a (C).
8.2 S10 = 9 ×
1
4
1
1
4
1 10
-
-c m
= 12 × 1
4
1 10
-c
e m o= 12 - 12
4
1 10
c m = 12 - 3
4
1 9
c m
A opção correta é a (C).
9
Considere as sucessões (an) e (bn) definidas, respetivamente, por:
an =
n
n
1 2
2 1
-
+
e bn =
n
n
2
2
+
-
Sabendo que A = lim an e B = limbn , tem-se que:
(A) A = 2B (B) A = B (C) A = -B (D) A = B + 1
A = -1 e B = 1
A opção correta é a (C).
10
O valor de lim
n
cos
n
n
2
é:
(A) 0 (B) 1 (C) -1 (D) +3
A sucessão cosn é limitada e lim
n
1
2
= 0 ; logo, lim
n
cos
n
n
2
= 0 .
A opção correta é a (A).
u3p77h2
000707 328-351.indd 331 01/07/16 13:41

90. 332
Avaliação global de conhecimentos
11
Dada uma sucessão (un) em que lim
n
(un) = +3 , indique qual das seguintes
afirmações é necessariamente verdadeira.
(A) (un) é monótona.
(B) (un) é limitada inferiormente.
(C) (un) é limitada superiormente.
(D) (un) tem todos os termos positivos.
Por definição, existe p ! IN , tal que un H 1 sempre que n H p .
Então, un é limitada inferiormente pelo mínimo de {u1, …, up - 1, 1} .
A opção correta é a (B).
RESPOSTA ABERTA
Nas questões desta secção, apresente o seu raciocínio de forma clara, indicando todos
os cálculos que tiver de efetuar e as justificações necessárias.
12
Considere a sucessão de termo geral un =
n
n
2
3 1
+
-
.
12.1
Verifique se 2,8 é termo da sucessão (un) .
12.2
Mostre que (un) é monótona.
12.3
Mostre que (un) é limitada e indique um minorante e um majorante
do conjunto dos seus termos.
12.4
Justifique que (un) é convergente.
12.5
Mostre, recorrendo à definição de sucessão convergente, que lim
n
un = 3 .
12.1
un = 2,8 +
n
n
2
3 1
+
-
= 2,8 + 3n - 1 = 2,8n + 5,6 +
+ 0,2n = 6,6 + n = 33 ! IN
Logo, 2,8 é termo da sucessão (un) .
12.2
un + 1 - un =
( )
n
n
n
n
3
3 1 1
2
3 1
+
+ -
-
+
-
=
=
( )( )
( )( ) ( )( )
n n
n n n n
3 2
3 2 2 3 1 3
+ +
+ + - - +
=
=
( )( )
( )
n n
n n n n n n
3 2
3 6 2 4 3 9 3
2 2
+ +
+ + + - + - -
=
=
( )( )
n n
3 2
7
+ +
0, 6n ! IN
Logo, (un) é monótona.
000707 328-351.indd 332 01/07/16 13:41

91. 333
Domínio 3 SUCESSÕES
12.3
Tem-se que 3n - 1 0, 6n ! IN ; logo, un 0, 6n ! IN e, assim,
0 é um minorante de (un) . Tem-se, também, que:
( )
n
n
n
n
n
n
2
3 1
2
3 6
2
3 2
1
+
-
+
+
=
+
+
= 3, 6n ! IN
Logo, 3 é um majorante de (un) e, portanto, (un) é limitada.
12.4
Pelas alíneas anteriores, (un) é monótona e limitada; logo, é também
convergente.
12.5 Dado d 0 , tem-se:
qun - 3| d +
n
n
2
3 1
3
+
-
- d +
n
n n
2
3 1 3 6
+
- - -
d +
+
n 2
7
+
-
d + 7 d(n + 2) +
7
d
n + 2 + n
7
d
- 2
Assim, basta tomar para ordem p o primeiro natural superior a
7
d
- 2 ,
e tem-se que, para n H p , un pertence à vizinhança de 3 de raio d .
Conclui-se, assim, que limun = 3 .
13
Um auditório tem 14 cadeiras na primeira
fila, 18 na segunda, 22 na terceira,
e assim sucessivamente.
13.1
Calcule o número de cadeiras
na décima segunda fila.
13.2
O auditório tem 15 filas. Determine a sua lotação máxima.
13.1
Seja (un) a sucessão do número de cadeiras em cada fila. A sucessão
(un) é uma progressão aritmética de termo geral un = u1 + r(n - 1) ,
em que u1 = 4 e r = 4 . Logo, u12 = 14 + 4 × (12 - 1) = 58 cadeiras.
13.2
S15 =
u u
2
1 15
+
× 15 =
2
14 14 4 14
#
+ +
= 630 lugares
14
Calcule a soma dos 25 primeiros termos de uma progressão aritmética (wn)
sabendo que w2 + w4 = 28 e w5 + w7 = 52 .
Sabe-se que wn = w1 + r(n - 1) . Então:
w w
w w
28
52
2 4
5 7
+ =
+ =
* +
w r w r
w r w r
3 28
4 6 52
1 1
1 1
+ + + =
+ + + =
* +
w r
r r
14 2
28 4 10 52
1 = -
- + =
) +
+
w r
r
14 2
4
1 = -
=
) +
w
r 4
6
1 =
=
)
Assim, S25 =
w w
2
1 15
+
× 25 =
2
4 24
6 6 #
+
+
× 25 = 1350 .
000707 328-351.indd 333 01/07/16 13:41

92. 334
Avaliação global de conhecimentos
15
Um carpinteiro pretende construir uma estante para livros
como a representada na figura ao lado.
Os comprimentos das prateleiras são decrescentes e estão
em progressão aritmética.
A primeira prateleira mede 1 metro e a última mede 60 cm .
Determine o número de prateleiras da estante sabendo que o carpinteiro gastou
exatamente 5,6 metros lineares de madeira nas prateleiras.
Seja (un) a sucessão do comprimento, em centímetros, de cada prateleira. Então:
Sn =
u u
2
n
1 +
× n + 560 =
2
100 60
+
× n +
80
560
= n + n = 7 prateleiras
16
Prove que a soma de duas progressões aritméticas é ainda uma progressão
aritmética de razão igual à soma das razões das progressões iniciais.
Caderno de Apoio do 11.º ano
Sejam (un) e (vn) duas progressões aritméticas de razão r e r' , respetivamente.
Tem-se que:
un + vn = ^u1 + (n - 1)rh + ^v1 + (n - 1)r'h = (u1 + v1) + (n - 1)(r + r') ,
que é o termo geral de uma progressão aritmética de razão r + r' e de primeiro
termo u1 + v1 .
17
O número de sócios de um clube de ténis,
fundado em 2001, pode ser modelado por
uma progressão geométrica.
Devido a um problema no programa informático
que registava o número de sócios, perderam-se
os registos relativos aos anos iniciais do clube.
No entanto, sabe-se o número de sócios
relativamente aos anos de 2013, 2014 e 2015,
os quais constam na tabela ao lado.
17.1
Determine qual o valor da razão da progressão
geométrica que determina o número de sócios
existentes em cada ano e conclua que o número
de sócios aumenta 20 % a cada ano que passa.
17.2 Determine:
a)
quantos sócios fundaram o clube.
b)
qual é o número de sócios previstos para o ano 2025.
Ano N.o
de sócios
2013 500
2014 600
2015 720
000707 328-351.indd 334 01/07/16 13:41

93. 335
Domínio 3 SUCESSÕES
17.1
Seja (un) a progressão geométrica do número de sócios do clube
em cada ano, com razão r . Então:
r = u
u
500
600
13
14
= = 1,2
Logo, o número de sócios em cada ano é mais 20 % do que no ano anterior.
17.2 a) u13 = u1 × 1,212
+ 500 = u1 × 1,212
+ u1 á 56,0783
O clube foi fundado por 57 sócios.
b) Utilizando o valor de u13 , dado no enunciado:
u25 = u13 × 1,212
á 4458,0502
No ano de 2025, prevê-se ter 4459 sócios.
18
Os três primeiros termos de uma progressão geométrica são dados, para um
determinado valor de x , respetivamente, por x - 2 , x + 1 e x + 7 .
Determine o termo geral dessa sucessão.
Adaptado do Caderno de Apoio do 11.º ano
x
x
x
x
1
7
2
1
+
+
=
-
+
+ (x + 7)(x - 2) = (x + 1)2
+
+ x2
- 2x + 7x - 14 = x2
+ 2x + 1 + 3x - 15 = 0 + x = 5
Assim, a razão da sucessão é
5 1
5 7
+
+
= 2 e o primeiro termo é 5 - 2 = 3 .
Logo, um termo geral dessa sucessão será un = 3 × 2n - 1
.
19
Seja (un) uma sucessão monótona crescente e de termos todos positivos.
Considere a sucessão (vn) definida por vn = u
1
n
.
19.1
Justifique que (vn) é convergente.
19.2
Sabendo que lim(un) = 2 , determine o valor de:
a) limvn
b) lim[vn × (vn - 2)]
c) lim
u 2
1
n-
19.1
Tem-se que vn + 1 = u u
1 1
n n
1
1
+
= vn, 6n ! IN porque un + 1 un .
Logo, (vn) é decrescente. Como (un) é positiva, (vn) também é positiva.
Assim, 0 é um minorante de (vn) . Como (vn) é decrescente e minorada,
é também convergente.
000707 328-351.indd 335 01/07/16 13:41

94. 336
Avaliação global de conhecimentos
19.2 a) limvn = lim u
1
n
=
lim u
1
n
=
2
1
b) lim6vn × (vn - 2)@ = limvn × lim(vn - 2) =
=
2
1
×
2
1
2
-
c m = -
4
3
c) lim
u 2
1
n -
=
( )
lim u 2
1
n -
=
0
1
- = -3
Observe-se que (un) é crescente; logo:
un 2 un - 2 0 e un 2
20
Considere as sucessões:
un =
n
n
1
2 1
+
-
; vn = 2n3
- 10 ; wn =
n
3 2
4
3
-
e xn = 4 - n 3
+
20.1
Prove, utilizando a definição de limite, que:
a) un 2 b) vn +3 c) wn 0 d) xn -3
20.2
Determine a ordem p a partir da qual se tem:
a) u 2
n- 0,01 b) wn ! V0,1(0)
20.3 Calcule:
a) lim(unwn) b) lim(vnwn) c) lim
n
xn
20.1 a) Dado d 0 , tem-se:
qun - 2u d +
n
n
1
2 1
2
+
-
- d +
+
n
n n
1
2 1 2 2
+
- - -
d +
n
1
3
+
-
d + 3 d(1 + n) +
+
3
d
1 + n + n
3
d
- 1
Assim, basta tomar para p ! IN o primeiro natural superior a
3
d
- 1 ,
e tem-se que, para n H p , un pertence à vizinhança de 2 de raio d .
Conclui-se, assim, que un 2 .
b) Dado L 0 , tem-se:
vn L + 2n3
- 10 L + n3
L
2
10
+
+ n
L
2
10
3 +
Assim, basta tomar para p ! IN o primeiro natural superior
a
L
2
10
3 +
, e tem-se todos os termos seguintes superiores a L .
Conclui-se, assim, que vn +3 .
000707 328-351.indd 336 01/07/16 13:41

95. 337
Domínio 3 SUCESSÕES
c) Dado d 0 , tem-se:
qwnu d +
n
3 2
4
3
-
d +
n
3 2
4
3
-
d +
+ 4 d(3n3
- 2) +
4
d
3n3
- 2 +
3
4
d
+
3
2
n3
+
+ n
3
4
3
2
3
d
+
Assim, basta tomar para p ! IN o primeiro natural superior
a
3
4
3
2
3
d
+ e tem-se que, para n H p , wn pertence à vizinhança
d de 0 .
Conclui-se, assim, que wn 0 .
d) Dado L 0 , tem-se:
xn -L + -xn L + -4 + n 3
+ L + n 3
+ L + 4
n + 3 L2
+ 8L + 16 + n L2
+ 8L + 13
Assim, basta tomar para p ! IN o primeiro natural superior a
L2
+ 8L + 13 , e tem-se todos os termos seguintes menores que -L .
Conclui-se, assim, que xn -3 .
20.2 a) qun - 2u 0,01 +
n
n
1
2 1
2
+
-
- 0,01 +
n
1
3
+
-
0,01 +
+ 3 0,01 + 0,01n +
,
,
0 01
2 99
n + n 299
Logo, p = 300 .
b) wn ! V0,1(0) + qwnu 0,1 +
n
3 2
4
3
-
0,1 + 4 0,3n3
- 0,2 +
+
,
,
0 3
4 2
n3
+ 14
3
n
Logo, p = 3 .
20.3 a) lim(unwn) = 2 × 0 = 0
b) lim(vnwn) = lim ( )
n
n
2 10
3 2
4
3
3
-
-
F = lim
n
n
3 2
8 40
3
3
-
-
=
= lim
n
n
n
n
3
2
8
40
3
3
3
3
-
-
d
d
n
n
= lim
n
n
3
2
8
40
3
3
-
-
=
3
8
c) lim
n
xn
= lim
n
n
4 3
- +
= lim
n n
4
1
3
+
-
f p = -1
000707 328-351.indd 337 01/07/16 13:41

96. 338
Avaliação global de conhecimentos
21
Considere a sucessão definida por:
an = 5 -
n
2
1 4
-
21.1
Mostre que (an) é uma progressão aritmética e indique a razão.
21.2
A sucessão é limitada? Justifique a sua resposta.
21.3
Prove, usando a definição de limite, que an +3 .
21.4
Calcule o valor de a20 + a21 + … + a30 .
21.5 Determine:
a) lim(an)2
b) lim n
a a
n n
2 -
21.1 an + 1 - an = 5 -
( )
n
2
1 4 1
- +
-
n
5
2
1 4
-
-
c m =
= -
n
2
1 4 4
- -
+
n
2
1 4
-
= 2
Logo, (an) é uma progressão aritmética de razão 2 .
21.2
A sucessão não é limitada porque é uma progressão aritmética de razão
diferente de zero.
21.3 Dado L 0 , tem-se:
an L + 5 -
n
2
1 4
-
L +
n
2
1 4
-
-L + 5 +
+ -4n -2L + 9 + n
L
4
2 9
-
Assim, basta tomar para p ! IN o primeiro natural superior
a
L
4
2 9
-
, e tem-se todos os termos seguintes superiores a L .
Conclui-se, assim, que an +3 .
21.4 a20 + a21 + … + a30 =
a a
2
20 30
+
× 11 =
=
2
5
2
1 4 20
5
2
1 4 30
# #
-
-
+ -
-
× 11 =
=
2
10
2
79
2
119
+ +
× 11 =
2
10
2
79
2
119
+ +
× 11 = 599,5
21.5 a) lim(an)2
= (+3)2
= +3
b) lim n
a a
n n
2 -
= lim n
n n
5
2
1 8
5
2
1 4
-
-
- -
-
c m
=
= lim
n
n n
2
1 8 1 4
- + + -
= lim
n
n
2
4
= 2
000707 328-351.indd 338 01/07/16 13:42

97. 339
Domínio 3 SUCESSÕES
22
Considere a sucessão:
bn = (-1)n
- n
22.1
Justifique que a sucessão (bn) é não monótona.
22.2
Prove, utilizando a definição de limite, que bn - 3 .
22.3 Calcule:
a) lim(bn)2
b) lim
b
b
n
n 1
+
22.1
Tem-se que b1 = -2 , b2 = -1 e b3 = -4 . Logo, b1 b2
e b2 b3 . Portanto, (bn) é não monótona.
22.2
Tem-se que (-1)n
- n G 1 - n . Assim, dado L 0 , 1 - n -L +
+nL+1 . Logo, tomando pHL+1 natural, vem nHpun -L .
Portanto, bn -3 .
22.3 a) lim(bn)2
= (-3)2
= +3
b) lim
b
b
n
n 1
+
= lim
( )
( )
n
n
1
1 1
n
n 1
- +
- + +
+
=
= lim
( )
( )
n n
n n n
1
1
1
1
1
n
n 1
-
+
-
+ +
+
d
d
n
n
=
0 1
0 1 0
+
+ +
= 1
23
Calcule o limite das sucessões cujo termo geral se indica, identificando
as indeterminações encontradas:
a) an =
n
n
1 2
3 1
-
-
b) bn =
n
n
3
2
2
+
+
c) cn =
n n
n n
1
2
2
3
+ +
+
d) dn =
n
n
2
4 1
+
+
e) en =
n
n
5
1 4
2
+
-
f) fn =
n n
n
1
3
2
+ +
+
g) gn = n n
2
2
+ -
h) hn =
1 3
3 4
n
n
1
-
-
+
i) in = 3n
- 4 × 22n
j) jn =
sin
n
n n
2
2
+
-
k) kn = 4-n
(3n
- 2)
l) ln =
cos
n n
n n
n
2 3
2
2
2
-
+
000707 328-351.indd 339 01/07/16 13:42

98. 340
Avaliação global de conhecimentos
a) liman = lim
n
n
1 2
3 1
-
-
= lim
n n
n n
1
2
3
1
-
-
c
c
m
m
= -
2
3
aIndeterminação 3
3 k
b) limbn = lim
n
n
3
2
2
+
+
= lim
n n
n
n
3
1
1
2
2
2
+
+
c
d
m
n
= lim
n
n
3
1
1
2
2
+
+
H= limn = +3
aIndeterminação 3
3 k
c) limcn =lim
n n
n n
1
2
2
3
+ +
+
=lim
n n n
n
n
1
1 1
1
2
2
2
3
2
+ +
+
d
d
n
n
= lim
n
n
2
3
= limn = +3
aIndeterminação 3
3 k
d) limdn = lim
n
n
2
4 1
+
+
= lim
n n
n n
2
1
4
1
+
+
c
c
m
m
=
1
4
= 2
aIndeterminação 3
3 k
e) limen = lim
n
n
5
1 4
2
+
-
= lim
n
n
n n
1
5
1
4
2
+
-
c m
=
1
4
-
= -4
aIndeterminação 3
3 k
f) limfn = lim
n n
n
1
3
2
+ +
+
= lim
n n
n n
n
1
1
1
1
1
2
+
+ +
e
c
o
m
=
=
0
1
1 0
+ +
= 1 aIndeterminação 3
3 k
g) limgn = lim n n
2
+ -
_ i = lim
n n
n n n n
2
2 2
+ +
+ - + +
_ _
i i
=
= lim
n
n n
n
2
2
+
+ -
+
=
2
3 3
+ +
= 0 ^Indeterminação +3+ (-3) h
h) limhn = lim
1 3
3 4
n
n
1
-
-
+
= lim
3
3
1
3
3 1
3
4
n
n
n
n
-
-
d
d
n
n
=
3
1
-
= -
3
1
aIndeterminação 3
3 k
i) limin = lim(3n
- 4 × 22n
) = lim(3n
- 4n + 1
) = lim 4
4
3
4
n
n
-
c
e m o
H =
= +3(0 - 4) = -3 ^Indeterminação +3 + (-3) h
000707 328-351.indd 340 01/07/16 13:42

99. 341
Domínio 3 SUCESSÕES
j) limjn = lim
sin
n
n n
2
2
+
-
= lim
sin
n
n
n
n
2 2
2 2
+
-
+
d n =
= lim sin
n
n
n
n
1
2
1
2
1
2
2
#
+
-
+
f p
Tem-se que lim
n
n
1
2
1
2
+
=
1
0
= 0 , lim
n 2
1
2
+
= 0 e sinn é limitada.
Logo:
lim sin
n
n
n
n
1
2
1
2
1
2
2
#
+
-
+
f p= 0 - 0 = 0
aIndeterminação 3
3 k
k) limkn = lim^4-n
(3n
- 2)h = lim
4
3 2
n
n
-
= lim
4
3
4
2
n
n
n
-
d n =
= lim
4
3
4
2
n
n
-
c m
= G = 0 -
2
3
+
= 0 (Indeterminação 0 × 3)
l) limln = lim
cos
n n
n n
n
2 3
2
2
2
-
+
= lim
cos
n
n
n
n n
2 3
2
2
2
-
+
=
= lim
cos
n
n n
2 3
2
-
+
= lim
cos
n
n
n
n
2 3
2
2 3
-
+
-
d n =
= lim cos
n
n
n
2
3
2
2 3
1
#
-
+
-
f p
Tem-se que lim
n
2
3
2
-
= -
3
2
, lim
n
2 3
1
-
= 0 e cosn é limitada.
Logo:
lim cos
n
n
n
2
3
2
2 3
1
#
-
+
-
f p = -
3
2
+ 0 = -
3
2
aIndeterminação
0
0
k
000707 328-351.indd 341 01/07/16 13:42

100. 342
Avaliação global de conhecimentos
24
Considere a sucessão (un) cujos primeiros termos são:
2, 20, 200, …
24.1
Escreva o termo geral de (un) admitindo que se trata de uma progressão
geométrica.
24.2
Justifique que un +3 .
24.3
Determine a soma:
20 000 + 200 000 + … + 20 000 000 000
24.1 Como
0
2
200
= 10 , (un) é uma progressão geométrica de razão 10
e de 1.o
termo 2 . Portanto, tem-se un = 2 × 10n - 1
.
24.2
Como (un) é uma progressão geométrica de primeiro termo positivo
e de razão maior do que 1 , un +3 .
24.3 2 × 104
+ 2 × 105
+ … + 2 × 1010
= u5 + u6 + … + u11 =
= 2 × 104
×
1 10
1 107
-
-
= 22 222 220 000
25
Em janeiro de 2010 o André decidiu começar
uma poupança, depositando no banco
1000 euros. No mês seguinte pôs menos
10 % do que tinha posto no mês anterior
e assim sucessivamente.
25.1
Justifique que o dinheiro que o André
deposita no banco, em cada mês,
é dado pela sucessão (bn) definida por:
,
b
b b
1000
0 9
n n
1
1 #
=
=
+
*
, 6n ! IN
25.2
Determine um termo geral de (bn) e indique o dinheiro que foi colocado
no banco em março de 2012.
25.3 Para p ! IN , determine uma expressão algébrica para a soma Sp
dos p primeiros termos desta sucessão.
25.4
Determine limSn e interprete o valor obtido no contexto da situação
apresentada.
000707 328-351.indd 342 01/07/16 13:42

101. 343
Domínio 3 SUCESSÕES
25.1
O primeiro depósito é de 1000 € ; logo, b1 = 1000 .
Como em cada mês o André deposita menos 10 % do que no mês
anterior, significa que deposita 90 % do que depositou no mês anterior.
Portanto:
bn + 1 = 0,9 × bn, 6n ! IN
25.2
A sucessão (bn) é uma progressão geométrica de razão 0,90
e de 1.o
termo 1000 .
Logo, bn = 1000 × 0,9n - 1
. Assim, em março de 2012, o 27.o
mês,
depositou:
b27 = 1000 × 0,926
á 64,61 €
25.3
Sp = 1000 ×
,
,
1 0 9
1 0 9p
-
-
= 10 000 × (1 - 0,9p
)
25.4 limSn = lim^10 000 × (1 - 0,9n
)h = 10 000 × (1 - 0) = 10 000
Como (Sn) é crescente, é majorada por 10 000 . Qualquer que seja
a duração da poupança do André, o valor acumulado nunca ultrapassará
os 10 000 € .
26
A soma, Sn , dos n primeiros termos da sucessão (vn) é dada por:
Sn = 2n2
, 6n ! IN
26.1
Justifique que (vn) é uma progressão aritmética de razão 4 .
26.2
Determine um termo geral de vn .
26.3
Calcule lim
( )
v
S
n
n
2
.
26.1
Tem-se que 6n ! IN :
vn = Sn - Sn - 1 = 2n2
- 2(n - 1)2
=
= 2n2
- 2n2
+ 4n - 2 = 4n - 2
que é uma progressão aritmética de razão 4 .
26.2
vn = 4n - 2
26.3 lim
( )
v
S
n
n
2
= lim
( )
n
n
4 2
2
2
2
-
= lim
n n
n
16 16 4
2
2
2
- +
=
= lim
n
n
n 4
2
2
2
2
2
-
c m
=
2
16
=
1
8
000707 328-351.indd 343 01/07/16 13:42

102. 344
Avaliação global de conhecimentos
27
Considere a sucessão de triângulos isósceles, de altura h , em que a base
do primeiro triângulo mede 8 , a do segundo mede 4 , a do terceiro 2 ,
e assim sucessivamente.
u3p78h2
4
8 2 1 0,5
27.1
Prove que a sucessão das áreas dos triângulos (an) tem de termo geral:
an = h × 23 - n
27.2 Determine h se a8 =
80
13
.
27.3
Sabendo que h = 16 , determine a soma de todas as áreas dos triângulos,
ou seja, limSn , em que Sn é a soma das áreas dos n primeiros triângulos.
27.1
O comprimento de cada base é uma progressão geométrica (bn)
de primeiro termo 8 e razão
2
1
. Assim:
an =
h b
2
n
#
=
h
2
8
2
1 n 1
# #
-
c m
= h × 4 ×
2
1 n 1
-
c m =
= h × 4 × 21 - n
= h × 23 - n
27.2
a8 =
80
13
+ h × 23 - 8
=
80
13
+ h =
80
416
+ h = 5,2
27.3
Por 27.1, tem-se que an = 16 × 23 - n
, progressão geométrica
de razão
1
2
e de primeiro termo 64 . Logo:
Sn = 64 ×
1
2
1
1
2
1 n
-
- c m
= 128 × 1
2
1 n
- c
e m o
Então:
limSn = lim 128 1
2
1 n
# - c
e m o
H = 128 lim 1
2
1 n
- c m
= G =
= 128 × 1 = 128
000707 328-351.indd 344 01/07/16 13:42

103. 345
Domínio 3 SUCESSÕES
28
Considere a sucessão (un) definida por:
u
u
u
2
2
3
n
n
1
1
=
=
+
+
*
,6n ! IN
28.1
Recorrendo ao princípio de indução matemática, justifique que todos
os termos de (un) são positivos e prove que (un) é monótona decrescente.
28.2
Justifique que (un) é convergente.
28.3
Determine limun .
28.1 Pretende-se provar que 6n ! IN, un + 1 un .
Para n = 1 , tem-se u2 =
2
3 2
+
=
2
5
2 = u1 , que é verdade.
Hipótese: Para um certo n ! IN , un + 1 un .
Tese: un + 2 un + 1
Demonstração:
un + 2 =
u
2
3 n 1
+ +
Por hipótese, obtém-se:
un + 2
u
2
3 n
+
= un + 1
Portanto, pelo princípio de indução, 6n ! IN, un + 1 un .
28.2 Como u1 0 , tem-se que
u
2
3 1
+
0 . Facilmente se observa que,
usando o princípio de indução, se obtém todos os termos de (un) positivos.
Assim, 0 é um minorante de (un) . Como (un) é decrescente e minorada,
implica que é também convergente.
28.3 limun + 1 = lim
u
2
3 n
+
Como limun + 1 = limun , vem:
limun = lim
u
2
3 n
+
+ 2 limun = lim u
3 n
+ +
+ 2 limun = lim u
3 n
+ 4(limun)2
= 3 + limun +
+ 4(limun)2
- limun - 3 = 0 + limun =
8
1 1 4 4 3
! # #
+
+
+ limun =
8
1 7
!
+ limun = 1 0 limun = -
4
3
Verificando as soluções:
• 2 × 1 = 3 1
+ ; logo, 1 é solução da equação inicial.
•
2 ×
4
3
-
c m= -
2
3
! 3
4
3
- ; logo, -
4
3
não é solução da equação.
000707 328-351.indd 345 01/07/16 13:42

104. 346
preparação para o teste 7
PREPARAÇÃO PARA O TESTE 7
I
Para cada uma das questões deste grupo, selecione a opção correta de entre
as alternativas que lhe são apresentadas.
1
Considere a sucessão (un) definida pelo termo geral:
un = 10 - q3 - nu
Indique a afirmação verdadeira:
(A) un +3
(B) (un) tem exatamente 13 termos positivos.
(C) (un) é monótona.
(D) 10 é um majorante de (un) .
Pode-se escrever un =
n n
n n
7 3
13 3
se
se
1
H
+
-
) . Então:
(A)
Falsa. Para n H 3 , limun = -3 ; e para n 3 , limun = +3 .
(B) Falsa.
7 + n 0 / n 3 + -7 n 3 + n ! {1, 2}
13 - n 0 / n H 3 + 3 G n 13 + n ! {3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Assim, (un) tem exatamente 12 termos positivos.
(C)
Falsa. Para n 3 , (un) é crescente, mas para n H 3 , (un) é decrescente;
logo, (un) não é monótona.
(D)
Verdadeira. Tem-se un = 10 - n
3-
n
3 0
1
2
-
10 ; logo, 10 é um
majorante de (un) .
A opção correta é a (D).
2
O limite da sucessão de termo geral vn =
3 1
2 3
n
n 1
-
- +
é:
(A) -3 (B) -2 (C)
3
2
(D) 3
lim
3 1
2 3
n
n 1
-
- +
= lim
3 1
3
1
3
3
2
3
n
n
n
n
-
-
d
d
n
n
= -
1
3
= -3
A opção correta é a (A).
000707 328-351.indd 346 01/07/16 13:42

105. 347
Domínio 3 SUCESSÕES
3
Nas figuras seguintes, estão representados os três termos de uma sucessão.
u3p82h1
D C
A B
D C
A B
D C
A B
D C
A B
D C
A B
O 1.o
termo é um quadrado azul com 1 cm de lado. Em cada termo seguinte
cada quadrado é dividido em quatro quadrados congruentes, com dois deles
coloridos de azul.
Considere a sucessão das áreas dos quadrados azuis em cada figura.
A área total de todos os quadrados azuis nesta sucessão é:
(A) 1 (B)
2
3
(C)
3
4
(D) 2
Seja (an) a sucessão das áreas dos quadrados azuis em cada figura.
Então, tem-se que an = 1 ×
2
1 n 1
-
c m . Logo:
Sn = 1 ×
1
2
1
1
2
1 n
-
- c m
= 2 × 1
2
1 n
- c
e m o
Assim:
limSn = lim 2 1
2
1 n
# - c
e m o
H = 2lim 1
2
1 n
- c m
= G = 2
A opção correta é a (D).
4
Para p ! IR , considere, num referencial o.n. Oxyz :
• o plano a definido pela equação x + y + z = 20 ;
• a reta r de equação (x, y, z) = (1, 0, -4) + k(2, 2, p), k ! IR .
O valor de p para o qual a reta r é paralela ao plano a é:
(A) -4
(B) -2
(C) 1
(D) 2
(1, 1, 1) $ (2, 2, p) = 0 + 4 + p = 0 + p = -4
A opção correta é a (A).
000707 328-351.indd 347 01/07/16 13:42

106. 348
preparação para o teste 7
5
Considere o triângulo [ABC]
representado na figura.
Sabe-se que:
• AB = 2
• AC
WB = 30°
Seja a = BA
WC .
Qual das expressões seguintes representa BC em função de a ?
(A) 4sina
(B) 6sina
(C) 4cosa
(D) 6cosa
Teste Intermédio do 11.o
ano, 2012
h = 2sina e sin30° =
BC
h
+ BC =
sin
2
1
2 a
= 4sina
A opção correta é a (A).
II
Nas questões seguintes, apresente o seu raciocínio de forma clara, indicando todos
os cálculos que tiver de efetuar e as justificações necessárias.
1
Considere as sucessões (un) e (vn) definidas, respetivamente, por:
un =
n
n
2 11
1 3
-
-
e
v
v v
2
1
1
n
n
1
1
=
= +
+
*
,6n ! IN
1.1 Prove que (un) não é monótona.
1.2 Prove, usando a definição de limite, que limun = -
2
3
e justifique que
(un) é limitada.
1.3 A figura ao lado é ilustrativa
dos termos da sucessão (vn) .
Sabendo que (vn) é monótona
e limitada, calcule o valor para o qual tende
o quociente entre o lado maior e o lado menor
dos retângulos assim formados.
1.1 Como u1 =
2 11
1 3
-
-
=
9
2
, u2 =
2 2 11
1 3 2
#
#
-
-
=
7
5
e
u6 =
2 6 11
1 3 6
#
#
-
-
= -17 , tem-se que u1 u2 mas u2 u6 .
Logo, (un) não é monótona.
u3p82h2
A
h
C
B
a
2
30º
u3p83h1
241
342 543
845
000707 328-351.indd 348 20/07/16 16:18

107. 349
Domínio 3 SUCESSÕES
1.2 Dado d 0 , sempre que 4n - 22 0 , tem-se que:
u
2
3
n + d +
n
n
2 11
1 3
2
3
-
-
+ d +
+
n
n n
4 22
2 6 6 33
-
- + -
d +
n
4 22
31
-
-
d
n 6
+
H
31 d(4n - 22) +
+
31
d
4n - 22 + n
4
31
d
+
2
11
Assim, basta tomar para ordem p o primeiro natural superior a
4
31
d
+
2
11
e a 6 e, assim, tem-se que todos os termos seguintes, un ,
com n H p , pertencem à vizinhança de -
2
3
e de raio d .
Conclui-se que un -
2
3
.
Como toda a sucessão convergente é limitada, (un) é limitada.
1.3 Como (vn) é monótona e limitada, existe limvn e é finito.
Tem-se que limvn + 1 = lim v
1
1
n
+
d n . Como limvn + 1 = limvn , vem:
limvn = lim v
1
1
n
+
d n + limvn = 1 +
lim v
1
n
+
+ (limvn)2
= limvn + 1 + (limvn)2
- limvn - 1 = 0 +
+ limvn =
2
1 1 4
! +
+ limvn =
2
1 5
!
Como (vn) é positiva, limvn =
2
1 5
+
(número de ouro).
2
Dada uma progressão aritmética (wn) , sabe-se que w6 = 5 e w14 = 9 .
2.1
Determine uma expressão simplificada do termo geral de (wn) .
2.2
Calcule a soma de todos os 30 termos consecutivos a partir do 10.o
termo, inclusive.
2.3 Calcule:
a) lim w
w
n
n 1
+
b) lim w w
n n
2 -
` j
2.1 w14 = w6 + 8r + 9 = 5 + 8r + r =
2
1
w6 = w1 + 5 ×
2
1
+ 5 = w1 +
2
5
+ w1 =
2
5
Logo, wn =
2
5
+ (n - 1) ×
2
1
=
n
2
+ 2 .
2.2 S =
w w
2
10 29
+
× 30 =
2
2 2
2
10
2
29
#
+ +
× 30 = 352,5
000707 328-351.indd 349 01/07/16 13:42

108. 350
preparação para o teste 7
2.3 a) lim w
w
n
n 1
+
= lim n
n
2
2
2
2
1
+
+
+
= lim
n
n
4
5
+
+
= lim
n
n
4
1
5
1
+
+
= 1
b) lim w w
n n
2 -
` j =
= lim n
n
2
2
2
+ - +
d n = lim
n
n
n
n
2
2
2
2
2
2
+ +
+ - -
+
c
f
m
p=
= lim
n
n
n
2
2
2
2
+ + +
f p= lim
n n n n
1 2
2
1 2
2
1
2 2
+ + +
f p=
=
0
2
1
+
= +3
3
O Sr. Silva possui 10 depósitos para armazenar
água. Sabe-se que o depósito com menor
capacidade permite armazenar 1000 litros
de água, o segundo 1500 litros, o terceiro
2250 litros, e assim sucessivamente.
Determine qual é a capacidade máxima de água que o Sr. Silva consegue
armazenar nos seus depósitos.
Apresente o resultado arredondado à unidade de litro.
Seja (un) a sucessão da capacidade, em litros, de cada depósito.
Tem-se que (un) é uma progressão geométrica de razão 1,5 e de 1.o
termo 1000 .
Logo, un = 1000 × 1,5n - 1
e S10 = 1000 ×
,
,
1 1 5
1 1 510
-
-
á 113 330 L .
4
Para x ! IR{0} , considere, num referencial o.n. xOy , os vetores u(1, 1)
e v^x, x2
h .
4.1
Supondo que u v
_ i
T =
3
r
, determine o valor exato de x .
4.2
Prove, usando o método de indução, que 6x ! IN , u $ v é par.
000707 328-351.indd 350 01/07/16 13:42

109. 351
Domínio 3 SUCESSÕES
4.1
u $ v = u v cos u v
_ i
T + x + x2
= 2 x x
2 4
+ cos
3
r
+
+ 2x + 2x2
= x x
2 2
2 4
+ 4x2
+ 8x3
+ 4x4
= 2x2
+ 2x4
+
+ 2x2
+ 8x3
+ 2x4
= 0 + 2x2
(1 + 4x + x2
) = 0 +
+ 2x2
= 0 0 1 + 4x + x2
= 0 + x = 0 0 x =
2
4 16 4
!
- -
+
IR{ }
x 0
+
!
x = 0 0 x = -2 + 3 0 x = -2 - 3
Verificação:
Para x = -2 + 3 , tem-se:
2 2 3
- +
_ i + 2 2 3
2
- +
_ i = 2 2 3 2 2 3
2 4
- + + - +
_ _
i i +
+ -4 + 2 3 + 2 4 4 3 3
+
-
_ i =
= 2 4 4 3 3 2 4 4 3 3 4 4 3 3
+ + + +
- - -
_ _ _
i i i +
+ 10 - 6 3 = 14 8 3 2 49 56 3 48
- + - +
_ i +
+ 10 - 6 3 = 208 120 3
-
Proposição falsa. Logo, -2 + 3 não é solução da equação inicial.
Para x = -2 - 3 , tem-se:
2 2 3
- -
_ i + 2 2 3
2
- -
_ i = 2 2 3 2 2 3
2 4
- - + - -
_ _
i i +
+ -4 - 2 3 + 2 4 4 3 3
+ +
_ i =
= 2 4 4 3 3 2 4 4 3 3 4 4 3 3
+ + + + + + +
_ _ _
i i i +
+ 10 + 6 3 = 14 8 3 2 49 56 3 48
+ +
+ +
_ i +
+ 10 + 6 3 = 208 120 3
+
+ 100 + 120 3 + 108 = 208 + 120 3 +
+ 100 + 108 = 208
Logo, -2 - 3 é o valor de x .
4.2 Para x = 1 , tem-se u $ v = 1 + 1 = 2 , que é verdade.
Hipótese: Para um certo x ! IN , x + x2
é par.
Tese: x + 1 + (x + 1)2
é par
Demonstração:
x + 1 + (x + 1)2
= x + 1 + x2
+ 2x + 1 = (x + x2
) + 2x + 2
Por hipótese, x + x2
é par; logo, x + 1 + (x + 1)2
é par porque
é a soma de números pares.
Portanto, pelo princípio de indução, 6x ! IN, x + x2
é par, ou seja,
6x ! IN, u $ v é par.
000707 328-351.indd 351 01/07/16 13:42