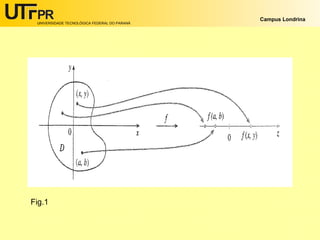
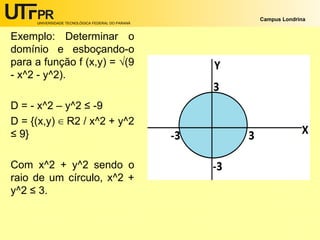
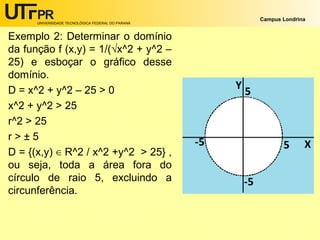
Uma função de duas variáveis mapeia cada par ordenado de números reais (x, y) de um subconjunto do plano cartesiano R2 para um único valor real. O documento explica o que é o domínio de uma função de duas variáveis e fornece exemplos de como determinar e representar graficamente o domínio de funções específicas.

1. Campus Londrina
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
FUNÇÕES DE DUAS VARIÁVEIS
E SEU DOMÍNIO
Lucas Peixoto Ferreira
Paulo Beraldo Junior
2013

2. Campus Londrina
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Uma função f de duas variáveis é uma
regra que associa, a cada par ordenado
de números reais (x,y) de um conjunto D,
um único valor real denotado por f(x,y). O
conjunto D é o domínio de f, e sua
imagem o conjunto de valores possíveis
de f, ou seja {f(x,y)/(x,y) ∈ D}.
2º Semestre de Química

3. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Londrina
Então uma função de duas variáveis é
aquela cujo o domínio é um subconjunto
de R2 e a imagem é um sub conjunto de R.
Visualizamos essa função pelo diagrama
de setas onde o domínio é representado
como um subconjunto do plano x,y. (fig. 1).

4. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Fig.1
Campus Londrina

5. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Londrina
Se uma função f é dada e o seu domínio
não é especificado, então entende-se
como domínio de f todo o conjunto de
valores (x,y) para os quais a expressão
dada fornece um numero real definido.

6. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Londrina
ex: f(x,y)= x2 -3xy+y3-1
A expressão para f esta bem definida em todos os
valores (x,y) logo o domínio de f são todos os reais D:
{(x,y) ∈ R2 }. (representado graficamente por toda área
em cinza no plano x,y).

7. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Exemplo: Determinar o
domínio e esboçando-o
para a função f (x,y) = √(9
- x^2 - y^2).
D = - x^2 – y^2 ≤ -9
D = {(x,y) ∈ R2 / x^2 + y^2
≤ 9}
Com x^2 + y^2 sendo o
raio de um círculo, x^2 +
y^2 ≤ 3.
Campus Londrina

8. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Exemplo 2: Determinar o domínio
da função f (x,y) = 1/(√x^2 + y^2 –
25) e esboçar o gráfico desse
domínio.
D = x^2 + y^2 – 25 > 0
x^2 + y^2 > 25
r^2 > 25
r>±5
D = {(x,y) ∈ R^2 / x^2 +y^2 > 25} ,
ou seja, toda a área fora do
círculo de raio 5, excluindo a
circunferência.
Campus Londrina

9. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Londrina
Bibliografia
• STEWART, J. Cálculo. Vol. II. 5.ed. São
Paulo: Thomson Learning, 2007.
• THOMAS, George B. Cálculo. Vol. II.
10.Ed. São Paulo: Pearson Addison
Wesley, 2003.

10. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Londrina
Bibliografia
• STEWART, J. Cálculo. Vol. II. 5.ed. São
Paulo: Thomson Learning, 2007.
• THOMAS, George B. Cálculo. Vol. II.
10.Ed. São Paulo: Pearson Addison
Wesley, 2003.