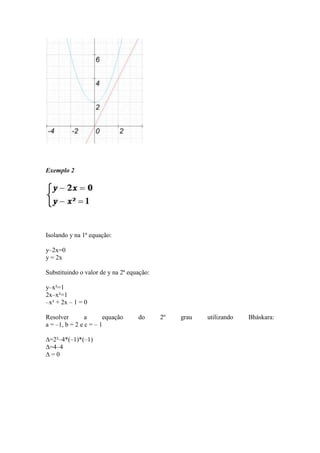
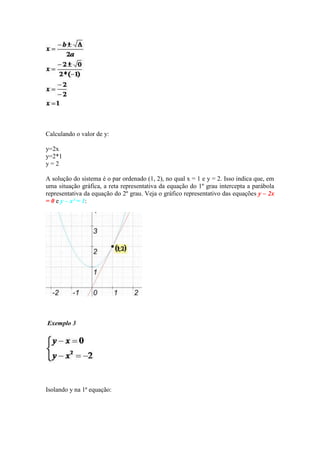
1) Um sistema de equações é formado por expressões iguais ao número de variáveis. 2) Sistemas podem envolver equações de 1o e 2o grau, resolvidas pelo método da substituição. 3) Exemplos mostram sistemas com soluções reais ou não, dependendo se as equações se interceptam.

1. Sistema de Equações do 1º e do 2º Grau
Um sistema de equações é formado por duas ou mais expressões, no qual o número de
equações deve ser igual ao número de variáveis. Por exemplo, se uma das funções
possui três variáveis: x, y e z, devemos ter três equações para que o sistema permita
possíveis soluções dentro dos números reais.
O sistema pode ser formado por diferentes tipos de equações. Vamos abordar os
sistemas envolvendo equações do 1º e do 2º grau. O método de resolução, nesses casos,
é o da substituição. Observe:
Exemplo 1
Isolando y na 2ª equação:
y–2x=0
y = 2x
Substituindo o valor de y na 1ª equação:
y–x²=2
2x–x²=2
–x²+2x–2=0
x² – 2x + 2 = 0
Resolver
a
a = 1, b = 2 e c = 2
equação
do
2º
grau
utilizando
Bháskara:
∆=b²–4ac
∆=2²–4*1*2
∆=4–8
∆=–4
Nesse caso, a equação não possui raízes reais e, dessa forma, não existe ponto em
comum entre as equações y – x² = 2 e y – 2x = 0. Observe o gráfico referente a elas:

2. Exemplo 2
Isolando y na 1ª equação:
y–2x=0
y = 2x
Substituindo o valor de y na 2ª equação:
y–x²=1
2x–x²=1
–x² + 2x – 1 = 0
Resolver
a
equação
a = –1, b = 2 e c = – 1
∆=2²–4*(–1)*(–1)
∆=4–4
∆=0
do
2º
grau
utilizando
Bháskara:

3. Calculando o valor de y:
y=2x
y=2*1
y=2
A solução do sistema é o par ordenado (1, 2), no qual x = 1 e y = 2. Isso indica que, em
uma situação gráfica, a reta representativa da equação do 1º grau intercepta a parábola
representativa da equação do 2º grau. Veja o gráfico representativo das equações y – 2x
= 0 e y – x² = 1:
Exemplo 3
Isolando y na 1ª equação:

4. y–x=0
y=x
Substituindo o valor de y na 2ª equação:
y–x²=–2
x–x²=–2
–x² + x + 2 = 0
Resolver
a
equação
a = –1, b = 1 e c = 2
do
2º
grau
utilizando
Bháskara:
∆=b²–4ac
∆=1²–4*(–1)*2
∆=1+8
∆=9
Calculando o valor de y, de acordo com y = x:
Quando x = –1, y = –1.
Quando x = 2, y = 2.
A solução do sistema são os pares ordenados (–1, –1) e (2, 2). Nessa situação, as
equações y – x = 0 e y – x² = –2 possuem dois pontos em comum. Observe o gráfico: