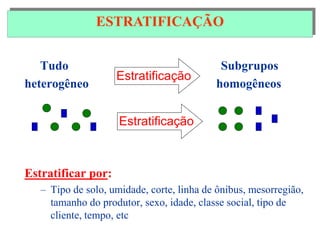
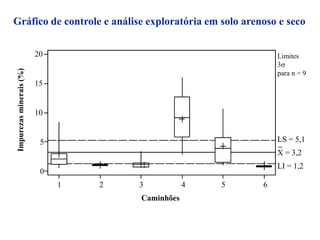
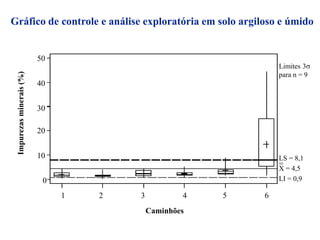
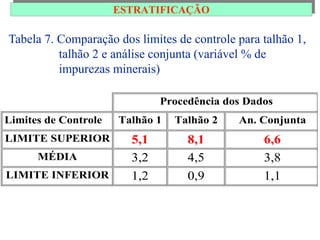
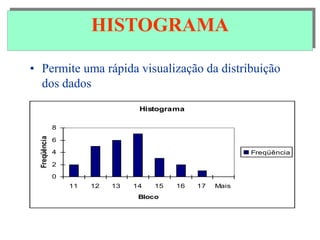
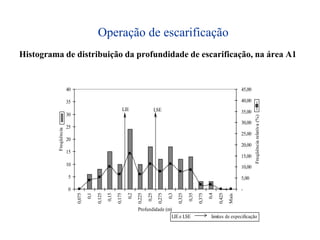
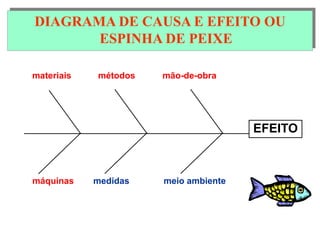
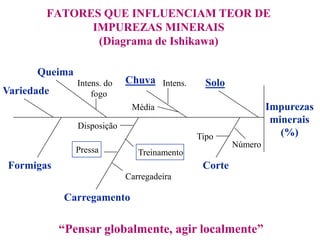
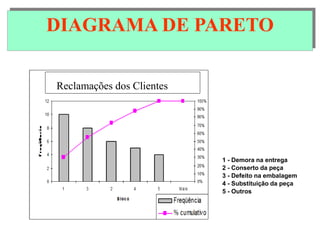
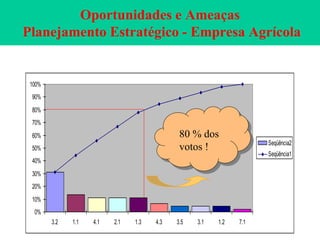
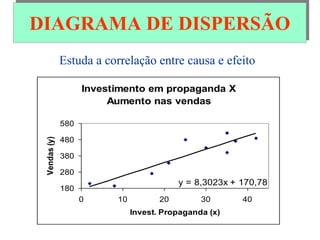
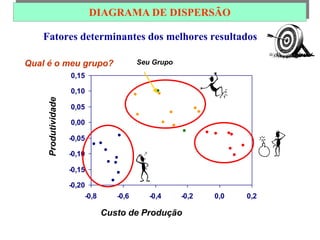
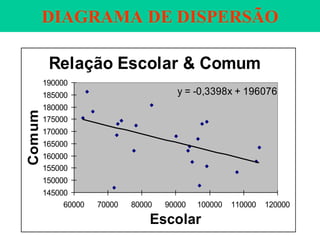
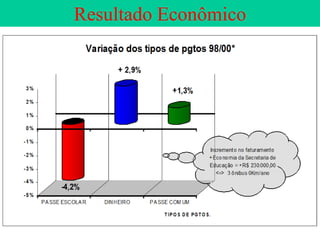
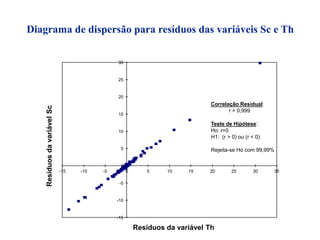
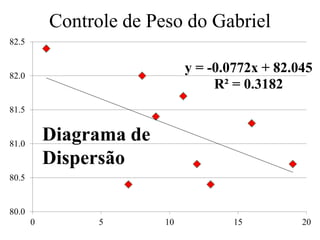
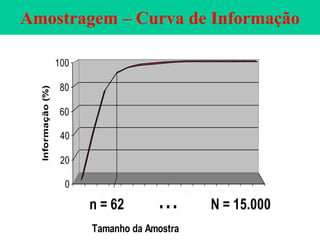
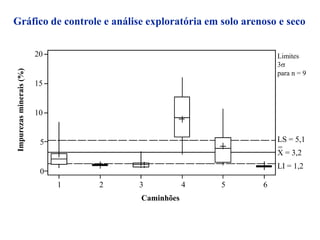
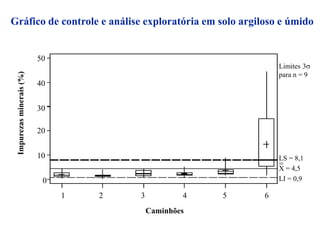
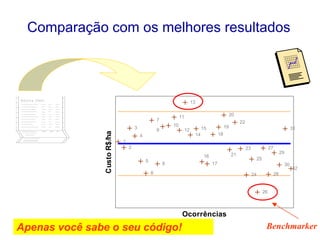
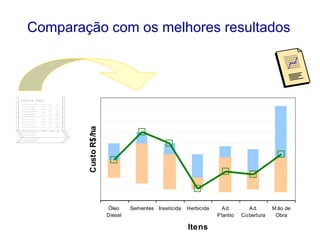
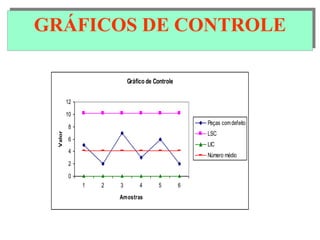
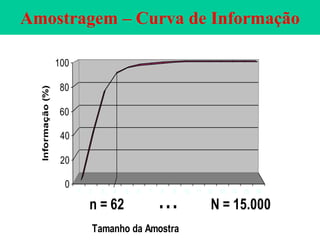
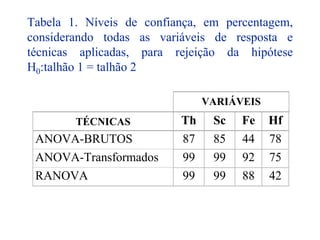
O documento descreve sete ferramentas estatísticas para controle da qualidade propostas por Ishikawa: folha de verificação, estratificação, diagrama de causas e efeitos, diagrama de Pareto, histograma, diagrama de dispersão e gráficos de controle. Essas ferramentas podem resolver aproximadamente 95% dos problemas de qualidade em qualquer organização.