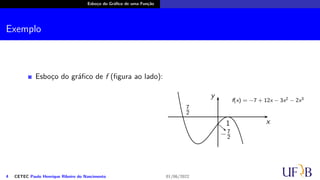
O documento descreve os passos para esboçar o gráfico de uma função, listando propriedades como domínio, paridade, pontos de descontinuidade, interseções com os eixos, comportamento no infinito, pontos críticos, entre outros. O documento fornece um exemplo detalhado de como esboçar o gráfico da função f(x) = (x2 − 1)3.

1. Cálculo Diferencial e Integral I
Universidade Federal do Recôncavo da Bahia
01/06/2022
Paulo Henrique Ribeiro do Nascimento

2. Esboço do Gráfico de uma Função
Os passos
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

3. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

4. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

5. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

6. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

7. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

8. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

9. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

10. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

11. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

12. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

13. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

14. Esboço do Gráfico de uma Função
Os passos
Para esboçar o gráfico de uma função, determinaremos/verificaremos:
seu domínio;
sua paridade;
seus pontos de descontinuidade e a existência de assíntotas verticais;
suas interseções com os eixos coordenados;
seu comportamento no infinito (existência de assíntota horizontal);
existência de assíntotas oblíquas;
seus intervalos de monotonicidade (crescimento e decrescimento);
seus extremantes;
seus pontos de inflexão
suas concavidades;
seu esboço gráfico.
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

15. Esboço do Gráfico de uma Função
Exemplo
Example 1.
Esboçar o gráfico da função f(x) = (x2 − 1)3.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

16. Esboço do Gráfico de uma Função
Exemplo
Solução:
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

17. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = ((−x)2 − 1)3 = (x2 − 1)3 = f(x). Portanto, a função é par e
seu gráfico possui simetria com respeito ao eixo das ordenadas (eixo-y).
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −1 e, se y = 0, então
x = ±1; a curva passa pelos pontos (1, 0), (−1, 0) e (0, −1).
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

18. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = ((−x)2 − 1)3 = (x2 − 1)3 = f(x). Portanto, a função é par e
seu gráfico possui simetria com respeito ao eixo das ordenadas (eixo-y).
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −1 e, se y = 0, então
x = ±1; a curva passa pelos pontos (1, 0), (−1, 0) e (0, −1).
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

19. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = ((−x)2 − 1)3 = (x2 − 1)3 = f(x). Portanto, a função é par e
seu gráfico possui simetria com respeito ao eixo das ordenadas (eixo-y).
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −1 e, se y = 0, então
x = ±1; a curva passa pelos pontos (1, 0), (−1, 0) e (0, −1).
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

20. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = ((−x)2 − 1)3 = (x2 − 1)3 = f(x). Portanto, a função é par e
seu gráfico possui simetria com respeito ao eixo das ordenadas (eixo-y).
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −1 e, se y = 0, então
x = ±1; a curva passa pelos pontos (1, 0), (−1, 0) e (0, −1).
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

21. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = ((−x)2 − 1)3 = (x2 − 1)3 = f(x). Portanto, a função é par e
seu gráfico possui simetria com respeito ao eixo das ordenadas (eixo-y).
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −1 e, se y = 0, então
x = ±1; a curva passa pelos pontos (1, 0), (−1, 0) e (0, −1).
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

22. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
x6
= +∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 6x(x2
− 1)2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = 0, x = 1 e x = −1, que são os
pontos críticos de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

23. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
x6
= +∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 6x(x2
− 1)2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = 0, x = 1 e x = −1, que são os
pontos críticos de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

24. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
x6
= +∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 6x(x2
− 1)2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = 0, x = 1 e x = −1, que são os
pontos críticos de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

25. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
x6
= +∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 6x(x2
− 1)2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = 0, x = 1 e x = −1, que são os
pontos críticos de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

26. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = 6(x2
− 1)(5x2
− 1).
Logo, f′′
(0) > 0 e 0 é ponto de mínimo relativo de f; f′′
(±1) = 0 e, neste caso, o
teste da segunda derivada nada nos diz.
Usando, então, o teste da primeira derivada para analisar a mudança de sinal, temos:
f′
(x) < 0, para todo x < 0; então x = −1 não é ponto extremo de f.
f′
(x) > 0, para todo x > 0; então x = 1 não é ponto extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

27. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = 6(x2
− 1)(5x2
− 1).
Logo, f′′
(0) > 0 e 0 é ponto de mínimo relativo de f; f′′
(±1) = 0 e, neste caso, o
teste da segunda derivada nada nos diz.
Usando, então, o teste da primeira derivada para analisar a mudança de sinal, temos:
f′
(x) < 0, para todo x < 0; então x = −1 não é ponto extremo de f.
f′
(x) > 0, para todo x > 0; então x = 1 não é ponto extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

28. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = 6(x2
− 1)(5x2
− 1).
Logo, f′′
(0) > 0 e 0 é ponto de mínimo relativo de f; f′′
(±1) = 0 e, neste caso, o
teste da segunda derivada nada nos diz.
Usando, então, o teste da primeira derivada para analisar a mudança de sinal, temos:
f′
(x) < 0, para todo x < 0; então x = −1 não é ponto extremo de f.
f′
(x) > 0, para todo x > 0; então x = 1 não é ponto extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

29. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = 6(x2
− 1)(5x2
− 1).
Logo, f′′
(0) > 0 e 0 é ponto de mínimo relativo de f; f′′
(±1) = 0 e, neste caso, o
teste da segunda derivada nada nos diz.
Usando, então, o teste da primeira derivada para analisar a mudança de sinal, temos:
f′
(x) < 0, para todo x < 0; então x = −1 não é ponto extremo de f.
f′
(x) > 0, para todo x > 0; então x = 1 não é ponto extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

30. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = 6(x2
− 1)(5x2
− 1).
Logo, f′′
(0) > 0 e 0 é ponto de mínimo relativo de f; f′′
(±1) = 0 e, neste caso, o
teste da segunda derivada nada nos diz.
Usando, então, o teste da primeira derivada para analisar a mudança de sinal, temos:
f′
(x) < 0, para todo x < 0; então x = −1 não é ponto extremo de f.
f′
(x) > 0, para todo x > 0; então x = 1 não é ponto extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

31. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = 6(x2
− 1)(5x2
− 1).
Logo, f′′
(0) > 0 e 0 é ponto de mínimo relativo de f; f′′
(±1) = 0 e, neste caso, o
teste da segunda derivada nada nos diz.
Usando, então, o teste da primeira derivada para analisar a mudança de sinal, temos:
f′
(x) < 0, para todo x < 0; então x = −1 não é ponto extremo de f.
f′
(x) > 0, para todo x > 0; então x = 1 não é ponto extremo de f.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

32. Esboço do Gráfico de uma Função
Exemplo
Existência de assíntotas oblíquas:
m = lim
x→±∞
f(x)
x
= lim
x→±∞
x6
x
= ±∞ e, portanto, não existe assíntota oblíqua.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

33. Esboço do Gráfico de uma Função
Exemplo
Existência de assíntotas oblíquas:
m = lim
x→±∞
f(x)
x
= lim
x→±∞
x6
x
= ±∞ e, portanto, não existe assíntota oblíqua.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

34. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

35. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

36. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

37. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

38. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

39. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

40. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = 6(x2
− 1)(5x2
− 1) = 0 implica que x = ±1 e x = ±
√
5
5
.
f′′
(x) > 0, se x ∈ (−∞, −1) ∪
(
−
√
5
5
,
√
5
5
)
∪ (1, ∞) e f′′
(x) < 0 se
x ∈
(
−1, −
√
5
5
)
∪
(√
5
5
, 1
)
.
Conclusão:
f tem C.P. nos intervalos (−∞, −1),
(
−
√
5
5
,
√
5
5
)
e (1, ∞).
f tem C.N. nos intervalos
(
−1, −
√
5
5
)
e
(√
5
5
, 1
)
.
e as abscissas dos pontos de inflexão de f são x = ±1 e x = ±
√
5
5
.
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

41. Esboço do Gráfico de uma Função
Exemplo
Esboço do gráfico de f (figura ao lado):
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

42. Esboço do Gráfico de uma Função
Exemplo
Esboço do gráfico de f (figura ao lado):
x
y
−1
−1 1
f(x) = (x2 − 1)3
3 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

43. Esboço do Gráfico de uma Função
Exemplo
Example 1.
Esboçar o gráfico da função f(x) = −7 + 12x − 3x2 − 2x3.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

44. Esboço do Gráfico de uma Função
Exemplo
Solução:
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

45. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = −7 + 12(−x) − 3(−x)2 − 2(−x)3 = −7 − 12x − 3x2 + 2x3.
Portanto, a função não é par e nem ímpar.
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −7 e se y = 0, então
x = 1 ou x = −7/2 (Verifique!);
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

46. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = −7 + 12(−x) − 3(−x)2 − 2(−x)3 = −7 − 12x − 3x2 + 2x3.
Portanto, a função não é par e nem ímpar.
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −7 e se y = 0, então
x = 1 ou x = −7/2 (Verifique!);
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

47. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = −7 + 12(−x) − 3(−x)2 − 2(−x)3 = −7 − 12x − 3x2 + 2x3.
Portanto, a função não é par e nem ímpar.
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −7 e se y = 0, então
x = 1 ou x = −7/2 (Verifique!);
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

48. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = −7 + 12(−x) − 3(−x)2 − 2(−x)3 = −7 − 12x − 3x2 + 2x3.
Portanto, a função não é par e nem ímpar.
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −7 e se y = 0, então
x = 1 ou x = −7/2 (Verifique!);
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

49. Esboço do Gráfico de uma Função
Exemplo
Solução:
Domínio: Claramente, temos Dom(f) = R.
Paridade: f(−x) = −7 + 12(−x) − 3(−x)2 − 2(−x)3 = −7 − 12x − 3x2 + 2x3.
Portanto, a função não é par e nem ímpar.
Pontos de descontinuidade: Não existem pois a função é contínua.
Intersecções com os eixos coordenados: se x = 0, então y = −7 e se y = 0, então
x = 1 ou x = −7/2 (Verifique!);
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

50. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
−2x3
= ∓∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 12 − 6x − 6x2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = −2 e x = 1, que são os pontos
críticos de f.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

51. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
−2x3
= ∓∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 12 − 6x − 6x2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = −2 e x = 1, que são os pontos
críticos de f.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

52. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
−2x3
= ∓∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 12 − 6x − 6x2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = −2 e x = 1, que são os pontos
críticos de f.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

53. Esboço do Gráfico de uma Função
Exemplo
Comportamento no infinito: lim
x→±∞
(x2
− 1)3
= lim
x→±∞
−2x3
= ∓∞. Com isso, não
existem assíntotas horizontais.
Pontos críticos de f:
Temos que f′
(x) = 12 − 6x − 6x2
.
Logo, resolvendo a equação f′
(x) = 0, obtemos x = −2 e x = 1, que são os pontos
críticos de f.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

54. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = −6 − 12x.
Logo, f′′
(1) < 0 e 1 é a abscissa do ponto de máximo relativo de f. f′′
(2) > 0 e 2 é
abscissa do ponto de mínimo.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

55. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = −6 − 12x.
Logo, f′′
(1) < 0 e 1 é a abscissa do ponto de máximo relativo de f. f′′
(2) > 0 e 2 é
abscissa do ponto de mínimo.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

56. Esboço do Gráfico de uma Função
Exemplo
Máximos e mínimos relativos de f:
Temos que: f′′
(x) = −6 − 12x.
Logo, f′′
(1) < 0 e 1 é a abscissa do ponto de máximo relativo de f. f′′
(2) > 0 e 2 é
abscissa do ponto de mínimo.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

57. Esboço do Gráfico de uma Função
Exemplo
Existência de assíntotas oblíquas:
m = lim
x→±∞
f(x)
x
= lim
x→±∞
=
−2x3
x
= −∞ e, portanto, não existem assíntotas
oblíquas.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

58. Esboço do Gráfico de uma Função
Exemplo
Existência de assíntotas oblíquas:
m = lim
x→±∞
f(x)
x
= lim
x→±∞
=
−2x3
x
= −∞ e, portanto, não existem assíntotas
oblíquas.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

59. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

60. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

61. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

62. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

63. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

64. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

65. Esboço do Gráfico de uma Função
Exemplo
Pontos de inflexão e Concavidade
f′′
(x) = −6 − 12x = 0 implica que x = −
1
2
.
f′′
(x) > 0 se x < −
1
2
e f′′
(x) < 0 se x > −
1
2
.
Conclusão: o gráfico de f tem
C.P. em
(
−∞, −
1
2
)
.
C.N. em
(
−
1
2
, ∞
)
.
A abscissa do ponto de inflexão de f é −
1
2
.
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

66. Esboço do Gráfico de uma Função
Exemplo
Esboço do gráfico de f (figura ao lado):
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

67. Esboço do Gráfico de uma Função
Exemplo
Esboço do gráfico de f (figura ao lado):
x
y
7
2
1
−7
2
f(x) = −7 + 12x − 3x2 − 2x3
4 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

68. Esboço do Gráfico de uma Função
Referências
M. B. Gonçalves and D. M. Flemming.
Cálculo A.
Pearson Education, 5 edition, 2007.
H. L. Guidorizzi.
Um curso de cálculo, volume 1.
Grupo Gen-LTC, 5 edition, 2000.
A. Howard.
Cálculo, um novo horizonte, volume 1.
Bookman, Porto Alegre, 2000.
E. L. Lima.
Curso de Análise, volume 1.
IMPA, Rio de Janeiro, 2000.
5 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022