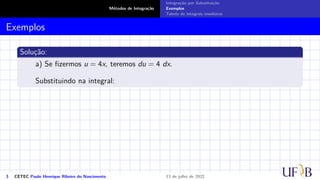
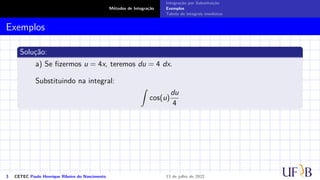
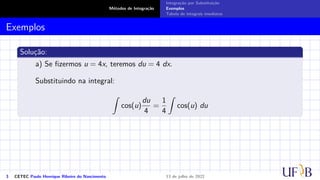
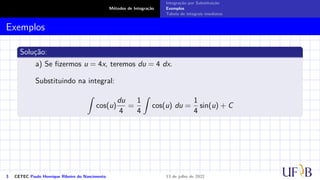
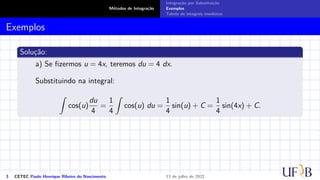
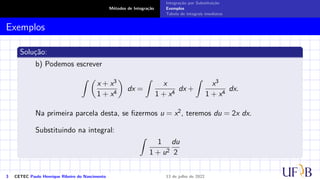
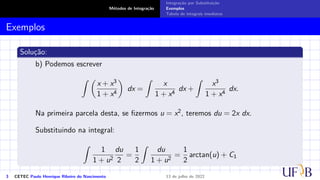
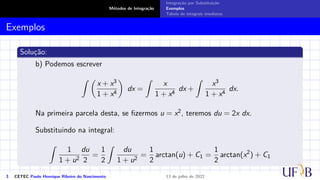
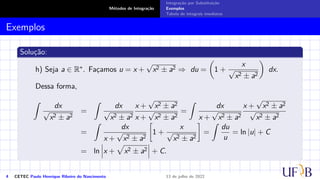
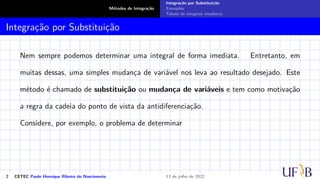
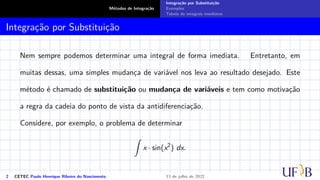
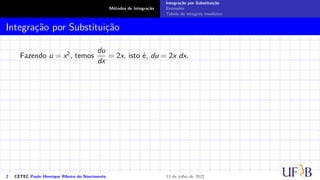
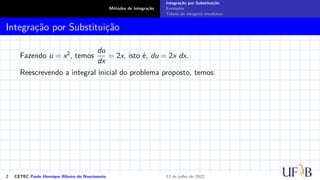
O documento discute o método de integração por substituição. Ele introduz o método formalmente, mostrando como realizar a substituição de variáveis em uma integral indefinida para obter o resultado desejado. Em seguida, apresenta exemplos passo a passo de como aplicar a técnica para resolver integrais específicas.








![Métodos de Integração
Integração por Substituição
Exemplos
Tabela de integrais imediatas
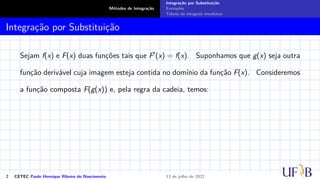
Integração por Substituição
Sejam f(x) e F(x) duas funções tais que F′(x) = f(x). Suponhamos que g(x) seja outra
função derivável cuja imagem esteja contida no domínio da função F(x). Consideremos
a função composta F(g(x)) e, pela regra da cadeia, temos:
[F(g(x))]′
2 CETEC Paulo Henrique Ribeiro do Nascimento 13 de julho de 2022](https://image.slidesharecdn.com/gcet146s14a-220713220915-6ca39ea9/85/GCET146-S14a-pdf-17-320.jpg)
![Métodos de Integração
Integração por Substituição
Exemplos
Tabela de integrais imediatas
Integração por Substituição
Sejam f(x) e F(x) duas funções tais que F′(x) = f(x). Suponhamos que g(x) seja outra
função derivável cuja imagem esteja contida no domínio da função F(x). Consideremos
a função composta F(g(x)) e, pela regra da cadeia, temos:
[F(g(x))]′
= F′
(g(x)) · g′
(x)
2 CETEC Paulo Henrique Ribeiro do Nascimento 13 de julho de 2022](https://image.slidesharecdn.com/gcet146s14a-220713220915-6ca39ea9/85/GCET146-S14a-pdf-18-320.jpg)
![Métodos de Integração
Integração por Substituição
Exemplos
Tabela de integrais imediatas
Integração por Substituição
Sejam f(x) e F(x) duas funções tais que F′(x) = f(x). Suponhamos que g(x) seja outra
função derivável cuja imagem esteja contida no domínio da função F(x). Consideremos
a função composta F(g(x)) e, pela regra da cadeia, temos:
[F(g(x))]′
= F′
(g(x)) · g′
(x) = f(g(x)) · g′
(x),
2 CETEC Paulo Henrique Ribeiro do Nascimento 13 de julho de 2022](https://image.slidesharecdn.com/gcet146s14a-220713220915-6ca39ea9/85/GCET146-S14a-pdf-19-320.jpg)
![Métodos de Integração
Integração por Substituição
Exemplos
Tabela de integrais imediatas
Integração por Substituição
Sejam f(x) e F(x) duas funções tais que F′(x) = f(x). Suponhamos que g(x) seja outra
função derivável cuja imagem esteja contida no domínio da função F(x). Consideremos
a função composta F(g(x)) e, pela regra da cadeia, temos:
[F(g(x))]′
= F′
(g(x)) · g′
(x) = f(g(x)) · g′
(x),
isto é, F(g(x)) é uma primitiva de f(g(x)) · g′(x).
2 CETEC Paulo Henrique Ribeiro do Nascimento 13 de julho de 2022](https://image.slidesharecdn.com/gcet146s14a-220713220915-6ca39ea9/85/GCET146-S14a-pdf-20-320.jpg)