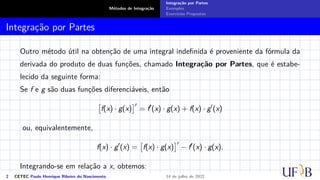
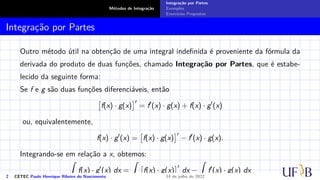
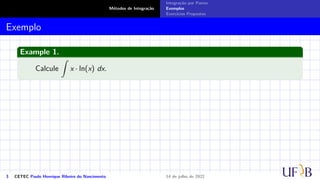
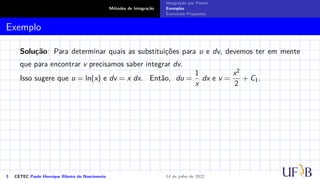
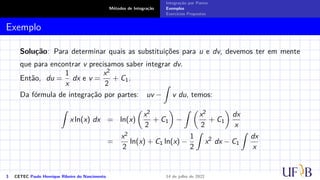
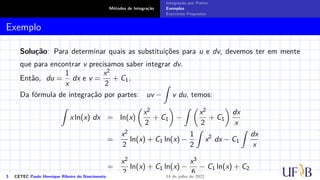
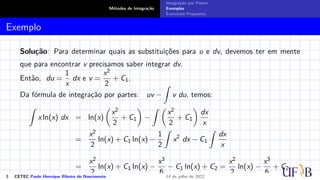
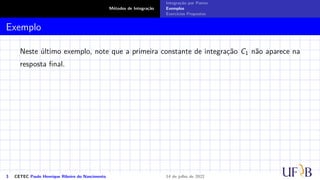
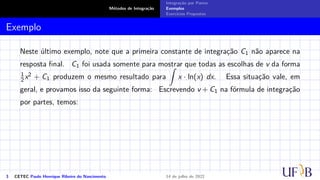
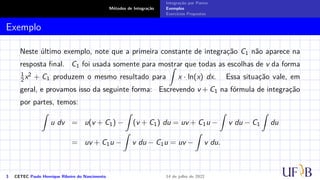
O documento discute o método de integração por partes. Ele define a fórmula de integração por partes, mostrando como separar uma integral indefinida em duas partes através da derivada do produto de duas funções. Exemplos e exercícios são fornecidos para demonstrar como aplicar este método para calcular integrais indefinidas.

1. Cálculo Diferencial e Integral I
Universidade Federal do Recôncavo da Bahia
14 de julho de 2022
Prof.: Paulo Henrique

2. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

3. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
Se f e g são duas funções diferenciáveis, então
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

4. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
Se f e g são duas funções diferenciáveis, então
f(x) · g(x)
′
= f′
(x) · g(x) + f(x) · g′
(x)
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

5. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
Se f e g são duas funções diferenciáveis, então
f(x) · g(x)
′
= f′
(x) · g(x) + f(x) · g′
(x)
ou, equivalentemente,
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

6. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
Se f e g são duas funções diferenciáveis, então
f(x) · g(x)
′
= f′
(x) · g(x) + f(x) · g′
(x)
ou, equivalentemente,
f(x) · g′
(x) =
f(x) · g(x)
′
− f′
(x) · g(x).
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

7. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
Se f e g são duas funções diferenciáveis, então
f(x) · g(x)
′
= f′
(x) · g(x) + f(x) · g′
(x)
ou, equivalentemente,
f(x) · g′
(x) =
f(x) · g(x)
′
− f′
(x) · g(x).
Integrando-se em relação a x, obtemos:
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

8. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Outro método útil na obtenção de uma integral indefinida é proveniente da fórmula da
derivada do produto de duas funções, chamado Integração por Partes, que é estabe-
lecido da seguinte forma:
Se f e g são duas funções diferenciáveis, então
f(x) · g(x)
′
= f′
(x) · g(x) + f(x) · g′
(x)
ou, equivalentemente,
f(x) · g′
(x) =
f(x) · g(x)
′
− f′
(x) · g(x).
Integrando-se em relação a x, obtemos:
Z
f(x) · g′
(x) dx =
Z
f(x) · g(x)
′
dx −
Z
f′
(x) · g(x) dx
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

9. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

10. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
f′
(x) · g(x) dx (1)
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

11. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
f′
(x) · g(x) dx (1)
que é chamada de fórmula de Integração por Partes.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

12. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
f′
(x) · g(x) dx (1)
que é chamada de fórmula de Integração por Partes.
Esta fórmula pode ser simplificada fazendo
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

13. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
f′
(x) · g(x) dx (1)
que é chamada de fórmula de Integração por Partes.
Esta fórmula pode ser simplificada fazendo
u = f(x) e dv = g′
(x) dx =⇒ du = f′
(x) dx e v = g(x),
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

14. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
f′
(x) · g(x) dx (1)
que é chamada de fórmula de Integração por Partes.
Esta fórmula pode ser simplificada fazendo
u = f(x) e dv = g′
(x) dx =⇒ du = f′
(x) dx e v = g(x),
resultando na seguinte versão da fórmula de integração por partes:
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

15. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
e escrevemos esta última equação da seguinte forma:
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
f′
(x) · g(x) dx (1)
que é chamada de fórmula de Integração por Partes.
Esta fórmula pode ser simplificada fazendo
u = f(x) e dv = g′
(x) dx =⇒ du = f′
(x) dx e v = g(x),
resultando na seguinte versão da fórmula de integração por partes:
Z
u dv = u · v −
Z
v du. (2)
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

16. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Observe, que esta fórmula nos permite expressar uma integral indefinida em termos de
outra que pode ser mais fácil de calcular, escolhendo adequadamente u e dv.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

17. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Observe, que esta fórmula nos permite expressar uma integral indefinida em termos de
outra que pode ser mais fácil de calcular, escolhendo adequadamente u e dv.
O termo por partes é do fato que este processo separa o integrando em duas partes.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

18. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Observe, que esta fórmula nos permite expressar uma integral indefinida em termos de
outra que pode ser mais fácil de calcular, escolhendo adequadamente u e dv.
O termo por partes é do fato que este processo separa o integrando em duas partes.
É importante a escolha adequada de dv que, em geral, fazemos representar a parte
mais complicada do integrando que possa ser prontamente integrada, pois v será uma
primitiva de dv.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

19. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Observe, que esta fórmula nos permite expressar uma integral indefinida em termos de
outra que pode ser mais fácil de calcular, escolhendo adequadamente u e dv.
O termo por partes é do fato que este processo separa o integrando em duas partes.
É importante a escolha adequada de dv que, em geral, fazemos representar a parte
mais complicada do integrando que possa ser prontamente integrada, pois v será uma
primitiva de dv.
Resumimos este processo de integração da seguinte forma:
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

20. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Olhamos uma função h que queremos integrar, como o produto de duas funções, uma
das quais é a derivada de uma função já conhecida, isto é,
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

21. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Olhamos uma função h que queremos integrar, como o produto de duas funções, uma
das quais é a derivada de uma função já conhecida, isto é,
h(x) = f(x) · g′
(x),
com g sendo uma função conhecida.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

22. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Olhamos uma função h que queremos integrar, como o produto de duas funções, uma
das quais é a derivada de uma função já conhecida, isto é,
h(x) = f(x) · g′
(x),
com g sendo uma função conhecida.
Como vimos, temos que
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

23. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Olhamos uma função h que queremos integrar, como o produto de duas funções, uma
das quais é a derivada de uma função já conhecida, isto é,
h(x) = f(x) · g′
(x),
com g sendo uma função conhecida.
Como vimos, temos que
Z
h(x) dx =
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
g(x) · f′
(x) dx.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

24. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Olhamos uma função h que queremos integrar, como o produto de duas funções, uma
das quais é a derivada de uma função já conhecida, isto é,
h(x) = f(x) · g′
(x),
com g sendo uma função conhecida.
Como vimos, temos que
Z
h(x) dx =
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
g(x) · f′
(x) dx.
Esperamos, então, que nossa escolha para as funções f e g tenha sido boa, de maneira
que conheçamos uma primitiva para g · f′.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

25. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Usando novas variáveis, u e v, podemos representar a igualdade acima de uma forma
mais simples u = f(x) e dv = g′(x) dx, implicando em du = f′(x) dx e v = g(x) e,
portanto, com essas novas variáveis, a fórmula que obtivemos acima,
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

26. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Usando novas variáveis, u e v, podemos representar a igualdade acima de uma forma
mais simples u = f(x) e dv = g′(x) dx, implicando em du = f′(x) dx e v = g(x) e,
portanto, com essas novas variáveis, a fórmula que obtivemos acima,
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
g(x) · f′
(x) dx
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

27. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Usando novas variáveis, u e v, podemos representar a igualdade acima de uma forma
mais simples u = f(x) e dv = g′(x) dx, implicando em du = f′(x) dx e v = g(x) e,
portanto, com essas novas variáveis, a fórmula que obtivemos acima,
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
g(x) · f′
(x) dx
se reduz a seguinte versão da fórmula de integração por partes
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

28. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Integração por Partes
Usando novas variáveis, u e v, podemos representar a igualdade acima de uma forma
mais simples u = f(x) e dv = g′(x) dx, implicando em du = f′(x) dx e v = g(x) e,
portanto, com essas novas variáveis, a fórmula que obtivemos acima,
Z
f(x) · g′
(x) dx = f(x) · g(x) −
Z
g(x) · f′
(x) dx
se reduz a seguinte versão da fórmula de integração por partes
Z
u dv = u · v −
Z
v du.
2 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

29. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Calcule
Z
x · ln(x) dx.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

30. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

31. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

32. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

33. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Isso sugere que u = ln(x) e dv = x dx.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

34. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Isso sugere que u = ln(x) e dv = x dx. Então,
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

35. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Isso sugere que u = ln(x) e dv = x dx. Então, du =
1
x
dx e v =
x2
2
+ C1.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

36. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Isso sugere que u = ln(x) e dv = x dx. Então, du =
1
x
dx e v =
x2
2
+ C1.
Da fórmula de integração por partes: uv −
Z
v du, temos:
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

37. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Isso sugere que u = ln(x) e dv = x dx. Então, du =
1
x
dx e v =
x2
2
+ C1.
Da fórmula de integração por partes: uv −
Z
v du, temos:
Z
x ln(x) dx
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

38. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Então, du =
1
x
dx e v =
x2
2
+ C1.
Da fórmula de integração por partes: uv −
Z
v du, temos:
Z
x ln(x) dx = ln(x)
x2
2
+ C1
−
Z
x2
2
+ C1
dx
x
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

39. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Então, du =
1
x
dx e v =
x2
2
+ C1.
Da fórmula de integração por partes: uv −
Z
v du, temos:
Z
x ln(x) dx = ln(x)
x2
2
+ C1
−
Z
x2
2
+ C1
dx
x
=
x2
2
ln(x) + C1 ln(x) −
1
2
Z
x2
dx − C1
Z
dx
x
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

40. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Então, du =
1
x
dx e v =
x2
2
+ C1.
Da fórmula de integração por partes: uv −
Z
v du, temos:
Z
x ln(x) dx = ln(x)
x2
2
+ C1
−
Z
x2
2
+ C1
dx
x
=
x2
2
ln(x) + C1 ln(x) −
1
2
Z
x2
dx − C1
Z
dx
x
=
x2
2
ln(x) + C1 ln(x) −
x3
6
− C1 ln(x) + C2
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

41. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Para determinar quais as substituições para u e dv, devemos ter em mente
que para encontrar v precisamos saber integrar dv.
Então, du =
1
x
dx e v =
x2
2
+ C1.
Da fórmula de integração por partes: uv −
Z
v du, temos:
Z
x ln(x) dx = ln(x)
x2
2
+ C1
−
Z
x2
2
+ C1
dx
x
=
x2
2
ln(x) + C1 ln(x) −
1
2
Z
x2
dx − C1
Z
dx
x
=
x2
2
ln(x) + C1 ln(x) −
x3
6
− C1 ln(x) + C2 =
x2
2
ln(x) −
x3
6
+ C2.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

42. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Neste último exemplo, note que a primeira constante de integração C1 não aparece na
resposta final.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

43. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Neste último exemplo, note que a primeira constante de integração C1 não aparece na
resposta final. C1 foi usada somente para mostrar que todas as escolhas de v da forma
1
2 x2 + C1 produzem o mesmo resultado para
Z
x · ln(x) dx.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

44. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Neste último exemplo, note que a primeira constante de integração C1 não aparece na
resposta final. C1 foi usada somente para mostrar que todas as escolhas de v da forma
1
2 x2 + C1 produzem o mesmo resultado para
Z
x · ln(x) dx. Essa situação vale, em
geral, e provamos isso da seguinte forma:
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

45. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Neste último exemplo, note que a primeira constante de integração C1 não aparece na
resposta final. C1 foi usada somente para mostrar que todas as escolhas de v da forma
1
2 x2 + C1 produzem o mesmo resultado para
Z
x · ln(x) dx. Essa situação vale, em
geral, e provamos isso da seguinte forma: Escrevendo v + C1 na fórmula de integração
por partes, temos:
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

46. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Neste último exemplo, note que a primeira constante de integração C1 não aparece na
resposta final. C1 foi usada somente para mostrar que todas as escolhas de v da forma
1
2 x2 + C1 produzem o mesmo resultado para
Z
x · ln(x) dx. Essa situação vale, em
geral, e provamos isso da seguinte forma: Escrevendo v + C1 na fórmula de integração
por partes, temos:
Z
u dv = u(v + C1) −
Z
(v + C1) du = uv + C1u −
Z
v du − C1
Z
du
= uv + C1u −
Z
v du − C1u = uv −
Z
v du.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

47. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Neste último exemplo, note que a primeira constante de integração C1 não aparece na
resposta final. C1 foi usada somente para mostrar que todas as escolhas de v da forma
1
2 x2 + C1 produzem o mesmo resultado para
Z
x · ln(x) dx. Essa situação vale, em
geral, e provamos isso da seguinte forma: Escrevendo v + C1 na fórmula de integração
por partes, temos:
Z
u dv = u(v + C1) −
Z
(v + C1) du = uv + C1u −
Z
v du − C1
Z
du
= uv + C1u −
Z
v du − C1u = uv −
Z
v du.
Assim, é desnecessário escrevermos a constante de integração quando calculamos v a
partir de dv.
3 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

48. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Determine
Z
x3
· ex2
dx.
4 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

49. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
4 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

50. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Usando integração por partes, com u = x2 e dv = xex2
, temos então que
du = 2x dx e v =
1
2
ex2
, em que v foi obtido pelo método de mudança de variável.
Da fórmula de integração pr partes, temos
Z
x3
ex2
dx = x2
1
2
ex2
−
Z
1
2
ex2
2x dx
=
1
2
x2
ex2
−
Z
xex2
dx
=
1
2
x2
ex2
−
1
2
ex2
+ C.
4 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

51. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Determine
Z
x cos(x) dx.
5 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

52. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
5 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

53. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Seja u = x e dv = cos(x) dx. Então du = dx e v = sin(x). Pela fórmula (??)
Z
x cos(x) dx = x sin(x) −
Z
sin(x) dx
= x sin(x) + cos(x) + C.
5 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

54. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Determine
Z
x2
sin(x) dx.
6 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

55. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
6 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

56. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Fazendo u = x2 e dv = sin(x) dx, temos du = 2x dx e v = − cos(x).
Portanto, pela fórmula de integração por partes, temos:
Z
x2
sin(x) dx = −x2
cos(x) −
Z
− cos(x)2x dx = −x2
cos(x) +
Z
2x cos(x) dx.
A integral do segundo membro é semelhante à primeira integral, exceto que em vez de
sin(x) temos cos(x). Aplicando, novamente, a integração por partes, sendo u = 2x e
dv = cos(x), temos du = 2 dx e v = sin(x). Assim,
Z
x2
sin(x) dx = −x2
cos(x) +
2x sin(x) −
Z
2 sin(x) dx
= −x2
cos(x) + 2x sin(x) + cos(x) + C = −(x2
+ 2) cos(x) + 2x sin(x) + C.
6 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

57. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Determine
Z
xex
dx.
7 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

58. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
7 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

59. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Façamos
u = x ⇒ du = dx e dv = ex
dx ⇒ v = ex
.
Logo,
Z
xex
dx = xex
−
Z
ex
dx = xex
− ex
+ C
= (x − 1)ex
+ C.
7 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

60. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Determine
Z
2x ln(x) dx.
8 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

61. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
8 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

62. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Façamos
u = ln(x) ⇒ du =
1
x
dx e dv = 2x dx ⇒ v = x2
.
Logo,
Z
2x ln(x) dx = x2
ln(x) −
Z
x2 1
x
dx
= x2
ln(x) −
Z
x dx
= x2
ln(x) −
x2
2
+ C.
8 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

63. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Example 1.
Determine
Z
sec3
(x) dx.
9 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

64. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
9 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

65. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Solução: Temos que I =
Z
sec3
(x) dx =
Z
sec(x) sec2
(x) dx
Façamos
u = sec(x) ⇒ du = sec(x) tan(x)dx e dv = sec2
(x) dx ⇒ v = tan(x).
Logo,
I = sec(x) tan(x) −
Z
tan(x) sec(x) tan(x) dx = sec(x) tan(x) −
Z
tan2
(x) sec(x) dx
9 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

66. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exemplo
Como tan2(x) = sec2(x) − 1, temos que:
I = sec(x) tan(x)−
Z
(sec2
(x)−1) sec(x) dx = sec(x) tan(x)−
Z
sec3
(x)dx
| {z }
I
+
Z
sec(x) dx.
Como
Z
sec(x) dx = ln | sec(x) + tan(x)| + C1, temos
2I = sec(x) tan(x) + ln | sec(x) + tan(x)| + C
9 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

67. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
Exercício 1.1.
Mostre, pelo método de integração por partes, as seguintes fórmulas:
a
Z
ln(x) dx = x ln(x) − x + C
b
Z
arctan(x) dx = x arctan(x) −
1
2
ln(1 + x2
) + C
c
Z
eax
cos(bx) dx =
eax
a2 + b2
[b sin(bx) + a cos(bx)]
d
Z
eax
sin(bx) dx =
eax
a2 + b2
[a sin(bx) − b cos(bx)]
10 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

68. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
10 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

69. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
10 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

70. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
10 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

71. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
10 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

72. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
Exercício 1.1.
Determine:
a
∫
x sin(5x) dx;
b
∫
xe
4x
dx;
c
∫
(x + 1) cos(2x) dx;
d
∫
e
x
cos
(
x
2
)
dx;
e
∫
ln(x) dx;
f
∫
ln(1 − x) dx;
g
∫
x ln(x) dx;
h
∫
ln(ax + b)
√
ax + b
dx;
i
∫
x sec
2
(x) dx;
j
∫
x · arctan(x) dx;
k
∫
sec
3
(x) dx;
l
∫
csc
3
(x) dx;
m
∫
√
x ln(x) dx;
n
∫
ln(x
2
+ 1) dx;
o
∫
x
2
ln(x) dx;
p
∫
(x − 1) sec
2
(x) dx;
q
∫
x(ln(x))
2
dx;
r
∫
e
−2x
sin(x) dx;
s
∫
x
3
e
x2
dx;
t
∫
x
3
cos(x
2
) dx;
u
∫
e
−x
cos(2x) dx;
v
∫
x
2
sin(x) dx;
w
∫
x sec(x) tan(x) dx.
11 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

73. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Exercícios Propostos
11 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

74. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Respostas:
a −
x cos(5x)
5
sin(5x)
25
+ C
b e4t
4
(
t − 1
4
)
+ C
c 1
2
sin(2x) (x + 1) +
cos(2x)
4
+ C
d 2
5
sin
(
x
2
)
ex 4
5
ex
cos
(
x
2
)
+ C
e x(ln(x) − 1) + C
f ln(1 − x) · (1 − x) + C
g x2
2
(
ln(x) − 1
2
)
+ C
h 2
√
ax+b
a
(ln(ax + b) − 2) + C
i x tan(x) ln | cos(x)| + C
j x2
2
arctan(x) − x
2
arctan(x)
2
+ C
k 1
2
tan(x) sec(x) + 1
2
ln | sec(x) tan(x)| + C
l −1
2
cot(x) csc(x) + 1
2
ln | csc(x) − cot(x)| + C
m 2
3
x
3
2 ln |x| − 4
9
x
3
2 + C
n x ln(x2
) − 2x arctan(x) + C
o x3
3
(
ln(x) − 1
3
)
+ C
p (x − 1) tan(x) + ln | cos(x)| + C
q x2
2
(
(ln |x|)2
− ln |x| 1
2
)
+ C
r − e−2x
5
(cos(x) + sin(x)) + C
s ex2
2
(x2
− 1) + C
t 1
2
(x2
sin(x2
) cos(x2
)) + C
u e−x
5
(2 sin(2x) − cos(2x)) + C
v −x2
cos(x) sin(x) cos(x) + C
w x sec(x) − ln | sec(x) + tan(x)| + C
11 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022

75. Métodos de Integração
Integração por Partes
Exemplos
Exercícios Propostos
Referências
M. B. Gonçalves and D. M. Flemming.
Cálculo A.
Pearson Education, 5 edition, 2007.
H. L. Guidorizzi.
Um curso de cálculo, volume 1.
Grupo Gen-LTC, 5 edition, 2000.
A. Howard.
Cálculo, um novo horizonte, volume 1.
Bookman, Porto Alegre, 2000.
E. L. Lima.
Curso de Análise, volume 1.
IMPA, Rio de Janeiro, 2000.
J. Stewart.
Cálculo, volume 1.
Cengage Learning, São Paulo, 6 edition, 2009.
12 CETEC Paulo Henrique Ribeiro do Nascimento 14 de julho de 2022