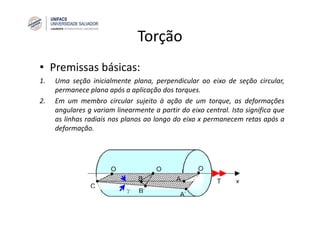
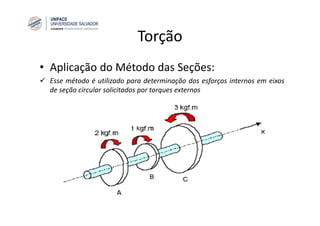
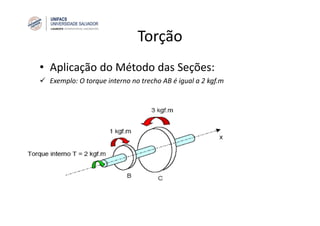
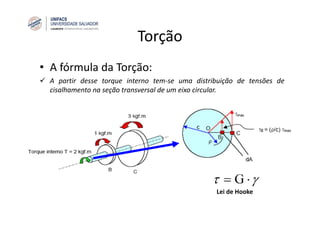
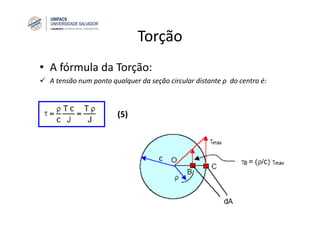
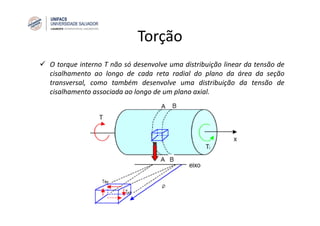
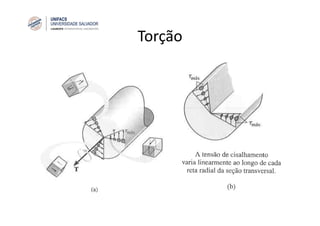
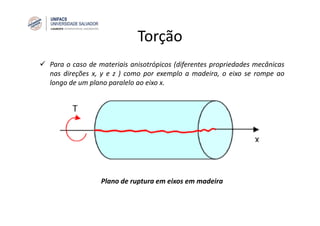
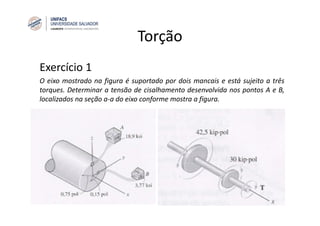
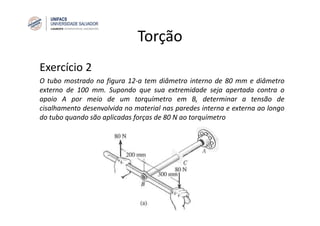
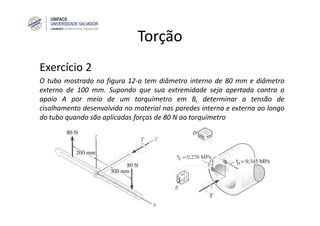
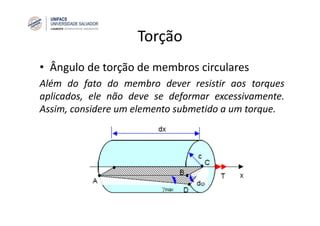
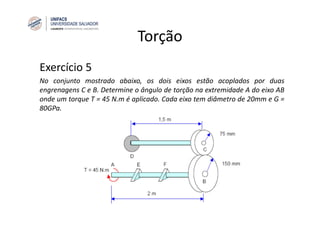
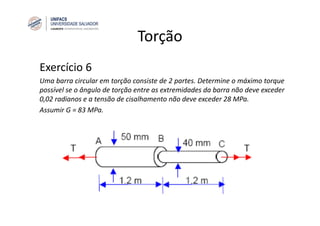
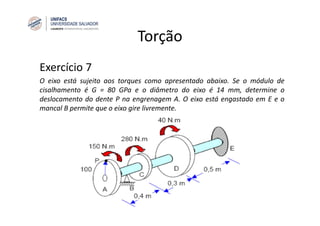
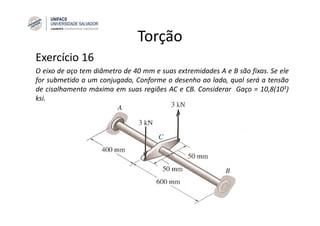
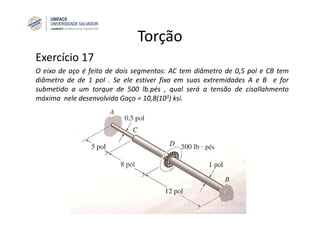
O documento discute o conceito de torção em eixos circulares. Define torque e momento, apresenta as premissas básicas da torção e a fórmula para cálculo da tensão de cisalhamento em eixos circulares sujeitos a torque. Apresenta também exemplos de cálculo de tensões em eixos e tubos sob ação de torque.

1. Torção
Prof. Eng. André Soares
Disciplina: Resistência dos Materiais II

2. Torção
• Definições:
Torque: O que é?
É o momento que tende a torcer o membro em
torno de seu eixo longitudinal.

3. Torção
• Definições:
Momento: O que é?
É uma grandeza que representa a magnitude da
força aplicada a um sistema rotacional a uma
determinada distância de um eixo de rotação
FrM
rrr
×=

4. Torção
• Definições:
Torque: O que é?
É força aplicada a uma determinada distancia
que tende a torcer o membro em torno de seu
eixo longitudinal.

5. Torção
Se o eixo estiver preso em
uma extremidade e for
aplicado um torque na
outra extremidade, o
plano sombreado se
distorcerá e assumirá uma
forma obliqua.

6. Torção
• Premissas básicas:
1. Uma seção inicialmente plana, perpendicular ao eixo de seção circular,
permanece plana após a aplicação dos torques.
2. Em um membro circular sujeito à ação de um torque, as deformações
angulares g variam linearmente a partir do eixo central. Isto significa que
as linhas radiais nos planos ao longo do eixo x permanecem retas após a
deformação.

7. Torção
ATENÇÃO
Estas premissas são válidas somente para eixos circulares.

8. Torção
• Aplicação do Método das Seções:
Esse método é utilizado para determinação dos esforços internos em eixos
de seção circular solicitados por torques externos

9. Torção
• Aplicação do Método das Seções:
Exemplo: O torque interno no trecho AB é igual a 2 kgf.m

10. Torção
• A fórmula da Torção:
A partir desse torque interno tem‐se uma distribuição de tensões de
cisalhamento na seção transversal de um eixo circular.
γτ ⋅= G
Lei de Hooke

11. Torção
• A fórmula da Torção:
O torque interno na seção transversal é a soma dos torques infinitesimais
atuantes em cada área dA.
Onde o momento polar de inércia de área J é dado da forma:
(1)
(2)

12. Torção
• A fórmula da Torção:
O momento polar de inércia para o caso particular de uma seção circular é
da seguinte forma:
Substituindo a eq. (3) na eq. (1), a expressão da tensão máxima atuando na
superfície mais externa do eixo é:
(3)
(4)

13. Torção
• A fórmula da Torção:
A tensão num ponto qualquer da seção circular distante ρ do centro é:
(5)

14. Torção
• A fórmula da Torção:
Para tubos circulares de raio interno ρ e raio externo c, o momento polar de
inércia pode ser calculado como segue:
(6)
(7)

15. Torção
• A fórmula da Torção:
Para tubos circulares de raio interno ρ e raio externo c, o momento polar de
inércia pode ser calculado como segue:
eixo.doexternoraio
al;transversseçãodaáreadapolarinérciademomento
eixo;doallongitudincentrodelinhada
tornoemaplicadaequilibriodemomentodoequaçãopelaeseçõesdasmétodo
peloodeterminadéSeu valoral.transversseçãonaatuaqueinternoptorque
;externasuperfícienaocorrequeeixo,nomáximatocisalhamendetensão
=
=
=
=
c
J
T
τ
J
CT ⋅
=maxτ

16. Torção
O torque interno T não só desenvolve uma distribuição linear da tensão de
cisalhamento ao longo de cada reta radial do plano da área da seção
transversal, como também desenvolve uma distribuição da tensão de
cisalhamento associada ao longo de um plano axial.

17. Torção

18. Torção
Para o caso de materiais anisotrópicos (diferentes propriedades mecânicas
nas direções x, y e z ) como por exemplo a madeira, o eixo se rompe ao
longo de um plano paralelo ao eixo x.
Plano de ruptura em eixos em madeira

19. Torção
• Atenção!
O conteúdo estudado nesse curso não deve ser aplicado para o estudo de
eixos maciços de seção transversal não circular.
O conteúdo estudado nesse curso não deve ser aplicado para estudos de
torção em tubos de paredes finas com seções diferentes de círculos.

20. Torção
Exercício 1
O eixo mostrado na figura é suportado por dois mancais e está sujeito a três
torques. Determinar a tensão de cisalhamento desenvolvida nos pontos A e B,
localizados na seção a‐a do eixo conforme mostra a figura.

21. Torção
Exercício 1
O eixo mostrado na figura é suportado por dois mancais e está sujeito a três
torques. Determinar a tensão de cisalhamento desenvolvida nos pontos A e B,
localizados na seção a‐a do eixo conforme mostra a figura.

22. Torção
Exercício 2
O tubo mostrado na figura 12‐a tem diâmetro interno de 80 mm e diâmetro
externo de 100 mm. Supondo que sua extremidade seja apertada contra o
apoio A por meio de um torquímetro em B, determinar a tensão de
cisalhamento desenvolvida no material nas paredes interna e externa ao longo
do tubo quando são aplicadas forças de 80 N ao torquímetro

23. Torção
Exercício 2
O tubo mostrado na figura 12‐a tem diâmetro interno de 80 mm e diâmetro
externo de 100 mm. Supondo que sua extremidade seja apertada contra o
apoio A por meio de um torquímetro em B, determinar a tensão de
cisalhamento desenvolvida no material nas paredes interna e externa ao longo
do tubo quando são aplicadas forças de 80 N ao torquímetro

24. Torção
• Transmissão de Potência
Eixos e tubos de seção circular são freqüentemente
utilizados para transmissão de potência. Quando
utilizados para esse propósito os eixos são submetidos a
torques que dependem da potência gerada pela
máquina e da velocidade angular do eixo.
fTPTP πω =⇒= 2

25. Torção
• Transmissão de Potência
A potência P é definida como o trabalho realizado por
unidade de tempo, no SI a potência é expressa em watts,
quando o torque é medido em (N . m) e ω é medido em
(rad/s),temos então 1W = 1N.m/s. No Sistema FPS temos
: 1 hp=550 pés.lb/s
fTPTP πω =⇒= 2

26. Torção
• Transmissão de Potência
CV014,1HP1
W5,735CV1
=
=

27. Torção
• Projeto de elementos circulares em torção
Uma vez conhecido o torque a ser transmitido pelo eixo,
e selecionado a máxima tensão de cisalhamento, as
proporções do membro tornam‐se fixas. Assim, tem‐se:
J/C é utilizado para projetar eixos
maciços ou perfurados
maxτ
T
C
J
=
admττ =max

28. Torção
Exercício 3
Selecione dois eixos maciços para transmitir 200 cv de potência cada um, de
forma que nenhum deles ultrapasse a tensão de cisalhamento de 7 kgf/mm2.
Um desses eixos deve operar a 20 rpm, e o outro a 20.000 rpm.
(1CV = 4500 kgf.m/min, ω (rad/min) = 2π ƒ(rpm))

29. Torção
Exercício 4
Um eixo é feito de liga de aço com tensão de cisalhamento admissível τadm =
12 ksi. Supondo que o diâmetro do eixo seja de 1,5 pol, determinar o torque
máximo T que pode ser transmitido. Qual seria o torque máximo T’ se fosse
feiro um furo de 1 pol de diâmetro ao longo do eixo? Traçar o gráfico da
distribuição de cisalhamento‐tensão ao longo de uma reta radial em cada caso.

30. Torção
• Ângulo de torção de membros circulares
Além do fato do membro dever resistir aos torques
aplicados, ele não deve se deformar excessivamente.
Assim, considere um elemento submetido a um torque.

31. Torção
• Ângulo de torção de membros circulares
Expressão geral para o ângulo de Torção.
Quando temos o torque e a seção transversal constante
ao longo do comprimento do eixo, tem‐se:
GJ
LT
⋅
⋅
=φ
Ø = ângulo de torção de uma extremidade do eixo em relação à outra, medido em
radianos
Т = torque interno, determinado pelo método das seções e pela equação do
momento na condição de equilíbrio aplicada em torno da linha de centro do eixo.
L = comprimento
J = momento de inércia polar do eixo
G = módulo de elasticidade ao cisalhamento do material

32. Torção
ATENÇÃO
O conteúdo estudado nesse curso não deve ser aplicado para
o estudo de eixos maciços de seção transversal não circular.
O conteúdo estudado nesse curso não deve ser aplicado para
estudos de torção em tubos de paredes finas com seções
diferentes de círculos.

33. Torção
Exercício 5
No conjunto mostrado abaixo, os dois eixos estão acoplados por duas
engrenagens C e B. Determine o ângulo de torção na extremidade A do eixo AB
onde um torque T = 45 N.m é aplicado. Cada eixo tem diâmetro de 20mm e G =
80GPa.

34. Torção
Exercício 6
Uma barra circular em torção consiste de 2 partes. Determine o máximo torque
possível se o ângulo de torção entre as extremidades da barra não deve exceder
0,02 radianos e a tensão de cisalhamento não deve exceder 28 MPa.
Assumir G = 83 MPa.

35. Torção
Exercício 7
O eixo está sujeito aos torques como apresentado abaixo. Se o módulo de
cisalhamento é G = 80 GPa e o diâmetro do eixo é 14 mm, determine o
deslocamento do dente P na engrenagem A. O eixo está engastado em E e o
mancal B permite que o eixo gire livremente.

36. Torção
Elementos Estaticamente Indeterminados
Carregados com Torque
∑ Mx = 0
L = LAC + LBC

37. Torção
Elementos Estaticamente Indeterminados
Carregados com Torque
ØA/B = 0
Condição de
Compatibilidade Necessária
TA LAC / JG ‐ TB LBC / JG = 0
TA = T (LBC / L)
TB = T (LAC / L)

38. Torção
Exercício 8
O Eixo de aço maciço mostrado
ao lado tem diâmetro de 20
mm. Se for submetido aos dois
torques , quais serão as reações
nos apoios fixos A e B ?

39. Torção
Exercício 9
O Eixo mostrado na figura ao lado esta
composto por um tubo de aço unido a
um núcleo de latão.Supondo que seja
aplicado um torque de T = 250 lb.pés à
sua extremidade, esquematizar a
distribuição cisalhamento tensão ao
longo de uma reta radial da área da
seção transversal.Supor, também, que
Gaço = 11,40(103) ksi e Glatão
= 5,20(103) ksi.

40. Torção
Exercício 9
Um motor de 200 kW gira a 250 rpm. Para a engrenagem em B é transmitido
90 kW e para a engrenagem em C 110 kW. Determine o menor diâmetro
permissível d se a tensão admissível é de 50 MPa e o ângulo de torção entre o
motor e a engrenagem C é limitado a 15°. Considerar G = 80 Gpa e 1kW »
60000 Nm/mim.

41. Torção
Exercício 10
O conjunto consiste em dois
segmentos de tubos de aço
galvanizados acoplados por uma
redução em B. O tubo menor tem
diâmetro externo de 0,75 pol e
diâmetro interno de 0,68 pol,
enquanto o tubo maior tem
diâmetro externo de 1 pol e
diâmetro interno de 0,86 pol.
Supondo que o tubo esteja
firmemente preso à parede em C,
determinar a tensão de
cisalhamento máxima desenvolvida
em cada seção do tubo quando o
conjugado mostrado é aplicado ao
cabo da chave

42. Torção
Exercício 11
Um tubo de aço com diâmetro externo de 2,5 pol transmite 35 hp quando gira
a 2700 rev/min. Determinar o diâmetro interno do tubo com aproximação de
1/8 pol se a tensão de cisalhamento admissível é τ adm = 10 ksi

43. Torção
Exercício 12
Um eixo maciço tem diâmetro de 0, 75 pol. Supondo que seja submetido aos
torques mostrados, determinar a tensão de cisalhamento máxima
desenvolvida nas regiões BC, DE,CD e EF. Os mancais A e F permitem rotação
livre do eixo.

44. Torção
Exercício 13
O eixo de aço está submetido à
carga de torção mostrada, a)
Determinar a tensão de
cisalhamento desenvolvida nos
pontos A e B. o eixo onde A e B
estão localizados tem raio
externo de 60 mm.b) Determinar
a tensão de cisalhamento
máxima absoluta nele
desenvolvida e desenhar a
distribuição cisalhamento‐tensão
ao longo de uma reta radial em
que ele atinja o máximo.

45. Torção
Exercício 14
O Eixo de aço A‐36 tem 2 m de comprimento e diâmetro externo de 40 mm.
Quando gira a 80 rad/s, transmite 32 kW de potência do motor E para o gerador
G . Determinar a menor espessura do eixo se a tensão de cisalhamento
adimissível τadm = 140 MPa e o eixo não pode ter uma torção maior que 0,05 rad.

46. Torção
Exercício 15
O Eixo de aço A‐36 tem 3 m de comprimento e diâmetro externo de 50 mm.
Requer‐se que transmita 35 kW de potência do motor E para o gerador G .
Determinar a menor velocidade angular que o eixo pode ter se a máxima torção
admissível é de 1 grau.

47. Torção
Exercício 16
O eixo de aço tem diâmetro de 40 mm e suas extremidades A e B são fixas. Se ele
for submetido a um conjugado, Conforme o desenho ao lado, qual será a tensão
de cisalhamento máxima em suas regiões AC e CB. Considerar Gaço = 10,8(103)
ksi.

48. Torção
Exercício 17
O eixo de aço é feito de dois segmentos: AC tem diâmetro de 0,5 pol e CB tem
diâmetro de de 1 pol . Se ele estiver fixo em suas extremidades A e B e for
submetido a um torque de 500 lb.pés , qual será a tensão de cisallahmento
máxima nele desenvolvida Gaço = 10,8(103) ksi.

49. Torção
Exercício 18
O conjunto de aço A‐36 consiste em um tubo com raio externo de 1 pol e
espessura parede de 0,125 pol. Por meio de uma chapa rígida em B, ele é
acoplado ao eixo maciço AB de 1 pol de diâmetro. Determinar a rotação da
extremidade C do tubo se um torque de 200 lb.pol for aplicado nessa extremidade.
A extremidade A do eixo tem apoio fixo

50. Torção
Exercício 19
As extremidades estriadas e as
engrenagens acopladas ao eixo de
aço A‐36 estão submetidas aos
torques mostrados. Determinar o
ângulo de torção da extremidade
B em relação à extremidade A. O
eixo tem diâmetro de 40 mm.
Considerar G= 75x109 N/m2.

51. Prof. André Felipe Leite Soares
Engenheiro Mecânico
andreflsoares@gmail.com