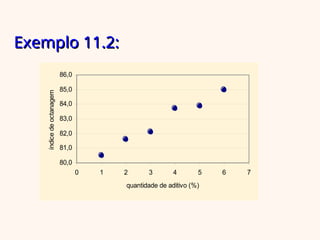
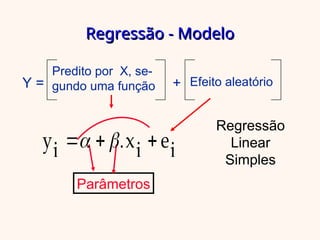
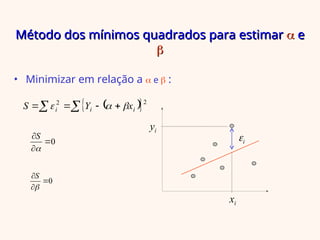
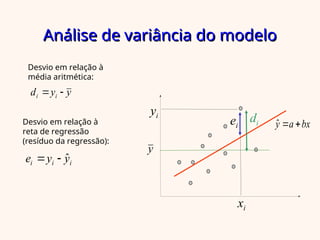
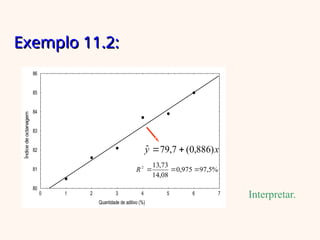
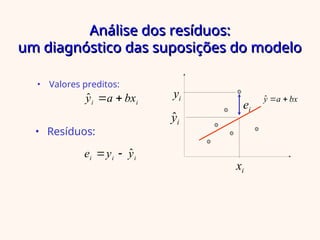
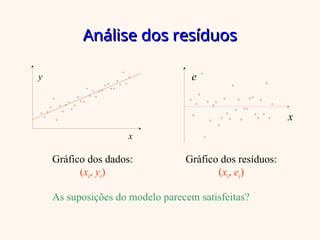
O documento aborda a regressão linear simples, apresentando como determinar a relação entre uma variável independente (x) e uma dependente (y) utilizando o método dos mínimos quadrados. Inclui exemplos práticos, análise de variância e interpretação do coeficiente de determinação para avaliar a qualidade do ajuste do modelo. Além disso, discute as suposições do modelo e a análise dos resíduos para validar as suposições feitas.

1. Regressão linear simples
Regressão linear simples
Variável independente,
X
Variável dependente,
Y
Temperatura do forno (0
C) Resistência mecânica da cerâmica (MPa)
Quantidade de aditivo (%) Octanagem da gasolina
Renda (R$) Consumo (R$)
Memória RAM do computador (Gb) Tempo de resposta do sistema (s)
Área construída do imóvel (m2
) Preço do imóvel (R$)

2. Exemplo 11.2:
Exemplo 11.2:
• X = % de aditivo
• Y = Índice de octanagem da
gasolina
X Y
1 80,5
2 81,6
3 82,1
4 83,7
5 83,9
6 85,0
Resultados de n = 6
ensaios experimentais:

3. Exemplo 11.2:
Exemplo 11.2:
80,0
81,0
82,0
83,0
84,0
85,0
86,0
0 1 2 3 4 5 6 7
quantidade de aditivo (%)
índice
de
octanagem

4. Regressão - Modelo
Regressão - Modelo
Y =
Predito por X, se-
gundo uma função Efeito aleatório
+
Parâmetros
Regressão
Linear
Simples
yi .xi ei
  
 

5. Modelo de regressão linear simples
Modelo de regressão linear simples
• Em termos das variáveis:   X
Y
E 
 

• Em termos dos dados: Yi =  + xi + i
• Suposições:
– os termos de erro (1, 2, ..., n) são variáveis aleatórias
independentes;
– E{i} = 0;
– V{i} = 2
; e
 i tem distribuição normal (i = 1, 2, ..., n).

6. Método dos mínimos quadrados para estimar
Método dos mínimos quadrados para estimar 
 e
e


• Minimizar em relação a  e  :
yi
xi
i
 
 

 



2
2
i
i
i x
Y
S 


0




S
0




S

7. Método dos mínimos quadrados para estimar
Método dos mínimos quadrados para estimar 
 e
e


• Resultado das derivadas parciais:
     
 2
2








i
i
i
i
i
i
x
x
n.
y
x
y
x
n.
b =
n
x
b
y
a = i
i 
 
Estimativa de :
Estimativa de  :
Reta de regressão construída com os dados:
bx
a
y 

ˆ

8. Qualidade do ajuste
Qualidade do ajuste
• Ajustou-se uma equação de
regressão entre X e Y. E a
qualidade do ajuste?
– análise de variância do modelo
– análise dos resíduos

9. Reta de regressão e resíduos
Reta de regressão e resíduos
• Valores preditos:
• Resíduos:
i
i bx
a
y 

ˆ
i
i
i y
y
e ˆ


yi
xi
ei
i
ŷ
bx
a
y 

ˆ

10. Análise de variância do modelo
Análise de variância do modelo
yi
xi
ei
di bx
a
y 

ˆ
y
y
y
d i
i 

i
i
i y
y
e ˆ


Desvio em relação à
média aritmética:
Desvio em relação à
reta de regressão
(resíduo da regressão):

11. Somas de quadrados
Somas de quadrados
SQT
variação total
SQR
variação explicada
pela equação de
regressão
SQE
variação não
explicada
 
 
2
y
yi =  
 
2
ˆ y
yi +  
 
2
ˆi
i y
y

12. Somas de quadrados
Somas de quadrados
 
 
n
y
y
y
y
SQT i
i
i
2
2
2 

 



  


 



 i
i
i
i
i
i y
x
b
y
a
y
y
y
SQE 2
2
ˆ
SQE
SQT
SQR 

Coeficiente de determinação:
SQT
SQE
SQT
SQR
R 

 1
2

13. Medida da qualidade do ajuste:
Medida da qualidade do ajuste:
Coeficiente de determinação (R2
)
R2
=
Variação
total
Variação
explicada
=
 (yi - y)2
 (yi - y)2
^
0  R2
 1 Matematicamente, R2
é o
quadrado do Coef. de Correlação
de Pearson.

14. Exemplo 11.2:
Exemplo 11.2:
Quantidade de aditivo (%)
Índice
de
octanagem
80
81
82
83
84
85
86
0 1 2 3 4 5 6 7
x
y )
886
,
0
(
7
,
79
ˆ 

%
5
,
97
975
,
0
08
,
14
73
,
13
2



R
Interpretar.

15. Fonte de
variação
gl SQ QM Razão f
Regressão 1
Erro n – 2
Total n – 1
Análise de variância do modelo
Análise de variância do modelo
 
 

2
ˆ y
y
SQR i
1
SQR
QMR 
QME
QMR
f 
 
 
 2
ˆi
i y
y
SQE
 
 
 2
y
y
SQT i
2


n
SQE
QME

16. Teste de significância do modelo
Teste de significância do modelo
• H0:  = 0 e H1:   0
• Distribuição de referência para a razão f :
distribuição F com gl = 2 no numerador e
gl = n – 2 no denominador (Tabela 6).
  X
Y
E .

 


17. Exemplo 11.2:
Exemplo 11.2:
Fonte de variação gl SQ MQ Razão f
Regressão 1 13,73 13,729 156,26
Erro 4 0,35 0,088
Total 5 14,08
Usar a Tabela 6 e fazer o teste de significância do modelo.

18. Suposições do modelo
Suposições do modelo
– os termos de erro (1,
2, ..., n) são variáveis
aleatórias
independentes;
– E{i} = 0;
– V{i} = 2
; e
 i tem distribuição
normal (i = 1, 2, ..., n).
• Modelo: Yi =  + xi + i
x
E{Y}= +x
y

19. Análise dos resíduos:
Análise dos resíduos:
um diagnóstico das suposições do modelo
um diagnóstico das suposições do modelo
• Valores preditos:
i
i bx
a
y 

ˆ
i
i
i y
y
e ˆ


• Resíduos:
yi
xi
ei
i
ŷ
bx
a
y 

ˆ

20. Análise dos resíduos
Análise dos resíduos
x
y e
x
Gráfico dos dados:
(xi, yi)
Gráfico dos resíduos:
(xi, ei)
As suposições do modelo parecem satisfeitas?

21. Análise dos resíduos
Análise dos resíduos
Gráfico dos dados:
(xi, yi)
Gráfico dos resíduos:
(xi, ei)
As suposições do modelo parecem satisfeitas?
O que pode ser feito? (Ver livro)
x
y
resíduo
0
x

22. Análise dos resíduos
Análise dos resíduos
Gráfico dos dados:
(xi, yi)
Gráfico dos resíduos:
(xi, ei)
As suposições do modelo parecem satisfeitas?
O que pode ser feito? (Ver livro)
x
y
e
0
x

23. Análise dos resíduos
Análise dos resíduos
Gráfico dos resíduos: (xi, ei)
As suposições do modelo parecem satisfeitas?
O que pode ser feito? (Ver livro)
resíduo
0 x