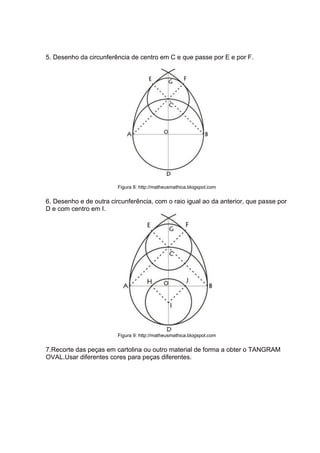
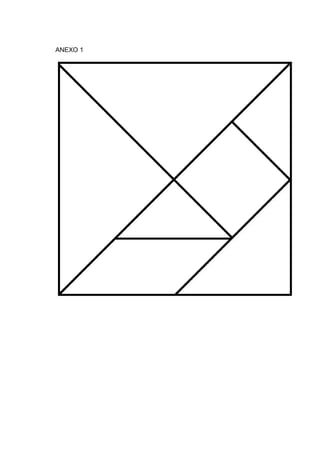
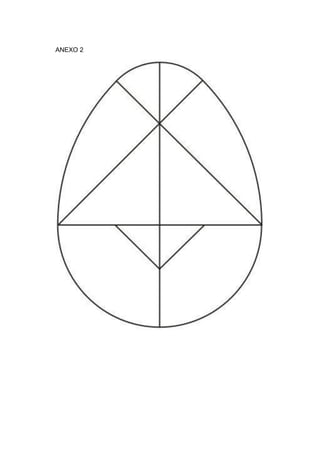
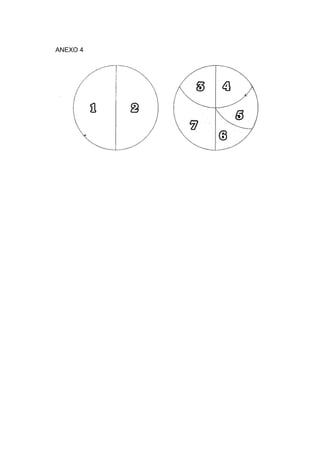
O documento descreve vários tipos de quebra-cabeças tangram, incluindo suas peças, construção e como podem ser usados em atividades educacionais. É fornecida instrução detalhada sobre como construir tangrams clássicos, ovais, de coração partido e de círculos partidos, além de exemplos de figuras que podem ser formadas e sugestões de atividades para diferentes séries do ensino fundamental.