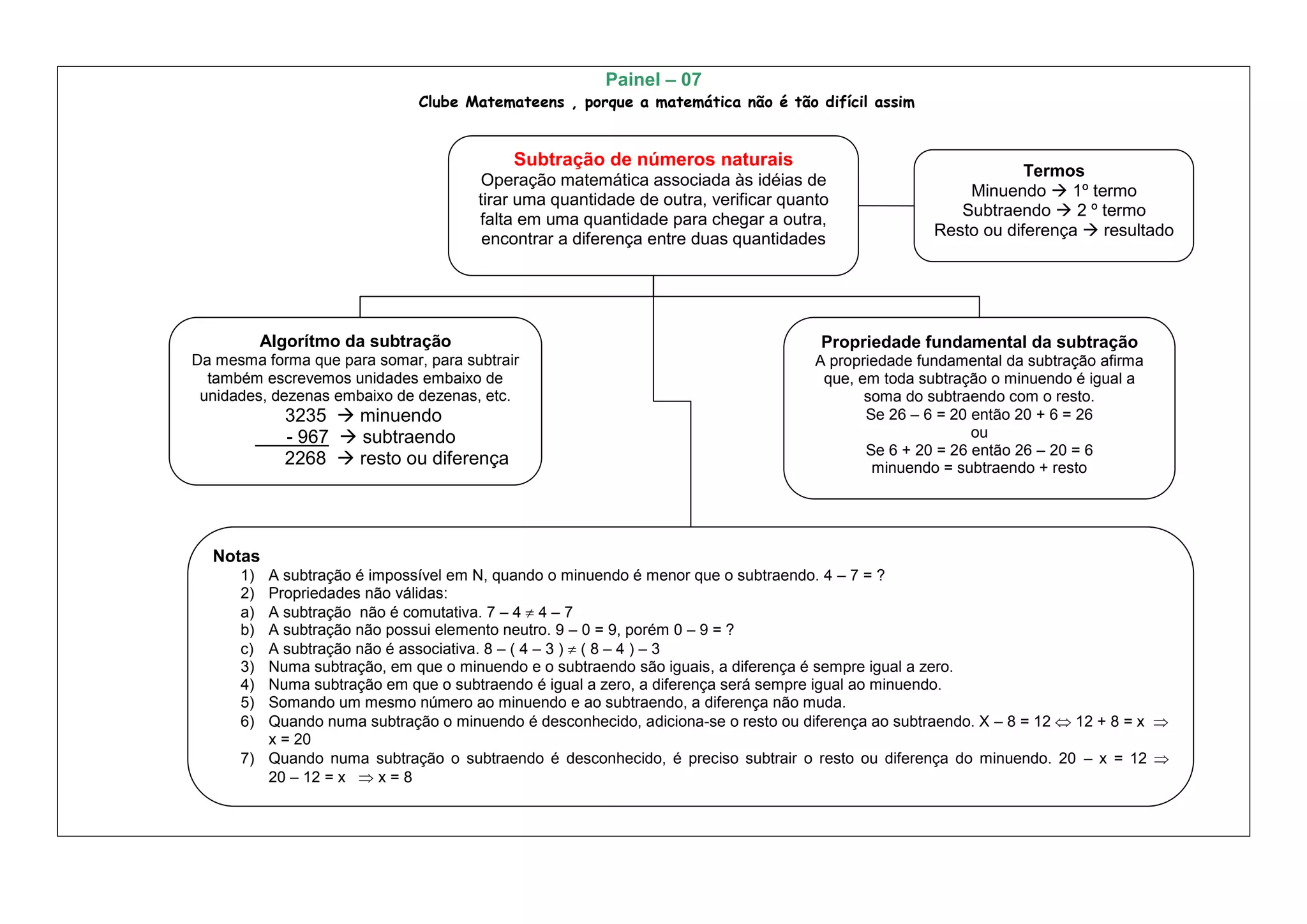
A subtração de números naturais envolve retirar uma quantidade de outra para encontrar a diferença entre elas. Ela segue um algoritmo de escrever as unidades embaixo das unidades e as dezenas embaixo das dezenas, da direita para a esquerda. Sua propriedade fundamental afirma que o minuendo é igual à soma do subtraendo com o resto.

1. Painel – 07
Clube Matemateens , porque a matemática não é tão difícil assim
Subtração de números naturais
Termos
Operação matemática associada às idéias de
Minuendo  1º termo
tirar uma quantidade de outra, verificar quanto
Subtraendo  2 º termo
falta em uma quantidade para chegar a outra,
encontrar a diferença entre duas quantidades Resto ou diferença  resultado
Algorítmo da subtração Propriedade fundamental da subtração
Da mesma forma que para somar, para subtrair A propriedade fundamental da subtração afirma
também escrevemos unidades embaixo de que, em toda subtração o minuendo é igual a
unidades, dezenas embaixo de dezenas, etc. soma do subtraendo com o resto.
3235  minuendo Se 26 – 6 = 20 então 20 + 6 = 26
- 967  subtraendo ou
Se 6 + 20 = 26 então 26 – 20 = 6
2268  resto ou diferença minuendo = subtraendo + resto
Notas
1) A subtração é impossível em N, quando o minuendo é menor que o subtraendo. 4 – 7 = ?
2) Propriedades não válidas:
a) A subtração não é comutativa. 7 – 4  4 – 7
b) A subtração não possui elemento neutro. 9 – 0 = 9, porém 0 – 9 = ?
c) A subtração não é associativa. 8 – ( 4 – 3 )  ( 8 – 4 ) – 3
3) Numa subtração, em que o minuendo e o subtraendo são iguais, a diferença é sempre igual a zero.
4) Numa subtração em que o subtraendo é igual a zero, a diferença será sempre igual ao minuendo.
5) Somando um mesmo número ao minuendo e ao subtraendo, a diferença não muda.
6) Quando numa subtração o minuendo é desconhecido, adiciona-se o resto ou diferença ao subtraendo. X – 8 = 12  12 + 8 = x 
x = 20
7) Quando numa subtração o subtraendo é desconhecido, é preciso subtrair o resto ou diferença do minuendo. 20 – x = 12 
20 – 12 = x  x = 8