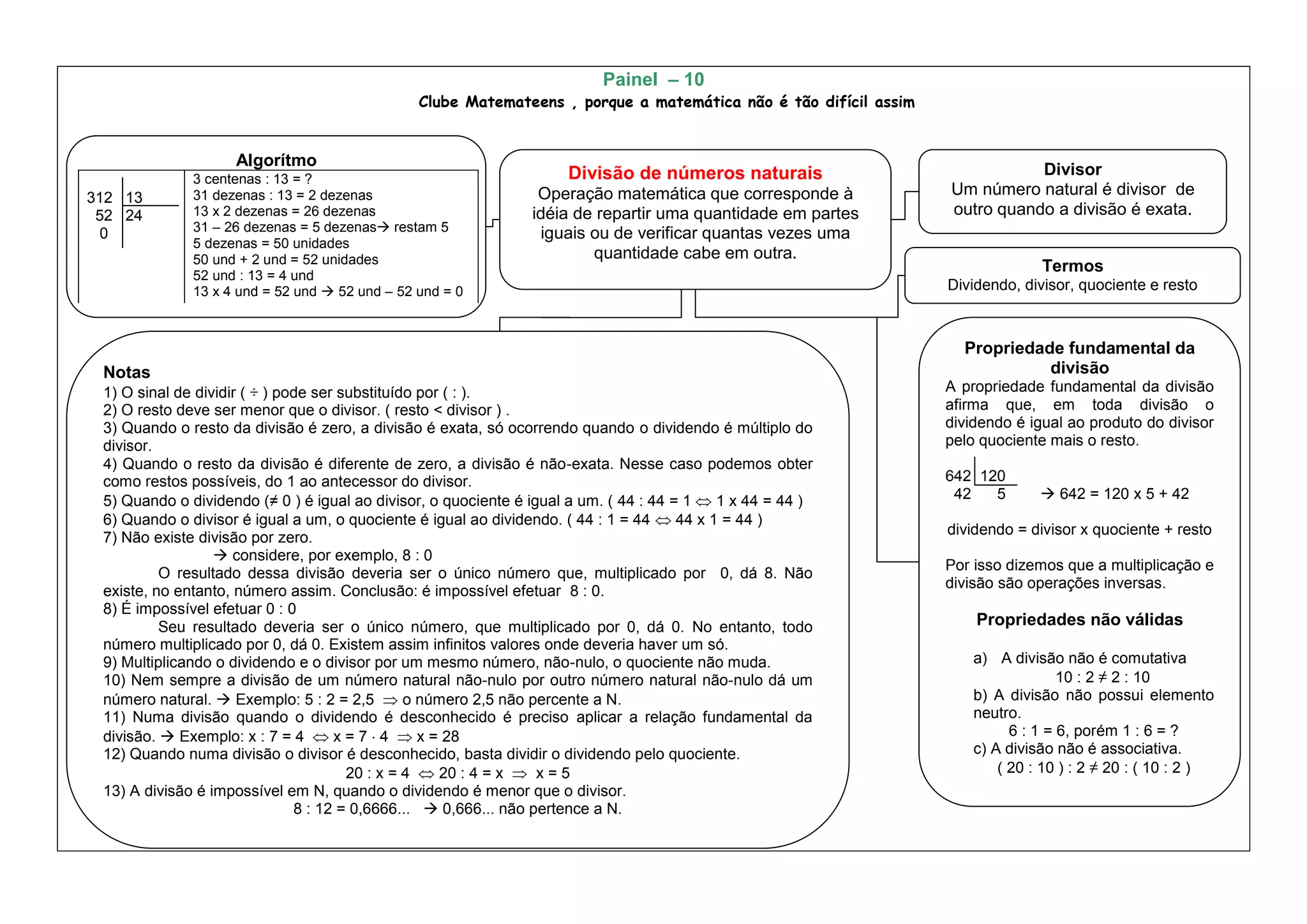
1) O documento explica os conceitos fundamentais da divisão de números naturais, incluindo divisor, dividendo, quociente e resto. 2) É definida a propriedade fundamental da divisão, que afirma que o dividendo é igual ao produto do divisor pelo quociente mais o resto. 3) São apresentadas várias notas importantes sobre a operação de divisão e suas propriedades.

1. Painel – 10
Clube Matemateens , porque a matemática não é tão difícil assim
Algorítmo
Divisão de números naturais Divisor
3 centenas : 13 = ?
312 13 31 dezenas : 13 = 2 dezenas Operação matemática que corresponde à Um número natural é divisor de
52 24 13 x 2 dezenas = 26 dezenas idéia de repartir uma quantidade em partes outro quando a divisão é exata.
0 31 – 26 dezenas = 5 dezenas restam 5 iguais ou de verificar quantas vezes uma
5 dezenas = 50 unidades
50 und + 2 und = 52 unidades quantidade cabe em outra.
Termos
52 und : 13 = 4 und
13 x 4 und = 52 und  52 und – 52 und = 0 Dividendo, divisor, quociente e resto
Propriedade fundamental da
Notas divisão
1) O sinal de dividir ( ÷ ) pode ser substituído por ( : ). A propriedade fundamental da divisão
2) O resto deve ser menor que o divisor. ( resto < divisor ) . afirma que, em toda divisão o
3) Quando o resto da divisão é zero, a divisão é exata, só ocorrendo quando o dividendo é múltiplo do dividendo é igual ao produto do divisor
divisor. pelo quociente mais o resto.
4) Quando o resto da divisão é diferente de zero, a divisão é não-exata. Nesse caso podemos obter
como restos possíveis, do 1 ao antecessor do divisor. 642 120
5) Quando o dividendo (≠ 0 ) é igual ao divisor, o quociente é igual a um. ( 44 : 44 = 1  1 x 44 = 44 ) 42 5  642 = 120 x 5 + 42
6) Quando o divisor é igual a um, o quociente é igual ao dividendo. ( 44 : 1 = 44  44 x 1 = 44 )
dividendo = divisor x quociente + resto
7) Não existe divisão por zero.
 considere, por exemplo, 8 : 0
Por isso dizemos que a multiplicação e
O resultado dessa divisão deveria ser o único número que, multiplicado por 0, dá 8. Não
divisão são operações inversas.
existe, no entanto, número assim. Conclusão: é impossível efetuar 8 : 0.
8) É impossível efetuar 0 : 0
Seu resultado deveria ser o único número, que multiplicado por 0, dá 0. No entanto, todo Propriedades não válidas
número multiplicado por 0, dá 0. Existem assim infinitos valores onde deveria haver um só.
9) Multiplicando o dividendo e o divisor por um mesmo número, não-nulo, o quociente não muda. a) A divisão não é comutativa
10) Nem sempre a divisão de um número natural não-nulo por outro número natural não-nulo dá um 10 : 2 ≠ 2 : 10
número natural.  Exemplo: 5 : 2 = 2,5  o número 2,5 não percente a N. b) A divisão não possui elemento
11) Numa divisão quando o dividendo é desconhecido é preciso aplicar a relação fundamental da neutro.
divisão.  Exemplo: x : 7 = 4  x = 7  4  x = 28 6 : 1 = 6, porém 1 : 6 = ?
12) Quando numa divisão o divisor é desconhecido, basta dividir o dividendo pelo quociente. c) A divisão não é associativa.
20 : x = 4  20 : 4 = x  x = 5 ( 20 : 10 ) : 2 ≠ 20 : ( 10 : 2 )
13) A divisão é impossível em N, quando o dividendo é menor que o divisor.
8 : 12 = 0,6666...  0,666... não pertence a N.