A conquista da matematica

Caro professor,
Este material foi organizado pensando em você.
Ele possui todas as resoluções dos exercícios da coleção;
assim, fi cará mais fácil identifi car a complexidade de
cada exercício, agilizando seu trabalho em sala de aula.
O formato em CD permite a impressão seletiva, auxiliando
a elaboração e a correção de provas e trabalhos.
Os autores

SUMÁRIO
6o . ano
O ser humano vive cercado por números......................................................................................................................... 5
Calculando com números naturais................................................................................................................................... 7
Divisibilidade: divisores e múltiplos................................................................................................................................... 19
Geometria: as ideias intuitivas........................................................................................................................................... 29
A forma fracionária dos números racionais.................................................................................................................. 32
A forma decimal dos números racionais.......................................................................................................................... 47
Medindo comprimentos e superfícies................................................................................................................................. 59
Volume e capacidade.............................................................................................................................................................. 67
Medindo a massa.................................................................................................................................................................... 70
7o . ano
Potências e raízes................................................................................................................................................................... 75
O conjunto dos números inteiros...................................................................................................................................... 84
O conjunto dos números racionais................................................................................................................................... 102
Estudando as equações........................................................................................................................................................ 117
Estudando as inequações..................................................................................................................................................... 147
Estudando os ângulos.......................................................................................................................................................... 155
Estudando triângulos e quadriláteros........................................................................................................................... 165
Razões e proporções............................................................................................................................................................... 167
Grandezas proporcionais..................................................................................................................................................... 185
Porcentagem............................................................................................................................................................................ 200
8o . ano
Os números reais.................................................................................................................................................................... 207
Introdução ao cálculo algébrico...................................................................................................................................... 211
Estudo dos polinômios.......................................................................................................................................................... 214
Estudo das frações algébricas........................................................................................................................................... 230
Equações do 1o. grau com uma incógnita......................................................................................................................... 236
Porcentagem e juro simples.................................................................................................................................................. 245
Sistema de equações do 1o. grau com duas incógnitas.................................................................................................. 248
Geometria................................................................................................................................................................................. 259
Ângulos formados por duas retas paralelas com uma reta transversal............................................................... 262
Polígonos................................................................................................................................................................................. 265
Estudando os triângulos..................................................................................................................................................... 270
Estudando os quadriláteros............................................................................................................................................... 276
Estudando a circunferência e o círculo.......................................................................................................................... 282
9 o . ano
Noções elementares de estatística.................................................................................................................................... 291
Estudando as potências e suas propriedades................................................................................................................... 296
Calculando com radicais..................................................................................................................................................... 304
Equações do 2o. grau.............................................................................................................................................................. 338
Função polinomial do 1o. grau............................................................................................................................................ 388
Função polinomial do 2o. grau (ou função quadrática).............................................................................................. 397
Segmentos proporcionais...................................................................................................................................................... 411
Semelhança.............................................................................................................................................................................. 419
Estudando as relações trigonométricas no triângulo retângulo.......................................................................... 430
Estudando as relações trigonométricas nos triângulos........................................................................................... 442
Estudando as áreas das figuras geométricas planas................................................................................................... 453
Estudando a circunferência e o círculo.......................................................................................................................... 465

SUMÁRIO
6o . ano
O ser humano vive cercado por números............................................................ 5
Calculando com números naturais.................................................................... 7
Divisibilidade: divisores e múltiplos.................................................................... 19
Geometria: as ideias intuitivas........................................................................... 29
A forma fracionária dos números racionais....................................................... 32
A forma decimal dos números racionais............................................................. 47
Medindo comprimentos e superfícies................................................................... 59
Volume e capacidade.......................................................................................... 67
Medindo a massa............................................................................................... 70

5
O SER HUMANO VIVE CERCADO POR NÚMEROS
Explorando, página 10.
1. Resposta em aberto.
3. Respostas pessoais.
1 − Uma história muito antiga
Exercícios, página 14.
1. a3; b1; c4; d2
3.
a) 8h19min
b) 1, 2, 3, 4 e 5
c) X
Desafio!, página 15.
b)
c)
d)
e)
Brasil real, página 16.
1.
a) XVIII c) MDCCLXXXVII
b) XIX d) MDCCCLXXXIX
2. MDCCCXL  1840; MDCCCLXXXIX  1889;
MDCCCLXXIX  1879; MDCCCLIV  1854;
MDCCCLII  1852
2 – E o nosso sistema de numeração?
Exercícios, páginas 19 e 20.
1.
a) São iguais. b) cinco; 5
3. sete; 7; .
Existem outras maneiras.
4.
a) 3 e) 8
b) 4 f) 1
c) 5 g) 3
d) 6 h) 5
5.
a) 302
b) 1
c) 12 322
d) 45 667
e) 100
f) 1 000
g) 10 000
h) 100 000
i) 901
j) 19 900
6.
a) 887 d) 0
b) 99 e) 11 999
c) 9 470 f) 7 000
7.
a) 1 001 c) 4 002
b) 20 010 d) 6 006
8.
a) 636 e 640
b) 1 324 e 1 328
c) 19 552 e 19 556
9.
a) 1 001 e 1 005
b) 9 007 e 9 011
c) 20 219 e 20 223
11.
a) 4 algarismos; 7, 5, 0 e 4
b) 4 algarismos; 1 e 0
c) 4 algarismos; 5
d) 6 algarismos; 1, 7, 4 e 0
Chegou a sua vez!, página 21.
1. “Os campeões em cada copa”
2. Os anos da copa, os países que sediaram
a competição e os respectivos campeões.
Editoria de arte

6
3. www.fifa.com
4.
a) 5 e) 3
b) 2 f) 1
c) 2 g) 1
d) 4 h) 0
5.
a) 10 b) 7 c) 1
6. 6
1. Desenhar: a) 10 bolinhas, b) 13 bolinhas,
c) 21 bolinhas, d) 11 bolinhas.
2.
a) Desenhar 1 bolinha, 31 bolinhas,
12 bolinhas e 11 bolinhas.
b) Somente no caso do item b, em que
houve um aumento de 18 .
c) Nos casos dos itens a e c. No item
a, diminuição de 9 ; no item c,
diminuição de 9 .
3.
a) Diminuiu. c) 50; 7
b) 5; 70
4.
a) Diminuiu.
b) Passou de 800 para 8.
c) Passou de 1 para 100.
5.
a) Trocá-lo de lugar com o 0; 7 650.
b) Trocá-lo de lugar com o 5; 7 065.
c) Trocá-lo de lugar com o 6; 6 057.
Brasil real, páginas 25 e 26.
1.
a) Rússia: Dezessete milhões, setenta
e cinco mil e quatrocentos. Canadá:
Nove milhões, novecentos e setenta
mil, seiscentos e dez. China: Nove
milhões, quinhentos e setenta e dois
mil e novecentos. Estados Unidos: Nove
milhões, trezentos e setenta e dois mil,
seiscentos e quatorze.
b) 8 514 215 km2; oito milhões, quinhentos
e quatorze mil, duzentos e quinze
quilômetros quadrados
2.
a) Sete mil e quatrocentos quilômetros.
b) Quarenta e oito mil quilômetros
quadrados.
c) Dois milhões, cento e sessenta e
seis mil e oitenta e seis quilômetros
quadrados.
d) Vinte e quatro mil, quatrocentos e
trinta quilômetros quadrados; vinte e
dois mil quilômetros quadrados.
4.
a) Nove milhões, novecentos e trinta mil,
quatrocentos e setenta e oito.
b) Cento e sessenta e nove milhões,
setecentos e noventa e nove mil, cento
e setenta.
c) Resposta em aberto.
5.
a) 600 000 e 600
b) 6 000
c) 6
d) 6 000 000
e) 60 000 000
1. 257, 275, 527, 572, 725, 752
a) 752
b) 257
2.
a) Mil e vinte e sete.
b) Resposta em aberto.
5. 2 106 504
6. Quatro números: 123, 345, 567 e 789.
Tratando a informação, página 27.
1. Resposta pessoal.
a) O número é 99.
b) Acima: 34, 42 e 50; abaixo: 66, 74 e 82.
c) Na coluna que vemos mais à esquerda,
em que estão os números 1, 9, 17...
d) 217 e 218.
e) 8 números; resposta em aberto.

7
Calculando com números naturais
Chegou a sua vez!, páginas 31 a 33.
1.
a) Multiplicação.
b) Subtração.
c) Adição.
d) Subtração.
e) Divisão.
f) Multiplicação.
g) Divisão.
2.
a) 6 3 3 5 18 R 18 ovos
18 2 6 5 12
12 ovos R 1 dúzia
7 dias R 7 3 5 5 35
R$ 35,00
b) • 205 2
005 102
1
102 alunos
• sobrou 1 pera.
c) • 27 1 3 5 30 R 30 camelos
• 30 1 35 1 15 5 80 R 80 camelos
d) 95 2 7 5 88 R 88 camelos
3 – Ideias associadas à adição
Brasil real, páginas 35 a 37.
1.
a) 91 1 38 1 14 1 101 5 244 R 244 km
b) 28 596 1 244 5 28 840 R 28 840 km
c) 28 840 1 244 5 29 084 R 29 084 km
d) 30 000 2 29 084 5 916 R 916 km
2.
a)
Ouro Prata Bronze Total
Argentina 257 278 362 897
Brasil 241 283 402 926
Canadá 347 546 681 1 574
Cuba 781 531 481 1 793
EUA 1 748 1 295 873 3 916
México 157 217 408 782
b) EUA, Cuba, Canadá, Brasil, Argentina,
México.
c) 4o. lugar
3.
a) Representam as regiões brasileiras.
d) Resposta em aberto.
a) 23 1 21 1 22 1 25 1 21 1 24 5 136 R
R 136 nascimentos
b) Abril.
c) Fevereiro e maio.
1.
a) Ivo: 9 070 1 13 620 1 10 090 5 32 780 R
R 32 780 pontos
Beto: 8 230 1 14 740 1 9 980 5 32 950 R
R 32 950 pontos
Guto: 10 060 1 12 900 1 10 120 5 33 080 R
R 33 080 pontos
b) Ivo: 13 620 1 10 090 5 23 710 R
R 23 710 pontos
Beto: 14 740 1 9 980 5 24 720 R
R 24 720 pontos
Guto: 12 090 1 10 120 5 22 210 R
R 22 210 pontos
2. 54 307 1 6 128 5 60 435 R 60 435
habitantes
3. 376 1 1 144 5 1 520 R 1 520 livros
4. O “segredo” é: o número acima é igual à
soma dos dois números abaixo dele.
Exemplo: 90 5 54 1 36
?
d e
a b c
90 84 110 121
54 36 48 62 59
a 5 90 1 84 ⇒ a 5 174
b 5 84 1 110 ⇒ b 5 194
c 5 110 1 121 ⇒ c 5 231
d 5 174 1 194 ⇒ d 5 368
e 5 194 1 231 ⇒ e 5 425
? 5 368 1 425 ⇒ ? 5 793
Editoria de arte

8
5. N 5 330 1 792 1 428 R N 5 1 550 R
R N 5 1 550 crianças
6. 215 1 175 1 245 1 175 5 810
7. 965 1 1 028 1 692 5 2 685 R 2 685 pessoas
8. 11 296 1 1 649 5 12 945 R 12 945 crianças
9.
a) 319 1 426 1 565 5 1 310 R 1 310 pessoas
b) Hidroginástica.
c) 565 2 319 5 246 R 246 pessoas
7 8 3
2 6 10
9 4 5
4 – Ideias associadas
à subtração
1. 1 891 2 66 5 1 825
2.
a) região Norte
b) 151 107, cento e cinquenta e um mil,
cento e sete.
133 717, cento e trinta e três mil,
setecentos e dezessete.
105 203, cento e cinco mil, duzentos
e três.
85 606, oitenta e cinco mil, seiscentos
e seis.
3.
a) 4 282 2 3 736 5 546 R 546 metros
b) 10 912 2 9 218 5 1 694 R 1 694 metros
4. 99 999 999 2 60 141 715 5 39 858 284 R
R 39 858 284 veículos
1.
12 1 13 1 14 5 39
1a linha: 12 1 17 5 29
? 5 39 2 29 R ? 5 10
3a linha: 9 1 14 5 23
? 5 39 2 23 R ? 5 16
1a coluna: 12 1 16 5 28
? 5 39 2 28 R ? 5 11
3a coluna: 10 1 14 5 24
? 5 39 2 24 R ? 5 15
2.
a) 875
b) Não é possível.
c) Não é possível.
d) 0
3. Em 2009; 2 010 2 1 692 5 318 R
R 318 participantes a mais
4. 36 290 2 27 545 5 8 745 R 8 745 reais
5. 2 590 2 2 431 5 159 R 159 m3
1. 3 002 2 1 496 5 1 506
2.
a) 9 105 2 5 299 5 3 806
b) 10 210 2 6 226 5 3 984
3.
a) ? 5 6 991 1 6 429 R ? 5 13 420
b) ? 5 15 000 2 7 995 R ? 5 7 005
1.
a) 120 c) 150
b) 18 d) 60
2.
a) 85 2 8 5 73 (1a vez)
73 2 8 5 65 (2a vez)
.
.
.
13 2 8 5 5 (10a vez)
b) 19
3. Alternativa b.
7 000 1 700 1 700 1 70 1 70 1 7 1 7 5
5 8 554
a) 3 530 2 3 048 5 482 R 482 quilowatts-
-hora

9
b)
1. 58 2 46 1 20 5
5 12 1 20 5 32
2. 50 2 (10 1 25) 2 1
3. (53 2 38 1 40) 2 51 1 (90 2 7 1 82) 1 101 5
5 (15 1 40) 2 51 1 (83 1 82) 1 101 5
5 55 2 51 1 165 1 101 5
4 1 165 1 101 5 270
4. 50 2 (71 2 37 1 6)
5. Respostas possíveis:
a) 11 1 20 2 (10 1 15)
b) 10 1 11 1 15 1 20
c) 15 1 11 1 20 2 10
d) 10 1 20 2 (11 1 15)
6. 40 2 25 212 1 10 2 7 1 8 5 14
Chegou a sua vez!, páginas 49 e 50.
1.
a) Para representar fenômenos físicos,
químicos, sociais, econômicos etc. Para
explicar símbolos ou cores usados nos
gráficos, mapas etc.
b) Unesco, Embaixada de Cuba e
Ministério da Educação.
c) Há quanto tempo alguns países
oferecem escola para todas as crianças.
e) Países; tempo (em anos) em que todas
as crianças daquele país estão na
escola.
f) 134 2 6 5 128 R 128 anos
44 2 6 5 38 R 38 anos
2.
a) • 1 927 2 1 804 5 123 R 123 anos
• 1 960 2 1 927 5 33 R 33 anos
• 1 974 2 1 960 5 14 R 14 anos
• 1 987 2 1 974 5 13 R 13 anos
• 1 999 2 1 987 5 12 R 12 anos
5 – Ideias associadas à multiplicação
Explorando, páginas 50 e 51.
1. Todas as parcelas são iguais.
2.
a) 6
b) 4
c) 4 1 4 1 4 1 4 1 4 1 4
d) Todas as parcelas são iguais.
e) 24
3.
a) 4 3 6 5 24 R 24 tipos
tipos de pão recheios
b) Respostas em aberto.
4.
a) 1 3 1 5 1 • Resposta pessoal.
b) 2 3 2 5 4 • Resposta em aberto.
c) 3 3 3 5 9
d) 4 3 4 5 16
e) 5 3 5 5 25
f) 6 3 6 5 36
5.
a) 3 3 4 5 12 ou 4 3 3 5 12
b) 2 3 6 5 12 ou 6 3 2 5 12
c) 6 3 2 5 12 ou 2 3 6 5 12
d) 1 3 8 5 8 ou 8 3 1 5 8
e) 7 3 7 5 49
f) 3 3 5 5 15 ou 5 3 3 5 15
6.
a) 2 3 6 5 12 R 12 maçãs (Seu Agenor)
2 3 12 5 24 R 24 maçãs (Dona Berta)
b) 5 3 6 5 30 R 30 maçãs (Seu Agenor)
5 3 12 5 60 R 60 maçãs (Dona Berta)
1. 6 3 50 5 300 R 300 laranjas
2. 13 3 43 5 559 R 559 azulejos
3. 27 560 3 4 5 110 240 R 110 240 habitantes
Editoria de arte

10
4. São 6 opções diferentes.
saia blusa branca amarela vermelha
preta
cinza
Saia
blusa branca
preta
blusa amarela
blusa vermelha
saia
blusa branca
cinza
blusa amarela
blusa vermelha
5.
a) 16 3 6 5 96 R 96 trens
b) 96 3 125 5 12 000 R 12 000 passageiros
6.
Quantidade de pães 1 2 3 4 5 6 7
Preço total
2
reais
4
reais
6
reais
8
reais
10
reais
12
reais
14
reais
7.
a) 3 7
3 8
2 9 6
b) 3 7
3 4 8
2 9 6
1 4 8 0
1 7 7 6
8. 12 3 9 5 108 R 108 litros
9.
1a vez 2a vez
vertical: 64 3 2 5 128 128 3 2 5 256
3a vez 4a vez
256 3 2 5 512 512 3 2 5 1 024
1a vez 2a vez
horizontal: 32 3 2 5 64 64 3 2 5 128
3a vez 4a vez
128 3 2 5 256 256 3 2 5 512
10.
a) 24 3 35
24 3 (30 1 5)
(24 3 30) 1 (24 3 5)
720 1 120
700 1 20 1 100 1 20
700 1 100 1 40 5 840
1 1
1
b) 35 3 24
353 (20 1 4)
(35 3 20) 1 (35 3 4)
700 1 140
700 1 100 1 40
800 1 40 5 840
c) 45 3 92
45 3 (90 1 2)
(45 3 90) 1 (45 3 2)
4 050 1 90
4 000 1 50 1 90
4 000 1 140 5 4 140
d) 92 3 45
92 3 (40 1 5)
(92 3 40) 1 (92 3 5)
3 680 1 460
3 600 1 80 1 400 1 60
4 000 1 80 1 60
4 000 1 140 5 4 140
a) 7 3 8 5 56
b) 8 3 6 5 48
1.
a) (1 1 2 1 4 1 8) 3 48 5 720
b) (1 1 4 1 8) 3 23 5 299
2.
a) 27 323
2
7
3 0 7 3
2 4 0 0 5 6 8
12 1 7 0 0 6 3 9
3 2 3
b) 18 872
0
1
1 3 4 8 3
0 1 0 3 0 4 0 8 1
0 4 1 2 11 6 3 2 4
8 8 7 2
1. 81 2 7 3 11 5 81 2 77 5 4
2. a 5 10 1 3 3 2 ⇒ a 5 10 1 6 ⇒ a 5 16
b 5 10 3 3 1 2 ⇒ b 5 30 1 2 ⇒ b 5 32
a  b

11
3. (12 1 8) 3 5 5 100
4. 50 2 (6 3 8 1 2) 5 50 2 (48 1 2) 5 50 2 50 5 0
5. (20 2 3 3 6) 3 2 5 (20 2 18) 3 2 5 2 3 2 5 4
6. (3 3 7 1 2 3 15) 3 (81 2 4 3 20) 5 (21 1 30) 3
3 (81 2 80) 5 51 3 1 5 51
7.
a) 4 3 2 1 4 3 5
b) 3 3 (3 1 3 1 2)
c) 2 3 (8 1 8) 1 3 3 4. Existem outras
respostas.
8.
a) 150 1 5 3 25
b) 150 1 5 3 25 5 150 1 125 5 275 R
R 275 reais
9.
a) 30 3 2 1 30 3 3
b) 30 3 2 1 30 3 3 5 60 1 90 5 150 R
R 150 balões
10.
a) Alex
b) 30 1 2 3 25 1 3 3 20
c) 30 1 2 3 25 1 3 3 20 5 30 1 50 1 60 5
5 140 R 140 reais
d) 360 2 140 5 220 R 220 reais
5 12 6
2 3 10
30 15 4
a) 1 2 7 M1 2 1 1 1 5 1 1 1 M2 MR 80
b) 1 5 3 4 7 M1 1 2 3 1 9 M1 MR 933
c) 2 1 3 1 2 M1 1 3 3 1 0 M2 MR 122
d) 5 8 M1 5 1 3 1 1 2 1 6 1 9 M2 MR 23
1. Vale 150 milhões.
2. 106 716 367 669
3.
a) 1 200 2 1 5 1 119 anos
b) 1 750 2 1 200 5 550 anos
c) 1 850 2 1 750 5 100 R 100 anos
d) 1950 2 1 850 5 100 R 100 anos
e) 2 005 2 1 950 5 55 R 55 anos
a) Ouro: hipismo, vela (nas categorias
laser e star), vôlei masculino, vôlei de
praia masculino; Prata: vôlei de praia
feminino e futebol feminino; Bronze:
judô masculino e atletismo masculino.
b) Sim.
c) Não, quintuplicou.
d)
I. (4 2 4) 3 (4 1 4) 1 1 5 0 3 8 1 1 5
5 0 1 1 5 1 (Tóquio)
II. 3 3 2 2 4 1 3 3 (3 2 3) 5 6 2 4 1
1 3 3 0 5 6 2 4 1 0 5 2 1 0 5 2
(Montreal ou Munique)
III. 4 2 4 1 4 2 1 5 0 1 4 2 1 5 4 2 1 5
5 3 (Barcelona ou México)
IV. 4 2 0 3 4 2 (2 2 2) 5 4 2 0 2 0 5 4
(Moscou)
V. 2 3 2 2 4 1 3 3 3 2 3 5 4 2 4 1
1 9 2 3 5 0 1 9 2 3 5 9 2 3 5 6 (Seul)
VI. 4 1 4 2 4 1 4 5 8 2 4 1 4 5 4 1 4 5 8
(Los Angeles)
VII. (3 1 2) 3 (9 2 7) 5 5 3 2 5 10
(Atenas)
VIII. 2 3 (3 1 4) 2 2 5 2 3 7 2 2 5 14 2 2 5
5 12 (Sidney)
IX. 4 3 4 2 (5 2 4) 5 16 2 1 5 15
(Atlanta)
e) Resposta em aberto.
6 – Ideias associadas à divisão
1.
a) Sim.
72 
 4
(divisão exata)
32 18
0
b) Número de candidatos em cada grupo: 18
72 
 4
32 18
0
2.
a) 6 3 12 5 72 R 72 perguntas
b) 72 
 3
2 R 2 perguntas

8 2
c) Como são 2 perguntas por participante
e há 32 candidatos, são 64 perguntas.
Como havia 72 perguntas, sobrarão
8 perguntas.

12
3.
a) 8 
 2
0 4
b)
• 6 
 2
0 3
• 8 
 2
0 4
c) Não; sobra um pedaço de 2 quadrinhos
roxos.
3 3 4 5 12 R 12 quadrinhos roxos
12 
 1
 0
2 1
d) Não; fica faltando um pedaço de
1 quadrinho para completar a barrinha azul.
4 3 2 5 8 R 8 quadrinhos vermelhos
e)
• 9 : 3 5 3 R cabem 3 barrinhas verde-
-claras em uma barrinha azul.
• 10 : 5 5 2 R cabem 2 barrinhas
amarelas em uma barrinha alaranjada.
• 7 
4 R faltam 3 quadrinhos para
3 1 a barrinha roxa completar a

barrinha preta.
1. 75 : 15 5 15 R 15 vezes
2.
a) Resposta em aberto.
b) 184 : 4 5 46 R 46 papéis
3. 1 352 : 4 5 338
4. 344 : 8 5 43 R 43 reais
5. 476 : 50 5 9 R 9 cupons e resta 26 reais.
50 2 26 R Precisa gastar 24 reais
6. 10 000 : 400 5 25 R 25 voltas
7. 6 970 : 85 5 82 R 82 toneladas
8. 6 160 : 560 5 11 R 11 viagens
1. 8 : 0
2. 12 : 24
3. 0 : 10
4. 1
5. 32 : 8 5 4
32 3 5 5 160
160 : ? 5 4 ⇒ ? 5 160 : 4 ⇒ ? 5 40, logo
devo multiplicar o divisor por 5, porque
40 5 8 3 5.
1.
a) n 5 9 3 7 1 2
n 5 63 1 2
n 5 65
b) n 5 11 3 16 1 5
n 5 176 1 5
n 5 181
c) n 5 64 3 25 1 10
n 5 1 600 1 10
n 5 1 610
2. n 5 45 3 17
n 5 765
3. Se o divisor é 12, o resto maior possível é
11, então:
n 5 12 3 9 1 11
n 5 108 1 11
n 5 119
4. n 5 6 3 35 1 5
n 5 210 1 5
n 5 215 R 215 laranjas
1. x 5 (20 : 4) 3 5
x 5 5 3 5
x 5 25
y 5 20 : (4 3 5)
y 5 20 : 20
y 5 1
a) x 1 y 5 25 1 1 5 26
b) x 3 y 5 25 3 1 5 25
c) x : y 5 25 : 1 5 25
2.
a) 105 : 5 1 30 5 21 1 30 5 51
b) 201 2 64 : 4 5 201 2 16 5 185
c) 65 : 5 2 10 5 13 2 10 5 3
d) 162 : 9 3 9 5 18 3 9 5 162
3.
N 5 85 : 5 1 3 3 15 2 50
N 5 17 1 45 2 50
N 5 62 2 50
N 5 12

13
4.
a) (7 3 7 1 5) : (18 2 15 : 3 1 5) 3 2 5
5 (49 1 5) : (18 2 5 1 5) 3 2 5
5 54 : (13 1 5) 3 2 5
5 54 : 18 3 2 5
5 3 3 2 5 6
b) (30 2 5 3 6) : (7 1 2 3 10) 3 (40 2 30 1 5) 5
5 (30 2 30) : (7 1 20) 3 (10 1 5) 5
5 0 : 27 3 15 5
5 0 3 15 5 0
5.
a 5 (36 : 6 2 5) 3 2
a 5 (6 2 5) 3 2
a 5 1 3 2
a 5 2
b 5 36 : (6 2 5) 3 2
b 5 36 : 1 3 2
b 5 36 3 2
b 5 72
b : a 5 72 : 2 5 36
6.
2 1 30 : 5 1 (9 3 6 2 4) : 5 2 (40 : 10 1 3) 5
5 2 1 6 1 (54 2 4) : 5 2 (4 1 3) 5
5 2 1 6 1 50 : 5 2 7 5
5 2 1 6 1 10 2 7 5
5 8 1 10 2 7 5
5 18 2 7 5 11
N 5 3 ? 11 5 33
7.
20 1 (40 2 30) : 5
1.
236 296 
 4
3 6 59 074 R 59 074 domicílios
0 2 9
1 6
0
2.
316 2 0 0 
 1
 2
7 6 26 350 R 26 350 pacientes
4 2
6 0
0 0
3.
a) 18 000 2 10 000 5 8 000 R 8 000
espécies
b) 18 000 : 2 000 5 9 R 9 vezes
c) 100 formigas (1 000 000 : 10 000)
d) Resposta possível: As formigas são
muito úteis, pois comem os parasitas
das plantas.
7 – Resolvendo problemas
1.
a) Washington; Atlético-PR
b) Paulo Nunes e Renaldo; 18 gols
(34 2 16 5 18)
c) maior: Vasco (22 1 21 1 29 5 72); menor:
São Paulo (19); diferença: 53 gols
d) 29 2 16 5 13 R 13 gols
e) Sim. Washington (34) em 2004 fez o
dobro de Souza (17) em 2006.
f) Respostas em aberto.
2.
a) • 8
• 17; 10
• PDT 1 1 2
PFL 1 — 1
PMDB 4 3 7
PP — 1 1
PPS 2 — 2
PSB 1 2 3
PSDB 4 2 6
PT 4 1 5
b) PT (5), PSDB (6) e PMDB (7). São
números naturais consecutivos.
c) Nenhum dos três, pois todos elegeram
4 governadores no 1o turno.
d) O PSB elegeu 3 governadores. O único
partido que elegeu 6 governadores
(dobro de 3) foi o PSDB.
e) Nenhum, pois dos partidos que
elegeram 5 ou mais governadores, o
máximo abrangido foi 4 regiões (das 5
regiões brasileiras).
Exercícios, páginas 79 a 81.
1.
a) 4 1 5 1 3 1 1 5 13 R 13 alunos
b) 4 1 5 1 3 1 1 1 2 1 5 5 20 R 20 alunos
2.
340 3 6 5 2 040 R 2 040 metros
3.
320 2 (87 1 218) 5
5 320 2 305 5 15 R 15 alunos
4.
125 3 (3 2 2) 1 230 3 (6 2 4) 1 312 3 (8 2 5) 5
5 125 3 1 1 230 3 2 1 312 3 3 5
5 125 1 460 1 936 5 1 521 R 1 521 reais

14
5.
a) 1 hora 5 60 minutos e 1 minuto 5 60
segundos, logo:
1 hora 5 60 3 60 5 3 600 segundos
7 3 (3 600 : 20)
5 7 3 180 5 1 260 R 1 260 vezes
b) em 1 hora goteja 1 260 vezes, em 2 horas:
2 3 1 260 5 2 520 R 2 520 vezes
c) 30 minutos é igual à metade de uma
hora, então:
1 260 : 2 5 630 vezes
d) 90 minutos é o triplo de 30 minutos,
então:
630 3 3 5 1 890 R 1 890 vezes
6. 9 3 (7 2 1) 3 8 3 12 5
5 9 3 6 3 8 3 12 5
5 54 3 8 3 12 5
5 432 3 12 5 5 184 R 5 184 reais
7. 10 1 (10 1 2) 1 2 ? 10 1 10 : 2 5
5 10 1 12 1 2 ? 10 1 10 : 2 5
5 10 1 12 1 20 1 5 5 47 R 47 crianças
8. 12 3 450 1 20 3 750 1 8 3 1 200 5
5 5 400 1 15 000 1 9 600 5 30 000 R
R 30 000 reais
9. Arrecadado na venda:
250 3 40
gasto na produção:
250 3 12 1 4 000
lucro obtido 5 arrecadado – gasto:
250 3 40 2 (250 3 12 1 4 000) 5
5 10 000 2 (30 000 1 4 000)
5 10 000 2 7 000 5 3 000 R 3 000 reais
10. (15 3 50 1 10 3 100) 3 3 5
5 (750 1 1 000) 3 3 5
5 1 750 3 3 5 5 250 R 5 250 reais
11. 108 horas com programação
160 2 108 R horas com consertos
quantia recebida:
108 3 40 1 (160 2 108) 3 25 5
108 3 40 1 52 3 25 5
4 320 1 1 300 5 5 620 R 5 620 reais
12. 1a- fileira: 1, então 64 2 1 5 63,
sobram 63 bandeiras.
2a- fileira: 1 1 2 5 3, então 63 2 3 5 60,
3a- fileira: 3 1 2 5 5, então 60 2 5 5 55,
4a- fileira: 5 1 2 5 7, então 55 2 7 5 48,
5a- fileira: 7 1 2 5 9, então 48 2 9 5 39,
sobram 39 bandeiras
6a- fileira: 9 1 2 5 11, então 39 2 11 5 28,
7a- fileira: 11 1 2 5 13, então 28 2 13 5 15,
8a- fileira: 13 1 2 5 15, então 15 2 15 5 0.
13. Gastou na 1a- loja:
300 : 2 1 2 5
5 150 1 2 5 152 5
Ao sair da 1a- loja tinha:
300 2 152 5 148
Gastou na 2a- loja:
148 : 2 1 2 5
5 74 1 2 5 76
148 2 76 5 72
Gastou na 3a- loja:
72 : 2 1 2 5
5 36 1 2 5 38
72 2 38 5 34 R 34 reais
14.
Número no visor: 347
Ao apertar a tecla D:
347 3 2 5 694
Ao apertar a tecla S:
694 1 1 5 695
Ao apertar a tecla D:
695 3 2 5 1 390
15. (28 3 50) : 100 5
5 1 400 : 100 5 14 R 14 notas
16. Gastou na livraria Todas as Letras:
9 3 24 5 216
Gastaria na livraria Escrita (um livro):
24 2 6 5 18
Teria comprado na livraria Escrita:
216 : 18 5 12 R 12 livros

Editoria de arte
15
17. Se vendeu 82 assinaturas, vendeu 32
assinaturas a mais que 50.
50 3 15 1 32 3 20 1 600 5
5 750 1 640 1 600 5 1 990 R 1 990 reais
1. couraçado: (M, 2), (M, 3), (M, 4), (M, 5) e (M, 6).
submarino: (N, 10).
cruzador: (D, 12), (E, 12), (F, 12) e (G, 12).
destroyer: (K, 13) e (L, 13).
hidroavião: (F, 5), (E, 6) e (G, 6).
2. Praça do Sol, alternativa a.
3. D4, E3, F4, E5, alternativa d.
8 – Potenciação de
números naturais
1.
a) 3 3 3 5 9
b) 5 3 5 5 25
c) 7 3 7 5 49
2. Todos os fatores são iguais.
3.
a) 5 3 5 3 5 5 125 c) 7 3 7 3 7 5 343
b) 9 3 9 3 9 5 729
1.
a) 38 000 000 5 38 3 106; 6 000 000 5 6 3 106;
17 000 000 5 17 3 106
b) 180 5 18 3 10; 330 000 5 33 3 104;
6 000 000 5 6 3 106; 1 000 5 103
2.
a) 23 5 8 R Curitiba
b) 32 5 9 R Belo Horizonte
c) 6 3 22 5 6 3 4 5 24 R Recife
d) 52 5 25 R Brasília ou Fortaleza
e) 52 5 25 R Salvador
1. 5 3 5 3 5 3 5 ou 54
2. 209
3.
a) 25 5 2 3 2 3 2 3 2 3 2 5 32
b) 37 5 3 3 3 3 3 3 3 3 3 3 3 3 3 5 2 187
c) 110 5 1. Todo número natural, diferente
de zero, elevado a zero é igual a 1.
d) 150 5 1. O número 1 multiplicado
cinquenta vezes dá 1.
e) 0100 5 0. O número 0 (zero) multiplicado
cem vezes dá 0 (zero).
f) 106 5 1 000 000. Toda potência de
10 é igual ao número formado pelo
algarismo 1 seguido de tantos zeros
quantas forem as unidades do
expoente.
4.
a) 52 5 25 e 25 5 32, logo 52  25
b) 74 5 2 401 e 103 5 1 000, logo 74 . 103
c) 43 5 64 e 29 5 512, logo 43  29
d) 110 5 1 e 101 5 10, logo 110  101
5. 4 3 4 ou 42
6.
14243
14243
5
5
1442443
1442443
8
8
144424443
144424443
10
10
144424443
144424443
11
11
a) c)
b) d)
7. 62 5 36
63 5 216, logo n 5 3
8. Não, todas estão corretas.
9.
a) 72 b) 63
10. 100 000 é formado de 5 zeros, então o
expoente dessa potência é 5.
11. Sim; 169 5 144 1 25

16
12.
a) 4 3 107 5 4 3 10 000 000 5 40 000 000
(quarenta milhões)
b) 9 3 105 5 9 3 100 000 5 900 000
(novecentos mil)
c) 106 5 1 000 000 (um milhão)
d) 2 3 103 5 2 3 1 000 5 2 000 (dois mil)
13. Se 1 000 m 5 1 km e 108 5 100 000 000,
então 100 000 000 : 1 000 5
5 100 000 R 100 000 km
Logo, 3 3 108 5 3 3 100 000 5 300 000 R
R 300 000 km
14.
a) 400 000 5 4 3 100 000 5 4 3 105 R
R 4 3 105 km
b) 120 mil 5 120 000 5 12 3 10 000 5 12 3 104
150 mil 5 150 000 5 15 3 10 000 5 15 3 104
c) 2 500 5 25 3 100 5 25 3 102
d) 100 mil 5 100 000 5 105
3 milhões 5 3 000 000 5 3 3 106
37 milhões 5 37 000 000 5 37 3 106
1.
a) A raiz quadrada de 81 é 9,
porque 9 3 9 5 81.
b) A raiz quadrada.
2.
a) 4 52 , pois 22 5 4
b) 49 57 , pois 72 5 49
c) 64 58 , pois 82 5 64
d) 121 511 , pois 112 5 121
e) 144 512 , pois 122 5 144
f) 225 515, pois 152 5 225
3. 9, 16, 36, 49 e 64, pois possuem raízes
quadradas exatas no conjunto dos
números naturais.
4.
169 513 R 13 metros, pois 132 5 169
1. N 5 412 1 312 1 212 ⇒ N 5 1 681 2 961 1
1 441 ⇒ N 5 720 1 441 R N 5 1 161,
então temos: 1 1 1 1 6 1 1 5 9
2. 302 : (72 3 3 2 102 2 2) 5
5 900 : (49 3 3 2 100 2 2) 5
5 900 : (147 2 100 2 2) 5
5 900 : (47 2 2) 5
5 900 : 45 5 20
3.
a) 72 2 40 1 18 : 32 2 100 5
5 49 2 40 1 18 : 9 2 1 5
5 49 2 40 1 2 2 1 5
5 9 1 2 2 1 5 11 2 1 5 10
b) (62 2 52) 3 33 2 102 5
5 (36 2 25) 3 27 2 100 5
5 11 3 27 2 100 5
5 297 2 100 5 197
c) 62 : (23 1 1) 3 (32 2 5) 5
5 36 : (8 1 1) 3 (9 2 5) 5
5 36 : 9 3 4 5
5 4 3 4 5 16
d) (7 3 3 1 112) 3 103 5
5 (7 3 3 1 121) 3 1 000 5
5 (21 1 121) 3 1 000 5
5 142 3 1 000 5 142 000
e) (7 3 32 2 1) : (82 2 2 3 31) 5
5 (7 3 9 2 1) : (64 2 2 3 31) 5
5 (63 2 1) : (64 2 62) 5
5 62 : 2 5 31
4.
a) 25 1 42 2 23 3 3 5
5 32 1 16 2 8 3 3 5
5 32 1 16 2 24 5
5 48 2 24 5 24
b) (25 1 42 2 23) 3 3 5
5 (32 1 16 2 8) 3 3 5
5 (48 2 8) 3 3 5
5 40 3 3 5 120
c) 25 1 (42 2 23) 3 3 5
5 32 1 (16 2 8) 3 3 5
5 32 1 8 3 3 5
5 32 1 24 5 56
5. (34 2 26 2 100) : (52 2 23) 5
5 (81 2 64 2 1) : (25 2 23) 5
5 (17 2 1) : 2 5
5 16 : 2 5 8
Logo, 82 5 64.

17
1.
a) 81 2 102 19 22 3 3 1 3 5
5 9 3 2 3 100 1 19 3 4 5
5 18 3 100 1 76 5
5 1800 1 76 5 1876, século XIX
b) 1877
2.
a) A segunda expressão.
• (2 36 )2 23 (103 22) (34 2 144 ) 3 1 3 ; 2 3 1 5
5 (2 3 6)2 1 8 3 (1 000 : 4) 2 (81 3 2 1 12) 5
5 122 1 8 3 250 2 (162 1 12) 5
5 144 1 8 3 250 2 174 5
5 144 1 2 000 2 174 5
5 2 144 2 174 5 1 970
• 112 100 54 9 3 0 15 40 8 3 210 2 1 3( ; ) 1( 2 ; ) 1 5
5 121 2 10 1 625 3 30 1 (15 2 5)3 1 210 5
5 121 2 10 1 625 3 1 1 103 1 210 5
5 121 2 10 1 625 1 1 000 1 210 5
5 111 1 625 1 1 000 1 210 5
5 736 1 1 000 1 210 5
5 1 736 1 210 5 1 946
b) 1 970 1 13 5 1 983
c) (210 25 ) 4 2 3 5
5 (1 024 2 5) 3 2 5
5 1 019 3 2 5 2 038
d) Até 2006 o Brasil foi pentacampeão,
como em 1970 ele já foi tricampeão, o
Brasil ganhou duas vezes a nova taça.
3.
5 3 202 2 103 : 52 1 32 5
5 5 3 400 2 1 000 : 25 1 9 5
5 2 000 2 40 1 9 5
5 1 960 1 9 5 1 969
b) 2006
a) 56 5 5 3 5 3 5 3 5 3 5 3 5 5 15 625
b) 65 5 6 3 6 3 6 3 6 3 6 5 7 776
c) 97 5 9 3 9 3 9 3 9 3 9 3 9 3 9 5
5 4 782 969
d) 79 5 7 3 7 3 7 3 7 3 7 3 7 3 7 3 7 3 7 5
5 40 353 607
e) 210 5 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3
3 2 5 1 024
f) 220 5 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3
3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3
3 2 3 2 3 2 5 1 048 576
1.
a) • verde; • azul e verde; • não consta no
gráfico
b) 9 2 5 5 4 R 4 times
c) 1988, 1990, 1995, 1997
2.
1ª partida: 2 . 0 (vitória)
2ª partida: 1  4 (derrota)
3ª partida: 3 5 3 (empate)
4ª partida: 0  5 (derrota)
São 5 vitórias, 3 empates e 2 derrotas,
então:
5 3 3 1 3 3 1 1 2 3 0 5
5 15 1 3 1 0 5 18 R 18 pontos
Retomando o que aprendeu, páginas 97 e 98.
1. Alternativa c.
3 exercícios em 10 minutos
6 5 3 3 2; então, 6 exercícios em 10 3 2
minutos
 6 exercícios em 20 minutos
2. Alternativa b.
2 3 20 2 2 3 8 5
5 40 2 16 5 24 R 24 reais
3. Alternativa b.
(1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40)
(8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52)
Termos comuns: 16, 28 e 40.
4. Alternativa a.
60 
 6
00 10
60 
 7
4 8

18
60 
 8
4 7
60 
 1
 1
5 5
A única divisão exata é 60 : 6.
5. Alternativa c.
2 3 1 5
6 4
36 64
100 10
5 1 5
5 5
6. Alternativa b.
(43 1 42 1 4) : 7 1 2 3 (3 1 32 1 33) 5
5 (64 1 16 1 4) : 7 1 2 3 (3 1 9 1 27) 5
5 84 : 7 1 2 3 39 5
5 12 1 78 5 90
7. Alternativa d.
Eu: 1 320 figurinhas
Meu primo: 1 320 : 2 5 660 R 660 figurinhas
Minha irmã: 660 3 3 5 1 980 R 1 980
figurinhas
8. Alternativa b.
3 3 5 3 10 5 15 3 10 5 150 R 150 mililitros
Logo, são necessários 2 frascos do
medicamento.
9. Alternativa d.
2 1 3 5 5 5 8 5 11 5 14 5 17 5 20 5
23 5 26 5 29 5 32
10. Alternativa a.
1ª) 838 1 162 5 1 000
2ª) 160 3 15 5 2 400
3ª) 3 600 : 2 5 1 800
4ª) 1 864 2 17 5 1 847
11. Alternativa d.
Fernanda:
1 3 16 1 1 3 32 1 3 3 64 5
5 16 1 32 1 192 5 240 R 240 pontos
Rita:
1 3 16 1 1 3 32 1 1 3 64 5
5 16 1 32 1 64 5 112 R 112 pontos
Paula:
1 3 16 1 0 3 32 1 2 3 64 5
5 16 1 0 1 128 5
5 144 R 144 pontos
Marcos:
1 3 16 1 0 3 32 1 4 3 64 5
5 16 1 0 1 256 5
5 272 R 272 pontos
1.
a) 8 estados (AM, AC, RO, RN, AL, SE, SC,
RS)
b) Santa Catarina e Rio Grande do Sul.
c) São Paulo, Minas Gerais e Rio de Janeiro.
d) de 501 a 2 000 casos
2.
a) • região Norte • região Nordeste
• região Norte • região Sudeste
b) 449 1 466 1 1 793 1 1 668 1 1 188 5
5 5 564 R 5 564 municípios
c) 1 371 236 1 3 349 405 1 4 919 940 1
1 21 509 157 1 8 708 546 5
5 39 858 284 R 39 858 284 veículos
d) 191 094 1 85 284 1 116 436 1 14 758 1
1 32 982 5 440 554 R 440 554 pessoas
3.
A região Nordeste tem 9 estados. O 9 é um
quadrado perfeito porque 9 5 32.
A região Norte tem 7 estados. O 7 não é um
quadrado perfeito porque nenhum número
elevado ao quadrado dá 7.
A região Centro-Oeste e a região Sudeste
têm 4 estados cada uma. O 4 é um
quadrado perfeito porque 4 5 22.
A região Sul tem 3 estados. O 3 não é um
quadrado perfeito porque nenhum número
elevado ao quadrado dá 3.
Assim, somente nas regiões Nordeste,
Centro-Oeste e Sudeste o número de
estados é um quadrado perfeito.

19
Divisibilidade: divisores e múltiplos
9 – Noção de divisibilidade
1.
a) 36 ; 2 5 18 e) 36 ; 12 5 3
b) 36 ; 3 5 12 f) 36 ; 18 5 2
c) 36 ; 4 5 9 g) 36 ; 36 5 1
d) 36 ; 6 5 6 h) 36 ; 1 5 36
2.
a) 23 ; 1 5 23
b) 23 ; 23 5 1
c) Nenhum.
3. 1, 2, 3, 4, 6 e 12.
4. 1 e 13.
5.
a) 1, 3, 5 e 15.
b) 1, 5 e 25.
c) 1 e 19.
d) 1, 2, 3, 5, 6, 10, 15 e 30.
6. 20, 18, 264 e 1 000. Os números pares são
divisíveis por 2.
7. 1
1.
a) 109 3
19 36
1 (não)
c) 202 11
92 18
4 (não)
b) 119 9
29 13
2 (não)
d) 310 5
10 62
0 (sim)
2.
37 9
1 4
(não)
45 9
0 5
(sim)
54 9
0 6
(sim)
62 9
8 6
(não)
72 9
0 8
(sim)
79 9
7 8
(não)
81 9
0 9
(sim)
93 9
03 10
(não)
99 9
09 11
0 (sim)
3.
a) 900 15
00 60
(sim)
d) 900 30
00 30
(sim)
b) 900 20
100 45
0 (sim)
e) 900 40
100 22
20 (não)
c) 900 25
150 36
00 (sim)
f) 900 60
300 15
00 (sim)
4.
a) 1 305 3
10 435
15
0 (sim)
b) 1 1 3 1 0 1 5 5 9, e 9 é divisível por 3.
5. 297
6. 555
7.
a) 719 23
029 31
6
Para ser divisível, o
resto deve ser 0,
como o resto é 6, então,
este é o menor número
que deve ser subtraído.
b) 706 13
56 54
4
Se sobra 4 para se ter 13
que é o divisor e assim
obter resto 0 (para
ser divisível), o menor
número natural que se
deve adicionar é 9.
8. 3
9. Números entre 40 e 50: 41, 42, 43, 44, 45,
46, 47, 48 e 49. O único número que é
divisível por 6 e 7 ao mesmo tempo é 42.
10. De 10 a 15, o número 60 é divisível por 10,
12 e 15; então, temos:
60 10
0 6
6 grupos de 10 equipes
60 12
0 5

20
60 15
0 4
Chegou a sua vez, página 105.
1.
a) 42 5
2 8
d) 45 5
0 9
b) 43 5
3 8
e) 46 5
1 9
c) 44 5
4 8
2.
Quociente Resto
32 6
32 3
32 12
3. 56 373 236
47 2 238
09 17
7 08
2 093
1 888
205
Desafio, página 105.
Pelas informações dadas, o total de
exercícios é um número:
• que está entre 50 e 100;
• divisível por 7, porque se contar de 7 em
7 não sobra resto;
• ímpar, porque contando de 2 em 2
sobra 1;
• não é divisível por 3, porque sobra 1
quando contado de 3 em 3.
Os números que atendem às informações
acima são 77 e 91, mas como 77 ao ser
dividido por 5 deixa resto 2; então, o
número de exercícios que João resolveu é
91, porque:
77 5
27 15
2
91 5
41 18
1
10 – Critérios de divisibilidade
1.
a) 259, 295, 529, 592, 925, 952
b) Para ser divisível por 2, o número deve
ser par, então são divisíveis por 2 os
números 592 e 952.
c) Para ser divisível por 3, o número deve
ter por soma de seus algarismos um
número divisível por 3. Como todos os
números são formados por 2, 5 e 9, e
2 1 5 1 9 5 16, que não é divisível por 3,
então nenhum deles é divisível por 3.
2.
a) Sim, porque 12 756 é um número par.
b) Sim, porque 1 1 2 1 7 1 5 1 6 5 21 é
divisível por 3.
c) Sim, porque: 56 4
16 14
0
d) Não, porque não termina em 0 ou 5.
e) Sim, porque é divisível por 2 e por 3 ao
mesmo tempo.
f) Não, porque: 756 8
36 94
4
3.
a) 5 1 0 1 0 1 1 5 6, não é divisível por 9.
b) 5 1 n 1 0 1 1 5 n 1 6
n 1 6 deve ser um número divisível por
9 e o menor possível; logo, n 1 6 5 9;
então, n 5 3.
4.
a) • 3? Sim, porque 4 1 0 1 3 1 0 1 2 1 0 5 9.
• 4? Sim, porque 20 é divisível por 4.
• 8? Não, porque 020 não é divisível por 8.
b) O menor número formado pelos três
últimos algarismos que é divisível por
8 é 24; logo, devemos substituir n por 4.
5. a) 3 000 e 3 300
b) 3 000
6. Números entre 50 e 60: 51, 52, 53, 54, 55,
56, 57, 58 e 59. Divisível por 2: 52, 54, 56 e
58. Divisível por 3: 5 1 1 5 6; 5 1 4 5 9;
5 1 7 5 12. O número procurado é 54,
porque, para ser divisível por 6, basta ser
divisível por 2 e por 3 ao mesmo tempo.

21
7.
a) Para ser divisível por 2, d pode ser 0, 2,
4, 6 ou 8, mas como deve também ser
divisível por 3, 3 1 2 1 5 1 d 5 10 1 d,
deve ser o menor número possível
divisível por 3, então d 5 2.
b) Para ser divisível por 9: 7 1 0 1 b 1
1 3 5 10 1 b deve ser o menor número
possível divisível por 9, então b 5 8.
1.
a) Várias respostas possíveis; por
exemplo: 1902, 1905, 1908, 1971, 2001.
b) 1908 e 1980.
2.
a) Divisíveis por 2: 250, 1 050, 340, 350,
188, 60, 90 e 202. Divisíveis por 3: 1 050,
60, 90 e 171. Divisíveis por 2 e por 3 ao
mesmo tempo: 1 050, 60 e 90.
b) Seis.
c) Divisíveis por 3: 1 050, 60, 90 e 171.
Divisíveis por 4: 340, 188 e 60. Divisíveis
por 3 e por 4 ao mesmo tempo: 60.
d) 90 e 171.
1.
13 23 22 27 22 25
6
132
6
1 1 1 1 1
5 5
22 2. 12 5 29 13 11
5
70
5
14 1 1 1 1
5 5 R 14 reais
3.
a) Sendo 4 bimestres e 6 a média de
aprovação, a soma mínima para
aprovação é:
4 ? 6 5 24
b) 24 2 (5 1 8 1 8) 5 24 2 21 5 3
11 – Divisores, fatores e múltiplos
de um número natural
1. 1 e 10; 2 e 5; isto é, 1, 2, 5 e 10.
2. 1, 2, 5 e 10.
3. Os fatores de um número são também
seus divisores.
4. 1 3 20 5 20; 2 3 10 5 20; 4 3 5 5 20
5. 1, 2, 4, 5, 10 e 20.
6. Sim.
7.
a) 22 R 1 3 22; 2 3 11
b) 60 R 1 3 60; 2 3 30; 3 3 20; 4 3 15;
5 3 12; 6 3 10
c) 17 R 1 3 17
8.
a) 22 R 1, 2, 11 e 22
b) 60 R 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60
c) 17 R 1 e 17
9. Os fatores de um número são também
seus divisores.
1.
a) Não. c) Sim.
26 5 1 3 26 72 5 1 3 72
26 5 2 3 13 72 5 2 3 36
b) Sim. 72 5 3 3 24
48 5 1 3 48 72 5 4 3 18
48 5 2 3 24 72 5 6 3 12
48 5 3 3 16 72 5 8 3 9
48 5 4 3 12 d) Não.
48 5 6 3 8 86 5 1 3 86
86 5 2 3 43
2.
a) Sim. b) Não.
92 5 1 3 92 c) Não.
92 5 2 3 46 d) Sim.
92 5 4 3 23
3.
a) 2, porque 14 5 2 3 7
b) 2, 3, 6 e 9, porque 18 5 2 3 9 e 18 5 3 3 6
c) 5, porque 25 5 5 3 5
d) 3, 5 e 9, porque 45 5 3 3 15 e 45 5 5 3 9
e) 2, 3, 6 e 9, porque 54 5 2 3 27,
54 5 3 3 18 e 54 5 6 3 9
f) 2, 5 e 10, porque 70 5 2 3 35,
70 5 5 3 14 e 70 5 10 3 7
4. Divisores de 15: 1, 3, 5 e 15
Divisores de 25: 1, 5 e 25
Divisores de 15 e também de 25: 1 e 5
5. Divisores de 14: 1, 2, 7 e 14.
Divisores de 35: 1, 5, 7 e 35.
a) Os divisores de 14 que não são
divisores de 35: 2 e 14
b) Os divisores de 35 que não são
c) Os divisores de 14 que são também

22
6. Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20,
30 e 60. Maior divisor de 60 sem ser 60 é 30.
7. 0, 15, 30, 45, 60, 75
8. 300 13
40 23
1
Para ser múltiplo, a divisão deve ser exata.
Então, tirando 1, que é o resto, de 300, o
número obtido será o maior múltiplo de 13
menor que 300.
300 2 1 5 299
9. 100 13
09 7
Para ser múltiplo, a divisão deve ser exata.
Então, adicionando a 100 o que falta para o
resto ser 13 (13 2 9 5 4), obtemos o menor
múltiplo de 13 maior que 100.
100 1 4 5 104
10.
a) 202
b) 36
c) 0
d) 0 e 4
e) 4
f) Números naturais menores que 500 e com
3 algarismos iguais: 111, 222, 333 e 444.
Múltiplos de 2: 222 e 444.
Múltiplos de 3: 111, 222, 333 e 444.
Múltiplos de 2 e 3: 222 e 444.
11. Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24,
27 e 30.
Múltiplos de 5: 0, 5, 10, 15, 20, 25 e 30.
Múltiplos comuns de 3 e 5: 0, 15 e 30.
12. 15
13.
a) 2008 e 2020
b) três: 1992, 1996 e 2000
c) Década de 1980: 1984, 1988
Década de 1990: 1992, 1996 e 2000
Década de 2000: 2000, 2004 e 2008
Desafio!, páginas 116 e 117.
1.
6
1
5
2
1
5
4
6
8
7
3
3
0 2
2 5 5 2
0
4 8
9
Por 2, porque 5 148 é par.
Por 3, porque 5 1 1 1 4 1 8 5 18.
Por 4, porque 48 é divisível por 4.
Por 6, porque é divisível por 2 e por 3.
Por 9, porque 5 1 1 1 4 1 8 5 18.
12 – Números primos
Exercícios, página 120
1.
a) 15
b) 5 casas
c) Século 21, 21 não é um número primo.
2. Não, pois é divisível por 7.
3.
a) 26 1 3 5
5 64 1 3 5 67 R é primo porque não
é divisível nem por 2, nem por 3, nem
por 5, nem por 7, e prosseguindo as
divisões:
67 11
1 6 R quociente menor que o divisor
b) 42 1 52 5
5 16 1 25 5 41 R é primo porque não é
divisível nem por 2, nem por 3, nem por 5, e:
41 7
6 5 R quociente menor que o divisor
c) 472 2 372 2 232 5
5 2 209 2 1 369 2 529 5
5 840 2 529 5 311 R é primo porque
não é divisível nem por 2, nem por 3,
nem por 5, e prosseguindo as divisões:
311 7
31 44
3
311 11
91 28
3
311 13
51 23
12
311 17
141 18
05
311 19
121 16
07
R quociente menor
que o divisor
4. 47 é primo porque não é divisível nem por
2, nem por 3, nem por 5, e:
47 7
5 6
R quociente menor que o divisor

23
51 não é primo, é divisível por 3.
83 é primo porque não é divisível nem por
2, nem por 3, nem por 5, e prosseguindo as
divisões:
83 7
83 11
13 11
7 7
R quociente menor
que o divisor
91 7
21 13
0
97 é primo porque não é divisível por 2, nem
por 3, nem por 5, e prosseguindo as divisões:
97 7
97 11
27 13
9 8
R quociente menor
6
que o divisor
5.
a) 131 é primo porque não é divisível
por 2, nem por 3, nem por 5, e
prosseguindo as divisões:
131 7
131 11
61 18
21 11
5
0
R quociente igual
ao divisor
b) 253 não é primo porque é divisível por 11:
253 7
43 36
1
253 11
33 23
0
c) 211 é primo porque não é divisível
por 2, nem por 3, nem por 5, e
prosseguindo as divisões:
211 7
01 30
211 11
101 19
2
211 13
81 16
03
211 17
41 12
7
R quociente menor
que o divisor
d) 391 não é primo porque é divisível por 17:
391 7
41 55
7
391 11
61 35
6
391 13
01 30
391 17
51 23
0
6. O “segredo” é que o número de cima é igual
à soma dos dois números abaixo dele:
63 5 33 1 30; 47 5 30 1 17; 38 5 17 1 21
a) a 5 63 1 47 5 110
b 5 47 1 38 5 85
c 5 110 1 85 5 195; O número 195
b) Não, pois 195 é divisível por 5.
1. Nenhum deles é primo. O 15 é divisível
por 5, o 36 e o 1 532 são pares.
2. Sim (7 1 3 1 6 1 7 5 23), 23 é primo
porque só tem dois divisores naturais: o 1
e ele mesmo.
3.
a) 23, 31, 131, 5 e 13.
b) Não, pois 299 (que é o total) é múltiplo
de 13 (299 ; 13 5 23).
4. Um, o 13.
13 – Decomposição em fatores primos
1.
a) 2 3 23 5 46 c) 3 3 19 5 57
b) 5 3 17 5 85 d) 7 3 11 5 77
2.
b) 32 3 5 3 17
c) 24 3 32 3 11
d) 72 3 11
Alternativas b, c e d.
3. Não; 3 3 22 3 11
4. 112 2
56 2
28 2
14 2
7 7
1
112 5 24 3 7
5. (152 1 255) ; (32 1 1) 5 48 2
24 2
12 2
6 2
3 3
1
48 5 24 3 3
5 (225 1 255) ; (9 1 1) 5
5 480 ; 10 5 48
6.
a) 48 5 24 3 3

24
b) 50 2
25 2
5 5
1
50 5 2 3 52
c) 80 2
40 2
20 2
10 2
5 5
1
80 5 24 3 5
d) 99 3
33 3
11 11
1
99 5 32 3 11
e) 108 2
54 2
27 3
9 3
3 3
1
108 5 22 3 33
f) 132 2
66 2
33 3
11 11
1
132 5 22 3 3 3 11
g) 210 2
105 3
35 5
7 7
1
210 5 2 3 3 3 5 3 7
h) 180 2
90 2
45 3
15 3
5 5
1
180 5 22 3 32 3 5
i) 234 2
117 3
39 3
13 13
1
234 5 2 3 32 3 13
7. 23 3 53
8. 1 200 2
600 2
300 2
150 2
75 3
25 5
5 5
1
1 200 5 24 3 3 3 52
a 5 4, b 5 1, c 5 2
a 1 b 1 c 5 4 1 1 1 2 5 7
9. 240 2
120 2
60 2
30 2
15 3
5 5
1
240 5 24 3 3 3 5
x 5 4
10. 1 620 2
810 2
405 3
135 3
45 3
15 3
5 5
1
1 620 5 22 3 34 3 5
n 5 34
11.
a) 22 3 5 3 112 5
5 4 3 5 3 121 5
5 20 3 121 5 2 420
b) 22 3 7 3 13 5
5 4 3 7 3 13 5
5 28 3 13 5 364
c) 33 3 17 5
5 27 3 17 5 459
1. 75 3
25 5
5 5
1
75 5 3 3 52
2.
a) América Latina
b) A coluna vermelha indica a expectativa
de vida de 1965 a 1970, e a coluna azul
indica a expectativa de vida de 2000 a
2005.
c) África
d) 44 2
22 2
11 11
1
44 5 22 3 11
49 7
7 7
1
49 5 72
54 2
27 3
9 3
3 3
1
54 5 2 3 33

25
67 5 1 3 67 (número primo)
70 2
70 5 2 3 5 3 7
35 5
7 7
1
76 2
38 2
19 19
1
76 5 22 3 19
56 2
28 2
14 2
7 7
1
56 5 23 3 7
65 5
13 13
1
65 5 5 3 13
3.
a) 1 580 2
790 2
395 5
79 79
1
1 580 5 22 3 5 3 79
650 2
325 5
65 5
13 13
1
650 5 2 3 52 3 13
4 000 2
2 000 2
1 000 2
500 2
250 2
125 5
25 5
5 5
1
4 000 5 25 3 53
20 2
10 2
5 5
1
20 5 22 3 5
15 000 2
7 500 2
3 750 2
1 875 3
625 5
125 5
25 5
5 5
1
15 000 5 23 3 3 3 54
b) Resposta possível: As principais causas
dessa ameaça são a caça, o comércio
clandestino, no qual as aves são
capturadas enquanto filhotes, ainda no
ninho, e a degradação em seu hábitat
natural.
14 – Máximo divisor comum,
mínimo múltiplo comum
1.
54, 72 2 R fator comum
27, 36 2
27, 18 2
3, 1 3
1, 1
m.d.c. (54, 72) 5 2 3 32 5 18
2.
a) 50, 75 2
25, 75 3
1, 1
m.d.c. (50, 75) 5 52 5 25
b) 112, 70 2 R fator comum
56, 35 2
28, 35 2
14, 35 2
7, 35 5
1, 1
m.d.c. (112, 70) 5 2 ? 7 5 14

26
c) 150, 250 2 R fator comum
75, 125 3
1, 5 5
1, 1
m.d.c. (150, 250) 5 2 ? 52 5 50
d) 90, 225 2
1, 5 5
1, 1
m.d.c. (90, 225) 5 32 ? 5 5 45
e) 56, 84, 210 2 R fator comum
28, 42, 105 2
14, 21, 105 2
7, 21, 105 3
7, 7, 35 5
7, 7, 7 7 R fator comum
1, 1, 1
m.d.c. (56, 84, 210) 5 2 ? 7 5 14
f) 504, 588 2 R fator comum
126, 147 2
21, 49 3
1, 7 7
1, 1
m.d.c. (504, 588) 5 22 ? 3 ? 7 5 84
g) 39, 65, 91 3
13, 65, 91 5
13, 13, 91 7
1, 1, 1
m.d.c. (39, 65, 91) 5 13
h) 144, 216, 288 2 R fator comum
72, 108, 144 2 R fator comum
18, 27, 36 2
9, 27, 18 2
1, 3, 1 3
1, 1 1
m.d.c. (144, 216, 288) 5 23 ? 32 5 72
3. 96, 144, 240 2 R fator comum
6, 9, 15 2
1, 3, 5 3
1, 1, 5 5
1, 1, 1
N 5 24 ? 3 5 48
4. 90, 126 2 R fator comum
5, 7 5
1, 7 7
1, 1
2 ? 32 5 18
1.
a) 30, 75 2
15, 75 3
5, 25 5
1, 5 5
1, 1
m.m.c. (30, 75) 5 2 ? 3 ? 52 5 150
b) 18, 60 2
9, 30 2
9, 15 3
3, 5 3
1, 5 5
1, 1
m.m.c. (18, 60) 5 22 ? 32 ? 5 5 180
c) 66, 102 2
33, 51 3
11, 17 11
1, 17 17
1, 1
m.m.c. (66, 102) 5 2 ? 3 ? 11 ? 17 5 1 122
d) 36, 54, 90 2
18, 27, 45 2
9, 27, 45 3
3, 9, 15 3
1, 3, 5 3
1, 1, 5 5
1, 1, 1
m.m.c. (36, 54, 90) 5 22 ? 33 ? 5 5 540

27
e) 48, 20, 40, 36 2
24, 10, 20, 18 2
12, 5, 10, 9 2
6, 5, 5, 9 2
3, 5, 5, 9 3
1, 5, 5, 3 3
1, 5, 5, 1 5
1, 1, 1, 1
m.m.c. (48, 20, 40, 36) 5 24 ? 32 ? 5 5 720
2. 8, 10 2
4, 5 2
2, 5 2
1, 5 5
1, 1
m.m.c. (8, 10) 5 23 ? 5 5 40
3. 12, 20 2
6, 10 2
3, 5 3
1, 5 5
1, 1
m.m.c. (12, 20) 5 22 ? 3 ? 5 5 60
4. 15, 25, 40 2
15, 25, 20 2
15, 25, 10 2
15, 25, 5 3
5, 25, 5 5
1, 5, 1 5
1, 1, 1
m.m.c. (15, 25, 40) 5 23 ? 3 ? 52 5 600
600 minutos 5 10 horas
5. 20, 24, 30 2
10, 12, 15 2
5, 6, 15 2
5, 3, 15 3
5, 1, 5 5
1, 1, 1
m.m.c. (20, 24, 30) 5 23 ? 3 ? 5 5 120
6. 15, 18 2
15, 9 3
5, 3 3
5, 1 5
1, 1
m.m.c. (15, 18) 5 2 ? 32 ? 5 5 90
Os ônibus partirão juntos depois de
90 minutos, ou seja, 1 hora e 30 minutos,
depois das 8 horas, ou seja, às 9 horas e
30 minutos.
7. 4, 5, 10 2
2, 5, 5 2
1, 5, 5 5
1, 1, 1
m.m.c. (4, 5, 10) 5 22 ? 5 5 20
8. 12, 15, 24 2
6, 15, 12 2
3, 15, 6 2
3, 15, 3 3
1, 5, 1 5
1, 1, 1
m.m.c. (12, 15, 24) 5 23 ? 3 ? 5 5 120
múltiplos comuns de 12, 15 e 24:
{ 120, 240, 360, ...}
17 17 17
127 247 367
Como a quantidade de figurinhas está
entre 200 e 300, só pode ser 247.
2 1 4 1 7 5 13
a) Números destacados: 165, 13, 2 000,
10, 20, 25, 45.
6 são divisíveis por 5, porque terminam
em zero ou 5.
b) 165 3
55 5
11 11
1 1
Divisores de 165 R 1, 3, 5 e 11.
c) (I) 80, 50 2 R fator comum
40, 25 2
20, 25 2
10, 25 2
1, 5 5
1, 1
m.d.c. (80, 50) 5 2 ? 5 5 10
(II)
50
50 m
80 m
50 60 70 80
40
40
30
30
20
20
10
10
9 1 6 1 9 1 6 5 30
30 2 4 5 26 mudas

Contamos 4 árvores 2 vezes.
Editoria de arte

28
Retomando o que aprendeu, página 130.
1. múltiplos de 2 e 3 ao mesmo tempo 5
5 múltiplos de 6.
M6 5 {0, 6, 12, 18, 24, 30, 36, 42, 48, 54, ...}
8 casas: 6, 12, 18, 24, 30, 36, 42, 48
2. 12c5
Divisível por 3 ⇒ 1 1 2 1 c 1 5 R deve ser
múltiplo de 3
1 1 2 1 c 1 5 5 8 1 c
c pode ser: 1 (8 1 1 5 9)
4 (8 1 4 5 12)
7 (8 1 7 5 15)
1 1 4 1 7 5 12
3. 90, 135 2
45, 135 3
15, 45 3
5, 15 3
5, 5 5
1, 1
m.m.c. (90, 135) 5 270
múltiplos de 270 5 {0, 270, 540, 810, 1 080, ...}
3 algarismos: 270, 540 e 810.
4. Alternativa a.
2, 3, 5 2
1, 3, 5 3
1, 1, 5 5
1, 1, 1
m.m.c. (2, 3, 5) 5 30
Como sobra 1, possíveis resultados:
{31, 61, 91, 121, ...}
Como é múltiplo de 7: 91 exercícios
5. Alternativa d.
1 800 2
900 2
450 2
225 3
75 3
25 5
5 5
1
1 800 5 23 ? 32 ? 52
1 800 5 2a ? 3b ? c2
Temos: a 5 3
b 5 2
c 5 5
Portanto: a 1 b 1 c 5 3 1 2 1 5 5 10
6. Alternativa d.
N 5 488a9b
488a9b é múltiplo de 5, portanto b 5 0 ou
b 5 5.
488a9b é múltiplo de 3, portanto 4 1 8 1 8 1
1 a 1 9 1 b deve ser múltiplo de 3.
 29 1 a 1 b deve ser múltiplo de 3.
Possibilidades:
b a a 1 b
0 1 1
0 4 4
0 7 7
5 2 7
5 5 10
5 8 13
7. Alternativa e.
n.o exibido: 4, 8, 12, 16, 20, 24
Total de bolas: 4 1 8 1 12 1 16 1 20 1 24 5 84
8. Como (213466917 2 1) e (230402457 2 1) são
primos, o m.m.c. (a) será igual ao produto
dos dois e o m.d.c. (b) será igual a 1,
portanto: ba 5 1a 5 1
9. Alternativa b.
6, 15 2
3, 15 3
1, 5 5
1, 1
m.m.c. (6, 15) 5 2 ? 3 ? 5 5 30
linha A R
30
6
55
10. Alternativa c.
18, 48 2
9, 24 2
9, 12 2
9, 6 2
9, 3 3
3, 1 3
1, 1
m.m.c. (18, 48) 5 24 ? 32 5 144

29
Geometria: As ideias intuitivas
15 – Ponto, reta e plano
1. Respostas em aberto.
1. c; c; a; b; c; b
2. Plana.
3.
a) Plana. b) Não plana.
1. a, b, d, f e h.
2. f
16 – A reta
1. Infinitas retas.
2. Uma única reta.
3. Inclinada.
4.
a) Concorrentes. d) Paralelas.
b) Concorrentes. e) Concorrentes.
c) Concorrentes.
5.
a) Vertical. b) Concorrentes.
1. Cláudio trabalha na rua Visconde de
Inhaúma, e Sueli, na rua Comandante
Marcondes Salgado.
2. Paralelas.
3. Não.
1. Seis: PA,PB,PC,PD,PE e PF .
2. PA,PB,PC,PD,PE,PF,EF; 7 segmentos.
3.
a) 8 b) 7 c) 4
4.
a) BC ou BD ou AC
b) AB ou AC
c) AB ou CD ou BC
5.
a) AB e MN
b) BN , BC ou CN
c) AB e AM ou AC e AB
6. 10 segmentos.
7. Nas figuras 3, 6 e 7.
8.
a) V c) V
b) F d) V
1.
a) 6 unidades. b) 2 unidades.
2.
a) 4u
b) 2u
c) 1u
d) 6u
e) 6u
f) 10u
3. 38 quarteirões.
4. Figuras a, d, e, h
17 – Giros e ângulos
1. Em todas elas, há a ideia de volta ou giro
em torno de algo.
2. a e C; b e A; c e D; d e B.
Editoria de arte

30
Exercícios, página 149 e 150.
1. Alternativa a.
2. A 5 908; B 5 458; C 5 1308; D 5 958
3.
a) 3 horas c) maior e) 180o
b) 9 horas d) 1 volta
18 – Polígonos
1. A, simples; B, simples; C, simples; D, não
simples, E não simples.
2. A, D; B, C, E.
3. Quando a origem da linha coincide com a
sua extremidade, é fechada; quando não
coincide, é aberta.
4. B, C.
6. Quadro B.
1. Sim; é uma figura geométrica plana
limitada por uma linha fechada simples,
formada apenas por segmentos de reta.
2. Porque ela não é limitada por uma linha
formada por segmentos de reta.
3.
a) Sim.
b) Quadrilátero.
4. Sim; polígono não convexo.
5.
a) Octógono.
b) Quadrilátero.
6. 6 lados; hexágono.
7. Triângulo.
8. Sim.
9. Como os polígonos são regulares, todos os
lados têm a mesma medida.
5 cm
3 cm
5 3 6 5 30 
30 unidades
3 3 8 5 24 
24 unidades
1.
a) Não, em A Lua não temos nenhum
deles.
b) Tanto em Estação Central do Brasil (nos
postes, por exemplo) como em São
Paulo (nos prédios e estruturas, por
exemplo) aparecem representações de
retas paralelas e de retas concorrentes.
c) Estruturas com triângulos, telhados,
janelas dos prédios, por exemplo.
d) Estação Central do Brasil: triângulos,
quadriláteros e pentágonos. A Lua:
nenhum; São Paulo: quadriláteros e
triângulos.
19 – Triângulos e quadriláteros
Sim, há dois lados Não há lados Sim, os lados opostos
paralelos. paralelos. são paralelos.
1. 1: escaleno; 2: equilátero; 3: isósceles.
2.
a) 1 e 3 b) 2 e 4
3. Triângulo equilátero.
4.
a) Triângulo isósceles.
b) Triângulo escaleno.
5.
a) 6 triângulos. b) Equilátero.
6.
A B
C
D E
F
G
H
I
J
a) 4 (B, F, H, I)
b) 6 (A, C, D, E, G, J)
c) 1 (C)
d) 2 (A, J)
7.
Editoria de arte
Editoria de arte
Editoria de arte
Editoria de arte

31
8.
A
L B
K C
M
J D
I E
H F
G
São 20 triângulos, a saber:
2 triângulos grandes de lados G1: AE , EI e
IA; G2: CG, GK e KC.
6 triângulos médios de lados:
M1: AD, DJ e JA
M2: BE , EH e HB
M3: CF , FL e LC
M4: DG , GJ e JD
M5: FI , IL e LF
M6: HK, KB e BH
12 triângulos pequenos de lados:
P1: AB , BL e LA
P2: BC, CD e DB
P3: DE , EF e FD
P4: FG , GH e HF
P5: HI , IJ e JH
P6: JK , KL e LJ
P7: BD , DM , e MB
P8: DF , FM e MD
P9: FH , HM e MF
P10: HJ , JM e MH
P11: JL , LM e MJ
P12: LB , BM e ML
1.
a) Alagoas e Sergipe.
b) Maranhão, Piauí, Rio Grande do Norte,
Paraíba e Pernambuco.
c) Pentágono.
d) 8 lados; octógono.
2.
a) Retângulo: espera-se que os alunos,
pelo menos, reconheçam que
um retângulo é um polígono de 4
lados (quadrilátero) com 4 ângulos
internos retos (que medem 90o).
Outras características ainda podem
ser citadas: é um polígono convexo,
é um paralelogramo etc. Losango:
quadrilátero, paralelogramo, os quatro
lados têm mesma medida.
b) 1: Amazonas
2: Pará
3: Amapá
1.
3.
4.
5. Há várias possibilidades.
Editoria de arte
Editoria de arte
Editoria de arte
Editoria de arte

A forma fracionária dos números racionais
20 – A ideia de fração
1.
a) 3 b) 5
2. Mesa 1 – comidos
 4 dos 8 ou
4
8
sobraram  4
dos 8 ou
4
8
Mesa 2 – comidos
 2 8
2
8
dos ou
sobraram  6
dos 8 ou
6
8
Mesa 3 − comidos
 5 8
5
8
dos ou
sobraram  3
dos 8 ou
3
8
Mesa 3.
1. a, b, d, e, f, h, i
2.
a) 1
4
b) 1
10
3.
a) 7
8
; c) 7
1
8
12
5
12
;
b) 3
10
; d) 1
7
10
6
5
6
;
4. 1
8
5.
a) 3
7
b) 6
7
6. 7
12
7. 5
12
8. 17
30
9. c, b, d
1.
a) Norte: Acre, Amazonas, Roraima,
Rondônia, Pará, Amapá e Tocantins
Sudeste: Minas Gerais, Espírito Santo,
Rio de Janeiro e São Paulo
Sul: Paraná, Santa Catarina e Rio
Grande do Sul
Centro-Oeste: Goiás, Mato Grosso,
Mato Grosso do Sul e Distrito Federal
Nordeste: Maranhão, Piauí, Ceará, Rio
Grande do Norte, Paraíba, Pernambuco,
Alagoas, Sergipe e Bahia
b) 26 estados
c) A região Nordeste é composta de
9 estados, então a fração é
9
26
.
d) A região Sul é composta de 3 estados,
então a fração é 3
26
.
e) A região Norte é composta de
7 estados, e a região Nordeste, de 9,
então juntas têm 16 estados, portanto
mais que a metade dos estados
brasileiros (26).
2.
a) 10 partes
b) 5
10
3.
a) 22 carros deram a largada, e 5 carros
não completaram a corrida.
Então: 22  5  17  17 carros
completaram a corrida.
Logo, 17
22
é a fração dos participantes
dessa corrida que completaram o
circuito.
b) Nesse período, 6 pilotos brasileiros
venceram o GP Brasil de F1, em
Interlagos, de 24 corridas realizadas.
Assim, a fração correspondente é 6
24
.
32

33
21 – Resolvendo problemas que
envolvem frações
1.
a) arremessos: 60
5
5
corresponde a 60
1
5
corresponde a 60  5  12
3
5
corresponde a 3  12  36  36
arremessos
b) Se acertou 60 arremessos e 36 foram
de 3 pontos, então acertou:
60  36  24  24 arremessos de
2 pontos
c) 3  36 1 2  24 
 108  48  156  156 pontos
2.
a) 40
670
3.
a) 12
30
b) No primeiro dia foram 30 testes:
5
5
corresponde a 30
1
5
3
5
corresponde a 3  6  18  18 testes
No segundo dia foram 40 testes:
8
8
corresponde a 40
1
8
5
8
corresponde a 5  5  25  25 testes
Na segunda fase este candidato
acertou: 18  25  43  43 testes
4. a) Número de
questões
Área do conhecimento
14 Língua Portuguesa
6 Língua Estrangeira
6 Geografia
6 História
10 Matemática
6 Física
6 Química
6 Biologia
b) 60 questões
c) 30 questões
d) total de questões: 60
5
5 corresponde a 60
1
5
corresponde a 60  5  12  12
questões
e) total de questões: 60
errou: 20
acertou: 60  20  40
fração de acerto: 40
60
f) 24
60
1. Número de alunos: 36
9
9
corresponde a 36
1
9
corresponde a 36  9 = 4  4 alunos
2.
a) 1 litro  1 000 mililitros
5
5
corresponde a 1 000
1
5
corresponde a 1 000  5  200 
 200 mililitros
b)
250
1000
c) 500
3.
1
3 corresponde a 16
3
3
corresponde a 3  16  48  48 cocos
4. 6
corresponde a 24
6
1
6
corresponde a 24  6  4  4 faltas
Compareceram:
24  4  20  20 candidatos
5.
a) 3
corresponde a 42
3
1
3
corresponde a 42  3  14  14 alunos

34
b) 42  14  28  28 alunos
6. 1
corresponde a 75
6
6
6
corresponde a 6  75  450
N  450 brinquedos
7. Primeiro colocado:
2
2
corresponde a 600
1
2 corresponde a 600  2  300  300 reais
Segundo colocado:
3
3
corresponde a 600
1
3
corresponde a 600  3  200  200 reais
Terceiro colocado:
600  (300  200) 
 600  500  100  100 reais
8. 1a redução:
2
2
corresponde a 2 048 e 1 024
1
2
corresponde a 2 048  2 = 1 024 e
1 024  2  512
2a redução:
2
2
corresponde a 1 024 e 512
1
2
corresponde a 1 024  2  512 e
512  2  256
3a redução:
2
2
corresponde a 512 e 256
1
2
corresponde a 512  2  256 e
256  2  128
Então, n é 3.
9.
4
4 corresponde a 2 400 000
1
4
corresponde a 2 400 000  4  600 000
3
4
corresponde a 3  600 000  1 800 000 
 1 800 000 reais
10. 3
corresponde a 9
1
8
8
8
8
corresponde a 8  3  24  24 alunos
11. 2
corresponde a 12 000
7
1
7
corresponde a 12 000  2  6 000
7
7
corresponde a 7  6 000  42 000 
 42 000 pessoas
12. 5
corresponde a 120
1
8
8
8
8
corresponde a 8  24  192  192
candidatos
13.
a) 2
corresponde a 18
2
1
2
corresponde a 18  2  9  9
quadradinhos
b) 3
corresponde a 18
3
1
3
2
3
quadradinhos
c) 6
corresponde a 18
6
1
6
5
6
quadradinhos
d) 9
corresponde a 18
9
1
9
4
9
quadradinhos

35
14.
10
10 corresponde a 30
1
10
7
10
corresponde 7  3  21
Faltaram:
30 − 21 = 9 → 9 dias
15. 1a loja:
4
4
corresponde a 300
1
4
Gastou: 75  2  77
2a loja e 3a loja:
Gastou: 77
Restam: 300  3  77 
 300  231  69  69 reais
22 – Comparando números
fracionários
1.
a) 1
5
; 2
5
; 3
5
; 4
5
; 5
5
b) 1
5
 2
5
 3
5
 4
5
 5
5
2.
a)
1
10 
1
8 
1
6 
1
5 
1
4 
1
3 
1
2
b) 2 partes;
2
4
1
2 5
c) 6 partes;
6
10
3
5 5
d) 8 partes;
4
4
8
8 5
3.
1
2
2
3
4
5
5 4
5 6
5 8
5
10 Exercícios, página 177.
1.
a) 2, 3 e 4.
b) Os dois comeram a mesma quantidade.
c) Sara:
1
4 ; Lara:
1
8
d) • 3; 5
• 2; 3
2. Sim.
3. O metrô.
4.
a)
1
1
3
. 6 (V)
2
1
6
.
6 b)
1
3
2
5 6 (V)
2
2
6
5
6 c)
1
3
3
 6 (V)
2
3
6

6 d)
2
3
1
3  (F)
e)
2
3
3
3 5 (F)
f)
1
2
5
5 10 (V)
2
2
10
5
10 g)
2
3
3
5 6 (F)
4
3
6
5
6 h)
2
3
2
. 6 (V)
4
2
6
.
6 23 – Obtendo frações equivalentes
1.
3 2
a)
2
7 e
6
21 d)
16
10 e
8
5
3 (sim) 2 (sim)
3 4
b)
5
9 e
15
18 e)
8
4 e
2
1
2 (não) 4
(sim)
7 3
c)
3
10 e
21
70 f)
15
12 e
5
2
7 (sim) 6 (não)

36
2.
3 5
a) 5
9  15
27 c)
5
8 
25
40
3 5
4
b)
11
3 
44
12
4
3.
4
5
9 36 5
a então: a  5  4  a  20
4
4.
10 4
1
10
3
2
5
20 5
12
20 5
10 4
5 2
5
25
9
4
5 20 10
18
20 5
5 2
5.
a) A maior é
7
8 .
b) 4 3
5
6
20
7
21
5 24
8
5
24 4 3
6.
2
a)
7
9
14
5 x então: x  9  2  x  18
2
3
b)
3
11
9
5 x então: x  11  3  x  33
3
4
c)
1
x
8 5
32 então: x  1  4  x  4
4
 7
d)
7
x
2 5
14 então: x  7  7  x  49
 7
7
e)
x
7
21
49 5 então: x  21  7  x  3
37
 6
f) 5
8
30
5 x
então: x  8  6  x  48
 6
3
g)
3 9
x 15 5 então: x  15  3  x  5
3
5
h)
x
4
5
20 5 então: x  5  5  x = 1
5
1.
 4 2
3
7 irredutível
4
12
1
3 5
2
10
1
5 5
4 2
2
5
6 irredutível
10
8
5
4 5
1
3 irredutível
2
2.
5
a)
20
25 b)
20
25
4
5 5
 5
 5
3.
15
20
3
4 5
5
4.
a)
105
63 calculando o m.d.c. (105, 63), temos:
105, 63 3  fator comum
35, 21 3
35, 7 5
1, 1
m.d.c. (105, 63)  3  7  21
21
105
63
5
3 5
21

37
b) m.d.c. (63, 105) = 21
21
63
105
3
5 
21
5.
5
a) 5
60
1
12   1
12
h
5
b)
15
60
m.d.c. (15, 60)
15, 60 2
15, 30 2
1, 1
m.d.c. (15, 60)  3  5  15
15
15
60
1
4   1
4
h
15
c)
30
60 m.d.c. (30, 60)  30
30
30
60
1
2  
1
2 h
30
d)
10
60 m.d.c. (10, 60)  10
10
10
60
1
6   1
6
h
10
e) 45
m.d.c. (45, 60)  15
60
15
45
3
3
60
 4  4
h
15
f)
60
60
60
60
60
1
1  → 1 h
60
6. manhã:
10  30  300  300 alunos
tarde:
6  40  240  240 alunos
m.d.c. (240, 300)  60
60
2 4 0
300
4
5 
60
7.
a) 8  5  4  12  10  1  40  40 alunos
b) 8  4  10  22  22 meninos
2
22
40
11
20 
2
c) 40  22  18  18 meninas
2
18
40
9
20 
2
d) 4  12  16 m.d.c. (16, 40)  8
8
16
40
2
5 
8
4
e) 4
12
1
3 
4
1.
a) Itália: 8 medalhas
b) 7 medalhas.
c) 7
; essa fração não pode ser
8
simplificada, pois já está na forma
irredutível.
d) 7
19
; essa fração não pode ser
simplificada, pois já está na forma
irredutível.
2.
a) 52a  quinquagésima segunda;
16a  décima sexta
b)
5
285 ou
1
57
c) Estados Unidos, China, Rússia e
Austrália
d) 35  32  27  17  111  111
medalhas

38
e)
111
285 m.d.c. (111, 285)  3
3
111
285
37
95 
7
f)
44
285 ; essa fração não pode ser
simplificada.
12
g
f
60
24
e
d
24
60
90
36
b
c
12
a
54
*
m.d.c. (60, 90)  30
30
∗ 
60
90
2
2
 → ∗ 3
3  
2
3
30
18
2
3 54 
a → a  2  18  a  36
18
18
2
3
36
 b
 b  3  18  b  54
18
4
2
3 12 
c  c  2  4  c  8
4
8
2
3 24 
d  d  2  8  d  16
8
12
2
3
24
 e
 e  3  12  e  36
12
20
2
3 60 
f  f  2  20  f  40
20
6
2
3
12
 g
 g  3  6  g  18
6
24 – Reduzindo duas ou mais
frações ao mesmo denominador
Exercício, página 184.
a)
1
2
1
4
e m.m.c. (2, 4)  4
2
1
2
2
4 
2
2
4
e 1
4
b)
1
6 ,
1
8 m.m.c. (6, 8)  24
4 3
1
4
1
3
6
 24 8

24 4 3
4
3
24 ,
24
c)
3
8 ,
5
6 ,
7
12 m.m.c. (8, 6, 12) = 24
3 4 2
3
9
5
20
7
8

24 6

24 12
14
24 
3 4 2
9
20
14
24 ,
24 ,
24
d) 3
4
, 5
18
, 2
9
, 1
6
m.m.c. (4, 18, 9, 6)  36
9 2 4 6
3
27
5
10
2
8
1
4

36 18

36 9

36 6
6
36 
9 2 4 6
27
, 10
, 8
, 6
36
36
36
36
e) 3
7
, 2
5
, 9
14
, 11
10
m.m.c. (7, 5, 14, 10)  70
10 14 5 7
3
30
2
28
9
45
11
7

70 5

70 14

70 10
77
70 
10 14 5 7
30
, 28
70
70
, 45
70
, 77
70
Editoria de arte

6
7   b) 5
12
4
9   b)
4
12    
5
8    

38
28

58
6
12

4
12
2
12
16

39
f)
7
20 ,
14
15 ,
9
10 ,
11
30
m.m.c. (20, 15, 10, 30)  60
3 4 6 2
7
21
14
56
9
54
11
20

60 15

60 10

60 30
22
60 
3 4 6 2
21
60 ,
56
60 ,
54
60 ,
22
60
Azul:
5
8 (livros); cor-de-rosa:
1
4 (DVDs);
amarelo:
1
8 (CDs)
25 – Adição e subtração
1.
a) 3
7
3
7
6
11
 12

12 2.
a) 7
9
3
9
7
7
5
2
 7

7 3.
a) 8
9
b) 5
8
c) 0 d)
1
2 e) 2
15
4.
a) 6
12
1
6
6
12
2
12
b) 3
8
1
4
3
8
2
8
5.
2
1
3
 4 m.m.c. (3, 4)  12
8
3
11
12
 12

12 6.
1
2
4
 5 m.m.c. (4, 5)  20
5
8
13
20
 20

20 7.
a) 5
9
b) 4
9
8.
a)
1
2
1
5
 3
 6 m.m.c. (2, 3, 6)  6
3
6
2
5
10
 6
 6

6 2
10
6
5
3 
2
b)
3
5
1
4
 6
 2 m.m.c. (4, 6, 2)  12
9
10
6
12
 12
 12 
19
12
6
13

12
12  
c) 5
6
1
1
   m.m.c. (6, 2, 3)  6
2
3 5
6
3
2
 6

6  
2
6
2
6
 0
 
d) 1
1
5
3
   m.m.c. (2, 3, 6, 4)  12
2
3
6
4 6
4
10
9
12
 12
 12
 12 
2
12
10
9
 12

12  
12
9
3
12

12
12 :3
3
12
 
1
4 
3
9.

1 1
10
1
2
 
 

 
 m.m.c. (10, 2)  10

1  1
10
5
10
 
 

 

6
10  
1 
10
10
6
4

10
10 2
4
10
2
5 
2
Editoria de arte
Editoria de arte

40
10. Sim.
1 a 5
1 1 1
b 1 5
5 5 5
1 1 c 5 d
1
2
5
4
2
4
5
4
d5 d5 d5
7
4
1 ⇒ 1 ⇒
1
4
1
2
1
2
1
4
2
4
1
4
1
4
1a5 ⇒a5  ⇒a5  ⇒a5
2
4
5
4
5
4
2
4
b1 b  b
3
4
5 ⇒ 5 ⇒ 5
1 7
4
7
4
1 7
4
4
4
3
4
1c5 ⇒c5  ⇒c5  ⇒c5
26 – A forma mista
1.
a)
b)
c)
d)
2.
1
4
5
a) 5
1
20
1
21
1 4
5 4
1 4
5
4 b) 10
1
3
10
1
30
1
31
1 3
5 3
1 3
5
3 2
3
5
c) 5
2
15
2
17
1 3
5 3
1 3
5
3 7
10
1
d) 1
7
10
7
17
1 10
5 10
1 10
5
10 3.
1
1
6
1
6
1
7
5 1
1 6
5 6
1 6
5
6 7
6
13
35
26
9
3
 15
5 30
 30
5 30
5
10 4.
15
1
2
1
1 12
3 5
1
1
1 2
1 1
3 515 12
5
1
1
1 2
1
3 527 5
3
2
1 6
1
6 527 5
5
→
5
1 6
6 527 5
27
5
6
27
quilômetros
5.
1
4
5
2
7
1 1
3
1 10 5
4
7
1 5
1 1 1
10 51 1
5
2
3
30
30
24
30
20
21
1 30
1 30
1 30
1
30 5 5
125
30
5 5
25
6
a) 4
1
4
3
3
1
1
 3
 2
 2

1
4
4
2
2 b) 1
2
1
3
3
4
, e
c) Elas são iguais.
d) No bolo de rolo; 4
1
4
.
e) A maior soma é a do bolo de rolo.
Cuca de manteiga
1
3
1
3
3
1 3
2
1 4
1 4 5
1
3
1
3
3
1 3
2
1 1 4
1
4 5 5
4
12
6
36
9
9
1 12
1 12
1 12
1
12 5 5
64
12
16
3
5 5 5
5
1
3
1
4
1
2
2
4
5
4
21
5
1
5
4
5 17
3
2
5
5
3 33
10
3
5
3
10 15
2
1
5
7
2 Editoria de arte
Editoria de arte

41
Bolo de rolo
4
1
4
3
1
 2
 2
4
2 5
1
1
 4
   
2 54 2
5
3
4
2
4
1
 4

2 58 5
1
1

2
2 59 5
9
9
1
2
1

5
3 f) Resposta em aberto.
g) Respostas em aberto.
1.
1
2
2
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
1
10
, , , , , , , , ,
1. Fração
irredutível
 2

 3

 4

 5

 6

1
2
2
4
3
6
4
8
5
10
6
12
1
3
2
6
3
9
4
12
5
15
6
18
3
4
6
8
9
12
12
16
15
20
18
24
5
6
10
12
15
18
20
24
25
30
30
36
2.
a) 4
3
12
 5 d) 5
5
5 6
12510
b) 2
4
8
 5 e) 1
9
9 2
1055
c) 5
1
1
 f)
10
5 2 2
3
22
 11
5
3 1 1
3.
3
4
1
2  5
2
3
2 1
4.
1 1
a)
1
3
4
4
 7
5 21 e)
9
8
4
1
 5
45
10 2 5
1 1
b) 7
8
3
21
 f)
2
5 16 4
45
1
10  5
9
8
5 2
1 1 5 2
c)
3
5
1
3  5 g) 45
5
9
4
8
9
 510
1 3 1 1
1 2 5
d) 2
7
11
7  5 h) 8
11
2
9
45
4
 510
1 1 1 2
5. 2
5
 10 54→→ 44 quilogramas
1
6.
1
1
2
1
 2
2 5
3
2
5
2
5  5
15
4
3
3
4
3
3
4
ou → de xícara de chá
1 1
7.
5
8
4
1
 5
5
2 2 1
8.
1
4  5
3
5 12  21 5
12 5
4
63→→ 6633 quilômetros
1
7 cheios + 7 pela
metade →
→ 10
1
2
; 3
em
1
2
cada bandeja ou
27 – Multiplicação
1.
5
2  5 → 2,5 quilos ou dois quilos e
meio
a) 5
1
2
b) 8 3 2,5 5 20 → 20 reais
2.
a) 6 metades de maçã
b) 5 metades de maçã
c) 5
2
2
1
2
ou
d) 3
5
2
2
1
2
; ou
e) 5 amigas
Editoria de arte

42
28 – Divisão
1.
•
1
4
4
1
3 51 •
7
11
11
7
3 51
•
5
4
4
5
3 51 •
13
10
10
13
3 51
a) 1
b) Os dois fatores são frações nas quais
o numerador de uma é igual ao
denominador da outra, e vice-versa.
2.
a) 2 vezes b) 3 vezes c) 4 vezes
3.
a) 2 vezes b) 4 vezes c) 6 vezes
1.
7
4 , inverso de
4
7
2. 4
15
3.
a) 5
1
4
5
4
1
; 5 3 520
b) 7
1
2
7
2
1
; 5 3 514
c) 1
4
1
1
1
; 5
5 4
3 5
5
20 d) 1
2
1
1
1
; 7
5 2
3 7
5
14 e) 5
8
5
1
5
; 2
5 8
3 2
5
16 1
f) 7
10
7
1
; 14
5 10
3 5
20 1
14
2
g) 1
11
4
4
; 1
4
5 3 11
5
11 h) 1
4
11
11
; 1
11
5 3 4
5
4 i) 0
5
9
0
9
5
; 5 3 50
4. 4
1
5
4
5
1
; 5 3 520→20 xícaras
5.
2
2
3
1
6
2
3
6
1
; 5 3 54 →4 copos
1
155
6. 465
3
4
465
4
3
; 5 3 5620 → 662200 pacotes
1
7.
5
1
2
1
10
1
11
5 5
1 2
5 2
1 2
5
2 1
11
2
1
2
11
2
2
1
; 5 3 511→11 aventais
1
8.
a) 6
1
2
1
12
1
13
5 6
1 2
5 2
1 2
5
2 1
13
2
1
2
13
2
2
1
; 5 3 513
1
b) 10
1
2
10
2
1
; 5 3 520
9.
a) 1
4
2
1
3
3
; 3
5 4
3 2
5
8 b) 1
5
4
1
7
7
; 7
5 5
3 4
5
20 1 1
c)
5
6
5
1
; 3
5 3 5
2 5
6
3
5
2 1
1
d)
7
8
1
7
; 4
5 3 5
2 7
8
4
1
2
1 2
e) 3
5
9
3
2
; 10
5 5
3 5
3 10
9
1 3
3
f) 1
40
1
3
; 30
5 3 5
4 1
40
30
1
4
10.
a)
2
3
4
1
; 5
1 2 5 b)
1
2
5
5
2 8
; 4 5
1 1 1
2
3
5
4
1
2 1 5 3 5
5 3 5
1
2
4
5 2
5
8
2 2 1
5
6
1
2 1
5 5
1
2
1
2
2 0
5 5
5
6
3
8
4
1
6
6
3 5 5 5
11. 4
1
2
4
2
1
; 5 3 58→8 pacot es
12.
5 3
a) 10
3
10
3
9
8
8
9 ; 55 3 5
15
4
1 4
b) 4
1
4
1
1
5
5
1 ; 55 3 5
4
5
 

43
c) 1
6
1
6
7
1
1
 7   
7
6
d)
7
4
2
3
7
4
3
2
21
8
:   
Sandra: 20 anos
Virgínia: 20
1
10
 20
2
20
1
10
  20 
1
 20  2  18  18 anos
Maria: 2  18
2  18  36  36 anos
Eu:
9
3
4
 36 27  27 anos
1
29 – As frações e a porcentagem
1.
a) 8% 
8
100 c) 43% 
43
100
b) 19% 
19
100 d) 120% 
120
100
2. 50%
3. setor A
4. Alternativa a.
5. Alternativa d.
6.
a) 6% de 35 000  6  1% de 35 000
35 000  100  350
6% de 35 000  6  350  2 100 
 2 100 eleitores
b) 35 000  2 100  32 900 
 32 900 eleitores
7. 1 650 pessoas
8. 9 250 reais
9.
a) 2; 25% b) 4; 50% c) 75%;
6
8 ou
3
4
a)
1 000
900
800
700
600
500
400
300
200
361
792
928
b) 1 025 + 20% de 1 025 = 1 025 + 205 = 1 230
Foram realizados 1 230 transplantes.
c) 61% de 6 200  61  1% de 6 200 6 200  100  62
61  62  3782
6 200  3 782  2 418  2 418 pacientes
30 – Resolução de problemas
1.
a) 24 000 000
1
8
 3 000 000  3 milhões
de reais
4 800 000
b) 24 000 000
3
5
 14 400 000 
 14 400 000 reais
c) 24 000 000  (3 000 000  14 400 000) 
 24 000 000  17 400 000  6 600 000 
 6 600 000 reais
2.
I 
1
7 III 
2
6 
1
3
II 
1
4 IV 
3
12 
1
4
Frações equivalentes: II e IV
3.
1
2
7
6
13
3
 7
 21
 21

21 21
13
8
21  21

21
100
1999 2003 2004 Ano
Quantidade de
transplantes
Editoria de arte

44
4.
70
560
3
8


 210
1
560  210  770  770 alunos
5.
3
56
30 000
1
56
30 000310 000
56
56
5610 000560 000
6.
 560 000 habitantes
3
4
1
5
15
20
4
20
11
20
   
11
20
44
1
20
44 11 4
20
20

20 4

 
 80
 
7.
2
5
1
4
8
20
5
20
13
20
   
13
20
65
1
20
65 13 5

  
20
20
 
205100 100 quilômetros
(comprimento da estrada)
100  65  35  35 quilômetros (faltam
duplicar)
8.
a)
8
8
5
3
 8

8 b)
5
8
25
1
8
2555
3
8
3515  15 litros
c) 1
5
8
8
8
8540 40 litros
1
2  
d) 40 2

40 2  1
 
2 

 

40   4
1

2
2 
 

 

5
2 
8
40 
2
5
 40 
 16  16 latas
1
9.
2
5
1
8
5
13
13
 4
 20
 20
 (quanto
20
20 foi vendido da peça)
20
20
13
7
7
 20
 20
20 (o que sobra da
7 peça)
20
1 400
1
20
1 4007200

20
20
20 2004 000  R$ 4 000, 00 (preço
de toda a peça)
4 000  5  800 800 metros
10.
180
a) 3600
1
20
 180  180 eleitores
1
deixaram de votar
b) 3 600  180  3 420  3 420 eleitores
votaram
171
3 420
1
20
1
285
c) 3 420
1
12
votaram em
branco
1
684
d) 3 420
3
5
anularam o voto
 2 052  2 052 votos para o
1
candidato vencedor
3 420  (2 052  285  171) 
 3 420  2 508  912  912 votos
para o candidato que perdeu
e) 2 052  912  1 140  1 140 votos
200
11. 800
1
4
 200  R$ 200,00 (metade do
1
meu salário)
2  200  400  R$ 400,00 (meu salário)
 105 reais
 80 litros

8
21
40
1
21
40 8 5
21
21
21 5 105

 
 

45
12.
a) 1o dia: 3
5
5
5
3
2
2 5 (percurso que falta)
5
5 2o dia:
2
3
2
4
3 5
5
15 3
5
4
9
4
13
13
1 5 1 5 → (fração
15
15
15
15
15 do percurso rodado nestes dois dias)
b)
15
15
13
2
2
2 → 15
5 15
15 (fração do
percurso que ainda falta para
completar a viagem)
c)
2
15
5 600
5 5
1
15
600;2 300
15
15
515330054 500 → 44 5 50000 quilômetros
(percurso total)
13.
a) Estado A
2 400 000
12 000 000
4
5
3 = 9600000  9 600 000
1 toneladas
Estado B
3200 000
9600 000
2
3
3 5 6 400 000  6 400 000
1 toneladas
Produção do estado A  9 600 000
toneladas
Produção do estado B  6 400 000
toneladas
O estado A produz mais trigo.
b) 9 600 000  6 400 000  3 200 000
O estado A produz 3 200 000 toneladas
a mais que o estado B.
14.
14
14
9
5
→ 5
2 5 (fração dos alunos
14
14
14 que obtiveram notas maiores que 6,0)
5
5300
14
1
14
5300;5560
14
14
5143605840  840 alunos
participaram da olimpíada
15.
60
240
3
4
3 5180  180 meninas
1
120
240
1
2
3 5120  120 (número de meninas
1 pensado pelo gerente)
1802120560  60 meninas não ganharão
brinde
1. Alternativa b.
1.
15333
1
3 5
515 331 5 1
3
3

 

 
515 1 5 99
3
1
3
3

 

 

100
3
5153 5
500  500 rotações
2.
:12
12
60
1
5 5
:12
3. Alternativa d.
13
65
1
5
3 51 3 13 cartas entregues
1 no 1o andar
65213552  52 cartas
4. Alternativa d.
60
420
5
7
3 5300 → 300 candidatos rejeitados 1
42023005120 → 120 candidatos aceitos

46
5. Alternativa c.
1
5 parte pintada
20
1
5
20
100 5 5 20%
20
6.
1
2
19
7
1
2
1
6
3 1

 

 


 

 
; 2 1 5
19
14
3
6
1
6

 

 
; 1
5 2 1 5

19
14
2
6
; 1
5 1 5
3
19
14
6
2
3 1
5 1 5
7
57
14
1
5 1 5
57
14
14
14
71
14
5 1 5 5
5
1
14
→ 1
5
14 está entre
os números naturais 5 e 6.
7. Alternativa a.
3
1
9
5
14
5
1 3
5 15
1 15
5
15 15
15
14
1
1
2 → 15
5 15
15 fração que representa
o número de jogos que perdeu
1
52
15
15
15
51532530→30 (total de jogos do
torneio)
3
5
330518 18 jogos vencidos
1
3
330510 10 jogos empatados
183311031554110564  64 (total de
pontos da equipe)
8. Alternativa c.
Fábrica A:
3 17
10
3 170 551  51 kg
1
Fábrica B:
Dobro de 51  102  102 kg
Fábrica C:
170  (51  102) 
= 170  153  17  17 kg
9. 1o termo  1
2o termo 
1
2  metade do 1o termo
1
4
1
2
1
1
; 2
3 metade do
2
2 3o termo 5 5 5 5
2o termo
O segredo desta sequência é:
O termo seguinte é igual à metade do
termo anterior.
4o termo 5 5 5
1
4
1
1
1
; 2
4
3
2
8 1
8
1
1
1
; 2
8
3
2
16 5o termo 5 5 5
1
16
1
1
1
; 2
16
3
2
32 6o termo 5 5 5
A soma do 5o e do 6o termos é:
1
1
2
1
3
16
1 32
5 32
1 32
5
32 10. Alternativa d.
100  (45  20) 
 100  65  35  35 bolas amarelas
35
100
 porcentagem de bolas amarelas
11. Alternativa d.
25
100
25% 5 5
1
4
=
3
16
6
16
5 5
3
8
3
16
5 1
4
16
5 5
1
4
Editoria de arte

A forma decimal dos números racionais
31 – Trocando dinheiro
1. água: trinta e cinco reais e trinta e nove centavos; luz: sessenta e cinco reais e trinta e seis
centavos.
2.
a) R$ 9,04 b) R$ 6,23 c) R$ 29,37 d) R$ 57,28 e) R$ 128,09
4.
a) 3 3 0,10 5 0,30; 6 3 0,05 5 0,30;
1 3 0,25 1 1 3 0,05 5 0,30
b) 35 centavos; qualquer produto, menos o cappuccino; posso adquirir, também, leite e carioca
ou dois cariocas (sobrando ainda 5 centavos) etc.
2.
a) R$ 0,04; quatro centavos d) R$ 1,25; um real e vinte e cinco centavos
b) R$ 0,32; trinta e dois centavos e) R$ 0,05; cinco centavos
c) R$ 0,47; quarenta e sete centavos f) R$ 13,50; treze reais e cinquenta centavos
4. R$ 930,00; resposta em aberto.
32 – Representação decimal
a) Uma placa representa a décima parte ou 1
10
.
b) Uma barra representa a centésima parte ou
1
100 .
c) Um cubinho representa a milésima parte ou
1
1000 .
1.
415
100
400 10
5
100
400
100
10
100
5
100
4
1
10
5
100
5 1 1 5 1 1 5 1 1 54,15
4 inteiros
1 décimo
5 centésimos
47

2.
a)
52
10
50 2
10
50
10
2
10
5
2
10
1
5 5 1 5 1 5 5 ,
2
5 inteiros 2 décimos
b)
52
100
50 2
100
50
100
2
100
5
10
2
100
1
5 5 1 5 1 5 0 ,
52
5 décimos 2 centésimos
c)
77
10
70
7
10
70
10
7
10
7
7
10
5 1 5 1 5 1 57,7
7 inteiros 7 décimos
d) 77
100
70 7
100
70
100
7
100
7
10
7
100
1
5 5 1 5 1 5 0 ,
77
7 décimos 7 centésimos
e) 7
10
50,7
f) 7
100
50,07
3.
a) 1 3 1
3
10
1
3
10
10
10
3
10
13
10
, 5 5 1 5 1 5
b)
13
100
c) 13
1000
d) 4 002 4
2
1000
4
2
1000
4 000
1000
2
1000
4 002
1000
, 5 5 1 5 1 5
e) 85
1000
f) 3
10
g) 2 47 2
47
100
2
47
100
200
100
47
100
247
100
, 5 5 1 5 1 5
h) 135
1000
4.
a) Um real e dezenove centavos. d) Três reais e cinquenta e quatro centavos.
b) Cinco reais e vinte e nove centavos. e) Sessenta e seis centavos.
c) Sete reais e quarenta e seis centavos.
5. a)
8
10
50,8 b)
42
100
50,42 c) 225
100
52,25 d)
406
100
54,06
;2
6. a) 2 2
22
10
11
5
, 5 5
;2
;4
b) 0 44
44
100
11
25
, 5 5
;4
;25
c) 0 25
25
100
1
4
, 5 5
;25
;2
d) 2 4 2
4
10
20
10
4
10
24
10
12
5
, 5 5 1 5 5
;2
48

49
;50
e) 2 50 2
50
100
2
50
100
200
100
50
100
250
100
5
2
, 5 5 1 5 1 5 5
;50
;2
f) 6 6 6
6
10
6
6
10
60
10
6
10
66
10
33
5
, 5 5 1 5 1 5 5
;2
7.
a) 0,35  trinta e cinco centésimos
b) 18,427  dezoito inteiros e
quatrocentos e vinte e sete milésimos
c) 0,004  quatro milésimos
d) 5,9  cinco inteiros e nove décimos
8.
350
1
2
50
100
5 50,50
350
33 – Propriedade geral dos
números decimais
1. As duas, porque 1,50 5 1,5.
2. 2,03; 2,030; 2,0300
3.
a) 0,07000 e 0,07 5 d) 9,32 e 9,3200 5
b) 6 e 6,000 5 e) 2,025 e 2,25 
c) 0,015 e 0,150  f) 9 e 9,00 5
4.
5,010 5 5,01 5 5,0100 5 5,01000
5.
a) 3,7; 7,01; 3,016; 10,01; 1,0004
b) 0,605; 0,28; 0,095
c) 0,605
d) 0,095
6.
a) 9,4 e 4,9
9,4  4,9, pois 9  4
b) 7 e 7,1
7  7,1, pois 7 5 7,0 e 0  1
c) 4,230 5 4,23
d) 2,081 e 2,0095
2,081  2,0095, pois 2,081 5 2,0810 e
810  95
e) 3,6 e 3,601
3,6  3,601, pois 3,6 5 3,600 e 600  601
f) 0,95 5 0,9500
g) 1,37 e 1,037
1,37  1,037, pois 1,37 5 1,370 e 370  37
h) 0,064 e 0,12
0,064  0,12, pois 0,12 5 0,120 e 64  120
7.
a) entre 0 e 0,5: 0,016; 0,405; 0,057
b) entre 0,5 e 1: 0,98; 0,71
c) entre 1 e 1,5: 1,02; 1,1
8. Caixa B, pois: 4,5  4,28  4,5 5 4,50 e
50  28
9. O portão da frente, pois: 4,3  4,18  4,3 =
= 4,30 e 30  18
1.
a) Não, pois apesar do aumento do
número de habitantes da Grande Rio,
esse número ainda não ultrapassa a
marca que a região da Grande São
Paulo tinha em 2000.
b) 23,2 milhões  21,1 milhões  20,4 mi-lhões
 17,8 milhões  11,9 milhões 
 10,6 milhões
a) 2005
b) 33,220 milhões  33,644 milhões 
 33,818 milhões  34,649 milhões 
 35,139 milhões
d) 1980: 25 inteiros e 23 milésimos;
1990: 28 inteiros, seiscentos e vinte e
oito milésimos; década: série de 10;
decênio, período de 10 anos.

50
34 – Adição e subtração de
números decimais
1.
a) 16,9 1 7,6 5 24,5
16,9
1 7,6
24,5
b) 35,2 2 9,8 5 25,4
35,2
2 9,8
25,4
c) 0,85 1 1,376 5 2,226
0,850
11,376
2,226
d) 25 2 18,25 5 6,75
25,00
218,25
6,75
e) 2,33 1 2,033 1 2,666 5 7,029
2,330
2,033
12,666
7,029
f) 15 2 9,85 1 3,275 5
5 5,15 1 3,275 5 8,425
15,00 5,150
2 9,85 13,275
5,15 8,425
2.
b 5 3,6 1 2,7 5 6,3
c 5 2,7 1 5,4 5 8,1
amarelo:
d 5 a 1 b 5 9,7 1 6,3 5 16
e 5 b 1 c 5 6,3 1 8,1 5 14,4
azul:
f 5 d 1 e 5 16 1 14,4 5 30,4
f
d e
a b c
6,1 3,6 2,7 5,4
3,4 2,7 0,9 1,8 3,6
5.
a) Equipe B; 0,716  0,698, pois 716  698
b) 0,716 2 0,698 5 0,018
0,716
20,698
0,018
6. 7,4 2 4,78 5 2,62  2,62 m
7,40
24,78
2,62
7. 2,5 − 1,35 5
5 1,15  1,15 m
2,50
21,35
1,15
8. Comprimento: 0,25 1 1,70 1 0,15 1 3,80 1
1 0,15 1 4,10 1 0,25 5 10,40  10,40 m
0,25
1,70
0,15
3,80
ou 0,15
4,10
1 0,25
10,40
Largura: 0,25 1 3,80 1 0,15 1 4,50 1 0,25 5
5 8,95  8,95 m
0,25
3,80
0,15
4,50
10,25
8,95
Editoria de arte
0,381
10,589
0,970
menor, pois 0,970  1  0  1
3. 3,000
21,899
1,101
4. O “segredo” é: o número acima é igual à
soma dos dois números abaixo dele.
Ex.: 6,1 5 3,4 1 2,7
verde:
a 5 6,1 1 3,6 5 9,7

51
9.
a) 1,4 1  5 10
 5 10 2 1,4
 5 8,6
b) 80,75 1  5 100
 5 100 2 80,75
 5 19,25
c) 345,27 1  5 1 000
 5 1 000 2 345,27
 5 654,73
10. x 5 (51,7 1 8,36) 2 (16,125 1 7,88)
x 5 60,06 2 24,005
x 5 36,055
51,70 16,125 60,060
1 8,36 1 7,880 224,005
60,06 24,005 36,055
Soma 5 1,6 1 2,1 1 1,4 5 5,1
A 5 5,1 2 (2,1 1 1,3)
A 5 5,1 2 3,4
A 5 1,7
B 5 5,1 2 (1,5 1 A)
B 5 5,1 2 (1,5 1 1,7)
B 5 5,1 2 3,2
B 5 1,9
C 5 5,1 2 (1,6 1 1,5)
C 5 5,1 2 3,1
C 5 2,0
D 5 5,1 2 ( C 1 1,3)
D 5 5,1 2 ( 2,0 1 1,3)
D 5 5,1 2 3,3
D 5 1,8
1.
a) 1950 2 1960
b) 1920 2 1940
c) 2,99 2 1,50 5 1,49
d) Verdadeira.
2.
a) 18 a 39 anos
b) 36,4 2 35,3 5 1,1  1,1%
c) 22,1 2 17,8 5 4,3  4,3%
d) 20,8 2 16,7 5 4,1  4,1%
35 – Multiplicação com números
decimais
1.
a) 10 1 08 10
108
100
108
10
3 , 5 3 5 510,8
b) 100 0 572 100
572
1000
572
10
3 , 5 3 5 557,2
c) 10 0 92 10
92
100
92
10
3 , 5 3 5 59,2
d) 1000 0 0029 1 000
29
10 000
29
10
3 , 5 3 5 52,9
2. 22,5 cm 5 0,225 m
0,225 3 1 000 5 225  225 m
3.
a) 539,5
5
95
10
5 95
10
475
10
3
3 5 5 5 47 ,
5
b) 731,25
7
125
100
7 125
100
875
100
3
3 5 5 5 8 ,
75
c) 12 3 8,3
8,3
3 1 2
1 6 6
1 8 3 0
9 9,6
d) 25 3 0,64
0,64
3 25
320
1 1280
16,00
e) 3 3 0,989
0,989
3 3
2,967
f) 7,2 3 4,8
7,2
34,8
5 7 6
1 2 8 8 0
3 4,5 6
g) 0,9 3 10,5
1 0 , 5
3 0 , 9
9, 4 5
10,0
2 1,4
8,6
100,00
2 80,75
19,25
1000,00
2 345,27
654,73

52
h) 7,25 3 0,6
7,2 5
3 0,6
4,3 5 0
i) 9,9 3 5,5
9,9
3 5,5
4 9 5
14 9 5 0
54,4 5
j) 0,96 3 0,5
0,9 6
3 0,5
0, 4 8 0
4.
a) 0,7 3 0,9 3 3,5 5
5 0,63 3 3,5 5
5 2,205
0, 7 0,6 3
3 0, 9 33,5
0, 6 3 3 1 5
1 8 9 0
2,2 0 5
b) 14,2 3 0,4 3 2,5 5
= 5,68 3 2,5 =
= 14,2
1 4,2 5,6 8
3 0, 4 3 2,5
5,6 8 2 8 4 0
1 1 1 3 6 0
1 4,2 0 0
c) 3,21 3 0,9 3 1,07 5
= 2,889 3 1,07 =
= 3,09123
3, 2 1 2,8 8 9
3 0,9 3 1,0 7
2, 8 8 9 2 0 2 2 3
1 2 8 8 9 0 0
3,0 9 1 2 3
d) 1,7 3 3 3 5,29 5
5 5,1 3 5,29 5
5 26,979
1,7 5,2 9
3 3 3 5,1
5,1 5 2 9
1 2 6 4 5 0
2 6,9 7 9
5. A 5 257 3 0,006 e B 5 3 3 1,025
A 1 B 5 (257 3 0,006) 1 (3 3 1,025)
A 1 B 5 1,542 1 3,075
A 1 B 5 4,617
2 5 7 1,0 2 5 1,5 4 2
30,0 0 6 3 3 13,0 7 5
1,5 4 2 3,0 7 5 4,6 1 7
6.
a) 9,05 2 2,5 3 2,5 5
5 9,05 2 6,25 5 2,80
2,5 9,0 5
32,5 26,2 5
1 2 5 2,8 0
5 0 0
6,2 5
b) (6 2 1,07) 3 3,1 5
5 4,93 3 3,1 5
5 15,283
6,0 0 4,9 3
21,0 7 33,1
4,9 3 4 9 3
1 1 4 7 9 0
1 5,2 8 3
7. 4 3 22,6 1 8 3 13,8 5
5 90,4 + 110,9 5
5 200,8  200,8 cm
2 2,6 1 3,8 1 1 0,4
3 4 3 8 1 9 0,4
9 0,4 1 1 0,4 2 0 0,8
8. 3,8 × 31 5
5 117,8  117,8 h
3,8
3 3 1
3 8
1 1 1 4 0
1 1 7,8
9. 12 3 (199 3 3,3 2 651) 5
5 12 3 (656,7 2 651) 5
5 12 3 5,7 5
5 68,4  68,4 anos
1 9 9 6 5 6,7 5,7
3 3,3 2 6 5 1,0 3 1 2
5 9 7 5,7 1 1 4
1 5 9 7 0 1 5 7 0
6 5 6,7 6 8,4
10. a) Estimativa: 30; valor exato: 30,6.
b) Estimativa: 150; valor exato: 148,5.
c) Estimativa: 63; valor exato: 63,9.
d) Estimativa: 56; valor exato: 55,3.
e) Estimativa: 72; valor exato: 73,08.

53
1.
a) Verdadeira, pois: 3,5 3 145,4 5 508,9 .
. 509
1 4 5, 4
3 3, 5
7 2 7 0
4 3 6 2 0
5 0 8, 9 0
b) (138,1 3 4) 2 509 5
5 552,4 2 509 5 43,4  43,4 m
1 3 8,1 5 5 2,4
3 4 2 5 0 9,0
5 5 2,4 4 3,4
c) 160 1 138,1 5 298,1
2 3 140,8 5 281,6
298,1  281,6
1 6 0,0 1 4 0,8
1 1 3 8,1 3 2
2 9 8,1 2 8 1,6
2.
a) Consumo médio 5
312 304 287
3
903
3
301 301
+ +
= = →
5 301  301 kWh
b) Meta de consumo 5 consumo médio 3 0,8
Meta de consumo 5 301 3 0,8 5 240,8 
 240,8 kWh
3.
a) 4,8 1 70,0 1 16,2 1 12,0 1 120 1 45 1
1 6,0 1 1,1 1 7,0 1 13,5 5
5 295,6  295,6 kWh
b) 295,6 3 0,40 5 118,24  R$ 118,24
c) Redução do consumo:
2956 20
295 6 20
, %
,
, ,
, ,
5
5 5
100
5 5
5 → kWh
Economia em reais:
59,12 3 0,40 5 23,648  23,65  R$ 23,65
3
3
3
2956 020
59 12 59 12
36 – Divisão com números decimais
1. a) 63 5 10 63 5
1
10
, ; 5 , 3 563,530,156,35
1
10
50,1
b) 502 ; 100 5 5,02

É o mesmo que multiplicar por 0,01. A
vírgula é deslocada duas casas para a
esquerda.
c) 37 ; 10 5 3,7

É o mesmo que multiplicar por 0,1. A
vírgula é deslocada uma casa para a
esquerda.
d) 5 006 ; 1 000 5 5,006

É o mesmo que multiplicar por 0,001.
A vírgula é deslocada três casas para a
esquerda.
e) 5,7 ; 10 5 0,57
f) 106,2 ; 100 5 1,062
2. De 6,1 para 0,61 a vírgula foi deslocada
uma casa para a esquerda. É o mesmo
que multiplicar por 0,1 ou dividir por 10.
3. C D U d
1 2 4 ,1 1 7
0 5 1 7 , 3  7,3 litros
0 U d
4.
3 100
140,40 ; 2,16 5 14 040 ; 216 5
5 65 3 100
DM UM C D U
1 4 0 4 0 2 1 6
1 0 8 0 6 5  65 dólares
0 D U
5. 162,80 ; 2,96 5 55  55 litros
DM UM C D U
1 6 2 8 0 2 9 6
1 4 8 0 5 5
0 D U
6. N 3 3,5 5 91
N 5 91 ; 3,5 5 910 ; 35 5 26
N 5 26
9 1 0 3 5
2 1 0 2 6
0
[
[

54
7. 62,1 ; 27 5 2,3
C D U d
6 2 1 2 7 0
8 1 0 2 , 3
0 U d
8. A 5 (17,25 2 8,47) ; 2
A 5 8,78 ; 2
A 5 4,39
1 7 , 2 5
2 8 , 4 7
8 , 7 8
9.
a) 37 ; 100 5 0,37  0,37 metro
b) 1,50 ; 100 5 0,015  0,015 metro
10.
a) 10,6 ; 2 5 5,3
C D U d
1 0 6 2 0
6 0 5 , 3
0 U d
b) 7,25 ; 5 5 1,45
C D U d c
7 2 5 5 0 0
2 2 5 0 1 , 4 5
2 5 0 0 U d c
0
c) 0,36 ; 3 5 0,12
D U d c
3 6 3 0 0
3 6 0 0 , 1 2
6 0 0 U d c
0
d) 14,4 ; 12 5 1,2
C D U d
1 4 4 1 2 0
2 4 0 1 , 2
0 U d
e) 30,6 ; 20 5 1,53
C D U d c
3 0 6 2 0 0
1 0 6 0 1 , 5 3
6 0 0 U d c
0
f ) 171,6 ; 26 5 6,6
UM C D U d
1 7 1 6 2 6 0
1 5 6 0 6 , 6
0 U d
11. 1468,32 ; 552 5 2,66  R$ 2,66
CM DM UM C D U d c
1 4 6 8 3 2 5 5 2 0 0
3 6 4 3 2 0 2 , 6 6
3 3 1 2 0 0 U d c
0
12. 897 ; 78 5 11,5
C D U d
8 9 7 7 8
1 1 7 1 1 , 5
3 9 0 D U d
0
13. a) 70,8 ; 0,6 5 118 d) 21,4 ; 2,14 5 10
C D U UMC D U
7 0 8 6 2 1 4 0 2 1 4
1 0 1 1 8 0 0 1 0
4 8
0
b) 5 ; 0,8 5 6,25 e) 0,14 ; 2,8 5 0,05
D U d c
5 0 8
2 0 6 , 2 5
4 0 U d c
0
c) 13 ; 5,2 5 2,5 f) 5,12 ; 0,064 5 80
C D U d UM C D U
1 3 0 5 2 5 1 2 0 6 4
2 6 0 2 , 5 0 0 8 0
0 U d
14.
a) (1,2 1 4,8) ; 0,24 5
5 6,0 ; 0,24 5 25
11,2 6 0 0 2 4
1 4,8 1 2 0 2 5
6,0 0
C D U d c
8 7 8 2 0 0
7 8 0 4 , 3 9
1 8 0 0 U d c
0
D U d c
1 4 0 0 2 8 0
0 0 , 0 5
U d c

55
b) 24,8 ; 4 1 45,5 ; 5 5
5 6,2 1 9,1 5 15,3
2 4 8 4 0 4 5 5 5 0
0 8 0 6,2 0 5 0 9,1
0 0
6,2
1 9,1
1 5,3
c) (0,05 ; 0,005) ; 0,5 5
5 10 ; 0,5 5 20
5 0 5 1 0 0 5
0 0 1 0 0 0 2 0
d) (2 3 1,1 1 3,83) ; 0,9 5
5 (2,2 1 3,83) ; 0,9 5
5 6,03 ; 0,9 5 6,7
1,1 13,8 3 6 0 3 9 0
3 2 + 2,2 0 6 3 0 6,7
2,2 6,0 3 0
15. 512 ; 1,6 5 320  320 milhas
5 1 2 0 1 6
3 2 3 2 0
0 0
16. D 5 (0,012 1 1,5) ; 1,68
D 5 1,512 ; 1,68
D 5 0,9
0,0 1 2 1 5 1 2 0 1 6 8 0 0,9
11,5 0 0 0 0,9 3 3
1,5 1 2 2,7
Logo: 3 3 D 5 3 3 0,9 5 2,7
17. 9,9 ; 0,55 5 18  18 metros
9 9 0 5 5
4 4 0 1 8
0 0
18.
a) 15,7 ; 3,14 5 5
1 5 7 0 3 1 4
0 5
b) Em cada oscilação completa, o pêndulo
passa pelo observador duas vezes; logo,
neste intervalo, ele vê o pêndulo passar
10 vezes.
1.
a) 7 3 6
1 3 1 2 , 1 6
1 0
4 0
4
b) 2 9 7
1 0 4 , 1
3
c) 1 1 7
4 0 1,5 7 1
5 0
1 0
3
d) 1 0 0 3 3
1 0 0 0,3 0 3
1
e) 1,3 ; 0,6 5 13 ; 6
1 3 6
1 0 2 , 1
4
2.
a) 2 6 7
5 0 3 , 7 1
1 0
3
b) 67,2 ; 13 5 672 ; 130
6 7 2 1 3 0
2 2 0 5 , 1 6
9 0 0
1 2 0
c) 7 2 1 1
6 0 6,5 4
5 0
6
d) 8,7 ; 2,3 5 87 ; 23
8 7 2 3
1 8 0 3 , 7 8
1 9 0
4

56
37 – Os números decimais e o
cálculo de porcentagens
1.
a) 3
3
100
%5 e
3
100
50,03, então 3% 5
5 0,03
b) 16
16
100
%5 e
16
100
50,16, então 16% 5
5 0,16
c) 21
21
100
%5 e 21
100
50,21, então 21% 5
5 0,21
d) 42
42
100
%5 e
42
100
50,42, então 42% 5
5 0,42
e) 55
55
100
%5 e
55
100
50,55, então 55% 5
5 0,55
f) 150
150
100
%5 e
150
100
51,50, então 150% 
5 1,50
2. Custo atual: 980,00 1 15% de 980,00
15
150
100
%5 50,15
15% de R$ 980,00 é o mesmo que
980,00 3 0,15:
980,00 3 0,15 5 147,0000 5 147,00
9 8 0,0 0
3 0,1 5
4 9 0 0 0 0
1 9 8 0 0 0 0
1 4 7,0 0 0 0
9 8 0,0 0
1 1 4 7,0 0
1 1 2 7,0 0
Custo atual:
980,00 1 147,00 5 1 127,00  R$ 1 127,00
3.
a) 51% de 3 340 é o mesmo que
0,51 3 3 340:
0,51 3 3 340 5 1 703,40 5 1 703,4
3 3 4 0
3 0,5 1
3 3 4 0
1 1 6 7 0 0 0
1 7 0 3,4 0
b) 120% de 2 500 é o mesmo que
1,20 3 2 500:
1,20 3 2 500 5 3 000,00 5 3 000
2 5 0 0
3 1,2 0
5 0 0 0 0
1 2 5 0 0 0 0
3 0 0 0,0 0
4. 35% de 1 020 telhas
1 020 3 0,35 5 357  357 telhas
1 0 2 0
3 0,3 5
5 1 0 0
1 3 0 6 0 0
3 5 7,0 0
5.
a) 85% de 16,8 metros quadrados
16,8 3 0,85 5 14,280 5 14,28 metros
quadrados
1 6,8
3 0,8 5
8 4 0
1 1 3 4 4 0
1 4,2 8 0
b) 16,8 2 14,28 5 2,52  2,52 metros
q uadrados
1 6, 8 0
2 1 4, 2 8
2, 5 2
6. 8
8
100
%5 50,08 40
40
100
%5 50,40
8% de 40% 5 0,08 3 0,40 5 0,032
0,0 8
3 0,4 0
0,0 3 2 0
7. (3% de 250) 1 (7% de 150) 2 (4% de 90) 5
5 (0,03 3 250) 1 (0,07 3 150) 2 (0,04 3 90) 5
5 7,5 1 10,5 2 3,6 5 18,0 2 3,6 5 14,4
8.
a) 88  100%
x  35%
88 100
x 35 5 → x 5
⋅ →
88 35
100
 x 5 30,80  R$ 30,80
b) uma calça  R$ 88,00 2 R$ 30,80 5
5 R$ 57,20
duas calças  2 3 R$ 57,20 5
5 R$ 114,40

57
38 – Potenciação de números
decimais
1.
a) (3,7)2  3,7  3,7  13,69
b) (0,6)3  0,6  0,6  0,6  0,216
c) (2,5)2  2,5  2,5  6,25
d) (0,3)4  0,3  0,3  0,3  0,3  0,0081
e) (2,4)0  1
f) (4,1)2  4,1  4,1  16,81
g) (1,5)3  1,5  1,5  1,5  3,375
h) (3,02)1  3,02
2. (0,4)3  0,064
1  0,064  0,936
Falta 0,936.
3.
a) (1,2)2  (0,9)2  1,44  0,81  2,25
b) (1,2  0,9)2  (2,1)2  2,1  2,1  4,41
4. 5
5
100
% 0,05 e (0,05)2  0,05  0,05 
 0,0025
5. x  (0,6)2  (0,8)2
x  3,6  6,4  1,0  1
6. a  4  (0,4)2
a  4  0,16  25
b  0,4  42
b  0,4  16  6,4
Logo, a  b.
7. (0,8  0,15  0,3)3  5,4  (0,5)2 
 (0,8  0,5)3  5,4  0,25 
 (0,3)3  5,4  0,25 
 0,027  5,4  0,25 
 0,005  0,25  0,255
a) 11% de 1 290 692,5 quilômetros
quadrados
1 290 692,5  0,11  141 976,17 
 141 976,17 quilômetros quadrados
b) 7,3% de 1 290 692,5 quilômetros
quadrados
1 290 692,5  0,073  94 220,552 
 94 220,552 quilômetros quadrados,
aproximadamente
c) 1 290 692,5  94 220,552  1 196 472 
 1 196 472 quilômetros quadrados,
aproximadamente
d) Espírito Santo, Paraná, Rio de Janeiro e
Santa Catarina.
1. Alternativa c.
Espaço ocupado pelas 16 pessoas:
16  0,30  4,8
Espaço entre as 16 pessoas:
1a 2a 3a 15a 16a
...
1 2 15
15  0,55  8,25
Comprimento da fila:
4,8  8,25  13,05  13,05 m
2. Alternativa b.
52  3  (4,1  1,8) 
 52  3  2,3  52  6,9  45,1
3. Alternativa c.
5,00  (3  0,20  1,50) 
 5,00  (0,60  1,50) 
 5,00  2,10  2,90  R$ 2,90
4. Alternativa e.
Pessoas com curso universitário completo:
75% de 320; logo, 0,75  320
0,75  320  240  240 pessoas
Total de pessoas do grupo: 320
Pessoas sem curso universitário completo:
320  240  80  80 pessoas
5. Alternativa a.
Quantidade de vinho na pipa:
63  0,7  44,1  44,1 litros
Quantidade de garrafas de 0,9 litro que a
pipa pode encher:
44,1  0,9  49  49 garrafas
Editoria de arte

58
6. 1 dólar vale R$ 2,85, 1 500 dólares valem:
1 500 3 2,85 5 4 275  R$ 4 275,00
7. Em um quilômetro lança 27,7 gramas, em
8 quilômetros lança:
8 3 27,7 5 221,6  221,6 gramas
8. Alternativa a.
; 4 ; 4 ; 4
40 10 2,5 ?
? 5 2,5 ; 4
? 5 0,625
9. Valdir andou 41,04 quilômetros.
Irmão de Valdir andou a terça parte de
41,04 quilômetros:
41,04 ; 3 5 13,68  13,68 quilômetros
10. Preço do litro de suco de laranja na
indústria A:
1,80 ; 1,50 5 1,20  R$ 1,20 o litro
Preço do litro de suco de laranja na
indústria B:
1,20 ; 0,80 5 1,50  R$ 1,50 o litro
Como 1,20  1,50, a indústria A vende o
suco mais barato.
11. Alternativa b.
185,8 2 176,9 5 8,9  8,9 milhões
12. Alternativa a.
37,8 2 0,5 5 37,3  37,3 graus
13. Alternativa d.
1o número decimal
(9 ; 2 1 4 3 1,25) 5 (4,5 1 5,0) 5 9,5
2o número decimal: (2 3 1,05 2 6,4 ; 4) 5
5 (2,10 2 1,6) 5 0,5
Produto desses dois números:
9,5 3 0,5 5 4,75
14. Alternativa b.
1320 40 1320
1
40
; 5 3 , mas
3 25
1
40
25
1000
25
100
1
10
5 5 3
3 25  
0,25 0,1
Logo: 1 320 ; 40 5 1 320 3 0,25 3 0,1.
15. Alternativa b.
Total de metros de fita:
4,86 3 10 5 48,6  48,6 m
Total de centímetros de fita:
1 m 5 100 cm; logo, 48,6 m é 48,6 3 100 5
5 4 860  4 860 cm
Total de pedaços de fita medindo 18 cm:
4 860 ; 18 5 270  270 pedaços
16. Alternativa b.
Comprimento da estrada de A a B:
103,2 quilômetros
Comprimento da estrada de B a C:
3
4 de 103,2 
3
4 3 103,2
3 25
Sendo
3
4
75
100
5 50,75, logo:
3 25
3
4
3103,250,753103,2577,4 
 77,4 quilômetros
Comprimento da estrada de A a C:
103,2 + 77,4 5 180,6  180,6 quilômetros
17. Expectativa de vida:
(3,5 3 416 2 715) ; 10 5 (1 456 2 715) ; 10 5
5 741 ; 10 5 74,1  74,1 anos
18.
1a 2a 3a 10a 11a
árvore árvore árvore ... árvore árvore
1a 2a 10a
distância distância distância
105 ; 10 5 10,5  10,5 metros
19. Alternativa c.
Preço da passagem em janeiro de 2009:
R$ 1,50
Reajuste da passagem em janeiro de 2010:
20% de R$ 1,50 
20
100
31,50
20
100
31,5050,2031,5050,30
Preço da passagem em janeiro de 2010:
1,50 1 0,30 5 1,80  R$ 1,80
Desconto para estudante:
10% de R$ 1,80 
10
100
31,80
10
100
31,8050,1031,8050,18
Preço da passagem para estudante em
janeiro de 2010:
1,80 2 0,18 5 1,62  R$ 1,62
Editoria de arte

59
Medindo comprimentos e superfícies
39 – Unidades de medida de
comprimento
2. Mariana, porque encontrou a menor
quantidade de palmos.
3. Marcos, porque encontrou o menor valor
em pedaços de barbante.
1.
a) km b) m c) mm d) cm
2. Distância em que se originou o
relâmpago:
340 3 5 5 1 700 R 1 700 metros
3. Distância entre as duas cidades:
74 milhas
Valor de uma milha: 1,609 km,
aproximadamente
Distância entre as duas cidades, em
quilômetros:
74 3 1,609 5 119,066 R 119,066 km,
aproximadamente
4. Comprimento do meu passo: 56 cm
Comprimento do meu pé: 24 cm
Comprimento do móvel: 1 passo e 2 pés
Comprimento do móvel em centímetros:
56 1 2 3 24 5 56 1 48 5 104 R 104 cm
5. Distância do ponto A ao ponto B: 84,5 km
Distância do ponto B ao ponto C:
3 3 84,5 5 253,5 R 253,5 km
6.
a) Maior: Júpiter, com 143 000 km; menor:
Mercúrio, com 4 860 km.
b) 12 756 km
c) 12756
6800
.1,8
d) 365 − 122 5 243 R 243 dias
Alternativa b.
Reginaldo: 600 metros
Lúcia: 700 metros
40 – Transformação das unidades
de medida de comprimento
1. Alternativa b.
43,2 R 43,2 3 100 5 4 320 R 4 320 cm
4 320 ; 24 5 180 R 180 lacinhos
2. Comprimento da sala: 5 400 mm
Se 1 mm 5 0,001 m, então:
5 400 3 0,001 5 5,4 R 5,4 m
Se 1 mm 5 0,000001 km, então:
5 400 3 0,000001 5 0,0054 R 0,0054 km
A unidade de medida mais conveniente
para medir a sala é o metro.
3. 18 mm 5 (18 ; 10) cm 5
18
10
cm 5
5 (18 3 0,1) cm 5 1,8 cm
4. Meu passo corresponde a 56 cm.
Meu pé corresponde a 25 cm.
Comprimento do terreno: 18 passos e 2 pés
18 3 56 1 2 3 25 5 1 008 1 50 5 1 058 R
R 1 058 cm
1 058 cm 5 (1 058 ; 100) m 5
1058
100
m 5
5 (1 058 3 0,01) m 5 10,58 m
5.
a)
1
2 m 5
5
10 m 5 0,5 m 5 (0,5 3 100) cm 5
5 50 cm
b)
2
5 m 5
4
10 m 5 0,4 m 5 (0,4 3 100) cm 5
5 40 cm
c)
9
4 km 5
225
100 km 5 2,25 km 5
5 (2,25 3 1 000) m 5 2 250 m
d)
18
5 m 5
360
100 m 5 3,60 m 5 (3,60 ; 1 000) km 5
5 (3,60 3 0,001) km 5 0,0036 km
6. 1 polegada 5 25 mm
1
2 ( )polegada 5
5
10

 

 
polegada
25 mm 5 25 5
10
3

 

 
mm 5 (25 3 0,5) mm 5
5 12,5 mm
Sendo 1 mm 5 0,1 cm, então:
12,5 mm 5 (12,5 3 0,1) cm 5 1,25 cm

60
7. 1 milha 5 1 609 m
Se 1 m 5 0,001 km, então:
1 milha 5 (1 609 3 0,001) km 5 1,609 km
85 milhas 5 (85 3 1,609) km 5 136,765 km
8. 64 m correspondem a 6 400 cm
Para ter 20 retalhos, cada um deve medir:
6 400 ; 20 5 320 R 320 cm
9. 10 km correspondem a 10 000 m
Logo: 10 000 1 150 5 10 150 R 10 150 m
10. Comprimento da tábua: 3,10 m
Uma das partes tem 98 cm de
comprimento, correspondendo a 0,98 m.
Restam: 3,10 − 0,98 5 2,12 R 2,12 m
As duas outras partes têm o mesmo
comprimento, logo cada uma mede:
2,12 ; 2 5 1,06 R 1,06 m
11. Os 385 metros foram medidos com 97 cm,
o que corresponde a 0,97 m, logo há 0,03 m
de tecido a menos em cada metro vendido.
Então: 385 3 0,03 5 11,55 R 11,55 m de
tecido a menos
12.
a) Se cada centímetro corresponde a 10,5 km,
então a distância real entre as duas
cidades é:
10,5 3 15 5 157,5 R 157,5 km
b) 68 250 m correspondem a 68,250 km,
logo a distância desta cidade ao mar,
no mapa, é:
68,250 ; 10,5 5 6,5 R 6,5 cm
15. Alternativa a.
Dois armários de 1,60 m de comprimento
ocupam:
1,60 3 2 5 3,20 R 3,20 m
Comprimento da parede: 5 m
Espaço livre:
5 − 3,20 5 1,80 R 1,80 m
Comprimento da estante: 1 m
1,80 − 1 5 0,80 R 0,80 m (sobra)
16. Alternativa b.
Percorreu no Brasil: 12,5 km
Percorreu na Inglaterra: 9 milhas
Uma milha corresponde a 1 600 m, e
1 600 m correspondem a 1,6 km, então na
Inglaterra percorreu:
9 3 1,6 5 14,4 R 14,4 km
Comparando o que percorreu nos dois
países, temos:
12,5 , 14,4 e 14,4 − 12,5 5 1,9 R 1,9 km a mais
17. Alternativa c.
1 m corresponde a 100 m, logo 4 m
correspondem a:
4 3 100 5 400 R 400 m
41 – Perímetro de um polígono
1. frente: 35 m; fundo: 22 m
metragem do fio: 35 1 22 1 35 1 22 5
5 114 R 114 m
2. frente: 30 m; fundo: 30 m
metragem do fio de arame: 30 3 4 5
5 120 R 120 m
3. 30 1 40 1 50 5 120 R 120 m
1.
a) 3 1 4,1 1 1,5 1 3,8 5 12,4 R 12,4 cm
b) triângulo equilátero R três lados de
mesma medida
2,9 3 3 5 8,7 R 8,7 cm
c) Reduzindo todas as unidades a cm,
temos:
0,3 dm corresponde a 3 cm
12 mm correspondem a 1,2 cm
25 mm correspondem a 2,5 cm
3 1 3,6 1 1,2 1 3,1 1 2,5 5 13,4 R 13,4 cm
2. medida do comprimento: 10,2 cm
medida da largura: metade do comprimento
10,2 ; 2 5 5,1 R 5,1 cm
perímetro do retângulo:
10,2 1 5,1 1 10,2 1 5,1 5 30,6 R 30,6 cm
3. lajota hexagonal: 6 lados medindo 65 cm
65 cm correspondem a 0,65 m
perímetro da lajota:
6 3 0,65 5 3,90 R 3,90 m
4. medida do comprimento: 12 m
medida da largura:
1
3
do comprimento
12
1
3
3 54R 4 m
extensão do muro:
12 3 2 1 4 3 2 5 24 1 8 5 32 R 32 m
5. Se a medida dos lados são três números
consecutivos, e o menor é 5, então os
outros dois são 5 1 1 e 5 1 1 1 1, isto é, 6
e 7; logo, o perímetro deste triângulo é:
5 1 6 1 7 5 18 R 18 cm

61
6.
a) O perímetro do retângulo e o do
quadrado são iguais, então esse
perímetro é:
7,2 3 2 1 10,6 3 2 5 14,4 1 21,2 5 35,6 R
R 35,6 cm
b) Tendo o quadrado quatro lados de mesma
medida, o lado do quadrado mede:
35,6 ; 4 5 8,9 R 8,9 cm
7.
a) medida do lado da praça: 24,5 m
perímetro da praça:
24,5 3 4 5 98,0 R 98 m
4 voltas ao redor da praça:
98 3 4 5 392 R 392 m
b) medida do comprimento do pé de Ana:
0,8 m
número de passos dados:
392 ; 0,8 5 490 R 490 passos
8. perímetro do quadrado: 20 cm
medida do lado do quadrado:
20 ; 4 5 5 R 5 cm
Este triângulo equilátero tem como medida
de lado a mesma medida do lado do
quadrado, então seu perímetro é:
3 3 5 5 15 R 15 cm
9. Total de metros de arame: 70
a) terreno quadrado de 17,2 m de lado
perímetro do terreno:
17,2 3 4 5 68,8 R 68,8 m (sim)
b) terreno retangular com 24,5 m de
comprimento e 11,8 m de largura
perímetro do terreno:
2 3 24,5 1 2 3 11,8 5 49 1 23,6 5
5 72,6 R 72,6 m (não)
10. Alternativa d.
perímetro da folha retangular: 40 cm
medida de um lado: 4 cm
soma das medidas de outros lados:
40 2 4 2 4 5 32 R 32 cm
dois lados de mesma medida:
32 ; 2 5 16 R 16 cm
medidas dos outros lados: 16 cm, 4 cm e 16 cm
11. Alternativa d.
medida do lado do quadradinho 5 1 cm
figura X tem 20 lados:
seu perímetro é 20 3 1 5 20 R 20 cm
figura Y tem 18 lados:
figura Z tem 32 lados:
Brasil real, página 269 e 270.
1.
a) 1 km corresponde a 1 000 m, logo
30 223 km correspondem a 30 223 000 m.
b) São 30 223 km de linhas de tráfego, sendo
1 916 km de linhas eletrificadas, logo:
30 223 2 1 916 5 28 307 R 28 307 km
são linhas de trens movidos a diesel.
c) 30 223 km de linhas de tráfego
14 500 km de linhas estão em São Paulo,
Minas Gerais e Rio Grande do Sul
Logo: 30 223 2 14 500 5 15 723 R
R 15 723 km não pertencem às três
cidades acima citadas.
2.
a) Se 1 m corresponde a 0,001 km, então
8 836 m correspondem a 8,836 km.
b) Se a extensão total da ponte é 13 290 m
e 8 836 m estão sobre o mar:
13 290 2 8 836 5 4 454 R 4 454 m estão
sobre a terra. Como 1 m corresponde a
0,001 km, a extensão da ponte sobre a
Terra é 4,454 km.
c) largura total da ponte: 26,60 m
Como 1 m corresponde a 100 cm, a
largura da ponte, em cm, é 2 660 cm.
3.
a) Rio Amazonas: 6 868 km que
correspondem a 6 868 000 m.
rio Nilo: 6 695 km que correspondem a
6 695 000 m.
6 868 000 2 6 695 000 5 173 000 R
R 173 000 m a mais
b) 6 868 ; 65 . 105,66
c) Se 20 km correspondem a 1 cm, então
65 km correspondem a:
65 ; 20 5 3,25 R 3,25 cm
4.
a) 1 m corresponde a 0,001 km, então
250 000 m correspondem a 250 km
b) o quilômetro
5.
a) Londres e Nova Iorque; 400 km
b) São Paulo; 60 km
c) 450 km
d) linha de Paris: 200 km
linha de Chicago: 150 km
200 2 150 5 50 R 50 km

62
42 – Unidades de medida de
superfície
1. 61
2. 69
Resposta em aberto.
1. Alternativa c.
2. Alternativa b.
3. A figura possui 22 quadrados. Como a
área de cada um corresponde a 1 cm2,
logo a área da figura é 22 cm2.
1.
a) 1 dm2 corresponde a 0,01 m2, logo
21 dm2 correspondem a 0,21 m2.
b) 1 cm2 corresponde a 0,0001 m2, logo
1 250 cm2 correspondem a 0,125 m2.
c) 1 km2 corresponde a 1 000 000 m2.
d) 1 hm2 corresponde a 10 000 m2, logo
0,72 hm2 corresponde a 7 200 m2.
2. 1 dm2 corresponde a 0,01 m2.
3. 1 hm2 corresponde a 10 000 m2, que
representa a área de um quadrado de
100 m de lado:
100 3 100 5 10 000 R 10 000 m2
4.
1,3 km2 corresponde a 1 300 000 m2.
1 ha corresponde a 10 000 m2, logo 103 ha
correspondem a 1 030 000 m2.
Então: 1,3 km2  103 ha
5.
1 600 cm2 correspondem a 0,16 m2.
100 caixas com 2 dúzias de piso:
100 3 24 5 2 400 R 2 400 pisos
2 400 3 0,16 5 384 R 384 m2 de piso
6.
10 000 m2 correspondem a 1 ha.
70 000 m2 correspondem a 7 ha.
1 ha é ocupado por 20 bois.
7 ha:
7 3 20 5 140 R 140 bois
7.
a) 7 km2 correspondem a 7 000 000 m2.
7 000 000 m2 correspondem a 700 ha.
60% de 700 ha ⇒
⇒
60
100
370050,637005420 ha
b) 700 2 420 5 280 R 280 ha
1. 3 488 – 1 300 = 2 188
O crescimento foi de 2 188 kg/ha.
2.
a) Minas Gerais
b) Amapá
c) estado de maior área (Minas Gerais):
1 888 922 ha
estado de menor área (Amapá): 87 581 ha
1 888 922 2 87 581 5 1 801 341 R
R 1 801 341 ha
1 801 341 ha correspondem a
18 013 410 000 m2.
3.
a) 225 000 ; 2,5 5 90 000 R R$ 90 000,00
b) Em São Paulo, 1 alqueire corresponde a
2,42 ha.
2,5 alqueires correspondem a
2,5 3 2,42 5 6,05 R 6,05 ha.
c) Na Bahia, 1 alqueire corresponde
a 96 800 m2.
2,5 alqueires correspondem a:
2,5 3 96 800 5 242 000 R 242 000 m2
4.
a) Na região Norte.
b) 160 alqueires por R$ 595,00 o alqueire
595 3 160 5 95 200 R R$ 95 200,00
c) 1 alqueire corresponde a 27 225 m2
160 alqueires correspondem a:
160 3 27 225 5 4 356 000 R 4 356 000 m2
d) 1 alqueire corresponde a 2,7225 ha
160 alqueires correspondem a 435,6 ha
435,6 ha para 20 trabalhadores dá:
435,6 ; 20 5 27,78 R 21,78 ha para
cada um
5. 1 alqueire corresponde a 48 400 m2.
3,5 alqueires correspondem a:
3,5 3 48 400 5 169 400 R 169 400 m2
6. 4,84 ha correspondem a 1 alqueire.
31,46 ha correspondem a:
31,46 ; 4,84 5 6,5 R 6,5 alqueires

63
7.
a) 5 822 km2 correspondem a 5 822 000 000 m2.
1 ha corresponde a 10 000 m2.
5 822 000 000 m2 correspondem a:
5 822 000 000 ; 10 000 5 582 200 R
R 582 200 ha
b) 1 alqueire corresponde a 4,84 ha.
582 200 ha correspondem a:
582 200 ; 4,84 5 120 289,25 R
R 120 289,25 alqueires
8.
a) 1 ha corresponde a 10 000 m2.
10 000 m2 correspondem a 0,01 km2.
38 000 3 0,01 5 380 R 380 km2
b) 1 alqueire corresponde a 4,84 ha.
38 000 ; 4,84 . 7 851,24 R
R 7 851,24 alqueires, aproximadamente
43 – Áreas das figuras
geométricas planas
a) Resposta pessoal.
b) Resposta pessoal.
c) Resposta pessoal.
d) Resposta pessoal.
1.
a) medida do lado: 8 cm
área: 8 3 8 5 64 R 64 cm2
b) medida da base: 12 cm
medida da altura: 6 cm
área: 12 3 6 5 72 R 72 cm2
c) medida da base menor: 4 cm
medida da base maior: 6 cm
( 6 1 4 )3
3
área:
2
5
5
3
5
10 3
2
15 R 15 cm2
d) medida da base menor: 5 cm
medida da base maior: 7 cm
( 7 1 5 )3
4
área:
2
5
5
3
5
12 4
2
24 R 24 cm2
2. medida da base: 8 cm
medida da altura: 5,2 cm
área: 8 3
52
2
5
,
41 6
2
5 5
20 8
,
, R 20,8 cm2
medida da altura: 1
2
de 10 cm
1
2
31055 R 5 cm
área: 10 3 5 5 50 R 50 cm2
medida da altura: 2
3
de 18 cm
2
3
318512 R 12 cm
área:
18 12
108 3
2
5 R 108 cm2
5.
a) medida do lado: 15 cm
área: 15 3 15 5 225 R 225 cm2
b) 45 m2 correspondem a 450 000 cm2
450 000 ; 225 5 2 000 R 2 000 pisos
área: 25 16
200 3
2
5 R 200 cm2
1 cm2 corresponde a 0,0001 m2
200 cm2 correspondem a:
200 3 0,0001 5 0,02 R 0,02 m2
80 peças de 0,02 m2 de área cada uma:
80 3 0,02 5 1,6 R 1,6 m2
7. medida do comprimento: 8 m
medida da altura: 2,75 m
área: 8 3 2,75 5 22 R 22 m2
1 lata pinta 10 m2.
2 latas pintam 20 m2.
Sobraram 2 m2, então é necessária uma 3a lata.
8.
a) área da sala: 4,20 3 4,50 5 18,9 R 18,9 m2
área do corredor: 2,50 3 1,50 5 3,75 R 3,75 m2
área do 1o dormitório: 3 3 4,5 5 13,5 R
R 13,5 m2
área do 2o dormitório: 4 3 4 5 16 R 16 m2
Carpete necessário:
18,9 1 3,75 1 13,5 1 16 5 52,15 R 52,15 m2
b) área do banheiro: 2,50 3 3 5 7,50 R 7,50 m2
área da cozinha: 4 3 4 5 16 R 16 m2
área da área de serviço: 1,70 3 4 5
5 6,80 R 6,80 m2
cerâmica necessária: 7,50 1 16 1 6,80 5
5 30,30 R 30,30 m2

64
c) medida da frente: 4,20 1 2,50 1 3 5
5 9,70 R 9,70 m
medida dos fundos: 4,50 1 4 5 8,50 R 8,50 m
área do apartamento: 9,70 3 8,50 5
5 82,45 R 82,45 m2
preço do apartamento: 82,45 3 500 5
5 41 225 R R$ 41 225,00
9. área das paredes da frente e do fundo:
4 3 2,70 5 10,80 R 10,80 m2
área das paredes laterais: 3 3 2,70 5
5 8,10 R 8,10 m2
área total para revestir:
2 3 10,80 1 2 3 8,10 − (2 3 1,60 1 2) 5
5 21,60 1 16,20 − 5,20 5
5 37,80 − 5,20 5 32,60 R 32,60 m2
10. área das paredes da frente e do fundo:
8 3 4 5 32 R 32 m2
área das paredes laterais:
3 3 5 5 15 R 15 m2
área da porta:
1,5 3 2 5 3,0 R 3,0 m2
área da janela:
3 3 1 5 3 R 3 m2
área do teto:
8 3 5 5 40 R 40 m2
área a ser pintada:
2 3 32 1 2 3 15 1 40 − (3 1 3) 5
5 64 1 30 1 40 − 6 5
5 134 − 6 5 128 R 128 m2
1 lata pinta 40 m2.
Sobram 8 m2, então é necessária mais uma
lata R 4 latas
11. Alternativa b.
área total:
17 3 24 3 2 1 5 3 24 3 2 1 17 3 5 3 2 5
5 816 1 240 1 170 5 1 226 R 1 226 cm2
12. área do telhado:
2 3 10 3 40 5 800 R 800 m2
Para cobrir 1 m2 usam-se 20 telhas.
Para cobrir 800 m2:
800 3 20 5 1 600 R 1 600 telhas
13.
a) cor-de-rosa: 3 u por 8 u; verde: 2 u por 12 u
b) Não, o perímetro do retângulo cor-de-
-rosa é 22 u, e o do retângulo verde é 28 u.
c) Ambos têm medida de área igual a 24 u2.
d) Há várias soluções.
1.
a) 6 cm
3 cm A1 A2 5 cm
2 cm
A1: 4 3 3 5 12 R 12 cm2
A2: 2 3 5 5 10 R 10 cm2
Atotal 5 12 1 10 5 22 R 22 cm2
b) 5 cm
3 cm A1 A2
7 cm
2 cm
A: 5 3 3 5 15 R 15 cm2
1A: 3 3 2
3 2
22
5 → cm
Atotal 5 15 1 3 5 18 R 18 cm2
2.
A1 A2 A3
1 m 1 m
1 m
1 m
3 m
5 m
A1: 1 3 1 5 1 R 1 m2
A2: 1 3 5 5 5 R 5 m2
A3: 1 3 1 5 1 R 1 m2
Atotal 5 1 1 5 1 1 5 7 R 7 m2
3. Alternativa a.
A2
4 m
A3
4 m
4 m
A4 m 1 4 m
1 m
2 m
5 m
Editoria de arte
Editoria de arte
Editoria de arte
Editoria de arte
R 3 cm2

65
A1: 4 3 4 5 16 R 16 m2
A m 2
4 3
3 5 →
2
2
; 6 6
A3 ; 4 3 3 5 12 R 12 m2
Atotal 5 16 1 6 1 12 5 34 R 34 m2
4. Alternativa c.
perímetro da figura:
3 1 4 1 5 1 4 1 4 1 4 1 4 5 28 R 28 m
largura da porta: 1 m
rodapé: 28 2 1 5 27 R 27 m
5. Alternativa d.
10 m
16 m 16 m
34 m
20 m
20 m
A
m
;
( )
34 10 16
2
44 16
2
352 352 2
1
5
5 5
→
3
3
6.
a) Aquadra: 18,29 3 36,57 5 668,8653 R
R 669 m2, aproximadamente
b) Ajogo: 10,97 3 23,77 5 260,7569 R
R 261 m2, aproximadamente
c) Tela:
(17,07 3 2 1 34,77 3 2) 3 3 5
5 (34,14 1 69,54) 3 3 5
5 103,68 3 3 5 311,04 R 311,04 m2
7. área da quadra oficial:
20 3 12 5 240 R 240 m2
área do pátio da escola:
40 3 32 5 1 280 R 1 280 m2
área livre que restou no pátio:
1 280 2 240 5 1 040 R 1 040 m2
1.
a) área do campo:
110 3 75 5 8 250 R 8 250 m2
b) placas de grama necessárias:
8 250 ; 3,5 . 2 357 R aproximadamente
2 357 placas de grama
c) Sim.
2.
a) ano de inauguração: 1960
ano da 1a corrida: 1978
tempo que levou para receber a 1a corrida:
1978 2 1960 5 18 R 18 anos
b) total de metros a percorrer: 305 909
total de quilômetros a percorrer:
305 909 metros correspondem a
305,909 quilômetros
c) total de metros percorridos: 305 909
total de voltas dadas: 71
metros percorridos em cada volta:
305 909 ; 71 . 4 308,6 R 4 308,6 m,
aproximadamente
d) total de voltas a percorrer: 71
total de voltas dadas: 53
total de voltas que faltaram dar:
71 2 53 5 18 R 18 voltas
metros percorridos aproximadamente
em cada volta: 4 308,6
4 308,6 m correspondem a 4,3086 km
quilômetros que faltavam para
completar o circuito:
4,3086 3 18 . 77,55 R 77,55 km,
aproximadamente
1. 20 habitantes por quilômetro quadrado
2. densidade demográfica brasileira:
d
habi tes
km
169799170
tan
5 5 5
8514215
19 ,
94 2
habitantes por quilômetro quadrado
3. 20 2 19,94 5 0,06
a) no período 1994-1995
b) 18 758 – 14 039 = 4 719
Ocorreram 4 719 km2 a menos de
desmatamento.
c) Expansão da pecuária e da agricultura,
a grilagem de terras públicas e a
exploração predatória de madeira.
d) Mato Grosso e Pará.
1. Todas têm a mesma área.
2. 16
3. 8
Editoria de arte

66
1. Alternativa b.
1a hora: 512 m
:2
2a hora: 256 m
:2
3a hora: 128 m
:2
4a hora: 64 m
:2
5a hora: 32 m
Distância percorrida:
512 1 256 1 128 1 64 1 32 5 992 R 992 m
2. Alternativa c.
5mesas
de comprimento: 85 cm
correspondema0,85m
de largura: 60 cm
correspondema0,60m






metros necessários para cada mesa:
2 3 0,85 1 2 3 0,60 5
5 1,70 1 1,20 5 2,90 R 2,90 m
metros necessários para as 5 mesas:
5 3 2,90 5 14,50 R 14,50 m
6 mesas quadradas de lado 70 cm
correspondem a 0,70 m necessários para
cada mesa:
4 3 0,70 5 2,80 R 2,80 m
metros necessários para as 6 mesas:
6 3 2,80 5 16,80 R 16,80 m
total de metros necessários para todas as
mesas:
14,50 1 16,80 5 31,30 R 31,30 m
3. Alternativa a.
largura: 3,50 m; comprimento: 6,30 m
contorno da sala: 2 3 3,50 1 2 3 6,30 5
5 7,0 1 12,6 5 19,6 R 19,6 m
comprimento da peça de gesso:
70 cm que correspondem a 0,7 m.
total de peças de gesso necessárias:
19,6 ; 0,7 5 28 R 28 peças
4. Alternativa d.
1o telefone
2o telefone
3o telefone
4o telefone
18o telefone
19o telefone
arte
de km 28 ...................... km 640
Editoria área da região A:
1 2 3 4 5 ......................
18 19 20
8 3 8 5 64 R 64 m2
640 28 612 612 km
área da região B:
4 3 4 5 16 R 16 m2
quantidade de vezes que a região A
representa a região B:
64 ; 16 5 4 R 4 vezes Para serem colocados os 19 telefones, é
preciso dividir a distância acima calculada,
de acordo com a figura, em 20 partes
iguais. Então a distância entre cada
telefone será:
612 ; 20 5 30,6 R 30,6 km
5. Alternativa c.
2 km2 correspondem a 2 000 000 m2.
1 ha corresponde a 10 000 m2, logo
2 000 000 m2 correspondem a:
2 000 000 ; 10 000 5 200 R 200 ha
6. área da cartolina:
75 3 30 5 2 250 R 2 250 cm2
área recortada da cartolina:
20 3 10 3 10 5 2 000 R 2 000 cm2
área restante:
2 250 2 2 000 5 250 R 250 cm2
7. Alternativa a.
área reservada para o plantio de laranja:
3
36005450→450 ha
4
1 ha corresponde a 10 000 m2.
10 000 m2 correspondem a 0,01 km2, então
450 ha correspondem a:
450 3 0,01 5 4,5 R 4,5 km2
8.
a) área da placa:
1
2
1
2
1
4
1
4
2 0 25 2 3 5 → m que corresponde a , m
1 m2 de piso necessita:
1 ; 0,25 5 4 R 4 placas
b) área a ser coberta: 55 m2
área da placa: 0,25 m2
quantidade de placas usadas:
55 ; 0,25 5 220 R 220 placas
9. Alternativa e.
quantidade de pisos na caixa:
12 3 1,5 5 18 R 18 pisos
área ocupada pelos pisos de uma caixa:
18 3 0,25 5 4,5 R 4,5 m2
área ocupada pelos pisos das 20 caixas:
20 3 4,5 5 90 R 90 m2
10. Alternativa b.
área a ser gramada:
5
7
4200 3000 3000 2 3 5 → m
quantidade de placas necessárias:
3 000 ; 2 5 1 500 R 1 500 placas
11. Alternativa c.

67
VOLUME E CAPACIDADE
44 – Medindo o espaço ocupado
Figura A: 42
Figura B: 210
Figura C: 24
Figura D: 12
45 – Volume do paralelepípedo
retângulo
1. V 5 30 3 18 3 12 5 6 480 R 6 480 m3
2. V 5 2,5 3 2,5 3 2,5 5 (2,5)3 5 15,625 R
R 15,625 m3
3. V 5 8 3 5 3 1,5 5 60 R 60 m3
4. Vcubo 5 4 3 4 3 4 5 64 R 64 m3
Vparalelepípedo 5 8 3 4 3 2 5 64 R 64 m3
Os volumes são iguais.
5. V 5 3,40 3 2,10 3 0,80 5 5,712 R 5,712 m3
6. V 5 0,20 3 0,10 3 0,05 5 0,001 R 0,001 m3
46 – Unidades de medida de volume
1.
a) 1 dm3 corresponde a 0,001 m3.
840 dm3 correspondem a:
840 3 0,001 5 0,840 R 0,840 m3
b) 1 mm3 corresponde a 0,000 000 001 m3.
14 500 000 mm3 correspondem a:
14 500 000 3 0,000 000 001 5 0,0145 R
R 0,0145 m3
c) 1 dm3 corresponde a 0,001 m3.
1 000 dm3 correspondem a:
1 000 3 0,001 5 1 R 1 m3
2.
a) 1 m3 corresponde a 1 000 dm3.
3,5 m3 correspondem a:
3,5 3 1 000 5 3 500 R 3 500 dm3
b) 1 cm3 corresponde a 0,001 dm3.
1 250 3 correspondem a:
1 250 3 0,001 5 1,25 R 1,25 dm3
c) 1 m3 corresponde a 1 000 dm3.
1
4
m3 corresponde a:
1
4
3 1 000 5 250 R 250 dm3
3. V 5 1 3 1 3 1 5 1 R 1 m3
1 m3 corresponde a 1 000 dm3.
4. volume máximo de um bujão: 13,5 dm3
volume gasto: 2
3
313,559,0 →9,0 dm3
volume que resta:
13,5 2 9,0 5 4,5 R 4,5 dm3
1 dm3 corresponde a 0,001 m3.
4,5 dm3 correspondem a:
4,5 3 0,001 5 0,0045 R 0,0045 m3
5. 1 m3 corresponde a 1 000 dm3.
1 golpe retira 100 dm3.
7 golpes retiram:
7 3 100 5 700 R 700 dm3
resta de ar após o 7o golpe:
1 000 2 700 5 300 R 300 dm3
1 dm3 corresponde a 0,001 m3.
300 dm3 correspondem a:
300 3 0,001 5 0,3 R 0,3 m3
1.
a) 97% de água salgada; resta 3% de água doce
1,36 bilhão 5 1,36 3 1 000 000 000 5
5 1 360 000 000 R 1 360 000 000 km3
volume de água do planeta:
3% 3 1 360 000 000 5
5 0,03 3 1 360 000 000 5
5 40 800 000 R 40 800 000 km3
b) volume de água doce do Brasil:
13,7% 3 40 800 000 5 0,137 3 40 800 000 5
5 5 589 600 R 5 589 600 km3
c) volume de água doce na bacia do
Paraná:
7% 3 5 589 600 5 0,07 3 5 589 600 5
5 391 272 R 391 272 km3
d) volume de água doce no Brasil:
5 589 600 km3
volume de água doce em São Paulo:
89 434 km3
porcentagem de água doce brasileira
em São Paulo:

68
89 434 ; 5 589 600  0,016 R
aproximadamente, 1,6%
2. leitura do mês: 1 946 m3
leitura do mês seguinte: 2 018 m3
consumo: 2 018 2 1 946 5 72 R 72 m3
1 m3 corresponde a 1 000 dm3.
72 m3 correspondem a 72 000 dm3.
47 – Unidades de medida
de capacidade
1. V 5 10 3 7 3 2,5 5 175 R 175 m3
1 m3 corresponde a 1 000 L.
175 m3 correspondem a 175 000 L.
2. V 5 10 3 10 3 10 5 1 000 R 1 000 cm3
1 cm3 corresponde a 0,001 L.
1 000 cm3 correspondem a 1 L.
3. V 5 1,2 3 1,2 3 1,2 5 1,728 R 1,728 m3
1,728 m3 corresponde a 1 728 L.
gasto diário: 432 L
dias necessários para esvaziar a caixa-d’água:
1 728  432 5 4 R 4 dias
4.
a) 1,6 m corresponde a 16 dm.
50 cm correspondem a 5 dm.
45 cm correspondem a 4,5 dm.
volume da banheira:
16 3 5 3 4,5 5 360 R 360 dm3 ou 360 L
b) água para o banho:
16 3 5 3 3 5 240 R 240 dm3 ou 240 L
c) R$ 1,50 o metro cúbico de água:
1 dm3 corresponde a 0,001 dm3.
240 dm3 correspondem a 0,240 m3.
preço do banho: 1,50 3 0,240 5 0,36 R
R R$ 0,36
5. Alternativa c.
V 5 1,00 3 1,20 3 0,80 5 0,96 R 0,96 m3
1 m3 corresponde a 1 000 dm3 ou 1 000 L.
0,96 m3 corresponde a 960 dm3 ou 960 L.
1.
a) Registro no hidrômetro: 98,6777 m3
98,6777 m3 correspondem a 98 677,7
dm3 ou 98 677,7 L.
b) leitura do hidrômetro da esquerda:
1 088,9808 m3
1 088,9808 m3 correspondem a
1 088 980,8 L.
leitura do hidrômetro da direita:
79,6569 m3
79,6569 m3 correspondem a 79 656,9 L.
2. desperdício de água em um dia: 1 600 L
desperdício de água em 7 dias:
1 600 3 7 5 11 200 R 11 200 L
desperdício de água em 30 dias:
1 600 3 30 5 48 000 R 48 000 L
3.
a) ducha gasta: 135 L
chuveiro gasta
1
3
da ducha:
1
3
3135545→45 L
b) Usando ducha, gastam-se:
30 3 135 5 4 050 R 4 050 L
usando chuveiro, gastam-se:
30 3 45 5 1 350 R 1 350 L
c) em 15 minutos, gastam-se: 45 L
em 5 minutos, gastam-se: 15 L
em 30 dias, economizam-se:
30 3 15 5 450 R 450 L
4. Com a torneira aberta, gastam-se de água: 12 L
Com a torneira aberta apenas para molhar
a escova e enxaguar a boca: 2 L
economia de água: 10 L
Em uma quinzena, com 4 escovações por
dia, economizam-se:
15 3 4 3 10 5 600 R 600 L
5. gasto diário de uma torneira malfechada: 48 L
desperdício em um mês:
48 3 30 5 1 440 R 1 440 L
desperdício em uma hora:
48 ; 24 5 2 R 2 L
6.
a) gasto de uma torneira aberta,
1
4
de
volta, por 15 minutos: 108 L
gasto de uma torneira aberta, 1
4
de
volta, por 5 minutos:
108 ; 3 5 36 R 36 L
b) gasto de uma torneira, uma volta
aberta, por 15 minutos: 380 L
gasto de uma torneira, uma volta
aberta, por 30 minutos:
380 3 2 5 760 R 760 L

69
c) gasto de uma torneira aberta meia-
-volta por 15 minutos: 280 L
gasto de uma torneira aberta meia-volta,
por 3 minutos: 280 ; 5 5 56 R 56 L
litros de água ingeridos por dia por
uma pessoa: 2 L
quantidade de dias para ingerir 56 L:
56 ; 2 5 28 R 28 dias
1. O volume também dobra.
2. Em ambos os casos o volume também
dobraria.
3. O volume do bloco ficaria multiplicado
por 8.
48 – Outras unidades de medidas
para medir capacidade
1.
a) 1 mL corresponde a 0,001 L.
1 200 mL correspondem a 1,2 L.
b) 1 cL corresponde a 0,01 L.
85 cL correspondem a 0,85 L.
c) 1 hL corresponde a 100 L.
2 hL correspondem a 200 L.
d) 1 dm3 corresponde a 1 L.
87 dm3 correspondem a 87 L.
e) 1 m3 corresponde a 1 000 L.
3,5 m3 correspondem a 3 500 L.
f) 1 cm3 corresponde a 0,001 dm3 ou
0,001 L.
2. 1 mL corresponde a 0,001 L.
500 mL correspondem a 0,5 L ou
1
2 L.
3. 1 m3 corresponde a 1 000 dm3 ou 1 000 L.
0,36 m3 corresponde a 360 L.
4. 1 L corresponde a 1 dm3.
400 L correspondem a 400 dm3.
1 dm3 corresponde a 1 000 cm3.
400 dm3 correspondem a 400 000 cm3.
capacidade de cada frasco: 50 cm3
quantidade de frascos necessários:
400 000 ; 50 5 8 000 R 8 000 frascos
5. 1 cm3 corresponde a 0,001 dm3 ou 0,001 L.
7 500 000 cm3 correspondem a 7 500 L.
6. 1 cL corresponde a 0,01 L.
33 cL correspondem a 0,33 L.
7. volume do tanque: 0,06 m3
volume de gasolina no tanque:
3
30,0650,045→0,045m3
4
falta para encher o tanque:
0,06 – 0,045 5 0,015 R 0,015 m3
0,015 m3 corresponde a 15 L.
8. 1 L corresponde a 1 000 mL.
10 000 L corresponde a 10 000 000 mL.
quantidade de garrafas usadas:
10 000 000 ; 250 5 40 000 R 40 000 garrafas
1. Uma solução é encher de água o balde
menor e passar todo o conteúdo para o
balde maior. A seguir, encher novamente
o balde menor e passar para o maior a
parte suficiente para completá-lo. O que
restar no balde menor será 1 litro de
água.
2. Uma solução é encher de leite o
recipiente de 500 mL e passar parte desse
leite para o copo de 200 mL, enchendo-o.
O que restar no recipiente de 500 mL
serão os 300 mL de leite necessários para
a receita.
1. medidas do sólido R comprimento:
40 cm; largura: 20 cm; altura: 60 cm
V 5 40 3 20 3 60 5 48 000 cm3
2. volume do 1o sólido: 1,2 m3
volume do 2o sólido:
5
8
1 2 0 75 075 3 3 , 5 , → , m
R 0,75 m3
3. volume do cubo A:
2 3 2 3 2 5 8 R 8 cm3
volume do cubo B:
0,5 3 0,5 3 0,5 5 0,125 R 0,125 cm3
quantidade de vezes em que o cubo B cabe
no cubo A:
8 ; 0,125 5 64 R 64 vezes

70
4. volume da caixa:
6 3 3 3 2 5 36 R 36 cm3
volume do paralelepípedo:
2 3 1,5 3 1 5 3 R 3 cm3
quantidade de paralelepípedos para encher
a caixa:
36 ; 3 5 12 R 12 paralelepípedos
5. volume do reservatório após a
evaporação:
5 3 1,20 3 (1,20 – 0,05) 5
5 5 3 1,20 3 1,15 5 6,9 R 6,9 m3
6. 1 hora equivale a 60 minutos.
1 minuto equivale a 60 segundos, logo 1
hora equivale a:
60 3 60 5 3 600 R 3 600 segundos
a cada 20 segundos goteja 7 vezes, logo em
3 600 segundos vai gotejar:
(3 600 ; 20) 3 7 5 180 3 7 5 1 260 R 1 260 gotas
volume de cada gota: 0,2 cm3
volume total de água que vaza:
1 260 3 0,2 5 252 R 252 cm3
1 cm3 corresponde a 0,001 dm3.
252 cm3 correspondem a 0,252 dm3.
7. volume do reservatório: 10 m3
10 m3 correspondem a 10 000 dm3 ou 10 000 L.
Retirando 2 200 L, restam:
10 000 – 2 200 5 7 800 R 7 800 L
2a retirada de água:
1
3780052600→2600 L
3
Restam: 7 800 – 2 600 5 5 200 R 5 200 L
8. suco consumido em cada refeição: 750 mL
suco consumido diariamente:
750 3 2 5 1 500 R 1 500 mL
suco consumido em uma semana:
1 500 3 7 5 10 500 R 10 500 mL
1 mL corresponde a 0,001 L, logo 10 500 mL
correspondem a 10,5 L.
9. volume da caixa-d’água: 105 m3
consumo diário:
4
5
105 84 84 3 3 5 → m / dia
84 m3/dia correspondem a 84 000 L/dia.
10. quantidade de gotas a cada 5 minutos:
100 gotas
quantidade de gotas em 1 minuto:
100 ; 5 5 20 R 20 gotas
1 hora corresponde a 60 minutos.
quantidade de gotas em 1 hora:
60 3 20 5 1 200 R 1 200 gotas
volume de cada gota: 3 mL
volume total das gotas em 1 hora:
1 200 3 3 5 3 600 R 3 600 mL
1 mL corresponde a 0,001 L.
3 600 mL correspondem a 3,6 L.
3,6 L 1 L
11. quantidade de óleo comprada:
100 3 120 5 12 000 R 12 000 L
capacidade de cada recipiente: 750 mL
1 mL corresponde a 0,001 L.
750 mL correspondem a 0,75 L.
quantidade necessária de recipientes:
1 200 ; 0,75 5 16 000 R 16 000 recipientes
Medindo a massa
49 – Unidades de medida de massa
50 – Transformação das unidades
de medida de massa
1.
a) um pacote de arroz: quilograma;
b) carga de um caminhão: tonelada;
c) um comprimido: miligrama;
d) laje de concreto: tonelada;
e) uma pessoa: quilograma;
f) ovo de codorna: grama
2.
a) g b) kg c) g d) g e) kg f) kg
3.
a) 1 kg corresponde a 1 000 g.
2,3 kg correspondem a 2 300 g.
b) 3
kg corresponde a:
4
3
4
310005750→750 g

71
c) 1 mg corresponde a 0,001 g.
950 mg correspondem a 0,95 g.
d) 1 quilate corresponde a 0,2 g.
24 quilates correspondem a:
24 3 0,2 5 4,8 R 4,8 g
4. 3,6 ; 0,2 5 18 R 18 quilates
5.
a) 1 sanduíche é feito com 270 g.
200 sanduíches são feitos com:
200 3 270 5 54 000 R 54 000 g
1 g corresponde a 0,001 kg.
54 000 g correspondem a 54 kg.
b) 1 kg corresponde a 1 000 g.
17,55 kg correspondem a 17 550 g.
270 g de carne para 1 sanduíche R
R 17 550 de carne para:
17 550 ; 270 5 65 R 65 sanduíches
6. 1 kg corresponde a 0,001 t.
83 000 kg correspondem a:
83 000 3 0,001 5 83 R 83 t
7. 1 kg corresponde a 1 000 g.
6 kg correspondem a 6 000 g.
quantidade de pedaços de 750 g cada:
6 000 ; 750 5 8 R 8 pedaços
8. 1 kg corresponde a 1 000 g.
1 000 g custam R$ 5,00.
100 g custam:
5 ; 10 5 0,50 R R$ 0,50
700 g custam:
7 3 0,50 5 3,50 R R$ 3,50
9. Alternativa a.
Emagreceu 450 g, ficou com:
64 000 – 450 5 63 550 g
63 550 g correspondem a 63,550 kg ou 63 kg
e 550 g.
10. Alternativa b.
quantidade de goiabada:
quantidade consumida:
250 1 200 1 450 5 900 R 900 g
quantidade que restou:
2 000 – 900 5 1 100 R 1 100 g
1.
a) volume do reservatório: 30 m3
30 m3 correspondem a:
30 3 1 000 5 30 000 R 30 000 L
b) 1 L corresponde a 1 kg.
30 000 L correspondem a 30 000 kg.
2. 1 m3 corresponde a 1 000 dm3 ou 1 000 L.
40 m3 correspondem a 40 000 L.
Se em cada litro (dm3) há 0,5 kg, em 40 000 L há:
40 000 3 0,5 5 20 000 R 20 000 kg
1 tonelada corresponde a 1 000 kg.
20 000 kg correspondem a 20 toneladas.
3. Seis embalagens de 0,5 kg correspondem
a:
6 3 0,5 5 3,0 R 3 kg
1 kg corresponde a 1 000 g.
quantidade de embalagens de 250 g:
3 000 ; 250 5 12 R 12 embalagens
4.
a) 25 cm correspondem a 0,25 m.
volume da laje:
5 3 3,2 3 0,25 5 4 R 4 m3
b) 4 m3 correspondem a 4 000 dm3.
Se 1 dm3 corresponde a 1,5 kg,
4 000 dm3 correspondem a:
4 000 3 1,5 5 6 000 R 6 000 kg
5. 1,5 m corresponde a 15 dm.
1,20 m corresponde a 12 dm.
80 cm correspondem a 8 dm.
volume do tanque:
15 3 12 3 8 5 1 440 R 1 440 dm3 ou 1 440 L
1 litro tem 0,7 kg, 1 440 L têm:
1 440 3 0,7 5 1 008 R 1 008 kg
1 kg corresponde a 0,001 t.
1 008 kg correspondem a:
1 008 3 0,001 5 1,008 R 1,008 t
6.
a) 1,20 m de comprimento correspondem
a 12 dm.
80 cm de largura correspondem a 8 dm.
45 cm de altura correspondem a 4,5 dm.
volume de água no reservatório:
12 3 8 3 4,5 5 432 R 432 dm3 ou 432 L
b) massa de 1 L de água: 1 kg
massa de 432 L de água: 432 kg
1.
a) 1 quarta corresponde a 12 kg.
45 quartas correspondem a:
45 3 12 5 540 R 540 kg
1 @ corresponde a 15 kg.
540 kg correspondem a:
540 ; 15 5 36 R 36 @

72
b)
1
4
de um quintal corresponde a 1 @.
1 quintal corresponde a:
4 3 15 5 60 R 60 kg
c) 1 @ corresponde a 15 kg.
30,5 @ correspondem a:
30,5 3 15 5 457,5 R 457,5 kg
d) boi: 510 kg
510 ; 15 5 34 R 34 @
1 @ custa R$ 46,00, 34 @ custam:
34 3 46 5 1 564 R R$ 1 564,00
vaca: 465 kg
465 ; 15 5 31 R 31 @
1 @ custa R$ 42,00, 31 @ custam:
31 3 42 5 1 302 R R$ 1 302,00
preço pago pelos animais:
1 564 1 1 302 5 2 866 R R$ 2 866,00
2.
a) 1 t corresponde a 1 000 kg.
28,5 milhões de toneladas
correspondem a:
28,5 milhões 3 1 000 5 28,5 bilhões R
R 28,5 bilhões de quilogramas
b) aumento de produção:
30 400 000 – 28 500 000 5 1 900 000 R
R 1,9 milhão de toneladas
1 tonelada corresponde a 1 000 kg ou,
em arrobas:
1 000 ; 15 . 66,67 @
1 900 000 toneladas correspondem a:
1 900 000 3 66,67  126 673 000 R
R 126,7 milhões de arrobas
1. 1 pote de fermento equivale a 5 caixas de
gelatina.
2 potes de fermento equivalem a 10 caixas
de gelatina.
1 pote de chocolate equivale a 2 potes de
fermento, logo:
1 pote de chocolate equivale a 10 caixas de
gelatina.
4 potes de chocolate equivalem a 40 caixas
de gelatina.
2 kg de açúcar equivalem a 40 caixas de
gelatina.
2. 2 kg de açúcar correspondem a 2 000 g de
açúcar.
4 potes de chocolate equivalem a 2 000 g.
1 pote de chocolate equivale a:
200 ; 4 5 500 R 500 g
1. 1 bloco tem 1
1
4
t, 20 blocos têm:
1
1
4
20
5
4
3 5 320525 R 25 t
2. 1 m3 tem 150 g de massa.
1,2 kg corresponde a 1 200 g, logo 1 200
correspondem a:
1 200 ; 150 5 8 R 8 m3 de massa
3. massa da laje: 42 toneladas
42 toneladas correspondem a 42 000 kg.
quantidade de blocos que formam a laje: 28
massa de cada bloco:
42 000 ; 28 5 1 500 R 1 500 kg
4. A produção dobra a cada ano.
Em 2007, a produção foi de 125 kg.
em 2008 a produção foi de 250 kg, em 2009
foi de 500 kg, em 2010 foi de 1 000 kg e,
em 2011, a produção será de 2 000 kg ou
2 toneladas.
5. cada bolinha: 0,25 kg
1 kg corresponde a 1 000 g.
0,25 kg corresponde a:
0,25 3 1 000 5 250 g
28 bolinhas têm:
28 3 250 5 7 000 R 7 000 g
caixa com as bolinhas: 7,35 kg ou 7 350 g
caixa tem: 7 350 2 7 000 5 350 R 350 g
6. 1 pacote de feijão equivale a 500 g.
12 pacotes de feijão equivalem a:
12 3 500 5 6 000 R 6 000 g
consumo de feijão por semana:
1,5 kg corresponde a 1 500 g.
6 000 g serão consumidos em:
6 000 ; 1 500 5 4 R 4 semanas
7.
a) volume de concreto na laje:
20 3 8 3 0,25 5 40 R 40 m3
b) 1 m3 de concreto tem 1 000 kg.
1 000 kg correspondem a 1 t, logo:
1 m3 de concreto tem 1 t, 40 m3 de
concreto têm 40 t.

SUMÁRIO
7o . ano
Potências e raízes.............................................................................................. 75
O conjunto dos números inteiros....................................................................... 84
O conjunto dos números racionais..................................................................... 102
Estudando as equações...................................................................................... 117
Estudando as inequações................................................................................... 147
Estudando os ângulos....................................................................................... 155
Estudando triângulos e quadriláteros............................................................... 165
Razões e proporções........................................................................................... 167
Grandezas proporcionais................................................................................... 185
Porcentagem...................................................................................................... 200

75
Potências e raízes
Abertura, página 7.
• Pra pensar, sem se cansar: Com quantos
cubinhos se faz um cubo?
Depende do tamanho do cubo.
• Procure no dicionário: Qual a diferença
entre censo e recenseamento?
Censo: conjunto dos dados estatísticos
dos habitantes de uma cidade, província,
estado, nação etc., com todas as suas
características.
Recenseamento: arrolamento de pessoas
ou de animais.
• Número quadrado: E quantos quadradinhos
terá o próximo número da sequência?
A sequência começa com 4 quadradinhos,
depois passa para 16 e depois para 256.
Logo, o próximo número da sequência será
65 536.
• Preste bem atenção e conte de forma
certeira: Quantos são os quadrados?
São 14 quadrados no total: nove quadrados
com 1 palito, quatro quadrados com 2
palitos e um quadrado com 3 palitos.
1 – Potência de um número
racional
a) Desdobrando a folha, verificamos que
ela ficou dividida em 8 partes iguais.
b) Desdobrando a folha, verificamos que
c) Desdobrando a folha, verificamos que
d) De acordo com os itens anteriores, se
dobrarmos a folha:
• 6 vezes, ela ficará dividida em 64
partes iguais.
partes iguais.
partes iguais.
Resposta em aberto.
1.
a) 10 3 10 3 10 5 103
b) 0,9 3 0,9 3 0,9 3 0,9 3 0,9 5 (0,9)5
c) 7 3 7 3 7 3 7 3 7 3 7 3 7 3 7 3 7 3 7 5
5 710
d) 2
5
2
5
2
5
2
3 5
 
 
e) 1 5 1 5 1 5 1 5 1 5 1 5
, 3 , 3 , 3 , 3 20
, 3... ,
5(1,5)20
fatores
f)
3
3
3
3
3
4 7
7
7
7
7
 
 
 
 
 
 
 
 
 
 
3 3 3 5
g) 1 1 1 1 1 1
100 3 3 3 3...3 5

100
fatores
2.
a) 46 5 4 3 4 3 4 3 4 3 4 3 4
b) (0,7)3 5 (0,7) 3 (0,7) 3 (0,7)
c) 1
8
1
8
1
8
2  
 
 
 
 
 
5 3
d) 104 5 10 3 10 3 10 3 10
3. De acordo com as figuras, temos:
a) 4 3 4 5 42
b) 2 3 2 3 2 5 23
4.
a) 63 5 6 3 6 3 6 5 216
b) 105 5 10 3 10 3 10 3 10 3 10 5 100 000
c) 72 5 7 3 7 5 49
d) 112 5 11 3 11 5 121
e) 90 5 1
f) (0,3)3 5 (0,3) 3 (0,3) 3 (0,3) 5 0,027
g) (1,8)2 5 (1,8) 3 (1,8) 5 3,24
h) 1
5 1
1
1
1
1 2
2
2
2
2
 
 
 
 
 
 
 
 
 
 
5 3 3 3 32
2
1
32
 
 
5
1 4  
i) 2
5
2
5
2
5
2
5
2
5
 
 
 
 
 
 
 
 
 
5 3 3 3 5
6
625
j) (2,5)0 5 1
5. De acordo com a figura, cada aresta tem
8 cubinhos; logo, o total de cubinhos será:
83 5 8 3 8 3 8, ou seja, 512 cubinhos.
6. De acordo com a figura, temos:
132 5 13 3 13 5 169
7.
a) (0,2)2 5 (0,2) 3 (0,2) 5 0,04
b) Escrevendo 0,04 na forma de fração
irredutível, temos:
0 04
4
100 4
1
25
4


, 5 5

76
c) Escrevendo 0,04 na forma percentual,
temos: 0,04 3 100 5 4%.
8. Das expressões, temos:
(11 1 3)2 5 (14)2 5 14 3 14 5 196
112 1 32 5 121 1 9 5 130
Logo, as expressões não são iguais,
pois 196 ≠ 130.
9. De acordo com o enunciado, vem:
N 5 2 3 (0,9) 2 (0,9)2
N 5 1,8 2 0,81
N 5 0,99
10.
a) x 5 24 3 22
x 5 2 3 2 3 2 3 2 3 2 3 2 5 64
y 5 28
y 5 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 5 256
Logo, x  y.
b) x 5 22 3 52
x 5 2 3 2 3 5 3 5 5 100
y 5 (5 3 2)2
y 5 (10)2
y 5 10 3 10 5 100
Logo, x 5 y.
11. Como 40% 5 0,4, então, o quadrado de
40% será:
(0,4)2 5 (0,4) 3 (0,4) 5 0,16
12. 10x 5 100 ou 10x 5 102 ⇒ x 5 2
8o 5 y ⇒ y 5 1
Logo, x 2 y 5 2 2 1 5 1.
2 – Propriedades da potenciação
1. De acordo com o esquema, temos:
33 5 3 3 3 3 3 5 27
Portanto, Larissa usou 27 cubinhos.
2. De acordo com os resultados obtidos por
Carlos, temos:
a)
• 22 3 23 5 4 3 8 5 32
• 25 5 32
• 34 3 32 5 81 3 9 5 729
• 36 5 729
b)
• 22 3 23 5 32 e 25 5 32
Logo, 22 3 23 5 25.
• 34 3 32 5 729 e 36 5 729
Logo, 34 3 32 5 36.
c)
• 25 : 23 5 32 : 8 5 4
• 22 5 4
• 35 : 32 5 243 : 9 5 27
• 33 5 27
d)
• 25 : 23 5 4 e 22 5 4
Logo, 25 : 23 5 22.
• 35 : 32 5 27 e 33 5 27
Logo, 35 : 32 5 33.
e)
• (23)2 5 (8)2 5 8 3 8 5 64
• 26 5 2 3 2 3 2 3 2 3 2 3 2 5 64
• (32)2 5 (9)2 5 9 3 9 5 81
• 34 5 3 3 3 3 3 3 3 5 81
• (22)3 5 (4)3 5 4 3 4 3 4 5 64
f)
• (23)2 5 26, pois (23)2 5 64 e 26 5 64.
• (32)2 5 34, pois (32)2 5 81 e 34 5 81.
• (22)3 5 26, pois (22)3 5 64 e 26 5 64.
3.
a)
• 23 5 2 3 2 3 2 5 8
• 33 5 3 3 3 3 3 5 27
• 23 3 33 5 8 3 27 5 216
• (2 3 3)3 5 (6)3 5 6 3 6 3 6 5 216
b)
• 32 5 3 3 3 5 9
• 52 5 5 3 5 5 25
• 32 3 52 5 9 3 25 5 225
• (3 3 5)2 5 (15)2 5 15 3 15 5 225
c)
• 53 5 5 3 5 3 5 5 125
• 23 5 2 3 2 3 2 5 8
• 53 3 23 5 125 3 8 5 1 000
• (5 3 2)3 5 (10)3 5 10 3 10 3 10 5 1 000
d)
• 22 5 2 3 2 5 4
• 42 5 4 3 4 5 16
• 22 3 42 5 4 3 16 5 64
• (2 3 4)2 5 (8)2 5 8 3 8 5 64
Resposta em aberto.
1.
a) 75 3 74 5 75 + 4 5 79
b) (132)6 5 132 3 6 5 1312
c) 85 : 84 5 85 2 4 5 81
d) (x10)3 5 x10 3 3 5 x30
e) (0,6)10 : (0,6)7 5 (0,6)10 2 7 5 (0,6)3

77
3 3 3 3 9  
f) 3
4
3
4
3
4
 

 

 
 
 
 
 
3
5 5
20 15 20 15 5  
g) 7
9
7
9
7
9
7
9
 
 
 
 
 
 
 
2
 5 5
h) (0,9)8 3 (0,9) 3 (0,9)3 5 (0,9)8 + 1 + 3 5
5 (0,9)12
i) ( , ) ( , ) ( , ) 1 7 1 7 1 7 10 4 10 4 40 

5 5 3
2.
a 5 213; b 5 27; c 5 25
a) a 3 b 5 213 3 27 5 213 1 7 5 220
b) b : c 5 27 : 25 5 27 2 5 5 22
c) a 3 c 5 213 3 25 5 213 1 5 5 218
d) a : b 5 213 : 27 5 213 2 7 5 26
e) a2 5 (213)2 5 213 3 2 5 226
f) b3 5 (27)3 5 27 3 3 5 221
g) a 3 b 3 c 5 213 3 27 3 25 5 213 1 7 1 5 5 225
h) a : c 5 213 : 25 5 213 2 5 5 28
i) c4 5 (25)4 5 25 3 4 5 220
3. Sendo x 5 104 e y 5 103, temos:
x3 5 (104)3 5 104 3 3 5 1012
y4 5 (103)4 5 103 3 4 5 1012
Logo, x3 5 y4.
4.
a) (5 3 11 3 23)3 5 53 3 113 3 233
b) (23 3 3)4 5 (23)4 3 34 5 212 3 34
c) (35 : 52)2 5 (35)2 : (52)2 5 310 : 54
d) 2,3)4 (2,1)5 (2,3) (2,1) (2,3 3 4 3 5 3
(0,6) 3 (1,1)54 5 )12(2,1)15 (2,3)4 (2,1)5 (2,3) 2,1) (2,3 3 4 3 5 3
  





  





55 (0,6)4 3 (1,1)4 5 )12(2,1)15
7 7 7  
e) 1
7
2
3
1
7
2
3
 
 
 

 

 
 
 
 
 
3 5 3
f) (2,3)4 (2,1)5 3 (2,3)4 3 (2,1)5 3 (2,3
  





5 5 )12(2,1)15
5.
a) a2 3 b2 5 (a 3 b)2
Como a 3 b 5 6, temos:
a2 3 b2 5 62 5 36
b) a3 3 b3 5 (a 3 b)3
a3 3 b3 5 63 5 216
6. giga: 1 000 000 000 5 109
mega: 1 000 000 5 106
miria: 10 000 5 104
quilo: 1 000 5 103
hecto: 100 5 102
deca: 10 5 101
7.
a) 35 000 5 35 3 103
b) 60 000 000 5 6 3 107
c) 920 000 5 92 3 104
d) 92 000 000 000 5 92 3 109
8. 9 5 32; 27 5 33; 729 5 36
(9 27) 729 (3 3 ) 3 (3 ) 3 3 3
3  5 3  5  5  5
3
3
3
2 3 6 2 3 6 5 6
5
6
5
5 5
1
26 3 1
1
3
5 5 2
9.
a) (29 3 211 3 23) : (27)3 5 (29 1 11 1 3) : 27 3 3 5
5 223 : 221 5 223 2 21 5 22 5 4
b)
(0,4)2 (0,4) (0,4) (0,4) (0,4) 10 9 7 2 10 



 3 3 5  3 (0,4)91711 5
5 (0,4)20 : (0,4)17 5 (0,4)20 2 17 5 (0,4)3 5
5 (0,4) 3 (0,4) 3 (0,4) 5 0,064
10. a 5 27 3 34 3 72; b 5 25 3 32 3 7;
c 5 25 3 3 3 7
a) a : b
(27 3 34 3 72) : (25 3 32 3 7) 5 27 2 5 3 34 2 2 3
3 72 2 1 5 22 3 32 3 7 5
5 4 3 9 3 7 5 252
b) a : c
(27 3 34 3 72) : (25 3 3 3 7) 5 27 2 5 3 34 2 1 3
3 72 2 1 5 22 3 33 3 7 5
5 4 3 27 3 7 5 756
c) b : c
(25 3 32 3 7) : (25 3 3 3 7) 5 25 2 5 3 32 2 1 3
3 71 2 1 5 20 3 31 3 70 5
5 1 3 3 3 1 5 3
11.
( 10
)
( 10 10
)
10
10 10
10
10 10
10
4 7
8 3
4 7
8 3 3
28
5
3
3
24 3 5
3
5
5
3
3
28
24 3
28
10
10 1 5 5
10 27
5 1028 : 1027 5 1028 2 27 5 101 5 10
12. Sabendo que 1 024 5 210 e 64 5 26, temos:
1 0242 : 643 5 (210)2 : (26)3 5 210 3 2 : 26 3 3 5
5 220 : 218 5 220 2 18 5 22 5 4
13.
a) Se o raio do Sol é 7 3 1010 cm e 1 km 5
5 105 cm, então, o raio do Sol será:
7 3 1010 : 105 5 7 3 1010 2 5 5 7 3 105 5
5 7 3 100 000 5 700 000
Logo, o raio do Sol tem
aproximadamente 700 000 km.

78
b) 150 000 000 km 5 15 3 107 km
c) A distância da Terra à Lua é 384 000 km;
logo, sendo 1 km 5 103 m, temos:
d 5 384 3 103 3 103 5 384 3 103 1 3 5
5 384 3 106  d 5 384 3 106 m
d) O raio da Lua é aproximadamente
1 700 km; logo, sendo
1 km 5 105 cm, temos:
rLua 5 1 700 3 105 5 17 3 102 3 105 5
5 17 3 102 1 5  rLua 5 17 3 107 cm
e) O raio da Terra é 3,765 vezes maior que
o raio da Lua. Como o raio da Lua é
aproximadamente 1 700 km, o raio da
Terra será, aproximadamente:
3,765 3 1 700 km 5 6 400,5 km
a) De acordo com a tabela de referências,
a maior distância entre os extremos do
Brasil é de Norte a Sul.
b) Sendo 1 km 5 103 m, temos:
4 402 km  4 402 3 103 m
4 325 km  4 325 3 103 m
a) 27 5 2 3 2 3 2 3 2 3 2 3 2 3 2 5 128
b) 36 5 3 3 3 3 3 3 3 3 3 3 3 5 729
c) 35 36 35 6 311 3 3 3 3 3
3 5 5 5 3 3 3 3 3 5 1 ...

11
vezes
5177147
d) 310 32 310 2 312 3 3 3 3 3
3 5 5 5 3 3 3 3 3 5 + ...

12
vezes
5531441
e) 26 3 26 5 26 1 6 5 212 5 2 3 2 3 2 3 2 3 ...
3 2 5 40
 96
12
vezes
f) (0,3)6 5 (0,3) 3 (0,3) 3 (0,3) 3 (0,3) 3
3 (0,3) 3 (0,3) 5 0,000729
g) (0,7)7 5 (0,7) 3 (0,7) 3 (0,7) 3 (0,7) 3
3 (0,7) 3 (0,7) 3 (0,7) 5 0,0823543
h) (2,25)5 5 (2,25) 3 (2,25) 3 (2,25) 3
3 (2,25) 3 (2,25) 5 57,665038
i) (32)4 5 32 3 4 5 38 5 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 5 6 561
j) (4)7 5 4 3 4 3 4 3 4 3 4 3 4 3 4 5
5 16 384
3 – Números quadrados perfeitos
a) Contando os quadradinhos de cada
figura, temos:
A: 36; B: 24; C: 64; D: 25; E: 72
b) Os quadrados são as figuras: A, C e D.
c) Os números correspondentes às áreas
dos quadrados são:
A: 36; C: 64; D: 25
1.
1 cm
1 cm
a) Sim, basta formar 5 fileiras com 5
quadrados em cada uma.
b) 25 é um quadrado perfeito, pois 25 5 52.
c) Não, pois o número de quadrados em
cada linha e em cada coluna não será
o mesmo.
d) Não, pois não há número natural que
elevado a 2 resulte em 29.
2.
a) 180 2
90 2
45 3
15 3
5 5
1 22 3 32 3 5
Como o fator 5 não apresenta expoente
par, 180 não é um quadrado perfeito.
b) 225 3
75 3
25 5
5 5
1 32 3 52
Como todos os fatores apresentam
expoente par, 225 é um número
quadrado perfeito.
c) 729 3
243 3
81 3
27 3
9 3
3 3
1 36
Como o fator apresenta expoente par,
729 é um número quadrado perfeito.

79
d) 1 000 2
500 2
250 2
125 5
25 5
5 5
1 23 3 53
Como os fatores não apresentam
expoente par, 1 000 não é um número
quadrado perfeito.
e) 1 024 2
512 2
256 2
128 2
64 2
32 2
16 2
8 2
4 2
2 2
1 210
Como o fator apresenta expoente par,
1 024 é um número quadrado perfeito.
f) 1 225 5
245 5
49 7
7 7
1 52 3 72
expoente par, 1 225 é um número
quadrado perfeito.
g) 1 600 2
800 2
400 2
200 2
100 2
50 2
25 5
5 5
1 26 3 52
quadrado perfeito.
h) 2 000 2
1 000 2
500 2
250 2
125 5
25 5
5 5
1 24 3 53
Como o fator 5 não apresenta expoente
par, 2 000 não é um quadrado perfeito.
i) 2 025 3
675 3
225 3
75 3
25 5
5 5
1 34 3 52
quadrado perfeito.
3. Para que 24 3 5x 3 112 seja um número
quadrado perfeito, devemos ter todos
os expoentes pares. Logo, os possíveis
valores para o expoente x, dentre os
números apresentados, são 6 e 10.
4. 38 3 114 é um quadrado perfeito, pois
todos os fatores apresentam expoente par.
5. Para que 2n 3 76 não seja um número
quadrado perfeito, basta que n seja um
número ímpar.
6. Os números quadrados perfeitos entre
100 e 300 são:
112 5 121; 122 5 144; 132 5 169; 142 5 196;
152 5 225; 162 5 256; 172 5 289
Logo, existem 7 números quadrados
perfeitos entre 100 e 300.
7. Entre 450 e 500, há um único quadrado
perfeito; logo, N vale 484.
a) A figura é formada por 42 ou 24
quadrados com lados medindo um
palito.
b) A figura é formada por 32 quadrados
com lados medindo dois palitos.
c) A figura possui 22 quadrados formados
por três palitos.
d) Para que não restem quadrados, devem
ser removidos da figura 32 palitos.

80
1.
a) 64 2
2
2 ,
32 2
16 2
8 2
4 2
2 2
1 26
26 5 (23)2 5 (8)2 5 8 3 8
Logo, 64 58 .
b) 49 7
7 7
1 72
72 5 7 3 7
Logo, 49 57 .
c) 25 5
5 5
1 52
1
25
1
5
1
5
2
2 ,
1
5
1
5
2
2
2
 
 
 
 
5 5 5 3
 
 
Logo,
1
25
1
5 5 .
d) 49 7
7 7
1 72
9 3
3 3
1 32
49
9
7
3
7
3
7
3
7
3
2
2
2
 
 
 
 
5 5 5 3
 
 
Logo,
49
9
7
3 5 .
e) 81 3
27 3
9 3
3 3
1 34
100 2
50 2
25 5
5 5
1 22 3 52
2
2 ,
0 81
81
100
3
2 5
( 3
)
( 2 5
)
9
10
9
10
4
2 2
2 2
2
( )
( )
5 5
3
5 5 5
3
 
 
 
 
2 9
10
5 0 81
81
100
3
2 5
( 3
)
( 2 5
)
9
10
9
10
4
2 2
2 2
2
( )
( )
5 5
3
5 5 5
3
 
 
 
 
 
 
2 9
9
5 10
3 10 5
5 (0,9) 3 (0,9)
Logo, 0,81 50,9 .
f) 36 2
18 2
9 3
3 3
1 22 3 32
100 2
50 2
25 5
5 5
1 22 3 52
2
2 ,
0 36
36
100
2 3
2 5
2 3
2 5
6
10
6
1
2 2
2 2
2
2
( )
( )
( )
( )
5 5
3
3
3
3 0
5 5 5
6
10
2  
 
 
 
5 0 36
36
100
2 3
2 5
2 3
2 5
6
10
6
1
2 2
2 2
2
2
( )
( )
( )
( )
5 5
3
3
3
3 0
5 5 5
6
10
6
10
2  
 
 
 
 
 
5 3 5
5(0,6) 3 (0,6)
Logo, 0,36 50,6 .
g) 4 2
2 2
1 22
10 000 2
5 000 2
2 500 2
1 250 2
625 5
125 5
25 5
5 5
1 24 3 54
0 0004
4
10000
2
2 5
( 2
)
( 2 5
)
( 2
)
( 4 25
)
2
4 4
2
2 22
2
,
5 5
2 3
5 5 5
3 3
( ( 2
100
0 0004
4
10000
2
2 5
( 2
)
( 2 5
)
( 2
)
( 4 25
)
2
4 4
2
2 22
2
,
5 5
2 3
5 5 5
3 3
( 2
)
( 100
)
2
100
2
2
2
 
 
5 5
 
 
 
2
2
0 02 002 100
100

 ( , ) ( , )
5 3 5 3
Logo, 0,0004 50,02 .
h) 16 2
8 2
4 2
2 2
1 24

2 2 2 2  
81
10 000 2
5 000 2
2 500 2
1 250 2
625 5
125 5
25 5
5 5
1 24 3 54
0 0016
16
10000
2
2 5
2
2 5
4
4 25
4
4 4
2 2
2 22
2
,
( )
( )
( )
( )
5 5
3
5 5
3 3 2
2
2
( )
( )
4
100
5 5
2
2 5
2
2 5
4
4 25
4
4 4
2 2
2 22
2
( )
( )
( )
( )
3
5 5
3 3 2
2
2
( )
( )
4
100
5 5
4
2 100

 4
100
4
100
( , ) ( , )
0 04 004
 
 
 
 
 
5 5 3 5 3
Logo, 0,0016 50,04 .
2.
169
400
13
20
13
20
169
400
2
 
5 ,pois 5  
Sendo x 5
169
400
, chegamos em x 5
13
20
.
3.
n2
121
2
2 196
2
11
1 5 5 5 5 3
11
14
11
14
11
14
( )
( )
 
 
 
 
4
 
 
Logo,n5
11
14 .
4.
210 3 52 3 72 5 (25 3 5 3 7)2 5 (1 120)2 5
5 (1 120) 3 (1 120)
Logo, 210 52 72 1120 3 3 5 .
5.
a) 484 2
242 2
121 11
11 11
1 22 3 112
22 3 112 5 (2 3 11)2 5 (22)2 5 22 3 22
Logo, 484 522 .
b) 729 3
243 3
81 3
27 3
9 3
3 3
1 36
36 5 (33)2 5 (27)2 5 27 3 27
Logo, 729 527 .
c) 676 2
338 2
169 13
13 13
1 22 3 132
22 3 133 5 (2 3 13)2 5 (26)2 5 26 3 26
Logo, 676 526 .
d) 256 2
128 2
64 2
32 2
16 2
8 2
4 2
2 2
1 28
28 5 (24)2 5 (16)2 5 16 3 16
Logo, 256 516 .
e) 1 764 2
882 2
441 3
147 3
49 7
7 7
1 22 3 32 3 72
1 764 5 22 3 32 3 72 5 (2 3 3 3 7)2 5
5 (42)2 5 42 3 42
Logo, 1764 542 .
f) 2 304 2
1 152 2
576 2
288 2
144 2
72 2
36 2
18 2
9 3
3 3
1 28 3 32
28 3 32 5 (24 3 3)2 5 (16 3 3)2 5 (48)2 5
5 48 3 48
Logo, 2304 548 .
6.
a) 4 84
484
100
22
10
 
 
 
 
2 2
2
22
10
22
10
2
,
( )
( )
5 5 5 5 3
2
10
 
5( , )3( , 4 84
484
100
22
10
 
 
 
 
2 2 2 2  
2 2
2
22
10
22
10
2
,
( )
( )
5 5 5 5 3
2
10
 
5( , )3( , )
Logo, 4,84 52,2 .

 
 
 
 
2 7 2 7  
2 2
2
 
 
 
 
2 6 2 6  
2 2
2
 
 
 
 
1 6 1 6  
2 1
2
82
b) 7 29
729
100
27
10
 
 
 
 
2 7 2 7  
2 2
2
27
10
27
10
2
,
( )
( )
5 5 5 5 3
7
10
 
5( , )3( , )
729
100
27
10
27
10
27
10
2
( )
( )
5 5 5 3
7
10
 
5( , )3( , )
Logo, 7,29 52,7 .
c) 6 76
676
100
26
10
 
 
 
 
2 6 2 6  
2 2
2
26
10
26
10
2
,
( )
( )
5 5 5 5 3
6
10
 
5( , )3( , )
676
100
26
10
26
10
26
10
2
( )
( )
5 5 5 3
6
10
 
5( , )3( , )
Logo, 6,76 52,6 .
d) 2 56
256
100
16
10
 
 
 
 
1 6 1 6  
2 1
2
16
10
16
10
2
,
( )
( )
5 5 5 5 3
6
10
 
5( , )3( , )
256
100
16
10
16
10
16
10
2
( )
( )
5 5 5 3
6
10
 
5( , )3( , )
Logo, 2,56 51,6 .
e) 0 1764
1764
10000
42
100
42
100
42
100
2
2
2
,
( )
( )
 
 
5 5 5 5
 
 
 
 
42
100
(0,42) (0,42)
3 5 3
42
100
42
100
42
100
2
2
2
( )
( )
 
 
5 5 5
 
 
 
 
42
100
(0,42) (0,42)
3 5 3
Logo, 0,1764 50,42 .
f) 0 2304
2304
10000
48
100
48
100
48
100
2
2
2
,
( )
( )
 
 
5 5 5 5
 
 
 
 
48
100
(0,48) (0,48)
3 5 3
48
100
48
100
48
100
2
2
2
( )
( )
 
 
5 5 5
 
 
 
 
48
100
(0,48) (0,48)
3 5 3
Logo, 0,2304 50,48 .
7. Se x 5 212 , temos:
212 5 (26)2 5 (64)2 5 64 3 64
Logo, x 5 64.
8.
1 521 3
507 3
169 13
13 13
1 32 3 132
n2 5 1 521 5 32 3 132 5 (3 3 13)2 5 (39)2 5
5 39 3 39
Logo, n 5 39.
a) 36 ovos valem 12 moedas de ouro R
triplicando-se a quantidade de ovos,
a quantidade de moedas de ouro
também triplica.
b) 54 galinhas valem 21 moedas de ouro
R triplicando-se a quantidade inicial
de galinhas, a quantidade de moedas
de ouro também triplica.
c) 60 bananas valem 5 moedas de prata,
já que cada 12 bananas valem uma
moeda de prata.
d) Transformando dúzias em unidades,
temos:
1 dúzia 5 12 unidades.
4 dúzias e
1
2 5 54 unidades.
Como 6 laranjas valem 2 moedas de ouro,
54 laranjas valem 18 moedas de ouro.
e) 3 quilogramas e 1
2
de café valem 21
moedas de prata, pois 1
2
quilograma
de café vale 3 moedas de prata.
f) 3 leitões valem 30 moedas de ouro, pois
1 leitão vale 10 moedas de ouro.
g) Não é possível responder a essa
questão, pois faltam dados.
a) Gráfico A: matrículas na Educação
Básica em 2007;
Gráfico B: matrículas na Educação
Básica em 2006 e 2007;
Gráfico C: matrículas na EJA entre 2000
e 2007.
b) Gráfico A: gráfico de setores;
Gráfico B: gráfico de barras;
Gráfico C: gráfico de linhas.
c) Sim, pois, de acordo com o gráfico A,
60,59% dos alunos foram matriculados
no Ensino Fundamental.
d) Sim.
Educação Infantil R de 7,0 para 6,4
Ensino Fundamental R de 33,2 para 31,7
Ensino Médio R de 8,9 para 8,3
EJA R de 5,6 para 4,9
e) De acordo com o gráfico C, a quantidade
de matrículas na EJA foi crescendo até
2006 e diminuiu em 2007.
1. Alternativa c.
Pelo sistema “mata-mata”, 8 times chegam
às quartas de final, ou seja, 23 times estão
participando dessa etapa.
2.
Alternativa b.
I) (3 1 5)2 5 32 1 52
(8)2 5 9 1 25
64 5 34 (Falso.)

 
5 2 5 2  
( , ) ( , )
83
II) (102)3 5 105
106 5 105 (Falso.)
III) 7  72 5 73
73 5 73 (Verdadeiro.)
IV) 100 5 0
1 5 0 (Falso.)
Apenas a igualdade III é verdadeira.
3. Alternativa a.
1a expressão:
(25 : 22) : 22 5 (25 2 2) : 22 5 23 : 22 5 21 5 2
2a expressão:
25 : (22 : 22) 5 25 : (22 2 2) 5 25 : 20 5 25 5 32
a) Verdadeiro, pois 2  32.
b) Falso, pois 2  32.
c) Falso, pois 2  32.
4. Alternativa d.
(27 : 24) 2 22 5 (27 2 4) 2 4 5 23 2 4 5 8 2 4 5 4
Logo, n 5 4.
5. Alternativa e.
a 5 (102 3 10)7 : (104)5
a 5 (102 1 1)7 : 1020
a 5 (103)7 : 1020
a 5 1021 : 1020
a 5 1021 2 20
a 5 101
a 5 10
b 5 47 410 4 4 2 5 7 3 3 

( )
b 5 47 10 4 4 2 35 1 1 


b 5 418 2 

: 435
b 5 436 : 435
b 5 436 2 35
b 5 41
b 5 4
Logo, a + b 5 10 + 4 5 14.
6. Alternativa a.
x 5 36 5 729
y 5 93 5 729
Logo, x 5 y.
7. Alternativa c.
Se x 5 27 3 38 3 7 e y 5 25 3 36, então:
x
y 5 (27 3 38 3 7) : (25 3 36) 5 27 2 5 3 38 2 6 3
3 7 5 22 3 32 3 7 5
5 4 3 9 3 7 5 252
Logo,
x
y 5 252.
8. Alternativa d.
970 mil toneladas R 970 000 toneladas R
R 970 000 000 quilogramas R 97 3 107 kg
9 Alternativa b.
Para que um número seja quadrado
perfeito, todos os expoentes dos fatores
devem ser par. Dentre os fatores dados,
o 5 é o único que tem expoente ímpar;
portanto, se multiplicarmos 24 3 32 3 53
por 5, obteremos um número quadrado
perfeito:
(24 3 32 3 53) 3 5 5 24 3 32 3 54
10. Alternativa c.
O quadrado perfeito entre 700 e 750 é 729.
729 R 7 1 2 1 9 5 18; portanto, 729 é
múltiplo de 3.
11. Alternativa d.
2 916 2
1 458 2
729 3
243 3
81 3
27 3
9 3
3 3
1 22 3 36
22 3 36 5 (2 3 33)2 5 (2 3 27)2 5 (54)2 5
5 54 3 54
Logo, 2916 554 .
12. Alternativa a.
27 04
2704
100
52
10
52
10
52
10
2
2
2
,
( )
( )
 
 
5 5 5 5
 
 
52
10
33 5 3
27 04
2704
100
52
10
52
10
52
10
2
2
2
,
( )
( )
 
 
5 5 5 5
 
 
 
52
5 2 5  
2 10
( , ) ( , )
33 5 3
Logo, 27,04 55,2 .
13. Alternativa e.
121
100 1 , 2 , 5 1 2 5
4 064 1 21 2
64
100
8
10
11
10
521 2 5 1 2 5
2 0,8 1,1 1,7
Logo, 4 1 0,64 2 1,21 51,7 .
14. Alternativa c.
81
100
9
10
x5 0 81 5 5 5
, 0,9
121
10000
11
100
y5 0 0121 5 5 5
, 0,11
Logo, x 2 y 5 0,9 2 0,11 5 0,79.

O conjunto dos números inteiros
Time
Pontos
ganhos
Gols
marcados
Gols
sofridos
Saldo de
gols
Cruzeiro 53 52 45 17
Atlético-PR 48 61 62 21
Corinthians 53 41 46 25
Santa Cruz 28 41 76 235
Fonte: www.cbfnews.uol.com.br . Acesso em: 18 jul. 2007.
e) Colocando as informações dos dois
times em uma tabela, vem:
Time
Gols
marcados
Gols
sofridos
Saldo de
gols
Flamengo 44 48 24
Palmeiras 58 70 212
De acordo com essa tabela, o Flamengo
possui o maior saldo de gols.
1. Representando as situações por números
inteiros, temos:
a) 28 pontos.
b) 26
c) 1550 reais.
d) 11 200 m
e) 142 8C
f) 121 gols.
g) 24 000 m
2. Como Heródoto nasceu em 484 antes de
Cristo, podemos representar essa data da
seguinte forma: 2484.
3. Como a equipe marcou 17 gols e sofreu 20
gols, o saldo de gols será indicado por: 23.
4. O nível do mar é representado pelo
número 0; logo, 395 metros abaixo do
nível do mar é representado por: 2395.
5. Como o monte Aconcágua tem 6 959 m de
altura, podemos representar sua altura da
seguinte forma: 16 959 m.
6. Considerando o saldo inicial de R$ 300,00
e efetuando as operações para cada
situação, temos:
a) 1300 2 250 5 150 R 150 reais.
b) 1300 1 200 5 1500 R 1500 reais.
c) 1300 1 100 5 1400 R 1400 reais.
d) 1300 2 320 5 220 R220 reais.
• O que é maior?: 7 graus Celsius abaixo de
zero ou 70 graus Celsius abaixo de zero?
27 8C 270 8C, pois 7 graus Celsius abaixo
de zero está mais próximo do marco zero
do que 70 graus Celsius abaixo de zero.
4 – A ideia de números inteiros
1.
a) O andar térreo é indicado pelo número
zero (0).
b) Os botões que indicam os andares
acima do térreo são:
11, 12, 13, 14, 15, 16, 17, 18, 19, 110
c) Os botões que indicam os andares
abaixo do térreo são:
21, 22, 23, 24, 25, 26
2.
a) Os times com saldo de gols positivo
são: São Paulo, Vasco e Cruzeiro. Já os
times com saldo de gols negativo são:
Corinthians, Atlético-PR e Santa Cruz.
b) Os saldos de gols positivos foram
indicados com o sinal de mais (1), e os
saldos negativos, com o sinal de menos
(2).
c) Como o saldo de gols é a diferença
entre o número de gols marcados e o
número de gols sofridos, temos:
5621
39
23
2
2
Como a quantidade de gols sofridos foi
maior, representamos o saldo de gols
da seguinte forma: 223.
d) Não; para que os times ficassem
ordenados do maior saldo de gols
para o menor, a tabela deveria ser
organizada da seguinte forma:
Time
Pontos
ganhos
Gols
marcados
Gols
sofridos
Saldo de
gols
São Paulo 78 66 32 134
Vasco 59 57 50 17
84

5 – O conjunto dos números
inteiros
1.
a) A profundidade é indicada por um
número negativo.
Logo, a profundidade referida será:
2300 m.
b) A altura é indicada por um número
positivo.
Logo, a altura referida será: 115 000 m.
c) A situação descrita será representada
por: 21 700 m.
d) A representação da profundidade que
o submarino alcança é: 2609 m.
2. Avião A: 250 km Avião B: 1150 km
3. De acordo com a figura, temos as
seguintes posições para as cidades
em relação à capital:
a) cidade A R 14
b) cidade B R 22
c) cidade C R 16
d) cidade D R 19
e) cidade E R 25
4. Se cada intervalo do exercício anterior
corresponder a 100 km, as posições das
cidades B e C em relação à capital serão:
Cidade B R 2200 km
Cidade C R 1600 km
5. De acordo com o exercício 3 e
considerando que cada intervalo na reta
representa a distância de 100 km, vem:
a) distância entre as cidades A e C R
200 km, pois há 2 intervalos entre os
pontos que representam a localização
dessas cidades.
b) distância entre as cidades A e D R
dessas cidades.
c) distância entre as cidades B e A R
dessas cidades.
d) distância entre as cidades E e B R
dessas cidades.
e) distância entre as cidades B e D R
1 100 km, pois há 11 intervalos entre os
dessas cidades.
f) distância entre as cidades E e A R
dessas cidades.
6.
a) 12, pois corresponde ao ponto R.
b) O ponto S, pois corresponde ao número
21.
c) o ponto Q, pois corresponde ao número
14.
d) 25, pois corresponde ao ponto P.
7. Fazendo a reta e localizando nela os pontos, temos:
c) B b) R f) P a) A e) C d) S
27 26 25 24 23 22 21 0 11 12 13 14 15 16 17
1. 23 000 m e 26 915 m.
2.
a) • A profundidade da exploração da
pesca na costa brasileira deve ser
indicada com número inteiro
negativo: 2200 m.
• A menor temperatura registrada
oficialmente na cidade de Caçador
é indicada por um número inteiro
negativo: 214 8C.
85

86
d) 1500 R o módulo é 500.
e) 0 R o módulo é 0.
f) 111 R o módulo é 111.
4. Os dois números inteiros diferentes que
possuem módulo igual a 20 são: 120 e
220.
5.
a) 111 511 R Módulo de mais onze é
igual a onze.
b) 230 530 R Módulo de menos trinta é
igual a trinta.
6. Não, pois o módulo de um número inteiro
está associado à distância; logo é sempre
positivo.
7.
a) 27 . 13
27 57 e 13 53 R 7 3
b) 235  160
235 535 e 160 560 R 35 60
c) 213 . 110
213 513 e 110 510 R 13 10
d) 250 5 150
250 550 e 150 550 R 50 5 50
8. Os números inteiros que têm módulo
menor que 3 são: 22, 21, 0, 11, 12.
22 52; 21 51; 0 50; 11 51; 12 52
9.
a) Dentre os números inteiros dados, os
que têm módulo menor que 30 são:
213, 120, 127, 225.
213 513; 120 520; 225 525; 127 527
b) Dentre os números inteiros dados, os
que possuem módulo entre 30 e 50 são:
232 e 240.
232 532 e 240 540
c) Dentre os números inteiros dados, 151
é o único que tem módulo acima de 50.
151 551.
10.
217 1 133 2 250
17 1 33 2 50
50 2 50
0
• A altitude do Pico da Neblina seria
indicada por um número inteiro
positivo: 13 014 m.
b) A temperatura máxima no deserto do
Saara durante o dia pode alcançar:
151 8C.
c) A temperatura noturna mínima no
deserto do Saara pode chegar a 24 8C.
6 – Módulo de um número inteiro
1.
a) De 15 a 0, há cinco intervalos; logo a
distância é 5.
b) De 28 a 0, há oito intervalos; logo a
distância é 8.
c) De 23 a 0, há três intervalos; logo a
distância é 3.
d) De 17 a 0, há sete intervalos; logo a
distância é 7.
e) De 22 a 15, há sete intervalos; logo a
distância é 7.
f) De 29 a 21, há oito intervalos; logo a
distância é 8.
g) De 12 a 17, há cinco intervalos, logo a
distância é 5.
h) De 24 a 14, há oito intervalos; logo a
distância é 8.
2.
a) De 90 km a oeste até 50 km a leste são
140 quilômetros, pois de 90 km até a
origem são 90 km, e da origem até
50 km são 50 km.
b) De 3 8C abaixo de zero até 12 8C
acima de zero há 15 graduações, pois
de 3 8C abaixo de zero até zero há 3
graduações, e de zero até 12 8C há 12
graduações.
c) De 80 km ao norte até 30 km ao sul são
110 quilômetros, pois de 80 km até a
origem são 80 km, e da origem até
30 km são 30 km.
d) De 251 8C até 227 8C são 24
graduações: 51 2 27 5 24.
3. Sendo o módulo de um número inteiro a
distância desse número até o zero, vem:
a) 131 R o módulo é 31.
b) 2300 R o módulo é 300.
c) 228 R o módulo é 28.

87
11.
a) O simétrico de 226 é 126, pois ambos
estão à mesma distância do zero.
b) O módulo de 265 é 65 (265 565), e o
oposto de 65 é 265, pois 65 e 265 estão
à mesma distância do zero.
12. 81  34 1 30
81  81 1 1
1 1 1
2
O oposto de 2 é 22.
13. O oposto de 24 é 14.
14. De acordo com o enunciado, esses
números são chamados números opostos
ou simétricos.
7 – Comparação de números
inteiros
1.
a) Estava mais quente no Rio de Janeiro
(130 8C) que em Montevidéu (122 8C).
b) Estava mais quente em Montevidéu
(122 8C) que em Tóquio (0 8C).
c) Estava mais quente em Tóquio (0 8C)
que em Londres (23 8C).
d) Estava mais quente em Londres (23 8C)
que em Oslo (210 8C).
e) Estava mais quente em Montevidéu
(122 8C) que em Oslo (210 8C).
f) Estava mais quente no Rio de Janeiro
(130 8C) que em Londres (23 8C).
2. De acordo com a tabela, nesse dia fez
mais frio em Oslo (Noruega).
1.
a) 22 26, pois 22 está mais próximo de
zero que 26.
b) 220 210, pois 220 está mais distante
de zero que 210.
c) 27 11, pois todo número positivo é
maior que um número negativo.
2. De acordo com a reta numérica, temos:
a) a 0, pois a está à direita de zero.
b) b 0, pois b está à esquerda de zero.
c) c 0, pois c está à direita de zero.
d) 0 d, pois 0 está à direita de d.
e) a b, pois a é positivo, e b é negativo.
f) a c, pois a está à direita de c.
g) d a, pois d é negativo, e a é positivo.
h) b c, pois b é negativo, e c é positivo.
i) b d, pois b está mais próximo de zero
que d.
3.
a) O menor número inteiro positivo da
figura é 128.
b) O maior número inteiro negativo da
figura é 221.
c) O maior número inteiro da figura é
175.
d) O menor número inteiro da figura é
296.
4.
a) 0 17 f) 230 16
b) 111 0 g) 17 120
c) 0 29 h) 211 230
d) 213 0 i) 21 15
e) 12 219 j) 220 23
5. O saldo nulo é igual a um saldo de gols
zero. Como a equipe A teve um saldo
negativo, e o número zero é maior que
qualquer número negativo, a equipe que
tem o maior saldo de gols é a equipe B.
6. Quanto mais à direita um número está
do outro, maior será esse número; logo,
colocando na ordem indicada, temos:
a) 2100, 270, 210, 0, 120, 180
b) 112, 17, 11, 2100, 2160, 2300, 2500
7.
a) Como o time Alegre sofreu mais gols
do que marcou, seu saldo é negativo:
27.
b) Como o time Bonito sofreu mais gols
do que marcou, seu saldo é negativo:
25.
22 21 0 11 12 13 14 15

Editoria de arte
88
c) Como 25 está à direita de 27, 25 é
maior que 27. Logo, a equipe Bonito
é que passou para a fase seguinte do
torneio.
8. Como 213 é menor que 29, pois 29 está
à direita de 213, a equipe que deverá ser
rebaixada é a equipe A.
9.
a) Os números que podem ser colocados
no lugar de x são: 24, 21, 0, 12 e 16,
pois todos esses números estão à
direita de 25.
b) Os números que podem ser colocados
no lugar de x são: 220, 27, 24, 21 e 0,
pois todos esses números respeitam a
condição x  0.
10.
a) A5{xZ| x.220} R Forma simbólica.
A 5 {219, 218, 217, 216, 215, 214, ...} R
R Nomeação dos elementos.
b) B5{xZ| x27} R Forma simbólica.
B 5 {... 213, 212, 211, 210, 29, 28} R
Nomeação dos elementos.
c) C5{xZ|25 x13} R Forma
simbólica.
C 5 {25, 24, 23, 22, 21, 0, 11, 12} R
Nomeação dos elementos.
11.
a) P5{xZ| x23} R P 5 {23, 22, 21, 0,
1, 2, ...}
b) Q 5{xZ|29x26}→Q 5{28,27,26}
c) R5{xZ| x2100} R R 5 {..., 2106,
2105, 2104, 2103, 2102, 2101}
12.
A5{xZ|26x13}
A 5 {25, 24, 23, 22, 21, 0, 11, 12}
a) Nesse conjunto, há três números
inteiros não negativos.
b) Nesse conjunto, há dois números
inteiros positivos.
c) O conjunto Z* é dos inteiros não nulos;
logo, pertencem ao conjunto A os
elementos: 25, 24, 23, 22, 21, 11 e 12.
8 – Adição de números inteiros
1.
a) Como a temperatura mínima era de
20 8C e subiu 8 8C, a temperatura
máxima em Brasília nesse dia foi:
(120 8C) 1 (18 8C) 5 28 8C.
b) Como a temperatura era 21 8C e
aumentou em 6 8C, a temperatura ao
meio-dia era: (21 8C) 1 (6 8C) 5 5 8C.
c) Como a temperatura era 28 8C à
meia-noite e subiu 7 8C ao meio-dia, a
temperatura ao meio-dia era: (28 8C) 1
1 (17 8C) 5 21 8C.
2.
a) Em Seul, a temperatura variou de
25 8C até 0 8C; logo, a temperatura
variou em 5 8C.
Em Buenos Aires, a temperatura variou
de 18 8C até 21 8C; logo, a temperatura
variou em 3 8C.
Em Berlim, a temperatura variou de
23 8C até 22 8C; logo, a variação da
temperatura foi de 5 8C.
Em Moscou, a temperatura variou de
No Cairo, a temperatura variou de
1. Analisando a pirâmide, verificamos que a
soma dos dois números inferiores é igual
ao número acima.
2. Como a pirâmide segue o mesmo segredo
da anterior, temos:
0
216 116
216 0 116
212 24 14 112
28 24 0 14 18
1.
a) (111) 1 0 5 111
b) 0 1 (213) 5 213
c) (234) 1 (23) 5 237

89
d) (28) 1 (251) 5 259
e) (121) 1 (121) 5 142
f) (149) 1 (260) 5 211
g) (2130) 1 (2125) 5 2255
h) (149) 1 (1121) 5 1170
i) (1820) 1 (2510) 5 1310
j) (2162) 1 (2275) 5 2437
2.
a) Para térreo  2  3  6, temos:
(12) 1 (13) 1 (26) 5 (15) 1 (26) 5 21
b) Para térreo  2  1  3, temos:
(22) 1 (21) 1 (13) 5 (23) 1 (13) 5 0
(térreo)
c) Para térreo  3  3, temos:
(23) 1 (13) 5 0 (térreo)
d) Para térreo  3  4  3  6, temos:
(23) 1 (14) 1 (13) 1 (26) 5 (23) 1 (26) 1
1 (14) 1 (13) 5 (29) 1 (17) 5 22
e) Para térreo  1  6  6  1, temos:
(21) 1 (16) 1 (26) 1 (11) 5 (21) 1 (11) 1
1 (16) 1 (26) 5 0 (térreo)
3.
a) De acordo com a tabela, cada grupo
obteve:
A R (113) 1 (118) 5 131
B R (212) 1 (134) 5 122
C R (23) 1 (125) 5 122
D R (128) 1 (25) 5 123
E R (121) 1 (118) 5 139
b) De acordo com a pontuação
total obtida no item anterior, os
três primeiros colocados foram
respectivamente os grupos E, A e D.
4. Representando o valor que Caio tem por
um número positivo, e o valor da retirada,
por um número negativo, temos:
(13 600) 1 (24 000) 5 2400.
Portanto, se Caio fizer essa retirada, seu
saldo será de 2400 reais.
5. Representando o prejuízo por um número
negativo (212), e o lucro, por um número
positivo (1 29), vem:
(212) 1 (129) 5 117
Logo, a florista teve um lucro de 17 reais.
6. Representando a data de nascimento de
Júlio César por 2100 e sabendo que ele
morreu com 56 anos, calculamos o ano de
sua morte: (2100) 1 (156) 5 244
Logo, Júlio César morreu no ano 244 ou
44 a.C.
7. Representando 31 a.C. por 231 e sabendo
que Marco Antônio morreu com 51 anos,
calculamos o ano de seu nascimento:
(231) 1 (251) 5 282
Logo, Marco Antônio nasceu em 282 ou
82 a.C.
8. Em 10 km há 10 000 m, pois 1 km 5 1 000 m.
Em 10 000 m há 50 vezes 200 m, pois
10 000  200 5 50.
Como a temperatura diminui cerca de
1 grau a cada 200 m de afastamento da
superfície terrestre, temos:
(120) 1 (250) 5 230
Logo, a temperatura na atmosfera a uma
altura de 10 km é 230 graus.
9. Valor ganho com as respostas corretas:
52 × 20 5 1 040 R R$ 1 040, 00
Como Carlos acertou 52 perguntas de um
total de 100, ele errou 48 perguntas; logo,
Carlos pagou pelas respostas erradas o
valor de:
48 × 22 5 1 056 R R$ 1 056, 00
Fazendo a diferença, vem:
(11 040) 1 (21 056) 5 216
Logo, Carlos perdeu 16 reais no programa.
10. Para determinar o valor de x em cada
caso, basta somar o resultado de cada
igualdade com o simétrico das parcelas
conhecidas. Assim, temos:
a) (113) 1 (29) 5 14
b) (210) 1 (16) 5 24
c) 0 1 (17) 5 17
d) (13) 1 (13) 5 16
e) (23) 1 (27) 5 210
f) (218) 1 (120) 5 12
11. De acordo com as operações do extrato,
podemos escrever:
(17 200) 1 (110 000) 1 (213 000) 1 (28 000) 1
1 (15 000) 5
5 (17 200) 1 (110 000) 1 (15 000) 1
1 (213 000) 1 (28 000) 5
5 (122 200) 1 (221 000)
5 11 200
Logo, o saldo de Sérgio no dia 6 de junho
era de 1R$ 1 200,00.
12.
a) (127) 1 (113) 1 (228) 5
5 (140) 1 (228) 5 112

275
2170 195
2140 230 1125
280 260 130 195
230 250 210 140 155
Editoria de arte
90
b) (250) 1 (230) 1 (212) 5
5 (280) 1 (212) 5 292
c) (190) 1 (275) 1 (247) 5
5 (190) 1 (2122) 5 232
d) (211) 1 (120) 1 (135) 1 (227) 5
5 (211) 1 (227) 1 (120) 1 (135) 5
5 (238) 1 (155) 5 117
e) (132) 1 (268) 1 (222) 1 (148) 5
5 (132) 1 (148) 1 (268) 1 (222) 5
5 (180) 1 (290) 5 210
f) (199) 1 (2100) 1 (2100) 1 (198) 1 (210) 5
5 (199) 1 (198) 1 (2100) 1 (2100) 1
1 (210) 5
5 (1197) 1 (2210) 5 213
g) (273) 1 (222) 1 (245) 1 (292) 1 (1250) 5
5 (2232) 1 (1250) 5 118
13. Como a e b são números inteiros opostos,
o resultado da adição de a 1 b é 0, pois
como a 5 2b, temos: (2b) 1 (1b) 5 0.
14. Sim; se a e b são números inteiros
positivos, a soma de a 1 b também será
positiva.
15. Sendo a 5 273, b 5 151 e c 5 217, temos:
a) a 1 b R (273) 1 (151) 5 222
b) a 1 c R (273) 1 (217) 5 290
c) b 1 c R (151) 1 (217) 5 134
d) a 1 b 1 c R (273) 1 (151) 1 (217) 5
5 (290) 1 (151) 5 239
1.
a) (120) 1 (218) 5 20 2 18 5 12
b) (230) 1 (121) 5 230 1 21 5 29
c) (281) 1 (217) 5 281 2 17 5 298
d) (137) 1 (152) 5 37 1 52 5 189
e) (215) 1 (122) 1 (26) 5 215 1 22 2 6 5
5 215 2 6 1 22 5 221 1 22 5 11
2. De acordo com a figura, vem:
A R (27) 1 (210) 5 27 2 10 5 217
B R (217) 1 (19) 5 217 1 9 5 28
C R (28) 1 (120) 5 28 1 20 5 112
3.
a) 7 1 17 5 124 g) 31 1 14 5 145
b) 28 2 2 5 210 h) 21 1 30 5 129
c) 29 1 14 5 15 i) 40 2 63 5 223
d) 24 2 4 5 28 j) 91 2 57 5 134
e) 19 2 23 5 24 l) 290 1 10 5 280
f) 240 2 11 5 251 m) 2100 1 104 5 14
4. A soma dos dois números inferiores é
igual ao número acima; com essa regra
preenchemos as linhas que faltam:
5.
a) 7 1 20 2 4 5 27 2 4 5 23
b) 217 1 14 1 3 5 217 1 17 5 0
c) 27 2 16 2 10 5 27 2 26 5 11
d) 225 2 21 2 40 5 246 2 40 5 286
e) 35 1 18 1 62 5 53 1 62 5 1115
f) 275 1 70 1 50 2 61 5 275 2 61 1 70 1
1 50 5 2136 1 120 5 216
g) 84 2 79 2 81 1 86 5 84 1 86 2 79 2 81 5
5 170 2 160 5 110
h) 264 2 96 2 77 1 200 5 2237 1 200 5
5 237
i) 292 1 17 1 34 1 20 5 292 1 71 5 221
j) 76 1 92 2 104 2 101 1 94 5 76 1 92 1
1 94 2 104 2 101 5 1262 2 205 5 157
l) 17 2 40 2 30 2 60 1 100 5 17 1 100 2
2 40 2 30 2 60 5 117 2 130 5 213
m) 81 1 19 2 95 2 105 1 260 2 110 5 81 1
1 19 1 260 2 95 2 105 2 110 5
5 1360 2 310 5 150
9 – Subtração de números inteiros
1. Para sabermos quantos anos Alexandre
viveu, basta subtrair o ano de nascimento
do ano de sua morte:

91
(2323) 2 (2356) 5 2323 1 356 5 33
Logo, Alexandre viveu 33 anos.
2. Para sabermos quantos anos Pitágoras
viveu, basta subtrair o ano de nascimento
do ano de sua morte:
(2496) 2 (2570) 5 2496 1 570 5 74
Logo, Pitágoras viveu 74 anos.
3.
a) A diferença entre os pontos das duplas
B e A é dada por:
(1230) 2 (2150) 5
5 1230 1 150 5
5 1380
Logo, a dupla B fez 380 pontos a mais
que a dupla A.
b)
• Rodada 2 R (1300) 2 (260) 5 300 1
1 60 5 360
A dupla A ganhou a rodada 2 com
360 pontos a mais.
• Rodada 3 R (1280) 2 (2120) 5 1280 1
1 120 5 400
A dupla B ganhou a rodada 3 com
400 pontos a mais.
• Rodada 4 R (1220) 2 (1150) 5 1220 2
2150 5 70
A dupla A ganhou a rodada 4 com 70
pontos a mais.
c) A expressão que representa o resultado
das rodadas da equipe A é:
(2150) 1 (1300) 1 (2120) 1 (1220)
d) A expressão que representa o resultado
das rodadas da equipe B é:
230 1 (260) 1 (1280) 1 (1150)
4. A diferença entre as temperaturas é dada
por:
(125) 2 (29) 5 125 1 9 5 34
Logo, a diferença é de 134 graus.
5.
a) 0 2 (217) 5 0 1 17 5 117
b) (29) 2 (116) 5 29 2 16 5 225
c) (113) 2 (120) 5 113 2 20 5 27
d) 0 2 (118) 5 0 2 18 5 218
e) (21) 2 (219) 5 21 1 19 5 118
f) (120) 2 (19) 5 120 2 9 5 111
g) (24) 2 (117) 5 24 2 17 5 221
h) (140) 2 (180) 5 140 2 80 5 240
i) (111) 2 (262) 5 111 1 62 5 173
j) (272) 2 (281) 5 272 1 81 5 19
1.
a) (130) 2 (210) 5 130 1 10 5 140 R 40
graus.
b) (143) 2 (137) 5 143 2 37 5 16 R 6
graus.
c) (143) 2 (212) 5 143 1 12 5 155 R 55
graus.
2.
a) A menor temperatura mundial ocorreu
na Antártida, na estação Vostok.
A temperatura foi de 289 8C.
(212) 2 (289) 5 212 1 89 5 177
Logo, a diferença das temperaturas
mínimas de Xanxerê e Vostok é de
77 graus.
b) (17) 2 (249) 5 17 1 49 5 156
Logo, a diferença de temperaturas
ocorridas em Browning, em 1916, foi
de 56 graus.
c) (158) 2 (289) 5 158 1 89 5 1147
Logo, a diferença entre a maior e a
menor temperatura registrada no
mundo foi de 147 graus.
d) Registrando as temperaturas negativas
em ordem crescente, temos:
289 249 212 210
10 – Adição algébrica
1.
a) 2 (19) 5 29
b) 2 (211) 5 111
c) 1 (213) 5 213
d) 1 (121) 5 121
e) 3 2 (22) 5 3 1 2
f) 2 (21 1 10) 5 11 2 10
g) 7 1 (6 2 3) 5 7 1 6 2 3
h) 1 2 (21 1 5) 5 1 1 1 2 5
i) 9 1 (24 2 2) 5 9 2 4 2 2
j) 2(1 1 1 2 4) 5 21 2 1 1 4
2.
a) 27 1 (113) 5 27 1 13 5 16
b) 10 2 (220) 5 10 1 20 5 130
c) 211 2 (26) 5 211 1 6 5 25
d) 32 1 (240) 5 32 2 40 5 28

92
3. Como Lucca considerou os valores
borrados como sendo a média aritmética
dos valores vizinhos, vem:
a) Às 9 horas R [(214) 1 (210)]  2 5
5 [224]  2 5 212
Logo, a temperatura às 9 horas era de
212 8C.
b) Às 11 horas R [(210) 1 (28)]  2 5
5 [218]  2 5 29
Logo, a temperatura às 11 horas era de
29 8C.
4.
a) 6 1 (29 1 1) 5 6 2 9 1 1 5 7 2 9 5 22
b) 8 2 (26 1 10) 5 8 1 6 2 10 5 14 2 10 5
5 14
c) 210 1 (6 2 4) 5 210 1 6 2 4 5 214 1
1 6 5 28
d) 2 1 (2 1 5 2 7) 5 2 1 2 1 5 2 7 5 9 2 7 5
5 12
e) 25 1 (2 2 4) 2 (7 2 1) 5 25 1 2 2 4 2
2 7 1 1 5 216 1 3 5 213
f) (25 1 3) 2 (5 2 9) 1 (8 2 1) 2 11 5 25 1
1 3 2 5 1 9 1 8 2 1 2 11 5 222 1 20 5
5 22
5. x 5 1 2 [4 1 (4 2 2 2 5) 2 (27 1 3)]
x 5 1 2 [4 1 4 2 2 2 5 1 7 2 3]
x 5 1 2 4 2 4 1 2 1 5 2 7 1 3
x 5 111 2 15
x 5 24
y 5 2 2 [7 2 (21 2 3 1 6) 2 8]
y 5 2 2 [7 1 1 1 3 2 6 2 8]
y 5 2 2 7 2 1 2 3 1 6 1 8
y 5 16 2 11
y 5 15
Como x 5 24 e y 5 15, temos x y.
6.
a) 30 1 [216 2 (27 1 10)] 5
5 30 1 [216 1 7 2 10] 5
5 30 2 16 1 7 2 10 5
5 37 2 26 5
5 111
b) 210 2 [11 1 (210 2 6) 1 1] 5
5 210 2 [11 2 10 2 6 1 1] 5
5 210 2 11 1 10 1 6 2 1 5
5 222 1 16 5
5 26
c) 18 2 (14 1 15) 2 [13 2 (16 2 21)] 5
5 18 2 14 2 15 2 [13 2 16 1 21] 5
5 18 2 14 2 15 2 13 1 16 2 21 5
5 134 2 63 5
5 229
d) 2(222) 2 [29 1 (27 2 23 2 26) 2 28] 5
5 122 2 [29 1 27 2 23 2 26 2 28] 5
5 122 2 29 2 27 1 23 1 26 1 28 5
5 199 2 56 5
5 143
e) 9 2 (210) 2 [221 2 (213 2 13 1 25)] 2
2 (218) 5
5 9 1 10 2 [221 1 13 1 13 2 25] 1 18 5
5 9 1 10 1 21 2 13 2 13 1 25 1 18 5
5 183 2 26 5
5 157
f) 11 1 [217 2 (222 1 16) 1 (229)] 2
2 (246 1 54) 5
5 11 1 [217 1 22 2 16 2 29] 1 46 2 54 5
5 11 2 17 1 22 2 16 2 29 1 46 2 54 5
5 179 2 116 5
5 237
7. Calculando o saldo de figurinhas para
cada dia da semana que João jogou, vem:
• 2a-feira R 217 1 43 1 14 1 23 2 45 5
5 262 1 80 5 118
• 3a-feira R 24 2 7 2 8 2 10 2 4 1 31 2
2 19 5 155 2 48 5 17
• 4a-feira R 19 2 21 1 36 2 100 2 35 1
1 100 5 1155 2 156 5 21
• 5a-feira R 223 1 24 2 25 1 26 2 27 1
1 28 5 275 1 78 5 13
• 6a-feira R 210 1 60 2 126 1 63 2 208 1
1 117 5 1450 2 334 5 1116
• Sábado R 299 1 85 2 121 2 310 1 420 1
1 115 5 2530 1 620 5 190
a) João ganhou mais figurinhas na 6a-feira.
b) João se saiu pior na 4a-feira.
c) De acordo com os saldos de figurinhas,
em cada dia da semana, vem:
118 1 7 2 1 1 3 1 116 1 90 5 234 2 1 5
5 1233
Logo, a quantidade de figurinhas de
João aumentou em 233.
Resposta em aberto.

212 000
2150 180
115 210 28
23 25 12 24
Editoria de arte
93
11 – Multiplicação de números
inteiros
a) (18) ? (29) 5 272
b) (26) ? (25) 5 130
c) (17) ? (14) 5 128
d) (19) ? (17) 5 163
e) (28) ? (16) 5 248
f) (15) ? (211) 5 255
g) 0 ? (113) 5 0
h) (26) ? (218) 5 1108
i) (13) ? (121) 5 163
j) (28) ? 0 5 0
l) (211) ? (221) 5 1231
m) (220) ? (117) 5 2340
n) (117) ? (117) 5 1289
o) (25) ? (232) 5 1160
2.
Segredo: a multiplicação dos dois
números inferiores é igual ao número
acima.
7.
a) x ? (216) 5 216 R x 5 11, pois 11 é o
elemento neutro da multiplicação de
números inteiros.
b) x ? (25) 5 (25) ? (19) R x 5 19, pois
pela propriedade comutativa, temos:
(19) ? (25) 5 (25) ? (19).
c) x ? (28) 5 0 R x 5 0, pois a
multiplicação de um número inteiro
por zero é sempre zero.
d) x ? (11) 5 111 R x 5 111, pois todo
número inteiro multiplicado por 11
resulta no próprio número.
8.
a) x ? (12) 5 26
Aplicando a operação inversa da
multiplicação, vem:
x 5 26  (12) R x 5 23
Logo, x deve ser substituído por 23.
b) (25) ? x 5 150
x 5 150  (25) R x 5 210
c) x ? (25) 5 210
x 5 210  (25) R x 5 12
Esses itens poderiam também ser
resolvidos da seguinte forma:
a) x ? (12) 5 26
x ? (12) 5 (12) ? (23)
Logo, x 5 23.
b) (25) ? x 5 150
(25) ? x 5 (25) ? (210)
Logo, x 5 210.
c) x ? (25) 5 210
x ? (25) 5 (25) ? (12)
Logo, x 5 12.
9.
a) O produto de dois números inteiros é
positivo quando esses dois números
possuem sinais iguais. Logo, em
8 quadradinhos, o resultado será
positivo.
b) O produto de dois números inteiros é
negativo quando esses dois números
possuem sinais diferentes. Logo, em
3.
a) (27) ? (111) ? (22) 5 (277) ? (22) 5 1154
b) (29) ? (25) ? (23) 5 (145) ? (23) 5 2135
c) (212) ? (26) ? (13) 5 (172) ? (13) 5 1216
d) (29) ? (29) ? (24) ? (21) 5 (181) ? (14) 5
5 1324
e) (28) ? (110) ? (17) ? (12) 5 (280) ? (114) 5
5 21 120
f) (28) ? (16) ? 0 ? (211) 5 (248) ? 0 5 0
5. 27 ? (16 2 8) 5 27 ? (22) 5 114 ou
27 ? (16 2 8) 5 27 ? (16) 1 (27) ? (28) 5
242 1 56 5 114
6. 25 ? (28 1 5) 5 25 ? (28) 1 (25) ? (15) 5
5 140 2 25 5 15

94
8 quadradinhos, o resultado será
negativo.
a) 81 1 (220) ? (14) 5
5 81 1 (280) 5
5 81 2 80 5
5 11
b) (24) ? (27) 2 30 5
5 (128) 2 30 5
5 128 2 30 5
5 22
c) 223 2 (26) ? (13) 5
5 223 2 (218) 5
5 223 1 18 5
5 25
d) (29) ? (16) 2 (12) ? (227) 5
5 (254) 2 (254) 5
5 254 1 54 5
5 0
e) 19 2 (24) ? (15) 5
5 19 2 (220) 5
5 19 1 20 5
5 139
f) 7 ? (23) 2 9 ? (26) 1 11 ? (22) 5
5 (221) 2 (254) 1 (222) 5
5 221 1 54 2 22 5
5 243 1 54 5
5 111
g) (15) ? (111) 2 37 2 (22) ? (114) 5
5 (155) 2 37 2 (228) 5
5 155 2 37 1 28 5
5 183 2 27 5
5 146
h) 18 2 3 ? (27) 1 9 ? (24) 2 20 5
5 18 2 (221) 1 (236) 2 20 5
5 18 1 21 2 36 2 20 5
5 139 2 56 5
5 217
2.
a) 2x 1 5y, para x 5 17 e y 5 22:
2 ? (17) 1 5 ? (22) 5
5 (114) 1 (210) 5
5 14
b) xy 1 2x, para x 5 26 e y 5 23:
26 ? (23) 1 2 ? (26) 5
5 2(218) 1 (212) 5
5 118 2 12 5
5 16
c) 3a 2 7b, para a 5 18 e b 5 27:
3 ? (18) 2 7 ? (27) 5
5 (124) 2 (249) 5
5 124 1 49 5
5 173
d) 2a 1 5b 2 10, para a 5 110 e b 5 22:
2 ? (110) 1 5 ? (22) 2 10 5
5 (120) 1 (210) 2 10 5
5 120 2 20 5
5 0
e) 3a 2 5b 1 4c, para a 5 21, b 5 21 e c 5 21:
3 ? (21) 2 5 ? (21) 1 4 ? (21) 5
5 (23) 2 (25) 1 (24) 5
5 23 1 5 2 4 5
5 27 1 5 5
5 22
f) 10 2 a 1 ab 2 2b, para a 5 21 e b 5 13:
10 2 (21) 1 (21) ? (13) 2 2 ? (13) 5
5 10 2 (21) 1 (23) 2 (16) 5
5 10 1 1 2 3 2 6 5
5 11 2 9 5
5 12
Desafios!, página 69.
1. As possíveis multiplicações de dois
números inteiros em que o resultado dá
120 são:
(11) ? (120); (21) ? (220); (12) ? (110);
(22) ? (210); (14) ? (15); (24) ? (25)
Para encontrar esses fatores, basta fatorar
o número 20:
20 2
10 2
5 5
1 22 ? 5

95
2. As possibilidades para que o produto de
dois números inteiros seja 16 são:
(11) ? (16); (21) ? (26); (12) ? (13); (22) ? (23).
Como a soma deve ser 25, os dois números
inteiros procurados são: 22 e 23.
As possibilidades para que o produto de
dois números inteiros seja 210 são:
(21) ? (110); (11) ? (210); (22) ? (15); (12) ?
?(25).
Como a soma deve ser 13, os dois números
inteiros procurados são: 15 e 22.
O gasto de Beto com o material escolar foi:
1 ? 2 1 5 ? 6 1 1 ? 5 1 1 ? 7 1 4 ? 1 5 2 1 30 1
1 5 1 7 1 4 5 48 R R$ 48,00
Como Beto levou R$ 50,00, ele conseguirá
comprar tudo o que precisa, e ainda
sobrarão 2 reais.
12 – Divisão de números inteiros
1.
a) Como o dividendo e o divisor têm
sinais diferentes, o resultado da divisão
será negativo.
b) Zero dividido por qualquer número
inteiro negativo será sempre zero.
c) Como o dividendo e o divisor têm o
mesmo sinal, o resultado da divisão
será positivo.
d) A divisão de zero por qualquer número
inteiro estritamente positivo será
sempre zero.
2.
a) (19)  (29) 5 21 R 21  Z; logo, essa
divisão pode ser efetuada no conjunto Z.
b) (22)  (11) 5 22 R 22  Z; logo, essa
divisão pode ser efetuada no conjunto Z.
c) (23)  (22) 5
3
2 R
3
2  Z; logo, essa
divisão não pode ser efetuada no
conjunto Z (o resultado não é inteiro).
d) (111)  (15) 5
11
5 R
11
5  Z; logo,
essa divisão não pode ser efetuada no
conjunto Z (o resultado não é inteiro).
e) 0  (15) 5 0 R 0  Z; logo, essa divisão
pode ser efetuada no conjunto Z.
f) (17)  0 R A divisão não é definida
para o divisor zero, portanto não pode
ser efetuada em Z.
3. Na divisão x  (28) 5 12, x 5 216, pois
(28) ? (12) 5 16.
4. Sim; Todo número dividido por ele mesmo
dá 1. Se o quociente for 21, é porque os
números têm mesmo módulo e sinais
contrários, ou seja, são opostos.
7.
a) (29)  (13) 5 23
b) (211)  (211) 5 11
c) (121)  (17) 5 13
d) (136)  (24) 5 29
e) 0  (120) 5 0
f) (231)  (131) 5 21
g) (145)  (23) 5 215
h) (152)  (12) 5 126
i) (265)  (25) 5 113
j) (290)  (16) 5 215
l) (164)  (116) 5 14
m) (239)  (213) 5 13
n) (196)  (224) 5 24
o) (2200)  (125) 5 28
p) (163)  (121) 5 13
q) (181)  (227) 5 23
8. Resolvendo as divisões do quadro, vem:
(2120)  (210) 5 112 (2200)  (250) 5 14
(260)  (112) 5 25 (196)  (216) 5 26
(180)  (28) 5 210 (148)  (124) 5 12
(1150)  (115) 5 110 (2121)  (111) 5 211
Somando os resultados obtidos, temos:
(112) 1 (25) 1 (210) 1 (110) 1 (14) 1 (26) 1
1 (12) 1 (211) 5
5 112 2 5 2 10 1 10 1 4 2 6 1 2 2 11 5
5 128 2 32 5 24
Logo, a soma dos resultados dessas
divisões dá 24.

96
a) 31 1 (240)  (12) 5
5 31 1 (220) 5
5 31 2 20 5
5 111
b) 210 2 20  (14) 5
5 210 2 (15) 5
5 210 2 5 5
5 215
c) (130)  (26) 1 (218)  (13) 5
5 (25) 1 (26) 5
5 25 2 6 5
5 211
d) 7  (27) 1 2 ? (26) 1 11 5
5 (21) 1 (212) 1 11 5
5 21 2 12 1 11 5
5 213 1 11 5
5 22
e) (236)  (24) 1 3 ? (23) 5
5 (19) 1 (29) 5
5 1 9 2 9 5
5 0
f) 35 2 6 ? (16) 1 (154)  (26) 5
5 35 2 (136) 1 (29) 5
5 35 2 36 2 9 5
5 35 2 45 5
5 210
g) 2 1 (275)  (25) 2 4 ? (21) 5
5 2 1 (115) 2 (24) 5
5 2 1 15 1 4 5
5 17 1 4 5
5 121
inteiros
1.
a) (11)2 5 (11) ? (11) 5 11
b (21)2 5 (21) ? (21) 5 11
c) (11)4 5 (11) ? (11) ? (11) ? (11) 5 11
d) (21)4 5 (21) ? (21) ? (21) ? (21) 5 11
e) (11)6 5 (11) ? (11) ? (11) ? (11) ? (11) ?
? (11) 5 11
f) (21)6 5 (21) ? (21) ? (21) ? (21) ? (21) ?
? (21) 5 11
g) (11)3 5 (11) ? (11) ? (11) 5 11
h) (21)3 5 (21) ? (21) ? (21) 5 21
i) (11)5 5 (11) ? (11) ? (11) ? (11) ? (11) 5
5 11
j) (21)5 5 (21) ? (21) ? (21) ? (21) ? (21) 5
5 21
k) (11)7 5 (11) ? (11) ? (11) ? (11) ? (11) ?
? (11) ? (11) 5 11
l) (21)7 5 (21) ? (21) ? (21) ? (21) ? (21) ?
? (21) ? (21) 5 21
2.
a) Podemos notar que, quando o expoente
é um número par, a potência é sempre
um número inteiro positivo.
b) Podemos notar que, quando o expoente
é um número ímpar, o sinal do resultado
vai depender do sinal da base.
1. Como x é um número inteiro negativo e
o expoente é par, a potência será sempre
um número inteiro positivo. Logo, x2 será
um número inteiro positivo.
2. Como a é um número inteiro negativo e o
expoente é ímpar, a potência tem sempre
o mesmo sinal da base. Logo, a3 será um
número inteiro negativo.
3.
a) (217)2 5 (217) ? (217) 5 1289
b) (115)3 5 (115) ? (115) ? (115) 5 13 375
c) (140)2 5 (140) ? (140) 5 11 600
d) (230)3 5 (230) ? (230) ? (230) 5 227 000
e) (25)4 5 (25) ? (25) ? (25) ? (25) 5 1625
f) (13)5 5 (13) ? (13) ? (13) ? (13) ? (13) 5
5 1243
g) (15)4 5 (15) ? (15) ? (15) ? (15) 5 1625

97
4.
a) (19)2 5 (19) ? (19) 5 181
b) (29)2 5 (29) ? (29) 5 181
c) (19)3 5 (19) ? (19) ? (19) 5 1729
d) (29)3 5 (29) ? (29) ? (29) 5 2729
e) (12)5 5 (12) ? (12) ? (12) ? (12) ? (12) 5
5 132
f) (22)5 5 (22) ? (22) ? (22) ? (22) ? (22) 5
5 232
g) (21)10 5 11 R Sendo 1 o módulo da
base, os produtos sempre serão 1.
Como o expoente é par, a potência é
positiva.
h) (23)4 5 (23) ? (23) ? (23) ? (23) 5 181
i) (27)3 5 (27) ? (27) ? (27) 5 2343
j) (2100)0 5 11
l) (21)101 5 21R Sendo 1 o módulo da
Como o expoente é ímpar, a potência
tem o sinal da base, que nesse caso é
negativo.
m) (225)2 5 (225) ? (225) 5 1625
n) (110)6 5 (110) ? (110) ? (110) ? (110) ?
? (110) ? (110) 5 11 000 000
o) (21)9 5 (21) ? (21) ? (21) ? (21) ? (21) ?
? (21) ? (21) ? (21) ? (21) 5 21
p) (21)200 5 11R Sendo 1 o módulo da
Como o expoente é par, a potência é
positiva.
q) (11)99 5 11R Sendo 1 o módulo da
Como o expoente é ímpar, a potência
tem o sinal da base, que nesse caso é
positivo.
5. Para a 5 (21)100 5 11 e b 5 (21)101 5 21,
temos:
a) a 1 b 5 (11) 1 (21) 5 0
b) a 2 b 5 (11) 2 (21) 5 11 1 1 5 12
6.
a) (28)5 ? (
28) ? (28)4 5 (28)5 1 1 1 4 5 (28)10
2 b) (12)6 5 (12) 6 ?
2 5 (12) 12 c) (210)9  (210)6 5 (210)9 2 6 5 (210)3
d) (19) ? (19)11 ? (19)8 5 (19)1 1 11 1 8 5 (19)20
e) (213)20  (213)14 5 (213)20 2 14 5 (213)6
f) (17)4 (17) (17) 3 4 3 12 

5 5 ?
g) (110)5 ? (110) ? (110)8 5 (110)5 1 1 1 8 5
5 (110)14
h) (120)7  (120)6 5 (120)7 2 6 5 (120)1
7.
a) (24)7 (24)10 (24) (24)8 2
? ? 5 



;
5 (2 ) (2 ) 5 1 1 4 4 7 10 1 16 



;
5 (24)18  (24)16 5
5 (24)18 2 16 5
5 (24)2 5
5 (24) ? (24) 5
5 116
b) (22)6 (22) (22) (22) 2 6 2 



; ? ? 5
5 5 ? (2 ) (2 ) 1 1 2 2 6 2 6 2 1 



;
5 (22)12  (22)9 5
5 (22)12 2 9 5
5 (22)3 5
5 (22) ? (22) ? (22) 5
5 28
a) (29)2 2 (15) ? (116) 5
5 181 2 (180) 5
5 181 2 80 5
5 11
b) (22)4  (116) ? (21)7 5
5 (116)  (116) ? (21) 5
5 (11)  (21) 5
5 21
c) (26)2 2 (27)2 1 130 5
5 136 2 (149) 1 1 5
5 136 2 49 1 1 5
5 137 2 49 5
5 212
d) 52 2 (23)3 1 (24)2 5
5 25 2 (227) 1 (116) 5
5 25 1 27 1 16 5
5 52 1 16 5
5 168

98
e) 4 ? (25)3 1 (220)2 5
5 4 ? (2125) 1 (1400) 5
5 2500 1 400 5
5 2100
f) 112 2 4 ? (25)2 1 100 5
5 121 2 4 ? (125) 1 1 5
5 121 2 100 1 1 5
5 122 2 100 5
5 122
g) 17 2 3 ? (22)2 2 (26)2 ? (21)7 5
5 17 2 3 ? (14) 2 (136) ? (21) 5
5 17 2 12 2 (236) 5
5 17 2 12 1 36 5
5 53 2 12 5
5 141
h) 7 ? (22)2 2 5 ? (22)3 2 102 5
5 7 ? (14) 2 5 ? (28) 2 100 5
5 28 1 40 2 100 5
5 68 2 100 5
5 232
14 – Raiz quadrada exata de
números inteiros
1.
a) 25 55
b) 64 58
c) 281 R Não existe em Z.
d) 1 51
2.
9 R É um número inteiro, pois 9 53.
37 R Não é um número inteiro, pois 62 5
5 36 e 72 5 49, e entre 6 e 7 não há
números inteiros.
80 R Não é um número inteiro, pois
82 5 64 e 92 5 81, e entre 8 e 9 não há
números inteiros.
Logo, 37 e 80 não representam
números inteiros.
3.
a) 36 56
b) 2 64 52(18)528
c) 100 510
d) 2 49 52(17)527
4.
a) 400 520, pois 202 5 400.
b) 2 900 52(130)5230, pois 302 5 900.
c) 2 2500 52(150)5250, pois 502 5 2 500.
d) 144 512, pois 122 5 144.
5. p512(2 100 )
p 5 1 2 (210)
p 5 1 1 10
p 5 111
Logo, p 5 111.
6. x5 81 42252 ;( )
x 5 9  (16 2 25)
x 5 9  (29)
x 5 21
Logo, x 5 21.
7. Não, pois não existe em Z raiz quadrada
de número negativo.
15 – Expressões numéricas
a) (27 2 4) ? (29 1 2) 2 (272 1 2)  (25 2 5) 1
1 (29 2 4 1 6) 5
5 (211) ? (27) 2 (270)  (210) 1 (27) 5
5 177 2 (17) 2 7 5
5 177 2 7 2 7 5
5 177 2 14 5
5 163
b) ( ) ( ) ( ) ( ) ( ) ( 2 2 2 1 2 2 2 2 2 1 1 2 2 2 9 3 1 7 10 4 3 5 4 36 1 3 ; ; ? 
( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 2 2 2 2 2 1 1 2 2 2 9 3 1 7 10 4 3 5 4 36 1 3 ; ; ? 

5
5 ? 5 ( ) ( ) ( ) ( ) ( ) ( ) 2 1 2 2 2 2 1 2 2 12 6 10 7 1 36 4 ; ; 

5 5 2 2 2 1 1 1 2 10 7 9 ( ) ( ) 

5 5 2 2 2 1 2 10 7 9 

5 22 2 10 1 7 2 9 5

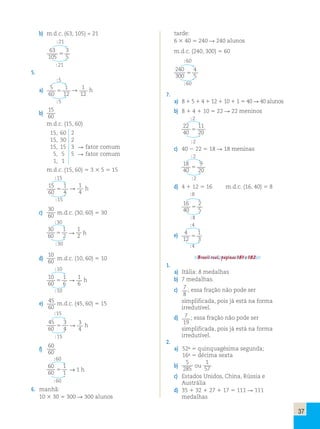
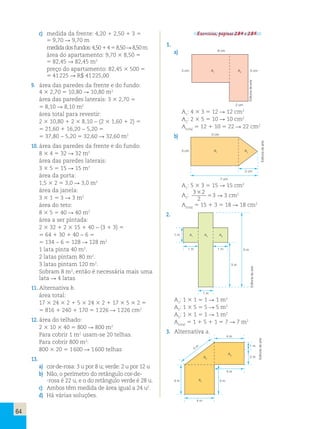
a idade biológica menor que a cronológica
0
25
210
215
220
225
230
25
26
212
213 215
216
221
223
227
229
235
30 anos 40 anos 50 anos 60 anos 70 anos
Homens
Mulheres
Editoria de arte
99
5 221 1 7 5
5 214
c) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 2 2 1 2 2 2 1 1 4 10 16 8 2 7 1 5 ? ? 5 ; 

) ( ) ( ) ( ) 2 1 2 2 2 1 8 2 7 1 5 ? 5 ; 
5 ? 5 ( ) ( ) ( ) 2 1 22 2 2 2 5 6 4 7 5 

5 5 2 22 2 1 30 4 7 5 

5 230 1 4 1 7 2 5 5
5 235 1 11 5
5 224
d) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 2 1 2 2 2 2 50 5 5 20 42 7 35 1 16 ; ; ; 

5
1 ( 2 42 ) ; ( 1 7 ) 2 ( 2 35 
) ; ( 2 1 2 16 ) 
5
5 5 ( ) ( ) ( ) ( ) ( ) 2 2 2 1 2 2 2 2 2 50 10 20 6 35 1 4 ; ; 

5 5 5 20 6 35 5 2 2 2 2 2 ( ) ( ) ; 

5 5 5 20 6 7 2 2 2 1 ( ) 

5 5 2 [20 2 6 2 7] 5
5 5 2 20 1 6 1 7 5
5 18 2 20 5
5 22
e) (26)2  (212) 2 (23)3 1 (22)5  (24)2 2 50 5
5 36  (212) 2 (227) 1 (232)  (116) 2 1 5
5 23 1 27 1 (22) 2 1 5
5 23 1 27 2 2 2 1 5
5 26 1 27 5
5 121
f) (2223)2 (225)1 302(2101 36 )2 (22)3252 ; ; 

5
5(25)2 (225)1 302(21016)2 (28)225 5 ; ; 
525 ; ( 2 25 ) 1 30 2  
( 2 4 ) 2 ; 
( 2 8 ) 2 25 5 5 5 2 1 2 1 2 2 1 30 16 8 25 ( ) ( ) ; 

5 5 2 1 2 2 2 1 30 2 25 ( ) 

5 5 2 1 1 2 1 30 2 25 

5 21 1 30 1 2 2 25 5
5 226 1 32 5
5 16
1.
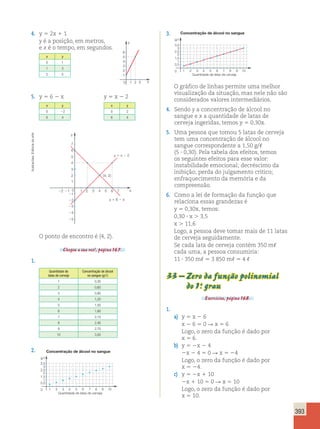
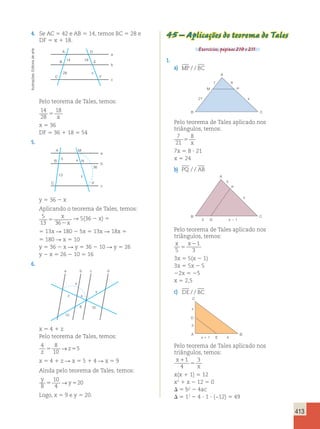
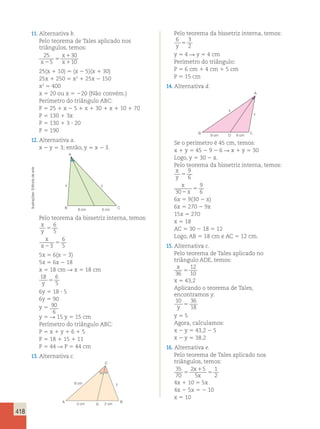
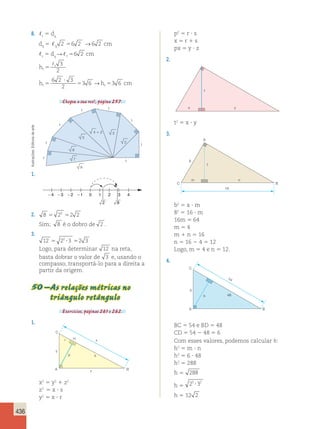
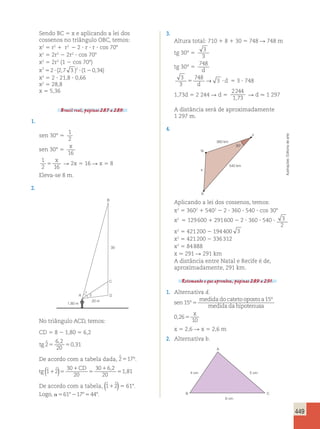
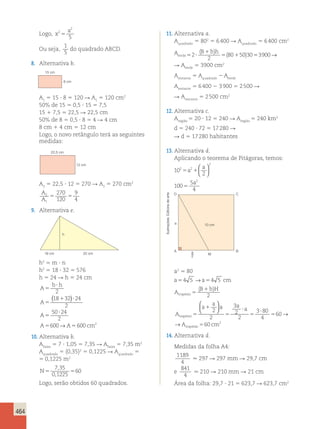
a) A mulher, pois ela consegue abater
mais anos da idade cronológica.
b) Como para um homem de 50 anos com
um estilo de vida saudável podemos
abater 15 anos, um homem de 50 anos
pode aparentar 35 anos.
c) O gráfico ficaria da seguinte forma:
2.
a) A fábrica teve lucro nos meses de
maio, julho, agosto, setembro, outubro,
novembro e dezembro. A fábrica teve
prejuízo nos meses de janeiro, fevereiro
e março.
b) O lucro foi maior em novembro.
c) Os meses que apresentam lucro zero
são os meses de abril e junho.
d) Lucro: 110 1 15 1 26 1 32 1 15 1 50 1
1 30 5 1178
Como o lucro da fábrica é dado em
milhares de reais, o lucro total nos
meses de lucro foi de R$ 178 000,00.
Prejuízo: 220 2 10 2 5 5 235
O valor absoluto do prejuízo total em
milhares de reais, foi de R$ 35 000,00.
Portanto, o lucro foi maior em
R$ 143 000,00.
3.
a) No eixo horizontal, a grandeza
representada é o tempo.
No eixo vertical, a grandeza
representada é a temperatura.
b) • A temperatura média é maior em
julho.
• A temperatura média é menor em
janeiro e fevereiro.
c) Em dezembro, a temperatura média
era de 0 8C e, em fevereiro, a
temperatura média era de 23 8C; logo,
a temperatura em dezembro é maior
que a temperatura em fevereiro, pois
0 8C 23 8C.

100
d) • De abril para maio, a temperatura
variou em 16 8C, pois
110 8C 2 4 8C 5 16 8C. Portanto,
houve um aumento de 6 8C nesse
período.
• De dezembro para janeiro, a
temperatura variou em 23 8C, pois
23 8C 2 0 8C 5 23 8C. Portanto,
houve uma queda de 3 8C.
e) A média da temperatura no
1o semestre é dada pela soma das
temperaturas médias de cada mês
dividido por 6:
( ) ( ) ( ) ( ) ( ) ( ) 2 1 2 1 2 1 1 1 1 1 1 3 3 1 4 10 15 6 

; 5
523232114110115 65 

;
5 5 2 1 7 29 6 

;
5 22  6 . 3,6 R .3,6 8C
Logo, a média da temperatura no
1o semestre foi de aproximadamente 3,6 8C.
• A média de temperatura no
2o semestre é dada por:
( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 1 1 1 1 1 18 17 12 7 3 0 6 

; 5
5 5 18 17 12 7 3 0 6 1 1 1 1 1 

;
5 57  6 5 9,5 R 9,5 8C
Logo, a média da temperatura no
2o semestre foi de 9,5 8C.
1. Alternativa b.
(23) 2 (21) 5 23 1 1 5 22
Logo, o simétrico do número obtido é 12.
2. Alternativa c.
A variação de temperatura é dada pela
diferença entre a temperatura final e a
inicial:
(22 8C) 2 (14 8C) 5 22 8C 2 4 8C 5 26 8C
Logo, a temperatura baixou 6 graus nesse
período.
3. Alternativa a.
(21)2 5 11 (I)
(21)3 5 21 (II)
Logo, a soma de (I) e (II) será:
11 2 1 5 0
4. Alternativa e.
Os números inteiros menores que 24 estão
à sua esquerda.
Daí vem:
24 27 210 212
Logo, dentre a sequência de números
apresentada, há 3 números menores que 24.
5. Alternativa b.
Primeiro, verificamos os resultados para as
potências apresentadas:
(13)5 5 1243 242 5 216 (21)10 5 11
(27)2 5 149 (22)3 5 28
Logo, há duas potências que representam
números inteiros negativos.
6. Alternativa c.
I) 224 5 (22)4 R Falsa, pois 224 5 216 e
(22)4 5 116.
II) 220 5 (22)0 R Falsa, pois 220 5 21 e
(22)0 5 11.
III) 223 5 (22)3 R Verdadeira, pois
223 5 28 e (22)3 5 28.
IV) (12)6 5 (22)6 R Verdadeira, pois
(12)6 5 132 e (22)6 5 132.
Logo, há 2 sentenças verdadeiras.
7. Alternativa c.
De acordo com os saldos do quadro, vem:
12 400 1 850 2 680 1 450 2 1 720 2 750 5
5 3 700 2 1 750 5
5 1550 R Crédito de R$ 550,00.
8. Alternativa b.
De acordo com o extrato bancário de
Roberto, vem:
1236 2 51 2 400 1 1 320 2 92 2 813 2 45 2
2 184 2 90 1 352 2 150 2 46 2 120 5
5 11 908 2 1 991 5 283
Logo, o saldo da conta de Roberto no dia
10/8 ficou negativo em 83 reais.
9. Alternativa b.
De acordo com o enunciado, podemos
escrever:
(210)2 ? x 5 2500
100 ? x 5 2500
100 ? x 5 25 ? 100
x 5 25
10. Alternativa d.
a3 2 3 ? a2 ? x2, para a 5 10 e x 5 2, temos:
(10)3 2 3 ? (10)2 ? (2)2 5

101
5 1 000 2 3 ? 100 ? 4 5
5 1 000 2 1 200 5
5 2200
11. Alternativa a.
(23)2 291(23)3 (23)2 ? 5 

;
5 ? 5 9 9 27 9 2 1 2 ( ) 

;
5 ? 5 9 9 27 9 2 2 

;
5 ? 5 9 36 9 2

;
5 2324  9 5
5 236
12. Alternativa d.
(210)3 2 9 ? (210)2 ? (22)2 5
5 21 000 2 3 ? (100) ? (4) 5
5 21 000 2 3 ? (400) 5
5 21 000 2 1 200 5
5 2 2 200
Logo, a metade do valor da expressão é:
22 200  2 5 21 100
13. Alternativa e.
A 5 (22)3 2 (28)  (22)
A 5 28 2 (14)
A 5 28 2 4
A 5 212
B5(22)? (21)? (11)? (12)? (21)? (12)?    (22)
B5 (12) ? (12) ? (22) ? (22)  
B5 (14) ? (14) 
B5 116
Logo, A 1 B 5 212 1 16 5 14.
14. Alternativa b.
(212)2  (27 2 11) 2 (24 1 2 2 1) ? (23)2 1
1 (22)4 ? (1 2 2)3 5
5 (1144)  (218) 2 (25 1 2) ? (19) 1 (116) ?
? (21)3 5
5 28 2 (23) ? (19) 1 (116) ? (21) 5
5 28 2 (227) 1 (216) 5
5 28 1 27 2 16 5
5 224 1 27 5
5 13
15. Alternativa a.
x 5 2(23)3 2 (22)3
x 5 2(227) 2 (26)
x 5 27 2 (64)
x 5 27 2 64
x 5 237
y 5 (22)3 2 (23)2 2 (25)0 1 (22)4
y 5 28 2 (19) 2 (11) 1 (116)
y 5 28 2 9 2 1 1 16
y 5 218 1 16
y 5 22
Logo, x ? y 5 (237) ? (22) 5 174.
16. Alternativa b.
a3 2 (b 2 c)3, para a 5 29, b 5 12 e c 5 110:
( ) ( ) ( ) 2 2 1 2 1 9 2 10 3 3 

5
527292 12210 5 3 

527292 28 5 3 

5 5 2 2 2 729 512 

5 2729 1 512 5
5 2217
17. Alternativa d.
x52 1 3 4 2 6 3 5 22 1 2 1 2 2 2 2 2 1 ( ) ( ) ( ) 

x52 1 1 8 2 22 1 1 2 2 2 1 ( ) ( ) ( ) 
x52 1 1 8 2 22 1 1 2 

x52 8 2 21 2 

x 5 2 2 8 2 2
x 5 28
Logo, o quadrado de x será 64, pois
x2 5 (28)2 5 64.

O conjunto dos números Racionais
Abertura, páginas 84 e 85.
• 1 5
10 1 é maior, menor, igual ou diferente
de 11,5?
São iguais, pois
5
10
50,5, então
1 1 0,5 5 1,5.
212 5
10 é maior, menor, igual ou
diferente de 21,5?
São iguais, pois 2 52
5
10
0,5, então
21 2 0,5 5 21,5.
16 – O conjunto dos números
racionais
1.
a) Racionais inteiros: 1, 2, 11, 12, 21 e
22.
b) Racionais escritos na forma
fracionária: 1
5
10
, 2
5
10
.
c) Racionais escritos na forma decimal:
11,5; 21,5.
2.
a) 25 pertence a Z e Q.
b) 17 pertence a IN, Z e Q.
c) 1
3
8
pertence a Q.
d) 22,7 pertence a Q.
3. Sim; o zero é um número racional, pois
podemos escrevê-lo na forma racional,
como por exemplo:
0
7 ;
0
12 etc.
4.
a) 24  IN g) 16 [ IN
b) 24 [ Z h) 16 [ Z
c) 24 [ Q i) 16 [ Q
d) 1
4
9  IN j) 21,6  IN
e) 1
4
9  Z l) 21,6  Z
f) 1
4
9 [ Q m) 21,6 [ Q
5.
6
12
6
;
a) 1 51
1
6 2
;
9
15
3
;
d) 2 52
3
3 5
;
10
30
10
;
b) 1 51
1
10 3
;
16
40
8
;
e) 1 51
2
8 5
;
5
40
5
;
c) 2 52
1
5 8
;
33
44
11
;
f) 2 52
3
11 4
;
6.
a) 1 2 10 2
0 05
; →
,
1
2
Logo, 2 52
0,5.
b) 13 4 13 4
10 3 25
20
0
; →
,
13
4
Logo, 1 51
3,25.
c) 21 5 21 5
10 4 2
0
; →
,
21
5
Logo,1 51
4,2.
d) 61 10 61 10
10 6 1
0
; →
,
61
10
Logo,2 52
6,1.
e) 1 20 100 20
0 005
; →
,
1
20
Logo, 1 51
0,05.
f) 3 50 300 50
0 006
; →
,
3
50
Logo, 2 52
0,06.
g) 27 100 270 100
700 0 27
0
; →
,
27
100
Logo, 1 51
0,27.
102

103
7
2

 
5
2

 
S D B A
C R
3 2 1 0 1 2 3
h) 39 6 39 6
30 6 5
0
; →
,
39
6
Logo, 2 52
6,5.
i) 23 10 23 10
30 2 3
0
; →
,
23
10
Logo,2 52
2,3.
7.
a) 10 951
9
10
,
15
10
5
;
b) 21 552 52
3
5 2
,
;
25
100
25
;
c) 20 2552 52
1
25 4
,
;
18
10
2
;
d) 11 851 51
9
2 5
,
;
2
1000
2
1
500 2
;
e) 20 ,
00252 52
;
55
10
5
;
f) 15 551 51
11
5 2
,
;
Um litro de água completa apenas
2
3 da
jarra. É fácil perceber que em 1
3
da jarra
cabe 0,5 litro de água. Logo, na jarra toda
cabe 1,5 litro de água.
17 – A reta numérica
1. Respondendo aos itens de acordo com a
reta numérica, vem:
a) 1
4
3
R Ponto R.
b) Ponto B R 2
1
3
.
c) Ponto S R 2
5
3
ou 21
2
3 .
d) 1
2
3
R Ponto A.
e) 13 R Ponto M.
2. Respondendo aos itens de acordo com a
reta numérica, vem:
a) Abscissa do ponto A R 12
b) Abscissa do ponto B R 2
3
2
ou 21
1
2
.
c) Imagem geométrica do número
1 1
3 1
2
ou

 
 R Ponto D.
d) Imagem geométrica do número
2 2
2 1
2
ou

 
 R Ponto E.
e) Abscissa do ponto C R 1
1
2
3. Fazendo a reta numérica e representando
nela os pontos, vem:
1. Alternativa d.
a) 0,40 0,31 R Comparação falsa, pois
0,40 está à direita de 0,31 na reta
numérica; logo, 0,40 0,31.
1
2  R Comparação falsa, pois 1 está
à direita de
b) 1
1
2 na reta numérica; logo,
1
1
2 . .
c) 0 4
4
10
,  R Comparação falsa, pois
4
50,4.
10
d) 2 1,9 R Comparação verdadeira,
pois 2 está à direita de 1,9 na reta
numérica; logo, 2 1,9.
2. Alternativa a.
De acordo com as posições marcadas na
figura, o ponto A está na metade entre os
pontos 0 e 1 km; logo, o ponto A representa
a posição 1
2
kmou 0,5 km.
O ponto B está na metade entre os pontos
1,5 km e 2 km; logo, o ponto B representa a
posição 1 75 1
3
4
, km5 km.
Editoria de arte

104
1.
a) Houve queda em três meses: fevereiro
(20,5%), maio (20,5%) e agosto (21,3%).
b) Houve crescimento em seis meses: janeiro
(1,8%), março (0,4%), abril (0,2%), junho
(2,9%), julho (1,4%) e setembro (1,7%).
c) Junho [2,9 – (20,5) 5 3,4 R 3,4%]
d) Maior: 2,9% R
2 9
100
29
1000
,
5 5 0,029
1 3 2
100
Menor: 21,3% R 2
5
13
1000
,
5 20,013
e) 1,8% R 0,018
20,5% R 20,005
0,4% R 0,004
0,2% R 0,002
1,4% R 0,014
1,7% R 0,017
Ordem decrescente: 2,9% . 1,8% . 1,7% .
.1,4% . 0,4% . 0,2% . 20,5% . 21,3%.
2.
a) Fazendo altitude nova menos a antiga, vem:
Pico da Neblina R 2 993,78 2 3 014,1 5
5 220,32
Logo, a diferença, em módulo, entre as
temperaturas estimadas para o Pico da
Neblina é de 20,32 m.
Pico 31 de Março R 2 972,66 2 2 992,4 5
5 219,74
temperaturas estimadas para o Pico 31
de Março é de 19,74 m.
Pico da Bandeira R 2 891,98 2 2 889,8 5
5 2,18
Logo, a diferença entre as
Bandeira é de 2,18 m.
Pico da Pedra da Mina R
R 2 770,0 2 2 787,0 5 28,39
Pedra da Mina é de 28,39 m.
Pico das Agulhas Negras R
R 2 791,55 2 2 787,0 5 4,55
temperaturas estimadas para o Pico
das Agulhas Negras é de 4,55 m.
Pico do Cristal R 2 769,76 2 2 780,0 5
5 210,24
temperaturas estimadas para o Pico
Cristal é de 10,24 m.
Monte Roraima R 2 734,06 2 2 739,3 5
5 25,24
temperaturas estimadas para o Monte
Roraima é de 5,24 m.
b) 4 picos: Pico da Neblina, Pico 31
de Março, Pico do Cristal e Monte
Roraima.
c) 3 picos: Pico da Bandeira, Pico da Pedra
da Mina e Pico das Agulhas Negras.
d) A maior diferença se deu entre as
medições do Pico da Pedra da Mina;
essa diferença é para mais.
e) Pico da Bandeira.
f) 2 739,3 2 770,0 2 780,0 2 787,0
2 889,8 2 992,4 3 014,1
g) No Amazonas.
18 – Adição algébrica de números
racionais
1.
a) 2 1 52 1 5
2 1
51
3
4
5
6
9
12
10
12
9 10
12
1
12
b) 12,35 2 3 5 20,65
c) 2 1 52 1 5
2 1
51
1
4
3
10
5
20
6
20
5 6
20
1
20
d) 20,48 2 1,6 5 22,08
e) 11,55 1 4,75 5 16,30
f) 2 1 52 1 5
2 1
52
7
6
8
9
21
18
16
18
21 16
18
5
18
g) 17,35 2 10 5 22,65
h) 22,91 1 3,07 5 10,16
2.
a) 2
3
5
6
1
2
4
6
5
6
3
6
4 1 5 2
3
6
6
6
1 2 5 1 2 5 5 51
1
2
3
5
6
1
2
4
6
5
6
3
6
4 1 5 2
3
6
6
6
1 2 5 1 2 5 5 51
1
b) 1 2 0,47 2 1,9 1 0,63 5
5 1,63 2 2,37 5
5 20,74
c) 24,7 1 2 2 1,75 1 1,48 5
5 26,45 1 3,48 5
5 22,97
d) 7
9
5
6
2
3
1
2
14
18
15
18
12
18
9
18
14 15 12 18 2 2 1 5 2 2 1 5
2 2

105
30
25
20
15
10
5
0
26
9
5
11
18
3
17
10
5
Ouro Prata Bronze
Brasil
Colômbia
Argentina
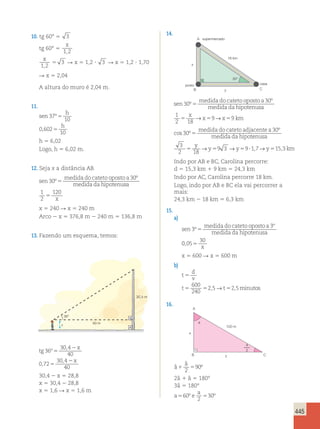
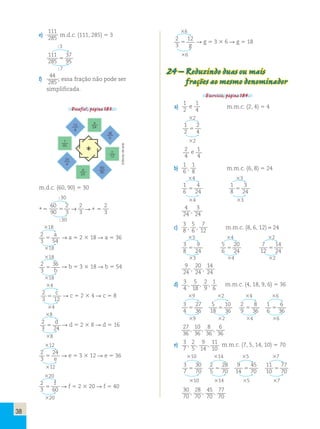
Medalhas conquistadas no Campeonato
Sul-Americano de Atletismo em 2006
15
18
12
18
9
18
14 2 15 2 12 1
9
18 2 2 1 5
5
5
2
2

52 52
23 27
18
4
18
2
2 9

3.
A 5 14,75 1 (17,21) 1 (210,92)
A 5 14,75 1 7,21 2 10,92
A 5 11,96 2 10,92
A 5 11,04
4. Para saber quantos graus a temperatura
aumenta, devemos fazer temperatura
final menos temperatura inicial. Assim,
temos:
a) (123,5) 2 (111,8) 5 123,5 2 11,8 5 11,7
Logo, a temperatura aumentou 11,7
graus.
b) (11,5) 2 (28,5) 5 11,5 1 8,5 5 10
Logo, a temperatura aumentou 10 graus.
5. Para x 5 20,67 e y 5 20,75, temos:
a) x 1 y 5 20,67 1 (20,75) 5 20,67 2
2 0,75 5 21,42
b) x 2 y 5 20,67 2 (20,75) 5 20,67 1
1 0,75 5 10,08
c) 1 2 x 2 y 5 1 2 (20,67) 2 (20,75) 5 1 1
1 0,67 1 0,75 5 12,42
6. A distância do ponto A até o ponto P é
o módulo de 210,75 m; logo, A está a
110,75 m de P.
A distância do ponto P até o ponto B é
113,65 m.
Portanto, a distância do ponto A ao B é dada:
10,75 m 1 13,65 m 5 24,40 m
7. Para a 5 21,75; b 5 13,6 e c 5 24,21,
temos:
a 2 b 1 c 5 21,75 2 (13,6) 1 (24,21) 5
5 21,75 2 3,6 2 4,21 5
5 29,56
8. Como a temperatura caiu 6 graus, temos:
13,5 8C 2 6 8C 5 22,5 8C
Logo, a temperatura registrada às 18 horas
nessa cidade era de 22,5 8C.
9. 2,5 2 [0,2 1 (23,7 1 5) 2 1,4] 5
5 2,5 2 [0,2 2 3,7 1 5 2 1,4] 5
5 2,5 2 0,2 1 3,7 2 5 1 1,4 5
5 17,6 2 5,2 5
5 12,4
Logo, o menor número inteiro maior que
12,4 é 13.
1.
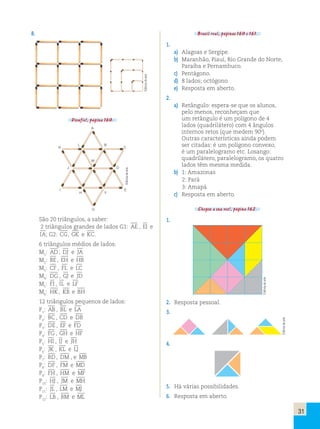
a) De acordo com as informações do
enunciado, podemos organizar a
seguinte tabela:
Campeonato Sul-Americano de Atletismo (2006)
Classifi-cação
País
Medalhas Total de
Medalhas
Total de
Ouro Prata Bronze Pontos
1o Brasil 26 11 17 54 498
2o Colôm-bia
9 18 10 37 317
3o Argen-tina
5 3 5 13 151
b)
2.
a) 53,89 m 2 33,81 m 5 20,08 m
b) 90,57 – 71,42 5 19,15 R 19,15 m R1 915 cm
3.
a) Sim. A diferença entre as marcas dos
dois atletas é 0,06 m
(53,95 m 2 53,89 m); Passaram-se
102 anos (2008 2 1906).
b) Sendo o dardo arremessado do local
onde o dardo da atleta anterior caiu,
a distância entre o local de arremesso
da primeira colocada e o da última
colocada será encontrada somando-se
a distância obtida por cada atleta:
53,95 1 49,88 1 46,74 1 43,81 1 43,75 1
1 41,94 1 41,46 1 41,08 1 40,11 5
5 402,72
Portanto, a distância seria de 402,72 m.
c) A diferença entre as marcas obtidas
pelas duas atletas é dada por:
53,95 2 71,42 5 217,47
Logo, o módulo dessa diferença é 17,47 m.
Aplicando a operação inversa da adição
para descobrir os valores desconhecidos,
completamos o quadro:
Editoria de arte

106
b) Triplo de 10,8:
3 ? (10,8) 5 12,4
0 ,
8

3
2 ,
4
c) Quádruplo de 1
7
6
:
4 7
? 1 51
6
14
3
2
3

 




d) Dobro de 26,5:
2 ? (26,5) 5 213
16 ,
5

2
13 ,
0
3.
a) 22 ? 2 3 ? 2 52
4
1
7
3
14
1
2

 

 

 

 

b)
7
9
2
7
2 ?1 ?2
1
6
1 1
1 3



















51
1
27
1 5
1 1 1
1 5
5 5 5
1 5
1
1
4 2 5 2 5
2

2 5 2 5 5
1
2 2 5 2 5
4

2 5 2 5 5
  19 – Multiplicação de números
c)
(21,5)? (10,36)? (12,7)5 
5 (20,54) ? (12,7) 5 21,458
d) (11,2)? (16)? (10,65)5 
5 (17,2) ? (10,65) 5 14,68
e) (20,8)? (20,45)? (20,5)5 
5 (10,36) ? (20,5) 5 20,18
4. (25) ? (21,8) 2 (17) ? (11,2) 5
5 19 2 (18,4) 5
5 19 2 8,4 5
5 10,6
5. O dobro de 6,25 m é: 2 ? 6,25 m5 12,50 m.
Como se trata de profundidade, podemos
representar esse valor pelo número
racional relativo: 212,50 m.
6. Se a cada quilômetro rodado consome-
-se 0,12 , de combustível, em 82,5 qui-lômetros
serão consumidos:
82,5 ? 0,12 5 9,9 R 9,9 ,
7. 5 ? (22,24) 1 3 ? (13,25) 5
5 (211,2) 1 9,75 5
5 211,2 1 9,75 5
5 21,45
8.
a) 5
4
1
4
9
1
2 1
? 2 1 ?1 5
4 1
2







 

racionais
1.
2
5
2
3
a) 1 ? 2 52
4
15

 

 


 

 

12
11 ( ) 
b) 24 ? 2 51 3
11
 

 

1
2
3
4
c) 1 ?1 51
3
8

 

 


 

 


1 
5
8

0 4 5

 1

(2 , ) 22 51
d) 2 ? 5 2 ?
8

2
 

 
 
( )



4
10
1
4 2




e) (26,4) ? (11,5) 5 29,60
26 ,
4
1 ,
5
320
64
9 ,
60

1
f) (20,7) ? (22,1) 5 11,47
2 ,
1
0 ,
7
1 ,
47

2.
a) Dobro de 2
5
8
:
2 5
? 2 52
8
5
4
1
4

 




1
4
1
2
3
4
2
3
7
6
11
12
23
12
23
12
11
12
12
12
2 5 51
→ 23
12
3
4
23
12
9
12
14
12
7
2 6

→ 1
1
2
2
2
1
2
→ 11
12
1
4
11
12
3
12
8
12
2
4 3

3
4
1
2
3
4
2
4
Editoria de arte
1
2

107
52 1 52 1 5
2 1
52
5
9
1
2
10
18
9
18
10 9
18
1
18
1 5
2 1
52
10
18
9
18
10 9
18
1
18
b) 7 2 5 ? (11,5) 5
5 7 2 7,5 5
5 20,5
c) 2
3
3
10
1
2
1
3
1
1
1







 

 
5 ? 1 2 1 ? 2





 


 

 
1
5
1
6
1
5
1
6
6
30
5
30
52 2 2 52 1 52 1 52
1
30
1
3
2

 


 

 
1
5
1
6
1
5
1
6
6
30
5
30
52 2 2 52 1 52 1 52
1
30
d) (20,28) ? (11,5) 2 (10,7) ? (20,72) 5
5 20,42 2 (20,504) 5
5 20,42 1 0,504 5
5 10,084
e) 0,625 2 (10,84) ? (10,6) 5
5 0,625 2 (10,504) 5
5 0,625 2 0,504 5
5 10,121
20 – Divisão de números racionais
1.
6
7
9
7
a) 1 2 5 1
6
7
2
1

 

 


 

 







; 






7
9
? 2 52
2
3
1
3
3
7
11
14
b) 1 1 5 1
3
71

 

 


 

 


 

 
14
11
; ?? 1 51
6
11
 2





5
27
10
9
c) 2 2 5 2
1
5
27
3

 

 


 

 






;







9
10
? 2 51
1
6
1
2
5
8
25
8
d) 2 1 5 2
5
8
1
1

 

 


 

 







; 





? 1 52
8
25
1
5
1
5
4
7
2 4
e) 1 51 ?1
7
1
2
2
1

 

 








 
;( ) 1 

 
51
2
7
f) (26) 12 (2 )
;1 5 ? 1 52
5
6 5
12
5
2
1
2

 

 


 

 
2.
a)  10
(12) ; (20,5) 5 (120) ; (25) 5 24
 10
b)  10
(22,1) ; (22,8) 5 (221) ; (228) 5 10,75
 10
210 28
140 0,75
0
c)  10
(17,31) ; (21,7) 5 (173,1) ; (217) 5 24,3
 10
73,1 17
051 4,3
00
d)  100
(20,18) ; (10,36) 5 (218) ; (136) 5 20,5
 100
180 36
000 0,5
e)  100
(10,66) ; (11,1) 5 (166) ; (1110) 5 10,6
 100
660 110
000 0,6
f)
 10
(230,4) ; (14) 5 (2304) ; (140) 5 27,6
 10
304 40
240 7,6
000
g)  100
(21,44) ; (20,24) 5 (2144) ; (224) 5 16
 100
 10
h) (16) ; (22,5) 5 (160) ; (225) 5 22,4
 10
60 25
100 2,4
000
3. Metade de 21,8% R (21,8) ; 2 5 20,9%
Logo, a queda foi de 20,9%.

4.
2
1
2
1
5
8
5
12
21
25
14
15






;









5
12  ;
 

 


 

 



5
8
5 2 1


 

 

 


 

 


 


21
25
; 2 ; 1
14
15

 5
5
8

5 2 ? 1
12
5
1
2
3
1





























21
25

;2 ?1
15
14
3
5
3
2







 

 

 

 
3
2
9
10

5 2 2 52
3
2
1
;
5
10
9



? 2 5
1 3








51
5
3
4
9
10
4
5
3
10
5
5 ?2 2 ? 2 52
10
1
1
1
1

 

 

 




9
10
3

 

 
2 2 5

52 1 52 1 5
2 1
51
10
9
10
3
10
9
30
9
10 30
9
20
9
52 1 52 1 5
2 1
51
10
9
10
3
10
9
30
9
10 30
9
20
9
e) 2
3



2 4
3
3


1




1 8
1
2
;(2 )1 1 ? 2





 

3
2 ;
 

 

 
1
4
2 1 2 5
2
3
1
2
1
2
5 ?2 12 21
1
4
1
1 2

 

 

 

 


 
 







1
2
3
? 2 5
  
1 1
1
1
1
1
2
3
1
2 3
2
6
3
2
6
6
6
6

 
52 2 22 52 2 1 52 2 1 5
 
2 3
1 1
1
1
1
1
2
3
1
2 2
3
2
6
3
2
6
6
6
6
 
 
52 2 22 52 2 1 52 2 1 5

1
2
;
52 52
1
6
4
6
2
2 3
;
)? 2 5
f)
(21,44);(10,48)2(20,9);(11,2)5  
5 23 2 (20,75) 5
55 23 1 0,75 5 
22,25
 1
7. 2 2 (10,8)  (10,5) 5
5 2 2 (11,6) 5
5 2 2 1,6 5
5 10,4
a) Valor da expressão na forma
4
10
2
;
fracionária: 1 51
2
2 5
;
.
b) Valor da expressão na forma decimal:
10,4.
8. x 5 (10,2)  (20,04) 2 3 ? (21,6)
x 5 25 2 (24,8)
x 5 25 1 4,8
x 5 20,2
5. 3 10
x 5 (15)  (212,5) 5 (150)  (2125) 5 20,4
3 10
500 125
000 0,4
Sendo x 5 20,4, temos:
a) Triplo de x R 3 ? (20,4) 5 21,2
3 10
b) Metade de x R (20,4)  2 5 (24)  (20) 5 20,2
3 10
40 20
00 0,2
6.
4
5
8
5
2 5
a) 2 1 2 2
4

 

 


 

 


 

 
; (1 ); 





1






1

4
5
5
5 2 ? 1 2
1 8
2
(12 4
5

 

 

5

 






1






1

4
5
5
5 2 ? 1 2
1 8
2
(12 4
)? 2 5
5

 

 

52 2 2 52 1 52 1 5
2 1
51
1
2
8
5
1
2
8
5
5
10
16
10
5 16
10
 

 

1
10
1 52 1 5
2 1
51
8
5
5
10
16
10
5 16
10
1
1
10
4 
8
5
2 3 1
b) 1 2 ? 2 5 1
4
8
5
 

 


 

 




;(1 )





 

3
4 1
 



  1
2
? 2 2 2 5
4 
5 1
1
4
8
5
 









 

3
4 1
52 1 52 1 5
 

 

 
1
2
? 2 2 2 5
2 1
52
4
5
3
4
16
20
15
20
16 15
20
1
20
1 5
2 1
52
15
20
16 15
20
1
20
c) (25,6)  (22,8) 2 (10,25)  (20,5) 5
5 12 2 (20,5) 5
5 12 1 0,5 5 12,5
d)
4
9
;(2 0 , 4 )5
2 ;(2 0 , 5 )4
4
5
5
5 ; 2 2 2
3
9
10
3
; 10 
 

 


 

 
5
5
10 )5 ; 2 2 ; 2
5 4
9
4
10
5
3

 

 


 

 
5
108

109
Desafios!, página 101.
1. Podemos representar o salário de Marcos
na forma de fração:
7
7
.
Depois de pagar a prestação
da casa, sobram para Marcos:
7
3
7 2
3
4
4
7
2 7
5
7
7
7 5 → do salário.
Com metade de
4
7 ele paga a prestação do
carro:
4
7
 2
5 ? 5 → do salário.
4
7
1
2
2
7
2
7
2
1
 6
1
2
1
2
1
2
 

 
 1
Dessa forma, após pagar o carro e a casa,
sobram para Marcos:
7
 3
2
7
3 1
2
7
5
7
2
2 1 5 2
5 2 5
7
7
7
7
7
7
7
 

 


 

 

5
7
2
7
2
7
5 →
7
7
5
7
7
2 5
2
5
7
2
7
2
7
5 → do salário.
De acordo com o enunciado, 2
7
representa
R$ 276,00; pois é o que sobra para Marcos.
Logo,
1
7
representa R$ 138,00.
Como 1
7
representa R$ 138,00;
7
7
representa:
7 ? 138 5 966
Portanto, o salário de Marcos é R$ 966,00.
2. Alternativa d.
Duas fotos coloridas custam: 2 ? R$ 3,60 5
5 R$ 7,20.
Logo, sobram para as cópias simples:
R$ 10,00 2 R$ 7,20 5 R$ 2,80
Como uma cópia simples custa R$ 0,15,
com R$ 2,80 poderei pagar:
2,80 : 0,15 5 18
Portanto, poderei pagar por 18 cópias
simples.
racionais
1.
9
10
9
10
a) 1 ?1 ?1
9
10

 

 


 

 


 

 
 1 1 1 3
1 1 9
10
55 1 5 1
9
10
 

 


 

 

b) (22,4) ? (22,4) ? (22,4) ? (22,4) ? (22,4) 5
5 (22,4)1 1 1 1 1 1 1 1 1 5 (22,4)5
11
8
11
8
c) 2 ?2 52
11
8

 

 


 

 


 
1 1 2 11

 

8
1

 
5 2

 

d) (10,05) ? (10,05) ? (10,05) 5 (0,05)1 1 1 1 1 5
5 (0,05)3
2.
 2
1
9
1
9
1
9
 

 
a) 2 52 ? 2 51


 

 


 

 

1
81
 2
1
4
1
4
1
4
b) 1 51 ?1 51
 

 


 

 


 

 

1
16
 6
1
2
1
2
1
2
 

 
 1
c) 2 52 ? 2 ? 2


 

 


 

 

1
2
1
2
1
2
 

 


 

 


 

 
? 2 ? 2 ? 2
2
1
64

 

 
51
2 52 ? 2 ? 2


 

 


 

 

1
2
1
2
1
2
 

 


 

 


 

 
? 2 ? 2 ? 2 2
1
64

 

 
51
d) (20,7)3 5 (20,7) ? (20,7) ? (20,7) 5
5 20,343
4
11
e) 2 51
1
 0
 

 

f) (10,9)3 5 (10,9) ? (10,9) ? (10,9) 5
5 10,729
7
3
g) 1 51
7
3
 1
 

 

h) (24,2)2 5 (24,2) ? (24,2) 5 117,64
i) (21,4)2 5 (21,4) ? (21,4) 5 11,96
j) (16,2)0 5 11
k) 1 51 ? 1 51
6
5
6
5
6
5
 2
 

 


 

 


 

 

36
25
3
10
3
10
l) 2 52 ?2
3
10
 2
 

 


 

 


 

 
51
9
100
3.
 2
5
7
5
7
5
7
 

 
a) 2 52 ? 2 51


 

 


 

 

25
49
b) (10,8)3 5 (10,8) ? (10,8) ? (10,8) 5
5 10,512
 4
1
2
1
2
1
2
 

 
c) 2 52 ? 2 ? 2


 

 


 

 

1
2
1
2
1
16

 

 


 

 
? 2 51
d) (22,5)2 5 (22,5) ? (22,5) 5 16,25
4.
1
2
x 5 2 1
2

 

 
( )
1
2
x 5 2 ? 1
1
2

 

 


 

 

x 52
1
4
a) Quadrado do número x:
 2
1
4
1
4
1
4
 

 
2 52 ?2 51


 

 


 

 

1
16
b) Cubo do número x:

110
 3
1
4
1
4
1
4
 

 
2 52 ? 2 ? 2


 

 


 

 

1
4
1
64

 

 
52
5.
 2
3
4
9
8
 

 
a) 2 2 5


 

 
 
9
16
8
9
5 1 ? 2 52
1
2
1
2
1
1












 2
7
9
7
6
5
6
 

 
b) 2 2 2 2 5


 

 


 

 
 
7
9
6
7
5 2 ? 2 2 1
25
3
1
3
2
1












6

 

 
5
2
3
25
36
24
36
25
36
51 2 51 2 52
1
36
c) 3 1
? 2 2 ?2 5
2
3 2
12 1
4

 

 


 

 
(2 ) 
3 1
? 2 2 ?1 5
8
12 1
16
3
4

 

 


 




(2 )
3
8
3
4
3
8
3
4
3
8
6
8
52 2 2 52 1 52 1 51
3
8

 

 

2
5
10 2
d) 2 ? 2 2 1
3
4
9
 2 2
 

 


 

 


 

(2 ) 
 
5
4
25
10 4
4
9 5
5 1 ? 21 1
9
 2
 





 

 


 
( ) 2 

 
5
8
5
 1
1
4
9

9
52 2 1 ? 1 5
1 4
1










8
5
( 1)
22 2 1 5
8
5
1
8
5
5
5
52 2 52 2 52
13
5
4
3
2
3
 ?? (15) 5 1 2 2 2 16
e) 2 2 2 2
7
25
 2 3
 

 


 

 


 

 
9
8
27
7
25
2
1

 

 


 

 



 




1
8
1
16
1
6

 

 

 

 
? (125)15
2 2
2
3
7
25
3

 


 

?? (15) 5 1 2 2 2 16
 
9
8
27
7
25
2
1

 

 


 

 



 




? (125)15
 2
3
16
27

9
5 1 ? 2 2
1 8
1










(27)5
5 26 2 (27) 5 26 1 7 5 11
6.
a) (22)3 2 (20,5)3 5
5 28 2 (20,125) 5
5 28 1 0,125 5 27,875
b) (22)2 2 (20,5)2 5
5 14 2 (10,25) 5
5 14 2 0,25 5 13,75
c) (22)2 2 (22) ? (20,5) 1 (20,5)2 5
5 14 2 (11) 1 (10,25) 5
5 14 2 1 1 0,25 5
5 4,25 2 1 5 13,25
7.
A 5 (20,25) : (22)2 2 (20,5)2 : (22)
A 5 (20,25) : (14) 2 (10,25) : (22)
A 5 20,0625 2 (20,125)
A 5 20,0625 1 0,125
A 5 10,0625
8.
(10,8) : (20,2)2 1 (22,7) : (20,3)2 5
5 (10,8) : (20,04) 1 (22,7) : (10,09) 5
5 20 1 (230) 5
5 20 2 30 5 210
9.
a5 5 5 2 2 1
2
1
8
3
 3
 

 


 

; b5 5 5 2 4 1
 
4
1
16
2
 2
 

 

Logo,
1
8
16
1
a
b 5 5 ? 5
2
1
2
Portanto, o quociente de a por b é 2.
10.
x5 5 2 6
1
6
1 ; y5 5 2 9
1
9
1
1
9
3
18
2
18
x1y5 1 5 1 5
5
18
Logo, x1y5
5
18
.
11.
a) 3 1
3
1
3
1
3
2
2
2 5 5 ? 5


 

 


 

 

1
9
b) 8 1
8
1
8
1
8
2
2
2 5 5 ? 5


 

 


 

 

1
64

c) (24) 1
4
1
4
1
4
3
3
 

 
2 5 2 5 2 ? 2


 

 


 

 


 

 
1
4
? 2 52
1
64
1
10
1
10
1
10
d) (2 ) 5 2 5 2 ? 2 51 2 10
1
100
2
2  
 
 
 
 
 

e) (29) 1
9
1
9
1
1
 

 
2 5 2 52


f) 10 1
10
1
10
1
10
3
3
 

 
25 5 ?


 

 


 

 



 

 
1
10
? 5
1
1000
2 2
5
1
2
5
g) 1 5 51
5
2
 1 1
 

 







h) 2 5
2
5 2
2 3
4
1
3
4
4
3
 2 2
 

 








 

 


 

 


 

 

2 4
3
4
3
16
9
5 2 ? 2 51

111
i) 2 5
2
5 2
2 3
2
1
3
2
2
3
 3 3
 

 








 
3  2

 


 

 


 

 


 
3
2
3
2
3
5 2 ? 2 ? 2
 
52
8
27

 

 2
3
 


 

 


 
2
3
2
3
5 2 ? 2 ? 2
 
52
8
27
j) 2 5
2
5 5
2 1
2
1
1
2
2 2
5 5
5 
 

 







(2 ) (2 )?(22)?(22)?(22)?(22)5232
5
2
(2 )?(22)?(22)?(22)?(22)5232
12. Para cada casa decimal que a vírgula
se desloca à direita, diminuímos uma
unidade negativa no expoente de base 10.
Daí vem:
a) 0,01 5 1022 c) 0,0015 1023
b) 0,00001 5 1025 d) 0,000001 5 1026
13.
2 5
6
6
5
a) 1 51 51
6
5
 2 2
 

 


 

 


 

 
6
5
36
25
?? 1 51 51
1 44

 

 
 ,

b) 10 1
10
1
10
1
10
4
4
 

 
2 5 5 ?


 

 


 

 



 

 


 

 
1
10
1
10
1
10000
? ? 5 5
0,0001
1
10
?

 


 

 



 

 


 

 
1
10
1
10
1
10000
? ? 5 5
0,0001

c) 2 1
2
1
2
1
2
3
3
 

 
2 5 5 ? ?


 

 


 

 

1
2
1
8
0 125

 

 
5 5 ,
d) 4 1
21 0 25 5 5 ,
4
14.
2 2 
a) 1 2
3
3
3
2
3
1
3
3 3
2 5 2 51
 

 


 

 


 

 

3
2
5 1 5 ? ? 51
3 3 (13) (13) (13) 27
 ( )
1
3
3
51
2 
 

 

3
2
5 1 5 ? ? 51
3 3 (13) (13) (13) 27
 ( )
2 2 
b) 5
3
1 5
3
3
3
2
3
4 4
2 5 2 51
 

 


 

 


 

 


2

5 1 5 1 ? 1
 

 


 

 

 
4 4 3
2
3
2
3
2

 


 

 


 

 
3
2
3
2
? 1 ? 1 51
81
16
2
3

 
51

 


2

5 1 5 1 ? 1
 

 


 

 


 
4 4 3
2
3
2
3
2

 


 

 


 

 
3
2
3
2
? 1 ? 1 51
81
16
2 2 
c) 1
3
1
2
2
6
3
6
1
6
2 2
2 5 2 52
 

 


 

 


 

 

2
2
5 5 ? 51
(26)2 (26) (26) 36
1
6
2
52
2 
 

 

2
2
5 5 ? 51
(26)2 (26) (26) 36
2 2 
d) 2 4
5
10
5
4
5
6
5
1 1
2 5 2 51
 

 


 

 

 
 

1 5
2
51
6
15.
a) 56 5 22 1 33 1 52, pois 56 5 4 1 27 1 25.
b) 154 5 21 1 33 1 53, pois 154 5 2 1 27 1 125.
c) 385 5 23 1 32 1 52 1 73, pois 385 5 8 1
1 9 1 25 1 343.
d) 160 5 22 1 30 1 52 1 72 1 92, pois 160 5
5 4 1 1 1 25 1 49 1 81.
22 – Raiz quadrada exata de
números racionais
1. De acordo com as figuras geométricas,
vem:
a) 36 56, pois 6 ? 6 ou 62 5 36.
b) 0,49 50,7, pois 0,7 ? 0,7 ou (0,7)2 5 0,49.
c) 4
9
2
3 5 , pois 2
3
2
3 ? ou 2
3
4
9
 2
 

 
 5 .
2.
a) 2 304 2
1 152 2
576 2
288 2
144 2
72 2
36 2
18 2
9 3
3 3
1 28 ? 32
2 304 5 28 ? 32 5 (24 ? 3)2 5 (16 ? 3)2 5 (48)2 5
5 48 ? 48
Como 2 304 5 48 ? 48, temos, pela
definição, que 2304 548.
b) 676 2
338 2
169 13
13 13
1 22 ? 132
676 5 22 ? 132 5 (2 ? 13)2 5 (26)2 5 26 ? 26
Como 676 5 26 ? 26, temos, pela
c) 1 764 2
882 2
441 3
147 3
49 7
7 7
1 22 ? 32 ? 72
1 764 5 22 ? 32 ? 72 5 (2 ? 3 ? 7)2 5 (42)2 5 42 ? 42
Como 1 764 5 42 ? 42, temos, pela

112
d) 2 500 2
1 250 2
625 5
125 5
25 5
5 5
1 22 ? 54
2
5 5 5 5 ?
2 500 5 22 ? 54 5 (2 ? 52)2 5 (2 ? 25)2 5 (50)2 5
5 50 ? 50
Como 2 500 5 50 ? 50, temos, pela
3.
a) Sendo x2 5 100, então x 5 10, pois:
25 2
; 
100 2
50 2
25 5
5 5
1 22 ? 52
100 5 22 ? 52 5 (2 ? 5)2 5 (10)2 5 10 ? 10
Portanto, x 5 10.
4 2
; 
b) Sendo x2 5 121, então x 5 11, pois:
121 11
11 11
1 112
121 5 112 5 11 ? 11
Portanto, x 5 11.
c) Sendo x2 1
16 5 , então x 5
1
4
, pois:
16 2
8 2
4 2
2 2
1 24
1
16
1
2
1
2
1
4
1
4
25 2
; 
1
2
5 5 5 5 ?
4 2 2 4
( )

 

 


 

 

 

 

Portanto, x 5
1
4
.
d) Sendo x2
16
;
4 2
; 
1
625 5 , 5 5
16
0 0016
16
10000
;
,
então x 5
1
25
ou x 5 0,004; pois:
625 5
125 5
25 5
5 5
1 54
1
625
1
5
1
5
1
25
1
2
5 5 5 5 ?
4 2 2 25
( )

 

 


 

 

1
25
0 04 004

 

 
5( , )? ( , )
1
625
1
5
1
5
1
25
1
4 2 2 25
( )

 

 


 

 

1
25
0 04 004

 

 
5( , )? ( , )
Daí, vem que x 5 0,04.
e) Sendo x 5 25 , então x 5 5, pois 5 ? 5 5
5 25.
f) Sendo x 5
36
49
, então x 5
6
7
, pois
6
7
6
7
36
49

 

 


 

 
? 5 .
4.
a) 12 25 1225
100
25 2
; 
49
4
7
2
7
2
7
2
25 2
2
, 5 5 5 5 5
;
 

 


 

 


 

 
7
2
(3,5) (3,5)
? 5 ?
12 25 1225
100
49
4
7
2
7
2
7
2
25 2
2
, 5 5 5 5 5
;
 

 


 

 


 

 
7
2
(3,5) (3,5)
? 5 ?
Como 12 25
49
4
, 5 53,5?3,5; temos, pela
definição: 12,25 53,5.
b) 12 96 1296
100
4 2
; 
324
25
18
5
18
5

1
3 6 4
2
2
, 5 5 5 5 5
;
 

 

8
5
18
5
 

 


 

 
? 5( , 12 96 1296
100
324
25
18
5
18
5
1
4
2
2
, 5 5 5 5 5
;
 

 

8
5
18
5
3 6 3 6

 

 


 

 
? 5( , )? ( , )
Como 12 96
324
25
, 5 53,6?3,6; temos,pela
definição: 12,96 53,6.
c) 30 25 3025
100
25 2
; 
121
4
11
2
11
2
25 2
2
, 5 5 5 5 5
;
 

 

5 5 
11
2
11
2
 

 


 

 
? 5( , 30 25 3025
100
121
4
11
2
11
2
25 2
2
, 5 5 5 5 5
;
 

 

11
2
11
2
5 5 5 5

 

 


 

 
? 5( , )? ( , )
Como 30 25
121
4
, 5 55,5?5,5; temos,
pela definição: 30,25 55,5.
d) 29 16 2916
100
4 2
; 
729
25
27
5
27
5

2
5 4 4
2
2
, 5 5 5 5 5
;
 

 

7
5
27
5
 

 


 

 
? 5( , 29 16 2916
100
729
25
27
5
27
5
2
4
2
2
, 5 5 5 5 5
;
 

 

7
5
27
5
5 4 5 4

 

 


 

 
? 5( , )? ( , )
Como 29 16
729
25
, 5 55,4 ?5,4; temos,
e) 0 0784 784
10000
16 2
; 
49
7
7
625
25 16
25
2 , 5 5 5 5
;
 

 


 

 


 

 

2 7
25
7
25
5 ? 5(0 0784 784
10000
16 2
; 
49
7
7
625
25 16
25
2 , 5 5 5 5
;
 

 


 

 


 

 

2 7
25
7
25
5 ? 5(0,28)? (0,28)
Como 0 0784
49
625
, 5 50,28?0,28; temos,

f) 0 1024 1024
10000
16 2
; 
64
8
8
625
25 16
25
2 , 5 5 5 5
;
 

 


 

 


 

 

2 8
25
8
25
5 ? 5(0,32)? (0,32)
64
625
8
25 2
8
25
2 5 5

 

 


 

 


 

 

2 8
25
8
25
5 ? 5(0,32)? (0,32)
Como 0 1024
64
625
, 5 50,32?0,32; temos,
5. Se a5
121
196
; então a5
11
4 , pois
11
4
11
14
121
196

 

 


 

 
? 5 .
6. a10 ? b4 5 (a5 ? b2)2 5 (a5 ? b2) ? (a5 ? b2)
Como a10 ? b4 5 (a5 ? b2) ? (a5 ? b2), temos, pela
definição, que a10 b4 a5 b2 ? 5 ? .
7. 441 521, pois 21 ? 21 5 441.
256 516, pois 16 ? 16 5 256.
900 530, pois 30 ? 30 5 900.
Então, temos:
441 1 256 2 900 52111623053723057
Logo, o valor da expressão é 7.
8. Se x 5
64
225
; então x 5
8
15
, pois
8
15
8
15
64
225

 

 


 

 
? 5 .
Logo, x 5
8
15
.
23 – Estudo das médias
1. Para determinar a média aritmética, basta somar os cinco números e dividir essa soma por
cinco:
( ) ( ) 5
25 22 13 15 30 2 1
2 1 2 1 2 1 1
5
2 2 2 1 1
5
5
25 22 13 15 30
5
60 45
5
15
5
52 52
3
2. Calculando a média aritmética ponderada, vem:
8 2 15 2 20 1
2 2 1
16 30 20
5
66
5
13 2 ? 1 ? 1 ?
1 1
5
1 1 1
5 5 ,
3. Calculando a média ponderada para compra de Cristina, vem:
3 21 2 12
3 2
63 24
5
87
5
17 4 ? 1 ?
1
5
1
5 5 ,
Logo, o preço médio por caneta foi R$ 17,40.
4. Calculando a média aritmética, vem:
2
3
1
6
3
4
3
8
12
2
12
9
12
3
19
12
3
19
12
1
3
19
36
1 1
5
1 1
5 5 ? 5
5. Calculando a altura média dos jogadores, vem:
1 90 199 2 01 208 2 12
5
10 1
5
2 02
, , , , , ,
1 1 1 1
5 5
, Logo, a altura média dos jogadores é 2,02 m.
113

6. Para calcularmos o custo de cada copo de refresco, devemos calcular a média ponderada
para o custo. Daí, vem:
8 50 2 85
8 2
400 170
10
570
10
57  1 
1
5
1
5 5
Logo, o custo de cada copo de refresco é 57 centavos.
7. Nos cinco resultados, o primeiro valor refere-se aos gols marcados pelo clube, e o segundo
valor refere-se aos gols sofridos por esse clube. Assim, temos:
Gols marcados R 4 1 3 1 2 1 4 1 1 5 14
Gols sofridos R 2 1 3 1 3 1 0 1 1 5 9
a) O clube marcou 14 gols.
b) O clube sofreu 9 gols.
c) A média de gols marcados é dada por:
4 3 2 4 1
5
14
5
1 1 1 1
5 5 2 ,
8 Logo, a média de gols marcados por esse clube foi de 2,8 gols.
d) A média de gols sofridos é dada por:
2 3 3 0 1
5
9
5
1 1 1 1
5 5 1 ,
8 Logo, a média de gols sofridos por esse clube foi de 1,8 gol.
8. Calculando a idade média dos jogadores dessa equipe, vem:
3  20 1 2  26 1 2  23 1 21 1 24 1 25 1 27 1
30
3 1 2 1 2 1 1 1 1 1 1 1 1 1
1
5
5
1 1 1 1 1 1 1
5 5
60 52 46 21 24 25 27 30
12
285
12
23,75
Logo, a idade média dos jogadores dessa equipe é 23,75 anos.
9. De acordo com as notas, calculamos a média do aluno no bimestre:
4 6 3 8 2 75 1 9
4 3 2 1
24 24 15 9
10
72
10
7 2  1  1  1 
1 1 1
5
1 1 1
5 5
,
,
Logo, a média desse aluno foi 7,2.
10. O preço médio do produto é dado por:
3500 30 8 500 24
 1  309
3500 8500
105000 204000
12000
1
5
1
5
000
12000
525,75
Logo, o preço médio desse produto, por unidade, foi R$ 25,75.
1.
a) 2004 R IDH de 0,798 (0,500 , 0,798 , 0,799 R categoria: médio)
2005 R IDH de 0,800 (0,800 5 0,800 R categoria: alto)
b) 0,800 . 0,798; foi maior.
c) Melhorou; porque quanto maior o IDH, melhor é a qualidade de vida da população.
d) Como o IDH de 2004 ficou 0,002 abaixo do mínimo para alcançar a categoria alto, o IDH de
2006 precisa ser no mínimo de 0,802 para que a média dos três anos esteja na categoria
alto.
114

2.
a) Calculando a média dos indicadores medidos em 2000, temos:
0 502 0 615 0 408
3
1 525
3
0 508
, , , ,
, 1 1
5 
Logo, o IDH dessa região em 2000 era 0,508.
b) Calculando a média dos indicadores medidos em 2005, temos:
0 420 0 648 0 540
3
1 608
3
0 536
, , , ,
1 1
5 5
, Logo, o IDH dessa região em 2005 era 0,536.
1.
a) Resposta em aberto. b) Resposta em aberto. c) Resposta em aberto.
2.
a) De acordo com o gráfico, nasceram nessa maternidade nesse dia:
4 1 2 1 2 1 1 1 1 5 10 R 10 crianças.
b) De acordo com o gráfico, 4 crianças nasceram com mais de 50 cm de altura: duas com
51 cm, uma com 52 cm e uma com 53 cm.
c) Nenhuma.
d) Calculando a média das alturas das crianças que nasceram nesse dia, temos:
4 47 2 48 2 51 52 53
4 2 2 1 1
188 96 102 52 53
1
 1  1  1 1
1 1 1 1
5
1 1 1 1
491
10
0 55 5
49,1
Logo, a média de altura das crianças foi 49,1 cm.
3.
a) Calculando a média das alturas do time feminino, vem:
1,7011,7611,7711,8011,8211,8211,8311,8711,9712,00 1 94 1 92
12
1 1
5
, ,
5
22 2
12
1 85
,
,
Logo, a altura média do time era 1,85 m.
b) Calculando a média das alturas do time masculino, vem:
2,0011,8612,1112,1111,9211,9111,9112,1112,0412,11 2 06 2 11
12
1 1
5
, ,
5
24 25
12
2 02
,
 ,
Logo, a altura média do time era 2,02 m.
c) 2,02 2 1,85 5 0,17
Logo, o time masculino é 0,17 m ou 17 cm mais alto que o time feminino.
d) De acordo com a tabela, a jogadora mais alta da seleção feminina é Alessandra.
e) De acordo com a tabela, a jogadora mais baixa da seleção feminina tem 1,70 m de altura.
f) A maior altura dos jogadores do time masculino é 2,11 m, e cinco jogadores possuem essa
altura.
g) Jogador mais baixo: 1,86 m.
Jogadora mais alta: 2,00 m.
A diferença entre essas alturas é:
1,86 m 2 2,00 m 5 20,14 m
O número racional negativo indica que o jogador é mais baixo do que a jogadora.
h) Iziane e Janeth possuem a mesma altura (1,82 cm).
i) De acordo com a tabela, 4 jogadores possuem altura inferior a 2,0 m.
115

116
1. Alternativa a.
(0,1 2 0,01) : (0,2 2 0,02) 5
5 (0,09) : (0,18) 5 10,5
2. Alternativa d.
Fazendo a diferença entre os pontos
considerados, temos:
21,5 2 (26,35) 5
5 21,5 1 6,35 5 14,85
Logo, a distância entre os dois pontos
considerados é 4,85 m.
3. Alternativa d.
x5(2121)? 5 2 2
4
2 1
2

 

 

x5(22)? 5 2 2 5(2 )? 2
4
8
4
1
2
2 3
4
1
2

 

 


 

 
1
2
3
2
1
2
2
4
2
4
2
2
 
2 51 2 5 5
1
)? 2
2 3
4
1
2

 

 
1
2
3
2
1
2
2
2
2 51 2 5 5
1
Sendo x 5 1, o cubo de x será:
(1)3 5 (1) ? (1) ? (1) 5 1.
4. Alternativa b.
3
2
1 3
2 2 ? 2 5 2 2
2
1 3
2
2
2

 

 


 

 


 

 



 

 
3
2
2
2
? 2 5
5
2
1
2
5
4
5 2 ? 52 52
1 25

 

 


 

 
 ,
21,25 está entre os inteiros 22 e 21.
5. Alternativa c.
x5 5 2 6
1
6
1
y5 5 5 ? 2 6 1
6
1
6
1
6
2
 2
 

 


 

 


 

 
5
1
36
1
6
1
36
6
36
1
36
x1y5 1 5 1 51
7
36
6. Alternativa e.
0,25 1 0,19 : (4 2 0,8 : 0,5 2 0,5) 5
5 0,25 1 0,19 : (4 2 1,6 2 0,5) 5
5 0,25 1 0,19 : (4 2 2,1) 5
5 0,25 1 0,19 : (1,9) 5
5 0,25 1 0,1 5 0,35
7. Alternativa d.
1
8
8
1
8. Alternativa a.
1
8
16
4
x5 2 2 2 2 2 ( ) ( ) 2 9 1 2 100 2 



;
x 5 [2(14) 2 3] ; [11 2 2]
x 5 [24 2 3] ; [21]
x 5 7
Se x 5 7, então x2 51 1 1
7
.
9. Alternativa c.
3 12 18 13 9 14
3 18 9
36 234 126
30
396
30
13 2 ? 1 ? 1 ?
1 1
5
1 1
5 5 ,
3 12 18 13 9 14
3 18 9
36 234 126
30
396
30
13 2 ? 1 ? 1 ?
1 1
5
1 1
5 5 ,
Logo, a média das idades dos alunos é
13,2 anos.
10. Alternativa e.
106 125 95 104
4
430
4
1 1 1
5 5 107 ,
5 Logo, a média de pontos da equipe A nesse
torneio é 107,5 pontos.
11. Alternativa a.
211 2 2 1 2 1
2
1
4
1 3
4
 2
 

 








 

 
; 5
5211 2 2 1 2 2
4
1
4
4
4
3
4
 2
 

 








 

 
; 
5
5211 2 1 2 3
4
4
4
3
4
 2
 

 





 

 

 
; 5
5211 1 2 5 1
4
3
4
 2
 

 








 

 
; 
5211 2 5 1
16
3
4

 

 

 

 
; 
16
16
1
16
3
4

 

 

 

 
5 2 1 2 5
; 
15
16
3
4

5 2 2 52
15
16
5
; ?? 2 51
4

 

 

 

 






4
3
5
4
1
1






12. Alternativa d.
11 6 13 8 10 7 14 2 15 4 2 1 2
, , (2 , ) (2 , ) , 11,6 13,8 10,7 5
2 1 1 1 1
5
12
11 6 13 8 10 7 14 2 15 4 2 1 2
, , (2 , ) (2 , ) , 11,6 13,8 10,7 14,2 15,4
2 1 1 1 1
5
12
5
2 1
5
5
2 1
52 52
365 29 2
5
7 3
5
1 46
, , ,
,
Logo, a média aritmética é 21,46.

 
2
3
2
2
1
2
 
2
9
4
4
2
2
3
 
? 2 2 2 5
5 ? 2

  
 

 


;

 
 

 

 
 
 

 


; 2 5 2 ; 2 5
5
2
1
8
18
4
4
1
8
18 16
4 
 
 
 
 
 
 
;
;
1
8
2 5
2
4
1
8
5 2 5
2
4
8
1
16
4
5 ? 2 52 52
4
2
9
4
4
5 ? 2
 

 



 
 

 

 
 
 

 


; 2 5 2 ; 2 5
5
2
1
8
18
4
4
1
8
18 16
4 
 
 
 
 
 
 
;
;
2 5
5 2 5
5 ? 2 52 52
4

117
ESTUDANDO AS EQUAÇÕES
• Qual o número cujo triplo mais 6 dá 21?
5, pois o triplo de 5 é 15 com mais 6 dá 21.
• No dicionário Aurélio, o significado das
palavras são:
Equivalente R de igual valor; aquilo que
equivale.
Equilíbrio R manutenção de um corpo na
posição normal, sem oscilações ou desvios;
igualdade de forças opostas.
Equilátero R que tem os lados iguais entre si.
Equidistante R que dista igualmente.
Equilibrista R pessoa que se conserva em
equilíbrio.
• Você já ouviu falar em “incógnita”?
x 1 y 5 67 e x 2 2y 5 46
x y x y
x y
→ 
67 67
1 5 5 2
2 5
2 46
I
II
Substituindo I em II, temos:
67 2 y 2 2y 5 46
23y 5 46 2 67
23y 5 221  (2 1)
3y 5 21
y 5
21
3
y 5 7
x 1 y 5 67
x 1 7 5 67
x 5 67 2 7
x 5 60
Logo, x 5 60 e y 5 7.
24 – Igualdade
As idades de Eva e Ivo
Sendo os dois números ímpares, a
diferença entre eles 6, e ainda a soma 40,
depois de algumas tentativas concluímos
que as idades são 17 e 23 anos.
Exercícios, página 119 e 120.
1.
a) 82 1 2 5 6 ? 11
Da equação, vem:
1o membro R 82 1 2
2o membro R 6 ? 11
b) 132 2 122 5 42 1 32
Da equação, vem:
1o membro R 132 2 122
2o membro R 42 1 32
2.
Sendo a 5 b e b 5 27, pela propriedade
transitiva, a 5 27.
3.
Pedro apenas mudou os termos de membro,
passando o termo do 1o membro para o
segundo e o do segundo para o 1o. Logo,
Pedro utilizou a propriedade simétrica.
4.
Sim, pois, pela propriedade simétrica,
21 5 x 1 1 R x 1 1 5 21.
5.
Sendo x 5 3y e 3y 5 z 2 2, pela
propriedade transitiva, x 5 z 2 2.
6.
Multiplicando o 1o membro por
1
7 , o
2o membro também deverá ser multiplicado
por
1
7 . Daí, vem:
21
1
7
( )? 3

2 membro o–
ou
7.
o–
Adicionando 26 ao 1o membro, o 2o
membro também deverá ser adicionado de
26. Daí, vem:
826  ou
2
2 membro 8.
a) x1256→x1 2 2 2 5622
x 5 4
b) x12521→x1 2 2 2 52122
x 5 23
9.
a) 3 21
1
3
3 21
1
3
x5 → ? x5 ?
x 5
21
3
x 5 7
b) 3 15
1
3
3 15
1
3
x52 → ? x52 ?
x 52
15
3
x 5 –5

118
25 – Equações
1.
Como cada sorvete custa R$ 3,00, temos:
a) 5 sorvetes custam: 5 ? 3 5 15 R 15 reais
b) 10 sorvetes custam: 10 ? 3 5 30 R 30 reais
c) 15 sorvetes custam: 15 ? 3 5 45 R 45 reais
d) x sorvetes custam: 3x reais
2.
Como o ponteiro da balança indicou 90 kg:
a) se ganhar 10 kg R 90 1 10 5 100 R 100 kg
b) se ganhar x kg R (90 1 x) R (90 1 x) kg
c) se perder 5 kg R 90 2 5 5 85 R 85 kg
d) se perder y kg R (90 2 y) R (90 2 y) kg
3.
Sendo a quantidade de carros no pátio da
concessionária igual a 30, temos:
a) se houvesse 3 vezes mais carros R
3 ? 30 5 90 R 90 carros
b) se houvesse t vezes mais carros R 30 ? t
c) se a quantidade de carros fosse
dividida por 3 revendedores R 30 : 3 5
5 10 R 10 carros
d) se a quantidade de carros fosse
dividida por n revendedores R 30 : n
1.
Sim, é uma equação, pois representa uma
igualdade e tem um elemento desconhecido.
2.
x 1 1 5 0 R é uma equação, pois
representa uma igualdade e tem um
elemento desconhecido.
x 2 1 5 0 R é uma equação, pois
representa uma igualdade e tem um
x 2 1  0 R não é uma equação, pois é
uma desigualdade.
x 1 1  0 R não é uma equação, pois é
uma desigualdade.
x 2 1  0 R não é uma equação, pois não
expressa uma igualdade.
x 5 21 R é uma equação, pois representa
uma igualdade.
3.
25 1 23 5 22 ? 10
Embora seja uma igualdade, essa sentença
não apresenta número desconhecido.
4.
Só há uma incógnita na equação, a
incógnita x.
5.
De acordo com as situações, escrevemos:
a) x 1 31 5 100
b) x 2 8 5 41
c) 2x 1 31 5 73
d) 3x 2 13 5 47
e) 1
2
1
3
x1 x535
f) 4x 5 x 1 72
6.
Idade atual de Karina: x
Logo, de acordo com o enunciado, podemos
escrever:
x 1 10 5 28
7.
Massa de uma das caixas: x
Logo, de acordo com o enunciado, podemos
escrever:
x 1 4x 5 20
8.
Largura: x; comprimento: x 1 10
Sendo o triplo da largura igual ao dobro do
comprimento, temos:
3x 5 2(x 1 10)
26 – Conjunto universo e conjunto
solução de uma equação
1.
O número cujo triplo mais 6 dá 21 é o
número 5.
Representando a situação na forma de
equação, temos:
3 ? x 1 6 5 21, sendo x o número
desconhecido.
2.
O número cuja metade mais o seu dobro
dá 20 é o número 8.
Representando a situação na forma da
equação, temos:
x
x
2
12 520 , sendo x o número desconhecido.
3.
O número que diminuído do seu triplo é
igual ao quádruplo do número menos 18 é
o número 3.
Representando a situação na forma da
equação, temos:
x 2 3x 5 4x 2 18, sendo x o número
desconhecido.

119
1.
a) x 2 7 5 0
x 5 7
S 5 {7}
b) x 1 9 5 0
x 5 29
S 5 {29}
3
8
c) x2 5
0
x 5
3
8
S5
3
8


d) x 1 1 5 0
x 5 21
S 5 , pois 21  IN.
e) x 2 10 5 3
x 5 3 1 10
x 5 13
S 5 {13}
f) x 2 6 5 210
x 5 210 1 6
x 5 24
S 5 {24}
g) 2x 5 216
x 52
16
2
x 5 28
S 5 {28}
d) y2 2 3y 5 8 2 y
(22)2 2 3 ? (22) 5 8 2 (22)
4 1 6 5 8 1 2
10 5 10 R sentença verdadeira
Logo, 22 é raiz da equação y2 2 3y 5 8 2 y.
e) 2
1
6
3
1
2
x1 5 x2
2
2
3
1
6
3
2
3
1
2
1
? 1 5 ? 2
1
 
 

 

 
4
1
1
1 5 2
3
6
2
2 8
6
1
4
1
1 6
5 2
2
2 9
3
3
6

5
3
2
3 2

3
2 5 → sentença verdadeira
Logo,
2
3 é raiz da equação
2
1
6
3
1
2
x1 5 x2
.
3. Para x 5 0:
(0)2 2 5 ? (0) 1 6 5 0
0 2 0 1 6 5 0
6 5 0 R sentença falsa
Para x 5 1:
(1)2 2 5 ? (1) 1 6 5 0
1 2 5 1 6 5 0
Para x 5 2:
(2)2 2 5 ? (2) 1 6 5 0
4 2 10 1 6 5 0
Para x 5 3:
(3)2 2 5 ? (3) 1 6 5 0
9 2 15 1 6 5 0
Logo, 2 e 3 são as raízes da equação
x2 2 5x 1 6 5 0.
4. Para x 5
1
2
:
2
1
2
1
2
3
1
2
2
3
1
? 2 5 ? 2
1

 

 
 
 
2
3 2 5 2
2
2
1
1
2
3
2
1
9
4
2 2
5 6
2
6 1
2
5
6 5 → sentença falsa
h) 4x 5 240
x 52
40
4
x 5 210
S 5 {210}
i) 8x 5 28
x 52
8
8
x 5 21
S 5 {21}
j) 8x 5 28
x 52
8
8
x 5 21
S 5 {21}
k)
x
3
54
x 5 3 ? 4
x 5 12
S 5 {12}
1
3
l) x1 5
2
3
2
3
x5 2
1
3
x 5
1
3
S5
1
3


2.
a) 7x 2 6 5 5x 1 4
7 ? (5) 2 6 5 5 ? (5) 1 4
35 2 6 5 25 1 4
Logo, o número 5 é raiz da equação
7x 2 6 5 5x 1 4.
b) 3 1
x
x 20
2 5 6
1
3 6 1
( 6
) ? ( )2 5 120
6
18 2 1 5 1 1 20
Logo, o número 6 não é raiz da equação
x
3 x 2 1
5 1 20
.
6
c) 8 1 5x 5 0
8 5
8
5
0
1
1 ? 2 5
1

 

 
8 1 (28) 5 0
8 2 8 5 0
Logo, 2
8
5
é raiz da equação 8 1 5x 5 0.

120
Para x 5
1
3
:
2
1
3
1
2
3
1
3
2
3
1
? 2 5 ? 2
1
 
 

 

 
2
1
2
2 5 1
3
2
2
3 4
6
3
3
2
2 6
5 3
2
3 1
6
1
3 5 → sentença falsa
Para x 5
1
6
:
2
1
6
1
2
3
1
6
2
3
1
? 2 5 ? 2
3
1
2

 

 

 

 
1
3
1
1
2
2 2
5 2
2
3 2
6
3
3
4
2 6
5 6
2
6 1
6
2 52
1
6 → sentença verdadeira
Logo,
1
6
é raiz da equação 2
1
2
3
2
3
x2 5 x2 .
5.
Substituindo x por 25 na equação, temos:
3 ? (25 1 2) 2 5 ? (25 1 3) 5 1
3 ? (23) 2 5 ? (22) 5 1
29 1 10 5 1
Logo, 25 é raiz da equação 3 ? (x 1 2) 2 5 ?
? (x 1 3) 5 1, pois, substituindo x por 25,
obtemos uma igualdade verdadeira.
27 – Equações equivalentes
1.
a) x 1 4 5 7 e x 5 7 2 4
x 1 4 5 7
x1 4 1(24)571(24)
x 5 7 2 4
x 5 3
x 5 7 2 4 R x 5 3
As equações são equivalentes, pois
apresentam a mesma solução.
b) x 1 2 5 9 e x 5 7
x 1 2 5 9
x1 2 1(22)591(22)
x 5 9 2 2
x 5 7
x 5 7
c) x 2 5 5 0 e x 5 25
x 2 5 5 0
x2 5 1 5 5015
x 5 15
x 5 25
As equações não são equivalentes, pois
apresentam soluções diferentes.
d) 2x 5 18 e x 5 9
2
2
18
2
x
5
x 5 9
x 5 9
e) 5x 5 215 e x 5 3
5x 5 215
5
5
15
5
x
52
x 5 23
x 5 3
As equações não são equivalentes, pois
apresentam soluções diferentes.
f) x 2 1 5 23 e x 5 22
x 2 1 5 23
x2 1 1 1 52311
x 5 22
x 5 22
g) 4x 5 16 e x 5 4
4x 5 16
4
4
16
4
x
5
x 5 4
x 5 4
h) x 1 2 5 25 e x 5 27
x 1 2 5 25
x1 2 1(22)5251(22)
x 5 25 2 2
x 5 27
x 5 27
2.
a) x 1 2 5 5
x1 2 2 2 5522
x 5 3
S 5 {3}
b) x 2 11 5 0
x2 11 1 11 50111
x 5 11
S 5 {11}

121
c) 4x 5 28
4
4
8
4
x
52
x 5 22
S 5 {22}
d) x 2 2 5 21
x2 2 1 2 52112
x 5 1
S 5 {1}
e) 6x 5 6
6
6
6
6
x
5
x 5 1
S 5 {1}
f) 4x 5 3x 1 9
4x23x5 3x 192 3x
x 5 9
S 5 {9}
g) 3x 5 7
3
3
7
3
x
5
x 5
7
3
S5
7
3


h) 5x 1 1 5 16
5x 11 21 51621
5
x
15
5
5
5
x 5 3
S 5 {3}
i) x
4
3
10 5
4
x
4
3
10
4
5
2
? 5 ?
x 5
6
5
S5
6
5


j) 10x 2 2 5 7x
10x2 2 1 2 57x12
10x27x5 7x 122 7x
3
x
2
5
3
3
x 5
2
3
S5
2
3


k) 6x 1 5 5 6
6x1 5 2 5 5625
6
x
1
5
6
6
x 5
1
6
S5
1
6


l) 8x 1 4 5 0
8x1 4 2 4 5024
8
x
4
52
8
8
4
8
4

x 52 52
1
4 2

S5 2
1
2


28 – Equações do 1°- grau
com uma incógnita
1.
a) 2x 2 8 5 8
2x 5 8 1 8
2x 5 16
x 5
16
2
x 5 8
S 5 {8}
b) 3x 1 1 5 19
3x 5 19 2 1
3x 5 18
x 5
18
3
x 5 6
S 5 {6}
c) 7y 2 4 5 10
7y 5 10 1 4
7y 5 14
y 5
14
7
y 5 2
S 5 {2}
d) 2t 1 1 5 28
2t 5 28 2 1
2t 5 29
t 52
9
2
S5 2
9
2


e) 11 2 3y 5 2
23y 5 2 2 11
23y 5 29 ? (21)
3y 5 9
y 5
9
3
y 5 3
S 5 {3}

122
f) 3x 5 27 1 x
3x 2 x 5 27
2x 5 27
x 52
7
2
S5 2
7
2


g) 9x 1 5 5 4x
9x 2 4x 1 5 5 0
5x 5 25
x 52
5
5
x 5 21
S 5 {21}
h) 20 5 26x 1 32
0 5 2 6x 1 32 2 20
6x 5 12
x 5
12
6
x 5 2
S 5 {2}
2.
a) 7x 1 1 2 5x 5 9
2x 1 1 5 9
2x 5 9 2 1
2x 5 8
x 5
8
2
x 5 4
S 5 {4}
b) y 1 9y 1 5 5 215
10y 1 5 5 215
10y 5 215 2 5
10y 5 220
y 52
20
10
y 5 22
S 5 {22}
c) 17x 2 1 5 15x 1 3
17x 5 15x 1 3 1 1
17x 5 15x 1 4
17x 2 15x 5 4
2x 5 4
x 5
4
2
x 5 2
S 5 {2}
d) 16 2 x 5 x 1 25
2x 5 x 1 25 2 16
2x 5 x 1 9
2x 2 x 5 9
22x 5 9 ? (21)
2x 5 29
x 52
9
2
S5 2
9
2


e) 20x 2 13 5 20 1 9x
20x 5 20 1 9x 1 13
20x 5 33 1 9x
20x 2 9x 5 33
11x 5 33
x 5
33
11
x 5 3
S 5 {3}
f) 21x 1 1 5 11x 1 6
21x 5 11x 1 6 2 1
21x 5 11x 1 5
21x 2 11x 5 5
10x 5 5
x5 5
5
10
1
5
5 2
;
;
S5
1
2


g) 9x 2 23 5 13x 2 27
9x 5 13x 2 27 1 23
9x 5 13x 2 4
9x 2 13x 5 24
24x 5 24 ? (21)
4x 5 4
x 5
4
4
x 5 1
S 5 {1}
h) 0,8 1 2x 5 x 1 3,5
2x 5 x 1 3,5 2 0,8
2x 5 x 1 2,7
2x 2 x 5 2,7
x 5 2,7
S 5 {2,7}
3.
Resolvendo as equações, temos:
10y 1 4 5 16y 2 8 9x 2 4 5 6x 1 8
10y 5 16y 2 8 2 4 9x 5 6x 1 8 1 4
10y 5 16y 2 12 9x 5 6x 1 12
10y 2 16y 5 212 9x 2 6x 5 12
26y 5 212 ? (21) 3x 5 12
6y 5 12 x 5 4
y 5
12
6
S 5 {4}
y 5 2
S 5 {2}
a) O valor do número y é 2.
b) O valor do número x é 4.
c) O produto de y por x:
y ? x 5 2 ? 4 5 8

123
d) O quociente de y por x:
2
;
y
2
x 5 4
5
1
2 2
;
4.
2x 2 6 5 10 3x 2 5 5 4 5x 2 7 5 8
2x 5 10 1 6 3x 5 4 1 5 5x 5 8 1 7
2x 5 16 3x 5 9 5x 5 15
x 5
16
2 x 5
9
3 x 5
15
5
x 5 8 x 5 3 x 5 3
S 5 {8} S 5 {3} S 5 {3}
Logo, as equações equivalentes são:
3x 2 5 5 4 e 5x 2 7 5 8, pois apresentam a
mesma solução.
5.
Chamando o número desconhecido de x,
vem:
3x 1 90 5 5x
3x 5 5x 2 90
3x 2 5x 5 290
22x 5 290 ? (21)
2x 5 90
x 5
90
2
x 5 45
S 5 {45}
Logo, o número é 45.
1.
a) 3 2 (3x 2 6) 5 2x 1 (4 2 x)
3 2 3x 1 6 5 2x 1 4 2 x
23x 1 9 5 x 1 4
23x 5 x 1 4 2 9
23x 5 x 2 5
2 3x 2 x 5 25
24x 5 25 ? (21)
4x 5 5
x 5
5
4
S5
5
4


b) 4 ? (x 2 2) 5 4 1 2 ? (x 2 1)
4x 2 8 5 4 1 2x 2 2
4x 2 8 5 2x 1 2
4x 5 2x 1 2 1 8
4x 5 2x 1 10
4x 2 2x 5 10
2x 5 10
x 5
10
2
x 5 5
S 5 {5}
c) 7x 2 3 ? (x 2 2) 5 3 ? (x 1 4)
7x 2 3x 1 6 5 3x 1 12
4x 1 6 5 3x 1 12
4x 5 3x 1 12 2 6
4x 5 3x 1 6
4x 2 3x 5 6
x 5 6
S 5 {6}
d) 2 ? (y 2 2) 1 5 ? (2 2 y) 5 23 ? (2y 1 2)
2y 2 4 1 10 2 5y 5 26y 2 6
23y 1 6 5 26y 2 6
23y 5 26y 2 6 2 6
23y 5 26y 2 12
23y 1 6y 5 212
3y 5 212
y 52
12
3
y 5 24
S 5 {24}
e) 2 ? (1 2 t) 1 1 5 3 ? (t 2 3) 2 2t
2 2 2t 1 1 5 3t 2 9 2 2t
22t 1 3 5 t 2 9
22t 5 t 2 9 2 3
22t 5 t 2 12
22t 2 t 5 212
23t 5 212 ? (21)
3t 5 12
t 5
12
3
t 5 4
S 5 {4}
f) 5 ? (m 1 1) 2 3 ? (2m 1 1) 5 4 ? (5 2 m)
5m 1 5 2 6m 2 3 5 20 2 4m
2m 1 2 5 20 2 4m
2m 5 20 2 4m 2 2
2m 5 18 2 4m
2m 1 4m 5 18
3m 5 18
m5
18
3
m 5 6
S 5 {6}
2.
Para que a expressão seja igual a zero,
devemos ter:
x 2 2 ? (3 2 2x) 5 0
x 2 6 1 4x 5 0
5x 2 6 5 0
5x 5 6
x 5
6
5
S5
6
5


Logo, devemos ter x 5
6
5
.

124
3.
3 ? (1,4 2 x) 1 5x 5 2 (x 2 4,8)
4,2 2 3x 1 5x 5 2x 1 4,8
4,2 1 2x 5 2x 1 4,8
2x 5 2x 1 4,8 2 4,2
2x 5 2x 1 0,6
2x 1 x 5 1 0,6
3x 5 0,6
x 5
0 ,
6
3
x 5 0,2
S 5 {0,2}
Logo, x 5 0,2.
4.
(m 2 3 ) ? x 1 3x 1 4 ? (m 2 5) 5 0
Sendo x 5 2, temos:
(m 2 3) ? 2 1 3 ? 2 1 4 ? (m 2 5) 5 0
(m 2 3) ? 2 1 6 1 4 ? (m 2 5) 5 0
2m 2 6 1 6 1 4m 2 20 5 0
6m 2 6 1 6 2 20 5 0
6m 5 20
m5 5
:
:
20
6
10
3
2
2
S5
10
3


Logo, a letra m é expressa pelo número
10
3
.
5.
Sendo as expressões iguais, temos:
3 ? (1,2x 2 2,4) 5 2 ? (1 1 1,5x) 1 2,8
3,6x 2 7,2 5 2 1 3x 1 2,8
3,6x 2 7,2 5 4,8 1 3x
3,6x 5 4,8 1 3x 1 7,2
3,6x 5 12 1 3x
3,6x 2 3x 5 12
0,6x 5 12
x 5
12
0,6
x 5 20
S 5 {20}
Logo, x 5 20.
1.
a) x
x
1 5 5
12
5
5 5
60
5
x x
1 5
5x 1 x 5 60
6x 5 60
x 5
60
6
x 5 10
S 5 {10}
b) x
x
2 52 7
3
7
7 7
21
7
x x
2 52
7x 2 x 5 221
6x 5 221
x 52 52
21
6
7
3
3 2
;
;
S5 2
7
2


c)
x x
5 2
1 521
2
5
10
10
210
10
x x
1 52
2x 1 5x 5 210
7x 5 210
x 5
210
7
x 5 30
S 5 {30}
d) 5
5
7
5 23x
35
7
5
21
5 7
2
7 x
35 5 5 2 21x
0 5 5 2 21x 2 35
21x 5 230
x 52 52
30
21
10
3
3 7
;
;
S5 2
10
7


e) 1
x x
1
2 52 1
4 6 2
2
3
2
12
6
x 8
x
3
2 12
52 12
1
12 2 2 6x 5 28x 1 3
26x 5 28x 1 3 2 2
26x 5 28x 1 1
26x 1 8x 5 1
2x 5 1
x 5
1
2
S5
1
2


f)
3
8
5
6 3
5
2
y y
2 5 2
9
24
20
24
8
24
60
24
y y
2 5 2
9y 2 20 5 8y 2 60
9y 5 8y 2 60 1 20
9y 5 8y 2 40
9y 2 8y 5 240
y 5 240
S 5 {240}

125
2.
Para A 5 B, temos:
x x
2
2
3
1 5 1
5
2
4 10
20
x x
8
20
20
20
15
20
1 5 2
10x 1 8 5 20 2 15x
10x 5 20 2 15x 2 8
10x 5 12 2 15x
10x 1 15x 5 12
25x 5 12
x 5
12
25
S5
12
25


3.
Chamando o número de x, temos:
3
5
1
2
? x1 x
2
5 3 ? 18
30
x x
15
30
20
30
1 5
18x 1 15 5 20x
18x 5 20x 2 15
18x 2 20x 5 215
22x 5 215 ? (21)
2x 5 15
x5 ou x5
15
2
7,5

15
7 5 2

S5 ou S5
{ , }.
4.
Chamando o número desconhecido de x:
x x
4 1 x
256
6
5 3
2
12
12
12
12
672
12
x x x
1 5 2
3x 1 2x 5 12x 2 672
5x 5 12x 2 672
5x 2 12x 5 2672
27x 5 2672 ? (21)
7x 5 672
x 5
672
7
x 5 96
S 5 {96}
5.
Representando o número por x:
x
x
1 5 x2 5
2 30
5
5 5
10
5
150
5
x x x
1 5 2
5x 1 x 5 10x 2 150
6x 5 10x 2 150
6x 2 10x 5 2150
24x 5 2150 ? (21)
4x 5 150
150
4
75
2
2
;
x5 5 ou x5
37 5
2
;
,
6.
Se a pessoa calça 38, temos que N 5 38, então:
38
5
4
x
5 17
152
4
5
x
28
5 4
1
4 152 5 5x 1 28
0 5 5x 1 28 2 152
0 5 5x 2 124
25x 5 2124 ? (21)
5x 5 124
x 5
124
5
x 5 24,8  24,8 cm
1.
a) x
x
2 2
4
3
1
4 5
0
3
3
12
3
5 ( )
1 4
3
0
x x
2 2
? 1
3x 2 12 2 1 ? (x 1 4) 5 0
3x 2 12 2 x 2 4 5 0
2x 2 12 2 4 5 0
2x 2 16 5 0
2x 5 16
x 5
16
2
x 5 8
S 5 {8}
b) x
2
2 5
x 8
2
4
(x ) x
1 8
2
8
2
2
2
? 2
2 5
1 ? (x 2 8) 2 8 5 2x
x 2 8 2 8 5 2x
x 2 16 5 2x
x 5 2x 1 16
x 2 2x 5 16
2x 5 16 ? (21)
x 5 216
S 5 {216}
c) x2 x
2 2
8
5
4
3
(x ) ? (x2 )
3 2
24
8 4
24
? 2
5
3 ? (x 2 2) 5 8 ? (x 2 4)
3x 2 6 5 8x 2 32
3x 5 8x 2 32 1 6
3x 5 8x 2 26
3x 2 8x 5 226
25x 5 226 ? (21)

126
5x 5 26
x 5
26
5
S5
26
5


d)
4
3
3
2
3
3
x x
2 5
2
x x
8
6
9
6
2 3
6
2 5
? ( 2 )
8x 2 9 5 2 ? (x 2 3)
8x 2 9 5 2x 2 6
8x 5 2x 2 6 1 9
8x 5 2x 1 3
8x 2 2x 5 3
6x 5 3
x5 5
3
6
1
3
3 2
;
;
S5
1
2


e) 3
8
x x x
1
4 3
2
5
1
2
( x) (x ) x
3 3
24
6 1
24
8
24
? 2
5
? 1
2
3 ? (3 2 x) 5 6 ? (x 1 1) 2 8x
9 2 3x 5 6x 1 6 2 8x
23x 5 6x 1 6 2 8x 2 9
23x 5 22x 2 3
23x 1 2x 5 23
21x 5 23 ? (21)
x 5 3
S 5 {3}
f)
t2 t t
5 1
1
2
2 3 5 3
2
3 14
12
(t ) t ? ( t1 )
6 5
12
4
12
4
12
1 3 14
12
? 2
2 5 2
6 ? (t 2 5) 2 4 5 4t 2 1 ? (3t 1 14)
6t 2 30 2 4 5 4t 2 3t 2 14
6t 2 34 5 t 2 14
6t 5 t 2 14 1 34
6t 5 t 1 20
6t 2 t 5 20
5t 5 20
t 5
20
5
t 5 4
S 5 {4}
2.
2 ? ( x
1
1
)
5 2
2
x 3
2 1
(x ) x
3
6
3
3
3
? 1
5 2
2 ? (x 1 1) 5 6 2 3x
2x 1 2 5 6 2 3x
2x 5 6 2 3x 2 2
2x 5 23x 1 4
2x 1 3x 5 4
5x 5 4
x 5
4
5
S5
4
5


4
5
Logo, x5 5
0,8 , e se encontra entre os
números inteiros 0 e 1.
3. 2
3
( ) ( ) 1
5 2 3
3 4 1
x
x x 11
2
1 ? 2 5
? 2
4
6
1 ( ) 
6 5 2 3
6
3 3 4 1
6
66
6
x x x
1
? ? 2
5
? ? 2

( ) 

4 6 5 2 3 3 3 4 1 66 x x x 1 ? ? 2 5 ? ? 2 1 ( ) 

( ) 

4x 1 6 ? [10x 2 15] 5 3 ? [12x 2 3] 1 66
4x 1 60x 2 90 5 36x 2 9 1 66
64x 2 90 5 36x 1 57
64x 5 36x 1 57 1 90
64x 5 36x 1 147
64x 2 36x 5 147
28x 5 147
x5 5
147
28
21
7
7 4
;
;
S5

21
4
2 m
( ) m m
6 3 2
4
3 ? 2 2
4. 3 2
7 2
1
2
5
? 2 m m m ( ) 
6
3 7 1
6
2 4
6
? ? 2
2
? 2
5

( ) ( )
6 3 2 3 7 1 2 4 ? ? 2 2 ? 2 5 ? 2 m m m ( ) 

( ) ( )
6 ? [3m 2 6] 2 21m 1 3 5 2m 2 8
18m 2 36 2 21m 1 3 5 2m 2 8
23m 2 33 5 2m 2 8
23m 5 2m 2 8 1 33
23m 5 2m 1 25
23m 2 2m 5 25
25m 5 25 ? (21)
5m 5 225
m52
25
5
m 5 25
Logo, a solução da equação é um número
negativo.

Esvaziou se x ervatório
Esvaziou se x ervatório
127
5.
a) x2 x
4 2 1
2
3
5
2
8
(x ) ? (x2 )
8 4
24
24
24
3 2
24
? 2
2 5
8 ? (x 2 4) 2 24 5 3 ? (x 2 2)
8x 2 32 2 24 5 3x 2 6
8x 2 56 5 3x 2 6
8x 5 3x 2 6 1 56
8x 5 3x 1 50
8x 2 3x 5 50
5x 5 50
x 5
50
5
x 5 10
Os números naturais divisores de 10
são: 1, 2, 5 e 10.
b) Sendo x 5 10, o valor numérico da
expressão 0 1
1
, ; x
será:
0 1
1
, ; 0,1;0,1 1 x 5 5
c) Sendo x 5 10, o quadrado de x será:
102 5 10 ? 10 5 100
De acordo com as dicas, podemos escrever:
idade de Eva R x
idade de Ivo R x 1 6
soma das idades igual a 40 R x 1 x 1 6 5 40
2x 1 6 5 40
2x 5 40 2 6
2x 5 34
x 5
34
2
x 5 17
Logo, Eva tem 17 anos, e Ivo tem 23 (17 1 6)
anos de idade.
29 – Usando equações na
resolução de problemas
1. De acordo com o enunciado:
janeiro: 180 atendimentos
fevereiro, março, abril e maio tiveram a
mesma quantidade de atendimento. Sendo
x para cada mês, o total de atendimento
nesses meses é 4x.
junho: 160 atendimentos
Como o total de atendimentos no
1o semestre foi de 1 400 pessoas:
180 1 4x 1 160 5 1 400
340 1 4x 5 1 400
4x 5 1 400 2 340
4x 5 1 060
x 5
1 060
4
x 5 265
Logo, foram atendidas 265 pessoas nesses
meses.
capacidade do reservatório: x
−
Esvaziou −
se x



se litros de água
−
1
3
1
3
400
:
Retirou
Restou no reservatório: x
capacidade total do res
3
5


ervatório
Esvaziou se x
se litros de água
−
1
3
1
3
400
:
Retirou
3
5


−

se litros de água
−
1
3
1
3
400
:
−
Retirou
3
5


se litros de água
−
1
3
1
3
400
:
Retirou
3
5


ervatório
1
3
400
3
5
x1 1 x5x
5
15
x x x
6 000
15
9
15
15
15
1 1 5
5x 1 6 000 1 9x 5 15x
14x 1 6 000 5 15x
14x 5 15x 2 6 000
14x 2 15x 5 26 000
2x 5 26 000 ? (21)
x 5 6 000
Logo, cabem no reservatório 6 000 litros de
água.
trabalham na matriz: x
trabalham nas filiais: 4x
Como o total de funcionários é 1 365,
temos:
x 1 4x 5 1 365
5x 5 1 365
x 5
1 365
5
x 5 273
Logo, na matriz trabalham 273 funcionários
e nas filiais trabalham
1 092 (4 ? 273) funcionários
total de eleitores pesquisados: x
votos no candidato A,
votosnocandidatoA do total x
votosnocandi
, 40% :
40
100



datoB do total x
indecisos


, % : t
:
35
35
100
3500


otal de eleitorespesquisados
votos no candidato A 40% do ttoottaall: x
votosnocandi
, 40% :
40
100
votos no candidato B,
35% do total:
datoB do total x
indecisos
, % : t
:
35
35
100
3500


votosnocandi
, 40% :
40
100
datoB do total x
indecisos
, % : t
:
35
35
100
3500


indecisos: 3 500
votosnocandi
, 40% :
40
100
datoB do total x
indecisos
, % : t
:
35
35
100
3500


votosnocandi
, 40% :
40
100
datoB do total x
indecisos
, % : t
:
35
35
100
3500



umsextodo total caiu paraadireita x
128
40
100
35
100
3500
x x
1 1 5x
40
100
x x x
35
100
350 000
100
100
100
1 1 5
40x 1 35x 1 350 000 5 100x
75x 1 350 000 5 100x
75x 5 100x 2 350 000
75x 2 100x 5 2350 000
225x 5 2350 000 ? (21)
25x 5 350 000
x 5
350000
25
x 5 14 000
Logo, foram pesquisados 14 000 eleitores.
total de pérolas: x
um sexto do total caiu
umsexto do total caiupparaara aa ddirireeititaa: x
umqu oparaa
:
1
6
int esquerda :
x
:
umterço seguroucomamão direita :
x
1
5
1
3


décimoseguroucomamão esquerda :
x
pérolas ficar
1
10
am presas no colar


total de pérolas no c
.


olar
um quinto para a
esquerda:
umqu oparaa
:
1
6
int esquerda x
umterço seguroucomamão direita x
um
:
:
1
5
1
3
x
pérolas ficar
1
10
am presas no colar
.


olar
um terço segurou com
a mão direita:
umqu oparaa
:
1
6
int esquerda x
umterço seguroucomamão direita :
x
1
5
1
3
x
pérolas ficar
1
10
am presas no colar
.


olar
um décimo segurou
com a mão esquerda:
1
10
x
umqu oparaa
:
1
6
int esquerda x
umterço seguroucomamão direita x
um
:
:
1
5
1
3
x
pérolas ficar
1
10
am presas no colar
.


total de pérolas olar
no colar
seis pérolas ficaram
presas no colar.
1
1
1
6
5
3
1
10
x1 x1 x1 x165x
5
30
x x x x x
6
30
10
30
3
30
180
30
30
30
1 1 1 1 5
5x 1 6x 1 10x 1 3x 1 180 5 30x
24x 1 180 5 30x
24x 5 30x 2 180
24x 2 30x 5 2180
26x 5 2180 ? (21)
6x 5 180
x 5
180
6
x 5 30
Logo, esse colar tinha 30 pérolas.
capacidade do tanque: x
ponteiro indicava: 1
5
x
colocou: 46,2 litros
nova indicação: 3
4
x
A soma do que o ponteiro indicava com
o que foi colocado corresponde à nova
indicação. Então:
1
5
46 2
3
4
x1 , 5 x
4
20
x x
924
20
15
20
1 5
4x 1 924 5 15x
4x 5 15x 2 924
4x 2 15x 5 2924
211x 5 2924 ? (21)
11x 5 924
x 5
924
11
x 5 84
Logo, a capacidade total do tanque é de
84 litros.
7. De acordo com o enunciado, podemos
montar o seguinte diagrama:
Turistas
Inglês Espanhol
42 x 30 x
16 não falam inglês nem espanhol.
A soma desses valores é o total de turistas
pesquisados. Assim, montamos a equação:
(422x)1x1(302x)116570
42 2x 1x 1302x116570
2x 1 88 5 70
2x 5 70 2 88
2x 5 218 ? (21)
x 5 18
Logo, 18 turistas falavam inglês e espanhol
ao mesmo tempo.
8. Do enunciado, podemos escrever:
comprimento da tábua maior: x
comprimento da tábua menor: 3
5
x
A soma das duas partes da tábua é igual a
120 cm de comprimento, então:
x1 x5
3
5
120
5
5
3
5
600
5
x x
1 5
5x 1 3x 5 600
8x 5 600
x 5
600
8
x 5 75
comprimento da tábua maior: 75 cm ou
0,75 m
comprimento da tábua menor:
3
75 45
5
1
15
? 5 cm ou 0,45 m

129
Portanto, o comprimento da menor parte
da tábua é 0,45 m.
9.
percurso total: x
primeiro dia: 3
5
x
segundo dia: 4
15
x
terceiro dia: 800 km
Somando os três dias, teremos o percurso total:
3
4
5
15
x1 x18005x
9
15
x x x
4
15
12 000
15
15
15
1 1 5
9x 1 4x 1 12 000 5 15x
13x 1 12 000 5 15x
13x 2 15x 5 212 000
22x 5 2 12 000 ? (21)
2x 5 12 000
x 5
12 000
2
x 5 6 000
Logo, o percurso total foi 6 000 km.
Portanto, a aeronave voou 3 600 km
3
6000 3600
5
1
1 200
? 5

 

 
no primeiro dia.
escrever:
pontos na região A: x
pontos na região B:
x
2
a) Como Caio acertou 5 flechas na região
A e 4 na região B, perfazendo 140
pontos, temos:
x
5 ? x1 4
? 5
2
140
2
1
5x 1 2x 5 140
7x 5 140
x 5
140
7
x 5 20
Logo, cada flecha certeira na região A
vale 20 pontos.
b) Lucca acertou 8 flechas na região A e 5
na região B. Logo, ele fez:
8 20 5
20
2
? 1 ? ? 160 1 50 5 210
pontos
10
1
Como Caio fez 140 pontos e Lucca 210
pontos, Lucca fez 70 pontos (210 2 140 5
5 70) a mais que Caio.
escrever:
1o bimestre: x
2o bimestre: 2x
3o bimestre: 4x
4o bimestre: 8x
5o bimestre: 16x
6o bimestre: 32x
O ano tem 6 bimestres e os acessos
dobravam a cada visita. Sendo o total de
visitas 756, podemos escrever:
x 1 2x 1 4x 1 8x 1 16x 1 32x 5 756
63x 5 756
x 5
756
63
x 5 12
Logo, foram feitas 12 visitas no 1o bimestre
de 2007.
total de entrevistados: x
entrevistados que liam a revista A: 1
3 ? x
entrevistados que liam a revista B: 2
5 ? x
entrevistados que liam a revista C: 832
Somando os entrevistados das revistas
A, B e C, teremos o total de pessoas
entrevistadas:
1
2
3
5
x1 x18325x
5
15
x x x
6
15
12 480
15
15
15
1 1 5
5x 1 6x 1 12 480 5 15x
5x 1 6x 2 15x 5 212 480
24x 5 212 480 ? (21)
4x 5 12 480
x 5
12480
4
x 5 3 120
Logo, foram entrevistadas 3 120 pessoas.
Tiago ficou com x figurinhas.
6 x
2
6 1 2 1 x 5 30 R
R x 5 30 – 8 R x 5 22

130
Guilherme ficou com (x 1 20) figurinhas.
Como foram rasgadas 36 das 200 figurinhas,
sobraram 164 figurinhas
(200 2 36 5 164). Então:
x 1 (x 1 20) 5 164
x 1 x 1 20 5 164
x 1 x 5 164 2 20
2x 5 144
x 5
144
2
x 5 72
Logo, Tiago tem 72 figurinhas, e Guilherme
tem 92 figurinhas (72 1 20 5 92).
15. Sabemos que 1 hora 5 60 minutos, então:
12 horas 5 12 ? 60 5 720 minutos
Do enunciado, podemos escrever:
volume de água drenada pelo
encanamento 1: 720 ? 30 5 21 600 litros de
água
volume de água drenada pelo
encanamento 2: 720 ? x
Como o total de água drenada é de 72 000
litros:
21 600 1 720x 5 72 000
720x 5 72 000 2 21 600
720x 5 50 400
x 5
50 400
720
x 5 70
Logo, o segundo encanamento drena 70 litros
de água por minuto.
Brasil Real, página 150.
1. Do enunciado, vem:
• 200 000 ligações com doação de 7 reais:
7 ? 200 000 5 1 400 000
• 100 000 ligações com doação de 15 reais:
15 ? 100 000 5 1 500 000
Como foram arrecadados 4 400 000 reais
com todas as ligações, podemos escrever
que as doações de 30 reais foram:
1 400 000 1 1 500 000 1 30 ? x 5 4 400 000
30x 5 4 400 000 2 1 400 000 2 1 500 000
30x 5 1 500 000
1500000
x 5
30
x 5 50 000
Logo, foram 50 000 ligações com doação de
30 reais.
2. Sendo o total arrecadado em 2006 de
4 400 000 reais, e 4 840 projetos sociais
apoiados por essa campanha, podemos
escrever:
4 400000
.909,10
4840
Logo, se o total arrecadado foi
dividido igualmente entre os projetos
sociais apoiados, cada um receberia,
aproximadamente, R$ 909,10.
3. Se 73 mil telespectadores fizessem 3 liga-ções
no valor de 30 reais cada uma, pode-mos
escrever:
73 000 ? 3 ? 30 5 6 570 000
Logo, seria arrecadado R$ 6 570 000,00.
4. Se os 73 mil telespectadores fizessem
3 ligações no valor de 7, de 15 e de 30 reais
cada uma, o total arrecadado seria:
73 000 ? 3 ? 7 1 73 000 ? 3 ? 15 1 73 000 ? 3 ? 30 5
5 1 1 533 000 1 3 285 000 1 6 570 000 5
5 11 388 000
Logo, seria arrecadado R$ 11 388 000,00.
Desafios, página 150.
1. I. Alternativa e.
Realizando uma única pesagem, podemos
separar a massa de 24 kg em dois pratos
com embalagens de 12 kg cada uma.
Logo, é possível montar pacotes de 12 kg
cada um.
II. Alternativa c.
Realizando exatamente duas pesagens,
podemos na primeira pesagem distribuir
12 kg entre os dois pratos, de modo que a
balança atinja novamente o equilíbrio.
Para uma segunda pesagem, podemos
formar pacotes de 6 kg. Com um pacote de
12 kg e outro de 6 kg, podemos montar um
pacote de 18 kg.
Logo, realizando duas pesagens, podemos
montar pacotes de 6 kg, 12 kg e 18 kg.
escrever:
total de abelhas: x
total numa flor de Kadamba: 1
5 ? x
pousou numa flor de Silinda: 1
3 ? x
voa sobre uma flor da Krutaja: 3

 1
1
? x2 x 3
5  

131
A abelha que sobra voa atraída pelo
perfume do jasmim.
Como o total de abelhas é x:
1
5
1
1
1
? x1 ? x1 3
? x2 x 115x 3
3
5

  
1
5
1
3
3
5
15
x x
3
15
 
 
x x 1
1 1 ? 2 1 5x
1
5
1
3
3
2
15
1
1
5
x x
x

1 1 ? 1 5x
 

 
1
5
1
3
2
5
x
x x 1
1 1 1 5x
3
5
1
3
x1 x115x
9
15
x x x
5
15
15
15
15
15
1 1 5
9x 1 5x 1 15 5 15x
9x 1 5x 2 15x 5 215
2x 5 215 ? (21)
x 5 15
Logo, o número de abelhas é 15.
30 – Aplicação das equações:
as fórmulas matemáticas
1. Resposta pessoal. Contando o número de
quadradinhos que forma cada figura, temos:
a) A figura é composta por 24
quadradinhos.
b) A figura é composta por 9 quadradinhos.
c) A figura é composta por 6 quadradinhos.
d) A figura é composta por 16 quadradinhos.
Para calcular, bastou contar o número de
quadradinhos que formava cada figura.
2. Se cada quadradinho tem 1 cm de lado,
sua área será 1 ? 1 5 cm2. Logo, a área de
cada figura será:
• figura a: 24 cm2, pois é formada por
24 quadradinhos.
• figura b: 9 cm2, pois é formada por
9 quadradinhos.
• figura c: 6 cm2, pois é formada por
6 quadradinhos.
• figura d: 16 cm2, pois é formada por
16 quadradinhos.
altura do retângulo: x
medida da base: 2 ? x
Sendo o perímetro do retângulo 60 cm,
podemos escrever:
x 1 2x 1 x 1 2x 5 60
6x 5 60
x 5
60
6
x 5 10
Logo, a altura do retângulo é 10 cm, e a
medida da base é 20 cm (2 ? 10).
2. Sendo as medidas dos lados desse
triângulo expressas por três números
inteiros consecutivos, e sabendo que um
dos lados mede x, podemos escrever:
x 1 (x 1 1) 1 (x 1 2) 5 27
x 1 x 1 1 1 x 1 2 5 27
3x 1 3 5 27
3x 5 27 2 3
3x 5 24
x 5
24
3
x 5 8
Logo, as medidas dos lados desse triângulo
são: 8 cm, 9 cm e 10 cm.
3. Sendo π 5 3,14, o comprimento da
circunferência igual a 314 cm, e sabendo
que esse comprimento é expresso por
C 5 2 ? π ? r:
314 5 2 ? 3,14 ? r
314 5 6,28r
6,28r 5 314 (simétrica)
r5 5
314
6 28
50
,
Logo, o raio da circunferência é 50 cm.
4. Sendo a área do trapézio expressa por:
A
B b h
5
( 1 )?
2
, em que a base maior (B)
mede 20 cm, a altura (h) mede 15 m e a
área (A) vale 270 m2, temos:
( 20 1b)?
5
270
2 5
20 15
2
270
1 ?
5
( b)
300 15
270 1
2
5
b
300 15
2
540
2
1
5
b

132
300 1 15b 5 540
15b 5 540 2 300
15b 5 240
b5
240
15
b 5 16
Logo, a base menor do terreno mede 16 m.
5. Chamando de x a frente do terreno,
podemos escrever:
frente do terreno: x
lateral do terreno: 3x
Como o contorno do terreno mede 80
metros:
x 1 3x 1 x 1 3x 5 80
8x 5 80
x 5
80
8
x 5 10
Logo, se for colocada grade na frente do
terreno, serão necessários 10 metros de
grade.
6. Sabemos que a área A de um retângulo é
dada por comprimento “a” vezes a largura
“b”. Sendo uma das dimensões igual a
12 m, e área igual a 360 m2, temos:
A 5 a ? b
360 5 12 ? b
12b 5 360 (simétrica)
b5
360
12
b 5 30
Logo, a outra dimensão mede 30 m.
7. Sabemos que o perímetro de uma figura
é a soma das medidas dos lados. Logo, de
acordo com a figura, podemos escrever:
3x 1 2 1 3x 1 6 1 3x 1 2 1 3x 1 2 5 36
12x 1 12 5 36
12x 5 36 2 12
12x 5 24
x 5
24
12
x 5 2
Portanto, o valor de x é 2 cm.
Retomando o que aprendeu, páginas 153 a 155.
1. Alternativa c.
Resolvendo a equação, temos:
3 5
2
2 9
3
8
x1 x
2
2
5
3 3 5
6
2 2 9
6
48
6
? 1
2
? 2
5
( x ) ( x )
48
6 ? ( x1 )2 ? ( x2 )5
9x 1 15 2 4x 1 18 5 48
5x 1 33 5 48
5x 5 48 2 33
5x 5 15
x 5
3 3 5 2 2 9
15
5
x 5 3
Verificando as alternativas:
a)
3 15
15
3
5
x
x
52
52 52
b)
3 27
27
3
9
x
x
5
5 5
c) 3x 5 9
x 5
9
3
x 5 3
d) 3 15
15
3
5
x
x
5
5 5
e) 3 9
9
3
3
x
x
x
52
52
52
Logo, a raiz da equação
3 5
2
2 9
3
8
x1 x
2
2
5
é, também, raiz da equação 3x 5 9.
2. Alternativa a.
2x 1 x 1 (x 1 4) 5 116 R soma dos três
números
2x 1 x 1 x 1 4 5 116
4x 1 4 5 116
4x 5 112
x 5
112
4
x 5 28
Portanto, os três números são: 28, 56
(2 ? 28 5 56) e 32 (28 1 4 5 32). Logo, o
produto desses três números é 28 ? 56 ? 32 5
5 50 176.
3. Alternativa b.
3x 2 (x 1 1) 5 2x 1 1
3x 2 x 2 1 5 2x 1 1
2x 2 1 5 2x 1 1

133
2x 5 2x 1 1 1 1
2x 5 2x 1 2
2x 1 x 5 2
3x 5 2
x 5
2
3
Logo, o valor de x é
2
3
.
4. Alternativa a.
2 ? (1 2 0,4) 1 x 5 4 ? (0,1x 2 0,4)
2 2 0,8x 1 x 5 0,4x 2 1,6
2 1 0,2x 5 0,4x 2 1,6
0,2x 5 0,4x 2 1,6 2 2
0,2x 5 0,4x 2 3,6
0,2x 2 0,4x 5 23,6
20,2x 5 23,6 ? (21)
0,2x 5 3,6
x 5
3 ,
6
0 ,
2
x 5 18
Logo, o valor de x é 18.
5. Alternativa e.
Sendo 4 ônibus na excursão, e cada ônibus
com 35 alunos, temos:
4 ? 35 5 140
Portanto, participaram da excursão 140
alunos. Como havia, ao todo, 150 pessoas
na excursão, concluímos que 10 pessoas
(150 2 140 5 10) eram professores.
Logo, 10 professores foram a esse passeio.
6. Alternativa b.
Capacidade total do tanque: x
Escoou 68 litros de água, ficando a terça
parte da capacidade total: 1
3 ? x
Com isso, podemos escrever:
1
3
x1685x
1
3
204
3
1 3
5
3 x
1x 1 204 5 3x
1x 5 3x 2 204
1x 2 3x 5 2204
22x 5 2204 ? (21)
2x 5 204
x 5
204
2
x 5 102
Logo, a capacidade do tanque é 102 litros.
7. Alternativa c.
Sendo o valor da média 12,5:
x2 1x1 x1 x1
( 4 ) 2 2 ( 6
) 12 ,
5 4
5
x2 1x1 x1 x1
5
4 2 2 12
4
12,5
6 8
4
12 5
x 1
5 ,
6 8
4
50
4
x 1
5
6x 1 8 5 50
6x 5 50 2 8
6x 5 42
x 5
42
6
x 5 7
Logo, o número x é 7.
8. Alternativa d.
Do enunciado, vem:
total de jogos: x
venceu: 3
5 ? x
empatou:
1
3 ? x
Perdeu 2 jogos.
Daí, podemos escrever:
3
1
5
3
1 x125x
9
15
x x x
5
15
30
15
15
15
1 1 5
9x 1 5x 1 30 5 15x
9x 1 5x 5 15x 2 30
9x 1 5x 2 15x 5 230
14x 2 15x 5 230
2x 5 230 ? (21)
x 5 30
A equipe venceu
3
5
dos jogos que
disputou, logo:
3
30
5
1
6
?
Portanto, a equipe venceu 18 jogos.
9. Alternativa b.
Sendo x a hora adicional e R$ 21,00 o valor
pago, temos:
6 1 3x 5 21
3x 5 21 2 6
3x 5 15
x 5
15
3
x 5 5
Logo, o carro ficou no estacionamento
5 horas adicionais mais a primeira hora,
ou seja, 6 horas (1 1 5 5 6).

134
10. Alternativa a.
Sendo o número x, temos:
x1 x5 x2
1
5
2 30
5
5
1
5
10
5
150
5
x x x
1 5 2
5x 1 1x 5 10x 2 150
5x 1 1x 2 10x 5 2150
24x 5 2150 ? (21)
4x 5 150
x 5
150
4
x 5 37,5
Logo, o número é 37,5.
11. Alternativa e.
total de recenseadores: x
Se cada recenseador visitar 100
residências, faltariam 60 residências:
100 ? x 1 60
Se cada recenseador visitar 102 residências,
todas seriam visitadas: 102 ? x
Daí, podemos escrever:
100x 1 60 5
102x → total de r
esidências

total de residências
100x 5 102x 2 60
100x 2 102x 5 260
22x 5 260 ? (21)
2x 5 60
x 5
60
2
x 5 30
Logo, foram contratados 30 recenseadores.
12. Alternativa c.
( ) 5
3 2 5
5 3
2
x
x 2 x 2 2
0
2
6
2
5 ( ) 
2 2 5
2
1 5 3
2
0
2
x x x
2
? 2
2
? 2

( )
6 2 2 5 1 5 3 0 x x x 2 ? 2 2 ? 2 5 ( ) 

( )
6x 2 2 ? [2x 2 10] 2 5 1 3x 5 0
6x 2 4x 1 20 2 5 1 3x 5 0
5x 1 15 5 0
5x 5 215
x 52
15
5
x 5 23
13. Alternativa a.
custo da bola de vôlei: x
custo da bola de basquete: x 1 40
Como foram compradas 6 bolas de
basquete e 10 bolas de vôlei, podemos
escrever:
10 ? x 1 6 ? (x 1 40) 5 1 280
10x 1 6x 1 240 5 1 280
16x 1 240 5 1 280
16x 5 1 280 2 240
16x 5 1 040
x 5
1 040
16
x 5 64
O custo de cada bola de basquete foi 105
reais (65 1 40 5 105). Como o professor
comprou 6 bolas de basquete, temos:
6 ? 105 5 630
Logo, foram gastos R$ 630,00 com as bolas
de basquete.
14. Alternativa b.
• total de amigos: x
• Se cada amigo recebeu 2 convites,
sobrarão 25 R 2x 1 25
• Se cada amigo recebeu 3 convites,
faltarão 15 R 3x 2 15
Daí, vem:
2x 1 25 5 3x 2 15
2x 5 3x 2 15 2 25
2x 5 3x 2 40
2x 2 3x 5 240
2x 5 240 ? (21)
x 5 240
A quantidade de convites disponíveis é:
2 ? 40 1 25 5 80 1 25 5 105
Logo, são 40 amigos e 105 convites.
Se cada amigo recebeu 4 convites, serão
necessários 160 convites (4 ? 40 5 160).
Como só há 105 convites disponíveis, ainda
faltariam 55 convites (160 2 105 5 55).
15. Alternativa c.
1a pergunta, ganhou: x
2a pergunta, ganhou: 2x
O candidato recebeu R$ 15 000,00 por ter
acertado as perguntas. Então:
x 1 2x 1 3x 1 4x 5 15 000
10x 5 15 000
x 5
15 000
10
x 5 1 500
Logo, o prêmio inicial era de R$ 1 500,00.

135
16. Alternativa b.
1a parte da tábua: 1,80 m
2a parte da tábua: 2x
3a parte da tábua: x
Como o comprimento total da tábua é de
5,85 metros, temos:
1,80 1 2x 1 x 5 5,85
1,80 1 3x 5 5,85
3x 5 5,85 2 1,80
3x 5 4,05
x 5
4 ,
05
3
x 5 1,35
Logo, o comprimento da segunda parte, em
metros, é 2,70 (2 ? 1,35 5 2,70).
31 – Equação do 1°- grau
com duas incógnitas
1. De acordo com cada situação, podemos
escrever:
a) x 1 y 5 61
b) 2x 2 7 5 y
c) 3x 1 5y 5 100
d) x 5 y 1 7 ou x 2 y 5 7
e) 1
2
? x52y
f) 2
3
3
5
? x2 ? y51
2. Sendo x a idade de Mariana e y a idade de
Gabriela podemos escrever:
x 2 y 5 2
3. Sendo x o preço do livro e y o preço do
caderno:
a) x 1 y 5 32
b) x 5 y 1 25
c) x 5 6 ? y
d) 2 ? x 1 5 ? y 5 60
4. Sendo x o número de carros e y o número
de motos:
a) Como no estacionamento há 20
veículos, temos: x 1 y 5 20
b) Sendo o número de carros igual ao triplo
do número de motos, temos: x 5 3y
c) Como o número de carros supera o
número de motos em 12, podemos
escrever: x 5 y 1 12
d) Sendo a metade do número de carros
igual a cinco vezes o número de motos:
1
2
? x55? y
e) Como no estacionamento há 42 rodas,
podemos escrever:
4x 1 2y 5 42
5. Sendo a equação 9 ? x 1 y 5 1:
a) (0, 1) R 9 ? 0 1 1 5 1
0 1 1 5 1
1 5 1 R igualdade
verdadeira, logo, o par ordenado é
solução da equação.
b) (1, 0) R 9 ? 1 1 0 5 1
9 1 0 5 1
9 5 1 R igualdade falsa,
logo, o par ordenado não é solução da
equação.
c) (1, 28) R 9 ? 1 1 (28) 5 1
9 2 8 5 1
1 5 1 R igualdade
verdadeira, logo, o par ordenado é
d) (21, 10) R 9 ? (21) 1 10 5 1
29 1 10 5 1
1 5 1 R
R igualdade verdadeira, logo, o par
ordenado é solução da equação.
6. Sendo a equação 2x 1 3y 5 1, vem:
a) (21, 21) R 2 ? (21) 1 3 ? (21) 5 1
22 2 3 5 1
25 5 1 R
R igualdade falsa, logo, o par ordenado
não é solução da equação.
b) (21, 1) R 2 ? (21) 1 3 ? (1) 5 1
22 1 3 5 1
1 5 1 R
R igualdade verdadeira, logo, o par
ordenado é solução da equação.
7. Sendo x a medida do lado do quadrado e y
a medida do lado do triângulo equilátero,
temos:
a) perímetro do quadrado: 4x
perímetro do triângulo: 3y
Logo, 4x 5 3y.
b) Se o lado do quadrado mede 15 cm, o
lado do triângulo medirá:

136
4 ? 15 5 3y
60 5 3y
3y 5 60
y 5
60
3
y 5 20
Logo, o lado do triângulo medirá 20 cm.
b) Se o lado do triângulo mede 12 cm, o
lado do quadrado medirá:
4x 5 3 ? 12
4x 5 36
x 5
36
4
x 5 9
Logo, o lado do quadrado medirá 9 cm.
8. Depois de algumas tentativas, o único par
ordenado que é solução das equações
x 1 y 5 3 e x 2 y 5 1, é o par (2, 1).
x 1 y 5 3
2 1 1 5 3
3 5 3 R verdadeira
x 2 y 5 1
2 2 1 5 1
1 5 1 R verdadeira
Outra maneira para a resolução seria:
Como o par ordenado tem de satisfazer
as duas equações, podemos isolar x
na primeira equação e substituí-lo na
segunda, ou seja:
x 1 y 5 3 R x 5 3 2 y (I) e x 2 y 5 1 (II)
Substituindo (I) em (II):
3 2 y 2 y 5 1
22y 5 1 2 3
22y 5 22 ? (21)
2y 5 2
y 5
2
2
y 5 1
Sendo x 5 3 2 y e substituindo o valor de y,
temos:
x 5 3 2 1
x 5 2
Logo, o par ordenado que satisfaz as
equações é (2, 1).
9. Sendo as equações x 1 2y 5 21 e x 2 2y 5
5 7, temos:
• (3, 22) em x 1 2y 5 1 R 3 1 2 ? (22) 5 21
3 2 4 5 21
21 5 21 R
R igualdade verdadeira
• (3, 22) em x 2 2y 5 7 R 3 2 2 ? (22) 5 7
3 1 4 5 7
7 5 7 R
Logo, o par (3, 22) é solução para as
equações x 1 2y 5 21 e x 2 2y 5 7.
10. Existem várias possibilidades de resposta.
Três possíveis respostas seriam os pares:
(7, 1); (3, 3); (5, 2)
• (7, 1) em x 1 2y 5 9 R 7 1 2 ? 1 5 9
7 1 2 5 9
9 5 9 R
• (3, 3) em x 1 2y 5 9 R 3 1 2 ? 3 5 9
3 1 6 5 9
9 5 9 R
• (5, 2) em x 1 2y 5 9 R 5 1 2 ? 2 5 9
5 1 4 5 9
9 5 9 R
11. Sendo a equação 4x 1 y 5 20, temos:
a) se x 5 0 R 4 ? 0 1 y 5 0
0 1 y 5 20
y 5 20
Logo, quando x 5 0, uma solução é o par
ordenado (0, 20).
b) se x52 ? 2 1y5
3
4
4 3
4
20
1
1
→

 

 
23 1 y 5 20
y 5 20 1 3
y 5 23
Logo, quando x 52
3
4 , uma solução é o
par ordenado 2
3
4
,23

 

 
.
12. Sendo a equação 10x 2 3y 5 7:
a) se y 5 1 R 10x 2 3 ? 1 5 7
10x 2 3 5 7
10x 5 7 1 3
10x 5 10
x 5
10
10
x 5 1
Logo, quando y 5 1, uma solução é o par
ordenado (1, 1).

137
13
3
b) se y5 10 x2 3
? 5
13
3
7
1
1
→

 

 
10x 2 13 5 7
10x 5 7 1 13
10x 5 20
x 5
20
10
x 5 2
Logo, quando y 5
13
3
, uma solução é o
par ordenado 2
13
3
,  
 
.
13. Sendo x 5 5y 1 6, o valor de y em cada
uma das equações será:
a) 2 ? x 1 y 5 34
2 ? (5y 1 6) 1 y 5 34
10y 1 12 1 y 5 34
11y 1 12 5 34
11y 5 34 2 12
11y 5 22
y 5
22
11
y 5 2
b) 3 ? x 2 2 ? y 5 221
3 ? (5y 1 6) 22y 5 221
15y 1 18 2 2y 5 221
13y 1 18 5 221
13y 5 2 21 2 18
13y 5 239
y 52
39
13
y 5 23
c) 5 ? x 5 y
5 ? (5y 1 6) 5 y
25y 1 30 5 y
25y 5 y 2 30
25y 2 y 5 230
24y 5 230
y 52 52
30
24
5
6
6 4


32 – Sistemas de duas equações do
1°- grau com duas incógnitas
considerar as seguintes possibilidades:
Número de
partidas vencidas
Número de
partidas perdidas
Número de partidas
disputadas (soma das
partidas vencidas com
as partidas perdidas)
Soma dos pontos
de acordo com as
partidas disputadas
0 4 0 1 4 5 4 0 ? (2) 1 4 ? (1) 5 4
1 3 1 1 3 5 4 1 ? (2) 1 3 ? (1) 5 5
2 2 2 1 2 5 4 2 ? (2) 1 2 ? (1) 5 6
3 1 3 1 1 5 4 3 ? (2) 1 1 ? (1) 5 7
4 0 4 1 0 5 4 4 ? (2) 1 0 ? (1) 5 8
2. O único par que satisfaz as duas
condições apresentadas é o par (3, 1), pois
3 1 1 5 4 é o número de partidas
disputadas e 3 ? (2) 1 1 ? (1) 5 7
corresponde aos pontos somados.
3. Sendo x o número de partidas vencidas
e y o número de partidas perdidas, e
sabendo que a equipe disputou 30 jogos
no total e somou 51 pontos, podemos
escrever as seguintes equações para essa
situação:
x 1 y 5 30 (I) e 2 ? x 1 1 ? y 5 51 (II)
Depois de algumas tentativas verificamos
que o único par ordenado que satisfaz as
equações I e II é o par (21, 9), ou seja, a
equipe venceu 21 partidas e perdeu 9.
Logo, a equipe teve 21 vitórias e 9 derrotas.
1.
a) Chamando a quantidade de figurinhas
de Carlos de x, e as de Celso de y, temos:
x 1 y
5
201
x 5
2
y

b) Chamando a quantidade de livros
com espessura de 3 cm de x, e com
espessura de 5 cm de y, temos:
x 1 y
5
15
x 1 y
5

3 5 50
2. Sendo o par ordenado (8, 1) e o sistema
x y
x y
8 0
3 5
2 5
2 5

, vem:
(8, 1) em x 2 8y 5 0 R 8 2 8 ? (21) 5 0
8 2 8 5 0
0 5 0 R
(8, 1) em x 2 3y 5 5 R 8 2 3 ? (1) 5 5
8 2 3 5 5
5 5 5 R

138
Logo, o par (8, 1) satisfaz as duas equações
e, por isso, é solução do sistema.
3. Sendo o par ordenado (23, 5) e o sistema
3 x 2 y
12
3 x 8 y
31
2 1 5
1 5

, vem:
(23, 5) em 2x 1 2y 5 12 R 2(23) 1 2 ? (5) 5 12
13 1 10 5 12
13 5 12 R igualdade
falsa
(23, 5) em 3x 1 8y 5 31 R 3 ? (23) 1 8 ? (5) 5 31
29 1 40 5 31
31 5 31 R igualdade
verdadeira
Logo, o par (23, 5) satisfaz apenas a
equação 3x 1 8y 5 31 e, por isso, não é
solução do sistema, pois não satisfaz a
primeira equação.
4.
a)
x y
x y
20
1 5
2 52
3 12

(II)
Da primeira equação, vem:
x 1 y 5 20 R x 5 20 2 y (I)
Substituindo I em II:
x 2 3y 5 212
(220y) 2 3y 5 212
20 2 y 2 3y 5 212
24y 5 212 2 20
24y 5 232 ? (21)
4y 5 32
y 5
32
4
y 5 8
Substituindo y em (I):
x 5 20 2 y
x 5 20 2 8
x 5 12
Logo, a solução do sistema é o par
ordenado (12, 8).
b)
( )
x 5
2
yI
x 2 y 5
II
2 5 3
( )
 

Substituindo (I) em (II), temos:
2x 2 5y 5 3
2 ? (2y) 2 5y 5 3
4y 2 5y 5 3
2y 5 3 ? (21)
y 5 23
x 5 2y
x 5 2 ? (23)
x 5 26
ordenado (26, 23).
5.
a)
x y
x y
10
1 5
1 5
3 14

Da primeira equação:
x 1 y 5 10 R x 5 10 2 y (I)
Da segunda equação, temos:
x 1 3y 5 14 R x 5 14 2 3y (II)
Comparando as equações (I) e (II):
10 2 y 5 14 2 3y
2y 5 14 2 3y 2 10
2y 5 4 2 3y
2y 1 3y 5 4
2y 5 4
y 5
4
2
y 5 2
x 5 10 2 y
x 5 10 2 2
x 5 8
ordenado (8, 2).
b)
( )  
y 6
xI
x y
5
2 5
3 2 54

3x 2 2y 5 54
22y 5 54 2 3x ? (21)
2y 5 254 1 3x
25413
x
y
2 ( )
5 II
Comparando as equações (I) e (II):
6
54 3
2
x
x
5
2 1
x x
12
2
1 54 3
2
5
? (2 1 )
12x 5 1 ? (254 1 3x)
12x 5 254 1 3x
12x 2 3x 5 254
9x 5 254

139
x 52
54
9
x 5 26
Substituindo x em (I):
y 5 6x
y 5 6 ? (23) 5 236
ordenado (26, 236).
6.
a)
x 1 y 5
6
I
x 5 y 1
2
II
( )
( )
 

Substituindo (II) em (I):
x 1 y 5 6
y 1 2 1 y 5 6
2y 5 6 2 2
2y 5 4
y 5
4
2
y 5 2
Substituindo y em (II):
x 5 y 1 2
x 5 2 1 2
x 5 4
ordenado (4, 2).
b)
( )
x 5
2
yI
x 1 y 5
II
2 5 9
( )
 

Substituindo a equação (I) em (II):
2x 1 5y 5 9
2 ? (2y) 1 5y 5 9
4y 1 5y 5 9
9y 5 9
y 5
9
9
y 5 1
x 5 2y
x 5 2 ? 1
x 5 2
ordenado (2, 1).
c)
x 1 y
5
x 2 y 5
II
5
1 ( )
  
Da primeira equação, temos:
x 1 y 5 5 R x 5 5 2 y (I)
x 2 y 5 1
(5 2 y) 2 y 5 1
5 2 y 2y 5 1
22y 5 1 2 5
22y 5 24 ? (21)
2y 5 4
y 5
4
2
y 5 2
x 5 5 2 y
x 5 5 2 2
x 5 3
ordenado (3, 2).
d)
2 3
3 2 8
x y
x y II
2 5
1 5 ( )
 

2x 2 y 5 3
2y 5 3 2 2x ? (21)
y 5 23 1 2x (I)
3x 1 2y 5 8
3x 1 2 ? (23 1 2x) 5 8
3x 2 6 1 4x 5 8
7x 5 8 1 6
7x 5 14
x 5
14
7
x 5 2
y 5 23 1 2x
y 5 23 1 2 ? (2)
y 5 23 1 4
y 5 1
ordenado (2, 1).
e)
( )
( )
 

y 5 3 x 1
2
I
x 2 y 52
II
2 4
2x 2 y 5 24
2x 2 (3x 1 2) 5 24
2x 2 3x 2 2 5 24
2x 5 24 1 2
2x 5 22 ? (21)
x 5 2

140
y 5 3x 1 2
y 5 3 ? (2) 1 2
y 5 6 1 2
y 5 8
ordenado (2, 8).
f)
2 5
8 5
x y
x y II
1 5
2 5 ( )
 

2x 1 y 5 5 R y 5 5 2 2x (I)
8x 2y 5 5
8x 2 (5 2 2x) 5 5
8x 2 5 1 2x 5 5
10x 5 5 1 5
10x 5 10
x 5
10
10
x 5 1
Substituindo x em (II):
8x 2 y 5 5
8 ? (1) 2 y 5 5
8 2 y 5 5
2y 5 5 2 8
y 5 23 ? (21)
y 5 3
ordenado (1, 3).
montar o seguinte sistema, sendo x carros
e y motos:
x 1 y
5
22
x 1 y 5
II
 

4 2 74 ( )
x 1 y 5 22 R x 5 22 2 y (I)
4x 1 2y 5 74
4 ? (22 2 y) 1 2y 5 74
88 2 4y 1 2y 5 74
22y 5 74 2 88
22y 5 214 ? (21)
2y 5 14
y 5
14
2
y 5 7
x 5 22 2 y
x 5 22 2 7
x 5 15
Logo, na revendedora há 15 carros e
7 motos.
8. Sendo x o preço do sorvete e y o preço do
doce:
x 2 y
5
4
x 1 y 5
II
2 13( )
 

Da primeira equação, podemos escrever:
x 2 y 5 4 R x 5 4 1 y (I)
x 1 2y 5 13
(4 1 y) 1 2y 5 13
4 1 y 1 2y 5 13
3y 5 13 2 4
3y 5 9
y 5
9
3
y 5 3
x 5 4 1 y
x 5 4 1 3
x 5 7
Logo, o preço do sorvete é 7 reais.
9. Chamando a lapiseira de x e a caneta de
y:
x 3
yI
x y II
( )
( )
5
1 5
24
 

x 1 y 5 24
3y 1 y 5 24
4y 5 24
y 5
24
4
y 5 6
x 5 3y
x 5 3 ? (6)
x 5 18
Logo, a lapiseira custa 18 reais, e a caneta
custa 6 reais.

141
10. Sabendo que o mais velho tem x anos,
podemos dizer que o mais novo tem y
anos. Assim:
x 2 y
5
x 1 y 5
II
4
20 ( )
 
 
Da primeira equação, podemos escrever:
x 2 y 5 4 R x 5 4 1 y (I)
x 1 y 5 20
(4 1 y) 1 y 5 20
4 1 y 1 y 5 20
2y 5 20 2 4
2y 5 16
y 5
16
2
y 5 8
x 5 4 1 y
x 5 4 1 8
x 5 12
Logo, os filhos do professor têm 12 e 8 anos.
11. Do enunciado, podemos montar o
seguinte sistema:
x 1 y 5
2 ,
85
II
x 5 y 1
0 ,
93
I
( )
()
 
 
x 1 y 5 2,85
(y 1 0,93) 1 y 5 2,85
y 1 0,93 1 y 5 2,85
2y 5 2,85 2 0,93
2y 5 1,92
y 5
1 ,
92
2
y 5 0,96
x 5 y 1 0,93
x 5 0,96 1 0,93
x 5 1,89
Logo, o comprimento da parte menor é
0,96 m, e o comprimento da parte maior é
1,89 m.
5
3
()
( )
x 5 ?
yI
x 1 y 5
1 60
II



 
,
Substituindo a equação (I) em (II), temos:
x 1 y 5 160
5
3
y1y5160
5
3
3
3
480
3
y y
1 5
5y 1 3y 5 480
8y 5 480
y 5
480
8
y 5 60
x5 ? y
5
3
5
3
x5 ?
60
1
20
x 5 100
Logo, já foram lidas 100 páginas do livro.
13.
De acordo com o enunciado:
x 5
4
y ()
I
x 1 y 5
30
II
( )
 
 
Substituindo a equação (I) em (II):
x 1 y 5 30
4y 1 y 5 30
5y 5 30
y 5
30
5
y 5 6
x 5 4y
x 5 4 ? (6)
x 5 24
Logo, 6 professores ensinam Matemática
nesse colégio.
1.
De acordo com as balanças, a soma de um
cubo com duas esferas equivale a 8 kg, e
uma esfera equivale à soma de um cubo
com 1 kg. Daí, podemos montar o seguinte
sistema, sendo a esfera x e o cubo y:
2 8
x 1 y 5
I
x 5 y 1
1
II
()
( )
 
 

142
Substituindo (II) em (I):
2x 1 y 5 8
2 ? (y 1 1) 1 y 5 8
2y 1 2 1 y 5 8
3y 5 8 2 2
3y 5 6
y 5
6
3
y 5 2
Substituindo y em (II):
x 5 y 1 1
x 5 2 1 1
x 5 3
Logo, como a esfera pesa 3 quilogramas,
para equilibrar a balança, serão
necessários 3 pesos de 1 quilograma.
2. Chamando de x o peso do cubo, de y o
peso da esfera e de z o peso da pirâmide,
de acordo com os valores marcados nas
balanças, podemos montar o seguinte
sistema:
x y z III
y z
x y
 ( )
1 1 5
1 5
1 5
23
11
 
 
2 28
Da segunda equação, vem:
y 1 z 5 11 R z 5 11 2 y (I)
Da terceira equação, temos:
2x 1 y 5 28 R y 5 28 2 2x (II)
x 1 y 1 z 5 23
x 1 y 1 (11 2 y) 5 23
x1 y 1112 y 523
x 1 11 5 23
x 5 23 2 11
x 5 12
Substituindo x em (II):
y 5 28 2 2x
y 5 28 2 2 ? (12)
y 5 28 2 24
y 5 4
z 5 11 2 y
z 5 11 2 (14)
z 5 11 2 4
z 5 7
Logo:
a) o cubo tem 12 kg.
b) a pirâmide tem 7 kg.
c) a esfera tem 4 kg.
1. Resolvendo o sistema:
x 1 y
5
67
x 2 y 5
II
2 46 ( )
 

x 1 y 5 67 R x 5 67 2 y (I)
x 2 2y 5 46
(67 2 y) 2 2y 5 46
67 2 y 2 2y 5 46
23y 5 46 2 67
23y 5 221 ? (21)
3y 5 21
y 5
21
3
y 5 7
x 5 67 2 y
x 5 67 2 (7)
x 5 67 2 7
x 5 60
Logo, o 14 Bis percorreu 60 metros, durante
7 segundos.
2. Resolvendo o sistema:
 

x 2 y
52
52
x 2 y 5
II
10 2 ( )
x 2 y 5 252 R 2 y 5 252 2 x ? (21)
y 5 52 1 x (I)
10x 2 y 5 2
10x 2 (52 1 x) 5 2
10x 2 52 2 x 5 2
9x 5 2 1 52
9x 5 54
x 5
54
9
x 5 6
y 5 52 1 x
y 5 52 1 6
y 5 58
Logo, D. Pedro II foi aclamado imperador com
6 anos de idade e reinou durante 58 anos.

143
montar o seguinte sistema:
y 5 x 1
21
( I
)
2 x 2 y 5
1840
( II
)

2x 2 y 5 1 840
2x 2 (x 1 21) 5 1 840
2x 2 x 2 21 5 1 840
x 5 1 840 1 21
x 5 1 861
y 5 x 1 21
y 5 1 861 1 21
y 5 1 882
Logo, o primeiro volume de Machado de
Assis foi impresso em 1861 e Papéis avulsos,
em 1882.
a) Borracha branca – látex Rjaneiro 2007
(0,28) e janeiro 2008 (0,28)
b) Lápis de cor R de 2,60 para 2,34
Caneta hidrográfica R de 4,80 para 4,74
Caneta esferográfica R de 0,58 para 0,53
Cola branca lavável R de 0,95 para 0,60
Caderno universitário (96 folhas) R
R de 8,56 para 8,19
c) Completando a tabela com as
diferenças de preço, temos:
Produto
Preço médio (em reais)
Variação de preço
Janeiro/2007 Janeiro/2008
Lápis preto no 2 (unidade) 0,36 0,39 (0,39 2 0,36) R 0,03
Lápis de cor (caixa com 12 cores) 2,60 2,34 (2,34 2 2,60) R 20,26
Caneta hidrográfica (conjunto com
4,80 4,74 20,06
12 cores)
Caneta esferográfica cristal (unidade) 0,58 0,53 20,05
Borracha branca – látex (unidade) 0,28 0,28 0
Cola bastão (10 g) 2,55 1,99 20,56
Cola branca lavável (40 g) 0,95 0,60 20,35
Régua plástica cristal (30 cm) 1,03 1,05 0,02
Caderno universitário/capa dura/
8,56 8,19 20,37
espiral/1 matéria (96 folhas) (96 folhas)
Caderno universitário/capa dura/
espiral/10 matérias (200 folhas)
14,72 15,42 0,70
Caderno brochura 1/4 de capa dura
(96 folhas)
2,16 2,41 0,25
Fonte: ,www.procon.sp.gov.br. Acesso em: 15 out. 2008.
d) As variações de preços que tiveram
queda estão indicadas com valores
negativos.
e) Pela tabela do item c, observamos que
o produto que apresentou a maior
queda de preço foi a cola bastão
(20,56).
f) Tabela R caderno universitário
(200 folhas) (0,70).
1. Alternativa c.
De acordo com o enunciado, Caio ganhou x
e Celso ganhou y, então:
2x 2 3y 5 10
2. Alternativa d.
I) (2 7,5) em 8x 1 5y 5 231 R
R 8 ? (27) 1 5 ? (5) 5 231
256 1 25 5 231
231 5 231 (igualdade
verdadeira)
Logo, I é verdadeira.
II) (10, 25) em 4x 2 5y 5 65 R
R 4 ? (10) 2 5 ? (25) 5 65
40 1 25 5 65
65 5 65 (igualdade verdadeira)
(10, 25) em x 5 2y R 10 5 2 ? (25)
10 5 210
(igualdade falsa)
Logo, II é falsa, pois (10, 25) não é
4 5 65
solução do sistema
x y
x y
2 5
5
2

.
III) x 5 y 1 6 (I)
5x 2 4y 5 10 (II)
5 (y 1 6) 2 4y 5 10
5y 1 30 2 4y 5 10
y 5 10 2 30
y 5 220
Logo, a afirmativa III é verdadeira.
IV) 27
1
2
,  
 
em 3x 1 2y 5 220 R
( ) 
→3 7 2
1
2
20
1
? 2 1 ? 52
21 1 20
20 20
1
2 1 52
2 52
 

 
(igualdade verdadeira)
Logo, a afirmativa IV é verdadeira.
Portanto, há três afirmações
verdadeiras.

144
3. Alternativa e.
Resolvendo o sistema:
3 4
( )  
x 2 y 5
II
x 2 y
5
8

Da equação x 2 y 5 8, temos:
x 2 y 5 8 R x 5 8 1 y (I)
3x 2 y 5 4
3 ? (8 1 y) 2 y 5 4
24 1 3y 2 y 5 4
2y 5 4 2 24
2y 5 220
y 52
20
2
y 5 210
Colocando y em (I):
x 5 8 1 y
x 5 8 1 (210)
x 5 8 2 10
x 5 22
Logo:
x 1 y 5 22 1 (210)
x 1 y 5 22 2 10
x 1 y 5 212
4. Alternativa b.
2 3
( )  
x 2 y 52
II
x y
2
2 1 52

2x 1 y 5 22 R y 5 22 1 x (I)
2x 2 y 5 23
2x 2 (22 1 x) 5 23
2x 1 2 2 x 5 23
x 5 23 2 2
x 5 25
y 5 22 1 x
y 5 22 1 (25)
y 5 27
Logo, x 2 y 5 25 2 (27)
x 2 y 5 25 1 7
x 2 y 5 2.
5. Alternativa a.
Montando um sistema com as duas
equações:
 
3 4 3
( ) x 1 y 5
II
x 1 6 y
5
8

Da equação x 1 6y 5 8, temos:
x 1 6y 5 8 R x 5 8 2 6y (I)
3x 1 4y 5 3
3 ? (8 2 6y) 1 4y 5 3
24 2 18y 1 4y 5 3
214y 5 3 2 24
214y 5 221 ? (21)
14y 5 21
y5 5
21
14
3
7
7 2
;
;
Colocando y em (I):
x582 6 ?
3
2
3
1

 

 
x 5 8 2 9
x 5 21
Logo:
x3 y3 3
3
5()  
3
2 2 1
22  
27
8 2 52 2
x3 y3 1
 
 
x3 27
2 y3 52 1
2
8 x3 y3 8
27
2 52 8
2
8 x3 y3 35
8 2 52
6. Alternativa d.
Sendo o preço da calça x e o preço da
camiseta y:
x 1 y
5
55
x 1 y 5
II
 

3 2 140 ( )
Da equação x 1 y 5 55, vem:
x 1 y 5 55
x 5 55 2 y (I)
Aplicando (I) em (II):
3x 1 2y 5 140
3 ? (55 2 y) 1 2y 5 140
165 2 3y 1 2y 5 140
2y 5 140 2 165
2y 5 225 ? (21)
y 5 25

145
Colocando y em (I):
x 5 55 2 y
x 5 55 2 25
x 5 30
Logo, o preço da calça é R$ 30,00, e o da
camiseta é R$ 25,00.
7. Alternativa c.
Chamando de x os candidatos aceitos e
de y os candidatos não aceitos, podemos
montar o seguinte sistema:
x 1 y 5
420
( II
)
y 5
5
xI
( )
 

x 1 y 5 420
x 1 5x 5 420
6x 5 420
x 5
420
6
x 5 70
Colocando x em (I):
y 5 5x
y 5 5 ? (70)
y 5 350
Logo, foram aceitos 70 candidatos.
8. Alternativa d.
Chamando de x os DVDs de música
brasileira e de y os de música estrangeira,
podemos montar o seguinte sistema:
x 1 y 5
36
II
x 5
3
yI
( )
( )
 

Aplicando a equação (I) em (II):
x 1 y 5 36
3y 1 y 5 36
4y 5 36
y 5
36
4
y 5 9
Colocando y em (I):
x 5 3y
x 5 3 ? (9)
x 5 27
Logo, são 27 DVDs de música brasileira.
9. Alternativa a.
Chamando os carros de x e as motos de
y, podemos montar o seguinte sistema de
equações:
x 1 y
5
36
x 1 y 5
II
 

4 2 126 ( )
x 1 y 5 36 R x 5 36 2 y (I)
4x 1 2y 5 126
4 ? (36 2 y) 1 2y 5 126
144 2 4y 1 2y 5 126
22y 5 126 2 144
22y 5 218 ? (21)
2y 5 18
y 5
18
2
y 5 9
Colocando y 5 9 em (I):
x 5 36 2 y
x 5 36 2 (9)
x 5 36 2 9
x 5 27
Logo, existem no pátio 27 carros.
10. Alternativa d.
Do enunciado, vem:
x 1 y
5
x 2 y 5
II
1
2
3
2 ( )

 
 
Da equação x1y5
1
2

, vem:
1
2
1
2

→ (I)
x1y5 x5 2y
x2y5
3
2

 1
3
2y 2y5 2
2  
1
2
3
2 2y2y5
3
2
22 5 2
1
2
y
22 5
2
2
y
22y 5 1 ? (21)
2y 5 21
y 52
1
2
Colocando y 52
1
2
em (I):
1
2
x5 2y
1
2
x5 2 2
1
2
 
 

146
Então:
1
2
x5 1
1
2
x 5
2
2
x 5 1
Logo, o menor desses dois números é 2
1
2
.
11. Alternativa c.
 Chamando de x a área do lote maior e de y
a área do lote menor:
x 1 y 5
2 600
( II
) x 2 y
5
200


x 2 y 5 200 R x 5 200 1 y (I)
x 1 y 5 2 600
(200 1 y) 1 y 5 2 600
200 1 y 1 y 5 2 600
2y 5 2 600 2 200
2y 5 2 400
y 5
2 400
2
y 5 1 200
Colocando y 5 1 200 em (I):
x 5 200 1 y
x 5 200 1 1 200
x 5 1 400
Logo, a área do lote maior é de 1 400
metros quadrados.
12. Alternativa a.
Chamando de x os livros com 3 cm de
espessura e de y os livros com 7 cm de
espessura, temos:
x 1 y
5
22
x 1 y 5
II
 

3 7 106 ( )
x 1 y 5 22 R x 5 22 2 y (I)
3x 1 7y 5 106
3 ? (22 2 y) 1 7y 5 106
66 2 3y 1 7y 5 106
4y 5 106 2 66
4y 5 40
y 5
40
4
y 5 10
x 5 22 2 y
x 5 22 2 10
x 5 12
Logo, foram colocados 12 livros com
espessura de 3 cm nessa pilha.
13. Alternativa c.
Somando uma das diagonais, encontramos
o número 2 1 5 1 8 5 15. Logo, a soma das
horizontais, verticais e diagonais deverá
ser 15. Pegando a primeira e a segunda
linha, podemos montar o seguinte sistema:
2 3 2 15 2 3 15 2 2 3 13
→ → ( )
→ y5152525→x1y55
y x x y x y II
1 1 5 1 5 2 1 5
1 1 1 5 1
x 5 5 y 15
x
 

x 1 y 5 5 R x 5 5 2 y (I)
2x 1 3y 5 13
2 ? (5 2 y) 1 3y 5 13
10 2 2y 1 3y 5 13
y 5 13 2 10
y 5 3
x 5 5 2 y
x 5 5 2 (3)
x 5 2
Logo:
x2 2 y2 5 (2)2 2 (3)2
x2 2 y2 5 4 2 9
x2 2 y2 5 25

Estudando as inequações
Introdução, página 170.
De acordo com o dicionário Aurélio, o
significado das palavras é;
• Inequação; desigualdade.
• Inegável; não negável; evidente.
• Ineficiente; sem eficiência.
• Inenarrável; inarrável.
• Inelegibilidade; não elegível.
• Inegociável; que não se pode negociar.
Todas as palavras começam com o prefixo
“in”, que é um prefixo que indica negação.
33 – Desigualdade
1. De acordo com a situação exposta no
enunciado, se Isa também levar sua
mochila, que tem as mesmas coisas
e é idêntica à de Bel, não muda nada,
segundo o princípio aditivo.
2. Sendo a desigualdade 52 1 22 , (5 1 2)2,
seu primeiro membro será 52 1 22.
3. Se x . 18 e 18 . y, concluímos, pela
propriedade transitiva, que x . y.
4. Se a . x, não podemos afirmar que x . a.
5. Sim; pelo princípio aditivo.
Sendo x 2 1 , 10, podemos escrever
x 2 1 1 1 , 10 1 1.
6. Sendo a desigualdade x 1 9 . 20, se
adicionarmos 29 aos dois membros,
teremos;
x191(29).201(29)→x 19 29 .2029→x.11
19 29 .2029→x.11. Logo, obtemos a desigualdade
x . 11.
7. Sendo 3x , 12, podemos afirmar, pelo
princípio multiplicativo, que x , 4. Então;
1
4
1
? 3 x , 12
? →x,
4
3
3
8. Dada a desigualdade 2x , 7, se
multiplicarmos ambos os membros por
21;
2x , 7 ? (21)
1x . 27
x . 27
Logo, a nova desigualdade é x . 27.
9. Dada a desigualdade 4x . 20, se
multiplicarmos ambos os membros por 1
4 ;
4x . 20
1
4
4 20
1
4
5
1
? x. ?
x . 5
Logo, a nova desigualdade será x . 5.
34 – Inequação
a) De acordo com as falas, o interessado que
tem a maior quantia é Nilton.
b) De acordo com as falas, podemos afirmar
a respeito das quantias de cada um;
• Ana tem menos de 6 000, pois se dobrasse
a quantia que tem não alcançaria 12 000.
• Nilton tem mais de 24 000, pois com
metade do valor que tem ele compraria o
carro e ainda lhe sobraria dinheiro.
• Ricardo tem 11 000, pois se comprasse o
carro por 11 000 não lhe sobraria nada.
• Kátia tem menos de 18 000, pois um
terço de suas economias não atingiria a
metade do valor pedido por Vágner, ou
seja, 6 000 reais.
c) Não é possível afirmar que quantia
Kátia tem exatamente, pois ela pode
ter qualquer quantia abaixo de 18 000
reais. Ricardo tem 11 000 reais, pois se
houvesse um desconto de 1 000 reais no
preço do carro ele compraria o carro e lhe
sobrariam 1 000 reais.
d) O máximo que Ana pode ter é a terça
parte do máximo que Kátia pode ter, pois
Kátia tem no máximo 6 000 reais, o que
não corresponde à metade do valor do
carro, e Ana tem menos de 6 000, pois se
147

148
dobrasse o que ela tem, ainda assim não
conseguiria comprar o carro.
e) De acordo com as falas, podemos fazer
as seguintes correspondências entre os
possíveis compradores e as sentenças
matemáticas;
x
.12000 2
R Nilton
W 5 11 000 R Ricardo
2y , 12 000 R Ana
m
,6000 R Kátia
3
f) O único interessado em uma situação que
pode ser traduzida por uma equação é
Ricardo.
1. Sim, 3x 2 2 , 1 é uma inequação, pois
representa uma desigualdade e tem um
2. (2 1 10) ; (2 1 4) , 2 1 10 ; 2 1 4
Não é uma inequação, pois, embora
represente uma desigualdade, não possui
3. O 1o membro é o lado esquerdo do sinal
de desigualdade, e o 2o membro é o lado
direito. Então;
a) 1 4
2
3 2 x,x1   1o membro
2o membro
b) x x
2
1
2 1
. 3
1
6  
1o membro 2o membro
4. Sendo x o número de letras e verificando
se a inequação x , 5 pode ser aplicada à
palavra;
a) matemática R não, pois tem 10 letras
e 10 . 5.
b) zero R sim, pois tem 4 letras e 4 , 5.
c) lado R sim, pois tem 4 letras e 4 , 5.
d) área R sim, pois tem 4 letras e 4 , 5.
e) quadrado R não, pois tem 8 letras e
8 . 5.
f) par R sim, pois tem 3 letras e 3 , 5.
5. De acordo com cada item, podemos
montar as seguintes desigualdades;
a) 2x 1 7 . 20
b) 2
3
x,2y
c) 4x 2 1 . 20
d) x1 x,
4
5
1
e) 3
1
2
x2 x.1
6. Se o lado do quadrado mede x, seu
perímetro p1 será;
p1 5 x 1 x 1 x 1 x R p1 5 4x
Como os lados do retângulo medem 7 m e
3 m, seu perímetro será;
p2 5 7 1 3 1 7 1 3 R p2 5 20
Sendo o perímetro do quadrado maior
que o perímetro do retângulo, podemos
escrever;
p1 . p2 R 4x . 20
7.
a) Sendo o custo da caneta x, e o custo da
lapiseira y;
x 1 y . 10, pois as duas juntas custam
mais de 10 reais.
b) Como o preço de três canetas é menor
que o preço de 5 lapiseiras;
3x , 5y
8. Sendo x o comprimento do terreno e 30
metros a medida da largura, temos;
a) o perímetro do terreno tem menos de
500 metros;
x 1 30 1 x 1 30 , 500
2x 1 60 , 500
b) A área do terreno tem mais de 300
metros quadrados, então;
30 ? x . 300
30x . 300
9. Do enunciado, podemos escrever;
capacidade do recipiente; x
Retirando 3 litros, temos x 2 3.
metade da capacidade do recipiente; 1
2
x
Retirando 3 litros desse recipiente ainda
sobra menos da metade da capacidade do
recipiente, então;
x23, x
1
2
35 – Inequação do 1°. grau com
uma incógnita
O salário de Paulo é obtido pela soma de
uma parte fixa de R$ 500,00 e uma parte
variável que corresponde a R$ 20,00 por
aparelho vendido.

149
a) Se Paulo vendeu 54 aparelhos, seu
salário será;
500 1 20 ? 54 5 500 1 1 080 5 1 580 R
R R$ 1 580,00
b) Sendo o salário mensal s, quando ele
vende p ou mais unidades todo mês,
temos;
s500120p
1.
a) x 1 15 . 21
x . 21 2 15
x . 6
S 5 {x ∈Q x. 6}
b) x 2 18 , 223
x , 223 1 18
x , 25
S 5 {x ∈Q x25}
c) 17 2 x , 30
2x , 30 2 17
2x , 13 ? (21)
1x . 213
x . 213
S 5 {x ∈Q x.213}
d) 11 2 9x  2x
29x  2x 2 11
29x 2 2x  211
211x  211 ? (21)
111x  111
x 
11
11
x  1
S5{x ∈Q x1}
e) 8x 1 19  10x 1 11
8x  10x 1 11 2 19
8x  10x 2 8
8x 2 10x  28
22x  28 ? (21)
12x  28
x 
8
2
x  4
S5{x ∈Q| x4}
f) 13x 2 1 , 9x 1 1
13x , 9x 1 1 1 1
13x , 9x 1 2
13x 2 9x , 12
14x , 2
2
4
2
;
x 5
1
2 2
;
 
 
S5 x ∈ x
 
 
Q | 1
2
g) 3 ? (x 2 1) 2 2x  13
3x 2 3 2 2x  13
x 2 3  13
x  13 1 3
x  16
S 5 {x ∈Q x 16}
h) 9 ? (x 2 2) 2 5 ? (x 2 3) , 1
9x 2 18 2 5x 1 15 , 1
4x 2 3 , 1
4x , 1 1 3
4x , 4
x 
4
4
x , 1
S 5 {x ∈Q| x1}
perímetro do retângulo; 5  x 1 5 1 x 5
5 2x 1 10
perímetro do quadrado; 11 1 11 1 11 1 11 5
5 44
Para o perímetro do retângulo ser maior
que o perímetro do quadrado, devemos
ter;
2 10 44
2 44 10
2 34
34
2
17
x
x
x
x
x
1 .
. 2
.
.
.
Logo, a medida do comprimento do
retângulo deve ser maior que 17 cm.
3. De acordo com o enunciado;
recipiente cheio; x
Tirando 2 litros, restam; x 2 2
Restará no recipiente uma quantidade
menor que 3
5
da capacidade do recipiente;
3
5
x
Com essas informações, podemos
escrever;
x22 x
3
5
5
5
x x
10
5
3
5
2 

150
5x 2 10 , 3x
5x , 3x 1 10
5x 2 3x , 10
2x , 10
x 
10
2
x , 5
Como do recipiente foram retirados 2
litros, podemos afirmar que a capacidade
do mesmo é; x 2 litros.
Logo, os possíveis valores racionais de x
são; 2 x , 5
4.
a)
x
x
2
5
3
2 1 21
3
10
6
6
6
6
6
6
x x
2 1 2
3x 2 10 1 6x , 26
9x 2 10 , 26
9x , 26 1 10
9x  4
x 
4
9
 
 
S5 x ∈ x
 
 
Q | 4
9
b) x2 x
. 1
1
2
1
3
3 ( 1
)
. 1 3(x 2 1) . 6 1 2x
3x 2 3 . 6 1 2x
3x . 6 1 2x 1 3
3x . 9 1 2x
3x 2 2x . 9
x . 9
S 5 {x ∈ Q| x . 9}
x2 x
6
6
6
2
6
c) x x
5
1
2
. 4
2
2 2
x x
4
20
5
20
10 2
20
. 2
? ( 2 )
4x . 5 2 10 ? (2 2 x)
4x . 5 2 20 1 10x
4x . 215 1 10x
4x 2 10x . 215
26x . 215 ? (21)
6x , 15
x 5
15
6
5
3
3 2
;
;
 
 
S5 x ∈ x
 
 
Q | 5
2
d) x11 x2
4
2
8

2 ? (x1 1
) 1 ? (x2 2
) 8

8
2 ? (x 1 1) 1 ? (x 2 2)
2x 1 2 x 2 2
2x x 2 2 2 2
2x x 24
2x 2 x 24
x 24
S 5 {x [ Q | x 24}
e) x
.2? (12 x
)
2
x 2 2 1
x
.
2
2
? ? 2 ( ) 

x x . ? ? 2 2 2 1 ( ) 

x . 2 ? [2 2 2x]
x . 4 2 4x
x 1 4x . 4
5x . 4
x 4
5
 
 
S5 x ∈ x.
 
 
Q | 4
5
f) x x
1
4
2
1
6
( x ) ( x
)
( x
) 11 ? 2
2 .2 1 2
2 .2 1
.2 1 1
.2
.2 1
2
? 2
.2 1
? 2
? 2 .2
2
3
3 1
12
2
12
4 2
12
3 1 2
4 x
2
3 x 3 2 4 x
8
3 x 3 10 4
x
3 x 10 4 x
3
3
x
( )
7 4
x
3 4 7
x x
x
x
x
S x x
( )
7 1
7
7
7
1
2 .2
2 .2 ? 2
1 1

5 
{ ∈Q| }
5. Resolvendo a inequação;
1
3
? ( x2 2
) x
 21
2
2 2
(x ) x
6
3
6
6
6
? 2
 2
2 ? (x 2 2) , 3x 2 6
2x 2 4 , 3x 2 6
2x , 3x 2 6 1 4
2x , 3x 2 2
2x 2 3x , 22
2x , 22 ? (21)

151
1x . 12
x . 2
Fazendo a verificação, temos;
• para 3, temos; 3 . 2 (sentença
verdadeira)
Logo, o número 3 pertence ao conjunto
3 ? (2x 2 1) , 5x 2 1
6x 2 3 , 5x 2 1
6x , 5x 2 1 1 3
6x , 5x 1 2
6x 2 5x , 2
x , 2
Fazendo a verificação dos números em
questão;
• para 26, temos; 26 , 2 (sentença
verdadeira)
verdadeira)
verdadeira)
• para 3, temos; 3 , 2 (sentença falsa)
Logo, os números 26, 23 e 0 pertencem
ao conjunto solução da inequação, e os
números 3 e 6 não pertencem a esse
conjunto.
1.
a)
São Paulo
Distância percorrida (km) Valor pago (R$)
1 3,50 1 2,10 5 5,60
2 3,50 1 2 ? 2,10 5 7,70
3 3,50 1 3 ? 2,10 5 9,80
... ...
12 3,50 1 12 ? 2,10 5 28,70
Rio de Janeiro
1 4,30 1 1,25 5 5,55
2 4,30 1 2 ? 1,25 5 6,80
3 4,30 1 3 ? 1,25 5 8,05
... ...
12 4,30 1 12 ? 1,25 5 19,30
Curitiba
1 3,50 1 1,80 5 5,30
2 3,50 1 2 ? 1,80 5 7,10
3 3,50 1 3 ? 1,80 5 8,90
... ...
12 3,50 1 12 ? 1,80 5 25,10
b) O valor da bandeirada é maior na
cidade do Rio de Janeiro, mas só esse
fato não garante que a corrida seja
mais cara no Rio, pois o valor do
quilômetro rodado não é o maior das
três cidades.
c)
1 3,50 1 1,80 5 5,30
2 3,50 1 2 ? 1,80 5 7,10
3 3,50 1 3 ? 1,80 5 8,90
... ...
12 3,50 1 12 ? 1,80 5 25,10
x 3,50 1 1,80 ? x
d) São Paulo R 3,50 1 2,10 ? x 5 20,00 R
R x 5
20 3 5
2 1
2 ,
, R x . 7,8. Portanto,
7 quilômetros.
Curitiba R 3,50 1 1,80 ? x 5 20,00 R
R x 5
20 3 5
1 8
2 ,
, R x . 9,2. Portanto,
9 quilômetros.
2.
a) Resolvendo a equação;
145 1 5 ? (x 1 571) . 64 2 7 ? (68 2 x)
145 1 5x 1 2 855 . 64 2 476 1 7x
5x 1 3 000 . 2412 1 7x
5x . 2412 1 7x 2 3 000
5x . 23 412 1 7x
5x 2 7x . 23 412
22x . 23 412 ? (21)
12x , 13 412
x 
3412
2
x , 1 706

152
Logo, o maior número inteiro que
satisfaz a equação dada é 1 705.
Portanto, a Música do Parnaso foi
impresso em 1705.
b) Resolvendo as inequações;
552 2 5 ? (x 2 221) , 8 ? (x 2 3) 2 11 ? (x 1
1 10) 2 221
552 2 5x 1 1 105 , 8x 2 24 2 11x 2 110 2
2 221
25x 1 1 657 , 23x 2 355
25x , 23x 2 355 2 1 657
25x , 23x 2 2 012
25x 1 3x , 22 012
22x , 22 012 ? (21)
12x . 12 012
x .
2012
2
x . 1 006
y1 y
1 , 2
? 2
2
86
12
40
9
13
4
2 105
18
1
36
( )
3 86
36
160
36
117
36
2 2 105
36
1
36
? 1
1 , 2
? ? 2
2
y y ( ) ( ) 

117
2 2 105
36
1
36
2
? ? 2
2
y ( ) 

3 86 160 117 2 2 105 1 ? 1 1 , 2 ? ? 2 2 y y ( ) ( ) 

3y 1 258 1 160 , 117 2 2 ? [210 2 2y] 2 1
3y 1 418 , 117 2 420 1 4y 2 1
3y 1 418 , 2304 1 4y
3y , 2304 1 4y 2 418
3y , 2722 1 4y
3y 2 4y , 2722
2y , 2722 ? (21)
1 y . 1 722
y . 722
Logo, o menor número natural que
satisfaz a primeira inequação é 1 007, e
o menor número natural que satisfaz a
segunda inequação é 723.
Portanto, a história de Genji foi escrita
em 1007, e Barbara Cartland escreveu
723 romances.
a) Observando os gráficos, podemos
concluir que o gráfico 1 é de barras ou
colunas, e o gráfico 2 é de linha.
b) O gráfico 1 trata da esperança de vida
do brasileiro ao nascer; o gráfico 2
trata da evolução da esperança de vida
no país, de 1960 a 2007.
c) IBGE significa Instituto Brasileiro de
Geografia e Estatística.
d) De acordo com o gráfico 2, vemos que,
em 1980 e em 2007, o sexo feminino é o
que tem maior esperança de vida.
e) 72,7 – 62,7 5 10 R 10 anos
f) De acordo com o gráfico, os anos em
que a esperança de vida do brasileiro
foi maior do que 60 anos foram os anos
de 1980, 1991, 2000 e 2004 e 2007.
1. Sendo x o número de funcionários
residentes na cidade A e sabendo que 50
trabalhadores vieram de outras cidades,
temos;
x . 50, pois o número de funcionários
que residem na cidade A deve ser sempre
maior que o número de funcionários
vindos de outras cidades.
2. Multiplicando os dois membros da
inequação 25x . 1 por (21);
25x . 1 ? (21)
15x , 21
5x , 21
3
5 ( )
1 2 1
x x
x
2 ? 1 ,
? 1 ( ) 
x x x
5
5
5 2 1
5
1 3
5
2
? ? 1
,

( )
5 5 2 1 1 3 x x x 2 ? ? 1 , ? 1 ( ) 

( )
5x 2 5 ? [2x 1 2] , x 1 3
5x 210x 2 10 , x 1 3
25x 2 10 , x 1 3
25x , x 1 3 1 10
25x , x 1 13
25x 2 x , 1 13
26x , 213 ? (21)
16x . 213
x .2
13
6
 
 
S5 x ∈ x.2
 
 
Q | 13
6

( x )
153
x2 x
7
5 1
10
1
(x ) x 
2 7
10 10
10
10
? 2
1
2 ? (x 2 7) 1 x 10
2x 2 14 1 x 10
3x 2 14 10
3x 10 1 14
3x 24
x 
24
3
x 8
Fazendo a verificação;
• para 23, temos; 23 8 (sentença
verdadeira)
verdadeira)
verdadeira)
verdadeira)
• para 9, temos; 9 8 (sentença falsa)
Logo, os números 23, 0, 5 e 8 fazem parte
do conjunto solução da inequação, e o
número 9 não faz parte desse conjunto.
5. De acordo com o enunciado;
11
18
7
15
1
12
x2 
110
180
84
180
15
180
x
2 
110x 2 84 , 15
110x , 15 1 84
110x , 99
x 5
99
110
9
11
11 10
;
;
Logo, os valores de x que satisfazem o
problema são os valores de x 
9
10
.
? ? 1 3
2 x
( ) x x
6 3 2
2 4
3 ? 2 2
3 2
7 2
1
2

? 2 x x x ( ) 
6
3 7 1
6
2 2 4
6
? ? 2
2
? 2


( ) ( )
6 3 2 3 7 1 2 2 4 ? ? 2 2 ? 2  ? 2 x x x ( ) 
( ) ( )
6 ? [3x 2 6] 2 21x 1 3 , 4x 2 8
18x 2 36 2 21x 1 3 , 4x 2 8
23x 2 33 , 4x 2 8
23x , 4x 2 8 1 33
23x , 4x 1 25
23x 2 4x , 25
27x , 25 ? (21)
17x . 225
x .2
25
7
25
7
. 3,57, então os números
Sendo x .2 2
inteiros negativos que fazem parte do
conjunto solução da inequação são 23, 22
e 21.
4x 2 1 , 2 1 3x
4x , 2 1 3x 1 1
4x , 3 1 3x
4x 2 3x , 3
x , 3
S 5 {0, 1, 2}
Logo, sendo U 5 IN, o conjunto solução da
inequação são os naturais 0, 1 e 2.
perímetro do triângulo; x 1 x 1 12 5 2x 1
1 12
perímetro do quadrado; 5 1 5 1 5 1 5 5 20
Sendo o perímetro do triângulo menor que
o perímetro do quadrado, temos;
2x 1 12 , 20
2x , 20 2 12
2x , 8
x 
8
2
x , 4
Logo, o valor inteiro de x é 3, pois x , 4.
( x ) x (x ) x2
3 2 1
2
2 1
6
10 2
3
6 1
2
? 1
2
1
.
? 1
2
3 3 2 1
? ? 1 3
6
1 2 1
6
2 10 2
6
2
? 1
.
? ? 1
2
x x x ( ) 

( ) ( ) 

?? 6 21
6
3 3 2 1
6
1 2 1
6
2 10 2
6
2
? 1
.
? ? 1
2
x x x ( ) 

( ) ( ) 

( x )
?? 6 21
6
3 3 2 1 1 2 1 2 10 2 3 6 ? ? 1 2 ? 1 . ? ? 1 2 ? x x x x ( ) 

( ) ( ) 

( 21)
3 3 2 1 1 2 1 2 10 2 3 6 ? ? 1 2 ? 1 . ? ? 1 2 ? x x x x ( ) 

( ) ( ) 

( 21)
3 ? [6x 1 3] 2 2x 2 1 . 2 ? [10x 1 20] 2 18x 1
1 3
18x 1 9 2 2x 2 1 . 20x 1 40 2 18x 1 3
16x 1 8 . 2x 1 43
16x . 2x 1 43 2 8
16x . 2x 1 35

154
16x 2 2x . 35
14x . 35
x. 5
35
14
5
7
7 2
;
;
 
 
S5 x ∈ x.
 
 
Q | 5
2
10. Alternativa d.
Resolvendo a inequação;
3x 2 7 . 3 ? (21 1 2x) 2 2x
3x 2 7 . 23 1 6x 2 2x
3x 2 7 . 23 1 4x
3x . 23 1 4x 1 7
3x . 4 1 4x
3x 2 4x . 4
2x . 4 ? (21)
1x , 24
x , 24
S 5 {x [ Q | x , 24}
Analisando as alternativas;
a) 0 [ S R falsa, pois 0 . 24.
b) 23 [ S R falsa, pois 23 . 24.
c) 24 [ S R falsa, pois 24 5 24.
d) 25 [ S R verdadeira, pois 25 , 24.
11. Do enunciado, podemos escrever a
seguinte inequação;
0,5 ? x 1 1,75 . 4
0,5x . 4 2 1,75
0,5x . 2,25
x .
2 ,
25
0 ,
5
x . 4,5
S 5 {x [ Q | x . 4,5}
Logo, x pode assumir valores maiores que
4,5.
12. 2x . 0 ? (21)
1x , 0
x , 0
Assim, todos os números racionais
negativos são solução dessa inequação.
Portanto, a afirmação é verdadeira.
13. Sendo a inequação x
x
 3
, temos;
x
x
 3
3
x x
3 
3
3x , x
3x 2 x , 0
2x , 0
x 
0
2
x , 0
Fazendo a verificação para os números
dados;
verdadeira)
verdadeira)
Logo, os números 29 e 26 fazem parte
do conjunto solução da inequação, e os
números 0, 3 e 12 não fazem parte da
solução dessa inequação.
14. Alternativa c.
Resolvendo as inequações;
5n 1 25 . 5 500
5n . 5 500 2 25
5n . 5 475
n .
5475
5
n . 1 095
28n 1 3 501 . 210 2 5n
28n . 210 2 5n 2 3 501
28n . 25n 2 3 291
28n 1 5n . 23 291
23n . 23 291 ? (21)
13n , 13 291
n 
3291
3
n , 1 097
Logo, o número de foguetes é um número
natural entre 1 095 e 1 097, portanto
1 096 foguetes.

155
Estudando os Ângulos
• O que eles têm em comum?
As figuras têm o formato em comum, mas
existem várias possibilidades de respostas.
36 – O ângulo e seus elementos
37 – Medida de um ângulo
1. De acordo com os elementos dos ângulos,
vem:
 
a) Vértice: B; lados: BA e BC
.
 
b) Vértice: O; lados: OMeON
.
2. De acordo com a figura, os ângulos são:
AÔB, AÔC, BÔC
3. As medidas dos ângulos indicados são:
a) med (AÔB) 5 208
b) med (AÔC) 5 488
c) med (AÔD) 5 558
d) med (AÔE) 5 908
e) med (AÔF) 5 1208
f) med (AÔG) 5 1808
g) med (BÔE) 5 med (AÔE) 2 med (AÔB) 5
5 908 2 208 5 708
h) med (EÔF) 5 med (AÔF) 2 med (AÔE) 5
5 1208 2 908 5 308
4. Sabemos que uma volta corresponde a
3608; logo, meia-volta corresponde a 1808.
5. Um ângulo de uma volta mede 3608.
6. Utilizando um transferidor, encontramos
as seguintes medidas:
a) med (ABˆ C) 5 458
b) med (GHˆ I) 5 1308
c) med (JLˆM) 5 208
d) med (NOˆ P) 5 1308
e) med (DFˆE) 5 208
f) med (QRˆS) 5 908
7. DFˆE  JLˆM e GHˆ I  NOˆ P.
8. Sabendo que os ângulos AÔB e MPˆQ são
congruentes e ainda que
med (AÔB) 5 508 e med (MPˆQ) 5 2x, temos:
med (AÔB) 5 med (MPˆQ) ⇒ 50 5 2x
2x 5 50
x 5
50
2
x 5 25
Logo, x 5 258.
9. Sendo as medidas de dois ângulos
congruentes expressas por
(2x 2 108) e (x 1 208), vem:
2x 2 10 5 x 1 20
2x 5 x 1 20 1 10
2x 5 x 1 30
2x 2 x 5 30
x 5 30
Logo, x 5 308.
Às 6 horas, o ângulo de abertura formada
pelos ponteiros do relógio será maior e
corresponderá a um ângulo de 1808, ou
seja, será um ângulo de meia-volta.
Portanto, o ângulo aumentou e passou a
ser 1808.
38 – Operações com medidas
de ângulos
1.
a) 18’
Como 1’ 5 60’’, temos:
18 ? 60 5 1 080 R 1 080’’
Logo, 18’ 5 1 080’’.
b) 2’ 15’’
2 ? 60 5 120 R 120’’
Logo, 2’ 15’’ 5 120’’ 1 15’’ 5 135’’.
c) 38
Como 18 5 60’ e 1’ 5 60’’, temos:
18 5 60 ? 60 5 3 600 R 3 600’’
Logo, 38 5 3 ? 3 600 5 10 800’’.

156
2.
a) 408
Como 18 5 60’, temos:
40 ? 60 5 2 400 R 2 400’
Logo, 408 5 2 400’.
b) 128 37’
12 ? 60 5 720 R 720’
Logo, 128 37’ 5 720’ 1 37’ 5 757’.
c) 2 040’’
2 040 ; 60 5 34 R 34’
2040 60
240 34
00
Logo, 2 040’’ 5 34’.
3.
a) 5 710’’
5 710 ; 60 5 95’ 10’’
5710
60
310 95 → 60 ? 95 1
10
10
95’ R Como 18 5 60’, temos:
95 ; 60 5 18 35’
95 60
35 1→60?1135
Logo, 5 710’’ 5 95’ 10’’ 5 18 35’ 10’’.
b) 53 400’’
53 400 ; 60 5 890’
53400 60
540 890 → 60 ?
890
000
890’ R Como 18 5 60’, temos:
890 ; 60 5 148 50’
890 60
290 14 → 60 ? 14 1
50
50
’’ ’
Logo, 53 400’’ 5 890’ 5 148 50’.
c) 43 471”
43 471 ; 60 5 724’ 31’’
43471 60
147 724 60 724 31
271
31
→ ? 1
724’ 31’’ R Como 18 5 60’, temos:
724 ; 60 5 128 4’
724 60
124 12 → 60 ? 12 1
4
4
Logo, 43 471’’ 5 724’ 31” 5 128 4’ 31’’.
4. Para comparar as medidas, devemos
trabalhar em uma mesma unidade, daí
vem:
a) 1 080’
1 080 ; 60 5 188
1080 60
480 18 → 60 ?
18
00
Logo, 208 é maior que 1 080’,
pois 1 080’ 5 188.
b) 720’
720 ; 60 5 128
720 60
120 12
00
Logo, 128 e 720’ são iguais, pois 720’ 5 128.
5. Simplificando as medidas, vem:
a)
20
80 1 20 1 60
1
’’
’’ 5 ’ ’’, pois ’ 5
’’
’

.
b)
25
12 145 14 25 1 60
2
’’
’ ’’ ’ ’’, ’ ’’.
’
5 pois 5

c)
20
200 3 20 1 60
3
’
’5 8 ’, pois °
5 ’.
8

d)
30 31
’’ ’
1 90 90 1 91 30 2 31 30 1 60
8 ’ ’’5 8 ’ ’’5 8 ’ ’’,pois 85 ’ e 1 60
1 1
’ ’’.
’
5
  8
30 31
1 90 90 1 91 30 2 31 30 1 60
8 ’ ’’5 8 ’ ’’5 8 ’ ’’,pois 85 ’ e 1 60
1 1
’ ’’.
’
5
  8
e)
40
’’
’’ ’ ’’, ’ ’’
’
5 100 5 1 40 1 60
8 5 8 pois 5

1
.
f)
10 1
’’ ’
8 120 70 8 121 10 10 1 10 1 60
8 ’ ’’5 8 ’ ’’5 8 ’ ’’,pois 85 ’’ ’ ’’.
’
e1 60
1 2
5
  8
10 1
’’ ’
8 120 70 8 121 10 10 1 10 1 60
8 ’ ’’5 8 ’ ’’5 8 ’ ’’,pois 85 ’’ ’ ’’.
’
e1 60
1 2
5
  8

157
Exercícios, página 196 a 197.
1.
a) 138 12’ 1 418 10’ 20’’
138 12’ 00’’
1 418 10’ 20’’
548 22’ 20’’
Logo, 138 12’ 1 418 10’ 20’’ 5 548 22’ 20’’.
b) 358 20’ 2 108 15’ 30’’
19’ 60’’
358 20'

00’’ 358 19’ 60’’
2 108 15’ 30’’  2 108 15’ 30’’
258 4’ 30’’
Logo, 358 20’ 2 108 15’ 30’’ 5 258 4’ 30’’.
c) 908 2 378 40’ 20’’
898 60’ 59’ 60’’

908
00’ 00’’ 898 60'

00’’ 898 59’ 60’’
2 378 40’ 20’’  2 378 40’ 20’’  2 378 40’ 20’’
528 19’ 40’’
Logo, 908 2 378 40’ 20’’ 5 528 19’ 40’’.
d) 348 51’ 12’’ 1 128 10’ 50’’
348 51’ 12’’
1 128 10’ 50’’
468 61’ 62’’
2’’ 2’
468 61’ 62'' 5 468 62' 2’’ 5 478 2’ 2’’
 1’  18
Logo, 348 51’ 12’’ 1 128 10’ 50’’ 5 478 2’ 2’’.
e) 2 ? (508 19’)
508 19’
3 2
1008 38’
Logo, 2 ? (508 19’) 5 1008 38’.
f) 4 ? (108 24’ 45’’)
2
108 24’ 45''
3 4
408 96’ 180’’
00’’ 39’
408 96’ 180'' 5 408 99' 5 41o 39’
 3’  18
Logo, 4 ? (108 24’ 45’’) 5 418 39’.
g) (278 36’ 33’’) ; 3
27° 36' 33'' 3
00 00 00 98 12’ 11’’
Logo, (278 36’ 33’’) ; 3 5 98 12’ 11’’.
h) (418 50’ 14’’) ; 2
41º 50' 14'' 2
1°1 60’ 208 55’ 7’’
110’
0 14’’
0
Logo, (418 50’ 14’’) ; 2 5 208 55’ 7’’.
i) 1808 2 548 12’ 49’’
1798 60’ 598 60’
1808

00’ 00’’ 1798 60'

00’’ 1798 59’ 60’’
2 548 12’ 49 ’’  2 548 12’ 49’’  2 548 12’ 49’’
1258 47’ 11’’
Logo, 1808 2 548 12’ 49’’ 5 1258 47’ 11’’.
j) 5 ? (28 55’ 30’’)
28 55’ 30’’
3 5
108 275’ 150’’
30’’ 37’
108 275’ 150'' 5 108 277’ 30’’ 5 148 37’ 30’’
 2’  48
Logo, 5 ? (28 55’ 30’’) 5 148 37’ 30’’.
2.
a) 158 12’ 35’’ 1 278 18’ 1 138 51’ 30’’
158 12’ 35’’
278 18’ 00’’
1 138 51’ 30’’
558 81’ 65’’
5”
558 81’ 65 ”
1’
22’

5 55° 82’
1°
5’’ 5 568 22’ 5’’
Logo, 158 12’ 35’’ 1 278 18’ 1 138 51’ 30’’ 5
5 568 22’ 5’’.
b) (508 2 158 20’) ; 5
49 60
° → °
° °
' '
' '
'
'
50 00 49 60
15 20 15 20
°
34 40
° 
2 2
°
° °
34 40 5
4
240
280
0
6 56
'
1 '
Logo, (508 2 158 20’) ; 5 5 68 56’.
c) 2 ? (188 15’ 1 308 27’ 40’’) 2 818 17’ 30’’
188 15’ 00’’ 488 42’ 40’’
1 30o 27’ 40’’ 3 2
488 42’ 40’’ 968 84’ 80’’

158
968 84’ 80’’
2 818 17’ 30’’
158 67’ 50’
7
7
7
15 8 8 8 67 50 16 8
8
8
7 50
8 
8 
8 
1
’ ” ’ ”
’
15 67 50 516 7 50
1
’ ” ’ ”
’
15 67 50 516 7 50
1
’ ” ’ ”
’
5
Logo, 2 ? (188 15’ 1 308 27’ 40’’) 2 818 17’ 30’’ 5
5 168 7’ 50’’.
3. A metade de 158 19’ 10’’ é:
15 19’ 10” 2
15 19’ 10” 2
60’
79’ 10”
60’
79’ 10”
’ ”
 7 39 35
 7 39 35
60”
70”
8
8
1
18
1

1
’
’ ”
60”
70”
8
8
1
18
1

1
’
Logo, a metade de 158 19’ 10’’ é 78 39’ 35’’.
4. Sendo a terça parte do ângulo 98 29’ 5’’,
o ângulo procurado será:
98 29’ 5’’
3 3
278 87’ 15’’
27'
27'
87 '
278 87 '
18
18
15’’ 5 288 27’ 15’’
Logo, o ângulo é 288 27’ 15’’.
5. Dividindo 1458 em 4 partes, vem:
145 8
4
1 8 60' 36 8
15'
0
Logo, dividindo 1458 por 4, encontramos
36° 15’’.
6. Calculando
2
3 de 378 40’, vem:
378 40’
3 2
20’
748 80’ 748 5 758 20
’
80’
1
8

75 20 3
0 20 25 6 40
’
’ ’ ”
’ ”
2 120
0
8
8
Logo,
2
3 de 378 40’ é 258 6’ 40’’.
7. Se dois ângulos somados medem 808, e
um deles mede 278 18’ 14’’, o outro ângulo
mede:
808 2 278 18’ 14’’ 5
798 60’ 59’ 60’’

80°
00’ 00’’ 798 60'

00’’ 798 59’ 60’’
2 278 18’ 14’’  2 278 18’ 14’’  2 278 18’ 14’’
528 41’ 46’’
Logo, o outro ângulo mede 528 41’ 46’’.
8. Se x representa cada uma das medidas a,
b, c e d, escrevemos:
a1b1c1d54428
x1x1x1x54428
4x54428
x 5
442
4
8
x51108 30’
442 4
2 10 30
8
8120’ 1 8 ’
0
Logo, a, b, c e d valem 1108 30’.
9. A soma de x com 388 25’ é igual a 1808, daí
vem:
x 1 388 25’ 5 1808
x 5 1808 2 388 25’
x 5 1418 35’
1798 60’
1808 00’ 1798 60’
2 388 25’  2 388 25’
1418 35’
Logo, x 5 1418 35’.
10. Sendo a soma das medidas dos ângulos Â,
Bˆ e Cˆ igual a 1808, podemos escrever:
598 20’ 1 358 50’ 20’’ 1 Â 5 1808
948 70’ 20’’ 1 Â 5 180o
Â 5 1808 2 948 70’ 20’’
Â 5 1808 2 958 10’ 20’’
Â 5 848 49’ 40’’
598 20’ 00’’
10
’
8 8
1 358 50’ 20’’ 94 70 20 95 10 20
1
8
’ ” ’ ”

5
948 70’ 20’’
1798 60’ 59’ 60”
180° 00’ 00’’ 1798 60' 00’’ 1798 59’ 60’’
2 958 10’ 20 ’’  2 958 10’ 20’’  2 958 10’ 20’’
848 49’ 40’’
Logo, o ângulo Â mede 848 49’ 40’’.

159
1. Utilizando um transferidor para
determinar a medida do ângulo,
concluímos que a lancha deve girar 308
para a direita para atracar no cais.
2. Mesmo utilizando a lente de aumento,
o ângulo continuará medindo 308, pois
permanece com a mesma abertura.
39 – ângulos consecutivos e
ângulos adjacentes
40 – Bissetriz de um ângulo
Construindo os ângulos, vem:
a) 458 Bissetriz de 458
45
bissetriz
b) 308 Bissetriz de 308
30
bissetriz
c) 758 Bissetriz de 758
75
bissetriz
d) 1208 Bissetriz de 1208
120
bissetriz
1. Existem várias possibilidades de resposta.
Uma delas seria: AÔB e BÔC são ângulos
consecutivos.
ˆB
ˆB
a) AÔB e BÔC são ângulos adjacentes.
b) AD e DC são ângulos adjacentes.
3. A bissetriz divide um ângulo em duas
partes iguais. Daí vem:
75 8
2
1
860 378 30
0
' '
Logo, cada ângulo obtido mede 378 30’.
4. Um ângulo raso tem 1808, então sua
bissetriz terá:
180 8
2
0 90
8
Logo, traçando a bissetriz de um ângulo
raso, encontramos dois ângulos de 908.

med (MÔB) 5 med (AÔM) 5 238, pois OM
é
bissetriz de AÔB.

med (AÔB) 5 2 ? med (MÔB), pois OM
é
bissetriz de AÔB.
med (AÔB) 5 2 ? 23° 5 468
Logo, med (AÔM) 5 238 e med (AÔB) 5 468.

med (AÔN) 5 med (NÔB) 5 158, pois ON
é
bissetriz de AÔB.

med (BÔM) 5 med (MÔC) 5 20o, pois OM
é
bissetriz de BÔC.
med (AÔC) 5 med (AÔN) 1 med (NÔB) 1
1 med (BÔM) 1 med (MÔC)
med (AÔC) 5 158 1 158 1 208 1 208 5 708
Logo, a medida do ângulo é 708.
41 – Ângulo reto, ângulo agudo
e ângulo obtuso
Na foto 1, o ângulo em destaque é reto.
Na foto 2, o ângulo em destaque é maior
que um ângulo nulo e menor que um reto;
logo, é um ângulo agudo.
Na foto 3, o ângulo em destaque é maior
que um ângulo reto e menor que um
ângulo raso; logo, é um ângulo obtuso.
Resposta em aberto.
Ilustrações: Editoria de arte

160
Chegou a sua vez!, página 206 e 207.
1.
a) Cada uma das partes indica um ângulo
de 1808.
b) Recortando ao meio as duas figuras do
item anterior, encontramos ângulos de 908.
2. De acordo com as dobraduras do círculo, vem:
a) Um ângulo de 1808 determina metade
do círculo.
b) A quarta parte do círculo determina
um ângulo de 908.
c) Dividindo o círculo em oito partes
iguais, formamos ângulos de 458.
3. Possível resposta:
180
90
45
45
4. 1 dobra R divide o círculo em 2 partes iguais;
2 dobras R divide o círculo em 4 partes
iguais;
iguais;
iguais.
Logo, para dividir o círculo em 16 partes
iguais, serão necessárias no mínimo 4 dobras.
5. Fazendo a tabela, vem:
Número de partes em que o círculo
foi dividido
Medida do ângulo que cada
parte representa
2 1808
4 908
8 458
16 22,58 ou 228 30’
6. Possível resposta:
Se considerarmos que Joaquina ganhou y,
podemos escrever:
Joana R 2y Jussara R y
2
Júlia R y
2
A soma de todas essas partes corresponde
a 3608 em um círculo; logo, escrevemos:
y y
2
y 1 y 1 1 5 360
8
2 2
3
y o 1 5
2
2
y 360
3y 1 y 5 360°
4y 5 360°
y 5
360
4
8
y 5 90°
Assim, temos:
Joaquina R y R 90°
Joana R 2y R 2 ? 90° 5 180°
Jussara R y
2
R 90
2
45 8
5 8
Júlia R
y
2 R
90
2
45 8
5 8
Portanto, podemos construir o seguinte
gráfico:
Jussara
Júlia
Joaquina
Joana
42 – Ângulos complementares e
ângulos suplementares
1.
a) Complemento de 88 R 908 2 88 5 828
b) Complemento de 358 18’ R 908 2 358 18’ 5
5 548 42’
c) Complemento de 898 R 908 2 898 5 18
2.
a) Suplemento de 908 R 1808 2 908 5 908
b) Suplemento de 1508 R 1808 2 1508 5 308
c) Suplemento de 188 43’ R 1808 2 188 43’ 5
5 1618 17’
3.
a) Complemento do ângulo R 908 2 x
b) Suplemento do ângulo R 1808 2 x
c) Metade do suplemento do ângulo R
R
180
8 2x
2
d) O quíntuplo do suplemento desse
ângulo R 5 ? (1808 2 x)
4. Complemento de 578 R 908 2 578 5 338
Metade de 338 R 338 ; 2 5 16,58 ou 168 30’
Logo, a metade do complemento de 578 é
168 30’.
5. Sabemos que dois ângulos são
complementares quando a soma deles é
igual a 908. Logo, o ângulo cuja medida é
igual à medida do seu complemento será
a bissetriz de 908, portanto 458.

161
6.
a) Como os ângulos são adjacentes
complementares, escrevemos:
358 1 x 5 908
x 5 908 2 358
x 5 558
b) Como os ângulos são adjacentes
suplementares, escrevemos:
x 1 1408 5 1808
x 5 1808 2 1408
x 5 408
c) Como os ângulos são adjacentes
x
2
1140851808
x
2
280
360
1 2
5
2 8 8
x 1 280° 5 360°
x 5 360° 2 280°
x 5 80°
d) Como os ângulos são adjacentes
complementares, escrevemos:
3x 1 2x 5 90°
5x 5 90°
x 5
90
5
8
x 5 18°
7. Como os ângulos são complementares,
escrevemos:
x
2 30
x 36 90
2 81 1 85 8
3
2
x
x 6 90
1 3
1 85 8
6
18
3 3
3
270
3
x x
8 8
1 1 5
6x x 18o 270o 1 1 5
7x 5 270° 2 18°
7x 5 252°
x 5
252
7
8
x 5 36°

8. med (BÔP) 5 med (PÔC) 5 658, pois OP
é
bissetriz de BÔC.
Como os ângulos BÔC e AÔC são
658 1 658 1 med (AÔC) 5 1808
med (AÔC) 5 1808 2 1308
med (AÔC) 5 508
Logo, med (AÔC) 5 508.
9. Chamando o ângulo de x, podemos
indicar o triplo da medida de seu
complemento por 3 ? (908 2 x) e escrever:
3 ? (90°2 x) 5 111°
270° 2 3x 5 111°
23x 5 111° 2 270°
23x 5 2159° ? (21)
3x 5 159°
x 5
159
3
8
x 5 53°
Logo, a medida desse ângulo é 538.
10. Chamando o ângulo procurado de x, como
os ângulos são suplementares, escrevemos:
x 1 938 50’ 5 1808
x 5 1808 2 938 50’
x 5 868 10’
Logo, o outro ângulo mede 868 10’.
11. Chamando o ângulo de x, o triplo da
medida de seu suplemento será
3 ? (1808 2 x); assim, temos:
3 ? (180°2 x) 5 x
540° 2 3x 5 x
23x 2 x 5 2540°
24x 5 2540° ? (21)
4x 5 540°
x 5
540
4
8
x 5 135°
Logo, o ângulo mede 1358.

12. med (AÔB) 5 med (BÔC) 5 x, pois OB
é a
bissetriz de AÔC.
Como AÔD e DÔE são suplementares,
escrevemos:
x 1 x 1 90° 1 40° 5 180o
2x 1 130° 5 180o
2x 5 1808 2 130°
2x 5 508
x 5
50
2
8
x 5 258
Logo, a medida de x é 258.
43 – Ângulos opostos pelo vértice
1.
a) De acordo com a figura, os pares de
ângulos congruentes são:
x e z, w e y, pois são opostos pelo vértice.

162
b) De acordo com a figura, os pares de
ângulos suplementares são:
x e y, y e z, z e w, w e z, pois são
ângulos adjacentes suplementares.
2. Os outros ângulos formados são 458, 1358
e 1358, pois 458 é oposto pelo vértice a 458,
e 1358 é suplementar a 458.
Logo, os três ângulos formados por essas
retas são 458, 1358 e 1358.
3. Nas figuras os ângulos destacados são
postos pelo vértice; assim, temos:
a) 3x 2 608 5 2x
3x 2 2x 5 608
x 5 608
b) 5x 2 98 5 2x 1 15°
5x 2 2x 5 15° 1 9°
3x 5 24°
x 5
24
3
8
x 5 8°
4. Como os ângulos são opostos pelo vértice,
podemos escrever:
6x 2 218 5 3x 1 40°
6x 2 3x 5 40° 1 21°
3x 5 61°
o
x
5
61
3
x 5 20° 20’
61 3
1 60 20 20
8
8 ' 8 '
0
Logo, a medida de x é 208 20’.
5.
a) x 1 1108 5 1808 (x e 110° são ângulos
suplementares.)
x 5 1808 2 1108
x 5 708
Se x 5 708, então a 5 708, pois a e x são
ângulos opostos pelo vértice.
Se o ângulo oposto a y é 110°, então
y 5 1108.
Logo, a 5 708, x 5 708 e y 5 1108.
b) x 5 458, pois o ângulo x é oposto pelo
vértice ao ângulo de 45° indicado na figura.
y 1 458 5 1808 (y e 45° são ângulos
suplementares.)
y 5 1808 2 458
y 5 1358
a 1 908 5 1808 (a e 90° são ângulos
suplementares.)
a 5 1808 2 908
a 5 908
Se a 5 908, então b 5 908, pois a e b são
ângulos opostos pelo vértice.
Logo, x 5 458, y 5 1358, a 5 908 e b 5 908.
b) Resposta possível:
• Na Praça dos Viajantes, Londrina (PR).
• Relógio de sol equatorial, em Santa
Catarina.
• Relógio de sol de Areia Preta, em
Natal (RN).
• Relógio solar de reclinação Sul,
Oficina Cerâmica Francisco
Brennand, em Recife (PE).
• No Mosteiro de São Bento (1847), na
cidade do Rio de Janeiro.
• Na Igreja de Santo Antônio (1712), em
Tiradentes (MG).
• Na Praça Nossa Senhora da
Conceição (1886), em Franca (SP).
• Na Praça Tiradentes (1857), na cidade
de Curitiba (PR).
• Em Sobral (CE), de 1989.
• Em Tefé (AM), de 1991.
• Em Feira de Santana (BA), de 1993.
c) Do texto, temos que, a cada 1 hora, o
Sol se desloca 15 graus; assim:
• em 2 horas R 2 ? 158 5 308.
• em 5 horas R 5 ? 158 5 758.
• em 8 horas R 8 ? 158 5 1208.
• em 12 horas R 12 ? 158 5 1808.
• em 18 horas R 18 ? 158 5 2708.
1. Alternativa b.
Como o ângulo é 228 30’, seu dobro será:
228 30’
3 2 44 60 45
00
8 8
 8
1
’5
448 60’
Logo, o ângulo mede 458.
2. Alternativa c.
Como os ângulos são congruentes,
escrevemos:
9x 2 438 5 7x 1 318
9x 2 7x 5 31° 1 438
2x 5 748

163
x 5
74
2
8
x 5 378
3. Alternativa a.
Escrevendo 278 58’ 120’’ na sua forma mais
simples, temos:
27 8 58 ’ 120 ” 27 8 60 ’
28
8
2
00
00
5 5
1
8
’
” ’
 
Logo, a forma mais simples do ângulo
será 288.
4. Alternativa e.
De acordo com o enunciado, temos:
med (AÔC) 5 med (AÔB) 1 med (BÔC)
med (AÔC) 5 258 1 47’ 28’’ 1 138 1 26’ 52’’
med (AÔC) 5 388 1 73’ 80’’
258 47’ 28’’
1 138 26’ 52’’
388 73’ 80’’
20
14
38 73 80 38 74 20 39 14 20
’ ” ’ ” ’ ”
8 8 8
1
5 5
1
8
’
” ’
 
Logo, o ângulo AÔC mede 398 14’ 20’’.
5. Alternativa a.
Como A 5 358 1 58’ 1 (808 53’ 2 528 27’),
temos:
A 5 358 1 58’ 1 (288 26’)
A 5 358 1 58’ 1 288 26’
A 5 638 1 84
1
24
’
24
’
’
 °
5 648 24’
808
4 1
53’
2 528 27’
288 26’
358 58’
1 288 26’
638 84’
’
Logo, A 5 648 24’.
6. Alternativa b.
Dividindo 718 29’ 35’’ em cinco ângulos
congruentes, temos:
718 29’ 35’’ 5
18
 160’ 148 17’ 55’’
89’ 35’’
4’ 1240’’
275’’
0
Logo, cada um dos ângulos obtidos medirá
148 17’ 55’.
7. Alternativa d.
Como mede (AÔC) 5
3
4 med (AÔB), temos:
med (AÔC)5 ?
3
4
248 12’36’’
248 12’ 36’’
3 3
728 36’ 108’’
med(AÔC)5
72 36 108
8 ’ ’’
4
48
72 36 108 72 37 48
’ ” ’ ”
8 8
1
8
”

5
med(AÔC)5
72 37 48
8 ’ ’’
4
72 37 48 4
0
’ ” 
1 60
108
0
18 9 27
8
8
’ ”
’ ”
”
1
med(AÔC)5188 9’27’’
Da figura, temos:
med (BÔC) 5 med (AÔB) 2 med (AÔC) 5
5 248 12’ 36’’ 2 188 9’ 27’’
248 12’ 36’’
2 188 9’ 27’’
68 3’ 9’’
Logo, med (BÔC) 5 68 3’ 9’’.
8. Alternativa c.
528 10’ 2 (818 50’ 2 358 10’) 5
5 528 10’ 2 (468 40’) 5
5 528 10’ 2 468 40’ 5
5 58 30’
818 50’
2 358 10’
468 40’
518 60’
528 10’ 518 70’
2 468 40’  2 468 40’
58 30’
Logo, multiplicando 6 por 58 30’, temos:
58 30’
0
3 6 30 180 33
8 8
3
8
’
’

5
308 180’
Portanto, seis vezes o valor da expressão
resulta em 338.
84
1
 °84
1
24
’
’
 °

164
9. Alternativa b.
O complemento de 378 28’ 50’’ é:
908 2 378 28’ 50’’
898 60’ 59’ 60’’
999000°°° 000000’’’ 000000””” 898 60’ 00’’ 898 59’ 60’’
2 378 28’ 50’’  2 378 28’ 50’’  2 378 28’ 50’’
528 31’ 10’’
Sendo 908 2 378 28’ 50’’ 5 528 31’ 10’’, então,
o dobro do valor será:
528 31’ 10’’
2
3 2 104 8 62 20 105 8
2 20
1
8
’ ” ’ ”
’

5
1048 62’ 20’’
Logo, o ângulo é 1058 2’ 20’’.
10. Alternativa c.
Com base no enunciado, temos:
Ângulo desconhecido R x
Terça parte da medida do suplemento
desse ângulo 180
o2x R .
3
Como a soma desses dois ângulos é 948,
escrevemos:
180
x
x
8
2
1
5
94 3
8
3
3
180
8 8
3
282
3
x x
1
2
5
3x 1 18082 x 5 2828
2x 5 2828 2 1808
2x 5 1028
x 5
102
2
8
x 5 518
Logo, a medida desse ângulo é 518.
11. Alternativa d.
Como os ângulos são adjacentes
suplementares, temos:
5x 1 2x 1 688 5 1808
7x 5 1808 2 688
7x 5 1128
x 5
112
7
8
x 5 168
Sendo os ângulos 5x e 2x 1 688, obtemos:
5 ? 16 5 808
2 ? 168 1 688 5 328 1 688 5 1008
Logo, o maior desses dois ângulos é 1008.
12. Alternativa e.
De acordo com a figura, temos:
508 5 x 1 208 (Ângulos opostos pelo vértice.)
x 1 208 5 508
x 5 50o 2 20o
x 5 30o
508 1 y 5 1808 (Ângulos adjacentes
suplementares.)
y 5 1808 2 508
y 5 1308
Logo, y 2 x 5 1308 2 308 5 1008.
13. Alternativa d.
1508 1 x 5 1808 (Ângulos adjacentes
suplementares.)
x 5 1808 2 1508
x 5 308
x 1 y 5 1508 (Ângulos opostos pelo vértice.)
30 1 y 5 1508
y 5 1508 2 308
y 5 1208
Logo, o valor de y é 1208.
14. Alternativa a.
Como os ângulos são opostos pelo vértice,
podemos escrever:
a 5 b R 3x 2 208 5 2x 1 108
3x 2 2x 5 108 1 208
x 5 308
Então, temos:
a 5 3x 2 208
a 5 3 ? 308 2 208
a 5 908 2 208
a 5 708
b 5 2x 1 108
b 5 2 ? 308 1 108
b 5 608 1 108
b 5 708
Logo, o valor de a 1 b 5 708 1 708 5 1408.
15. Alternativa c.
med (BÔE) 5 208

med (DÔE) 5 med (BÔE) 5 208, pois OE
é
bissetriz de DÔB.
med (CÔD) 5 908
med (BÔC) 5 med (BÔE) 1 med (DÔE) 1
1 med (CÔD)
med (BÔC)5 208 1 208 1 908 5 1308
Como os ângulos AÔC e BÔC são
suplementares, temos:
med (AÔC) 1 med (BÔC) 5 1808
med (AÔC) 1 1308 5 1808
med (AÔC) 5 1808 2 1308
med (AÔC) 5 508
Logo, o ângulo AÔC mede 508.

165
Estudando triângulos e quadriláteros
44 – Reconhecendo triângulos
45 – Uma relação entre as
medidas dos ângulos internos
de um triângulo
1. Fazendo as medições dos lados dos
triângulos, temos:
a) Como ABAC, ABBC e ACBC,
o triângulo é escaleno.
b) Como ABACBC, o triângulo é
equilátero.
c) Como ABAC, o triângulo é isósceles.
2. Fazendo as medições dos ângulos dos
triângulos, temos:
a) Todos os ângulos são menores que 908,
logo o triângulo é acutângulo.
b) O triângulo possui um ângulo de 908,
logo o triângulo é retângulo.
c) O triângulo possui um ângulo maior
que 908 e menor que 1808; logo, o
triângulo é obtusângulo.
3. Chamando o terceiro ângulo de x,
podemos escrever:
x 1 358 1 558 5 1808
x 5 1808 2 358 2 558
x 5 908
Logo, o terceiro ângulo mede 908.
4. Não, pois a soma dos ângulos internos de
um triângulo é igual a 1808.
5. Sendo x a medida do ângulo
desconhecido, podemos escrever:
x 1 x
1 50 8 5
180
8
2 x
5 180 8 2
50
8
2 x
5
130
8
130
x
8
5
2
x
5
65
8
Logo, a medida dos ângulos congruentes
é 658.
6.
a) Como 458, 908 e x são as medidas dos
ângulos internos do ABC, temos:
458 1 908 1 x 5 1808
x 5 1808 2 1358
x 5 458
b) Como x, x e x são as medidas dos
x 1 x 1 x 5 1808
3x 5 1808
x 5
180
3
8
x 5 608
c) Como 608, 388 e x são as medidas dos
608 1 388 1 x 5 1808
x 5 1808 2 988
x 5 828
d) Como x 1 1, x 1 2 e x são as medidas
dos ângulos internos do ABC, temos:
x 1 18 1 x 1 28 1 x 5 1808
3x 5 1808 2 38
3x 5 1778
o
x
5
177
3
x 5 598
Resposta em aberto.
Resposta em aberto.
46 – Reconhecendo quadriláteros
1.
a) De acordo com a ilustração, os
paralelogramos são as figuras 1, 3
e 4, pois apresentam lados opostos
paralelos dois a dois.
b) Entre os paralelogramos, os retângulos
são as figuras 3 e 4, pois possuem
quatro ângulos retos.
Entre os paralelogramos, o quadrado
é a figura 3, pois possui os quatro
lados congruentes e os quatro
ângulos retos.

166
c) Entre os quadriláteros desenhados,
os trapézios são as figuras 2 e 5, pois
possuem apenas dois lados paralelos.
d) O trapézio retângulo é a figura 2, pois
possui dois ângulos internos retos.
2. A união dos vértices C, M, L e C com
segmentos de reta forma um triângulo
equilátero, pois CMMLLC.
A união dos vértices, A, M, L, O e A, nessa
ordem, forma um quadrilátero, que é
retângulo, pois possui quatro ângulos retos
e os lados AMLO e MLAO.
Logo, os polígonos formados são um
triângulo equilátero e um quadrilátero, que
é retângulo.
Alternativa d.
b) Na 1a pintura: trapézio, retângulo e
triângulos.
Na 2a pintura: quadrados, triângulos,
paralelogramos, trapézios e um círculo.
47 – Uma relação entre as
medidas dos ângulos internos
de um quadrilátero
1. O quadrilátero em questão não é um
paralelogramo, pois os lados opostos não
são paralelos.
2. O paralelogramo em questão é um
quadrado, pois ele é retângulo e
losango. Daí, traçando uma de suas
diagonais, o quadrado ficará dividido
em dois triângulos retângulos isósceles.
Logo, esses triângulos são retângulos
isósceles.
3. Sabendo que o retângulo possui quatro
ângulos retos, ou seja, ângulos que
medem 908, e sendo a, b, c e d as medidas
dos quatro ângulos internos do retângulo,
vem:
a 5 908, b 5 908, c 5 908 e d 5 908
Daí, temos:
a 1 b 1 c 1 d 5 908 1 908 1 908 1 908 5 3608
Logo, a 1 b 1 c 1 d 5 3608.
4. Utilizando um transferidor, podemos
verificar as seguintes medidas para a, b, c
e d:
a 5 608, b 5 608, c 5 1208 e d 5 1208
Daí, temos:
a 1 b 1 c 1 d 5 608 1 608 1 1208 1 1208 5
5 3608
Logo, a 1 b 1 c 1 d 5 3608.
Observando o mapa, temos:
a) A Universidade de São Paulo se
encontra delimitada por um trapézio
retângulo.
b) Sim. Rod. da Glória e Av. Salvador.
c) Sim. A Rod. da Glória, a Av. Salvador e a
Av. Rui Marques formam um triângulo
retângulo.
f) Não, nesse mapa não encontramos
triângulos. Encontramos vários
quadriláteros, dentre eles, o trapézio
retângulo.

11
10 5 5
167
Razões e proporções
Abertura, página 231 e 232.
• De acordo com o Novo dicionário da
língua portuguesa, de Aurélio Buarque de
Holanda, os significados das palavras são,
entre outros:
Razoável  conforme à razão; moderado,
comedido.
Arrazoar  expor ou defender (causa,
assunto, argumento etc.) alegando razões;
censurar, repreender, arguir.
Raciocinar  fazer raciocínio; pensar,
refletir, considerar.
48 – Razão
1. Acertos  12 e erros  20 2 12 5 8
a) Utilizando uma fração para comparar
a quantidade de acertos com o total de
questões, vem: 12
20

3
5 .
4
4 5

b) Transformando
12
20 em decimal,
chegamos a 0,6.
c) Comparando as questões que Renata
errou com o número total de questões,
temos: 8
20

2
5 .
4
4 5

d) Transformando
8
20 em decimal,
chegamos a 0,4.
e) Como Renata acertou
3
5 das questões,
se a atividade valesse 10 pontos no
total, a pontuação obtida por Renata
seria: 3
5
10 6
1
2
 5 R 6 pontos.
2. Como Roberto acertou 76, vem:
a) Comparando o número de acertos com
o total de questões, temos:
76

4
19
100
5

4 25
b) O percentual de acertos foi de 76%.
c) Como Roberto acertou
19
25 das
questões, se fossem 50 testes, ele teria
acertado:
19
25
50 38
1
2
 5 R 38 testes.
d) Se fossem 25 testes, ele teria acertado:
19
25
25 19
1
1
 5 R 19 testes.
1. Determinando as razões, vem:
a) 5
20
1
4 5
b) Transformando 0,5 m em cm, vem:
0,5 m 5 50 cm
Logo, a razão será: 10
50
1
5 5 .
c) 12
15
4
5 5
d) Transformando 2 kg em g, vem:
2 kg 5 2 000 g
2000
2
5 5 .
e) Transformando 1 m2 em cm2, vem:
1 m2 5 1 m  1 m 5 100 cm  100 cm 5
5 10 000 cm2
5000
2
1 5 .
f) Transformando 200 km em cm, vem:
200 km 5 20 000 000 cm
Logo, a razão será:
4
20000000
1
5000000 5
número de participantes em
número de participante
2010
s em 2009
880
800
Logo, a razão entre o número de
participantes em 2010 e o número de
participantes em 2009 é
11
10 .
comprimento
72
80
9
10
medida da envergadura 5 5 5
0,9
Logo, a razão entre o comprimento e a
envergadura desse tipo de avião é 0,9.
a) A razão entre as medidas dos lados dos
quadrados é:
20
2
30
5
3 b) O perímetro do quadrado 1 é dado por:
20 cm 1 20 cm 1 20 cm 1 20 cm 5 80 cm;
o perímetro do quadrado 2 é dado por:
30 cm 1 30 cm 1 30 cm 1 30 cm 5 120 cm

168
Daí a razão entre o perímetro do quadrado
1 e o perímetro do quadrado 2 será:
80
2
120

3 c) A área do quadrado 1 é 400 cm2
(20  20  400); a área do quadrado 2
é 900 cm2 (30  30  900). Daí a razão
entre a área do quadrado 1 e a área do
quadrado 2 será: 400
900
4
9 
5. Tendo a equipe disputado 60 pontos e
acumulado 45 pontos, podemos escrever:
pontos acumulados
45
3
  
0,75
pontos disputados 60
4
Logo, o índice de aproveitamento dessa
equipe é 0,75.
6. a) De acordo com o esquema, as
quantidades de lajotas são:
• Total de lajotas pretas  2  20 5 40,
pois há 20 colunas verticais com
2 lajotas pretas cada uma.
• Total de lajotas brancas  8  20 5 160,
pois há 20 colunas verticais com
8 lajotas brancas cada uma.
• Total de lajotas brancas e pretas 
 200 lajotas (160 1 40 5 200).
Para o revestimento serão necessárias
200 lajotas.
b) número de lajotas pretas
40
200
total de lajotas  
1
5
c) número de lajotas brancas
160
200
total de lajotas  
4
5
d) número de lajotas pretas
número de lajotas brancas 
40
160
1
4 
e) A razão obtida no item d significa que,
para cada lajota preta, há 4 lajotas
brancas.
7. Do enunciado vem que o índice de
produtividade é a razão entre o lucro (L) e
o número de funcionários (n).
De acordo com a tabela, podemos escrever:
• 2008 
L
68000
n  16

4250
• 2009 
L
54000
n   12

4500
• 2010 
L
86400
n   20

4320
Logo, o índice de produtividade foi maior
em 2009.
8. Do enunciado vem que a razão entre o
fluxo de saída e o fluxo de entrada de
água expressa a eficiência do sistema.
De acordo com a tabela, podemos escrever:
• Sistema I 
 fluxo de saída
15
45
fluxo de entrada  
1
3
0,33
• Sistema II 
 fluxo de saída
10
40
1
4
fluxo de entrada   
0,25
• Sistema III 
 fluxo de saída
5
40
1
8
0,125
• Sistema IV 
 fluxo de saída
10
20
1
2
0,5
• Sistema V 
 fluxo de saída
5
20
1
4
0,25
Logo, entre os sistemas testados pela
indústria, o que apresenta maior eficiência
é o sistema IV, pois apresenta a maior razão.
1.
a) Determinando as razões entre a
população estimada de 2050 e a
população estimada de 2007 para os
Estados Unidos e o Brasil, temos:
• Estados Unidos  410
300
41
30 
• Brasil  250
190
25
19 
Logo, a maior razão é a dos Estados
Unidos, pois 41
30
1 37
25
19
 ,  1,32.
b) A razão entre a população da Índia em
2007 e a previsão da população indiana
em 2050 será de: 1130
1530
113
153  .
c) De acordo com a tabela, podemos fazer
o seguinte gráfico:
República
População
2 000
1500
1000
500
Popular da China
Índia Estados
Unidos
Brasil
2007
2050
População estimada
em milhões de habitantes
0
Países
Editoria de arte

169
d) Observando o gráfico, podemos
concluir que os países que apresentam
menor crescimento populacional no
período dado são: República Popular da
China e Brasil.
2.
a) Calculando as razões entre a produção
efetiva anual de energia elétrica e a
potência instalada para as usinas,
temos:
• Itaipu 
 90000000000
12600000
50000
7
5 7142,85
• Três Gargantas 
 84000000000
18200000
60000
13
5 4615,38
Logo, a razão é maior na usina
hidrelétrica de Itaipu.
b) Calculando a razão entre a potência
instalada e a área inundada pelo
reservatório para as usinas, temos:
• Itaipu 
 12600000
1350
28000
3
5 9333,33
• Três Gargantas 

18200000
1084
4550000
271
5 16 789,66
Logo, a razão é maior na usina
hidrelétrica de Três Gargantas.
49 – Algumas razões especiais
1. velocidade média
distância percorrida
tempo gasto 5 5
510
6
85
km
h
5 km/h
tempo gasto 5
510
6
85
km
h
5 km/h
Logo, a velocidade média do automóvel no
percurso foi de 85 km/h.
2.
a) De acordo com as informações, a
luz do Sol leva 500 segundos para
percorrer 150 000 000 km; assim temos:
velocidade média
tempo gasto 5 5
150000000
500
300000
km
s
5 km/s
tempo gasto 5
150000000
500
300000
km
s
5 km/s
Logo, a velocidade da luz no vácuo é
300 000 km/s.
b) Sabendo que 1 minuto 5 60 segundos,
500 segundos serão: 500
60
25
3 5 de
minuto, ou seja, 8 minutos e
20 segundos.
Logo, a luz do Sol leva cerca de 8 minutos
e 20 segundos para chegar à Terra.
3. Se a velocidade média do veículo é 95 km/h,
a cada hora ele percorrerá 95 km. Então:
a) Em 1 hora, ele percorrerá 95 km.
b) Em 2 horas, ele percorrerá 190 km
(2 ? 95 5 190).
c) Em 2 horas e meia, ele percorrerá
237,5 km (2,5 ? 95 5 237,5).
4. Calculando a velocidade média, temos:
velocidade média
tempo gasto 5 5
100
12
8 33
m
s
 , distância percorrida
velocidade média
tempo gasto 5 5
100
12
8 33
m
s
 , m/s
Logo, a velocidade média de Adriano foi
aproximadamente 8,33 m/s.
5. Do enunciado, temos:
• Comprimento no desenho  5 cm.
• Comprimento real R
R 3 m 5 (3 ? 100) cm 5 300 cm.
escala
comprimento no desenho
comprimento real 5 5
5
1
300 55 60
5
160
escala
5
1
300 55 60
5
160
Logo, a escala utilizada foi de
1
60 ou 1  60.
• Comprimento real R
R 2 m 5 (2 ? 100) cm 5 200 cm.
• Escala utilizada R 1 ; 40
• Comprimento no desenho R x
escala
comprimento real 5
Assim, temos:
35
1
40 200 5
x R x 5 5 cm ou
1
x
40 5
200
5
x
200 5
200
5
x
5
5 5


x 5 →x 5
cm



35
Logo, a largura da miniatura é 5 cm.

170
1.
a) Velocidade média 5
1000
15
R
velocidade média . 66,7 km/h
b) Velocidade média 5
1000
12,5 R
velocidade média 5 80 km/h
2. Com base no enunciado, temos:
• Comprimento real R 408 km 5
5 (408 ? 100 000) cm 5 40 800 000 cm
• Comprimento no desenho R 20,4 cm
escala
comprimentonodesenho
20,4
40800000
1
2000000 5
comprimento real 5
20,4
40800000
1
2000000 5 ou 1 ; 2 000 000.
Logo, a escala do mapa é 1 ; 2 000 000.
3.
a) Sabendo que
velocidade média
distânciapercorrida
tempogasto 5 ,
ou seja, v
d
m5 t , temos:
• De acordo com a tabela, a distância
de Caruaru a Fortaleza é 855 km. Se o
tempo de viagem é de 11 horas, temos:
v
km
h
855
11
km h m 5
77,7 / .
• De acordo com a tabela, a distância de
Brasília a Picos é 1 622 km. Se o tempo
de viagem é 21 horas, temos:
v
km
h
1662
21
km h m 5
79,1 / .
• De acordo com a tabela, a distância
de Aracaju a Anápolis é 1 800 km. Se o
tempo de viagem é 22,5 horas, temos:
v km h m 5
1800
22 5
80
,
/ .
b) Se a distância de Palmas a Bom Jesus
da Lapa é 1 598 km e a velocidade
média da motocicleta é 79,9 km/h, ele
percorrerá 79,9 km a cada hora. Então,
para percorrer 1 598 km, ele levará:
1598
79 9
comprimento real 5 → 1
5 20
. Portanto, o percurso
, km
h
h
comprimento real 5 → 1
10000000 99100000
foi feito em 20 horas.
c) Com base no enunciado, temos:
consumomédio
litros consumido 5 s
• Se a distância de Boa Vista a
Governador Valadares é 5 064 km e o
consumo de combustível foi 442 litros,
temos:
km
consumomédio
5064
422
12
5 km
,
. /,
• Se a distância de Araraquara ao Rio
de Janeiro é 694 km e o consumo de
combustível 50 litros, temos:
consumomédio
694
50
km
13 9
5 km
,
. , /,
• Se a distância de Mossoró a Vitória é
2 268 km e o consumo de combustível
foi 156 litros, temos:
km
consumomédio
2268
156
14 5
5 km
,
. , /,
d) Se a distância de São Luís a Campina
Grande é 1 530 km e o tempo para
percorrê-la foi 30 horas, temos:
v
km h m5 → m5 5 1530
d
t
v
km
h
30
51 /
Logo, a velocidade média do caminhão
foi 51 km/h.
e) Com base no enunciado, temos:
• Comprimento real R 2 268 km 5
5 (2 268 ? 100 000) cm 5 226 800 000 cm
• Comprimento no desenho R 11,34 cm
escala
11,34
226800000
5
escala
11,34
226800000
1
20000000 5 ou
1 ; 20 000 000.
Logo, a escala utilizada no mapa é
1 ; 20 000 000.
f) Com base no enunciado, temos:
• Comprimento real R 991 km 5
5 (991 ? 100 000) cm 5 99 100 000 cm
• Comprimento no desenho R x
escala
5 → 1
comprimento real 10000000 5 3 9,91
escala
x
5 59 91 59 91
10000000 99100000
→x , →x , cm
3 9,91
escala
x
→x , →x , cm
5 59 91 59 91
Logo, a distância no mapa entre Chuí e
Florianópolis é 9,91 cm.

171
Fazendo a pesquisa, concluímos que a
densidade do ouro é douro 5 19,32 g/cm3 e
da prata é dprata 5 10,49 g/cm3.
1. De acordo com o enunciado, temos:
densidade
14
25
kg
dm
, / 3
0 56 3
5 5 kg dm
Logo, a densidade do bloco é 0,56 kg/dm3.
densidade
8 1
3
g
cm
, 3
2 7 3
5 5 g cm
, /
Logo, a densidade dessa pedra é 2,7 g/cm3.
densidade
4 3
0 2
g
cm
, 21 5 3
,
3
5 5 g cm
, /
Logo, a densidade desse metal é 21,5 g/cm3.
4. De acordo com os dados dos bairros,
temos:
• Bairro A R densidadedemográfica
125000
24
hab
km
.
, ./km2
5 hab
5208 3 2
densidadedemográfica
125000
24
hab
km
.
, ./km2
5 hab
5208 3 2
• Bairro B R densidadedemográfica
83800
16
hab
km
.
, ./km2
5 5 hab
5237 5 2
83800
16
hab
km
.
, ./km2
5 5 hab
5237 5 2
Logo, o bairro B possui a maior densidade
demográfica.
1. Bahia: densidade demográfica 5
5
14 080654
564692 R densidade demográfica .
. 25 hab./km2
Paraná: densidade demográfica 5
5
10284503
199314 R densidade demográfica .
.51,6 hab./km2
2. De acordo com o mapa e sua legenda, temos:
a) O estado brasileiro que atingiu
40 milhões de habitantes em 2007 foi
São Paulo.
b) Os estados com a população de
10 milhões a menos de 20 milhões
de habitantes são quatro: Rio Grande
do Sul, Minas Gerais, Rio de Janeiro e
Bahia.
c) Os estados com a população de até
1 milhão de habitantes são três: Acre,
Roraima e Amapá.
3.
a) Densidade demográfica:
Região Norte:
14623316
3860000
R densidade
demográfica . 3,79 hab./km2
Região Nordeste:
51534 406
1560000
R
R densidade demográfica . 33 hab./km2
Região Sudeste:
77873120
930000
R
R densidade demográfica . 83,7 hab./km2
Região Sul:
26733595
577000
R densidade
demográfica . 46,3 hab./km2
Região Centro-Oeste:
13222854
1610000
R
R densidade demográfica . 8,2 hab./km2
1. Escrevendo as frações na forma
percentual, temos:
a)
51
100
551%
b)
6
100
56%
c)
15 4
100
15 4
,
5 , %
d)
3 5
11
20
55
100
5 555%
3 5
e)
3 20
1
5
20
100
5 520%
3 20

172
f)
3 25
3
4
75
100
5 575%
3 25
g)
3
8
?
5 0 375
5 37 5
0 375 100
, 5
100
,
, %
h) 7
16
?
5 0 4375
5 43 75
0 4375 100
, 5
100
,
, %
i)
2
3
?
. 0 , 666
66 6
0 666 100
100
,
5 5
, %
2. Escrevendo os números decimais na
forma percentual, temos:
a) 0 03
3
100
, 5 53%
b) 0 35
35
100
, 5 535%
c) 1 42
142
100
, 5 5142%
d) 0 625
62 ,
5
100
, 62 5
5 5 , %
e) 0 045
4 ,
5
100
, 4 5
5 5 , %
f) 0 228
22 ,
8
100
, 22 8
5 5 , %
3. A figura está dividida em 25 partes iguais,
das quais 9 partes estão pintadas de
vermelho, ou seja, temos a razão 9 para 25.
Daí:
3 4
9
25
36
100
5 536%
3 4
Logo, a área pintada de vermelho
representa 36% da área total.
4. A equipe acumulou 34 pontos dos
40 pontos disputados, ou seja, uma razão
de 34 para 40. Daí:
34
0 ,
85 0 , 85
?
100
5 5 5
85
%
40
100
Logo, o índice de aproveitamento dessa
equipe foi 85%.
5. Do enunciado, temos a razão 5 para 60,
pois 1 hora tem 60 minutos. Então:
5
. 0 ,
083 100
0 , 083
?
60
5 100
5
8 , 3
%
Logo, 5 minutos representam 8,3% de
uma hora.
6. Do enunciado, temos a razão 19 para 200.
Então:
19
200
?
. 0 , 095
9 5
0 095 100
100
,
5 5
, %
Logo, 19 pessoas representam 9,5% de
200 pessoas.
7. Podemos representar a quantidade de
itens de plásticos recolhidos por meio da
razão 250 para 400. Daí:
250
0 ,
625 ?
100
400
5 0 , 625
5 100
5
62 , 5
%
Logo, a quantidade percentual de itens de
plásticos recolhidos representa 62,5% do total.
8. De acordo com o gráfico, podemos representar
a quantidade de jogadores que concluíram
o Ensino Médio por meio da razão 68 para
112. Lembrar que o total de 68 jogadores que
concluíram o Ensino Médio inclui os jogadores
que possuem o superior incompleto.
Temos, então:
68
. 0 ,
60 0 , 60
?
100
60
%
12
5 100
5
Logo, o percentual de jogadores que
concluíram o Ensino Médio é
aproximadamente 60%.
Alternativa d.
a) Numeração cuja soma dos algarismos
é 8: 8, 17, 26, 35, 44, 53, 62, 71 e 80 R
R 9 números.
Logo, esse livro tem 9 páginas cuja soma
dos algarismos é 8.
b) A razão entre o número de páginas
com soma dos algarismos 8 e o total de
páginas é de 9 para 80. Então:
9
0 ,
1125 ?
100
5 0 , 1125
5 5
11 , 25
%
80
100
Logo, essa numeração representa 11,25%
do número total de páginas do livro.
• Total de fichas R 25
• Fichas ímpares R 13
• Fichas pares R 25 2 13 5 12
A razão entre o número de fichas pares e o
total de fichas é 12 para 25. Temos, então:
3 4
12
25
48
100
5 548%
3 4
Logo, as fichas com números pares
representam 48% do total de fichas.

173
11. De acordo com o gráfico, temos:
a) Estudantes inscritos por área:
• Engenharia
→
• Computação
→
•
Matemática
8  6 5
14
6  5 5
11
→

 
 
11 4 15
14 11 15 40
 5
Total5   5 estudantes
Logo, o total de estudantes que se inscreveram para fazer o estágio é 40.
b) A razão entre o número de estudantes de Matemática e o total de estudantes é 15 para 40.
Daí:
15
40

5 0 375
5 37 5
0 375 100
, 5
100
,
, %
Logo, os universitários de Matemática representam 37,5% do total de inscritos.
1.
a) 47% 2 44% 5 3%
b) De acordo com a tabela, a
participação feminina é maior que
a masculina nas áreas de: Ciências
Biológicas, Ciências Humanas,
Ciência da Saúde e Linguística, Letras
e Artes.
2.
a) Fittipaldi:
14
149
. 0,094 5
5
0 094 100
,  ,
100
9 4
100
5 5 9,4%
Piquet:
23
207
. 0,111 5
5
0 111 100
,  ,
100
11 1
100
5 5 11,1 %
Senna:
41
162
. 0,253 5
5
0 253 100
,  ,
100
25 3
100
5 5 25,3%
b) O melhor índice de aproveitamento
foi de Ayrton Senna, com 25,3% de
vitórias.
50 - Proporção
a) Fazendo a tabela, temos:
Tabela de descontos
Litros Descontos (em R$)
40 4
50 5
60 6
70 7
80 8
90 9
100 10
b) De acordo com a tabela do item
anterior, temos:
• Desconto para 40 litros R R$ 4,00
c) De acordo com a tabela, um desconto
de R$ 10,00 corresponde a 100 litros de
gasolina.
d) Sendo o desconto de R$ 1,00 para
cada 10 litros completos de gasolina,
temos que para 420 litros de gasolina o
desconto será de R$ 42,00, pois
3 42
1
10 420 5
x .
3 42
e) As razões estabelecidas com base na
tabela são:
• Desconto de 4 reais para 40 litros R
R
4
40
1
10
ou
R
5
50
1
10
ou

174
R
6
60
1
10
ou
R
7
70
1
10
ou
R
8
80
1
10
ou
R
9
90
1
10
ou
R
10
100
1
10
ou
f) Comparando as razões obtidas,
concluímos que são todas iguais a
1
10 .
51 – Propriedade fundamental das proporções
1. Aplicando a propriedade fundamental das proporções, temos:
a)
Produtodos extremos
Produtodosmeios
:
:
→
→
8 80 640
20
? 5
?? 5
? 5 ?
32 640
8 80 20 32
 
 
Logo, os números 8, 20, 32 e 80, nessa ordem, formam uma proporção.
b)
Produtodos extremos
Produtodosmeios
: , ,
:
→1 2?36543 2
→
 
 
6 72 43 2
1 2 36 6 72
? 5
? 5 ?
, ,
, ,
Logo, os números 1,2; 6; 7,2 e 36, nessa ordem, formam uma proporção.
c)
Produtodos extremos
Produtodosmeios
: ,
:
→
→
5 24 12
6
? 5
?1 5 9
5 24 6 1 5
,
, ,
5
? ?
 
 

Logo, os números 5; 6; 1,5 e 2,4 não formam uma proporção.
2. Aplicando a propriedade fundamental das
proporções, temos:
5
3 ,
5
8
5
x
5x 5 8 ? 3,5
5x 5 28
x 5
28
5
x 5 5,6
Logo, o valor de x é 5,6.
3. Aplicando a propriedade fundamental das
a)
6
10
15
5 x
6x 5 10 ? 15
6x 5 150
x 5
150
6
x 5 25
Logo, a quarta proporcional dos
números 6, 10 e 15 é o número 25.
b)
0 4
0 6
, 1 ,
2
,
5 x
0,4x 5 0,6 ? 1,2
0,4x 5 0,72
x 5
0 ,
72
0 ,
4
x 5 1,8
Logo, a quarta proporcional dos
números 0,4; 0,6 e 1,2 é o número 1,8.

175
4.
a)
x
3
8
12 5
12x 5 3 ? 8
12x 5 24
x 5
24
12
x 5 2
b)
10
x
7 5
21 ,
7x 5 10 ? 2,1
7x 5 21
x 5
21
7
x 5 3
c)
2
3
15
2
x
5
2 ? 2x 5 3 ? 15
4x 5 45
x 5
45
4
x 5 11,25
d)
x
x
1
2
5
6
6
2
3
3 ? (x 1 6) 5 2 ? (x 2 6)
3x 1 18 5 2x 2 12
3x 2 2x 5 212 2 18
x 5 230
e)
1
5
x
2
1 ,
5
5
x
1
1 ,
5 1 ? ( x 1 1,5) 5 5 ? (x 2 1,5)
x 1 1,5 5 5x 2 7,5
x 2 5x 5 27,5 2 1,5
24x 5 29 ? (21)
4x 5 9
x 5
9
4
x 5 2,25
f)
3
4
1
3
1
5 2x
3
4
1
3
1
2
x5 ?
3
1
x 4
5
6
6 ? 3x 5 4 ? 1
18x 5 4
x5 5
4
18
2
9
2
0,5 2 5
x
0,5x 5 2 ? 2
0,5x 5 4
x 5
4
0,5
x 5 8
Logo, serão necessários 8 ovos.
6. De acordo com o exposto, temos:
5
x
3 5
72 3x 5 5 ? 72
3x 5 360
x 5
360
3
x 5 120 R x 5 120 cm ou 1,2 m
Logo, a altura do bastão é 1,2 m.
1
25
12
5 x
1x 5 25 ? 12
x 5 300 R x 5 300 cm ou 3 m
Logo, o comprimento real é 3 m.
8. Do exposto pelo enunciado, temos:
1
2500
30
5 x
1x 5 2 500 ? 30
x 5 75 000 R x 5 75 000 habitantes
Logo, a população dessa cidade é
75 000 habitantes.
2
x
5 5
16 5x 5 2 ? 16
5x 5 32
x 5
32
5
x 5 6,4 R x 5 6,4 m/s
Logo, a velocidade de A é 6,4 m/s.
3
5
9
5 x
3x 5 5 ? 9
3x 5 45

176
x 5
45
3
x 5 15 R x 5 15 copos de água
Logo, deverão ser misturados 15 copos de
água.
• Para a medida real de 6,5 m ou 650 cm:
1
x
50 5
650 50x 5 650 ? 1
50x 5 650
x 5
650
50
x 5 13 R x 5 13 cm
• Para a medida real de 4,2 m ou 420 cm:
1
x
50 5
420 50x 5 420 ? 1
50x 5 420
x 5
420
50
x 5 8,4 R x 5 8,4 cm
Logo, as dimensões da cozinha no
desenho serão 13 cm e 8,4 cm.
1.
a) Se o interior de São Paulo tem 1 médico
para 659 habitantes e a quantidade de
médicos é 43 490, então a população
do interior é aproximadamente:
1
43490
659
5 x
x 5 659 ? 43 490
x 5 28 659 910 R x 5 28 659 910 habitantes
Logo, a população aproximada do
interior de São Paulo é 28 659 910
habitantes.
b) No estado de São Paulo a razão do
número de habitantes por médico
é 1 médico para 459 habitantes,
que é maior que a dos padrões
internacionais (1 médico para 1 000
habitantes).
No Brasil a razão do número de
habitantes por médico é 1 médico para
610 habitantes, que é maior que a dos
padrões internacionais (1 médico para
1 000 habitantes).
2. A medida no mapa da Rua Maria Antônia
é 3 cm e a escala do mapa é 1 ; 12 500.
Daí, temos:
1
12500
3
5 x
1x 5 3 ? 12 500
x 5 37 500 R x 5 37 500 cm ou 375 m
Logo, o comprimento real da Rua Maria
Antônia é aproximadamente 375 m.
escrever:
1
1450000
14 6
5
,
x
1x 5 14,6 ? 1 450 000
x 5 21 170 000 R x 5 21 170 000 cm ou
211,7 km
Logo, a distância real entre as cidades é
211,7 km.
52 – Outras propriedades das
proporções
1. Do enunciado temos x
y 5
5
3
e
x 1 y 5 32. Aplicando as propriedades das
x
5
→ x 1
y
5 1 3
→
x 1
y
8
y
5
3
y
5
3
y 5
3 Como x 1 y 5 32, temos:
32 8
y 3 5
8y 5 3 ? 32
8y 5 96
y 5
96
8
y 5 12
x 1 y 5 32
x 1 12 5 32
x 5 32 2 12
x 5 20
Logo, x 5 20 e y 5 12.
2. Sendo
a
b 5
7
8 e aplicando as propriedades
das proporções, temos:
a) a 1 b 5 45
a
b
a b
b 5
→ a 1
b
1 →
1
15
b
5
5
8 7
8
7 8
8
45 15
b 8 5
15b 5 8 ? 45
15b 5 360

177
b5
360
15
b 5 24
a 1 b 5 45
a 1 24 5 45
a 5 45 2 24
a 5 21
Logo, a 5 21 e b 5 24.
b) a 2 b 5 25
a
b
a b
b 5
→ a 2
b
2 →
2
1
b
5
52
8 7
8
7 8
8
Como a 2 b 5 −5, temos:
2 52
5 1
b 8
2b 5 25 ? 8
2b 5 240 ? (21)
b 5 40
a 2 b 5 25
a 2 40 5 25
a 5 25 1 40
a 5 35
Logo, a 5 35 e b 5 40.
x y → x 2
y x → x 2
y x
5 5
2 5 2
2 5
5 3 5
5 Como x 2 y 5 1,5, temos:
1 ,
5
x
3 5
5
3x 5 5 ? 1,5
3x 5 7,5
x 5
7 ,
5
3
x 5 2,5
x 2 y 5 1,5
2,5 2 y 5 1,5
2y 5 1,5 2 2,5
2y 5 21 ? (21)
y 5 1
Logo, os dois números são x 5 2,5 e y 5 1.
a b c a 1 b 1
c a a 1 b 1
c a
8 5 → → 5 5
2 8 1 5 1
2 5
8 15 5
8 Como a soma a 1 b 1 c 5 90, temos:
90
a
15 5
8 15a 5 8 ? 90
15a 5 720
a5
720
15
a 5 48 R a 5 48 cm
Tomando as igualdades duas a duas,
temos:
48
b
8 5
5 8b 5 5 ? 48
8b 5 240
b5
240
8
b 5 30 R b 5 30 cm
48
c
8 5
2 8c 5 2 ? 48
8c 5 96
c 5
96
8
c 5 12 R c 5 12 cm
Logo, os segmentos medem
a 5 48 cm, b 5 30 cm e c 5 12 cm.
5. Sendo os números x e y, temos:
• Soma de dois números é
15,4 R x 1 y 5 15,4.
• Razão R x y
7 4 5
Aplicando as propriedades das proporções,
temos:
x y → x 1
y x → x 1
y x
7 5
4 7 1
4 5
7 11 5
7 Como x 1 y 5 15,4, vem:
15 ,
4
x
11 5
7
11x 5 7 ? 15,4
11x 5 107,8
x 5
107 ,
8
11
x 5 9,8
x 1 y 5 15,4
9,8 1 y 5 15,4
y 5 15,4 2 9,8
y 5 5,6
Logo, o maior desses números é 9,8 e o
menor desses números é 5,6.
6. Aplicando as propriedades das

178
a)
x
5
y
x y
6
5
15
2 5



 
x
y
x y
y 5
→ x 2
y
2 →
2
1
y
5
5
5 6
5
6 5
5
Como x 2 y 5 15, temos:
15 1
y 5 5
y 5 5 ? 15
y 5 75
x 2 y 5 15
x 2 75 5 15
x 5 15 1 75
x 5 90
S 5 {(90,75)}
b)
x
5
y
x y
7
5
24
1 5



 
x
y
x y
y 5
→ x 1
y
1 →
1
12
y
5
5
5 7
5
7 5
5
24 12
y 5 5
12y 5 5 ? 24
12y 5 120
y 5
120
12
y 5 10
x 1 y 5 24
x 1 10 5 24
y 5 24 2 10
x 5 14
S 5 {(14,10)}
c)
x y
3 4
x y
35
5
1 5



 
x y → x 1
y x → x 1
y x
3 5
4 3 1
4 5
3 7 5
35
x
7 5
3 7x 5 3 ? 35
7x 5 105
x 5
105
7
x 5 15
x 1 y 5 35
15 1 y 5 35
y 5 35 2 15
x 5 20
S 5 {(15,20)}
d)
x y
2 5
y x
5
5
2 5



 
x y → y 2
x x → y 2
x x
2 5
5 5 2
2 5
2 3 5
2 Como y 2 x 5 6, temos:
6
x
3 5
2 3x 5 2 ? 6
3x 5 12
x 5
12
3
x 5 4
y 2 x 5 6
y 2 4 5 6
y 5 6 1 4
y 5 10
S 5 {(4,10)}
7. Conforme o enunciado, podemos
escrever:
• Suco de limão R x e água R y
• Proporção R x
y 5
2
9
• Limonada R x 1 y 5 5,5
Aplicando as propriedades das proporções,
temos:
x
2
→ x 1
y
2 1 9
→
x 1
y
11
y
5
9
y
5
9
y 5
9 Como x 1 y 5 5,5, temos:
5 5 11
,
y 5
9
11y 5 9 ? 5,5
11y 5 49,5
y 5
49 ,
5
11
y 5 4,5 R y 5 4,5 litros de água

179
x 1 y 5 5,5
x 1 4,5 5 5,5
x 5 5,5 − 4,5
x 5 1 R x 5 1 litro de suco de limão
Logo, serão necessários 1 litro de suco de
limão e 4,5 litros de água.
escrever:
x 1 y 5 16 R soma das idades dos dois
filhos
x
5
5
R razão entre as idades
y 3
Das propriedades das proporções, temos:
x
5
→ x 1
y
5 1 3
5
5
→
x 1
y
8
y
3
y
3
y 5
3 Como x 1 y 5 16, vem:
16 8
y 3 5
8y 5 3 ? 16
8y 5 48
y 5
48
8
y 5 6 R y 5 6 anos
x 1 y 5 16
x 1 6 5 16
x 5 16 2 6
x 5 10 R x 5 10 anos
Logo, as idades são 10 anos e 6 anos.
9. Denominando x os CDs clássicos e y
os CDs de música popular, podemos
escrever:
x 1 y 5 45 R total de CDs
x
1
y 5
4
R razão entre o número de CDs
x
1
→ x 1
y
1 1 4
5
5
→
x 1
y
5
y
4
y
4
y 5
4 Como x 1 y 5 45, vem:
45 5
y 4 5
5y 5 4 ? 45
5y 5 180
y 5
180
5
y 5 36 R y 5 36 CDs
x 1 y 5 45
x 1 36 5 45
x 5 45 2 36
x 5 9 R x 5 9 CDs
Logo, são 9 CDs clássicos e 36 CDs de
música popular.
10. Chamando os bombons de nozes de x e os
de frutas de y, podemos escrever:
x 1 y 5 60 R total de bombons
x y
5 R razão entre os bombons
7 5 Das propriedades das proporções, temos:
x y → x 1
y x → x 1
y x
7 5
5 7 5 5
7 12 5
1
7 Como x 1 y 5 60, vem:
60
x
12 5
7 12x 5 7 ? 60
12x 5 420
x 5
420
12
x 5 35 R x 5 35 bombons de nozes
x 1 y 5 60
35 1 y 5 60
y 5 60 2 35
y 5 25 R y 5 25 bombons de frutas
Logo, há nessa caixa 35 bombons de nozes
e 25 bombons de frutas.
11. Chamando diesel de x e álcool de y,
podemos escrever:
x
2
y 5
3
R razão entre diesel e o álcool
x 1 y 5 40 R total da mistura
x
2
→ x 1
y
2 1 3
→
x 1
y
5
y
5
3
y
5
3
y 5
40 5
y 3 5
5y 5 3 ? 40
5y 5 120
y 5
120
5
y 5 24 R y 5 24 litros de álcool

180
x 1 y 5 40
x 1 24 5 40
x 5 40 2 24
x 5 16 R x 5 16 litros de diesel
Logo, há na mistura 24 litros de álcool e
16 litros de diesel.
12. Chamando a massa de alumínio de x
e a massa de oxigênio de y, podemos
escrever:
x
7
y 5
8
R razão entre massas de alumínio
e oxigênio
x 1 y 5 51 R total de óxido de alumínio
x
7
→ x 1
y
7 1 8
→
x 1
y
15
y
5
8
y
5
8
y 5
51 15
y 8 5
15y 5 8 ? 51
15y 5 408
y 5
408
15
y 5 27,2 R y 5 27,2 g de oxigênio
x 1 y 5 51
x 1 27,2 5 51
x 5 51 2 27,2
x 5 23,8 R x 5 23,8 g de alumínio
Logo, a massa de alumínio será 23,8 g e a
massa de oxigênio será 27,2 g.
1.
a) Chamando o número de homens
eleitos de x e o número de mulheres de
y, podemos escrever:
x 1 y 5 27 R total de unidades
federativas
y
x 5
1
8
R razão entre o número
de mulheres eleitas e o
número de homens eleitos
Das propriedades das proporções,
temos:
y 1
x
1 1 8
→
y 1
x
9
x
5
8
x
5
27 9
x 8 5
9x 5 8 ? 27
9x 5 216
x 5
216
9
x 5 27 R x 5 27 homens
x 1 y 5 27
24 1 y 5 27
y 5 27 2 24
y 5 3 R y 5 3 mulheres
Logo, foram eleitas 3 mulheres para o
governo em 2006.
b) Resposta possível: Fazendo a pesquisa,
verificamos que os estados do Brasil
em que foram eleitas governadoras
em 2006 foram: Rio Grande do Sul, Rio
Grande do Norte e Pará.
2. Total de deputados federais eleitos:
45 1 468 5 513
Porcentagem de mulheres:
45
. 0,088 5
513
0 088 100
, ? 5 8,8%
100
3. Conforme o enunciado, temos:
• Estados que não elegeram mulheres em
qualquer dos cargos R 6
• Estados que elegeram 4 mulheres ou
mais R 3
Logo, a razão entre os estados que
elegeram 4 ou mais mulheres e os que não
elegeram mulheres é 3
6
1
2 5 .
4. Calculando 51,53% de 125 913 479:
51 53
100
125913479 64883216
,
? . mulheres
Logo, aproximadamente 64 883 216
mulheres estavam aptas a votar nas
eleições de 2006.
• Não houve candidatura feminina R
9 unidades federativas
• Total de unidades federativas R 27
Logo, a razão entre as unidades da
Federação com nenhuma candidatura
feminina e o total de unidades da
Federação é 9
27
1
3 5 .

181
• Total de candidaturas aprovadas pelo
TSE R 16 038
• Candidaturas aprovadas de mulheres
R 3 717
Daí a porcentagem de mulheres nessa
eleição foi:
3717
. 0 ,
2318 0 , 2318

100
23 18
16038
100
5 5
, %
Logo, a porcentagem de mulheres
candidatas em 2006 foi 23,18%.
Tratando a informação, páginas 264 e 265.
1.
a) De acordo com o gráfico, o assunto
de maior interesse das mulheres é
Notícias do momento.
b) De acordo com o gráfico, a expectativa
de vida das mulheres é 74,29 anos.
c) Somando as mulheres eleitas em 2004
nos cargos de vereadoras e prefeitas,
temos: 6 549 1 408 5 6 957.
Logo, em 2004 o total de mulheres
eleitas foi 6 957.
d) De acordo com o gráfico, o estado civil
da maioria das mulheres é solteira.
e) Sim, pois o número de mulheres eleitas
em 2002 para deputada estadual foi
129 e o de homens eleitos foi 906, o que
corresponde a pouco mais de 7 vezes
129.
2.
a) Reproduzindo a tabela, temos:
Estado População Área (km2) Sigla Capital
Acre 669 736 152 581,4 AC Rio Branco
Amapá 594 587 142 814,6 AP Macapá
Amazonas 3 232 330 1 570 745,7 AM Manaus
Pará 6 970 586 1 247 689,5 PA Belém
Paraná 10 261 856 199 314,9 PR Curitiba
Rio Grande
do Sul
10 845 087 281 748,5 RS Porto Alegre
Rondônia 1 534 594 237 576,2 RO Porto Velho
Roraima 391 317 224 299,0 RR Boa Vista
Santa Catarina 5 866 568 95 346,2 SC Florianópolis
Tocantins 1 305 728 277 620,9 TO Palmas
b) Os estados que compõem a região
Sul são Paraná, Santa Catarina e Rio
Grande do Sul. A população dessa
região é 10 261 856 1 10 845 087 1
1 5 866 568 5 26 973 511 R 26 973 511
habitantes.
E a superfície da região Sul é
199 314,9 1 281 748,5 1 95 346,2 5
5 576 409,6 R 576 409,6 km2.
c) Região Sul R Paraná, Santa Catarina e
Rio Grande do Sul
Densidade demográfica 5
5
10284503 5866252 10582840
1993149 95346 2 28174
1 1
, 1 , 1 8 5
26733595
5
, 576409,6
5
10284503 5866252 10582840
1993149 95346 2 28174
1 1
, 1 , 1 8 5
26733595
, 576409,6
. 46,4 hab./km2
d) A população da região Norte é:
655 385 1 587 311 1 3 221 939 1
1 7 065 573 1 1 453 756 1 395 725 1
1 1 243 627 5 14 623 316 habitantes.
E a área dessa região é:
152 581,4 1 142 814,6 1 1 570 745,7 1
1 1 247 689,5 1 237 576,2 1 224 299,0 1
1 277 620,9 5 3 853 327,3 R 3 853 327,3 km2.
Logo, a população e a superfície da
região Norte são, respectivamente,
14 623 316 habitantes e 3 853 327,3 km2.
e) A densidade demográfica da região
Norte é:
hab
km
5
14698878
3853327 3
.
3 2
,
. ,8 hab. / km2
hab
km
5
14698878
3853327 3
.
3 2
,
. ,8 hab. / km2
Logo, a densidade demográfica da
região Norte é 3,8 hab./km2.
f) A região que possui maior
superfície é a região Norte, pois
3 853 327,3 . 576 409,6.
g) A região que possui a maior densidade
demográfica é a região Sul, pois
46,8 . 3,8.
h)
Estado Densidade demográfica (hab./km2)
Acre 655 385/152 581,4 . 4,3
Amapá 587 311/142 814,6 . 4,1
Amazonas 3 221 939/1 570 745,7 . 2,0
Pará 7 065 573/1 247 689,5 . 5,7
Paraná 10 284 503/199 314,9 . 51,6
Rio Grande do Sul 10 582 840/281 748,5 . 37,6
Rondônia 1 453 756/237 576,2 . 6,1
Roraima 395 725/224 299 . 1,8
Santa Catarina 5 866 252/95 346,2 . 61,5
Tocantins 1 243 627/277 620,9 . 4,5

182
i) Aproveitando os dados da tabela,
elaboramos o gráfico de barras a
seguir.
Densidade demográfica (hab./km2)
0 10 20 30 40 50 60 70 (hab./km2)
Estados
Tocantins
Santa Catarina
Roraima
Rondônia
Rio Grande do Sul
Paraná
Pará
Amazonas
Amapá
Acre
j) Observando o gráfico, o estado que
possui a maior densidade demográfica
é Santa Catarina e o estado que possui
a menor densidade demográfica é
Roraima.
• Total de pessoas R 80 (I)
• Usam óculos R 25 (II)
Razão entre (II) e (I):
25
5
5 50,3125
80
16
Logo, a razão é 0,3125.
Alternativa c.
2. Sabendo que
velocidade média
tempogasto 5 ,
temos
200
25
8
m
s
5 m/s.
Logo, a velocidade média desse corredor
é 8 m/s.
Alternativa e.
3. Se a proporção é
d
v2
3
200 5 e v 5 30, temos:
d d
(30)
3
200 900
3
2 200 5 → 5
200d 5 3 ? 900
200d 5 2 700
d5
2700
200
d 5 13,5
Logo, o valor de d é 13,5.
Alternativa a.
1
x
75 5
12 75x 5 1 ? 12
75x 5 12
x 5
12
75
x 5 0,16 R x 5 0,16 m ou 16 cm
Logo, o comprimento do muro na maquete
será 16 cm.
Alternativa d.
5. 1
2
3
5
x2 x 1
4
, aplicando a propriedade
fundamental da proporção, temos:
3 ? (x 2 2) 5 1 ? (x 1 4)
3x 2 6 5 x 1 4
3x 2 x 5 4 1 6
2x 5 10
x 5
10
2
x 5 5
Logo, o quadrado de x é 25.
Alternativa b.
6. Sendo x o número de homens e y o
número de mulheres, temos:
x 1 y 5 320 R total de pessoas
x
9
y 5
7
R razão entre homens e mulheres
x
9
→ x 1
y
9 1 7
5
5
→
x 1
y
16
y
7
y
7
y 5
320 16
y 7 5
16y 5 7 ? 320
16y 5 2 240
y 5
2240
16
y 5 140
Editoria de arte

183
x 1 y 5 320
x 1 140 5 320
x 5 320 2 140
x 5 180
Logo, o número de homens é 180.
Alternativa c.
1
300
14
5 x
1x 5 14 ? 300
x 5 4 200 R x 5 4 200 cm ou 42 m
Logo, o comprimento real desse avião é 42 m.
Alternativa b.
escrever:
2
3
4
3
x
x 2
5
3 ? 2x 5 4 ? (x 2 3)
6x 5 4x 2 12
6x 2 4x 5 212
2x 5 212
x 52
12
2
x 5 26
2 6
y 15 5
6y 5 2 ? 15
6y 5 30
y 52
30
6
x 5 5
Logo, x2 1 y2 5 (26)2 1 (5)2 5 36 1 25 5 61.
Alternativa a.
1
50
9
5 x
1x 5 9 ? 50
x 5 450 R x 5 450 cm ou 4,5 m
1
50
10
5 y
1y 5 50 ? 10
y 5 500 R y 5 500 cm ou 5 m
Logo, as dimensões reais dessa cozinha
são 4,5 m e 5 m.
Alternativa b.
10. Conforme o enunciado, temos:
x
y
x y
y 5
→ x 1
y
1 →
1
11
y
5
5
5 6
5
6 5
5
550 11
y 5 5
11y 5 5 ? 550
11y 5 2 750
y 5
2750
11
y 5 250
x 1 y 5 550
x 1 250 5 550
x 5 550 2 250
x 5 330
Logo, o diâmetro da cratera de Vredefort
é 300 km.
Alternativa c.
montar a seguinte proporção:
x y → x 1
y x → x 1
y x
11 5
5 11 5 5
11 16 5
1
11 Como x 1 y 5 1448, temos:
144
x
16 5
11 16x 5 144 ? 11
16x 5 1 584
x 5
1584
16
x 5 99 R x 5 998
x 1 y 5 144
99 1 y 5 144
y 5 144 2 99
y 5 45 R y 5 458
Logo, x 2 y 5 998 2 458 5 548.
Alternativa c.
12. Conforme o enunciado:
• Distância entre A e B R 800 m 5 0,8 km
• Tempo gasto R 0,025 h
velocidade média
0 8
0 025
km
h
5 5 32
km h
,
,
/
Logo, a velocidade média da composição
nesse trecho é 32 km/h.
Alternativa a.
2
5
7
5 5
x 1
y
→ 2 1
5
x 1
y
→
x y
5
5
y
5
y

184
7
112
5
5 y
7y 5 5 ? 112
7y 5 560
y 5
560
7
y 5 80 R y 5 80 mm
x 1 y 5 112
x 1 80 5 112
x 5 112 2 80
x 5 32 R x 5 32 mm
Logo, y − x 5 80 2 32 5 48 mm.
Alternativa d.
14. Pelo enunciado, temos:
a
b
a b
b 5
→ a 1
b
1 →
1
5
b
5
5
3 2
3
2 3
3
Como a 1 b 5 908, pois o triângulo é
retângulo, vem:
90 5
b 3 5
5b 5 3 ? 90
5b 5 270
b5
270
5
b 5 54 R b 5 548
a 1 b 5 90
a 1 54 5 90
a 5 90 2 54
a 5 36 R a 5 368
Logo, essas medidas são: a 5 368 e b 5 548.
Alternativa d.
15. Conforme o enunciado, podemos escrever:
x R aroma de limão
y R aroma de coco
x
y
x y
y 5
→ x 1
y
1 →
1
8
y
5
5
3 5
3
5 3
3
Como x 1 y 5 2 400 (total de frascos), temos:
2400 8
y 3 5
x 1 y 5 2 400
x 1 900 5 2 400
x 5 2 400 2 900
x 5 1 500
8y 5 3 ? 2 400
8y 5 7 200
y 5
7200
8
y 5 900
Logo, foram adquiridos 1 500 frascos de
detergente cujo aroma é limão.
Alternativa d.
16. Sendo o primeiro maratonista x e o
segundo, y, podemos escrever:
x 2 y 5 3 R diferença entre velocidade
média
x
6
5
R razão entre velocidades
y 5
x
5
x 2
y
6 2 5
x 2
y
1
y
5
→ 5
→
6
y
5
y 5
3 1
y 5 5
x 2 y 5 3
x 2 15 5 3
x 5 3 1 15
x 5 18
1y 5 3 ? 5
y 5 15
Logo, a velocidade média do maratonista
mais veloz é 18 km/h.
Alternativa b.
17. Sendo x a altura da ladeira e y o
afastamento, podemos escrever:
x
x
10
x
1
510 y
y
5 100
y 5
10
%→ → R
R declividade da ladeira
Como o afastamento é de 50 m, vem:
x
1
50
5
10 10x 5 1 ? 50
10x 5 50
x 5
50
10
x 5 5 R x 5 5 m
Logo, a altura da ladeira é 5 m.
Alternativa b.
18. Sabemos que 13 km 5 1 300 000 cm, e
conforme o enunciado podemos escrever:
1
x
500000 1300000 5
500 000x 5 1 ? 1 300 000
500 000x 5 1 300 000
x 5
1300000
500000
x 5 2,6
Logo, o comprimento dessa estrada no
mapa é 2,6 cm.
Alternativa e.

185
Grandezas Proporcionais
Abertura, página 268 e 269.
Se um luthier demora 30 dias para fazer
um violino, 30 luthiers demorariam 1 dia
para fazer um violino.
53 – Números direta e
inversamente proporcionais
1.
a) Sim, pois cada convidado que chega à
festa deve levar duas garrafas de suco.
b) Como cada convidado deve levar duas
garrafas de suco, 6 convidados levaram
6 ? 2 5 12 garrafas de suco.
c) Se tivesse chegado o dobro de
convidados seriam 24 garrafas de suco.
Pois, como o número de convidados
dobrou, o número de garrafas de suco
também dobrará.
2. De acordo com as cenas, temos:
a) • cena 1 R cada pessoa receberá
12 pirulitos.
• cena 2 R cada pessoa receberá
6 pirulitos.
• cena 3 R cada pessoa receberá
3 pirulitos.
b) Sim, pois aumentando o número de
pessoas, diminuirá a quantidade de
pirulitos que cada pessoa vai receber.
c) Se há 3 pessoas e 12 pirulitos, cada
pessoa receberá 4 pirulitos.
d) Se o número de pessoas dobrar, cada
pessoa receberá 2 pirulitos. Pois,
dobrando o número de pessoas, o
número de pirulitos recebidos reduzirá
pela metade.
1. Fazendo a verificação se os números são
diretamente proporcionais, temos:
a) 4
16
1
4 5 9
36
1
4 5 7
28
1
4 5
Como 4
16
9
7
1
5 5 5 , os números
36
28
4 4, 9 e 7 são diretamente proporcionais
aos números 16, 36 e 28.
b) 7
50
2
175
35
10
7
2 5
Como 7
50
2
 175 , os números 7, 2 e 35
não são diretamente proporcionais aos
números 50, 175 e 10.
c) 6
14
3
7 5 12
7
18
4
9
2 5
Como
3
7
12
 7 , os números 6, 12 e 28
números 14, 7 e 4.
d) 1 5
4
3
8
,
5 2
3
2 4
2 5
24
25
,
, 5
Como 3
8
2
 3 , os números 1,5; 2 e 2,4
números 4, 3 e 2,5.
x y
40 72
32
128 5 5
Daí, temos:
x
32
40
5
128 128x 5 40 ? 32
128x 5 1 280
x 5
1280
128
x 5 10
y
72
32
128 5
128y 5 32 ? 72
128y 5 2 304
y 5
2304
128
y 5 18
Logo, x 5 10 e y 5 18.
3x 5 12 ? 30 5 104
Daí, temos:
3x 5 12 ? 30
3x 5 360
x 5
360
3
x 5 120
10y 5 12 ? 30
10y 5 360

186
y 5
360
10
⇒ y 5 36
Logo, os valores de x e y são
respectivamente 120 e 36.
4. Representando as parcelas por x, y e z,
podemos escrever:
x y z x 1 y 1
z x x 1 y 1
z x
5 5
⇒ 5
⇒ 5
3 7 4 3 1 7 1
4 3 14 3
x ⇒ x 1 y 1
z x
5
3 14 3
Como a soma das três parcelas é igual a
420, temos:
420
x
14 5
3 14x 5 3 ? 420
14x 5 1 260
x 5
1260
14
x 5 90
90
y
3 5
7 3y 5 7 ? 90
3y 5 630
y 5
630
3
y 5 210
90
z
3 5
4 3z 5 4 ? 90
3z 5 360
z 5
360
3
z 5120
Logo, as três parcelas são x 5 90, y 5 210 e
z 5 120.
5. Representando as parcelas por a, b e c,
podemos escrever:
2a 5 5b 5 4c 5 x
Daí, podemos tirar:
2
a x a x
2
5 ⇒ 5
b x b x
5
5
5 ⇒ 5
c x c x
4
4
5 ⇒ 5
Como a soma das três parcelas deve ser
380, temos:
a 1 b 1 c 5 380
x x x
2 5 4
1 1 5380
10
4
5
20
20
20
7600
20
x x x
1 1 5
10x 1 4x 1 5x 5 7 600
19x 5 7 600
x 5
7600
19
x 5 400
Substituindo x, obtemos:
x
a
400
2
5 5 5 2
200
b
x
400
5
5 5 5 5
80
c
x
400
4
5 5 5 4
100
Logo, as três parcelas são 200, 80 e 100.
6. Sendo a parte de Divo x e a parte de Dalva
y, temos:
a) Para a divisão em partes diretamente
proporcionais a 8 e 5, vem:
x y ⇒ x 1
y x ⇒ x 1
y x
5
5
5
8 5 8 1
5 8 13 8
Como a soma das três parcelas é 4 550,
temos:
4 550
x
13 5
8 13x 5 8 ? 4 550
13x 5 36 400
x 5
36 400
13
x 5 2 800
x 1 y 5 4 550
2 800 1 y 5 4 550
y 5 4 550 2 2 800
y 5 1 750
Logo, se a divisão for feita em partes
diretamente proporcionais, Divo
receberá R$ 2 800,00 e Dalva receberá
R$ 1 750,00.
b) Para a divisão em partes inversamente
proporcionais a 5 e 2, vem:
5x 5 2y 5 k
Daí, obtemos:
5
x k x k
y k y k
5 ⇒ 5 e 2
5
2
5 ⇒ 5
Como x 1 y 5 4 550, temos:
k k
5 2
1 545500
2
5
10
10
45550
10
k k
1 5
2k 1 5k 5 45 500
7k 5 45 500
k5
45500
7

187
x 5 6 500
Substituindo k, obtemos:
k
x
6500
5
5 5 5 5
1300
y
k
6500
2
5 5 5 2
3250
Logo, se a divisão for feita em partes
inversamente proporcionais, Divo
receberá R$ 1 300,00 e Dalva receberá
R$ 3 250,00.
7. Sendo x a massa do cobre e y a massa do
zinco, vem:
x y ⇒ x 1
y x ⇒ x 1
y x
5
5
5
7 3 7 1
3 7 10 7
40
x
10 5
7 10x 5 7 ? 40
10x 5 280
x 5
280
10
x 5 28
x 1 y 5 40
28 1 y 5 40
y 5 40 2 28
y 5 12
Logo, serão necessários 28 kg de cobre e
12 kg de zinco.
• preparação física R x
• treino de jogadas R y
• “racha” entre os jogadores R z
Daí, temos:
x y z ⇒ x 1 y 1
z x x 1 y 1
z x
5 5
5
⇒ 5
3 7 2 3 1 7 1
2 3 12 3
x 1 y 1
z x x 1 y 1
z x
5
3 1 7 1
2 3 12 3
⇒ 5
Como x 1 y 1 z 5 180, pois é o tempo total
do treino, vem:
180
x
12 5
3 12x 5 3 ? 180
12x 5 540
x 5
540
12
x 5 45
45
y
3 5
7 3y 5 7 ? 45
3y 5 315
y 5
315
3
y 5 105
45
z
3 5
2 3z 5 2 ? 45
3z 5 90
z 5
90
3
z 5 30
Logo, a 1a parte do treino durou 45
minutos, a 2a parte durou 105 minutos e a
3a parte durou 30 minutos.
• cimento R x
• saibro R y
• areia R z
Daí, temos:
x y z ⇒ x 1 y 1
z x ⇒ x 1 y 1
z x
5 5
5
5
1 2 4 1 1 2 1
4 1 7 1
x y z x 1 y 1
z x x 1 y 1
z x
5 5
⇒ 5
⇒ 5
1 2 4 1 1 2 1
4 1 7 1
Como x 1 y 1 z 5 420, pois é massa total
da mistura, vem:
420
x
7 5
1 7x 5 1 ? 420
7x 5 420
x 5
420
7
x 5 60
60
1 2 5
y
y 5 2 ? 60
y 5 120
60
z
1 5
4 z 5 4 ? 60
z 5 240
Logo, serão necessários 60 kg de cimento
para o preparo da mistura.
• transporte R x
• compras R y
• hospedagem R z
Daí, temos:
x y z ⇒ x 1 y 1
z x ⇒ x 1 y 1
z x
5 5
5
5
5 3 2 5 1 3 1
2 5 10 5
x y z x 1 y 1
z x x 1 y 1
z x
5 5
⇒ 5
⇒ 5
5 3 2 5 1 3 1
2 5 10 5
Como x 1 y 1 z 5 3 000, pois é o total
separado, vem:

188
3000
x
10 5
5 10x 5 5 ? 3 000
10x 5 15 000
x 5
15000
10
x 5 1 500
1500
y
5 5
3 5y 5 3 ? 1 500
5y 5 4 500
y 5
4500
5
y 5 900
1500
z
5 5
2 5z 5 2 ? 1 500
5z 5 3 000
z 5
3000
5
z 5 600
Logo, separei R$ 1 500,00 para transporte,
R$ 900,00 para compras e
R$ 600,00 para hospedagem.
• prêmio de Adriano R x
• prêmio de Beto R y
• prêmio de Carlos R z
Daí, temos:
5x 5 8y 5 4z 5 k
Logo, podemos tirar:
5
x k x k
y k y k
5 ⇒ 5 ; 8
5
5 ⇒ 5 ;
8
z k z k
4
4
5 ⇒ 5
Como o prêmio é de 460 reais, temos:
x 1 y 1 z 5 460
k k k
5 8 4
1 1 5460
8
5
40
40 40
18 400
40
k k k
1 1 5
8k 1 5k 1 10k 5 18 400
23k 5 18 400
k5
18 400
23
k 5 800
Substituindo k, obtemos:
k
x
800
5
5 5 5 5
160
y
k
800
8
5 5 5 8
100
z
k
800
4
5 5 5 4
200
Portanto, Adriano receberá R$ 160,00; Beto
receberá R$ 100,00 e Carlos receberá
R$ 200,00.
a) Sendo a área do parque x e
representando 95% por
95
100 , temos:
95
100
8400
5 x
95x 5 100 ? 8 400
95x 5 840 000
x 5
840000
95
x.8842,1
Logo, a área aproximada do parque é
de 8 842,1 metros quadrados.
b) Chamando de x a quantidade de cajus
produzidos por um dos cajueiros e y a
quantidade de cajus do outro cajueiro,
vem:
x y ⇒ x 1
y x x 1
y x
5
5
⇒ 5
3 497 3 1
497 3 500 3
Como os dois cajueiros produzem 80 000
frutos, temos:
80000
x
500 5
3 500x 5 3 ? 80 000
500x 5 240 000
x 5
240000
500
x 5 480
x 1 y 5 80 000
480 1 y 5 80 000
y 5 80 000 2 480
y 5 79 520
Logo, cada árvore produz
aproximadamente 480 e 79 520 cajus.
1. De acordo com a tabela, vem:
a) 4
10
2
5 5
b) 600
1500
2
5 5
c) As razões dos itens a e b são iguais.

189
d) Como as razões dos itens a e b são
iguais, as grandezas são diretamente
proporcionais.
a) 2
6
1
3 5
b) 15
5
53
c) As razões dos itens a e b são inversas.
d) Como as razões dos itens a e b
são inversas, as grandezas são
inversamente proporcionais.
3.
a) Sendo o comprimento do retângulo
40 cm e a largura 8 cm, temos:
A 5 8 ? 40 5 320 cm2
Logo, a área do retângulo é 320 cm2.
b) Se a largura for 6 cm, a área do
retângulo será:
A 5 6 ? 40 5 240 cm2
Logo, se a largura do retângulo for
6 cm a área será de 240 cm2.
c) Se a largura passar de 8 cm para 6 cm,
a razão será:
8
6
4
3 5
d) As áreas variam na razão:
320
240
4
3 5
e) As razões dos itens c e d são iguais.
f) Podemos verificar nos itens c e d que
as razões são iguais, logo as grandezas
são diretamente proporcionais.
4. De acordo com a tabela, temos:
a)
150
200
3
4 5
b)
300
400
3
4 5
c) A razões dos itens a e b são iguais.
d) Podemos verificar nos itens a e b que
as razões são iguais, logo as grandezas
são diretamente proporcionais.
5. De acordo com a tabela, temos:
a) 60
50
6
5 5
b) 80
96
5
6 5
c) As razões dos itens a e b são inversas.
d) Podemos verificar nos itens a e b que as
razões são inversas, logo as grandezas
são inversamente proporcionais.
1. De acordo com o gráfico, as grandezas
envolvidas são: consumo de gasolina
(em litros) e distância percorrida (em
quilômetros).
2. De acordo com o gráfico, as grandezas
são diretamente proporcionais, porque,
dobrando uma delas, a outra também
dobra; triplicando uma delas, a outra
também triplica... e assim por diante.
3. De acordo com o gráfico, com 1 litro de
gasolina, o carro percorre 15 km, como as
grandezas são diretamente proporcionais,
com 7 litros de gasolina, Fabrício
percorrerá 7 ? 15 5 105 km.
4. Como as grandezas são diretamente
proporcionais, se o carro percorrer
90 quilômetros ele consumirá
90
15
56
litros de gasolina, pois a cada 15 km ele
consome 1 litro de gasolina.
• Resposta pessoal.
54 – Regra de três simples
1. Representando por x o tempo procurado,
temos:
Tempo Clientes
5 3
x 36
Se duplicarmos o atendimento, o tempo
também duplicará. Logo, as grandezas são
diretamente proporcionais.
Daí, temos:
5
x
3 5
36 3x 5 5 ? 36
3x 5 180
x 5
180
3
x 5 60
Logo, Onofre vai levar 60 minutos ou 1
hora para atender os 36 clientes.
2. Representando por x a altura do edifício,
temos:
Altura (m) Sombra (m)
2 0,8
x 12
Se duplicarmos a sombra, também
duplicará a altura.
Logo, as grandezas são diretamente
proporcionais.

⇒190
Daí, temos:
2
0 8 5
12
0 8 5 2 ?
12
0 8 5
24
24
0 8
30
,
,
,
5 5
,
x
x
x
, , 5 5 ? 5 5 5
x ⇒ x ⇒ x ⇒x 56
x
Portanto, a altura do edifício é de 30 m.
3. Representando por x o número de páginas
procurado, temos:
Linhas Páginas
45 280
30 x
Se duplicarmos o número de linhas, a
quantidade de páginas cairá pela metade.
Logo, as grandezas são inversamente
proporcionais.
Daí, temos:
30x 5 45 ? 280
30x 5 12 600
x 5
12 600
30
5 5 ? 5 5 541
x 5 420
Portanto, seriam necessárias 420 páginas.
4. Representando por x o comprimento
procurado, temos:
Largura (cm) Comprimento (cm)
3 4
10,5 x
Duplicando a largura, também duplicará
o comprimento. Logo, as grandezas são
Daí, temos:
3
4
10 5 3 4 105 3 42 42
5 5 ? 5 5 514
3
, ,
x
⇒ x ⇒ x ⇒x
42 42
3
5 x
5 514
Portanto, o comprimento da foto ampliada
será de 14 cm.
5. Representando por x a massa de poeira
procurada, temos:
Massa (gramas) Volume (m3)
0,7 100
x 8 000
Duplicando o volume, também duplicará
o ar filtrado. Logo, as grandezas são
Daí, temos:
0 7
100 8 000
5 5 ? 5 5 541
, , 5 5 ? 5 5 5
x ⇒ 100 x 0 7 8 000 ⇒ 100 x 5600 ⇒x 5600
56
100
0 7
100 8 000
100 0 7 8 000 100 5600 5600
100
Portanto, serão retidos 56 gramas de
poeira.
6. Representando por x o comprimento
verdadeiro do fio, temos:
Corda (m) Fio (m)
2 40
2,05 x
Duplicando o comprimento do fio,
também duplicará o comprimento da
corda. Logo, as grandezas são diretamente
proporcionais.
Daí, temos:
2
40
2 05 2 40 2 05 2 82 82
2
, ,
x
⇒ x ⇒ x ⇒x
2
40
2 05 2 40 2 05 2 82 82
2
, ,
x
⇒ x ⇒ x ⇒x
Portanto, o comprimento verdadeiro do fio
é 41 m.
7. Representando por x a concentração de
álcool procurada, temos:
Lata de cerveja
Concentração
(gramas por litro)
1 0,3
5 x
Duplicando a ingestão de cerveja,
também duplicará a concentração de
álcool no sangue. Logo, as grandezas são
Daí, temos:
1
5 5 ⇒x 5 5 ? 03 , ⇒x
5 15
,
0 ,
3
x
Portanto, a concentração de álcool no
sangue seria de 1,5 grama por litro.
8. Representando por x a quantidade de dias
procurada, temos:
Comprimento (c) Dias
600 x
180 6
Duplicando o comprimento da rua,
também duplicarão os dias trabalhados.
Logo, as grandezas são diretamente
proporcionais.
Daí, temos:
600 180
6
180 6 600 180 3600 3600
180
20
x
5 ⇒ x5 ? ⇒ x5 ⇒x5 5
600 180
6
180 6 600 180 3600 3600
180
20
x
5 ⇒ x5 ? ⇒ x5 ⇒x5 5

191
Para concluir a obra serão necessários 20
dias. Como já foram trabalhados 6 dias,
faltam 14 dias para concluir a obra.
Portanto, o trabalho estará terminado em
14 dias.
9. Representando por x a velocidade média
procurada, temos:
Velocidade (km/h) Tempo (min)
75 40
x 50
Duplicando o tempo, a velocidade cairá
pela metade. Logo, as grandezas são
Daí, temos:
50 75 40 50 3000 3000
x5 ? ⇒ x5 ⇒x5 560
50
Portanto, a velocidade média do ônibus
será de 60 km/h.
10. Representando por x a distância de
Brasília a Salvador, no mapa, temos:
Real (km) Desenho (cm)
1 600 24
1 200 x
Duplicando a distância real, a distância no
desenho duplicará. Logo, as grandezas são
Daí, temos:
1600
24
x5 ? ⇒ x5 ⇒x5 520
Portanto, seriam necessários 20 caminhões.
1200 1600 1200 24 1600 28800 28800
1
5 5 ? 5 5
x
⇒ x ⇒ x ⇒x
600
518
1200 24 1600 28800 28800
1
⇒ x ⇒x
? 5 5
600
518
Portanto, no mapa a distância que separa
Brasília de Salvador é de 18 cm.
11. Representando por x a quantidade de
água procurada, temos:
Comprimento (m) Volume (litros)
8 45 000
10 x
Duplicando o comprimento, também
duplicará o volume. Logo, as grandezas são
Daí, temos:
8
45000
10 8 10 45000 8 450000 450000
5 5 ? 5 5 55625
8
x
⇒ x ⇒ x ⇒x 0
8 10 45000 8 450000 450000
5 ? 5 5 55625
8
⇒ x ⇒ x ⇒x 0
Portanto, cabem na piscina 56 250 litros de
água.
caminhões procurada, temos:
Caminhões Capacidade (m3)
16 5
x 4
Duplicando a capacidade dos caminhões,
a quantidade de caminhões cairá
pela metade. Logo, as grandezas são
Daí, temos:
4 516 4 80 80
4
13. Como a velocidade média do piloto é de
153 km/h, temos que o piloto percorre
153 km a cada hora. Transformando 153 km
para metros, vem 153 000 m. Daí, temos:
velocidade média
tempogasto 5 5
153000
3600
542,5m/distânciapercorrida
velocidademédia
tempogasto 5 5
153000
3600
542,5m/s
Logo, a velocidade média do piloto foi de
42,5 m/s.
14. De acordo com o enunciado, o problema
é inversamente proporcional, pois
duplicando a quantidade de operários o
tempo cairá pela metade. Representando
por x o tempo procurado, temos:
Operários Dias
16 48
30 x
30x 5 25 ? 48
30x 5 1 200
x 5
1 200
30
x 5 40
Logo, a cobertura estaria pronta em
40 dias.
15. Como a velocidade do piloto é de 25 m/s,
temos que o piloto percorre 25 metros a
cada segundo. Transformando 25 metros
para quilômetros, vem 0,025 km, e
transformando 1 segundo em hora, vem
1
hora
3600
Daí, temos:
velocidade5 5 ? 5 km h
0 025
1
3 600
0 025
3600
1
90
,
, /
Logo, a velocidade é de 90 km/h.

⇒ x ⇒ x ⇒x 1 , 5
, 5 , 5 ? , , , ,
5 5 5
53
? 5 5 510
5 5 5
192
duplicando a velocidade o tempo cairá
pela metade. Representando por x o
tempo procurado, temos:
Velocidade (km/h) Tempo (horas)
450 4
800 x
800x 5 4 ? 450
800x 5 1 800
x 5
1 800
800
x 5 2,25
Logo, o avião levaria 2,25 h ou 2h15min.
é diretamente proporcional, pois
duplicando o comprimento do muro
também duplicará o tempo. Como já
foram construídos 14 m do muro, ainda
faltam 35 m, e sendo x o tempo para
construir o restante do muro, temos:
Comprimento (m) Tempo (dias)
14 4
35 x
14
4
35 14 4 35 14 140 140
5 5 ? 5 5 510
14
x
⇒ x ⇒ x ⇒x
35 14 140 140
14
⇒ x ⇒x
Logo, o restante do muro será construído
em 10 dias.
5 5 ? 5 5 540
duplicando a área também duplicará
a quantidade de azulejos. Sendo x a
quantidade de azulejos procurada, temos:
Área (m2)
Quantidade de
azulejos
3 ? 6,5 5 19,5 390
15 x
19 5
390
, , , , , , ,
x5 ? , ⇒ x5 ⇒x5 ⇒x520
Logo, o comprimento da outra tela é de
20 m.
5 5 ? 5 5 520
15 195 15 390 195 5850 5850
5 5 ? 5 5 5
5 5 ? 5 5 540
5 5 ? 5 5 520
5 5 ? 5 5 5
19 5
, , ,
,
x
⇒ x ⇒ x ⇒x 300
195 5850 5850
19 5
,
,
⇒ x ⇒x 300
duplicando o comprimento da tábua
duplicará sua sombra. Sendo x o
comprimento da sombra procurada, temos:
Comprimento (m) Sombra (cm)
1,5 53
10,5 x
1 5
53
10 5 1 5 53 105 15 556 5 556 5
1 ,
5
x
10 5 1 5 53 105 15 556 5 556 5
1 ,
5
x
⇒ x ⇒ x ⇒x 371
Logo, o comprimento da sombra seria de
371 cm ou 3,71 m.
duplicando a largura o comprimento cairá
pela metade. Sendo x o comprimento
procurado, temos:
Comprimento (m) Largura (m)
50 1,20
x 3
3 50 12 3 60 60
3
21. De acordo com a tabela, o problema
duplicando a área pintada também
duplicará o tempo e a quantidade de tinta
usados. Sendo x o tempo procurado e y a
quantidade de tinta gasta, temos para o
tempo:
Área (m2) Tempo (h)
10 2
200 x
10
2
200 10 2 200 10 400 400
10
x
⇒ x ⇒ x ⇒x
10
2
200 10 2 200 10 400 400
10
x
⇒ x ⇒ x ⇒x
Para a quantidade de tinta, temos:
Área (m2) Tempo (ℓ)
10 1
200 y
10
1
200 10 1 200 10 200 200
10
y
⇒ y ⇒ y ⇒y
10
1
200 10 1 200 10 200 200
10
y
⇒ y ⇒ y ⇒y
Logo, o tempo será de 40 horas e serão
gastos 20 litros de tinta.
Alternativa d.
a) Se 100 gramas de açaí tem 250
quilocalorias, então 50 gramas terá 125
quilocalorias, pois se a massa caiu pela
metade as calorias também caíram
pela metade.

y ⇒ y ⇒ y ⇒y 100
1 7 97 5
193
b) As frutas apresentadas na tabela que
contêm menor quantidade de:
• carboidrato R caju
• proteínas R guaraná e maracujá
• quilocalorias de energia R caju e
pitanga
• gordura R maracujá e pitanga
c) Sendo x a quantidade de carboidratos
procurada no abacaxi e y a quantidade
procurada no guaraná, vem:
Consumo (gramas)
Carboidratos
(gramas)
100 12
120 x
100
12
120 100 12 120 100 1 440 1 440
5 5 ? 5 5 514 4
100
x
⇒ x ⇒ x ⇒x ,
100 12 120 100 1 440 1 440
⇒ x ⇒x ,
5 ? 5 5 514 4
x 100
Para a polpa de guaraná:
Consumo (gramas)
Carboidratos
(gramas)
100 17,5
80 y
100
17 5
y ⇒ y ⇒ y ⇒y .5735
80 100 80 17 5 100 1 400 1 400
100
14
,
, , ,
5 5 ? , 5 5 5
y
⇒ y ⇒ y ⇒y
80 17 5 100 1 400 1 400
100
14
⇒ y ⇒y
5 ? , 5 5 5
y Logo, foram consumidos 14,4 g de
carboidratos no abacaxi e 14 g de
carboidratos na polpa de abacaxi, ou
seja, a pessoa consumiu
14,4 1 14 5 28,4 g de carboidratos.
d) Sendo x a quantidade de proteínas
ingeridas com o consumo do cupuaçu,
vem:
Consumo (gramas) Proteínas (gramas)
100 1,7
7 x
100
1 7
7 100 78 1 7 100 132 6 132 6
100
1 3
,
5 5 ? , 5 , 5 , 5 ,
x
⇒ x ⇒ x ⇒x 26
1 7 100 132 6 132 6
5 , 5 , 5 ,
1 3
, 100
⇒ x ⇒x 26
Logo, a pessoa ingeriu 1,326 g ou
1 326 mg de proteínas.
e) Sendo x a quantidade de gordura
contida na polpa de açaí, temos:
Consumo (g) Gorduras (g)
100 12
35 x
100
12
35 100 12 35 100 420 420
5 ? ⇒ 5
5 5 ? 5 5 54 2
100
x
⇒ x ⇒ x ⇒x ,
12 35 100 420 420
? 5 5 54 2
100
⇒ x ⇒x ,
Logo, o suco continha 4,2 g de gordura.
f) Chamando de x a quantidade de
proteínas que o atleta deve ingerir e
transformando 65 kg para gramas,
temos:
Consumo (g) Massa do corpo (g)
1,5 1 000
x 65 000
1 5
1000 65000
, 5 1000 51,5?65000 1000 597500 x ⇒ x ⇒ x ⇒1 , 5
x 5 ⇒ 1000 x 51,5?65000 ⇒ 1000 x 597500 ⇒x 97
500
5 597,5
1000 65000
1000
Logo, um atleta de 65 kg deve ingerir
97,5 g de proteínas diariamente.
Chamando de y a quantidade de polpa
de cupuaçu necessária para ingerir
97,5 g de proteína, temos:
Consumo (g) Proteínas (g)
100 1,7
y 97,5
100
1 7 97 5
1 7 100 975 17 9750 9 750
, , ,
, , 1 ,
5 5 ? 5 5
1 7 100 975 17 9750 9 750
, , 1 ,
7
5 5 ? 5 5
Logo, seria necessária a ingestão de
5 735 g de cupuaçu.
55 – Regra de três composta
1. Indicando por x a quantidade de dias
procurada, podemos escrever:
Dias Táxis Consumo ()
30 25 100 000
x 36 240 000
As grandezas número de táxis e quantidade
de dias são inversamente proporcionais e
as grandezas número de dias e consumo de
combustível são diretamente proporcionais.
Daí, temos:
30 36
25
100 000
240 000
30 3600 000
x x 6 000 000
3 600 000x 5 30 ∙ 6 000 000
3 600 000x 5 180 000 000
x 5
180 000 000
3600 000
x 5 50
Logo, uma frota de 36 táxis consumiria
240 000 , de combustível em 50 dias.

194
2. Indicando por x a quantidade de litros de
água desperdiçados, podemos escrever:
Gotas por minuto Dias Água ()
20 30 100
30 50 x
As grandezas número de dias e gotas por
minuto são diretamente proporcionais à
quantidade de água desperdiçada.
Daí, temos:
20
2 30
100 2
100
? 5 ⇒
5
30
50
5
1
1
5
x x
2x 5 5 ∙ 100
2x 5 500
x 5
500
2
x 5 250
Logo, foram desperdiçados 250 litros de
água.
3. Indicando por x o número procurado,
podemos escrever:
Altura (m) Comprimento (m) Dias
2,5 30 24
2 25 x
As grandezas altura do muro e comprimento
do muro são diretamente proporcionais ao
número de dias.
Daí, temos:
2 , 5
30
15 24 37 ,
5
24
2
25
25
1
? 5 5 x x →
37,5x 5 25 ∙ 24
37,5x 5 600
x 5
600
37,5
x 5 16
Logo, o grupo de operários ergueria o muro
em 16 dias.
4. Chamando a quantidade de operários de
x, podemos escrever:
Operários Horas Calçados
16 8 240
x 10 600
A grandeza horas trabalhadas é
inversamente proporcional a número de
operários e a grandeza pares de calçados
é diretamente proporcional a número de
operários.
Daí, temos:
16 10
8
240
600
16 30
30
1
1
30
60 x x ? 5 → 5
30x 5 16 ∙ 60
30x 5 960
x 5
960
30
x 5 32
Logo, serão necessários 32 operários.
5. Chamando o número de dias de x,
podemos escrever:
Digitadores Páginas Dias
6 720 18
8 800 x
As grandezas número de digitadores e número
de dias são inversamente proporcionais; as
grandezas número de páginas e número de
dias são diretamente proporcionais. Daí,
temos:
1
8
720
18 ? 5 →
120
18
x 100
5 6
800
x 1
120
100
120x 5 18 ∙ 100
120x 5 1 800
x 5
1 800
120
x 5 15
Logo, em 15 dias 8 digitadores prepararão
800 páginas.
6. Sendo x o tempo procurado, podemos
escrever:
Velocidade (km/h) Horas por dia Dias
60 8 6
80 9 x
As grandezas velocidade e dias são
inversamente proporcionais; as grandezas
número de horas por dia e dias são
inversamente proporcionais. Daí, temos:
80
60
9
8
6 90
? 5 5 x x →
60
6
10
1
90x 5 6 ∙ 60
90x 5 360
x 5
360
90
x 5 4
Logo, o mesmo percurso seria feito em 4
dias.
7. Sendo x a quantidade de caixas que o
outro funcionário leva, podemos escrever:
Caixas por vez Tempo (min.) Total de caixas
4 3 240
6 5 x
As grandezas número de caixas por vez e total
de caixas são diretamente proporcionais;

195
as grandezas tempo e total de caixas são
inversamente proporcionais. Daí, temos:
4
5
240 ? 5 →
20
240
6
3
x 18
5 x 20x 5 18 ∙ 240
20x 5 4 320
x 5
4320
20
x 5 216
Logo, o funcionário mais devagar leva
216 caixas.
a) Do enunciado temos que, o total de
cimento gasto para construir a laje de
6 cm de espessura foi de 30 ? 40 5
5 1 200 kg de cimento. Sendo x a
quantidade de cimento gasto em uma
laje de 5 cm de espessura, temos:
Espessura (cm) Aumento (kg)
6 1 200
5 x
As grandezas espessura e cimento
são diretamente proporcionais, pois
dobrando a espessura da laje também
dobrará a quantidade de cimento
utilizado.
Daí, temos:
6
1200
x x 5 ? → 5
5 040x 5 100 ∙ 630
5 040x 5 63 000
x 5
? ? → 5 5 x
5 6 51200 6 6000 6000
? ? → 5 5 x
5 5 ? 5 5 51000
6
x
⇒ x ⇒ x ⇒x
51200 6 6000 6000
? 5 5 51000
6
⇒ x ⇒x
Logo, se a laje fosse de 5 cm de
espessura seria economizado
1 200 2 1 000 5 200 kg de cimento.
b) Se cada saco de cimento contivesse
50 kg e a laje tivesse 5 cm de
espessura, seriam utilizados
1000
50
520
sacos de cimento, pois a laje precisaria
de 1 000 kg de cimento.
1. Sendo x o número de celulares, podemos
escrever:
Número de
celulares (milhões)
Dias Residências
100 28 1 260
x 7 630
As grandezas número de celulares, número
de dias e residências são diretamente
proporcionais. Daí, temos:
100 28
7
180
1260
630
100 5040
630 1
63000
5040
x 5 12,5
Logo, 12,5 milhões de celulares sendo
carregados simultaneamente utilizam
a energia que pode abastecer por uma
semana 630 residências.
2. Chamando de x o número de livros
procurado, temos:
Minutos por mês
Usuários
(milhões)
Livros Páginas
80 100 4 900 000 475
16 2 x 95
As grandezas minutos por mês, número
de usuários e quantidade de livros são
inversamente proporcionais. Enquanto as
grandezas número de páginas e quantidade de
livros são inversamente proporcionais. Daí,
temos:
80
100
95
4900000 95000
16
2
475
1900
490000
40
4
25
1
0
x
80
16
100
2
95
475
4900000 95000
1900
490000
40
4
25
1
0
x
95 000x 5 1 900 ∙ 4 900 000
95 000x 5 9 310 000 000
9310000000
x 5
95000
x 5 98 000
Logo, seriam necessários 98 000 livros.
Tratando a Informação, páginas 290 e 291.
1.
a) Em cada 100 entrevistados, 18
afirmaram trabalhar em empresas
que estimulam a amizade entre
funcionários.
Para 300 000 entrevistados,
54 000 fariam tal afirmação, pois
18 300000
18
100
%de → ?300000554000
b) Do resultado, temos que menos de uma
em cinco pessoas considera-se amiga
do chefe. Sendo x o número de pessoas
que se considera amiga do chefe em
um grupo de 55 pessoas, temos:

⇒ x ⇒ x ⇒x 0
x ⇒ x ⇒ x ⇒⇒x ⇒x megawatts 5 5
⇒ x ⇒ x ⇒x 0
196
1
5 55
5 55 55
5 5 5 511
5
x ⇒ x ⇒x
Logo, menos de 11 pessoas se
consideram amigas do chefe em um
grupo de 55 pessoas.
c) Calculando um terço de 210
funcionários, temos:
1
3
?210570
funcionários. Como a empresa
promoveu atividades para estimular
a amizade entre seus colaboradores e
de acordo com o quadro I, o número
máximo de empregados satisfeitos que
a empresa deverá esperar será: (50% de
70)  70.
Daí, temos:
50
100
?70535
Logo, o número máximo de
empregados satisfeitos será de
35 1 70 5 105 funcionários.
2.
a) De acordo com a tabela, para cada
1 000 nascimentos, em São Francisco
do Conde, 38 crianças morrem.
Duplicando o número de nascimentos
também duplicará o número de
crianças mortas.
Daí, para 2 000 nascimentos, espera-se
que 76 crianças morram, ou seja, 1 924
crianças sobrevivam, pois 2 000 2 76 5
5 1 924.
Logo, para 2 000 nascimentos espera-se
que 1 924 crianças sobrevivam.
Daí, para 3 500 nascimentos e sendo x o
número de crianças mortas, temos:
38
1000 3500
x ⇒ 1000 x 38 3500 ⇒ 1000 x 133000 ⇒x 13300
0
5 5 ? 5 5
1000
⇒x5133
1000 38 3500 1000 133000 13300
5 ? 5 5
1000
⇒x5133
Se 133 crianças morrem, 3 500 2 133 5
5 3 367 crianças sobrevivem.
Logo, para 3 500 nascimentos espera-se
que 3 367 crianças sobrevivam.
b) De acordo com a tabela, para cada
1 000 nascimentos no Brasil, 26
crianças morrem. Daí, para 5 000
nascimentos e sendo x o número de
crianças que se espera que morram,
temos:
26
1000 5000
x ⇒ x ⇒ x ⇒
630000
100
x ⇒ 1000 x 26 5000 ⇒ 1000 x 130000 ⇒x 13000
0
5 5 ? 5 5
1000
⇒x5130
1000 26 5000 1000 130000 13000
5 ? 5 5
1000
⇒x5130
Se 130 crianças morrem, 5 000 2 130 5
5 4 870 crianças sobrevivem.
Logo, para 5 000 nascimentos no
Brasil espera-se que 4 870 crianças
sobrevivam.
c) Espera-se que sobrevivam menos
crianças, pois a tabela mostra que a
taxa de mortalidade nesse município
é maior que a taxa de mortalidade
nacional. Espera-se que sobrevivam
12 crianças a menos, em cada 1 000
nascimentos.
3.
a) Sendo x o tempo procurado, podemos
escrever:
Brasileiro Tempo (min.) Mês
1 80 1
3 x 5
Como as grandezas número de brasileiros
e meses são diretamente proporcionais
à grandeza tempo, vem:
1
1
80 ? 5 →
1
80
3
5
x 15
5 x x 5 15 ∙ 80 ⇒ x 5 1 200 min ou 20 h
Logo, os brasileiros falam, em média,
1 200 min ou 20 h ao celular durante
5 meses.
b) Representando por x a quantidade de
megawatts/hora procurada, temos:
Megawatts/hora Celulares (milhões)
315 100
x 2 000
As grandezas megawatts/hora e
número de celulares são diretamente
proporcionais.
Daí, temos:
315
100 2000
5 100 5315?2000 100 5630000
315
100 2000
5 100 5315?2000 100 5630000
630000
100
6300 ⇒x5 ⇒x5 6300 megawatts /
hora
Sendo y a quantidade de residências
procurada, temos:
Megawatts/hora Residências
315 1 260
6 300 y
As grandezas megawatts/hora e
número de residências são diretamente
proporcionais.
Daí, temos:

197
315
1260
6300 5 315 512606300 315 57938000
y
⇒ y ⇒ y ⇒
⇒ ⇒ 2 200⇒ 400
⇒ y ⇒⇒y5 ⇒y5 residências
315 1260 6300 315 7938000 5  5
y 7938000
315
25200
7938000
315
⇒y5 ⇒y5 25200
residências
Logo, seriam abastecidas 25 200
residências.
c) Chamando de x a quantidade de
minutos procurada, temos:
Linhas Telefones
Tempo
(segundos)
2 4 5
8 16 x
As grandezas número de linhas e
número de telefones são diretamente
proporcionais ao tempo. Daí, temos:
2
4
5 ⇒
2
5
 5 5
18
16
x 72
x
2 572 2 360 360
⇒ ⇒ ⇒
2
x x x
x
1
1
9
2
8
5  5 5
5
⇒ 80 segundos ou 3minutos
Logo, mantendo a mesma proporção,
levariam 3 minutos para vender 18
linhas e 16 telefones.
Retomando o que aprendeu, página 291 e 292.
a
28 b
12 15
20 5 5
Daí, a vem:
a a
28
a a a
28
5 5  5
5 5  5
a a
5 5
a a
b
15
20
20 15 28 20 420
420
20
21
5 5
12 15
2
5
⇒ ⇒ ⇒
⇒ ⇒
0
⇒ ⇒ ⇒
⇒ ⇒ ⇒
15 20 12 15 240
240
15
16
⇒ ⇒
b b
b b
5  5
5 5
b
15
20
20 15 28 20 420
420
20
21
12 15
2
5
⇒ ⇒ ⇒
⇒ ⇒
0
15 20 12 15 240
240
15
16
⇒ ⇒
b b
b b
5  5
5 5
Logo, a 1 b 5 21 1 16 5 37.
Alternativa c.
2. Representando por x, y e z as parcelas,
podemos escrever:
2x 5 5y 5 4z 5 k
2
x k x k
2
5 ⇒ 5
y k y k
5
5
5 ⇒ 5
4
z k z k
4
5 ⇒ 5
Como a primeira parcela é 200, vem:
x5 k 5 k k5  k5
2
200
2
ySendko k 5y 400, temoys:
400
5
5 5 5
5
y k y y
400
5
5 5 5
5
z k z z
5 5 5
80
4
400
4
100
⇒ ⇒
⇒ ⇒
z k z z
5 5 5
80
4
400
4
100
⇒ ⇒
⇒ ⇒
Logo, x 1 y 1 z 5 200 1 80 1 100 5 380.
Portanto, Caio dividiu o número 380.
Alternativa a.
3. Sendo x, y e z os trechos asfaltados pelas
empresas A, B e C, respectivamente,
temos:
x y z x y z z
5 5
⇒ ⇒
2 5 3 2 5 3 3
x y z z
⇒
10 3
Como x 1 y 1 z 5 420, vem:
420
10 3
1 1
1 1
5
1 1
5
z z z
⇒ ⇒ ⇒
10 3 420 10 1260
5 5  5
1260
10
⇒ z 5 ⇒
z
5
126
Logo, o trecho asfaltado pela empresa C foi
de 126 km.
Alternativa a.
4. Chamando de x, y e z a quantia que cada
pessoa vai receber, podemos escrever:
5x 5 2y 5 10z 5 k
5
x k x k
5
5 ⇒ 5
y k y k
2
2
5 ⇒ 5
z k z k
10
10
5 ⇒ 5
Como x 1 y 1 z 5 34 000, temos:
k k k
5 2 10
1 1 534000
2
5
10
10 10
340000
10
k k k
1 1 5
2k 1 5k 1 k 5 340 000
8k 5 340 000
k5
340000
8
k 5 42 500
Daí, temos:
x5 k x5 5
5
42 500
5
⇒ 8 500
y5 k y5 5
2
42 500
2
⇒ 21 250
z5 k z5 5
10
42 500
10
⇒ 4 250

⇒ x ⇒x ⇒x
10
,
? 5 5 5
198
Logo, a maior quantia paga será de
R$ 21 250,00.
Alternativa b.
5. Do enunciado, podemos escrever a partir
da informação II:
a b c a 1 b 1
c c a 1 b 1
c c
5 5
⇒ 5
⇒ 5
5 4 2 5 1 4 1
2 2 11 2
c ⇒ a 1 b 1
c c
5
2 11 2
Como a 1 b 1 c 5 33, temos:
33
11 2
c ⇒ 11 c 2 33 ⇒ 11 c 66 ⇒c 66
⇒c
5 5 ? 5 5 56
11
66 66
11
5 5 56
c ⇒c ⇒c
Daí, vem:
b 6
b b b
4
2 4
x ⇒ x ⇒ x ⇒x ⇒x
5 5 ? 5 5 5 ,
5 → 53⇒ 54 ?3⇒ 512
a 6
→ a 5 53⇒ a 55?3⇒ a
515
5
2 5
Logo, o filho mais velho tem 15 anos.
Alternativa d.
6. Sendo x o tempo procurado, temos:
Watts Tempo (horas)
40 15
60 x
Se duplicarmos a potência da lâmpada,
o tempo cairá pela metade. Logo, as
grandezas são inversamente proporcionais.
Daí, temos:
60 40 15 60 600 600
x5 ? ⇒ x5 ⇒x5 ⇒x510
60
Portanto, a lâmpada deverá funcionar por
10 horas.
Alternativa b.
7. Chamando de x o lado menor da foto
ampliada, temos:
2 5
3 5 14
x5 ? ⇒ x5 ⇒x5 ⇒x540
Logo, seriam necessárias 40 latas.
Alternativa d.
x5 ? ⇒ x5 ⇒x5 ⇒x580
Logo, a velocidade média na volta é de
80 km/h.
Alternativa c.
, x 5 ⇒ 3 , 5 x 5 2 , 5 ? 14 ⇒ 3 ,
5 x 35 ⇒x 35
5 5 ⇒x
5
10
,
3 ,
5
14 3 5 35 35
3 ,
5
x5 ? ⇒ x5 ⇒x5 ⇒x575
Logo, o lado menor da foto ampliada deve
medir 10 cm.
Alternativa b.
latas de óleo procurada, temos:
Lata (ℓ) Quantidade de latas
2 60
3 x
As grandezas são inversamente
proporcionais. Daí, vem:
3 2 60 3 120 120
3
açúcar procurada, temos:
Açúcar (kg) Frutas (kg)
3 2,5
x 4
As grandezas são diretamente
3
2 5 4
x ⇒ 2 5 x 3 4 ⇒ 2 5 x 12 ⇒x 12
⇒x
5 5 ? 5 5 5 ,
2 5
4 8
,
, ,
,
3
2 5 4
2 5 3 4 2 5 12 12
2 5
4 8
,
, ,
,
Logo, ela deverá utilizar 4,8 kg de açúcar.
Alternativa b.
10. Representando por x a velocidade média
na volta, temos:
Velocidade (km/h) Tempo (min.)
60 16
x 12
12 16 60 12 960 960
12
11. Representando por x o tamanho do tecido
procurado, temos:
Tecido (m) Largura (cm)
105 50
x 70
70 50 105 70 5250 5250
x5 ? ⇒ x5 ⇒x5 ⇒x575
70
70 50 105 70 5250 525 0
70
Logo, o tecido terá 75 m.
Alternativa e.
12. Chamando de x o tempo que o ponteiro
menor levará para percorrer 42 graus,
temos:
Ângulo (graus) Tempo (min.)
30 60
42 x

30
60
42 30 60 42 30 2 520 2 520
5 5 ? 5 5 584
30
x
⇒ x ⇒ x ⇒x ⇒x
42 30 2 520 2 520
5 5 584
30
⇒ x ⇒x ⇒x
Logo, o ponteiro menor levará 84 minutos
para percorrer 42 graus.
Alternativa e.
⇒ x ⇒ x ⇒x 102
9
13. Chamando de x o número de pacotes de
pão procurado, temos:
Pacotes Sanduíches
7 105
x 150
5 5 ? 5 5 5
7
105 150
x ⇒ 105 x 7 150 ⇒ 105 x 1050 ⇒x 1050
⇒x
5 5 ? 5 5 510
105
150 105 1050 1050
⇒ x ⇒x ⇒x
5 5 510
105
Logo, Cristina usará 10 pacotes de pão de
forma.
Alternativa a.
14. Sendo x o comprimento procurado,
podemos escrever:
Comprimento (m) Largura (m)
80 35
x 25
25 35 80 25 2 800 2 800
x5 ? ⇒ x5 ⇒x5 ⇒x5112
25
800 2 800
⇒x5 ⇒x5112
25
Logo, o comprimento deverá passar de
80 m para 112 metros, ou seja, o
comprimento deverá ser aumentado de
32 m, pois 112 2 80 5 32.
Alternativa d.
15. Sendo x a quantidade de recenseadores
que devem ser contratados, temos:
Residências Recenseadores
102 9
3 060 x
102
9
3060 102 9 3060 102 27540 27540
102
5 5 ? 5 5 x
3060 102 9 3060 102 27540 27540
102
x
⇒ x ⇒ x ⇒x ⇒x 270
Logo, precisam ser contratados 270
recenseadores.
Alternativa e.
16. Sendo x, y e z as quantias a serem pagas,
podemos escrever:
x y z x y z x
5 5
30 40 50 30 40 50 30
x y z x
120 30
1 1
1 1
5
1 1
5
⇒ ⇒
⇒
Como x 1 y 1 z 5 90 mil, temos:
90
120 30
x x x
⇒ ⇒ ⇒
120 30 90 102 2700
5 5 ? 5
2 700
120
⇒ x 5 ⇒ x
5
22
,5mil ou 22500
Daí, temos:
22500
30 40
y y
⇒ ⇒
30 40 22500
5 5 ?
30 900000 900000
⇒ y 5 ⇒ y
5
⇒ y 530000
30
22500
z z
⇒ ⇒
5 5 ?
30 50
30 50 22500
30 1125000 1125000
⇒ ⇒
z z
5 5
30
⇒y537500
Logo, o maior credor receberá R$ 37 500,00.
Alternativa a.
199

200
56 – Porcentagem
1.
Porcentagem
a) De acordo com a tabela, 10 crianças
fazem parte da turma de Roberto.
b)
• Quantidade de meninos: 6. Logo:
6
10
0 6
0 ,
6 ?
100
100
5 , 5 5
60
%
• Quantidade de meninas: 4. Logo:
4
10
0 4
0 ,
4 ?
100
100
5 , 5 5
40
%
• Quantidade de crianças
com cabelo preto: 5. Logo:
5
10
0 5
0 ,
5 ?
100
100
5 , 5 5
50
%
• Quantidade de crianças
com cabelo loiro: 3. Logo:
3
10
0 3
0 ,
3 ?
100
100
5 , 5 5
30
%
2. De acordo com o enunciado, a turma
tem 40 alunos, dos quais 26 têm 12 anos
completos. Daí, vem:
a) taxa percentual dos alunos
que já completaram 12 anos:
26
0 ,
65 100
5 0 , 65
?
5 5
65
%
40
100
b) Os 40 alunos representam 100% da
turma. Como 65% da turma têm 12 anos
completos, temos:
100% 2 65% 5 35%
Logo, 35% dos alunos ainda não
completaram 12 anos.
3. Do enunciado, temos que em 40 g de
óxido de magnésio há 24 g de magnésio.
Daí:
24
0 ,
6 100
5 0 , 6
?
5 5
60
%
40
100
Logo, a taxa percentual de magnésio na
substância é de 60%.
4. Do exposto, podemos escrever:
a) O clube de Antônio venceu 24 jogos,
dos 30 que disputou. Logo, a taxa
percentual de vitórias é de:
24
0 ,
8 100
5 0 , 8
?
5 5
80
%
30
100
O clube de Alfredo venceu 21 jogos,
dos 28 que disputou. Logo, a taxa
percentual de vitórias é de:
21
0 ,
75 100
5 0 , 75
?
5 5
75
%
28
100
Portanto, o time de Antônio teve 80%
de aproveitamento, e o time de Alfredo
teve 75% de aproveitamento.
b) O que apresentou melhor campanha
foi o clube A, o de Antônio.
5. Alternativa a.
Representando por x o valor que Luciana
ganha com a venda de cada sofá:
x 5 1,5% de 8 200 5 0,015 ? 8 200 5 123
Logo, Luciana ganhou R$ 123,00 com a
venda do sofá.
6. Sendo 100% o salário da funcionária,
8% são descontados para a Previdência
Social. Logo, sobra do salário:
100% 2 8% 5 92% R 92% do salário
Chamando de x o salário da funcionária:
x 5 92% de 420 5 0,92 ? 420 5 386,40
Portanto, a funcionária recebe R$ 386,40.
7. Com o desconto de 15%, o valor pago pelo
aparelho, em porcentagem, foi:
100% 2 15% 5 85% R 85% do valor original
Representando o valor original do
aparelho por x, podemos escrever:
85% de x 5 102 R 0,85 ? x 5 102 R
R x 5
102
0,85
R x 5 120
Logo, o preço original do aparelho de som
era R$ 120,00.
8. Representando por x o preço pago pela
mercadoria, podemos escrever:
• loja 1, desconto de 20%
Logo, o valor pago em porcentagem
será:
100% 2 20% 5 80% R 80% do valor
original, que é 120 reais.
Daí, temos:
x 5 80% de 120 5 0,8 ? 120 5 96 R
R R$ 96,00
Portanto, o valor pago na loja 1 será de
R$ 96,00.
• loja 2, desconto de 30%
Logo, o valor pago em porcentagem
será:

201
100% 2 30% 5 70% R 70% do valor
original, que é 140 reais.
Daí, temos:
x 5 70% de 140 5 0,7 ? 140 5 98 R
R R$ 98,00
Portanto, o valor pago na loja 2 será de
R$ 98,00.
Logo, o preço mais baixo é o da loja 1,
R$ 96,00.
9. Representando por x o número
de universitários que escolheram
computação:
x 5 35% de 40 5 0,35 ? 40 5 14 R
R 14 universitários
Logo, 14 universitários se inscreveram para
fazer estágio em computação.
10. Como 45% dos alunos não confirmaram a
ida no acampamento:
100% 2 45% 5 55% R 55% dos alunos já
confirmaram a inscrição.
Chamando de x os alunos que
confirmaram a inscrição, temos:
x 5 55% de 60 5 0,55 ? 40 5 33 R 33 alunos
Logo, 33 alunos confirmaram a inscrição.
• Estudam no turno da manhã: 15 ? 30 5
5 450 alunos
• Estudam no turno da tarde: 20 ? 25 5
5 500 alunos
• Total de alunos da escola: 450 + 500 5
5 950 alunos
• Como 52% dos alunos são meninas,
temos:
100% 2 52% 5 48% R 48% dos alunos
são meninos.
Representando por x a quantidade de
meninos:
x 5 48% de 950 5 0,48 ? 950 5 456
Logo, estudam nessa escola 456 meninos.
Brasil Real, páginas 297 e 298.
1.
a) Das 8 415 apreensões de répteis no
Brasil, em 2005, 6 347 foram no estado
do Amazonas. Logo, a taxa percentual
de apreensões é de:
6347
. 0 ,
754 100
0 , 754
?
75 , 4
%
8415
5 100
5
Portanto, a porcentagem de animais
apreendidos no Amazonas é de 75,4%.
b) Representando por x o número de
apreensões feitas no Sudeste brasileiro,
temos:
x 5 6% de 8 415 5 0,06 ? 8 415  505 R
R 505 répteis
Logo, no Sudeste brasileiro, foram
apreendidos 505 répteis.
espécies de répteis, temos:
x 5 6% de 6 300 5 0,06 ? 6 300  378 R
R 378 espécies de répteis
Logo, na Amazônia, há 378 espécies de
répteis diferentes.
3. De acordo com o texto, temos:
a) • Crianças de 5 a 9 anos que
trabalham: 280 228
• Crianças de 10 a 15 anos que
trabalham: 2 708 066
• Crianças de 16 ou 17 anos que
trabalham: 2 450 261
• Total de crianças: 5 438 555
Daí, vem:
Percentual de crianças que
trabalhavam na idade de 5 a 9 anos:
280228
5438555
?
. 0 , 0515
5 15
0 0515 100
100
,
5 5
, %
Logo, a porcentagem aproximada
das crianças entre 5 e 9 anos que
trabalhavam é de 5,15%.
b) Sendo x o número que representa 5,1%
das crianças que trabalham em via
pública:
x 5 5,1% de 5 438 555 5 0,051 ? 5 438 555 
 277 366
Logo, trabalham, em via pública,
aproximadamente 277 366 crianças.
c) Se 68,6% das crianças que trabalham
estão atrasadas na escola, então:
100% 2 68,6% 5 31,4%
31,4% das crianças que trabalham não
estão atrasadas na escola.
Se 80,5% das crianças que trabalham
frequentam a escola, e cerca de 31,4%
dessas crianças não estão atrasadas,
temos:
x 5 31,4% de (80% de 5 438 555) R
R x 5 31,4% de (0,805 ? 5 438 555) R
R x 5 31,4% de 4 378 036 R
R x 5 0,314 ? 4 378 036 R x 5 1 374 703
Logo, das que trabalham e frequentam
a escola, 1 374 703 crianças não estão
atrasadas nos estudos.

202
4.
a) A expressão “um em cada vez”
representa 10%, pois:
1
0 ,
1 100
0 1
?
10
100
5 , 5 5
10
%
b) Em 2000, um em cada dez chefes
de família não ganhavam um único
centavo. Esse número representa 10%
do total de chefes de família no Brasil.
Chamando de x o total de chefes de
família, temos:
10% dex 2600000 0,1 x 2600000
→ x
→ 000000
→ →
5 ? 5
2 600 000
0,1
x 26
5 5
Logo, havia 26 000 000 de chefes de
família no Brasil em 2000.
c) Se a cada chefe de família corresponde
um domicílio, em 2000 havia no Brasil
26 000 000 de domicílios, dos quais
2 600 000 estavam sem rendimentos.
d) Se 9,15% do total de residências do
país corresponde a 4 099 domicílios
sem rendimentos, e sendo x o total de
residências do país, temos:
9 , 15 % dex 4099 0 ,
0915 x
4099
4099
0 0915
44 7
x x
,
5 ? 5
5
→ →
→ →  97
Logo, nessa época, o Brasil tinha 44 797
domicílios.
e) • Usando o total de residências do
item c, temos:
170000000
26000000
6,5
Logo, com esses dados, havia,
em média, 6,5 pessoas em cada
domicílio.
• Usando o total de residências do
item d, temos:
170000000
44797
3794
Logo, com esses dados, havia, em
média, 3 794 pessoas em cada
domicílio.
f) O mais confiável é o resultado
encontrado no item c.
g) As informações numéricas desse artigo
são contraditórias.
h) Resposta em aberto.
Chegou a sua vez!, página 299 e 300.
2. Cada símbolo completo do CD representa
1 000 unidades vendidas. Daí, vem:
a)
R 500 unidades, pois
1
2
1000 500
1
500
? 5
1
4
1000 250
1
250
? 5
1
8
1000 125
1
125
? 5
b) As vendas em cada trimestre foram:
1o trimestre: 3 125 unidades
• A venda foi inferior a 3 500 unidades,
apenas no 1o trimestre.
• A venda foi superior a 3 500 unidades,
no 1o, no 2o , no 3o e no 4o trimestre.
• No 2o trimestre foram vendidas 500
unidades a mais que no 1o trimestre, pois:
3 625 2 3 125 5 500
• No 2o trimestre foram vendidas
250 unidades a menos que no 3o
trimestre, pois:
3 875 2 3 625 5 250
c) Organizando os dados em uma
tabela, temos:
Trimestre 1o 2o 3o 4o
Número de
CDs vendidos
3 125 3 625 3 875 4 750
d) Observando as figuras do gráfico,
verificamos que há 15 CDs completos
mais 3 partes com
1
8
de CD. Como cada
CD representa 1 000 unidades, temos:
15 ? 1 000 + 3
1
8
1000
1
125
? ? 5 15 000 +
+ 375 5 15 375
Logo, foram vendidas, no ano, 15 375 uni-dades
de CDs.

203
e) Construindo um gráfico de acordo com
a tabela indicada, temos:
Legenda
1 000 unidades
1º_ trimestre
2º_ trimestre
3º_ trimestre
4º_ trimestre
1. Alternativa c.
Do enunciado, temos:
1
?
4
5 0 25
5 25
0 25 100
, 5
100
,
%
Logo, esse número representa 25% dos
alunos da academia.
2. Alternativa d.
Do enunciado, temos:
8 5
0 47
18
0 47 ?
100
100
47
,
,
,
 5 5
%
Logo, o Brasil ocupa, aproximadamente,
47% da superfície da América do Sul.
3. Alternativa d.
Sabemos que, no gráfico de setores, 360o
corresponde a 100% em taxa percentual.
Daí, temos que 25% corresponde a um
ângulo de 90°. Logo, 75% corresponde a um
ângulo de 270o em um gráfico de setores.
Observando os gráficos, concluímos que
o único gráfico em que 75% corresponde
a um ângulo de 270o é o indicado pela
alternativa d.
4. Alternativa e.
Representando
7
2000 em porcentagem,
temos:
7
2000
?
5 0 0035
5 0 35
0 0035 100
, 5
100
,
, %
Logo, o aumento do comprimento é de
0,35%.
5. Alternativa d.
O valor percentual da passagem era de
100%, com o aumento de 16%, esse valor
passou a:
100% + 16% 5 116%
Logo, sendo x o novo preço da passagem:
x 5 116% de 15 R x 5 1,6 ? 15 R x 5 17,40
Portanto, o preço da passagem passou a ser
R$ 17,40.
6. Alternativa c. O valor percentual da
bicicleta é de 100%; como Luís quer
vendê-la com um lucro de 5%, o preço
percentual de venda será:
100% + 5% 5 105%
Logo, sendo x o preço de venda da bicicleta:
x 5 105% de 180 R x 5 1,05 ? 180 R x 5 189
Portanto, o preço de venda da bicicleta será
R$ 189,00.
7. Alternativa c.
50% de (10%)2 5 0,50 ? (0,10)2 5 0,50 ? 0,01 5
5 0,005
Logo, 50% do quadrado de 10% é 0,005.
8. A entrada do cinema custava R$ 13,00, o
que corresponde a 100%. Com o aumento
de 20%, o novo preço da entrada passará
a ser, em porcentagem:
100% + 20% 5 120%
Representando por x o novo preço da
entrada:
x 5 120% de 13 R x 5 1,20 ? 13 R x 5 15,60
Como a pessoa com 65 anos ou mais paga
meia-entrada:
15 60
2
7 80
,
5 ,
Logo, o preço da entrada desse cinema
para uma pessoa com 65 anos ou mais é
R$ 7,80.
Projeto
3. Resposta em aberto
4. Reproduzindo as figuras e desenhando os
eixos de simetria, temos:
5. Sim, pois os ângulos internos desse
losango são 60o e 120o, que são diversos de
360o.

206
SUMÁRIO
8o . ano
Os números reais............................................................................................... 207
Introdução ao cálculo algébrico....................................................................... 211
Estudo dos polinômios....................................................................................... 214
Estudo das frações algébricas........................................................................... 230
Equações do 1o. grau com uma incógnita............................................................. 236
Porcentagem e juro simples................................................................................. 245
Sistema de equações do 1o. grau com duas incógnitas.......................................... 248
Geometria.......................................................................................................... 259
Ângulos formados por duas retas paralelas com uma reta transversal.............. 262
Polígonos.......................................................................................................... 265
Estudando os triângulos................................................................................... 270
Estudando os quadriláteros.............................................................................. 276
Estudando a circunferência e o círculo............................................................. 282

207
OS NÚMEROS REAIS
• Pra pensar, sem se cansar!
169, pois o quadrado é formado por 13 3 13
quadradinhos.
1 – Raiz quadrada exata de um
número racional
1.
a) Área 12: 1 3 12, 2 3 6, 3 3 4
b) Área 16: 1 3 16, 2 3 8, 4 3 4
2. Sim, o de medidas 4 3 4.
3. Não, pois existem números inteiros cujo
quadrado seja 18.
4. Sim, um quadrado de lado 6, ou seja, 6 3 6.
152 5 225; 252 5 625; 452 5 2 025; 552 5
5 3 025;
652 5 4 225; 752 5 5 625; 852 5 7 225; 952 5
5 9 025.
a) 16
1 1 3 1 5 1 7 5 16
b) 25
1 1 3 1 5 1 7 1 9 5 25
c) 36
1 1 3 1 5 1 7 1 9 1 11 5 36
1.
a) 121 sim, 112 5 121
b) 169 sim, 132 5 169
c) 186 não
d) 441 sim, 212 5 441
2.
a) 625 5 54 (Expoente par), sim.
b) 784 5 24 3 72 (Expoentes pares), sim.
c) 1 200 5 24 3 31 3 52 (Nem todos os
expoentes são pares), não.
d) 1 156 5 22 3 172 (Expoentes pares), sim.
e) 2 000 5 24 3 53 (Nem todos os
expoentes são pares), não.
3.
a) 484 5 222  a raiz é 22.
b) 625 5 252  a raiz é 25.
c) 729 5 272 a raiz é 27.
d) 1 296 5 362  a raiz é 36.
e) 1 849 5 432  a raiz é 43.
f) 3 025 5 552  a raiz é 55.
g) 4 096 5 642  a raiz é 64.
h) 5 625 5 752  a raiz é 75.
4.
a) 2,25 5 1,5, pois (1,5)2 5 2,25
b) 3,61 5 1,9, pois (1,9)2 5 3,61
c) 4,41 5 2,1, pois (2,1)2 5 4,41
d) 7,84 5 2,8, pois (2,8)2 5 7,84
e) 10,89 5 3,3, pois (3,3)2 5 10,89
f) 27,04 5 5,2, pois (5,2)2 5 27,04
g) 37,21 5 6,1, pois (6,1)2 5 37,21
h) 51,84 5 7,2, pois (7,2)2 5 51,84

208
5.
a) A59,61m2 ∴ ,5 9,61 53,1m
b) A572,25m2 ∴ ,5 72,25 58,5m
2 – Raiz quadrada aproximada de
um número racional
1.
a) 150 .12, pois (122 5 144, 132 5 169)
b) 200 .14, pois (142 5 196, 152 5 225)
c) 350 .18, pois (182 5 324, 192 5 361)
d) 500 .22, pois (222 5 484, 232 5 529)
2.
a) 2 .1,4, pois ((1,4)2 5 1,96; (1,5)2 5 2,25)
b) 10 .3,1, pois ((3,1)2 5 9,61; (3,2)2 5 10,24)
c) 90 .9,4, pois ((9,4)2 5 88,36; (9,5)2 5
5 90,25)
d) 130 .11,4, pois ((11,4)2 5
5 129,96; (11,5)2 5 132,25)
e) 20 .4,4, pois ((4,4)2 5 19,36; (4,5)2 5
5 20,25)
f) 40 .6,3, pois ((6,3)2 5 39,69; (6,4)2 5
5 40,96)
g) 320 .17,8, pois ((17,8)2 5
5 316,84; (17,9)2 5 320,41)
h) 450 .21,2, pois ((21,2)2 5
5 449,44; (21,3)2 5 453,69)
3.
a) 3,6 .1,8, pois ((1,8)2 5 3,24; (1,9)2 5
5 3,61)
b) 7,2 .2,6, pois ((2,6)2 5 6,76; (2,7)2 5
5 7,29)
c) 10,7 .3,2, pois ((3,2)2 5 10,24; (3,3)2 5
5 10,89)
d) 18,5 .4,3, pois ((4,3)2 5 18,49; (4,4)2 5
5 19,36)
e) 54,6 .7,3, pois ((7,3)2 5 53,29; (7,4)2 5
5 54,76)
f) 69,27 .8,3, pois ((8,3)2 5
5 68,89; (8,4)2 5 70,56)
Chegou sua vez!, página 18.
a) 324 5 32 3 32 3 32 3 32 5 1 048 576
494 5 49 3 49 3 49 3 49 5 5 764 801
Como nos quadrados desses números,
as quartas potências também são
formadas pelos mesmos algarismos,
dispostos em outra ordem.
b) Resposta pessoal.
3 – Os números racionais e sua
representação decimal
1.
a) 3
5
50,6 30 5
0 0,6
b) 5
11
50,4545... 50 11
60 0,4545...
50
60
5
c)
7
5
51,4 7 5
20 1,4
0
d) 10
3
53,333... 10 3
10 3,33...
10
1
e)
1
5
50,2 10 5
0 0,2
f) 2
3
50,666... 20 3
20 0,666...
20
2
Nos casos a, c e e os decimais são exatos,
enquanto nos casos b, d e f temos dízimas
periódicas.
2. Tanto um como outro apresentam
infinitas casas decimais sem que haja
repetição periódica de algarismos.
1.
a)
7
10
50,7 d)
11
100
50,11
b)
31
10
53,1 e)
162
100
51,62
c)
6
100
50,06 f) 9
1000
50,009

209
g) 29
1 000
50,029 j) 163
10
516,3
h)
385
1000
50,385 k)
427
100
54,27
i)
82
10
58,2 l)
1104
1000
51,104
2.
a) 1
2
50,5
b) 7
3
52,333...
c) 9
5
51,8
d)
37
20
51,85
e)
35
11
53,1818...
f) 11
9
51,222...
g) 11
8
51,375
h)
33
25
51,32
i) 3
20
50,15
j) 13
90
50,1444...
k) 33
4
58,25
l)
25
6
54,1666...
4 – Os números irracionais
1.
a)
5
3
51,666... R infinita e periódica.
b) 7 52,645751... R infinita e não
periódica.
c)
13
5
52,6 R finita.
d) 0,202002000... R infinita e não
periódica.
e)
9
2
54,5 R finita.
f) 2,161616... R infinita e periódica.
g) 16 54 R finita.
h) 5,131131113... R infinita e não
periódica.
2. 40 56,324555320 R infinita e não periódica.
3.
a) 6,25 (racional)
b) 36 56 (racional)
c) 2,010010001... (irracional)
d) 30 55,47722... (irracional)
e) 2,4343... (racional)
f) 5,02 (racional)
g) 5
7
5 0,714285714285... (racional)
h) 6,161661666... (irracional)
i) 10 (racional)
j) 0,0025 (racional)
4. 39,69 56,3(racional)
5. 5 .2,23 ((2,23)2 5 4,9729; (2,24)2 5 5,0176)
6. Racionais: 26; 21,5; 2
2
3
; 0; 21
5
.
Irracionais: 22,171171117...; 2 .
7. Alternativa d.
30 55,4772255... (infinita e não periódica;
irracional)
8. Alternativa a.
50 57,0710678... (infinita e não periódica;
irracional)
9. 22
7
 7
...
53,14285714285714285
período período
período
Representação infinita e periódica
(período: 142 857); racional.
1.
a) C 5 2 3 3,14 3 9 5 56,52 ⇒ C .56,52 cm
b) C 5 2 3 3,14 3 1,5 5 9,42 ⇒ C .9,42 cm
c) C 5 2 3 3,14 3 0,25 5 1,57 ⇒ C .1,57 cm
2. C 5 2 pr ⇒ 50,24 5 2 3 3,14 3 r ⇒ 50,24 5
5 6,28 3 r ⇒ r 5 50 24
,
,
6 28
5 8 ⇒ r . 8 cm
3. O comprimento não é da roda, é do pneu.
0 ,
60
2
, ⇒ . ,
a) C523 , 14  5 1 884 C 1 884
m
b) d 5 5 000 3 1,884 5 9 420 ⇒ d .9 420 m
 
4. C5 5 5
C cm
2 314 20
4
125 6
4
31 4 31 4
, ,
, ⇒ . ,
5. C 5 2 3 3,14 3 6 5 37,68 ⇒ C .37,68 cm

210
6. C 5 2pr ⇒ 94,2 5 2 3 3,14 3 r ⇒ 94,2 5
5 6,28r ⇒ r 5 94 2
,
,
6 28
5 15 ⇒ r 5 15 cm 
Diâmetro: 30 cm
5 – Os números reais
1.
a) Pertencem a IN: 0 e 1
b) Pertencem a Z: 24, 0 e 1
c) Pertencem a Z, mas não a IN: 24
d) Pertencem a Q, mas não a Z: 22, 3, 2
1
4
e 0,666...
2.
a) Reais e naturais: 6
b) Reais e inteiros: 6 e 26
c) Reais e racionais: 6, 26 e 6,6
d) Reais e irracionais: 6
3. 5 52,23...
22
9
52,44...
∴ 22
9
é maior que 5
4.
a) 100  IR* e) 2 9 ∈ IR
b) 100  IR1 f) 29 ∉ IR
c) 100  IR2 g) 2p  IR2
d) 9 ∈ IR h) 2,66...  IR1
5.
a) 7 1 5 5 2,6 1 2,2 5 4,8
b) 7  2 5 2,6 3 1,4 5 3,6
c) 5 2(2 3 )52,211,753,9
d) 8 3 581,7513,6
e) 2 10 2 2 523,121,4524,5
f) 10  5 53,12,251,4
g) 211 7 52112,651,6
h) 52 5 5522,252,8
5
4
6. 2 1 5 2 1 5
2 1
1 1
5 5
25
16
16 25
16
9
16
2
2   
 
 
 
 
3
4
5 2 1 5
2 1
5 5
1
25
16
16 25
16
9
16
 
 
 
 
3
4
a) 2002 R
29 6
14 9
,
, . 2 vezes
2003 R
29 6
19 4
,
, . 1,5 vez
2004 R
29 6
23 5
,
, . 1,3 vez
2005 R
29 6
25 7
,
, . 1,2 vez
b) Holanda R50%
c) 1240 . 35,2
d) Aumento de 2006 para 2007 R
35,2 2 29,6 5 5,6
5 6
 , 0 19
5
29 6
0 19 100
100
19
100
,
,
,

5 . 19%
f) Resposta em aberto.
1. Aro 12 → Diâmetro: 12 polegadas 5
5 12 3 2,54 5 30,48 ⇒ 30,48 cm
 Raio 5 15,24 cm
C 5 2 3 3,14 3 15,24 5 95,7 ⇒ 95,7 cm
2.
a) 1,25 m de altura ⇒ Aro 20
Diâmetro: 20 polegadas 5 20 3 2,54 5
5 50,8 ⇒ 50,8 cm
Raio: 50 8
, 5 25,4 ⇒ 25,4 cm
2
C 5 2 3 3,14 3 25,4 5 159,5 ⇒ 159,5 cm
b) A resposta depende da altura do aluno.
1. 5 1764 542m
P 5 4 3 42 5 168 m
Alternativa b.
2. Diâmetro: 39 cm ⇒ Raio: 19,5 cm
C 5 2 3 3,14 3 19,5 5 122,46 ⇒ 122,46 cm
Alternativa a.
3. x
y
51 , 84 7 ,
2
40 , 96 6 ,
4
5 5
5 5
 

 x 2 y 5 7,2 2 6,4 5 0,8
Alternativa d.
4. 1 volta: C 5 2 3 3,14 3 1,5 5 9,42 ⇒ 9,42 cm
n.o de voltas: 489 84
,
,
9 42
5 52 voltas
Alternativa e.
5. 1 volta: C 5 2 3 3,14 3 5 5 31,4 ⇒ 31,4 m
7 voltas 5 7 3 31,4 5 219,8 ⇒ 219,8 m
Alternativa c.

211
INTRODUÇÃO AO CÁLCULO ALGÉBRICO
6 – O uso de letras para
representar números
1. Apenas números: a, b, e
Número e letras: c, f, g
Apenas letras: d
2.
a) A 5 a ? b ⇒ A 5 3 ? 6 5 18
b) A 5 2x ? y ⇒ A 5 (2 ? 6,2) ? 2,4 5
5 12,4 ? 2,4 5 29,76
c) A 5 2 ⇒ A 5 (2,5)2 5 6,25
4.
a) n 5 5 ⇒ 1 1 2 1 3 1 4 1 5 5 15
5 5 ( )
Soma 5 5 5 1
2
5 6
2
30
2
15
? 1
5
?
A fórmula é verdadeira para n 5 5.
n 5 10 ⇒ 1 1 2 1 3 1 4 1 5 1 6 1 7 1
1 8 1 9 1 10 5 55
Soma 5 10 10 1
5 5 ( )
2
10 11
2
110
2
55
? 1
5
?
A fórmula é verdadeira para n 5 10.
b) Soma 5 100 100 1
2
100 101
2
10100
2
? 1
?
5
5 5
5050 ( )
100 1
100 101
2
10100
2
1
?
5
5 5
5050 )
1.
a) x2 e) b 1 c
b) y3 f) a ? x
c) a g) 2y
d) b5 h) m
6
2.
a) 2x 1 2y c) x2 1 y2
b) (x 1 y) ? (x 2 y) d) x2 1 3x
7 – Expressões algébricas ou literais
1. 2x 1 5y
2. h 1 m
3. A 5 (4x) ? (3y) 5 12xy
4. P 5 5x 1 3y
5. x 2 3y
6. A 5 a2 1 bc
7.
a) 7x 1 10
b) 12y 1 9
8.
a) 2x 1 10, inteira.
b)
x
3y , fracionária.
c) a2 2 b3, inteira.
d) x2
4
, inteira.
e) x (a 2 b), inteira.
f) 2p 1 m2, inteira.
g) a3 2 b3, inteira.
h) 3b 2 ac, inteira.
8 – Valor numérico de uma
expressão algébrica
1.
a) 4 ? 22 2 2 ? 6 5 4 ? 4 2 2 ? 6 5 16 2 12 5 4
b) 4 ? (0,4)2 2 (0,4) ? (1,2) 5 4 ? 0,16 2 0,48 5
5 0,64 2 0,48 5 0,16
2. C 5 10 1 0,3 ? (P 2 1); P 5 18 kg
C 5 10 1 0,3 ? (8 2 1) 5 10 1 0,3 ? 7 5
5 10 1 2,1 5 12,1
O custo será de R$ 12,10.
3.
a) 5 ? 02 2 18 ? 0 2 8 5 0 2 0 2 8 5 −8
b) 5 ? (1,2)2 2 18 ? (1,2) 2 8 5
5 5 ? (1,44) 2 18 ? (1,2) 2 8 5
5 7,2 2 21,6 2 8 5 −22,4
c) 5 ? (−2)2 2 18 ? (−2) 2 8 5
5 5 ? 4 2 18 ? (−2) 2 8 5 20 1 36 2 8 5 48
4. N 5 103 1 2 ? 10t, t 5 5
N 5 103 1 2 ? 105 5 1 000 1 2 ? 100 000 5
1 000 1 200 000 5 201 000
Compraram o produto 201 000 pessoas.

7
4 2 1 5 2 5
212
5.
1
4
2x1 x , x5
x
1
4
1
1
1 8
4 4
4 2
2
2
2
7
2 1 5 4
2 1 5 4
2 5
4
5
4 4 2
1
4
2
1 2
8
4
5
2
6. N 5 105 ? 24t, t 5 2
N 5 105 ? 24 ? 2 5 100 000 ? 28 5
5 100 000 ? 256 5 25 600 000
O número de bactérias será 25 600 000.
7. p5
1 1
5 5
5 13 10
2
28
2
 
150
2 2 100

 2
( , ) ( , ) 551000?6,2556250
3 1000 1 1 5 1000 2 5
14 ⇒ p 5 14
p ? (p 2 a) ? (p 2 b) ? (p 2 c) 5
14 ? (14 2 5) (14 2 13) ? (14 2 10) 5
5 14 ? 9 ? 1 ? 4 5 504
6
1 2
8. y5 1 2 5 1 2 5
1 2 3 2 5 12 32 3
,
, , , ,
9. V5
1
5 5
14 4
1 5 3
14 4
4 5
3 2
,
,
,
,
, ⇒ V 5 3,2
5
4
10. N5 ?C1 C5
7, 24
5
4
N5 ? 24 1 7
5 1 5 1 5
120
4
7 30 7 37
1 5 1 5
120
4
7 30 7 37 ⇒ N 5 37
11.
a) 4 2 4
4
16 8
2
8
2
4
22 ?
5
2
5 5
1
4
1
4
b) 2 2 ? 2 ? 1 5 1 1 5
1 1
1 2 1 1
5
2
4
1
16
16 8 1
16
2
 
2 2  
( , ) ( , ) 551000?6,2556250
3 1000 1 1 5 1000 2 5
25
1
2
2
( )  
 
( )
6
5 1 1 5
1 1
5
1
4
1
2
4
1
16
16 8 1
16
25
1
2
 
6
c) 8 8 10
9
64 80
9
144
9
16 4
21 ?
5
1
5 5 5
64 80
9
144
9
16 4
1
5 5 5
d) 3 ? ((−2)2 2 (−2)2) 2 10 ? ((−2) 1 (−2)) ?
? ((−2) 2 (−2)) 5 3 ? (4 2 4) 2 10 ? (−4) ?
? 0 5 3 ? 0 1 40 ? 0 5 0 1 0 5 0
e) 2
3
1 1
2 3
3
1
1
3
1
1
9
2
2
2 2
2 2 2 5
2
2 5
2
2 5
 
 
( )  
 
 
 
2 1
22 5
2
5
1 9
9
8
9
1
2 3
3
1
1
3
1
1
9
2
2 2
2 5
2
2 5
2
2 5
( )  
 
 
 
2 1
22 5
2
5
1 9
9
8
9
f) 1 05
0 5 8 1
1 025
4 1
0 75
3
0 25
2 2
? 2 1
5
2
2 1
5
2
52
( , )
,
, ,
( ) ,
g)
g)
1
2
1
2
1
8
1
8
 

 ( )
 

 
( )
( )
(
3
3
3
3
2
2
8
8
2 2
1 2
5
2 2
1 2 )
5
1
2
5
2
5
2
1
8
1
8
65
8
63
8
64
64
65
63
g)
1
2
1
2
1
8
1
8
 

 
( )
 

 
( )
( )
(
3
3
3
3
2
2
8
8
2 2
1 2
5
2 2
1 2 )
5
1
2
5
2
5
2
1
8
1
8
65
8
63
8
64
64
65
63
h)
5 1
10
10 1
5
50 1
10
50 1
5
51
10
51
5
51
10
5
51
5
10
1
2
1
1
5
1
1
5 5 ? 5 5
5 1
10
10 1
5
50 1
10
50 1
5
51
10
51
5
51
10
5
51
5
10
1
2
1
1
5
1
1
5 5 ? 5 5
150
100
12. A510 ? 11 5 ? 1 5 ?
A510 ? 11 5 ? 1 5 ?
1. Cidade: 85% de 189,8 milhões R
189 800 000 R 100%
x R 85%
x 5 189800000 85
100
? R x 5 161 330 000 ou
aproximadamente 161,3 milhões
Campo: 189,8 – 161,3 5 28,5 R .28,5
milhões
2. Possível resposta: calculando a
porcentagem nos dois casos ou
calculando uma e subtraindo o resultado
do total.
3.
a) Brancos:
1898 49 4
, ? , . 93,76 R 93,76 milhões
100
b) Pardos:
1898 42 3
, ? , . 80,3 R 80,3 milhões
100
c) Negros:
189 8 7 4
, ? , . 14 R 14 milhões
100
d) Outros:
1898 08
, ? , . 1,5 R 1,5 milhão
100
4. Gráfico pictórico ou pictograma.
Não, pois, por exemplo, o percentual
de negros é nove vezes o percentual de
outros, isso significa que o número de
homenzinhos que representa os negros
(12) deveria ser nove vezes o número de
homenzinhos que representa os outros (2),
o que não acontece.
5.
Negros: 2 R 0,8%
x R 7,4%
x 5
2 7 4
0 8
? ,
, . 18,5 R 18,5 homenzinhos
Pardos:
2 42 3
0 8
? ,
, .105,8 R 105,8 homenzinhos
Brancos:
2 49 4
0 8
? ,
, 5 123,5 R 123,5 homenzinhos

( ( 2) ( 2)) (( 2) ( 2)) ( 2) ( 2)3 ( ) ?
2 2
2 5
213
9 – Uma consideração importante
1.
a) x 2 4 5 0 ⇒ x 5 4
b) 1 2 3a 5 0 ⇒ −3a 5 −1 ⇒ a 5 1
( 2)) (( 3
( ) ( 2) ( ?
2) ( 2)) ( 2) ( 2)3 c) 2 1 5x 5 0 ⇒ 5x 5 −2 ⇒ x 5 2
2
5
d) 2 2 2b 5 0 ⇒ −2b 5 −2 ⇒ b 5 1
2.
a) x 1 y 5 0 ⇒ x 5 −y
b) x 2 2y 5 0 ⇒ x 5 2y
c) 2x 1 y 5 0 ⇒ 2x 5 −y ⇒ x 5 2
y
2
1. Não, porque 8 1 0 1 7 5 15 não é divisível
por 9.
2. 8 1 x 1 7 5 18 ⇒ x 5 18 2 8 2 7 ⇒ x 5 3
3. xy 5 10x 1 y 5 9x 1 (x 1 y)
As parcelas são divisíveis por 9, então a
soma também o é.
1.
a) 88,1 1 84,7 1 17 5 189,8 R 189,8
milhões
b)
86700000
16800000
5,16 (Aproximadamente
5 vezes)
c) Idosos em 2025 R 2 ? 17 5 34 R 34
milhões
34 R 15%
x R 100%
x 5
2
34 100
15
? . 226,7 R 226,7 milhões
d) Solteiros: 79 900 000
2
Outros: 50 700 000 1 6 200 000 1 4 900 000 5
5 61 800 000
79 900 000 2 61 800 000 5 18 100 000
Existem 18 100 000 solteiros a mais que
os outros.
e) Católicos:
1898 73 6
, ? , . 139,7 R 139,7 milhões
100
f) 73 6
15 4
4 8
, %
, %
 ,
A área é 4,8 vezes maior,
aproximadamente. Justificativa em aberto.
2.
a) Os suecos.
b) 2o lugar.
c) Região Norte.
d) 3000
1400
 2,1 (Aproximadamente o dobro)
1. 2 2 2 2 2 1 2 1 2 ? 2 2
2
2
2 2 2 2 2 1 2 1 2 ? 2 2
2 2
2 55 1 ? 2 2 1 2 ? 2 2
2
2
4
2 ( ) ( ) ( ) ( )
2 2 2 2 2 8 5
2
54 ? (24)116125216116125 2
Alternativa a.
2.
0 4 0 5
0 4 0 5
0 2
0 1
2
, ,
, ,
,
,
( )? ( )
2
5
2
52
Alternativa e.
3. y 5 20 ? x 1 30
Alternativa d.
4. (−2)3 1 2 ? (−2)2 5 −8 1 2 ? 4 5 −8 1 8 5 0
Alternativa c.
5. A 5 4 ? ax 2 2 ? a2x 5 4 ? ax 2 2 ? (ax)2 5
4 ? 10 2 2 ? 102 5 4 ? 10 2 2 ? 100 5
5 40 2 200 5 −160
Alternativa b.
6. 3
2
50 40
150
2
? 1 5 1405751405115
Alternativa c.
7. x 5
( ) ( ) ( )
2 2 1 2 2 ? ? 2
?
5
1 1
5
1
5
9 9 4 5 2
2 5
9 81 40
10
9 11
10
2 x 5
2 2 1 2 2 ? ? 2
?
5
1 1
5
1
5
9 9 4 5 2
2 5
9 81 40
10
9 11
10
2
2 ( ) ( ) ( )
Alternativa a.
8. T 1
1 2
6
12 4 12 10
144
6
2
2
5 ? 1 ? 1 5
48 10 24 48 10 1 1 52 1 1 T C 1
1 2
6
12 4 12 10
144
6
5 ? 1 ? 1 5
48 10 24 48 10 34
2
1 1 52 1 1 5 º
T 2
1 2
6
18 4 18 10
324
6
2
2
5 ? 1 ? 1 5
72 10 54 72 10 1 1 52 1 1 T C 2
1 2
6
18 4 18 10
324
6
5 ? 1 ? 1 5
72 10 54 72 10 28
2
1 1 52 1 1 5 º
A temperatura diminuiu 6 8C.
Alternativa d.
1 2
2
9. A5 ? 2 5 2 5
2
5
1
2
2
3
1
4
2
3
3 8
12
5
12
B5 ?
2
2
2 52 2 5
52
 
1 1
2
2
3
2
3
1
3
2
3
3
3
 
5 1
12
A2B52 1 5
2 1
5
1
5 12
12
7
12
Alternativa b.
10. 11 ? (11 2 1) 1 1 5 11 ? 10 1 1 5 110 1 1 5
5 111 jogos
Alternativa e.

ESTUDO DOS POLINÔMIOS
214
10 – Monômio ou termo algébrico
1.
a) A 5 x ? y
b) P 5 x 1 y 1 x 1 y 5 2x 1 2y
c) O item b apresenta uma soma de dois
“termos” e o item a apresenta um
único “termo”.
2. P1 5 x 1 x 1 x 1 x 1 x 5 5x
P2 5 x 1 x 1 x 1 y 1 y 5 3x 1 2y
3.
a) (I) A 5 2a ? 3a 5 6a2
(II) A 5 a ? 2a 5 2a2
b) , 5 3a 1 a 5 4a
c) A 5 4a ? 2a 5 8a2
d) A área do retângulo ABCD é a soma da
área (I) com a área (II): 8a2 5 6a2 1 2a2
1. 5x
2. ab
3. V 5 (2a) ? (2a) ? (2a) 5 8a3
4. 6,20xy
5.
a) Sim.
b) Sim.
c) Não.
d) Sim.
e) Não.
f) Sim.
g) Não.
h) Sim.
i) Não.
j) Não.
6.
a)
Coeficiente
:
Parte literal :
a
7
3

b)
Coeficiente
:
Parte literal :
xy
21
5

c)
Coeficiente
:
2
Parte literal :
mn
2
3
2 4

 
 
d)
Coeficiente
Parte literal bc
: ,
:
20 06
3

e)
Coeficiente
:
Parte literal :
m
1
5
4

 
 
f)
Coeficiente
:
Parte literal :
a x y
1
3 5 2

g)
Coeficiente
: 6 ,
2
Parte literal :
x y
3 3

h)
Coeficiente
:
220
Parte literal :
a bc
4 3


 
 
i) Coeficiente
12
5

:
: .
Parte literal Nao tem
1. Grau 4: 5a3b, 26m2n2
2. 10a3x3y é do 7o grau.
3. m5x3y4 é do 3o grau em relação à variável x.
4. 2 1 n 1 2 5 13 ⇒ n 1 4 5 13 ⇒ n 5 9
5. x6 é o monômio de maior grau.
6. 28a4, 26a3, 7a2, 10a, 5
1.
a) 3
1
5
x2y,2 x2y
b) 4xy, 2xy
c) 2
1
2
x2,10x2
2.
a) a2 1 6a2 2 2a2 5 5a2
b) 17ax 2 18ax 5 2ax
c) xy xy
xy xy xy
1 5
1
5
3
5
5 3
5
8
5
d) 0,7x2y1 3,1x2y 5 3,8x2y
e) 10bc 2 12bc 1 7bc 2 3bc 5 2bc
f) 1
3
2 2 2 2 2 2 x y x y x y
x y x y x y x 1 2 5
4
9
5
6
6 8 15
18
2 2 2 2 2 2
1 2
5
2
18
1
3
4
9
5
6
6 8 15
18
2 2 2 2 2 2
2 2 2 2 2 2 2 2
x y x y x y
x y x y x y x y
1 2 5
1 2
5
2
18

215
g) ay ay ay
ay ay ay ay
1 2 5
1 2
52
3
4
4
4 3 16
4
9
4
ay ay ay ay
5
1 2
52
4 3 16
4
9
4
h) 0,9ab3 1 2,5ab3 2 5,2ab3 5 21,8ab3
3.
a) 0,6ab2 2 ab2 1 0,3ab2 1 0,5ab2 5 0,4ab2
b) 0,4 ? (21) ? (26)2 5 0,4 ? (21) ? 36 5 214,4
c) 0,4 ? (0,4) ? (20,2)2 5 0,4 ? (0,4) ? (0,04) 5
5 0,0064
4. 5x2y2 1 P 5 9x2y2 ⇒ P 5
5 9x2y2 2 5x2y2 ⇒ P 5 4x2y2
5.
a) 2ax c) 3ax
b) 22ax d) 7ax
6.
a) 7x 2 (22x 1 x) 1 (23x 1 5x) 5
5 7x 2 (2x) 1 2x 5 10x
b) 5y2 2 (24y2 1 7y2) 1 (2y2 1 9y2 2 11y2) 5
5 5y2 2 3y2 1 (23y2) 5 2y2
c) 10 3 2 5 8 ab ab ab ab ab ab 2 2 2 2 ( ) 1 5 

5 5 10 3 2 8 ab ab ab ab 2 2 2 2 ( ) 

5 5 10 3 13 ab ab ab 2 2

d) 2 5 2 4 2 8 xy xy xy xy xy xy xy 1 2 1 2 1 2 2 ( ) 

5
5 5 2 5 2 3 8 xy xy xy xy xy 1 2 1 2 2 

5 5 2 14 12 xy xy xy 1 2 2 

7.
a) 20 7 11 40 6 5 bc bc bc bc bc bc 2 2 2 2 2 1 ( ) 

5
5 5 20 7 35 5 bc bc bc bc 2 2 2 2 1 ( ) 

5 20bc 2 33bc 5 213bc
b) 15bc
8. 1,2ax 2 (20,6ax 1 3,4ax 2 2,9ax) 2
2 (7,3ax 2 0,8ax) 5 1,2ax 2 (20,1ax) 2
2 6,5ax 5 25,2ax
9. 2y 1 5y 1 3y 5 10y
1. d 5 9x 1 5x 1 18x 5 32x
2.
a) Porcentagem da frota de bicicletas por
região
Região
Quantidade
estimada
Porcentagem
Sudeste 26 400 000 44%
Nordeste 15 600 000 26%
Sul 8 400 000 14%
Centro-Oeste 4 800 000 8%
Norte 4 800 000 8%
b)
% bicicletas
Sudeste Nordeste Sul Centro- região
c) Total: 60 000 000 bicicletas
Transporte: 60 000 000 ? 0,50 5 30 000 000
Infantil: 60 000 000 ? 0,32 5 19 200 000
Lazer: 60 000 000 ? 0,17 5 10 200 000
Esporte: 60 000 000 ? 0,01 5 600 000
50%
45%
40%
35%
30%
25%
20%
15%
10%
5%
3.
a) Bicicletas.
b) Bicicletas.
c) 3
10
2 1 100
3 10 20 10
10
1000
10
x x x
x x x
1 1 1 5
1 1 1
( ) ⇒ 5
3
10
2 1 100
3 10 20 10
10
1000
10
x x x
x x x
1 1 1 5
1 1 1
( ) ⇒ 5
⇒33x11051000⇒33x5990⇒x530
Portanto:
Carros: 30%
Motos:
3
10
?3059%
Bicicletas: 2 ? 30 1 1 5 61%
1.
a) b8
b) 5x7
c) 14y2
d) 21,2a3
e) 20,75x2y3
f) mn 2
2 14
g) 2a5m2
2.
a) 20a6b3c5
b) 23ax3y2
c) 1,35y7
d) 0,1x5y3
e) 40m3n3p2
f) x4y4z3
g) 21,96a2m3n2
-Oeste
Norte
0%

216
3. P 5 4n 1 4n 1 4n 1 4n 1 4n 1 4n 1 4n 1
1 4n 1 4n 1 4n 1 4n 1 4n
P 5 48n
4. A 5 (3,5x) ? (1,6x) ⇒ A 5 5,6x2
5.
a) produto: (22a2x) ? (21,6ax) 5 3,2a3x2
b) 3,2 ? (20,5)3 ? (20,5)2 5
5 3,2 ? (20,125) ? (0,25) 5 20,1
5
4
 
 
6. (2 ) ( )
5
2
ax ? 2 ax2 5 a2x 52 a4x4
5
2
v.n. 5 2 ? 2 ? 2 52 ? ? 52
2 1
5
2
( )4 ( )4 16 1 40
7. 4a
8. (2a) ? (2m) ? (2m3) ? (2a) 5 a2m4
1
4
 
v.n.5 ? (2 2
) 5 ? 5
1
16
16 1
2
4  
9. 2
3
4
a2b
10. 5ab, 10a3b2, 20a5b3
Regra: multiplicar por 2a2b
Próximos termos: 40a7b4, 80a9b5, 160a11b6

último termo
11. 1
2
3
xy xy xy
2 6
2
9
2
2 2 2
2 2 2
1 1
xy 1 xy 1 xy 5 5
xy
2
12.
a) A 5 x ? (0,5x) 5 0,5x2
b) Aamarelos 5 12 ? (0,5x2) 5 6x2
c) Aazuis 5 12 ? (0,5x2) 5 6x2
d) Atotal 5 24 ? (0,5x2) 5 12x2
V1 5 a3 1 2a3 5 3a3
V2 5 a3 1 2a3 1 4a3 5 7a3
V3 5 2 ? (4a3) 1 2 ? (2a3) 1 2 ? a3 5
5 8a3 1 4a3 1 2a3 5 14a3
V4 5 2 ? (4a3) 1 2 ? (2a3) 1 2 ? a3 5
5 8a3 1 4a3 1 2a3 5 14a3
1.
a) a5
b) x
c) 1
d) 4x3
e) 23y3
f) 1
2
a3x
g) 24xy2
h)
1
3
i) 21,9xy4
j) 4n
k) 21,6b
l) 2
1
4
b2
m) 3
2
y
n) 10ax2
o) x2
p) 0,125mx
2. 4xy
3. (30a7x3)  (6a4x2) 1 (26a3x) 5
5 5a3x 2 6a3x 5 2a3x
4. ( ) ( ) ( ) 220 5 100 10 2 3 3 4 2 xy x y x y xy ? 5 



(10xy2)  510x2y2
( ) ( ) ( ) 220 5 100 10 2 3 3 4 2 xy x y x y xy ? 5 



(10xy2)  510x2y2
5. (20a4m2)  (29am 1 5am) 5
5 (20a4m2)  (24am) 5 25a3m
6. (210x3y)  (22xy) 5 5x2
Resposta errada.
7. (2x6 1 x6)  (2x3) 5 (3x6)  (2x3) 5 23x3
Resposta certa.
8. 23a3b3
1.
a) a10
b) 4x8
c) 2125y9
d) 100a4b2
e) 81x8y4
f) 1
25
m4n2
g) 0,25a2b4
h) a4m20x12
i)
4
9
x6y4
j) a14c21
k) x y 4 4
25
l) 0,01p10
2.
a) (1,5b2c3)2 5 2,25b4c6
b) (0,4a5b3)3 5 0,064a15b9
3. (22 ) (8 )5(4 ) (8 )5
1
2
xy 2 xy2 x2y2  xy2 x
4. (27y 1 10y 1 2y)3  (210y2 2 15y2) 5
5 (5y)3  (225y2) 5 (125y3)  (225y2) 5 25y
5.
a) (210x3)2 5 100x6
b) (100x6)  (5x4) 5 20x2

217
1
2
1
4
 
 
 
6. 2 2 1 5
1
16
2 5
4
4 9
2
 
 
a c a c c2 a8c20  
; ;
1
a8c18 c2 16

  
1 5
1
4
2 1 5
1
16
4 9
2
a c c2 a8c20  
 
 
 
;
1
a8c18 c2 16

  
1 5
5c21c252c2
1. A
( ) ( , ) ,
x ?
x x
5 5 5
,
x
5 25
2
12 5
2
6 25
2
2
Alternativa d.
5  
2. x x x
x 1
x
1 2 ? 5 x
2 ?
1
5
1
2
5
5
5
1
2
 

 

 
 
 

 

 
5
 x x x x
5 2 ? 5
2
? 5 ? 5 5
6
5
1
2
5
12 5
10
5
7
10
5
7
2
3
x
x
 

 

 

 
,5x
2
? 5 ? 5 5
5
5
7
10
5
7
2
3
x x x

 
,5x
Alternativa c.
3. Menor: 3,5x
Maior: 30 ? (3,5x) 5 10,5x
Produto: (3,5x) ? (10,5x) 5 36,75x2
Alternativa b.
4. 7
5
2
x 14 x 1
5
x x
2
19
2
x 9 5
1 5 5 5 ,
x
Alternativa a.
11 – Polinômios
1. 2x 1 3y
2. 45 1 0,50x
3. 4x 1 2y
4.
a) 10x 1 y
b) 10y 1 x
5.
a) 2a 1 b
b) 2a 2 b
6. a ? a 1 b ? a 1 b ? a 1 b ? b 5 a2 1 2ab 1 b2
1.
a) 5y 1 4y3 2 1 1 2y2 2 y3 2 y 1 7y2 2 1 5
5 3y3 1 9y2 1 4y 2 2
b) a2x 2 5a2x2 1 3a2x 2 7ax2 1 a2x2 2
2 2a2x 1 5ax2 5 2a2x 2 4a2x2 2 2ax2
c) 7a 1 5b 2 9c 1 13b 1 10c 2 5a 2 8b 1 c 5
5 2a 1 10b 1 2c
d) 6x 2 5y 1 3xy 1 2xy 2 5x 1 9y 1 4x 2
2 xy 2 y 5 5x 1 3y 1 4xy
e) 8x2 2 6x 1 1 1 7x 2 6x2 2 3 2 3x 2 x2 2 5 5
5 x2 2 2x 2 7
2. x2 2 0,2ax 1 2,5x2 2 a2 2 4,1ax 2 2x2 2 1,2a2 5
5 1,5x2 2 4,3ax 2 2,2a2 (trinômio)
3.
a) x2 1 ax 1 ax 1 ax 1 x2
b) A 5 x ? x 1 a ? x 1 a ? x 1 a ? x 1 x ? x 5
2x2 1 3ax
4. 0,5a 1 (2b 2 0,6ab 1 0,8a) 2 (0,7b 2 1,2ab) 5
5 0,5a 1 2b 2 0,6ab 1 0,8a 2 0,7b 1 1,2ab 5
5 1,3a 1 1,3b 1 0,6ab
5.
a) 7a2 2 5a2 1 9a 2 2 2 2a 1 a2 2 1 5
5 3a2 1 7a 2 3
b) 8ab 2 a 2 7b 1 5 2 5ab 1 2 2 b 1 4a 1
1 2ab 2 6b 5 5ab 1 3a 2 14b 1 7
c) 5a 1 3b 2 5a 1a2 4b 1 b 5a
d) 2x2 2 2xy 2 x2 1 3xy 1 y2 2 2y2 2 xy 5
5 x2 2 y2
6.
a) Binômios: a2 2 b2, x 1 2a
b) Trinômios: y2 2 2y 1 1, x2y2 1 4xy 1 4
7.
a) 23r2 1 5rs 1 9r2 1 rs 2 6s2 2 14s2 1
1 6r2 1 5rs 1 8s2 5 12r2 1 11rs 2 12s2
b) 12 ? (0,5)2 1 11 ? (0,5) ? (0,2) 2 12 ? (0,2)2 5
5 3 1 1,1 2 0,48 5 3,62
1. 6o grau.
2. 3o grau em relação a x.
3. 2x 1 x3 2 9x2 2 2 5 x3 2 9x2 1 2x 2 2
4. Incompleto; x3 1 0x2 1 0x 2 1.
5.
a) 5x5 1 7x4 1 2x3 2 5x2 2 x 1 3
b) 5o grau.
6. x5 1 0x4 1 0x3 1 0x2 1 0x 1 1
7.
a) 4o grau.
b) Incompleto.
c) x4 1 0x3 2 10x2 1 0x 1 9

218
1.
a) As medidas indicadas correspondem
aos perímetros.
b) 6x
2. P1 5 6x; P2 5 6x 1 6; P3 5 6x 1 12
3.
a) 6 ? (5x) 5 30x
b) 10 ? (6x) 5 60x
1. x2 2 9x 1 5 1 3x2 1 7x 2 1 5 4x2 2 2x 1 4
2.
a) 2x 1 5y
b) 3x 1 2y
c) 2x 1 5y 1 3x 1 2y 5 5x 1 7y
d) 5 ? 60 1 7 ? 300 5 300 1 2 100 5 2 400
Juntos gastaram R$ 2 400,00.
3. D 5 (5ax 2 10x 2 9a) 2 (3ax 2 8x 2 12a) 5
5 5ax 2 10x 2 9a 2 3ax 1 8x 1 12a 5
5 2ax 2 2x 1 3a
4.
1
2
a) P x a x
a
53 1 1 4
1 1 x1a1 x1a5
2
3
3 3
5 1
3 1 4 1 6 1
6
13 5 1
6
13
19
6
x
a a a a
x
a
b) 13 1
19 ?
6
6
? 1 5 13 1 19 5
32
5.
a) 0,6x 2 1
b) 0,4x 1 2
c) 0,6x 2 1 1 0,4x 1 2 5 x 1 1
d) (0,6x 2 1) 2 (0,4x 1 2) 5 0,2x 2 3
6.
a) Loja A: 0,6x 1 2y
b) Loja B: 0,4x 1 3y
c) Diferença: (0,6x 1 2y) 2 (0,4x 1 3y) 5
5 0,2x 2 y
7. (13x2 2 11x 2 15) 1 (27x2 2 2x 1 16) 5
5 6x2 2 13x 1 1
Ax2 1 Bx 1 C
A 5 6, B 5 213, C 5 1
A 1 B 1 C 5 6 1 (213) 1 1 5 26
8. (7x 1 2xy 1 3y 2 2x2y2) 2
2 (6x 2 13xy 1 2y 2 x2y2) 5
5 x 1 15xy 1 y 2 x2y2
9.
a) Oposto: 28x3 1 5x2 1 9x 2 4
b) A soma de qualquer número com seu
oposto é zero.
c) (8x3 2 5x2 2 9x 1 4) 2 (28x3 1 5x2 1 9x 2 4) 5
5 16x3 2 10x2 2 18x 1 8
10.
a) P1 1 P2 1 P3 5 (a 1 b 1 c) 1 (a 2 b 1 c) 1
1 (a 1 b 2 c) 5 3a 1 b 1 c
b) P1 1 P2 2 P3 5 (a 1 b 1 c) 1 (a 2 b 1 c) 2
2 (a 1 b 2 c) 5 a 2 b 1 3c
c) P1 2 P2 1 P3 5 (a 1 b 1 c) 2 (a 2 b 1 c) 1
1 (a 1 b 2 c) 5 a 1 3b 2 c
d) P1 2 P2 2 P3 5 (a 1 b 1 c) 2 (a 2 b 1 c) 2
2 (a 1 b 2 c) 5 2a 1 b 1 c
11.
a) P 1 Q 5 x2 1 a2 2 2ax 1 2x2 1 5ax 1 3a2 5
5 3x2 1 4a2 1 3ax
v.n. 5 3 ? (24)2 1 4 ? 102 1 3 ? 10 ? (24) 5
5 3 ? 16 1 4 ? 100 2 120 5
5 48 1 400 2 120 5 328
b) P 2 Q 5 x2 1 a2 2 2ax 2 2x2 2 5ax 2 3a2 5
5 2x2 2 2a2 2 7ax
v.n. 5 2(1,2)2 2 2 ? (0,5)2 2 7 ? (0,5) ? (1,2) 5
5 21,44 2 2 ? (0,25) 1 4,2 5
5 21,44 2 0,5 1 4,2 5 2,26
12.
a) 6a 2 15b 1 7c
b) 7y2 2 4ay 1 5a2
c) 22a3 1 5a2b 2 ab2 2 5b3
d) 2x2 1 2y2 1 4x2y2
e) 0,2a2 2 0,6b2 2 0,8c2
f) 4a2 2 4ab 1 5b2 1 2c2
g) 0,2x3 1 0,3x2 1 0,4x 2 6
h) 2ab 1 2a2b2
i) 3y3 2 6y2 1 3
1.
a) (ab 1 6) (ab 2 2) 5 a2b2 2 2ab 1 6ab 2 12 5
5 a2b2 1 4ab 2 12
b) (x 2 20) (x 1 9) 5 x2 1 9x 2 20x 2 180 5
5 x2 2 11x 2 180
2.
a) 2bx (1 2 a) 1 2x (a 2 b 2 c) 2 2x (a 2 c) 5
5 2bx 22abx1 2ax 2 2bx 2 2cx 2 2ax 1 2cx 2 2ax 1 5 2bx 22abx1 2ax 2 2bx 2 2cx 2 2ax 1 2cx 2 2ax 1 2cx 522abx
b) 3 2 6 3 3 5 a a b a a b b a b ( ) ( ) ( ) 2 2 2 2 2 

5
5 6a2 2 3ab 2 6a2 1 3ab 13ab25b253ab25b2
5 6a2 2 3ab 2 6a2 1 3ab 13ab25 b253ab25b2

219
2
3
3. A verde5 y ? 2
x 2 y 5 xy 2
y 4
3
2
3
( ) 2
4. a ? (a2 2 ab 1 b2) 1 b ? (a2 2 ab 1 b2) 5
5a32 a2b 1 ab2 1 a2b 2 ab2 1b35a31b3
5. 10 ? (x 1 4y) 5 10x 1 40y
6. V 5 3x ? y ? (x 1 y) 5 3x2y 1 3xy2
7. A 5 (3x 1 2y) ? (3x 2 y) 5
5 9x2 2 3xy 1 6xy 2 2y2 5
5 9x2 1 3xy 2 2y2
8. A 5 (a 1 b)2 5 (a 1 b) (a 1 b) 5
5 a2 1 2ab 1 b2
v.n. 5 42 1 2 ? 4 ? 2 1 22 5 16 1 16 1 4 5 36
9. Averde 5 (3x 1 y) ? (2x 2 y) 5
5 6x2 2 3xy 1 2xy 2 y2 5 6x2 2 xy 2 y2
v.n. 5 6 ? 22 2 2 ? 1 2 12 5 24 2 2 2 1 5 21
10. (1,2a 0,5b)(1,2a 0,5b) 1,44a2 0,6ab 0,6ab 0,6ab 1 1 5 2 1 1 2 0,25b2
0,5b)(1,2a 0,5b) 1,44a2 0,6ab 0,6ab 0,6ab 1 5 2 1 1 2 0,25b2
51,44a2 0,25b2 2
11.
a) (x 1 7) (x 1 5) 5 x2 1 12x 1 35
b) (y 2 6) (y 1 5) 5 y2 2 y 2 30
c) (2a 1 b) (a 2 2b) 5
5 2a2 2 4ab 1 ab 2 2b2 5 2a2 2 3ab 2 2b2
d) (3a 2 1,5x) (0,7a 2 5x) 5
5 2,1a2 2 15ax 2 1,05ax 1 7,5x2 5
5 2,1a2 2 16,05ax 1 7,5x2
e) (2x 1 1) (26x2 2 5x 1 3) 5
5 212x3 2 10x2 1 6x 2 6x2 2 5x 1 3 5
5 212x3 2 16x2 1 x 1 3
f) (a2 2 1) (2a2 2 2a 1 1) 5
5 2a4 2 2a3 1 a2 2 2a2 1 2a 2 1 5
5 2a4 2 2a3 2 a2 1 2a 2 1
g) (a1x)(a 2ax1x )5a 2 a x 1 ax 1 a x 2 ax 1x 5a 1x 2 2 3 2 2 2 2 3 3 3
(a1x)(a 2ax1 x )5a 2 a x 1 ax 1 a x 2 ax 1x 5a 1x 2 2 3 2 2 2 2 3 3 3
ax 1 a x 2 ax 1 x 5a 1x 2 2 2 3 3 3
12. (2x2 2 x 2 3) (3x2 1 x 2 2) 5
5 6x4 1 2x3 2 4x2 2 3x3 2 x2 1 2x 2 9x2 2
2 3x 1 6 5 6x4 2 x3 2 14x2 2 x 1 6  A 5
5 6; B 5 21; C 5 214; D 5 21 e E 5 6, logo:
A 1 B 1 C 1 D 1 E 5 6 2 1 2 14 2 1 1 6 5 24
13.
a) (x 1 6)2 5 (x 1 6) (x 1 6) 5 x2 1 12x 1 36
b) (a 2 2b)2 5 (a 2 2b) (a 2 2b) 5
5 a2 2 4ab 1 4b2
c) (1 1 3xy)2 5 (1 1 3xy) (1 1 3xy) 5
5 1 1 6xy 1 9x2y2
d) (x 1 y)3 5 (x 1 y) (x 1 y) (x 1 y) 5
5 x3 1 3x2y 1 3xy2 1 y3
14. VI 5 x ? (3x 1 1) ? 2x 5 6x3 1 2x2
VII 5 (x 1 1) ? x ? (x 1 3) 5 x3 1 4x2 1 3x
VI 1 VII 5 7x3 1 6x2 1 3x
15. A5(a1x)(a22ax1x2)5a32 a2x 1 ax2 1 a2x 2 ax2 1x35a31x3
A5(a1x)(a22ax1x2)5a32 a2x 1 ax2 1 a2x 2 ax2 1x35a31x3
B5(a2x)(a21ax1x2)5a31 a2x 1 ax2 2 a2x 2 ax2 2x35a32x3
B5(a2x)(a21ax1x2)5a31 a2x 1 ax2 2 a2x 2 ax2 2x35a32x3
A 2 B 5 (a3 1 x3) 2 (a3 2 x3) 5 2x3
16.
a) (x 2 2) (x 2 3) 2 (x 2 4) (x 2 5) 5
5 (x2 2 5x 1 6) 2 (x2 2 9x 1 20) 5 4x 2 14
b) (a3 b3)(a b) (a2 b2)(a2 b2) a4 a3b ab3 b4 2 1 2 1 2 5 1 2 2 2 (a3 b3)(a b) (a2 b2)(a2 b 2) a4 a3b ab3 b4 a4 a2 2 1 2 1 2 5 1 2 2 2 1 b2 a2b2 b4 2 1 5
(a3 b3)(a b) (a2 b2)(a2 b2) a4 a3b ab3 b4 a4 a2 2 1 2 1 2 5 1 2 2 2 1 b2 a2b2 b4 2 1 55a3b2ab3
c) ( ) ( ) ( ) ( ) a b a b b a a b ab a b ab 2 2 1 2 5 2 2 1 2 5 2 3 1 2 3 



( ) ( ) ( ) ( ) a b a b b a a b ab a b ab 2 2 1 2 5 2 2 1 2 5 2 3 1 2 3 



5 2 2 1 52 1 1 2 52 1 2 ( ) a b a b a ab ab b a ab 2 3 3 6 2 3 7 2 2 2 2 

5 2 2 1 52 1 1 2 52 1 2 ( ) a b a b a ab ab b a ab b 2 3 3 6 2 3 7 2 2 2 2 2 

d) (x21)(x11)13(x21)(x21)13(x21)115
5x21 x 2 x 21 13x22 3x 13x1 3 1 3x 2 3 11 54x223x
5x21 x 2 x 21 13x22 3x 13x1 3 1 3x 2 3 11 54x223x
17. (x2 xy y2)(x2 xy y2)(x2 y2) 2 1 1 1 2 5
5(x41 x3y 1 x2y2 2 x3y 2 x2y2 2 xy3 1x2y21 xy3 1y4)(x22y2)5(x41 x3y 1 x2y2 2 x3y 2 x2y2 2 xy3 1x2y21 xy3 1y4)(x22y2)55(x41x2y21y4)(x22y2)5x62 x4y2 1 x4y2 5(x41x2y21y4)(x22y2)5x62 x4y2 1 x4y2 2 x2y4 1 x2y4 2y65x6 y6 2
v.n. 5 26 2 (21)6 5 64 2 1 5 63
Pela ponta esquerda, na ordem:
B R D R C R A
Pela ponta direita, na ordem:
A R C R D R B
1.
a) Nordeste: x
Norte: 74,4 2 73,1 5 1,3 R x 1 1,3
Centro-Oeste: 77,5 – 73,1 5 4,4 R x 1 4,4
Sudeste: 77,9 – 73,1 5 4,8 R x 1 4,8
Sul: 78,2 – 73,1 5 5,1 R x 1 5,1
b) Sudeste: y
Norte: 68,3 – 69,8 5 –1,5 R y – 1,5
Centro-Oeste: 70,5 – 69,8 5 0,7 R y 1 0,7
Nordeste: 65,8 – 69,8 5 –4 R y – 4
Sul: 71,5 – 69,8 5 1,7 R y 1 1,7

220
2.
a) 82,3180,3180,3180,2179,1179177,9175,6172,5171,711 1 1
, , ,
5
65 637 50 8
13
958 4
13
.
.73,7
b) Japão: 82,3
África do Sul: 50,8
82,3 – 50,8 5 31,5
c) 82,3 – 71,7 5 10,6
1.
a) 27x2 1 2
b) a 2 b2
c) 7x2 2 4ax
d) 5y4 2 8y3 2 3
e) (x4y4 1 x4y6 2 x5y5)  (x4y4) 5 1 1 y2 2 xy
f) a3b 3 a
2 2
g) 2
5
3
x42 x21x23
1
3
h) 2 1
5
4
a2b2 ab
2.
a) (60a4x2 2 40a2x4 1 90a4x4)  (10ax) 5
5 6a3x 2 4ax3 1 9a3x3
b) (60a4x2 2 40a2x4 1 90a4x4)  (10a2x2) 5
5 6a2 2 4x2 1 9a2x2
c) (60a4x2 2 40a2x4 1 90a4x4)  (210a2x) 5
5 26a2x 1 4x3 1 9a2x3
3. (12a2x3 1 15a3x2)  (3ax) 5 4ax2 1 5a2x
4. ( ) ( ) ( ) x y x y x y x y x y xy xy xy 3 3 2 2 2 2 2 2 2 4 3 2 1 2 1 2 1 2 2 
; 5
) ( ) ( ) y x y x y x y x y xy xy xy 3 2 2 2 2 2 2 2 4 3 2 1 2 1 2 1 2 2 
; 5
2 2 2
2 2 1 2 1
5 5 x y x y x y xy xy xy x y xy x y 3 3 2 2 2 2 2 2 1 1 1 2 2 1 1 2 2 

;( )
5 xy xy xy x y xy x y 2 2 2 1 2 2 1 1 2 2 
;( )
5. ( ) ( ) ( ) 2 8 20 2 4 10 5 4 3 2 3 2 a a a a a a a 2 2 2 1 2 ; 

5
5 5 a a a a a a a 3 2 3 2 2 4 10 4 10 8 2 2 2 1 2 2 

( )
6. (6x2 1 13x 2 5)  (3x 2 1)
v.n. para x 5 20,5
6 x 1 13 x 2 5 3 x
2
1
6 x 2 x 2 x
5
2 1 1
15 5
15 5
0
2
2
x
x
2
2 1
v.n. 5 2 ? (20,5) 1 5 5 21 1 5 5 4
7.
12 x 1 5 x 2 2 3 x
1
2
12 x 8 x 4 x
1
3 2
3 2
0
2
2
x
x
2 2
1
8.
4 3 2 2
2 x 2 9 x 2 6 x 1 16 x 2 3 2 x 1 x
2
3
2 x 4 x 3 3 x 2 x 2
5 x
1
10
3
x
2
x x
3 16 3
2 22 1 2
3 2
x x x
10 1 5 2
15
x x
x x
2 1 2
3
2 3
2 2 1
0
2
2
P 5 x2 2 5x 1 1
v.n. 5 52 2 5 ? 5 1 1 5 1
9.
a)
x x x x
x x x x
3 6 2
2 3
2 2 1 2
2 1 2 2
x x
x x
2 2 1
x
x
3 2
3 2 2
2
2
6
2
3 6
3 6
2
2 1
2
0
Q 5 x2 2 x 2 3
R 5 0
b)
2 x 1 7 x 2 15 x
1
5
2 x 10 x 2 x
3
2 2 2
3 15
3 15
0
2
2
x
x
2 2
1
Q 5 2x 2 3
R 5 0

221
c)
3 2 2
x x x x x
x x x x
2 3 5 2
1 2 2 1 2
2 2 1 1
x x
x x
2 2
2 2 1
x
3 2
2
2
2 1
5
2
2 3
2 2
Q 5 x 1 1
R 5 22x 2 3
d)
x 2 1 x
2
1
x x x x
2 1 1 1
x
2
x x
2 1
x
x
3
3 2 2
2
2
1
1
1
1
0
2
2 1
Q 5 x2 1 x 1 1
R 5 0
e)
6 x 5 1 3 x 4 2 13 x 3 2 4 x 2 1 5 x 1 3 3 x 3
2 2 x
2
1
2 6 x 5 1 4 x 3 1 2 x 2 2
x 2
1 x
23
4 3 2
x x x x
x x x
3 2 9 2 2 1 5 1
3
3 4 2
2
2 1 1
x x
x x
9 6 3
9 6 3
2 1 1
1 2 2
0
3
3
Q 5 2x2 1 x 2 3
R 5 0
10.
4 2 2
x x x x
x x x
2 5 2 4 4
2 8 2 3
2 1 1 1 2
4 2 2
2 2 2
2 1 1
x x
x
3 2 4
3 2
12
2
2
2
x 28
Q 5 22x2 2 3
R 5 2x 2 8
Q 1 R 5 22x2 1 2x 2 11
11.
2 x 3 2 7 x 2
1 11 x 2 10 x
2
2
2 2 x 3 1 4 x 2 2 x 2
2 3 x
1
5
2 2
3 11 10
x x Ax
Bx C
2 1 2 11 1
2
2
2 1
5 52 5
x x
x
x
A B C
3 6
5 10
5 10
2 3 5
0
2
∴ , ,
5A 1 3B 1 2C 5 10 2 9 1 10 5 11
12.
5 3 2
x 2 x 1
5
x
4 2
2 2 10
x x x
2 1 2 1
3
6 x 6 x
30
5 4 3 2
x 2 x 5 x 7
x
2 1
2 1 1
( )
16 30 2 6
22 1 2 1
2 6 5
2 1 2 2 1
7 16 30
2 1 2 1
2
5 4 3 3
3 2
x x x
x x x x x
x x x
x3 2
2 x 6
x
5 x 10 x
30
5 x 10 x
30
2 1
2
1 2 1
2 2
1 2
0
v.n. 5 (22)3 2 (22) 1 5 5
5 28 1 2 1 5 5 21
13.
3 2
9 x 2 36 x 1 29 x 2 6 x
2
3
9 x 3 27 x 2 9 x 2
9 x
2
2 1 2 1
2
9 x 29 x
6
9
x
2 1 2
2
2
27
x
2 x
2
6
2 x
6
0
2 1
1
3
v.n.59? 2 2 9
? 2 1 5
1
3
2
2  
 
 
 
1
9
9
3
59? 1 1 2
5
51131256
14. (2x 1 3) ? (x 2 1) 1 6 5
5 2x2 2 2x 1 3x 2 3 1 6 5 2x2 1 x 1 3

222
15.
3 x 3 2 2 x 2
2 41 x 1 60 x
2
3
2 3 x 3 1 9 x 2 3 x 2
1 7 x 2 20 x
1
4
2
7 x 41 x
60
2 1 22 2 2
2 1 2 2
2 1 1
2
3 12 3 5
7 21 5 20
20 60 5 20
20 60 0
0
2
2
x x x
x x x
x x
¨ x
O terceiro fator é 3x 2 5.
16. P 5 (x2 2 1) ? (x 1 2) 1 (x 2 3) 5 x3 1 2x2 2 x 2 2 1 x 2 3
P 5 x3 1 2x2 2 5
x x x
x x x x
2 5 2
2 4 8
4 5
4 8
1 2 2
2 1 1 1
x
x x
x
x
3 2
3 2 2
2
2
2
2 1
8 2
5
8 16
2 1
11
Q 5 x2 1 4x 1 8
R 5 11
17. 3 3 15 2 12 60 2
4
x 2 x 2 x 1 x
2
x x x P
3 12 3 15
2 1 2 5
15 60
15
3
1
2
x
x
2 1
2
2
60
0
3 2 2
x x x x x
x x x x P2
3 2 15 2 12 1 60 2 7 1
10
3 3 21 2
30 3 6
2 1 2 1 5
2
6 x 2 42 x
1
60
6 x 2
42 x
60
2 1 2
0
P1 ? P2 5 (3x 2 15) ? (3x 1 6) 5
5 9x2 1 18x 2 45x 2 90 5 9x2 2 27x 2 90
1.
a) Média5
(74,4266,8)1(74,7267)1(74,9267,3)1(75,2267 6 75 5 67 9 75 8 68 2
6
, )1( , 2 , )1( , 2 , )
1 1 1 1 1
Média5 5 5
anos
7 6 7 7 7 6 7 5 7 6 7 6
6
45 6
6
7 6
, , , , , , ,
,
b) 76,4 – 74,4 5 2 ou 68,8 – 66,8 5 2

223
c)
Expectativa de vida ao nascer
Idade (em anos)
74,9
Ano
74,4
2000
74,7
2001
75,2
2002
2003
75,5
75,8
2004
2005
78
76
74
72
68
66
66,8
67,0
67,3
67,6
67,9
68,2
70
Homens
Mulheres
2.
a) Mais: Distrito Federal
Menos: Alagoas
b) Não, apenas o 2o e o 3o lugares: Santa
Catarina e Rio Grande do Sul.
1921 1
27
c) Média5 5
71 1
,
, anos
Abaixo da média estão 14 estados.
12 – Os produtos notáveis
1.
a) 49a2 2 1
b) 4 1 36x 1 81x2
c) 36x2 2 12xy 1 y2
d) 9 4
4
9
x21 ax1 a2
e) a8 2 m8
f) a6 1 12a3y2 1 36y4
g) m4 1 4m2n3 1 4n6
h) b c 2 2 2
1
9
a2
i) 9a2b2 1 6ab 1 1
2.
a) (2a2 1 0,6b) (2a2 2 0,6b) 5 4a4 2 0,36b2
b) (1 1 0,5x) (1 2 0,5x) 5 1 2 0,25x2
c) (abc 1 1,6) (abc 2 1,6) 5 a2b2c2 2 2,56
3. (3x 1 5) (3x 2 5) 5 9x2 2 25
Alternativa a.
4. (2x 2 y3)2 5 4x2 2 4xy3 1 y6
A resposta de Caio está errada.
5. (a2b) 1(a1b)(a2b)2(a1b) 5 2 2
2 1 x 2 x 5 2 x  
1
16
5 a2 22ab1 b2 1a22 ab 1 ab 2b22 a2 22ab2 b2 5a224ab2b2
1 ab 2b22 a2 22ab2 b2 5a224ab2b2
6. 1
1
4
1
1
4
1
1
16
 
 
 
v.n.512 ? 4 5 1
2 5 2 5
16
16
2 1 1 0
7. (2a 1 3)2 1 (a 2 5)2 5 4a2 1 12a 1 9 1 a2 2
2 10a 1 25 5 5a2 1 2a 1 34
8. (x 1)2 (x 1)2 2(x2 1) 1 1 2 2 2 5 x2 1 x 1 1 x2 2 x 1 2 x 2 1 2 1 2 (x 1)2 (x 1)2 2(x2 1) 1 1 2 2 2 5 x2 1 x 1 1 x2 2 x 1 2 x 1 5 2
2 1 2 1 2 2 4
9.
a) Verdadeira.
b) Falsa; (3y 2 a) (3y 1 a) 5 9y2 2 a2.
c) Falsa; (2c 1 a)2 5 4c2 1 4ac 1 a2.
d) Verdadeira.
10. (2a1b)226ab2(a2b)254a21 4ab 1 b2 2 6ab 2a21 2ab 2 (2a1b)226ab2(a2b)254a21 4ab 1 b2 2 6ab 2a21 2ab 2 b2 53a2
11. (3xy 1 7) (3xy 1 7) 5 (3xy 1 7)2 5
5 9x2y2 1 42xy 1 49
12. (x114)222(x2118x)55x211 8x 111622 x2 22 8x 5516
13. (a22b)22(a222ab14b2)5 a2 24ab1 4b2 2 a2 12ab2 4b2 (a22b)22(a222ab14b2)5 a2 24ab1 4b2 2 a2 12ab2 4b2 522ab
14. x2 1 y2 5 153; xy 5 36
(x 1 y)2 5 x2 1 2xy 1 y2 5 x2 1 y2 1 2xy 5
5 153 1 2 ? 36 5 153 1 72 5 225
15. a2 1 4b2 5 30; ab 5 5
(a 2 2b)2 5 a2 2 4ab 1 4b2 5
5 a2 1 4b2 2 4ab 5 30 2 4 ? 5 5
5 30 2 20 5 10
16. O outro é b 1 c, pois (b 2 c) (b 1 c) 5 b2 2 c2.
17. (b3 2 a) (b3 1 a) 1 (b2 2 a) (b2 1 a) 1
1 (b 2 a) (b 1 a) 5
5 b6 2 a2 1 b4 2 a2 1 b2 2 a2 5
5 b6 1 b4 1 b2 2 3a2
v.n. 5 (21)6 1 (21)4 1 (21)2 2 3 ? (21)2 5
5 1 1 1 1 1 2 3 5 0
18. O quadrado da soma de dois números
mais 5: (x 1 y)2 1 5.
Alternativa c.
19.
a) 6x
b) 6x
c) x2 1 6x 1 6x 1 36 5 x2 1 12x 1 36
20.
a) (a 1 b)3 5 a3 1 3a2b 1 3ab2 1 b3
b) (1 2 2a)3 5 1 2 6a 1 12a2 2 8a3
c) (2x 1 y)3 5 8x3 1 12x2y 1 6xy2 1 y3
d) (4y 21)3 5 64y3 2 48y2 1 12y 2 1

224
21. (a b)3 (a3 b3) 4ab (a b) 2 2 2 1 2 5
5 a3 23a2b13ab22 b3 2 a3 1 b3 14a2b24ab25a2b2ab2
2 a3 1 b3 14a2b24ab25a2b2ab2
13 – Fatorando polinômios
1.
a) 30 5 2 ? 15 5 3 ? 10 5 5 ? 6
b) 60 5 2 ? 30 5 3 ? 20 5 6 ? 10
c) 48 5 2 ? 24 5 3 ? 16 5 4 ? 12
d) 120 5 2 ? 60 5 3 ? 40 5 4 ? 30
Existem outras possibilidades.
2.
a) 180 5 22 ? 32 ? 51
b) 420 5 22 ? 31 ? 51 ? 71
c) 200 5 23 ? 52
d) 648 5 23 ? 34
3. ax 1 ay 5 a ? (x 1 y)
4.
a) x2 2 y2 5 (x 1 y) (x 2 y)
b) b2 2 c2 5 (b 1 c) (b 2 c)
1.
a) 10a 1 10b 5 10 (a 1 b)
b) 4a 2 3ax 5 a ? (4 2 3x)
c) a2 1 5ab 5 a ? (a 1 5b)
d) xy 1 y2 2 y 5 y ? (x 1 y 21)
e) 1
3
1
6
1
3
1
2
 
 
a1 b5 a1 b
f) 35c 1 7c2 5 7c ? (5 1 c)
g) 24x5 2 8x4 2 56x3 5 8x3 (3x2 2 x 2 7)
h) p ? a2 1 pab 1 pb2 5 p (a2 1 ab 1 b2)
i) 35x3y2 2 14x2y3 5 7x2y2 ? (5x 2 2y)
j) y 1 y3 1 y5 1 y75 y (1 1 y2 1 y4 1 y6)
k) xy 2 x3y3 5 xy ? (1 2 x2y2)
l) 120ax3 2 100ax2 1 60ax 5
5 20ax (6x2 2 5x 1 3)
m) a (m 1 1) 2 b (m 1 1) 5 (m 1 1) (a 2 b)
n) x (n 1 h) 1 y (n 1 h) 5 (n 1 h) (x 1 y)
o) b2m2 1 4b2mn 5 b2 ? m (m 1 4n)
p) 2
3
8
3
2
3
a51 a35 a3(a214)
q) a a a a
a a
2 2 2 2
1
3 5
2 4 1 1 5 ? ( 1 1 )
r) x (a 1 b) 1 y2 (a 1 b) 2 z (a 1 b) 5
5 (a 1 b) (x 1 y 2 z)
s) 5
4
3
4
1
4
x32 x25 x2 (5x23)
 
t) ab a b ab ab a
b
8 4 2 2
1
4 2
2 2
1 2 5 1 2
 
2.
a) 2mx2 2 2my2 5 2m (x2 2 y2)
b) v.n. 5 2 ? 10 ? 16 5 320
3. xy3 1 7xy2 23xy 5 xy ? (y2 1 7y 2 3)
v.n. 5 6 ? (20 2 3) 5 6 ? 17 5 102
4. a (2x 2 y) 1 b (2x 2 y) 1 c (2x 2 y) 5
5 (2x 2 y) (a 1 b 1 c)
v.n. 5 20 ? 12 5 240
5.
3x2y13xy253xy ? x1y
área
semiperímetro


( )
24
2
v.n.53?32? 5
1152
soma dos + velho
ac 1 ad 1 bc 1 bd 5 a(c 1 d) 1 b(c 1 d) 5 (c 1
d)
s
(a b)
soma dos novos

 1
1
soma dos + velho
ac 1 ad 1 bc 1 bd 5 a(c 1 d) 1 b(c 1 d) 5 (c 1
d)
s
(a b)
soma dos novos

 1
1
 ac 1 ad 1 bc 1 bd 5 59 ? 34 5 2 006
1.
a) a2 1 ab 1 ax 1 bx 5
5 a (a 1 b) 1 x (a 1 b) 5 (a 1 b) (a 1 x)
b) ax 2 x 1 ab 2 b 5
5 x (a 2 1) 1 b (a 2 1) 5 (a 2 1) (x 1 b)
c) a5 1 a3 1 2a2 1 2 5
5 a3 (a2 1 1) 1 2 (a2 1 1) 5
5 (a2 1 1) (a3 1 2)
d) bx2 2 2by 1 5x2 2 10y 5
5 b (x2 2 2y) 1 5 (x2 2 2y) 5
5 (x2 2 2y) (b 1 5)
e) cx 1 x 1 c 1 1 5
5 x ? (c 1 1) 1 1 ? (c 1 1) 5 (c 1 1) (x 1 1)
f) 2b2 1 2 2 b2k 2 k 5
5 2 (b2 1 1) 2 k (b2 1 1) 5 (b2 1 1) (2 2 k)
g) 5y3 2 4y2 1 10y 2 8 5
5 y2 (5y 2 4) 1 2 (5y 2 4) 5 (5y 2 4) (y2 1 2)

225
h) x
ax a
x
a
x x
a
211 2 5 2 1 2 5 2 1
2 2
1 1
2
1 11
2
( ) ( ) ( ) 
 
1 x
1
a
x x
a
2 1 2 5 2 1
2
1 11
2
( ) ( ) ( ) 
 
i) 15 1 5y 1 2ay 1 6a 5
5 5 (3 1 y) 1 2a (y 1 3) 5 (y 1 3) (5 1 2a)
j) a12 1 a8 2 a4 2 1 5 a8 (a4 1 1) 2 1 ? (a4 1 1) 5
5 (a4 1 1) (a8 2 1)
k) 2an 1 n 2 2am 2 m 5
5 n (2a 1 1) 2 m (2a 1 1) 5 (2a 1 1) (n 2 m)
l)
1
2
1
1
1
1 
 x1xy1y5 ( 1 1x)1y(x1 1 )5(x1 1
) 1y 2
2
2  
1
2
 
1
( 1 1x)1y(x1 1 )5(x1 1
) 1y 2  
2. ac 2 bc 1 ad 2 bd 5
5 c (a 2 b) 1 d (a 2 b) 5 (a 2 b) (c 1 d)
v.n. 5 (21, 1) ? (2, 5) 5 22,75
3.
a) ax 2 bx 1 cx 1 ay 2 by 1 cy 5
5 x (a 2 b 1 c) 1 y (a 2 b 1 c) 5
5 (a 2 b 1 c) (x 1 y)
b) am 1 bm 1 m 2 an 2 bn 2 n 5
5 m (a 1 b 1 1) 2 n (a 1 b 1 1) 5
5 (a 1 b 1 1) (m 2 n)
c) a (x 1 y) 1 b (x 1 y) 1 x (a 1 b) 1 y (a 1 b) 5
5 (x 1 y) (a 1 b) 1 (a 1 b) (x 1 y) 5
5 2 (a 1 b) (x 1 y)
4.
a) x2 2 xz 1 2xy 2 2yz 5
5 x (x 2 z) 1 2y (x 2 z) 5 (x 2 z) (x 1 2y)
b) v.n. 5 5 ? 27 5 135
5.
5 x 1 2 y
5
29
2 x 2 2 y
5
13
7 x 42 x
6
1
5 5
 

⇒
18
2
26
2
v.n. 5 ? 5 ? 5
9 13 117
1.
a) x2 2 81 5 (x 1 9) (x 2 9)
b) 100 2 a2 5 (10 1 a) (10 2 a)
c) b2 4 b b
  
2
2
2 25
5 1 5
2
5  
 
d) 1 2 m2n2 5 (1 1 mn) (1 2 mn)
e) 16x2 2 9y2 5 (4x 1 3y) (4x 2 3y)
f) 1
9
1
1
2 4
y 2 5 1 2
y 2 y 3
3
 
2  
 
 
g) 49h2 2 81p2 5 (7h 1 9p) (7h 2 9p)
h)
1
100
2 2 1
1
2x y 5 1xy 2xy 10
10

  
 
 
2
16 4 4 2 5 1 ? 2
2 c
i) b
c
b
c
b
 
 
 
 
j)
 
 
a a a  
1
25 4
1
5 2
1
5 2
2
2 5 1 ? 2
 
k) x4 2 y4 5 (x2 1 y2) (x2 2 y2)
l) a2b4 2 x2 5 (ab2 1 x) (ab2 2 x)
m) a6 2 b6 5 (a3 1 b3) (a3 2 b3)
n) x10 2 100 5 (x5 1 10) (x5 2 10)
o) y8 2 9 5 (y4 1 3) (y4 2 3)
p) r2 2 81s4 5 (r 1 9s2) (r 2 9s2)
2.
a) (x 2 5)2 2 16 5 (x 2 5 1 4) (x 2 5 2 4) 5
5 (x 2 1) (x 2 9)
b) (y 1 1)2 2 9 5 (y 1 1 1 3) (y 1 1 2 3) 5
5 (y 1 4) (y 2 2)
c) (a 1 b)2 2 c2 5 (a 1 b 1 c) (a 1 b 2 c)
d) (m 1 5)2 2 25 5
5 (m 1 5 1 5) (m 1 5 2 5) 5 m (m 1 10)
e) (3x 2 1)2 2 x2 5
5 (3x 2 1 1 x) (3x 2 1 2 x) 5
5 (4x 2 1) (2x 2 1)
f) (x3 1 2)2 2 x6 5
5 (x3 1 2 1 x3) (x3 1 2 2 x3) 5
5 2 (2x3 1 2)
3.
a) x2 2 (x 2 y)2 5 (x 1 x 2 y) (x 2 (x 2 y)) 5
5 (2x 2 y) ? y
b) x2 2 (x 1 2)2 5 (x 1 x 1 2) (x 2 (x 1 2)) 5
5 (2x 1 2)  (22)
4. a2b2 2 x2 5 (ab 1 x) (ab 2 x)
v.n. 5 7 ? 3 5 21
5. 9x2 2 y2 5 (3x 1 y) (3x 2 y)
v.n. 5 (26) ? (212) 5 72
1.
a) Sim; (x 1 3y)2.
b) Sim; (4a 2 3x)2.
c) Não.
d) Sim; (2x 2 1)2.
2. 4x2 1 16x 1 16 5 4 ? (x2 1 4x 1 4) 5
5 4 ? (x 1 2)2
Alternativa d.

226
3. x2 1 10x 1 25 5 (x 1 5)2  O lado mede
x 1 5.
4.
a) 4x2 2 12xy 1 9y2 5 (2x 2 3y)2
b) y2 1 10y 1 25 5 (y 1 5)2
c) 81n2 2 18n 1 1 5 (9n 2 1)2
d) 4a2 1 16ax 1 16x2 5 (2a 1 4x)2
e) 121x2y2 1 44xy 1 4 5 (11xy 1 2)2
f) x2 x x
2 2
5
1
1
2 1 25
5 2
5  
 
g) 100p2 2 20np 1 n2 5 (10p 2 n)2
h) y2 1 14y 1 49 5 (y 1 7)2
i) a6 1 12a3 1 36 5 (a3 1 6)2
j)
1
4
1
3
1
9
1
2
1
3
2
2
 
m 2 m1 5 m2
 
k) 4p2 2 28p 1 49 5 (2p 2 7)2
l) 16x4 1 8x2y 1 y2 5 (4x2 1 y)2
m) x2 2 2bcx 1 b2c2 5 (x 2 bc)2
n) m10 1 4m5n3 1 4n6 5 (m5 1 2n3)2
5.
a) Sim; (x 1 8y)2.
b) v.n. 5 102 5 100
6. (x2 1 2xy 1 y2) 1 (x2 2 2xy 1 y2) 5
5 (x 1 y)2 1 (x 2 y)2
v.n. 5 (29)2 1 132 5 81 1 169 5 250
7.
a) 11
b) 112x
c) 12a
d) 2abx
e) 19
f) 1x
8. 4a2 2 12a 1 9 5 (2a 2 3)2
v.n. 5 (27)2 5 49
a) a3 1 b3 5 (a 1 b) (a2 2 ab 1 b2)
b) m3 2 n3 5 (m 2 n) (m2 1 mn 1 n2)
c) x3 2 8 5 (x 2 2) (x2 1 2x 1 4)
d) a3 1 1 5 (a 1 1) (a2 2 a 1 1)
a) x x x
x x
ou
x x
2 25 0 5 5 0
5 0 5
5 0 5
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
x x
x x
ou
x x
5 5 0
5 0 5
5 0 5
1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
b) x x x x
x
ou
x x
2 12 0 12 0
0
12 0 12
2 5 2 5
5
2 5 5
⇒ ⇒
⇒

 
 
( )
x x x x
x
ou
x x
2 12 0 12 0
0
12 0 12
2 5 2 5
5
2 5 5
⇒ ⇒
⇒

 
 
( )
c) x x x x
x
ou
x x
2 5 0 5 0
0
5 0 5
1 5 1 5
5
1 5 52
⇒ ⇒
⇒

 
 
( )
x x x x
x
ou
x x
2 5 0 5 0
0
5 0 5
1 5 1 5
5
1 5 52
⇒ ⇒
⇒

 
 
( )
d) x x x
x x
ou
x x
2 1 0 1 1 0
1 0 1
1 0 1
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
x x x
x x
ou
x x
2 1 0 1 1 0
1 0 1
1 0 1
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
e) x x x
x x
ou
x x
2 64 0 8 8 0
8 0 8
8 0 8
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

   
( )( )
x x x
x x
ou
x x
2 64 0 8 8 0
8 0 8
8 0 8
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
f) x x x x
x
ou
x x
2 9 0 9 0
0
9 0 9
2 5 2 5
5
2 5 5
⇒ ⇒
⇒

 
 
( )
x x x x
x
ou
x x
2 9 0 9 0
0
9 0 9
2 5 2 5
5
2 5 5
⇒ ⇒
⇒

 
 
( )
g) x x x
x x
ou
x x
2 81 0 9 9 0
9 0 9
9 0 9
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
x x x
x x
ou
x x
2 81 0 9 9 0
9 0 9
9 0 9
2 5 1 2 5
1 5 52
2 5 5
⇒ ⇒
⇒
⇒

 
 
( )( )
h) x x x x
x
ou
x x
2 0 1 0
0
1 0 1
2 5 2 5
5
2 5 5
⇒ ⇒
⇒

 
 
( )
x x x x
x
ou
x x
2 0 1 0
0
1 0 1
2 5 2 5
5
2 5 5
⇒ ⇒
⇒

 
 
( )
i) x x x
x x
ou
x
2 0 36 0 0 6 0 6 0
0 6 0 0
2 5 1 2 5
1 5 52
2
, ( , )( ,)
, ,
⇒ ⇒
⇒
650⇒ 50 
 
 
x x x x
x x
ou
x
2 0 36 0 0 6 0 6 0
0 6 0 06
0
2 5 1 2 5
1 5 52
2
, ( , )( ,)
, ,
,
⇒ ⇒
⇒
650⇒ 50 6

 
 
x ,
1.
a) a4 2 b4 5 (a2 1 b2) (a2 2 b2) 5
5 (a2 1 b2) (a 1 b) (a 2 b)
b) 3x2 2 6x 1 3 5 3 ? (x2 2 2x 1 1) 5
5 3 ? (x 2 1)2

227
c) m2x 2 x 5 x ? (m2 2 1) 5
5 x ? (m 1 1) (m 2 1)
d) 5a2 1 30ab 1 45b2 5
5 5 (a2 1 6ab 1 9b2) 5 5 ? (a 1 3b)2
e) x3y 2 xy3 5 xy(x2 2 y2) 5
5 xy ? (x 1 y) (x 2 y)
f) m8 2 n8 5 (m4 1 n4) (m4 2 n4) 5
5 (m4 1 n4) (m2 1 n2) (m2 2 n2) 5
5 (m4 1 n4) (m2 1 n2) (m 1 n) (m 2 n)
g) x3 2 xy2 1 x2y 2 y3 5
5 x (x2 2 y2) 1 y (x2 2 y2) 5
5 (x2 2 y2) (x 1 y) 5
5 (x 1 y) (x 2 y) (x 1 y) 5
5 (x 1 y)2 (x 2 y)
h) a4 2 ax3 5 a (a3 2 x3) 5
5 a (a 2 x) (a2 1 ax 1 x2)
i) 1
p p  
1
2 p 4 1
1
1
5 1
1 p 2 1
2 p 2 16
4
4
5 1
1 p 2 1 4
 
1  
 
 
 
 
1
2
1
1
2
 
 
 
2
2 2 2 1 1 p 2 p 5 1 p 1 1
4
1
1
4
1
1
4
 
 
 
 
 
1
1
p 1
p 2
2

  
 
 
2
2 4
3
 
 
 
4
4
4
2
1 1 9
5 1 3
1 9
5 1
3 j) y3 y2 y y y2 y y y
 
2 4
3
 
 
 
y2 4
2
5 y 1 y 1 5 y y
9
1
3  
k) x3y 2 y 5 y (x3 2 1) 5 y (x 2 1) (x2 1 x 1 1)
l) ax2 2 a 1 bx2 2 b 5
5 a (x2 2 1) 1 b (x2 2 1) 5
5 (x2 2 1) (a 1 b) 5
5 (x 1 1) (x 2 1) (a 1 b)
2. 5x2 2 10xy 1 5y2 5 5 (x2 2 2xy 1 y2) 5
5 5 (x 2 y)2
v.n. 5 5 ? 62 5 5 ? 36 5 180
3. ab2 2 ac2 1 b3 2 bc2 5
5 a (b2 2 c2) 1 b (b2 2 c2) 5
5 (b2 2 c2) (a 1 b) 5 (b 1 c) (b 2 c) (a 1 b)
4. x3y 1 2x2y2 1 xy3 5 xy (x2 1 2xy 1 y2) 5
5 xy (x 1 y)2
v.n. 5 10 ? (25)2 5 10 ? 25 5 250
5. ax3 2 ax 1 bx3 2 bx 5
5 ax (x2 2 1) 1 bx (x2 2 1) 5
5 (x2 2 1) (ax 1 bx) 5
5 (x 1 1) (x 2 1) x (a 1 b) 5
5 x (a 1 b) (x 1 1) (x 2 1)
14 – Cálculo do m.m.c.
de polinômios
1.
a) m.m.c. (54, 72) 5 23 ? 33 5 216
54 5 21 ? 33
72 5 23 ? 32
b) m.m.c. (200, 100, 80) 5 24 ? 52 5 400
200 5 23 ? 52
100 5 22 ? 52
80 5 24 ? 5
c) m.m.c. (42, 63, 105) 5 2 ? 32 ? 5 ? 7 5 630
42 5 2 ? 3 ? 7
63 5 32 ? 7
105 5 3 ? 5 ? 7
d) m.m.c. (18, 24, 36, 72) 5 23 ? 32 5 72
18 5 2 ? 32
24 5 23 ? 3
36 5 22 ? 32
72 5 23 ? 32
2.
x
y
mmc x y
5 ?
5 ? ?
5 ? ? 5
5 7
2 5 7
2 5 7 2450
2
2

⇒ . . . ( , )
  2 2 3.
x
y
mmc x y
5 ? ?
5 ? ?
5 ? ? ? 5
2 3 11
3 5 11
2 3 5 11
3
2
3 2  

⇒ . . .( , ) 3960
4.
a
b
 
mmc a b
7 3 5 ?
5 ?
5 ? 5
2 5
2 5
2 5 16000
5 3
7 2

⇒ . . . ( , )
5.
a) m.m.c. (xy6, x4y5) 5 x4y6
b) m.m.c. (a5x2, a2y) 5 a5x2y
c) m.m.c. (xy3, x2y2, x4y) 5 x4y3
d) m.m.c. (3x6, 5x4) 5 15x6
e) m.m.c. (ab3, a4c2, bc) 5 a4b3c2
f) m.m.c. (x3y3, x4y2, x2y5) 5 x4y5
g) m.m.c. (9x3, 6ax2) 5 18ax3
h) m.m.c. (4a, 6a2b, 9b3) 5 36a2b3
i) m.m.c. (18a2b3, 24ab4) 5 72a2b4
j) m.m.c. (12b2c, 16bc5, 20b3c) 5 240b3c5
k) m.m.c. (15m3x, 10mx3, 20m2x2) 5
5 60m3x3
l) m.m.c. (14a2p6, 21a4p3, 42a5p5) 5 42a5p6

228
6.
a)
2
x 2
x x
8
2 10 2 5
mmc x x
8 5
2 5 2
5 2
( )
. .. ( )

b)
xy
x xy x x y
mmc x y x y
3
3 2 2
2 3
1 5 1
5 1
( )
. .. ( )
 

c) ax a ax a
x a x a x a
mmc a x a
2 5 2
2 5 1 2
5 1
2
2 2
( )
( )( )
. . . ( )(
 

x2a)
d)
xy x xy
y y y
2 ( )
mmc x y
1 5 1
1 1 5 1
5 1
5 5
10 25 5
5 2 2
( )
. . . ( )

e)
5
2 5 1
1
1
ax
x x x x
ax a ax
2 5 2 mmc ax x
2 5 2
( ) 5 2
( )
. .. ( )

 
 
f)
2 a 2 b 2
a b a b
3 a 3 b 3
a b
a 2 b 2
a b a b
( )( )
( )
( )( )
2 5 2 2
1 5 1
2 5 1 2

 

 
m.m.c.56(a1b)(a2b)
g)
x x x x
x x x
x x
m
2
2
7 7
49 7 7
( )
( )( )
( )
2 5 2
2 5 1 2
1 5 1
2 14 2 7
.

 
 
m.c.52x(x17)(x27)
h)
2 2 2
x x y x y 2
x xy x y
2 2 2 1
6 6 6 91
mmc 6
x
1 5 1
1 5 1
5
( )
( )
. .. (

11 y)
i)
x x x
x
x x x x
mmc x
2 2
6 9 3
3
3 3
2 1 5 2
2
3
2 5 2
4 3 3
5
( )
( )
( )
. . .

 
 
3(x23)3
j)
5 10 5 2
2 4 2 2
3 6 3 2
3
a a
a a
a a
mmc
1 5 1
1 5 1
1 5 1
5
( )
( )
( )
. . .

 
 
0(a12)
k)
2
( )( )
a a a
a a a
a a a
2 2
2
25 5 5
10 25 5
10 25 5
2 5 1 2
2 1 5 2
2 1 5 1
( )
( )2
5 2 5 2

 
 
m.m.c.5(a1 ) (a2 )
l)
x x x
x
x x
mmc x
2 2
2 1 1
1
3
2 2 2 1
2
2 1 5 2
2
2 5 2
5 2
( )
( )
( )
. . . (

 
 
1)3
7. a6 2 a5 1 a 2 1 5 a5 (a 2 1) 1 1 (a 2 1) 5
5 (a 2 1) (a5 1 1)
a10 1 2a5 1 1 5 (a5 1 1)2
m.m.c. 5 (a 2 1) (a5 1 1)2
8. 6x2 2 4xy 2 9px 1 6py 5
5 2x (3x 2 2y) 2 3p (3x 2 2y) 5
5 (3x 2 2y) (2x 2 3p)
4x2 2 12px 1 9p2 5 (2x 2 3p)2
m.m.c. 5 (3x 2 2y) (2x 2 3p)2
1. Custo do sanduíche:
1
5
1
2
2 5
10
7
10
x x
x x x
1 5
1
5
Custo de 50 sanduíches: 50
7
10
x
? 535
x
Lucro: 50x 2 35x 5 15x
Alternativa c.
2. n 5 1 ⇒ 12 1 3 ? 1 1 1 5 1 1 3 1 1 5 5
n 5 2 ⇒ 22 1 3 ? 2 1 1 5 4 1 6 1 1 5 11
n 5 3 ⇒ 32 1 3 ? 3 1 1 5 9 1 9 1 1 5 19
(5, 11, 19, ...)
Alternativa b.
3. V 5 2a ? (0,5a) ? (4,5a) 5 4,5a3
Alternativa b.
4. v.n. 5 2 ? (23)2 1 8 5 2 ? 9 1 8 5
5 18 1 8 5 26
Alternativa c.
5. xy x y
x y x y x y x y x y
4 2
2 4 8 16
2
, , 3 , 4 , 5 , 6 , 7
O 7o termo será 16x7y.
Alternativa a.
6. (2x13)22(2x21)2540⇒ 4x2 112x192 4x2 14x21540⇒
(2x13)22(2x21)2540⇒ 4x2 112x192 4x2 14x21540⇒
⇒16x18540⇒16x532⇒x52
7. P 5 2 (x 2 3) 1 2 (2x 1 1) 5
5 2x 2 6 1 4x 1 2 5 6x 2 4
Alternativa a.
8. A 5 (b 1 c) (a 1 10) 5
5 ab 1 ac 1 10b 1 10c
Alternativa a.
9. (x1y) 2( x1y)(2x1y)5x 1 xy 1 y 1 x 2 xy 1xy2 2 2 2 2 2 2 2 2 (x1y) 2( x1y)(2x1y)5x 1 xy 1 y 1 x 2 xy 1xy2 y 5 2 2 2 2 2 2 2 2 2
53x21xy5x(3x1y)
Alternativa b.

229
10.
3 2 2
3 2 15 2 12 1 60 2
4
3 12 3 15
2 1 2
15 60
3
2
1
x x x x
x x x
x
Q
2 1

x2 2
15 60
0
3 2 2
3 x 2 15 x 2 12 x 1 60 x 2 7 x
1
10
3 x 3 21 x 2
30 x 3 x
6
2 1 2 1 
6
2
x
Q
2
2
42 60
2 1
6 42 60
2 1 2
0
x
x x
Produto: Q1 ? Q2 5 (3x 2 15) (3x 1 6) 5
5 9x2 2 27x 2 90
Alternativa d.
11. V5
1
5 5
28 8
1 5 3
28 8
4 5
6 4
,
,
,
,
,
Alternativa e.
12. A 5 a ? c
Alternativa a.
13. P 5 (8x2 1 1) (3x 2 1) 1 (4x 2 2) 5
5 24x3 2 8x2 1 3x 2 1 1 4x 2 2 5
5 24x3 2 8x2 1 7x 2 3
P x x 3 x 2
x x
1 24 8 7 3 1
; 2 2 1 2 2
3 2 2
24 x 24 x 24 x 16 x
23
2 1 1 1
16
( ):
x x
x x
x
x
2
2
7 3
16 16
23 3
23 23
20
1 2
2 1
2
2 1
Resto: 20
14. (3x3 2 4x 1 6) 2 (5x3 2 8x2 2 9) 5
5 22x3 1 8x2 24x 1 15
Soma dos coeficientes:
22 1 8 2 4 1 15 5 17
Alternativa a.
15. a2x 1 b2x 1 a2y 1 b2y 5
5 x (a2 1 b2) 1 y (a2 1 b2) 5 (a2 1 b2) (x 1 y)
v.n. 5 (2,25) ? (0,8) 5 1,8
Alternativa b.
16. A 5 x2 2 9 5 (x 1 3) (x 2 3)
P 5 2 (x 1 3) 1 2 (x 2 3) 5 32 ⇒
⇒ 2x 1 6 1 2x 2 6 5 32 ⇒
⇒ 4x 5 32 ⇒ x 5 8
A 5 82 2 9 5 64 2 9 5 55 ⇒ 55 cm2
Alternativa d.
17. A5(a21)2 ? (a221)5(a222a11)(a221)5a42 a2 22a312a1 A5(a21)2 ? (a221)5(a222a11)(a221)5a42 a2 22a312a1 a2 21
A5a 2 a 1 a2 4 2 3 2 1
4 3 2
a a a a a
a a a a a
2 2 1 3 1
3 4
2 1 2 2 2
4 3 2 2
2 1 1 1 1
3 2
a a a
a
3
2 1
1 1 2
3
a a
4 a 3 a
1
4 a 12 a
4
2 11 1
1 2
2 1 1
15 1
3
2
2
2
a
Resto: 15a 1 3
Alternativa b.

230
15 – Fração algébrica
1. 50
x
2. x 2
y
n
3.
a) x  0
b) x  0
c) a 1 4  0 ⇒ a  −4
d) 2x 2 1  0 ⇒ x  1
2
4. c
2x1y
5.
2
x y 2
y
a) 15
3
5 5
x
b)
2 6
x x 2
2
3
3 2
x x 2
x
5 2
c)
x
x
x x
3 2
1
x
x
2 9
3
3 3
3
5
1 2
1
5 2
( )( )
d) a a
5 2 1
a
a
2 8 15
3
2
5 2
6. x 2
a
x
1. 1 ha 5 1 hm2 R 1 ha 5 0,01 km2
6 295 ha 5 6 295 ? 0,01 km2 5 62,95 km2
2. Distância: 316 km
Tempo: 22 – 17 5 5 R 5 horas
Velocidade média:
316
5
5 63,2 R 63,2 km/h
3. Distância: 182 km
Velocidade média: 81km/h
Tempo:
182
81
. 2,25 R aproximadamente
2,25 horas ou 2 horas e 15 minutos
10 horas 1 2 horas e 15 minutos 5 12 horas
e 15 minutos
4.
a)
182
x
b) 182
x11
5. Carol, pois fez o percurso em menos
tempo.
Estudo das frações algébricas
16 – Simplificação das frações
algébricas
O erro está na divisão por zero. Como
partimos da informação de que a 5 b, no
passo em que dividimos ambos os lados da
igualdade por (b 2 a), estamos na verdade
dividindo por zero, o que é um absurdo.
1.
a)
5 11
11 17
5
17
?
?
5
b)
2 3 7
3 5 7 11
2
55
? ?
? ? ?
5
c) 2 3
2 3
2
3
4
3
5 6
3 7
2
1
?
?
5 5
d) 2 5 11
? ?
? ?
2 5 11
2
5
2
25
5 7 3
5 5
4 9 3 2
2.
a) 70
220
2 5 7
2 5 11
7
? ?
? ?
5
2 22 5
b) 80
200
2 5
2 5
2
5
4
3 2 5
?
?
5
c)
135
180
3 5
2 3 5
3
2
3
4
3
?
? ?
2 2 2 5
5 5
d) 98
140
2 7
2 5 7
7
2 5
7
10
2
2 5
?
? ?
5
?
5
3.
a) 5
ab
bc
a
c 5
20 4
4
6 2 5
b) x y
x
y
x
c) 12
10
6
5
2
2
m x
mx
m
x 5
d) 2 2 3 2
a b c
a b
c
ab
5
4 4 2
m n 5
mn
e) 2
5
2
5
10 7
5 7
m
5
2 2
6 3 6 5
f) x y
x y
y
x

2
2 1 2
3
c 2 2
x
( ) ( ) 2 1 1
( )( ) (x )(x ) 1 2 x
3 ) ( x 3)( 2
x 2
x
( ) ( ) x x2 y
y 1 2
2 2 2 22 2 1 2 ( ) ( )
2 x xy y
1
231
g) 8
4 4
8
4
2
5
a2 x a 2
x a x
5
( ) 2
h) 2 2
1
2
1
3
3 2
3
2
h
h h
h
h h
h
5
2 2
h
5
( ) 2
2 2
2 2 5
4. ( )
( )
( )( )
( )( )
a b c
b c a
a b c a b c
b c a b c a
1 2
1 2
5
1 1 1 2
1 1 1 2
a 1 b 2
c
b 1 c 2
a
b c a b c
c a b c a
)( )
)( )
1 1 2
1 1 2
5
a 1 b 2
c
b 1 c 2
a
5.
a) ac c
c c
c a
c c
a
c
2
2
5
2
2
5
2
1
1
2 2
1
1
( )
( )
b) 3 3
3 3
3
3 1 1
x y
a
x y
a
x y
a
1
2
5
1
2
5
1
2
( )
( )
( ) ( ) 1
2 2
3 2 2 2
c) a b
a ab
a b a b
a a b
a b
a
2
2
5
1 2
2
5
( )
5 5
7 5
( ) ( ) 1
2 25 m
7 35
d) m
m
m m
m
5
7
2
2
5
1 2
2
5
( )
8 16 2
16
e) x x
x
x
x x
x
x
2
2
4
4 4
4
4
2 1
2
5
2
1 2
5
2
1
( )
( )( )
f)
2
2 2
2 2
4 4
a a
a a
a a
a
a
a
3 2
2
2
2
1
1 1
5
1
1
5
1
( )
( )
g) x ax
x a
x x 5
a
x a
2 5 x
3 15
3 5 3
1
1
5
1
1
5
( )
( )
1 1
( ) ( ) 2
2 2 1 xy
2 2
h) x y
xy
xy xy
c 2 2
x
2 xy
1
1
2
2
1
5
1 2
1
5
( )
6.
( ) ( ) 2 1 1
( )( ) (x )(x ) ( )( )
2 2 2 2 y y x
( )( ) 1
a) x 1 y 1 x y 2 x 1
xy
y x
x y x xy
y x
x
x x
x x
2 1
2 2 2
5
1 2 1
1
5
( )
( )
(y x)
a
b 1 5
2 5
x
2
x x
y
1
5 2
2
x x
( y x )( y x ) x y
1
1 1 2 1
y x
2 2 2 y y x
x y x xy
y x
2 1
2 2 2
5
1 2 1
1
5
( )
( )
(y x)
y
1
5 2
b)
( ) ( )
( ) ( )
( )
( )
a a
a a
a a
a a
a a
a a
2
2
2
2
1 1
1 1
1
1
2 1 1
2 2 2
5
1
2
5
1
2
5
a
a
1
2
1
1
c)
ax ay
x x y yx y
x 2
x
a x y
x y x y
( ) ( ) x x1
a
x y
2
2 2 2
5
( 2
)
2 2
5
( ) ( ) 2
( )( )
y
y 1 2
x y y ( ) ( )
d) ( )
x x y x
( ) ( )
x y y x y y
x x y
2 2
2 2 2
5
2 1 2 1
2 2
2 2
4 4 2 2 4 4 21
5
x x
x ( x 2
2
y
)
x y x y
1
2 2
2
m m
2 1
x x
x x
x
x y
x 1 2 2
2 2
5
4 ( )( )
1
x y y ( ) ( )
( )
( ) ( )
x x y x
x y y x y y
x x y
2 2
2 2 2
5
2 1 2 1
2 2
2 2
4 4 2 2 4 4 21
5
x ( x 2
2
y
)
x y x y
x
x y
x 1 2 2
2 2
5
4 1
( )( )
) ( )
y y x y y
1 2 1
2 2
4 4 21
x y
5
x ( x 2
2
y
)
x y x y
2 2 2 22 2 1 2 ( ) ( )
2 x xy y
1
x
x y
x 1 2 2
2 2
5
4 ( )( )
1
17 – Adição e subtração de
frações algébricas
1.
a) 3
2
5
3
9 10
6
19
6
a
b
a
b
a a
b
5
b) 7
3
2
4
28 6
2 12 2
b
x
a
x
bx a
x
1 5
1
c)
x
y
y
x
x y
2 2 2xy
d) 1
2
1 1
2
2
2 2
2
m m m
2
1 2 5
1 2
e)
3
2
1 3 2 2
x
x
y
y xy x
xy 2 1 5
f) x a
x
a x
a
1 2 2 2 2
ax a ax x
ax
a x
ax
1
2
2
5
1 2 1
5
g) x
x
x
x
x x x
x
x x
x
1
1
2
5
1 1 2
5
1 2 3 3
3
5 3
2 2
3
2
2
h) a b
a
a b
b
2 2 2 2
ab b a ab
ab
b a
ab
1
1
2
5
1 1 2
5
1
2 2 2 2
2.
a) 2
1 1
2 1 1
1 1
c
x
c x c x
x x
cx c cx c
1
1
2
5
2 1 1
1 2
5
1 2 1 2
c
2 c x 2 1 1 c x
1
1
cx c cx c
1
1
1 x
2
1
5
x 1 1 x
2
1
5
3
cx c
1 1
5
2
1 2 x x
1 1 1 2
b) 2
9
7
3
2 7 3
3 3
2 x 7 x
21
2 3
2 1
x x
5
2 2
1 2
5
2 1
1
( )
( )( ) ( )( 2
5
1 5 9
7
3
2 7 3
3 3
2 7 21
2 3
2 1
x x
5
2 2
1 2
5
2 1
1
( )
( )( ) ( )( 2
5
5 x
21
2 1
3 1 2
) ( x 3)( x
3)
c) 5
4
1
5 1 4
1
5 5 4
1
5
2
2
2
2
2
2
2
2
1
5
1 2 2
1
5
1 2 1
1
5
x x
x
x x
x
5
4
1
5 1 4
1
5 5 4
1
5
2
2
2
2
2
2
2
2
1
5
1 2 2
1
5
1 2 1
1
5
x x
x
x x
x
1
9
x2 1
d) y
y
y y
y
y
y
2
5
1 2 2
2
5
2 2
2
5
2
2
2
2
2
2 2 2
2
4 2
2
6
2
( )( ) 2 2
y
y
y y
y
y
y
2
5
1 2 2
2
5
2 2
2
5
2
2
2
2
2
2 2 2
2
4 2
2
6
2
( )( ) 2 2
e) x y
x y
x
x y
x y x x y
x y x y
1
2
5
2 1 1
1 2
5
( )( )
2 11 1 2
( x y )( x x y
x
x 2 y 1 x x 1
y
11 2 x2 1
2 xy 3 2 1
2
x y
1
x y
5
( x y )( x y
)
5
5
2
1 2
1 2
1 2
x y x y
x y
( )( ) (x y)(x y)

3 4 4
a a
a a
x2 x x2 2
x x
2 2
a x ax
) 1
)( )
( )(x2 ) 5
1 5
( )2 2 2 2 21 2
a b
ab 1
2 2 2 21 2 1 2 2 ( )
232
f) 3 4
a
a 16
a
1
4
3 4 4
4 4
3 4 4
2
a a
a a
a a
a
2
2
2
2
5
2 2 1
1 2
5
2 2 2
1
( )
( )( ) ( 4 4
2 a
8
5
2
)(a 2 ) ( a 1 4)( a
2
4)
3 4 4
4 4
a a
a
5
2 2 1
1 2
5
2 2 2
1
( )
( )( ) ( 4 4
2 a
8
5
2
)(a 2 ) ( a 1 4)( a
2
4)
5
2
a
a 1 a 2
a
5
1
2 4
4 4
2
4
( )
( )( )
x 2 2 2
x
g) 4
1
1
1
1
1
( ) ( )
( )( x) 5
4 1 1
2 2 1 1
1 1
2
2
x
x
x
x
x x x
2
2
1
1
1
2
5
2 x
1 2
1
1
1
1
( ) ( )
( )( x) 5
4 1 1
1 1
2
2 2 2
x
x
x
x
x x x
x
2
2
1
1
1
2
5
2 2 1 1
1 2
5
x2 2 1 x 2 x2 1 1 x 1
x2 2
1 2
5
( ) 2 1
2
1 2
4 1 2 1 2
1 1
4 4
1 1
x x
x x
( )( ) ( x)( x) 5
( )
1
2 2 2 2 2 2 2
1 2
5
5
5
2
4 1
1 1
4
1
x x
x x
x
x
( )
( )( )
2 1 1 1
1 2
5
2
1 2
1 2
1
4 4
1 1
x x
)( ) ( x)( x) 5
1
1 2
5
2
4 1
1 1
4
1
x x
x x
x
x
( )
( )( )
h) a
a b
a
a b
a a b a
a b a b
a ab a
2
2 a b
2
5
1 2
1 2
5
1 2
1
2
2 2
( ) 2 2 2
( )( ) ( )(a b
ab
5
) ( 1 )( 2 )
2 a b a b
b
a a b a
a b a b
a ab a
a b
5
1 2
1 2
5
1 2
1
2
( ) 2 2 2
( )( ) ( )(a b
ab
5
) ( 1 )( 2 )
2 a b a b
3.
x2 xy y2 2 2 3 2 2 2
3 x 2 3 3 2 3 3
2
x a
x ax
x 2 a
2
x x a x ax
( ) 5
( ) x
1
( x a )( x a
)
2
1
2
2
5
1 1 2
1 2
5
x2 xy y2 2 2 3 2 2 2
3ax 1 x2 2
3ax
x a x a
( )( )
5 1 2
3 3
x a x a
x
1 1 2
1 2
5
3ax 1 x2 2
3ax
x a x a
( )( )
5 1 2
5
4 2 4 2
1 2
5
2 2
2
x
x a x a
x
( )( ) x a
v . n .
?
5
( 1 )( 2
) 5
?
?
5 5
4 4
4 2 4 2
4 16
6 2
64
12
16
3
2
4.
b a
a b
1 2 1
2
1 ab 5
a2 2
v n . .5
1 ?
?
5
1
?
5 5
4 2 2
2 4
4 4
4 4
8
16
1
2 2
5.
a)
( )2 2 2 2 21 2
a b
ab 1
a b c b a c c a b 2 1 2
( ) ( ) ( ) ab ac ab b
( )( )( )
a b c b a c c a b 2 1 2
( ) ( ) ( ) ab ac ab b
2 2 2 2 21 2 1 2 2 ( )
1
1 x xy y y
x y
y
y
x y
x
x y
x y y xy
( )( )( )
y x y
2
1
2
1
5
1 2 2
1
5
( )
2
1
( ) 2 1
2 2
( ) 5
1 2
2 2 2 2
5 ( )( )( )
1
5
1
xy
y x y
x
( ) y(x y)
y
x y
2 2 2 2 21 2 1 2 2 ( )
x
x y
x y y xy
y x y
x xy y y
2
1
2
1
5
1 2 2
1
5
( )
2 2 2 2
1
5
1
xy
y x y
x
( ) y(x y)
x y y xy
y x y
x xy y y
1 2 2
1
5
( )
2 2 2 2
1
5
1
xy
y x y
x
( )
( ) y(x y)
b)
1
1
1
1
2
1
1 1 2
x
2
x x 2 1 1
x
x x x
1 2
x x
1
2
5
2 2 1 1
1 2
5
( ) ( )
( )( )
1
1
2
1
1 1 2
x
x 2 1 1
x
x x x
x x
2
2
1
2
5
2 2 1 1
1 2
5
( ) ( )
( )( )
5
2 2 2 1
1 2
5
2
1 2
5
( 2
)
1
x x x
x x
x
x x
x
x
1 1 2
1 1
2 2
1 1
2 1
( )( ) ( )( ) 1
2 2 2 1
1 2
5
2
1 2
5
2
1
x x x
x x
x
x x
x
x
1 1 2
1 1
2 2
1 1
2 1
( )( ) ( )( ) 1
( )(x2 ) x
1 1
6.
2 a 2
2 2 2 2 2 2 2 2
2 2 2
a b
a
a b
a aa b
a b a b
a a a
2
2
1
5
2 2
1 2
5
( )( )
b
1 )( 2 ) ( 5
a b a b
a ( 2 a 2
2 2 2 2 2 2 2 2
2 2 2
a b
a
a b
a aa b
a b a b
a a a
2
2
1
5
2 2
1 2
5
( )( )
b
a b a b
ab
a b a b
ab
( 1 )( 2 ) ( 1 )( 2
) a b
5
2 2
2
7.
m n
n
n
m n n
n
m
n
1 5
2 1
5
v n . .
( )
5
2
5 5
5
100
25
100
1
4
2
8.
2 3
2
x y
x y
x xy y x y
x y
2 1
2
2 2 5
2 1 2 2
2
( )
2 3
2
x y
x y
x xy y x y
x y
2 1
2
2 2 5
2 1 2 2
2
( )
5
2 1 2 1 2
2
5
2
2
5
2
2
5
2x2 3xy y2 2x2 4xy 2y2 2
x y
xy y
x y
y x y
x y
( )
5
2 1 2 1 2
2
5
2
2
5
2
2
5
2x2 3xy y2 2x2 4xy 2y2 2
x y
xy y
x y
y x y
x y
y
( )
9.
a
b
a b
ab
a a ab b ab
ab
1
2 5
1 1 1 2
5
2
2 2 2
a
b
a b
ab
a a ab b ab
ab
1
2 5
1 1 1 2
5
2
2 2 2
10.
a
a b a c
b
b c a b
c
( 2 )( 2 ) ( 2 )( 2
) (a c)(b c)
1
2 2
5
5
2 1 2 1 2
2 2 2
5
a b a c b c
c 1 ac 2
bc
( a 2 b )( a 2 c )( b 2
c
)
5
2 1 2 1 2
2 2 2
5
a b a c b c
c ac bc
a 2 b a 2 c b 2
c
5
2
2 2 2
5
( 2
)
2 2 2
5
2ab 2bc 2
a b a c b c
b a c
( )( )( ) a b a c b c
( )( )( )
2b
(a2b)(b2c)
5
2
2 2 2
5
2
2 2 2
5
2ab 2bc 2
a b a c b c
b a c
( )( )( ) a b a c b c
( )( )( )
2b
(a2b)(b2c)
11.
2 1
( ) ( ) ( )( )
a x
a
1 1
2 1 1
a x
a
a x a x a
2 1 1
( a )( a
)
1
2
1
2
1
5
1 1 2 2
1 2
5
5
ax 1 a 1 a2 2 a 2 ax 1
x 2
1 2
5
1 1 1
1 2
2 2
1 1 1 1
a a
ax a a x
( )( ) (a )(a ) 5

3x
m n
1 1 1 2 8 2 4
( a x a x ( x b a x xy ax ay
233
5
2 a
1 1 1
1 2
5
( 1 ) 1 ( 1
)
( 1 )( 2
)
5
ax x a a
a a
x a a a
a a
1 1
1 1
( )( ) 1 1
( 11 1
1
x a
1 1 1
1 2
5
1
2
) ( )
( a )( a
)
x a
a
1 1 1
1 2
5
a a a
a a
a
1 1
1 1
) ( )
( )( )
( 11 1
1
x a
1 1 1
1 2
5
1
2
) ( )
( a )( a
)
x a
a
12.
2
2
2 2 1
2
2
2
( 2 ) ( 2
)
( 2 )( 2
)
2
2
1
5
1 2 2
2 1
5
a
a
a
a
a a
a a
5
1 1 2 1 2
2 1
5
2 1
4 4 4 4
2 2
8
2 2
a a2 a a2
a a
a
( )( ) ( a)( a)
v n . .
( )( ) ( )
5
?
2 1
5
?
2 ?
52 52
8 6
2 6 2 6
8 6
4 8
6
4
3
2
1
? 4
5 5 ? 4 5
18 – Multiplicação e divisão de
frações algébricas
1. Comprimento: 11,5 m; peso: 4 a 6
toneladas.
2. Razão:
21
400
50,0525
3. Razão:
143
1250
50,1144
4. Razão:
143
138
51,04
1.
a) 2
7
3 6
7 2
a
x
b
xy
ab
x y
? 5
b) x
y
x
y
x
y
4 3
? 5
2
7
2
5
2
15
3 3
c) ax
bc
3 2
3 3 ? 5
xy
b c
ax y
b c
2 2
2 2
d) 9
10
9
10
2 2 2 1
9
10
3
4
2 32
4
2
2
m
x
x
m
m x
mx
m
x
? 5 5
e)
a b
xy
3 2 2
2 2 3 2 5 5 5
x y
a b
a b x y
a b xy
ax
y
3 2
3
2
2 2
f) a b
c
4
2 ? 5 5
c
a b
a bc
a bc
c
b
3 3
3
7
3 5
3 3 7
3 5 3
2.
x 2
a
a) 3
7
2 x
6
x
? b
5
7
ab b) 5
c ac
10
5
a
b c
2 10 b 2 c
2 2
a
b
? 5 5
c) 3
8
4 12
8
3
5 5 2 4
a
b
b
a
ab
a b a
? 5 5
d) 21
8
2
7
42
56
1 1 1 2 8 2 4
3
4
2
3
2
3 2
xy
ab
ab
y
ab xy
aby
bx
y
? 5 5
e) 8
4
8
4
2
2 3
6
8
3
8 2 3
6 3
x y ab
ab x y
2
ab
xy
ab xy
? 5 5 b x
a2 3 3
bc
f) 6
5 2
6
10
3
5
abc abc
bc
a
? 5 5
3. am
x
x y
a
amx y
a x
my
a
3
2
2
4
3 2
4 2 ? 5 5
4. 8
3
4
3
8
3
3
4
24
12
3
2
2
2
3
2
2
2
3 2
2 2
m
ax
bm
x
m
ax
x
bm
m x
abm x
; 5 ? 5 5
2m
ab
5.
xy
a c
a
x
1
? y
5 5 ? 4 5
axy
a cx
y
y
ac y
y
4
2 2 2
2
4
2
 
 
 
 
; ; 8
1
acy 8ac 5
xy
a c
a
x
y
axy
a cx
y
y
ac y
y
2 2 2
2
4
2
 
 
 
 
; ; 8
1
acy 8ac 5
6.
a) x
x
2
2 2 2
x
x
x x
x
x
x
1
?
2
5
1 2
5
2
2 2
2
4
2 2
2
( )( )
b) a
a b
ab
a b
2 2
5
a b
2 2
a b a b
5
a b
?
5
2
( )( ) 2 2
1 2
a b
5
1 2
5
2 2
4
c)
a
a
2 ( ) ( ) 4
a
ax
a a a
? 1 2
ax a
a
?
2
5
2 x
( 2
)
5
1
4
16 4 4
4
d) a
2 1 1 2
2
x y
x y
a
a a x y
x y x y
2
2 2
1 2 2
2 2
?
1
2
5
( 1 )( 2 ) ? ( 1
)
( 1 )( 2
)?? 2
5
1
2 1 2
1
(a )
a
x y
2 1 1 2
2
a
x y
x y
a
a a x y
x y x y
2
2 2
1 2 2
2 2
?
1
2
5
( 1 )( 2 ) ? ( 1
)
( 1 )( 2
)?? 2
5
1
2 1 2
1
(a )
a
x y
e)
3 a
15
4
2
5
15 2
2 2 5
3
?
1
5
? 1
2 2
x
xy y
a
a y x
x x a
y
2 x
1 2 ?
5
2
( )
( )( )
f) x
x xy
x y
y
x x y
x x y y
x
y
3
2
7 7 3 7 7 2
2
?
2
5
? 2
2 ?
5
( )
( )
g) x
a a
2 2 2 1
a a
x x
x a a
a a x x x
3
2
2
5 3
3
3 2
1 1
2
2
?
2
1
5
? 2
2 ? 1
5
( )
( ) ( ) 211
x
a a
a a
x x
x a a
a a x x x
3
2
2
5 3
3
3 2
1 1
2
2
?
2
1
5
? 2
2 ? 1
5
( )
( ) ( ) 211
h) ax x
m n
3 3
m n
a
x a m n
m n m n a
1
2
?
1
1
5
( 1 1 ) ? 3
( 1
)
1
1 2 1 2 2
( )( )( 1
)
5
2
ax x
m n
3 3
m n
a
x a m n
m n m n a
1
2
?
1
1
5
( 1 1 ) ? 3
( 1
)
1
1 2 1 2 2
( )( )( 1
)
5
3x
m 2
n
7.
x xy ax ay
ab b
a
a x
x y x a a
b a
2
4 2 2
2
?
2
2
5
( 1 ) ( 1 ) ? ( 2 )
( 22 ? 1 2
5
4 2
) ( ) ( )
ab b
a
a x
x y x a a
b a
2
4 2 2
2
?
2
2
5
( 1 ) ( 1 ) ? ( 2 )
( 22 ? 1 2
5
x 1
y
b a x
2
4 ) ( ) ( )
2
( )
a x a x ( )
v n . .
( )
( )
( )
5
? 1 2
2 ? 2
5
? 2
2 ?
5 5
2 1 3
2 5 1
2 2
2 4
2
4
1
2
( )

5
8 4 3
( )( )
2 x
2 2 2
 1 1 3

 
2 36
a 
 1

( ) ( ) 
 6
2 2 1
1
 1 1

234
8.
( ) ( )
( )
2 4 2 7
2
5
8 4 3
4 3
2
a b a b 2 5 2
xy
x y
a a b
a b
xy
   x y

 



4 3
5
x
 
a 
b 2

( )
4 3
2
2 5 2
x y
a a b
a b
xy
x y

 



4 3
5
x
a 
b 2

9.
a) x
a
2 1 1 1
a
x
x
a
a a
4 4 3
x
a



 
x

 


1
1
1
( )( )
x
a a
x
a
x


 


1
1 1 1
4 3
b) x y
x y
x
7
x xy
x y
x y
x
x x y x y










7 7 
7
7 1
2 ( ) ( )
x y
x y
x
7
x xy
x y
x y
x
x x y x y










7 7 
7
7 1
2 ( ) ( )
2 x
2 2 2
c) a
 1 1 3

x y
x y
a a
a a
x y x y
1 3 3
2 1


 

 
 

( )( )
( )( )
( 


( ) ( ) 
a 
3 
1
 
 1

 
y
a
a
x y a
)
( )
( )
1 2 ( )( 1
)
a
y
x y
a a
a a
x y x y
1 3 3
2 1


 

 
 

( )( )
( )( )
( 


3 
1
 
y
a
a
x y a
)
( )
( )
1 2 ( )( 1
)
d)
m
x y
2 36
( ) ( ) 
 6
xy
m
m m
x y
xy
m
2 2
m
2 2
2 2
2 12
6 6
2 6



 



( ) 2x
m
x y
xy
m
m m
x y
xy
m
2 2
m
2 2
2 2
2 12
6 6
2 6



 



( ) 2x
e) 3 2 2
9
3
1
y
y
2 1
9
y
y
 
2
3
4


7 6 2
4
6 3 2
2
6
2
a
x x
x
a
a
x x
x
a
a

 
x



( )
( )
3
1
2 1
9
2
3
4
6 3 2
2
6
2
a
x
x
a
a
x




( )
( )
2
  1 1

f) x x
x
1
x
1 1
2 2 1
x x x
x x
x
x x
x
2
2
4
3 2
2
2
1


 

 


(  ) (  )
(x x )
  
x
2
2 x
1
1
 
x
x
1 1
x x x
x x
x
x x
x
4
3 2
2
2
1


 

 


(  ) (  )
(x x )
x
2
2 x
1
1
 


10.
x x
ax bx a b
x
a b
x x
a b x
a b
 
x
2 2 1 1
 
1 1

  




 




( )
 
x
   

1 1 2
( ) ( ) ( ) (x  ) ( x
)
x
a b
x
a b
x x
a b x
a b
x
2 1 1
1 1

 




 




( )
 
  x
   
1 1 2
( ) ( ) ( ) (x  ) ( x
)
11.
a)
3 3 9
a
b
a
b
3

 

 

b)
2 2
2 4
2
4 2
a
x y
a
x y

 

 

c)
x y
x
2 2 2
x xy y
x


 
4
2
16
2
 
 
d) x
x
1 3 x 3 3 x 2
3 x
1 x


3
 
 
12.
a)
xy
a
a
x
1 2
ay
x
2
3
4
2
1
b)
a b
xy
y
a b
( a b ) ( a b
) 
xy
y
a b
a b
x
2 2 2
2 2
2
2




 



( )
a b
xy
y
a b
a b a b
xy
y
a b
a b
x
2 2 2
2 2
2
2




 



( )
13.
a
a
a
a
a
a
a
a
a
a
a
a a









 

3 3 2
9
3 3 2
3 3
2
5
2
5
( )( )
a
a
a
a
a
a
a
a
a
a
a
a a









 

3 3 2
9
3 3 2
3 3
2
5
2
5
3
( )( )
v.n.2 (5)32 (125)250
14.
a a
x x
x
a
x x
a a
a a
x
2
2
2
2
2
2
1
1






 

 

 

 

( )
(x
x x
a a
a x  
 
 

1
1 1
1 1
)
( )( )
( )( )
a a
x x
x
a
x x
a a
a a
x
2
2
2
2
2
2
1
1






 

 

 

 

( )
(x
( x )( x
)
( a )( a
)
a a
x x
a
 
 

( 
)
( 
)

 x
1
1 1
1 1
1
1
2
2 )
15.
a) 1
1
1
2
1 1 1
2
y
y
y
y
 
2   
 y y
 
 

 

 
   

 

 
 
y
y
y
 1


y ( 1 )( 1
1
1
1 1 1
2
2   
 y y
 
 

 

 
 
 

 

 
 
y
y
2
y
y y
y
y


 


1
1 1 1
( )( )
b)
x y
x y
x y
x y
x y x y
x y





 
 
  

 
 
1 1  
 
 
 
x y x x y
  

 
x y
x y
x y
x y
x y x y
x y





 

 

1 1  
 
 
x  y  x 
y
x 
y

 
 






2
2
y
x y
x y
x
y
x

 

 

 

 
c)
a
b
b
a
a b
a b
a b
ab
a b a
 


 


 
 
 

 

 
1
2 2 b
ab

 
 
a
b
b
a
a b
a b
a b
ab
a b a
 


 


 
 

 

 
1
2 2 b
ab

 
 

(a  b) (a 
b) (  )



ab
a
a b
a b
b
2 2
1.
a) Nos dias: 1, 6, 7, 8,14, e 15.
b) Abaixo da meta vigente.
c) Houve queda no consumo.
d) Houve aumento no consumo.

y 3
( ) (  x y
y xy x y
235
2. Consumo da lâmpada:
100 3 30
1000
9000
1000
9 9  
5 5 ⇒ kWh
Consumo do chuveiro:
4 400 1 30
1000
132 000
1 000
132 132  
 
 
2  2
( )
2 a a a
2 
5 5 ⇒ kWh
3.
a) Custo:
200 1 30
1000
0 28
6 000
1 000
 
 
2  2
( )
2 a a a
2 
0 28 168 1 68  
 , 5  , 5 , ⇒R$ ,
200 1 30
1000
0 28
6 000
1 000
0 28 168 1 68  
 , 5  , 5 , ⇒R$ ,
b) Custo:
900 1 30
1000
0 28
27 000
1 000
0 28 756 7 56  
 , 5  , 5 , ⇒R$ ,
900 1 30
1000
0 28
27 000
1 000
0 28 756 7 56  
 , 5  , 5 , ⇒R$ ,
c) Custo:
60 1 30
1000
0 28
1800
1000
2 1 1
2 3 x
2 2 2
0 28 0504 0 50  
 , 5  , 5 , ⇒R$ ,
0 28
1800
1000
5  , 5 , ⇒R$ ,
0 28 0504 0 50 , 2 1 1
2 3 x
2 2 2
4. Lâmpada de 75 W ⇒ consumo:
75 4 30
1000
9 000
1 000
9 9  
5 5 ⇒ kWh
Lâmpada eletrônica ⇒ consumo:
13  4 
30
1560
1 56 156 1000
1000
5 5 , ⇒ , kWh
2 3 2 2
Economia: 9 2 1,56 5 7,44 ⇒ 7,44 kWh
1. 1 1 5
5
ab
ab 2 5
a b
b 2
a
ab
5 5
Alternativa a.
2. x x
x
x x
x
3
2 3 x
2 6
2 3 2
2
2
5
2
2
5
( )
( )
Alternativa c.
x
x 5 5
1 x
2 2 2 2 2   2
2 2   2 2 2 a 2 ab  b 
a
 2
2 2 
3. ( ) ( )
a b a b a
a b a b a b
( ) ( )( )
5
  2 
  5 1
1 x
5
y x
x y
( )( )
( )

5
2 2
2
2
2 2
2 2
2 2 2 2
2
2
ab b a
a ab b a b
b
ab b
2 2 2 2 2   2
  2 2 2 a 2 ab  b 
a
2 2 
( a b )
a
( a b )( a b
)
5
  2 
5

5
2 2
2
2
2 2
2 2
2 2 2 2
2
2
ab b a
a ab b a b
b
ab b
 2
2 
5

2 2
2
2 2
2 2
2 2
2
2
ab b a
a b
b
ab b
5

5

2
2
b2
b a b
b
( ) a b
Alternativa b.
4.
0 49
1 4 2
0 7 0 7
2 0 7
2 ,

0 7
x 2
x
2
, 2
,
( , ) (, )
( , )
5
 2

5
x x
x
x
Alternativa c.
5. x y
1 2 
2
 5  2
x xy
x y
y x
x y
2 y x
2
2
2
5 
   

 

 
Alternativa a.
6. a a
a
a
a
a
a a
a a
2 5
2
 2
2 1 1
1
1 1
1
 
( )( )
( )
a
5 1
 
 
a a
a
a
a
a
a a
a a
2 5
2
 2
2 1 1
1
1 1
1
 
( )( )
( )
a
5 1
 
 
5
2
 2


2 2
5
2
2 
5
a a
a a
a
a a a
a a
a a a
( )
( )( )
( )
( )
1
1 1
1 1
1
1
2 2
Alternativa c.
7.
y x
xy
2 2 2 
2 2
 5
5
x2y xy2 2 2 2
(  )
( )
v n . .5

5 5
2 8
4
16
16
1 2
Alternativa d.
8.
x y
y xy x y
2 3 2 2
x y
y y x
y x
x 2 y
2

 2 5


2
5

 

 
( )
y
y y 
x

x y
y y x
y x
x 2 y
2

 2 5


2
5

 

 
( )
y
y y x
y x y x
x y
y x
3
( 
) 2 2

 2
5 2 5
5 −1 (x 2 y)
v.n. 5 −10
Alternativa c.
9. A
B
A B
x
x
2
2
 2 2
2
1 1
1
 
 
 
 
5
2  2
2
2  2
2
5
2
2

2
2
x x
x
x x
x
x
x
1
1
1
1 2
1
1
1 2
 
 
 
 
 x 5
5
2  2
2
2  2
2
5
2
2

2
2
x x
x
x x
x
x
x
1
1
1
1 2
1
1
1 2
 
 
 
 
 x 5
5
2
2

2 2
2
52
1 2
1
1 1
1 2
1
x
x
x
x
Alternativa b.
10)
1 1
1
1
1
a
a
a
2

2
1 1
1
1
a
a
a
a
2

2
5
1 1
1
a
a
a
a
2

2
5
5
1 1
a a2 a a
1
a
2
2 
2
5
1 1
1
a a2
a
2
2
5
5
1 1
a 2
a
a
2
2 5
a a
2 1
2 5
a
1
a2
Alternativa b.

236
Equações do 1.o grau
com uma incógnita
19 – Equações do 1.o grau
com uma incógnita
1. 35
35
7
1 540⇒3515540  O número é 35.
2. 32
32
2
32
4
1 1 556⇒3211618556
 A quantidade é 32.
3. 60
2
3
60
3
4
60 145 60
120
3
180
4
1  1  5 ⇒ 1 1 5145⇒601401455145
60
3
4
60 145 60
120
3
180
4
1  5 ⇒ 1 1 5145⇒601401455145
120
3
180
4
1 5145⇒601401455145
 A quantidade é 60.
1.
a) 11x 2 13 5 64
11x 5 64 1 13
11x 5 77
x 5 7
S 5 {7}
b) 17x 1 50 5 7x
17x 2 7x 5 250
10x 5 250
x 5 25
S 5 {25}
c) 13x 2 12 5 9x 1 16
13x 2 9x 5 16 1 12
4x 5 28
x 5 7
S 5 {7}
d) 12x 1 21 5 10x 1 16
12x 2 10x 5 16 2 21
2x 5 25
x 52
5
2
S5 2
5
2


e) 1,9x 2 3,6 5 x 2 10,8
1,9x 2 x 5 210,8 1 3,6
0,9x 5 27,2
x 5 28
S 5 {28}
f) 5 (x 1 2) 2 2 (3x 2 1) 5 13
5x 1 10 2 6x 1 2 5 13
5x 2 6x 5 13 2 10 2 2
2x 5 1
x 5 21
S 5 {21}
g) 7 (2 1 x) 5 35 1 5 (x 2 1,2)
14 1 7x 5 35 1 5x 2 6
7x 2 5x 5 35 2 6 2 14
2x 5 15
x5 5
15
2
7,5
S 5 {7,5}
h) 3 (x 1 1) 2 2 (x 2 1) 5 2(x 1 5)
3x 1 3 2 2x 1 2 5 2x 2 5
3x 2 2x 1 x 5 25 2 3 2 2
2x 5 210
x 5 25
S 5 {25}
2.
a) x x
20
4
1 1 5
3 3 240
x1 x
12
4
12
5
3x 2 4x 5 2240
2x 5 2240
x 5 240
S 5 {240}
b) 2
5
3
4
3
20
y2 5 y
8 y2 15
3
y
5
20
20
8y 2 3y 5 15
5y 5 15
y 5 3
S 5 {3}
c) 1
x
2
1
3
2 5 2 x
12
6 3
6
x 2 x1
2 12
6
2
5
23x 1 2x 5 12 2 6
2x 5 6
x 5 26
S 5 {26}

2
5 2 5 4 5 400
237
d) x2 x
10
9 6
1 5
10
2 20 3
18
180
18
x2 1 x
5
2x 1 3x 5 180 1 20
5x 5 200
x 5 40
S 5 {40}
e) x1 x
2
2
5
3
4
1
3
7
2
3 9 4 4
12
42
12
x1 2 x1
5
3x 2 4x 5 42 2 9 2 4
2x 5 29
x 5 229
S 5 {229}
f) 4 1
x2 x
10
2
4
5
2
4
2 5 2
2
8 2 40
x2 2 x
20
16 10 5
20
5
2 1
8x 2 5x 5 16 2 10 1 2 1 40
3x 5 48
x 5 16
S 5 {16}
3. 2m 1 400 5 4m 1 200
2m 2 4m 5 200 2 400
22m 5 2200
2m 5 200
m 5 100
Cada maçã tem 100 g.
4. p 5 3x 1 8 p 5 38
38 5 3x 1 8
23x 5 8 2 38
23x 5 230
3x 5 30
x 5 10
A criança de 38 quilogramas tem 10 anos.
5. x1 x
2
2
5
2
4
1
5
1
5 10 4 4
20
20
20
x1 2 x1
5
5x 2 4x 5 20 2 10 2 4
x 5 6
O número deve ser 6.
5
4
6. n5 x1
7 n 5 38
5
4
x17538
5 28
4
152
4
x 1
5
5x 5 152 2 28
5x 5 124
x 5 24,8
O pé 38 mede 24,8 cm.
7. (x 2 5) 1 (2x 2 9) 1 (3x 2 13) 1 (4x 2 3) 5 90
x 2 5 1 2x 2 9 1 3x 2 13 1 4x 2 3 5 90
x 1 2x 1 3x 1 4x 5 90 1 5 1 9 1 13 1 3
10x 5 120
x 5 12
Os números são: 7, 13, 23 e 45; logo,
o maior é 45.
8. c 5 10 1 0,3 (p 2 1) c 5 11,65
10 1 0,3 (p 2 1) 5 11,65
10 1 0,3p 2 0,3 5 11,65
0,3p 5 11,65 2 10 1 0,3
0,3p 5 1,95
p 5 6,5
A massa da encomenda foi de 6,5
quilogramas.
9. A 5 (x 1 5)  7 5 105
7x 1 35 5 105
7x 5 105 2 35
7x 5 70
x 5 10
O comprimento do retângulo é 15 cm.
10. x1 ? x1
5
2 3
3
8
( )
x1 x1
5
2 6
3
24
3
x 1 2x 5 24 2 6
3x 5 18
x 5 6
Karina tirou 6 na 1a fase e 9 na 2a fase.
11. 0,5x 1 0,3x 1 1 000 5 x
0,5x 1 0,3x 2 x 5 21 000
20,2x 5 21 000
0,2x 5 1 000
x 5 5 000
A indústria produziu 5 000 aparelhos.
12. V
x
5 V
1 5 ⇒ 5 220
x
V
x
20
1 5 1 1
4 4
∴ x x ⇒ x x ⇒ x x
⇒
5 4
20
4
20
5 400
20
2 52
∴ x x ⇒ x x 2
5 2 5 ⇒ 4 x 5 x
400
⇒
5 4
20
4
20
5 400
20
2 52
⇒ 2x 5 2400 ⇒
⇒ x 5 400
A distância é de 400 km.

238
13. v 1 d 5 7 ⇒ d 5 7 2 v
2v 1 1d 5 12 ⇒ 2v 1 7 2 v 5 12 ⇒
⇒ 2v 2 v 5 12 2 7 ⇒ v 5 5
d 5 7 2 5 5 2
Foram cinco vitórias e duas derrotas.
14. x 1 0,8x 5 900
1,8x 5 900
x 5 500
0,8  500 5 400
Rafael recebeu R$ 500,00, e Pedro recebeu
R$ 400,00.
15.
a) x 1 4 5 2x 2 7
x 2 2x 5 27 2 4
2x 5 211 ⇒ x 5 11
Roberto tem R$ 11,00.
b) Preço: 11 1 4 5 15
O chaveiro custa R$ 15,00.
16. 0 8 3000 0 6 5000
x
x ⇒ x ⇒ x1 0 92
x ⇒ x ⇒ x1 ⇒
, ? 1 , ? 1 ?2000 57000
100
2 400 1 3 000 1 20x 5 7 000
20x 5 7 000 2 2 400 2 3 000
20x 5 1 600
x5 5
1600
20
80
A montadora C vendeu 80% da produção.
1.
a) 19  2 5 38 ⇒ 38 jogos
b) 3 1
x x x
3
60
9
3
180
3
1
⇒ 5 ⇒ 5 ⇒ 5
x 1 ? 5 10 x 180 x
18
60
9
3
180
3
10 180 18
x x
x x
1
⇒ 5 ⇒ 5 ⇒ 5
 O Paraná clube venceu 18 partidas,
empatou 6 e perdeu 14.
c) 3  x 1 1  (38 2 x 2 4) 5 78
3x 1 38 2 x 2 4 5 78
3x 2 x 5 78 2 38 1 4
2x 5 44
x 5 22
O São Paulo teve 22 vitórias, 4 derrotas
e 12 empates.
2. x x x x
x
165
6 1 5 1 3 1 10
5 6 10 3 180
x1 x1 x1 x1 x
30
30
30
5
5x 1 6x 1 10x 1 3x 2 30x 5 2180
26x 5 2180
6x 5 180
x 5 30
 O colar tinha 30 pérolas.
1. Alto.
2.
a) Em educação.
b) Em renda.
c) América Latina: 0,80; mundo: 0,74;
países ricos: 0,94.
3. 0 92
0 87 093
3
0 92
1 8
3
2 76
3
1 8
3
,
, ,
,
, , ,
5
1 1
5
1
5
0 87 093
3
0 92
1 8
3
2 76
3
1 8
3
,
, ,
,
, , ,
5
1 1
5
1
5
⇒ 2,76 2 1,8 5 x ⇒ x 5 0,96
O índice educacional é 0,96.
20 – Equação fracionária do
1.o grau com uma incógnita
1.
a) 3
4
1 11
12 1 5 x
9 12
12
11
12
x
x
x
x
1
5
9x 2 11x 5 212
22x 5 212
2x 5 12
x 5 6
S 5 {6}
b) x
x
3 2
x
x
1
1
5 1
1 3
2
2 3
2
(x 1
) 2 x 1 ( 1 2
3
x
)
5
x
2
x
2x 1 6 5 2x 1 1 2 3x
2x 2 2x 1 3x 5 1 2 6
3x 5 25
x 52
5
3
S5 2
5
3


c) 1
6
3
2
1
x
x
1 5
2
x x 4 2
2 18
12
3 1
x x
2 12 2
x
x
x
1
5
( 2 )

2 3 2 2 2 2 2
239
2x 1 18x 5 3x 2 3
2x 1 18x 2 3x 5 23
17x 5 23
x 52
3
17
S5 2
3
17


d) x
x
2
1
5
3
3
3
5
5 3
5 3
3 3
5 3
( )
( )
( )
( )
x
x
x
x
2
1
5
1
1
5x 2 15 5 3x 1 9
5x 2 3x 5 9 1 15
2x 5 24
x 5 12
S 5 {12}
e) 2
2 1
5
5
x2 x 1
1
2 1
2 1 1
5 2 1
2 1 1
( )
( )( )
( )
( )( )
x
x x
x
x x
1
2 1
5
2
2 1
2x 1 2 5 10x 2 5
2x 2 10x 5 25 2 2
28x 5 27
8x 5 7
x 5
7
8
S5
7
8


f) 1
3
1
1
2
x
5 2
2 2 2 6
2 2
( 2 x
)
1
2
2
x
5
( 2
x
) 2 ( 2
2
x
)
4 2 2x 1 6 5 2 2 x
22x 1 x 5 2 2 4 2 6
2x 5 28
x 5 8
S 5 {8}
2. x
x
x
x
2
2
5 1
2
1
1
1
2 1
2 1
2 1
1 2
2 1
( )
( )
( )
( )
x
x
x x
x
2
2
5
2 1
2
2x 2 2 5 1 2 x 1 2x
2x 1 x 2 2x 5 1 1 2
x 5 3
S 5 {3}
3. 3
y 2
3
y2 4
5 1
y
3
4
3 4 2 4
( 2 ) 1 ( 2
)
4
y2
y y
y y y
5
( ) y y
2 ( 2
)
3y2 5 3y2 2 12y 1 2y 2 8
3y2 2 3y2 112y22y528
10y 5 28
y 52 52
8
10
4
5
S5 2
4
5


4. 1
1
3
2
2
5
x2 x 2
x 3
2
2
( )( )
x x ( )( ) ( )(
2 2 x x x x
( x 2 )( x 2 )( x
2
)
5
1 2 3
3 1 3 2 1 2
1 2 3
)
(x2 )(x2 )(x2 )
⇒
( )( )
x x ( )( ) ( )(
2 2 x x x x
2 3 2 2 2 2 2
( x 2 )( x 2 )( x
2
)
5
1 2 3
3 1 3 2 1 2
1 2 3
)
(x2 )(x2 )(x2 )
⇒
⇒ x2 2 3x 2 2x 1 6 5
5 3x2 2 9x 2 3x 1 9 2 2x2 1 4x 1 2x 2 4 ⇒
⇒ x2 2 3x 2 2x 2 3x2 1 9x 13x1 2x2 2 4x 22x592426⇒
⇒ x2 2 3x 2 2x 2 3x2 1 9x 13x1 2x2 2 4x 22x592426⇒
⇒ x 5 21
S 5 {21}
5.
a)
5
9
3
52
x22 x 1
3
5
3 3
3
52
(x1 )(x2 ) x 1
3
5
3 3
3 3
( x
)
5
2 2
1 2
( )( ) 3 3
x 1 x 2 ( x )( x
)
5 5 23x 1 9
3x 5 9 2 5
3x 5 4
x 5
4
3
S5
4
3


b) 2
2
1
2
1
2
x2 x 1
x
5
2 2 2
2 2
2 2
2 2
x x x x
x x x
x x
x x x
( ) ( )
( )( )
( )( )
( )( )
1 2 2
1 2
5
1 2
1 2
2x2 1 4x 2 x2 1 2x 5 x2 2 2x 1 2x 2 4
2x2 14x2 x2 12x2 x2 1 2x2 2x 524
6x 5 24
x 52 52
4
6
2
3
S5 2
2
3



240
c)
4
4
1
2
1
1
x22 x 1
x
5
4
2 2
1
2
1
1
(x1 )(x2 ) x 1
x
5
4 2
2 2
2 2
2 2
x xx
x x x
x x
x x x
1 2
1 2
5
1 2
1 2
( )
( )( )
( )( )
( )( )
4x 1 x2 2 2x 5 x2 2 4
4x1 x2 22x2 x2 524
2x 5 24
x 5 22
Como x ≠ 22, S 5 .
d)
1
5
2
5
7
1
y1 y 2
y2 25
5
2
1
5
2
5
7
1
y1 y 2
y 5 y 5
5
( 1 )( 2 )
( y 2 5 ) 1 2 ( y
1
5
)
7
5
( y 1 5 )( y 2
5
) ( y 1 5 )( y
2
5
)
y 2 5 1 2y 1 10 5 7
y 1 2y 5 7 1 5 2 10
3y 5 2
y 5
2
3
S5
2
3


e) 5 2
9
3
3
1
3
0 2
x
2
2
1
x x 1
x
2
2
5
5 2
3 3
3
3
1
3
0
x
2
x x x x
( )( )
1
2
5 1 2
1
5 2 3 3 3
( )( ) ( )( ) 4 1
x 2
x x x ( )(
2 1 2 2 1
3 3
2 1 2 2 x x
( x )( x )( x
)
0
3 3
x x x
x x x x
1 2
5
1 2
( ) ( )
( )( ) ( )( )
5x 2 2 1 9 2 3x 2 3 2 x 5 0
5x 2 3x 2 x 5 2 2 9 1 3
x 5 24
S 5 {24}
f)
3
1
1 1
5 2
y22 y y 1
1
3
1 1
1 1
5 2
(y1 )(y2 ) y y 1
1
3
1 1
( 1 1 )( 2 1 ) 2 ( 2
1
)
1 1
y
y y y
y y y y
5
( )( ) y y y
1 2 ( 1 )( 2
)
3y 5 y2 2 1 2 y2 1 y
3y y2 y2 y 1 2 1 2 52
2y 5 21
y 52
1
2
S5 2
1
2


g)
4
2
4
2
2
t
1
t t 2 4
1 2
t
5
2
4
2
4
2
2
t
1
t 1 t 2
t 2 t
2
5
( 1 )( 2 )
4 2 4 2
( t 2 ) 1 ( t
1
)
2
t
5
( t 1 2 )( t
2
2
) ( t 1 2 )( t
2
2
)
4t 2 8 1 4t 1 8 5 2t
4t 1 4t 2 2t 5 8 2 8
6t 5 0
t 5 0
S 5 {0}
6. 5
1 1
1
1
1
1
0
x
1
(x1 )(x2 ) x 2
x
2
1
5
5 1 1
( ) ( )
( )( ) ( )( )
1 1 2 2
1 1
0
1 1
x x x
x 1 x 2
x x
5
1 2
5x 1 x 1 1 2 x 1 1 5 0
5x 1 x 2 x 5 21 2 1
5x 5 22
x 52
2
5
O valor é 2
2
5
.
7. 3
1
1
3
4
1
x2 x 2
x 2
5
2
3 3 2 1 2
( )( ) ( )( ) 4 1
x x x x ( )(
2 2 1 2 2 x x
( x 2 1 )( x 2 3 )( x
2
2
)
5
2 23
)
1 3 2
(x2 )(x2 )(x2 )
⇒
3 3 2 1 2
1 3 2
2 2 2
5
2 23
)
1 3 2
(x2 )(x2 )(x2 )
⇒
⇒ 3x2 2 6x 2 9x 1 18 1 x2 22x 2 x 1 2 5
5 4x2 2 12x 2 4x 1 12 ⇒
⇒ 3x2 26x2 9x 1 x2 2 2x 2 x 2 4x2 1 12x 14x51221822⇒
⇒ 3x2 26x2 9x 1 x2 2 2x 2 x 2 4x2 1 12x 14x51221822⇒
⇒ 22x 5 28 ⇒
⇒ 2x 5 8 ⇒
⇒ x 5 4
S 5 {4}
8. 4 3 2
a 5 a 1
a 2
1 4 1
1
3 1 2
1
( )
( )
( )
( )
a
a a
a a
a a
2
2
5
2 1
2
4a 2 4 5 3a 2 3 1 2a
4a 2 3a 2 2a 5 23 1 4
2a 5 1
a 5 21
A expressão é verdadeira para a 5 21.

241
9. 128 224
6
⇒ 128 ( 6
) ⇒
( 6
) ( )
224
x
x x x x
6
x
x x
5
1
1
1
5
1
⇒ 128x 1 768 5 224x ⇒
⇒ 128x 2 224x 5 2768 ⇒
⇒ 296x 5 2768 ⇒
⇒ 96x 5 768 ⇒
x 5 8
Colônia A: 8 grupos.
Colônia B: 8 1 6 5 14 ⇒ 14 grupos
10. C 5 F 1 8x
12
2000 8 12 2000 8
5
1
x 1
⇒ 5
⇒
x
x
x
x
x
⇒ 12x 2 8x 5 2 000 ⇒
⇒ 4x 5 2 000 ⇒
x 5 500
Devem ser produzidas 500 camisetas.
11. 320 300
x 5
x 2
2 320 2
( x
)
300
( 2
) ( 2
)
x x
x
x x
2
2
5
2
320x 2 640 5 300x
320x 2 300x 5 640
20x 5 640
x 5 32
O 8o ano A tem 32 alunos, e o 8o ano B tem
30 alunos.
12. 240 400
t 5
t 1
2 240 2
( t
)
400
( 2
) ( 2
)
t t
t
t t
1
1
5
1
240t 1 480 5 400t
240t 2 400t 5 2480
2160t 5 2480
160t 5 480
t 5 3
t corresponde a 3 horas.
a) 3
10
15
15
2 5
3 2
150
10
75 2
10
⇒ ( ) 8

1 a x
a1 x1 a a x
3 2 75 150
x x x x
2 5 1 5
x x
1
z 1
⇒ ⇒ 2 5 1 ⇒
3
10
15
15
2 5
3 2
150
10
75 2
10
3 2 75 150
x x x x
2 5 1 5
x x
1
⇒ ⇒ 2 5 1 ⇒
150
10
75 2
10
3 2 75 150
x x
x x
2
5
1
⇒ 2 5 1 ⇒
⇒ x 5 225
Mangue Seco dista 225 km de Salvador.
b) 1
4
4
12
1
2
59
2 12

⇒ ( ) 8
12 16
4 12
2 12 11
2
2
5 2
2
2 2
2
5
2 2
y y
y
y
y
( ) ( )
4(y212)
⇒
1
4
4
12
1
2
59
2 12
12 16
4 12
2 12 11
2
2
5 2
2
2 2
2
5
2 2
y y
y
y
y
( ) ( )
4(y212)
⇒
⇒ y 2 12 2 16 5 2y 2 24 2 118 ⇒
⇒ y 2 2y 5 224 2 118 1 12 1 16 ⇒
⇒ 2y 5 2114 ⇒ y 5 114
Mangue Seco dista 114 km de Aracaju.
c) 3 4
5
1
15
1
10
1
z z 5z 2 1 5 1
90 24 2
30
3 6
30
2 1
5
z
z
z
2z 2 3z 5 6 2 90 1 24
2z 5 260
z 5 60
O comprimento da tartaruga-oliva
é 60 cm.
21 – Equações literais do
1o grau na incógnita x
1.
a) 5x 2 3a 5 12a
5x 5 12a 1 3a
5x 5 15a
x 5 3a
S 5 {3a}
b) 6x 1 p 5 4x 1 2p
6x 2 4x 5 2p 2 p
2x 5 p
p
x
5 2
S
p
5 2

c) a x
a
1 5
2
2
4
3
3 3 6
6
8 2
6
5
2
3x 1 2x 5 8a 2 3a 2 6a
5x 5 2a
a
x
52 5
S
a
5 2 5

d) x1b b 2
x x
1
1 5 5 3 10
0
6 6 10 10 3
30
0
30
x1 b1 b2 x1 x
5
6x 2 10x 1 3x 5 26b 2 10b

242
2x 5 216b
x 5 16b
S 5 {16b}
e) 5bx 1 2a 5 bx 1 3a
5bx 2 bx 5 3a 2 2a
4bx 5 a
x
a
b 5 4
S
a
0 b


5 b 4
, 
f) 3 (ax 1 b) 5 2 (ax 2 b)
3ax 1 3b 5 2ax 2 2b
3ax 2 2ax 5 22b 2 3b
ax 5 25b
x
5
b
52
a S
5
b
0 a


5 2 a
, 
g) (x 1 b) (x 2 b) 5 x (x 2 b3)
x2 1 b2 5 x2 2 xb3
x2 x2 xb3 b2 2 1 5
xb3 5 b2
x
b
b
5
2
3
x
1
b 5
S

1
0 5 b
b

, 
h) (a 2 b) x 1 (a 1 b) x 5 2a
ax2 bx 1ax1 bx 52a
2ax 5 2a
x
2
a
5
2
a x 5 1
S 5 {1}
i) x
x
a 5 1 2
2
2
a
c
2
2
x
a
ac x
a
5
1
2x 2 x 5 2ac
x 5 2ac
S 5 {2ac}
j) am
x
m
ax
b
1 2 5b
2 2 1 2
abm bx amx
bm
bm
bm
5
bx 2 amx 5 b2m 2 abm2
x (b 2 am) 5 bm (b 2 am)
bm b am
x
( )
( b am
)
5
2
2
x 5 bm
S 5 {bm}
2. 6hx 1 14 5 18 1 2hx
6hx 2 2hx 5 18 2 14
4hx 5 4
x
4
4
h 5
x
1
h 5
S

1
0 5 h
h

, 
3. b1x b 2
x 2
x
1
5
5 3 10
6 6 10 10
b1 x1 b2 x x
30
3
30
5
2
6x 2 10x 1 3x 5 26b 2 10b
2x 5 216b
x 5 16b
O número deve ser 16b.
4. x a
b
x b
a
2
2 2
5 2
2 1 2 2 2
ax a
ab
ab bx b
ab
2
5
ax 1 bx 5 a2 1 2ab 1 b2
x (a 1 b) 5 (a 1 b)2
x
a b
a b 5
( 1
)
( 1
)
2
x 5 a 1 b
S 5 {a 1 b}
5. x
a b
a
a b
5 2
bx
2
2 1
a b a b
5
( 1 )( 2
)
x a b aa b
( 1 ) 2 5 ( 2
)
2
bx
5
( a 1 b )( a 2
b
) ( a 1 b )( a 2
b
)
ax 1 bx 2 5a2 1 5ab 5 2bx
ax 1 bx 2 2bx 5 5a2 2 5ab
ax 2 bx 5 5a2 2 5ab
x (a 2 b) 5 5a (a 2 b)
x
5 a ( a b
)
( a b
)
5
2
2
x 5 5a
6. (m 2 n) x 1 (m 1 n) x 5 10m
x(m2 n 1m1 n)510m

⇒ ⇒3 4 20⇒
⇒ ⇒
( y
)
2 2
1 2
⇒ ⇒⇒
243
2mx 5 10m
x
10
m
5
2
m x 5 5
O número x vale 5.
1. Maior: Norte
Menor: Sul
2. Maior: Sudeste
Menor: Centro-Oeste
3.
Região
Superfície
(Área em km2)
População
Estimada (em no de
habitantes)
Centro-Oeste 1 600 000 13 000 000
Nordeste 1 600 000 52 000 000
Norte 3 900 000 15 000 000
Sudeste 900 000 80 000 000
Sul 600 000 27 000 000
4. Centro-Oeste:
13000000
1600000
⇒ ⇒3 4 20⇒
⇒ ⇒5 3 18⇒
8,1 hab./km2
Nordeste:
52000000
1600000
32 5 2 5 , hab./km
Norte:
15000000
3900000
3,8 hab./km2
Sudeste:
80000000
900000
88,9 hab./km2
Sul:
27000000
600000
45 2 5 hab./km
5. Maior: Sudeste
Menor: Norte
6. 1a situação: A densidade demográfica
diminui.
2a situação: A densidade demográfica
aumenta.
4
3 52 y1 y5 2 y5 y5
7. 2 (x 2 25,3) 5 67,5 2 3 (x 2 14,8)
2x 2 50,6 5 67,5 2 3x 1 44,4
2x 1 3x 5 67,5 1 44,4 1 50,6
5x 5 162,5
x 5 32,5
Região Nordeste.
1. 7 5 3 2 1 10 3 x x x x 2 1 2 1 2 52 2 1 ( ) ( ) 

7 5 3 2 1 10 3 x x x x 2 1 2 2 2 5 2 

7x 2 5x 2 3 1 2x 1 1 1 10 5 x 2 3
7x25x12x2x523 13 21210
3x 5 211
x 52
11
3
Alternativa b.
2. x x
x x
2
 5 2 5 x x
2 52
3
4
5
3
4
4 20
4
x x
x x
2
 5 2 5 x x
2 52
3
4
5
3
4
4 20
4
⇒ 2x 5 220 ⇒
⇒ x 5 20
y y
y y
1
⇒ ⇒5 3 18⇒
 5 1 5 y y
2 5
5
3
6
5
3
3 18
3
y y
y y
1
 5 1 5 y y
2 5
5
3
6
5
3
3 18
3
⇒ 2y 5 18 ⇒
⇒ y 5 9
 x 2 y 5 20 2 9 5 11
Alternativa d.
3. 3
4
3
2 3
4
3 4 2 4
4
x x
2
x x
x x
x x x
5 1
2 2
x x
5
2 1 2
2
( )
( ) ( )
( )
3
4
3
2 3
⇒ ⇒
4
3 4 2 4
4
x x
2
x x
x x
x x x
5 1
2 2
x x
5
2 1 2
2
( )
( ) ( )
( )
⇒3x253x2212x12x28⇒ 3x2 23x2 112x22x528⇒
⇒3x253x2212x12x28⇒ 3x2 23x2 112x22x528⇒
⇒10 8⇒
8
10
4
5
x52 x52 ⇒x52
5
3
3 3
3
5
3 3
3 3
5
2
1 1 2
5
( )( ) ( )( ) 3 3
y 1 y 2 y y y ( y )( y
)
5
3 3
3
3
5
3 3
3 3
( y
)
5
2
1 1 2
⇒ 5
⇒⇒
2 2
1 2
( )( ) ( )( ) 3 3
y 1 y 2 y y y ( y )( y
)
4
3 52 y1 y5 2 y5 y5
⇒5 3 9⇒3 9 5⇒3 4⇒
⇒5 3 9⇒3 9 5⇒3 4⇒

x
y 5
2
52  52
4
5
4
3
4
5
3
4
3
5
Alternativa a.
4. 280 1 3x 5 400 1 x
3x 2 x 5 400 2 280
2x 5 120
x 5 60 ⇒ 60 km
Alternativa a.
5. n
n
n
n
1
5
n n n n 1
1
1
1 1 5 1 1
3
7
7
12
( 3)( 12) ( 7)( 7)
n
n
n
n
1
1
5
n n n n 1
1
1 1 5 1 1
3
7
7
12
( 3)( 12) ( 7)( 7)

244
n2 1 12n 1 3n 1 36 5 n2 1 7n 1 7n 1 49
n2 112n13n 2n2 27n27n5149236
n 5 13
 n13 5 1313 5 16 54
Alternativa d.
6. 6 10
100
10
60 6
10
100 10 100
⇒ ⇒
10
5 2
1
1
1
5
t
t
1 2
t
t
t 1
6 10
100
10
60 6
10
100 10 100
⇒ ⇒
10
5 2
1
1
1
5
t
t
1 2
t
t
t 1
⇒ 6t 2 10t 5 260 ⇒ 24t 5 260 ⇒
⇒ t 5 15 ⇒ 15 anos
Alternativa d.
7. 0,25x 1 0,45x 1 12 5 x
0,7x 2 x 5 212
20,3x 5 212
0,3x 5 12
x 5 40
0,45x 5 0,45  40 5 18 ⇒ 18 jovens
Alternativa e.
8.
13000
10
2
4000
13000
10 2
⇒ 5 4000
⇒
x
x
5
1
x 1
⇒ 13000 ⇒ ⇒
10 2
4000 13000 4000 10 2
x
x
x x
1
5 5 ( 1 )
⇒ 13 000x 5 40 000 1 8 000x ⇒
⇒ 5 000x 5 40 000 ⇒ x 5 8
Alternativa c.

245
PORCENTAGEM E JURO SIMPLES
22 – Porcentagem
1. Acerto:
38
50
50,76 ou 76%
2. Falta:
7
20
50,35 ou 35%
3. Desconto:
17000
50000
50,34 ou 34%
4. Meninos:
720
1600
50,45 ou 45%
5. Ótimo:
105
250
50,42 ou 42%
Bom:
100
250
50,40 ou 40%
Regular:
30
250
50,12 ou 12%
Ruim:
15
250
50,06 ou 6%
6.
a) 396 1 9 1 18 1 27 5 450 kg
b) Plástico:
396
450
50,88 ou 88%
1.
Utilização Quantidade (litros)
Consumo 54
Higiene 50
Lavagem de roupa 24
Descarga 66
Outras 6
3. 110
829
.0,1326 ou 13,26%
4.
a)
Época
Consumo diário
de água
100 anos a.C. 12 litros
Romano antigo 20 litros
Século XIX 60 litros
Século XX 800 litros
b)
1000
800
600
400
200
0
Consumo diário de água
(em litros)
100 anos
a.C.
Romano
antigo
Século
XIX
Século
XX
1 000
800
600
400
200
0
Consumo diário de água (em litros)
12 20 60
100 anos
a.C.
800
Romano
antigo
Século
XIX
Século
XX
1. 0,24 ? 25 5 6
 6 professores.
2.
a) 0,18 ? 55 000 5 9 900
 9 900 habitantes têm mais de 50 anos.
b) 55 000 − 9 900 5 45 100
 45 100 habitantes têm 50 anos ou menos.
3. 0,227 ? 110 000 5 24 970
 R$ 24 970,00
4. 0,035 ? 4 800 − 168
 168 veículos por hora.
5.
a) Jovens: 0,48 ? 200 000 5 96 000
Homens adultos: 0,25 ? 200 000 5 50 000
Mulheres adultas: 0,27 ? 200 000 5 54 000
b) Jovens com E.F. completo 5
5 0,20 ? 96 000 5 19 200
Adultos com superior completo 5
5 0,05 ? 50 000 1 0,03 ? 54 000 5
5 2 500 1 1 620 5 4 120
6.
a) 0,45 ? x 5 27 ⇒ x 5
27
0,45
⇒ x 5 60 alunos
b) 0,55 ? 60 5 33  33 alunos
7. 0,65 ? x 5 26 ⇒ x 5
26
0,65
5 40  40 partidas

246
8. Não acertos de A: 0,10 ? 60 5 6
Não acertos de B: 0,30 ? 60 5 18
Não acertos de C: 0,55 ? 60 5 33
Total de não acertos: 57
9.
a) 0,81 ? x 5 427 ⇒ x 5
427
0 81
 527
, 
 527 espécies
b) 0,09 ? y 5 427 ⇒ y 5
427
0 09
 4744
, 
 4 744 espécies
1. [(0,24 ? 8 000) ? 0,25] ? 0,15 5
5 [1 920 ? 0,25] ? 0,15 5 480 ? 0,15 5 72
 72 entrevistados
2. 0,24 ? 0,25 ? 0,20 5 0,012
 1,2% dos entrevistados
1.
a) 0,98 ? 600 000 5 588 000 casos de malária.
b) Casos de dengue:
2006: 50 027
2007: 92 345
Aumento: 92 345 – 50 027 5 42 318
Taxa percentual:
42318
 0 ,
85 0 ,
85
?
100
85
5
50027
100
100
5 5 85%
2.
a) 14 039 – 11 532 5 2 507 R 2 507 km2
b)
2507
14 039
0 18
0 18 100
100
18
100
 ,
,
5
?
5 5 18%
c) Pará
46% de 11 532 R 11532 46
? R 5 304 km2
100
3.
a) Diferença: 5 912 2 4 707 5 1 205 milhões
de toneladas de CO2.
x ? 4 707 5 1 205 ⇒ x 5
1205
4707
0,25
 Aumento de 25%.
b) 0,08 ? 5 800 000 000 5 464 000 000 de
toneladas de CO2.
Total da China:
5 800 000 000 1 464 000 000 5 6 264 000 000
 O total da China foi de
aproximadamente 6,2 bilhões de
toneladas de CO2.
c) Brasil:
337
127
2,6
 O Brasil lança 2,6 vezes a média mundial.
d) Precisa diminuir:
337 000 000 − 300 000 000 5 37 000 000 t
x ? 337 000 000 5 37 000 000 ⇒
⇒ x 5
37000000
337000000
0,11
 O Brasil precisa reduzir em 11% suas
emissões de CO2.
23 – Juro Simples
1. Resposta em aberto. O aluno concluirá
que juro é uma espécie de “aluguel” que
se paga pelo uso de dinheiro emprestado
ou quando se paga uma mercadoria em
prestações.
2. 0,40 ? 1 200 5 480  Pagaria R$ 480,00.
Restaria para pagar: 1 200 − 480 5 720
 R$ 720,00.
3. Desconto: 0,10 ? 1 200 5 120
Preço a pagar: 1 200 − 120 5 1 080
 Pagaria R$ 1 080,00.
1.
a) Juros ao mês para pagar:
0,015 ? 5 200 5 78 reais
b) Total em 5 meses: 78 ? 5 5 390 reais
Total pago: 5 200 1 390 5 5 590 reais.
2.
a) Ao mês: 0,023 ? 1 800 5 41,40 reais
Em 5 meses: 5 ? 41,40 5 207 reais
b) Ao mês: 0,0196 ? 2 450 5 48,02 reais
Em 2 meses: 2 ? 48,02 5 96,04 reais
3. Rendeu ao mês: 3 000  3 5 1 000 reais.
Taxa: x ? 40 000 5 1 000 ⇒
⇒ x5 5
1000
40000
0,025  2,5% ao mês
4. Rendimento por ano: 389,12  2 5 194,56 reais
Total: 0,256 ? x 5 194,56 ⇒
⇒ x5 5
194 56
0 256
760
,
,
reais
5. Total de juros: 69 − 60 5 9 reais
9
60
Taxa: x ? 60 5 9 ⇒ x5 5
0,15
 A taxa de juros é de 15%.

247
6. Juro ao mês: 931  2 5 465,50 reais
Total: 0,019 ? x 5 465,50 ⇒
⇒ x5 5
465 50
0 019
24500
,
,
reais
1.
a) Gráfico de colunas triplas ou de
múltiplas colunas ou de colunas
comparativas.
b) Maior superfície: região Norte (45,3%)
Mais recursos hídricos:
região Norte (68,5%)
2a menor concentração de população:
região Norte (8,0%)
c) Região Nordeste (3,3%)
d) Região Sudeste (42,0%)
e) Não, pois a região Norte possui a maior
superfície (45,3%) e a segunda menor
concentração de população (6,98%).
f) A região Sudeste tem 6% do total
brasileiro, que por sua vez tem 12% do
total mundial, logo, a região Sudeste
tem 6% de 12% da água do planeta, ou
seja, 0,06 ? 0,12 5 0,0072 ou 0,72%.
g) Não. Maiores recursos hídricos: região
Norte (68,5%)
Maior população: região Sudeste (42%).
2.
b) • Geleiras e neves eternas:
0,689 ? 0,025 . 0,0172 ou 1,72%.
• Rios e lagos: 0,003 ? 0,025 . 0,000075
ou 0,0075% aproximadamente.
• Águas subterrâneas:
0,299 ? 0,025 . 0,0075 ou 0,75%.
• Solos, pântanos e geadas:
0,009 ? 0,025 . 0,000225 ou 0,0225%.
3.
1. 1
5
50,2 ou 20%
Alternativa c.
2. Alternativa a.
3. 15
375
50,04 ou 4%
Alternativa c.
4. V 5 3,5 ? 2,5 ? 2 5 17,5 m3
Falta 20% da capacidade para encher:
0,20 ? 17,5 5 3,5.
 3,5 ? 1 000 5 3 500 L
Alternativa e.
5. Número de meninos (x) menos 3 é igual a
60% do número de meninas (y).
(x – 3) 5 0,6 ? y
x 1 y 5 35 ⇒ y 5 35 − y
 x − 3 5 0,6 ? (35 − x) ⇒
⇒ x − 3 5 21 − 0,6x ⇒ x 1 0,6x 5 21 1 3 ⇒
⇒ 1,6x 5 24 ⇒ x5 5
24
1 6
15
,
 A classe tem 15 meninos.
Alternativa d.
6. 0,3 ? 0,4 ? 0,5 5 0,06 ou 6%.
Alternativa d.
7. Antes da liquidação:
60 1 0,2 ? 60 5 60 1 12 5 72 reais.
Durante a liquidação:
Desconto: 0,2 ? 72 5 14,40 reais.
Preço: 72 − 14,40 5 57,60 reais.
Alternativa d.
8. Juro ao mês: 0,04 ? 2 400 5 96 reais
Alternativa c.
9. Juro ao mês: 310  10 5 31 reais
31
0 05
Preço: 0,05 ? x 5 31 ⇒ x5 5
620
,
reais
Alternativa b.
10. Juro pago: 49 000 − 25 000 5 24 000 reais
Juro pago ao mês: 24 000  20 5 1 200
Taxa: x ? 25 000 5 1 200 ⇒
⇒ x5 5
1200
25000
0,048 ou 4,8% a.m.
Alternativa d.
Distribuição de água no corpo humano
sangue
rins
coração
músculos
fígado
pulmões
cérebro
81%
83%
75%
75%
86%
86%
75%

248
SISTEMA DE EQUAÇÕES DO 1.o GRAU
COM DUAS INCÓGNITAS
24 – Equação do 1º grau com duas
incógnitas
1.
a) x 1 8 1 x 1 8 5 4 ? y ou 2x 1 16 5 4y
b) x 5 7 e y 5 6
Sim, pois 2 ? 6 1 16 5 4 ? 7, ou seja,
12 1 16 5 28
2.
a) 4x 1 2y 5 48
b) x 5 10, y 5 4
Sim, pois 4 ? 10 1 2 ? 4 5 40 1 8 5 48.
1.
a) 3 ? 3 1 9 5 9 1 9 5 18, sim.
b) 3 1 2 ? 9 5 3 1 18 5 21, sim.
c) 2 ? 3 1 3 ? 9 5 6 1 27 5 33 ≠ 30, não.
2. y 5 2x 2 5
a) 3x 1 2 (2x 2 5) 5 4 ⇒ 3x 1 4x 2 10 5 4 ⇒
⇒ 3x 1 4x 5 4 1 10 ⇒
⇒ 7x 5 14 ⇒ x 5 2
b) x 2 4 (2x 2 5) 5 21 ⇒
⇒ x 2 8x 1 20 5 21 ⇒
⇒ x 2 8x 5 21 2 20 ⇒
⇒ 27x 5 221 ⇒ x 5 3
3. 5x 2 3y 5 31
a) y 5 3
5x 2 3 ? 3 5 31 ⇒ 5x 5 31 1 9 ⇒
⇒ 5x 5 40 ⇒ x 5 8
Solução: (8, 3)
b) x 5 5
5 ? 5 2 3y ⇒ 23y 5 31 2 25 ⇒
⇒ 23y 5 6 ⇒ y 5 22
Solução: (5, 22)
4. 7x 1 1 5 50 ⇒ 7x 5 50 2 1 ⇒
⇒ 7x 5 49 ⇒ x 5 7
Solução: (7, 1)
5. 6x 2 y 5 42
a) x 5 8
6 ? 8 2 y 5 42 ⇒ 48 2 y 5 42 ⇒
⇒ 2y 5 42 2 48 ⇒ 2y 5 26 ⇒ y 5 6
Solução: (8, 6)
b) y 5 0 ⇒ 6x 5 42 ⇒ x 5 7
Solução: (7, 0)
6. 4 ? (23) 1 3 ? 5 5 212 1 15 5 3, sim.
2 ? (23) 2 5 ? 5 5 26 2 25 5 231, sim.
 É solução das duas equações.
7. (4, 1)
25 – Sistema de equações do
1º grau com duas incógnitas
1.
a)
x 2
y
x y
5
1 5
30

b)
x y
x y
1 5
2 5
25
13

c)
x 1 y
5
x 5
y
150
2
3

   
d)
x y
x y
50
1 5
5 2
2 1

e)
x 1 y
5
x 5
y
1 300
5
4

 
 
f)
x 1 y
5
x 5
y
500
0,7

g)

x y
x y
8
1 5
1 5
5 10 55
h)

x y
x y
23
1 5
1 5
2 4 82
2.
3 ? 10 2 2 ? 7 5 30 2 14 5
16
2 ? 10 2 3 ? 7 5 20 1 21 5
41

Sim, (10, 7) é solução.
3.
( )
( )
4 ? 2 3 1 3 ? 5 52 12 1 15 5
3
2 ? 2 3 2 5 ? 5 52 6 2 25 52
31
 

Sim, (23, 5) é solução.

⇒ 
x23(2322x)5226⇒x1916x5226⇒x16x5226 x23(⇒ 
3? (22425y)22y524 ⇒272215y22y524 ⇒215y22y524172⇒
y y y
⇒ ⇒ y y 29
5
2 5 y 2 5 100 1
249
4.
2 1 2 2 2 0 3
3 1 2 2 3 4 7 8


? 2 5 2 5
? 1 ? 5 1 5

(1, 2) não é solução.
2 ? 2 2 1 5 4 2 1 5
3
3 ? 2 1 2 ? 1 5 6 1 2 5
8

(2, 1) é solução.
5. (3, 2)
6.
2
2
2
4 2 1 8 7
1 ? 52 1 5
2
2
2
2 1 3

 
 
2 2 52 2 52
(22, 2) não é solução.
1.
1
3
x y
1 5
x y
110
1 5
1
4
110

 
 
Alternativa b.
2. A incógnita x representa a quantia
economizada por Bento, e a incógnita y
a quantia economizada por Antônio.
3.
80
1
3
90 80 30 110
1
4
1 ? 5 1 5
80 90 20 90 110
? 1 5 1 5

 
 
O par correto é (80, 90).
Alternativa a.
2 5 100 58 1
4. Bento economizou: R$ 80,00.
Antônio economizou: R$ 90,00.
26 – Resolução de um sistema de
2 5 100 58 1
duas equações do 1º grau com
duas incógnitas
a)
x y
x y x y
20
8⇒ 8
1 5
2 5 5 1

(81y)1y520⇒y1y52028⇒2y512⇒y56
1y520⇒y1y5202 8⇒2y512⇒y56
x5816514
S5{(14,6)}
b)
3 18
x y
x y x y
2 5
1 5 10 ⇒ 5 10
2

3? (102y)2y518⇒3023y2y518⇒23y2y518230
3? (102y)2y518⇒3023y2y5 18⇒23y2y518230
⇒24y5212⇒y53
x5102357
S5{(7,3)}
c)
2 3 3 2
x 1 y 52 y 52 2
x
x 2 3 y
52
26
2322x)522 6⇒x1916x5226⇒x16x5226 2 9⇒
x23(2322x)5226⇒x1916x522 6⇒x16x5226 2 9⇒
⇒7x5235⇒x525
y52322? (25)52311057
S5{(25, 7)}
d)
x 1 5 y 52 24 x 52 24 2
5
y
x 2 y
52
3 2 4
3? (22425y)22y52 4 ⇒272215y22y524 ⇒215y22y524172⇒
3? (22425y)22y524 ⇒272215y22y52 4 ⇒215y22y524172⇒
⇒217y568⇒y524
x522425? (24)5224120524
S5{(24,24)}
e)
x y
5 1
2 5 ⇒ 5 1
5
10
2
x y 29 x 29
y

 
 
29
5
10
2
58 2
10
100 5
10
5 1
1
5
1
10
2
58 2
10
100 5
10
5 1
1
5
1
2 5 2
y y y y
⇒ ⇒ y y ⇒
29
5
10
2
58 2
10
100 5
10
5 1
1
5
1
2 5 2
y y y y
⇒ ⇒ y y ⇒
⇒23y542⇒y5214
x5291(214)515
S5{(15,214)}
f)
( )
3 5 2 1
3 3 3 2 3
x 2 y 5 x 2 y
1
y 2 x 2 y 1 x 52 2
y
( )
 

⇒
⇒
3 5 2 2 1
3 3 3 2 3
x 2 y 5 x 2 y
1
y 2 x 1 y 1 x 52 2
y

⇒
⇒
3 x 2 5 y 5 2 x 1 2 y
5
1
3 y 2 3 x 1 3 y 1 x 1 3 y
52
2

⇒
⇒
⇒ 
x y x y
3 1 1 3
2 9 2
2 5 5 1
2 1 52
x y
22 ? (1 1 3y) 1 9y 5 22 ⇒ 22 2 6y 1
1 9y 5 22 ⇒ 26y 1 9y 5 22 1 2 ⇒
⇒ 3y 5 0 ⇒ y 5 0
x 5 1 1 3 ? 0 5 1 1 0 5 1
S 5 {(1, 0)}

1 5 1 ) ( )⇒ ⇒
250
g)
x y x y
x
5 3
y x y
1
5
2
5 1 5 1
2
2⇒ 2 4

 
 
2 4
5
2 4
3
3 ( 3 4
) ( ⇒ )⇒ 1 5 1 ⇒
15
5 4
15
9 12 5 20
y y y y y y
1 1
5
y y 1 2 1
5
1
4
2 4
3
3 ( 3 4
) ( ⇒ )⇒ 1 5 1 ⇒
15
5 4
15
9 12 5 20
y y y y y
1
5
y y 1 2 1
5
1
3 4
15
5 4
15
9 12 5 20
y y
1
1
5
y y ⇒9y25y520212⇒4y58⇒y52
x52?214541458
S5{(8,2)}
h)
 ( )⇒
x y x y
x y x
2 2 2 4
5 1 5 1
2
5 1
10 2
2
 
 
2 4
10
2 4
2
2
4
10
10 20 20
1 1 ⇒ ⇒
10
y1 2y y y y
5
1
1
1
5
4
10
2 4
2
2
4
10
10 20 20
⇒ 1 1 ⇒
10
⇒y210y52012024⇒29y536⇒y524
2y y y y
5
1
1
1
5
y210y5201202 4⇒29y536⇒y524
x52? (24)1452814524
S5{(24,24)}
1.
a)
x y
x y
x
x
1 5
2 5
1
5
5
32
18
2 50
25
 

25 1 y 5 32
y 5 32 2 25
y 5 7
S 5 {(25, 7)}
b)
6 3 20
4 3 40
10 60
6
x y
x y
x
x
2 5
1 5
1
5
5
 

4 ? 6 1 3y 5 40
3y 5 40 2 24
3y 5 16
y 5
16
3
 
S5 6
16
3
,  
 
c)
7 x 6 y
23
5 x 6 y
21 1
1 5
1 5 ? 2 ( )
 

7 6 23
5 6 21
2
1
x y
x y
x
x
1 5
2 2 5 2
1
5
5
 

2
7 ? 1 1 6y 5 23
6y 5 23 2 7
6y 5 16
y5 5
16
6
8
3
S5 1
8
3
,  
 


d)
8 x 5 y
11
4 x 5 y
3 1
1 5
1 5 ? 2 ( )
 

8 5 11
4 5 3
4 8
2
x y
x y
x
x
1 5
2 2 5 2
1
5
5
 

8 ? 2 1 5y 5 11
5y 5 11 2 16
5y 5 25
y 5 21
S5{(2,21)}
e)
2 x 3 y
11
2 x 7 y
1 1
2 5
1 5 ? 2 ( )
 

2 2 3 5
11
2 7 1
2 2 5 2
10 10
1
x y
x y
y
y
1
2 5
5 2
 

2x23? (21)511
2x51123
2x58
x 54
S5{(4,21)}
f)
2 12
3 2
6
2 3
6
36
6
2 12 3
2 3
x y
x y x y
x y
x y
2 5
1 5
1
5
2 5 ?
⇒ 1

 
 
⇒ ( )
536
 

2 12
3 2
6
2 3
6
36
6
2 12 3
2 3
x y
x y x y
x y
x y
2 5
1 5
1
5
2 5 ?
⇒ 1

 
 
⇒ ( )
536
 

6 3 36
2 3 36
8 72
9
x y
x y
x
x
2 5
1 5
1
5
5
 


20
10
y x y
x y x 5 2 16 2
y x y
251
2?92y512
2y512218
2y526
y 56
S5{(9,6)}
g)
( ) ( ) 2 5 2
( ) ( )
3 2 2 3
18 2 32 3
3 6 2 6
18
x y
y y x
2 5 2 x y
2 1 5 1
 

⇒
y2361y56x19

⇒
) ( ) 2 5 2
) ( )
2 2 3
2 32 3
3 6 2 6
18
y
y x
2 5 2 x y
⇒
2 1 5 1
y2361y56x19

⇒
⇒
⇒ 3 2 6 6 ( )
6 18 9 36

3 2 0 2
6 19
x y
x y y
x y
x y
2 52 1
2 1 1 5 1
2 5 ?
2 1 545
 

2 6 6 ( )
⇒ 18 9 36
3 2 0 2
6 19
y
x y y
x y
x y
2 52 1
1 1 5 1
2 5 ?
2 1 545
 

6 2 4 5
0
6 19 45
2 1 5
15 45
3
x y
x y
y
y
1
5
5
 

3x22?350
3x56
x 52
S5{(2,3)}
h)
x y x y
x
y
2 x y
x y x y
x y
2
5
2
5 2
2
5
2
5
2
5 2
3
2
2
2 2
10
5 5
10
3
2
2 4
2

 
 
⇒

 
 
⇒

x y
x y
2 5
2 1 5 2
2 x y
y x y
2 x 2 2 y 2 5 x 1 5 y
5
0
3 x 2 2 y
52
4
x 2
y x y
5
x y
2
5
2
2 2
10
5 5
10
3
2
2 4
2
⇒

2 x 2 2 y 2 5 x 1 5 y
5
0
3 x 2 2 y
52
4
3 3 0
3 2 4
2 1 5
2 52
1
4
5 2
x y
x y
y
 

23x13? (24)50
23x512
x 524
S5{(24,24)}
2.
a)
3 20 4
1
3
2
2 6
x 1 y 2 x 5 1 5 x 2 y
16 2
y 1 x 2 y
5 1
3 20 4
2 2
6
3 6
x y
x y x
x y
x y
2 5 2
1
5
1
1
2 5 2
1
5
1 1

 
 
⇒ x
6
⇒

 
 
20 4
1
3
2
2 6
3 20 4
2 2
6
3 6
x y
x y x
x y
x y
2 5 2
1
5
1
1
2 5 2
1
5
1 1
⇒ x
6
⇒

 
 
⇒

 
⇒ ( )
3 4 20
2 3 6 2
3 16
3 4 3
x y
x y x
x y
x y
2 52 1
2 2 5 2
2 5
2 5 ? 2 
3 16
3 9 12
8 4
y
1
5
 

4
8
y5 5
1
2
3
1
2
x2 516
6 1
2
32
2
x 2
5
6x53211
6x533
x5 5
33
6
11
2
S5
11
2
1
2
,  
 


b)
5 2
2
3
5
2
7 1
2
5
3
2
25 10 2 6
10
x y
x
y x
y
1
2
5
2
1
2
5
2 1 2
( )

 
 
⇒
5
2 1 2
5
21 21 2 10
6
x
12
6

 
 
⇒
5 2
2
3
5
2
7 1
2
5
3
2
25 10 2 6
10
x y
x
y x
y
1
2
5
2
1
2
5
2 1 2
( )

 
 
⇒
5
2 1 2
20
10
5
21 21 2 10
6
x
12
6

   
⇒
⇒

1 2 5 1 x y
⇒
1 2 5 1
25 2 20 10 6
21 2 12 21 10
1 5 ? 2 (( )
( )
 

2x19y531 ? 5
⇒

⇒
25 2 20 10 6
21 2 12 21 10
1 5 ? 2 (( )
( )
 

2x19y531 ? 5
10 4 32
10 45 155
2 2 5 2
1 5
1
41 123
5
5
3
x y
x y
y
y
 

5x12?3516
5x51626
5x510
x 52
S5{(2,3)}
c)
2 x y x y
x y x y
1
1
x y x y
5
1
2
2
5
2 1 1
5
6 8
5
4 5
10
4 4 3 3
24
120
2

 
 
⇒ 4
5 5 4 4
20
200
20
x1 y2 x1 y
5

 
 
⇒

2 x y x y
x y x y
1
1
x y x y
5 10 (
10 100 60
y 2 5 10 5
x
1 52 x y
252
5
1
2
2
5
2 1 1
5
6 8
5
4 5
10
4 4 3 3
24
120
2
⇒ 4
5 5 4 4
20
200
20
x1 y2 x1 y
5

 
 
⇒
⇒ ( )  
x y
x y

⇒
7 120 9
2 5 ?
1 5
9 200
63 9 1080
9 200
64 1280
20
x y
x y
x
x
2 5
1 5
1
5
5
 

2019y5200
9y5200220
9y5180
y 520
S5{(20,20)}
3.
x y
x y
x
x
1 5
2 5
1
5
5
18
2 12
3
10

 
 
30
101y518
y518210
y 58
x22y1z5212
1022?81z5212
z5212210116
z 526
4.
 ( 1 ) 2 ( 2 ) 5 x 1 2 y
1 5
⇒ 2 3 5 6 4 3 ( )
2 18
x
5 2
5 2
5
2
1 x y
y
y
x
5 2
y x
1 2 5 2
1
5
3 10 5 10
2 10
10
10 5
( ) ( )

 
 
⇒
y
10
5 6 60
x y x
2
 ( ) ( ) 1 2 1 5
10 100
2
1 2
5
2

 
 
1 2 2 5 x y
⇒ 2 3 5 6 4 3 ( )
2 18
2 3 1 4
2 18
⇒
y
x
x y
2
2 5 2
1
5
2
2
10 5 10
2 10
10
10 5
) ( )
⇒
y
10
5 6 60
x y x
2
10 100
2
1 2
5
2

 
 
⇒
⇒
⇒ 2 10 5 10 (
5 6 10 100 60

2 52 ? )
x 2 y 1 y 52 2 x 5 y
10 5
x 1 y 2 x
52 1
( )
 

25x16y5240 ?2
⇒ 52 1
2 52 ? )
( )
 

25x16y5240 ?2
10 25 50
10 12 80
x y
x y
2 5 2
2 1 5 2
13 130
13 130
y
y
y
1
2 52
5
 

5 10
2x25?105210
2x5210150
2x540
x 520
a) x ? y 5 20 ? 10 5 200
b) x2 1 y2 5 202 1 102 5 400 1 100 5 500
c) x
20
10
y 5 5
2
5.
2 2 3 1 5 6
2 4
0 45
2 4 3 3 5 6
2
x y
x y
1 5
 
 
⇒
,
,
,
x1y
5
4
1 ,
8
4

 
 
⇒
2 2 3 1 5 6
2 4
0 45
2 4 3 3 5 6
2
x y
x y
1 5
 
 
⇒
,
,
,
x1y
5
4
1 ,
8
4

 
 
⇒
⇒

2 3 1 4 1
2 1
x y
x y
x y
x y
2 5 2 2
1 5
2 52 ?2
1 5
,
,
,
,8
 

⇒

2 3 1 4 1
2 1
x y
x y
x y
x y
2 5 2 2
1 5
2 52 ?2
1 5
,
,
,
,8
 

2 1 5
1 5
1
4 32
5
5
0 8
x y
x y
y
y
,
,
,
,
 

2x10,851,8
2x51,820,8
2x51
x5 5
1
2
0,5
 x3 y3 2 5
5(0,5)32(0,8)35
50,12520,5125
520,387
6.
x y
x z
1 5
1 5
1 5
y z
1
15
11
6

 
 
2x12y12z532(;2)⇒x1y1z516
1.
4a linha: 4 1 4 1 4 1 5 20 ⇒ 5 8
4a coluna: 8 1 1 8 1 8 5 26 ⇒ 5 2
2a linha: 8 1 1 2 1 2 5 18 ⇒ 5 6
2a coluna: 4 1 6 1 1 4 5 26 ⇒ 5 12
3a linha: 4 1 12 1 1 8 5 38 ⇒ 5 14

253
2. Usando a para Andréa, b para Balu e c
para Carlos, temos:
c 1 b 5 87 ⇒ c 5 87 2 b (substituindo na
2a equação)
c 1 a 5 123
a 1 b 5 66
87 123
66
123 87
66
2 1 5
1 5
2 5 2
1 5
b a
a b
a b
a b

⇒

⇒
⇒

a b
a b
a
a
2 5
1 5
1
5
5
36
66
102
2
51
51 1 b 5 66
b 5 66 2 51
b 5 15
c 5 87 2 b
c 5 87 2 15
c 5 72
 Andréa tem 51 kg, Balu tem 15 kg e
Carlos tem 72 kg.
1.
x y
x y
x
x
1 5
2 5
1
5
5
169
31
2
100

 
 
200
1001y5169
y51692100
y 569
 Os números são 100 e 69.
2.
x y
x y
110
1 5
5 1
3 18

1 5 ? ( 2
) 1 5
2 
2 5 2
( )  
( ) 
2 2 5 2
(3y118)1y5110⇒3y1y5110218⇒4y592⇒y523
3y1y5110218⇒4y592⇒y523
x53?23118569118587
 Os números são 87 e 23.
3.
2 2 128
20
x y
x y
1 5
5 1

36 2
21 2
2 2 42
2 4 50
2 8
2(y120)12y5128⇒2y14012y5128⇒2y12y5128240⇒
2y14012y5128⇒2y12y5128240⇒
⇒4y588⇒y522
x522120542
Área do retângulo: A 5 42 ? 22 5 924
 As dimensões do retângulo são
42 m ? 22 m e sua área é de 924 m2.
4. x y
x y
10 1
2 16
1 5
1
5
x y
x y
x
10
2 16
6
 

61y510
y51026
y 54
Usando x para número de vitórias e y para
número de derrotas, a equipe ganhou
6 jogos.
5. 3a parte: x
85 1 2x 1 x 5 235
2x 1 x 5 235 2 85
3x 5 150
x 5 50 ⇒ x 5 50 cm
 A segunda parte mede 100 cm e a
terceira, 50 cm.
6. Certos: x; errados: y
x y
x y
1 5 ?
2 5
5 2 110

2 2 72
5 2 110
7 182
26
x y
x y
x
x
1 5
2 5
1
5
5
 

261y536
y536226
y 510
 O jogador acertou 26 arremessos.
7. Se x é o número de galinhas e y o número
de ovelhas, temos:
x 1 y
5 ? 2
2 x 1 4 y
5
50
1 5
1
5
5
4
x y
x y
y
y
 

x14521
x52124
x 517
 Há no terreiro 17 galinhas e 4 ovelhas.
8. x – nível avançado; y – nível intermediário
x 1 y
5 300 ?  ( 
2
0 4
) 0 4 x 1 0 05 y
5
50
,
, ,


254
0 4 0 4 120
0 4 0 05 50
, ,
, ,
x y
x y
2 2 5 2
2 5
1
0 35 70
,
y
y
2 5 2
 

5 200
x12005300
x53002200
x 5100
Alunos do intermediário que escolheram
Espanhol: 0,05 ? 200 5 10.
 Não escolheram Espanhol 190 alunos do
nível intermediário.
9. x: mais velha; y: mais jovem
x y
x y
70
1 5
2 5 1
10 10

⇒
x y
x y
x
x
1 5
2 5
1
5
5
70
20
2 90
45

 
 
451y570
y570245
y 525
10. x: campeão; y: vice
x y
x y
1 5
5 1
173
7

⇒
x y
x y
x
x
1 5
2 5
1
5
5
173
7
2 180
90

 
 
901y5173
y5173290
y 583
 O campeão somou 90 pontos e o vice,
83 pontos.
11. x – caixas com capacidade para 50 livros.
y – caixas com capacidade para 70 livros.
x y
 1 5 27 ? ( 
2
50
) 50 x 1 70 y
5
1 650

50 50 1350
50 70 1650
2 2 5 2
1 5
1
20 300
5
5
1
x y
x y
y
y
 

5
x115527
x527215
x 512
 Foram utilizadas 12 caixas de 50 livros e
15 caixas de 70 livros.
12. x – prateleiras com vão de 20 cm.
y – prateleiras com vão de 30 cm.
x y
 1 5 24 ? ( 
2
20
) 20 x 1 30 y
5
600

20 20 480
20 30 600
2 2 5 2
1 5
1
10 120
5
5
12
x y
x y
y
y
 

x112524
x524212
x 512
 12 vãos de 20 cm e 12 vãos de 30 cm.
13. x – preço na loja A
y – preço na loja B
x 2 18
5
y
x 2 0,2
x 5
y

x2185x20,2x
x2x10,2x518
0,2x518
x 590
902185y
y 572
 A mercadoria custa R$ 90,00 na loja A e
R$ 72,00 na loja B.
1. Outras soluções:
a 5 2, b 5 2, c 5 4; a 5 5, b 5 1,25, c 5 6,25;
a 5 6, b 5 1,2, c 5 7,2.
1.
x y
x y
544 1
5 8 2
1 5
2 5
1 5 5
1 2 2 x 60 2 x
30 1
,
,
, ,
 

⇒ ⇒
x 5 30,1 (30,1‰ ou 30,1 em 1 000)
 Em 2000, o índice de mortalidade infantil
foi de 30,1 (30,1% ou 30,1 por 1 000).

255
2. x y
544 1
5 8 2
1 5
2 5
2 5 5
x y
1 2 2 y 48 6 y
24 3
,
,
, ,
 

⇒ ⇒
y 5 24,3 (24,3 ‰ ou 24,3 em 1 000)
 Em 2005 o índice foi de 26,6, ou seja,
26,6% ou 26,6 por 1 000.
1.
a)
2 1
3
1
2
1
2
2 1
3
3
3
2
2 2
x
y
y
x
x
y
y
y
y
x
1
1
5
1
5
1
1
5
1
1
1
5

 
 
⇒
( )
x
x
2
1
1
2( 2)





⇒
⇒

 

2 2 3
1
⇒ ( )
2 3 1
2 2
2 2
2 2 2
x y
x y
x y
x y
2 5 2
2 1 5
2 5
2 1 5 ?
2 2 5
2
2 4 4
2 1 5
3 6
2
x y
x y
y
y
1
5
5
 

2x2252
2x5212
2x = 4
x 52
S5{(2,2)}
b)
x y
x
y
x y
x
y
y
y
x y
x y
1 5
5
1 5
5
1
 1
1 5
2 5 ?
9
2
1
9
2
2
2
9
2 0

 
 
⇒

 
 
⇒
(21)
 

x y
x
y
y
y
x y
x y
5
5
1 5
5
1 5
2 5 ?
9
1
9
2
2
2
9
2 0
⇒

 
 
⇒
(21)
 

x y
x y
1 5
2 1 5
y
y
1
5
5
9
2 0
3 9
3
 

x1359
x5923
x 56
S5{(6,3)}
c)
2 2 3
1
1
1
3
2 3 2
3
1 3
1
x y
y x
x y
x
y x
y
y
5 1
2
5
2
2 5
2
2 2
5
2

 
 
⇒
( )( ) ( 221)( 23)

 
 
x
1
3
2 3 2
3
1 3
1
x y
y x
x y
x
y x
y
y
5 1
2
5
2
2 5
2
2 2
5
2

 
 
⇒
( )( ) ( 221)( 23)

 
 
⇒
x
⇒

 

⇒ ( )
2 3 2
1 3
2 3 2
2 2
x y
x y
x y
x y
2 5
2 52 1
2 5
2 5 ? 2
2 3 2
2 2 4
2 1 5 2
2
2
x y
x y
2 5
y
y
1
2 52
5
 

2x23?252
2x5216
2x58
x 54
S5{(4,2)}
d)
 2 2
1
3
3 7
1
2
6 3
3
2 2
3
x y
x y
x y
x
x y
x y
x y
x
1
1
5
2
1
5
1
1
5
 
 
⇒
( ) 1
2
1
5
( y
)
1
1
x y
x
x
x
( ) ( )





⇒
2 2
2 3 7
3 7
2 3 7
2 2
3
3 7
1
2
6 3
3
2 2
3
x y
x y
x y
x
x y
x y
x y
x
1
1
5
2
1
5
1
1
5
 
 
⇒
( ) 1
2
1
5
( y
)
1
1
x y
x
x
x
( ) ( )





⇒
2 2
2 3 7
3 7
2 3 7
⇒

⇒ ( ) 
6 3 2 2 0
2 2 3 7
4 0 2
2 7
x y x y
x y x
x y
x y
1 2 2 5
2 2 5
1 5 ?


2 2 5
⇒

⇒ ( ) 
6 3 2 2 0
2 2 3 7
4 0 2
2 7
x y x y
x y x
x y
x y
1 2 2 5
2 2 5
1 5 ?


2 2 5
8 2 0
2 7
7 7
1
x y
x y
x
x
1 5
2 2 5
1
5
5
 

4 ?11y50
y5024
y 524
S5{(1,24)}
2.
x
y
y
x
x
y
y
y
y
x
x
x
1
1
5
1
5
1
1
5
1
1
1
5
1
4
3
1
2
2
4
4
3
3
3
2
2
4 8

 
 
⇒
1
2 5 2
2 1 5
2
3 4
4 2 8





⇒

⇒
x y
x y
x
y
y
x
x
y
y
y
y
x
x
x
1
1
5
1
5
1
1
5
1
1
1
5
1
4
3
1
2
2
4
4
3
3
3
2
2
4 8

 
 
⇒
1
2 5 2
2 1 5
2
3 4
4 2 8





⇒

⇒
x y
x y

256
⇒ ( )  
2 52 ?
2 1 5

⇒
x y
x y
1 2
4 2 8
2 2 2
4 2 8
2 6
3
x y
x y
x
x
2 52
2 1 5
1
2 5
5 2
 


232y521
2y52113
2y52
y 522
a) y 2 x 5 22 2 (23) 5 22 1 3 5 1
b) xy5 23  22 5
3
2 ( ) ( )
c) (x 1 y) (x 2 y) 5 (23 2 2)(23 1 2) 5
5 (25) ? (21) 5 5
3. Fração:
x
y
x
y
x
y
x
y
y
y
x
y
y
y
5
1
5
5
1
5
1
1
7
4
2
3
2
4
4
7
4
2
2 2
3 6
2 2

 
 
⇒
( ) ( )





 

 

2 1 5 2
4 x 2 7 y
5
0
2 x 2 3 y
5 6 ? 2
2
2 52
⇒ ( )
x
y
x
y
x
y
y
y
x
y
y
y
5
1
5
5
1
5
1
1
7
4
2
3
2
4
4
7
4
2
2 2
3 6
2 2

 
 
⇒
( ) ( )





 

4 x 2 7 y
5
0
2 x 2 3 y
5 6 ? 2
2
⇒ ( )
y
y
x
y
y
5
1
5
1
1
7
4
2
3 6
2 2
) ( )
⇒ ( )
 

4 x 2 7 y
5
0
2 x 2 3 y
5 6 ? 2
2
4 7 0
4 6 12
2 1 5 2
12
12
x y
x y
2 5
y
y
1
2 52
5
 

4x27?1250
4x584
x 521

x
y 5
21
12
4. Fração:
x
y
x
y
x
y
x
y
y
y
1
1
5
2
2
5
1
1
5
1
1
2
2
5
6
2
2
1
2
6 12
6 2
5 10
6 2

 
 
⇒
( ) (( )
( ) ( )





⇒
2 4
2 2
2
2 2
6 5 10 12
x y
2
y
y
x y
2 2
x y
5
2
2
2 5 2
2 522214

⇒
x
y
x
y
x
y
y
y
1
1
5
2
2
5
1
1
5
1
1
2
2
5
6
2
2
1
2
6 12
6 2
5 10
6 2

 
 
⇒
( ) (( )
( ) ( )




⇒
2 4
2 2
2
2 2
6 5 10 12
x y
2
y
y
x y
2 2
x y
5
2
2
2 5 2
2 522214

⇒
⇒ ( )
⇒
6 x 2 5 y
52
2
2 x 2 y
5 2 ? 2
3
6 5 2
6 3 6
2 8
2 8
4
x y
x y
y
y
y
1
2 52
5
5
 

2x2452
2x5214
2x56
x 53

x
y 5
3
4
1.
Produto Variação em %
Alimentação
Arroz – tipo 2 (5 kg) 0,95
Feijão carioquinha (1 kg) 0,00
Açúcar refinado (5 kg) 1,58
Café em pó – papel laminado (500 g) 1,25
Farinha de trigo (1 kg) 21,20
Farinha de mandioca torrada (500 g) 21,42
Batata (kg) 21,43
Cebola (kg) 22,01
Alho (kg) 5,12
Ovos brancos (dúzia) 22,84
Margarina (250 g) 25,50
Extrato de tomate (350–370 g) 4,79
Óleo de soja (900 mL) 0,39
Leite em pó integral (400–500 g) 20,75
Macarrão com ovos (500 g) 0,00
Biscoito maisena (200 g) 0,90
Carne de primeira (kg) 2,01
Carne de segunda sem osso (kg) 20,42
Frango resfriado inteiro (kg) 0,52
Salsicha avulsa (kg) 2,84
Linguiça fresca (kg) 0,46
Queijo mozarela fatiado (kg) 0,76
Limpeza
Sabão em pó (1 kg) 21,52
Sabão em barra (unidade) 22,44
Água sanitária (L) 1,12
Detergente líquido (500 mL) 2,67
Higiene pessoal
Papel higiênico fino branco (4 unidades) 21,67
Creme dental (90 g) 22,34
Sabonete (unidade 90–100 g) 0,00
Desodorante spray (90–100 mL) 6,67
Absorvente aderente (10 unid.) 6,85
2.
a) 16 produtos
b) 12 produtos
3.
a) Maior aumento: absorvente aderente R
R 6,85%
b) Maior queda: margarina R
R 25,50%

 


3 2 3 5 0  2
1 26 2
257
4. 2x13157
2x5723
2x54
x 52
Razão
y
1
x 5 2
5
0,5
Alternativa a.
2.
v 2 c
5
c 5
v
5000
0,75

v20,75v55000
0,25v55000
v 5
5000
0,25
v 520000
200002c55000
2c55000220000
2c5 215000
c 515000
 O preço de custo é R$ 15 000,00.
Alternativa c.
3.
5  v p
2 5 2
v p
v p
v p
v p
3 0
2 5
2 52 1
2 26
⇒

⇒ ( )
v2p524
⇒
 

Variação semanal do custo médio
no período de 9/10/2008 a 16/10/2008
Detergente líquido
Salsicha avulsa
Carne de primeira
Alho
( )
( )
,
,
Absorvente aderente
Desodorante spray
Sabonete
Creme dental
Papel higiênico
Sabão em barra
Sabão em pó
Carne de segunda sem osso
Macarrão com ovos
Leite em pó integral
Extrato de tomate
Ovos brancos
Água sanitária
Queijo mozarela fatiado
Linguiça fresca
Frango resfriado inteiro
Biscoito maisena
Óleo de soja
Cebola
Batata
Farinha de mandioca torrada
Farinha de trigo
Margarina
Café em pó
Açúcar refinado
Feijão carioquinha
Arroz – tipo 2
x50,8195⇒x5 ⇒x 5
v 5 3  p
v 3 p
0 1 
⇒
v 2 3 p
5
0
2 5  2
v 2 26 5 p
2
2
v 2 p
52 2 1
26

⇒ ( )
v2p524
⇒
3 0
2 1 5
2 5
1
5
5
v p
v p
p
p
24
2 24
12
 

v5312
v 536
 Há 36 bolas vermelhas na caixa.
Alternativa d.
4.
A 4
B
A B
5
1 5
260

4B1B526
5B5260
B552
A54 52
A5208
Diferença: A 2 B 5 208 2 52 5 156.
A diferença entre os valores das
assinaturas é de R$ 156,00.
Alternativa b.
5.
a)
1 , 46 x 1 109 , y
5
9 ,
48
1 , 53 x 1 103 , y
5
9 ,
71

b)
1 , 46 x 1 109 , y
5 9 , 48 3
103
,
1 , 53 x 1 103 , y
5 9 , 71 32
109
,
 

1 , 5038 x 1 1 , 1227 y
5
9 ,
7644
1 , 6677 x 1 , 1227 y
10 ,
5839
2 2 5 2

 
 
1
20,1639x 520,8195 (321)
0 1639
0 8195
0 1639
, 5
1,46 3 5 1 1,09y 5 9,48 ⇒
7,3 1 1,09y 5 9,48 ⇒ 1,09y 5 9,48 2 7,3
1 09 218
2 ,
18
1 ,
09
y 5 ⇒ y5 ⇒y 5
, , 2
 Noêmia comprou 5 latas de extrato
de tomate e 2 potes de margarina.
1.
x y
x
y
x y
x y
2
1 5
2
2
5
2 1
5
2 1
5
2
3 2
1
2
1
2
2
2 4 3
6
3
6
2 1
2
4
2

 
 
⇒

 

 
⇒
⇒

 

⇒ ( )
2 3 3 4
2 4 1
2 3 7
2 3 1
x y
x y
x y
x y
1 5 1
2 5 2
1 5
2 5  2
2 1 3 5
7
2 3
2 1 5 2
4 4
1
x y
x y
y
y
1
5
5
 

6,00% 4,00% 2,00% 0,00% 2,00% 4,00% 6,00%
8,00% 8,00%

5
258
5. Usando f para massa do frasco e r para
massa do remédio, temos:
f 1 r
5
f r
r
f r
f
1 5
1 5 ? 2
1
5
420
2
235
420 1
2
2
470
2

 
 
⇒
 ( )
 
 

f r
f r
2 2 5 2
1 5
420
2 470

f 550 g
O frasco tem 50 g.
Alternativa e.
6.
1
3
1
1
5
3 2 1
1
y
3 1
3
x y x y
3
y x
x
2 2
x y
5 2
2
2 2
5
2
2
( )

 
 
⇒ ( )( ) ( ) 2
5 2
1
3 2 2
( )

 
 
⇒
y x
1
3
1
1
3 2 1
1
y
3 1
3
x y x y
3
y x
x
2 2
x y
5 2
2
2 2
5
2
2
( )

 
 
⇒ ( )( ) ( ) 2
5 2
1
3 2 2
( )

 
 
⇒
y x
⇒

⇒ ( )  
2 1 52 1
2 1 52
2 1 52 ? 2
2 1 52
x y
x y
x y
x y
3 1
2 3 2
2 2
2 3 2 
2 2 4
2 3 2
2 1 52
2
x y
x y
2 5
y
1
5
 

2x12522
2x52222
2x5 24
x 54

x
y
y
x 2 5 2 5
2
5 5
4
2
2
4
8 2
4
6
4
3
2
Alternativa b.
7. Para x igual a ingresso de não estudante e
y para ingresso de estudante, temos:
x 1 y
5 100 ? ( 2
4
) 8 x 1 4 y
5
620
 

⇒
⇒
 

4 4 400
8 4 620
4 220
2 2 5 2
1 5
1
5
5
55
x y
x y
x
x
x1y5100
551y5100
y5100255
y 545
Foram vendidos 45 ingressos de estudante.
Alternativa a.
8.
a b
a c
1 5
1 5
1 5
b c
a b c
1
1 1 5
1200
1500
1100
2 2 2 3

 
 
800 (;2)⇒a1 b1c51900
Alternativa c.

GEOMETRIA
259
27 – Introdução
28 – A reta
1. São paralelas.
2. São paralelas.
3. Os segmentos são do mesmo
comprimento. As setas nas extremidades
criam a ilusão de que AB é maior que CD.
4. Nenhum.
1. Por um ponto de um plano passam
infinitas retas.
     
, , , , ,
2. 6 semirretas: AB AC BA BC CA CB
10.
a) CD ou GF
b) DF ou CG
c) BD ou AC
29 – Ângulos
Na 1.a figura:
a 5 c 5 d 5 908 1 458 5 1358
b 5 458 1 908 1 458 1 458 5 2258
e 5 1808 1 458 5 2258
Na 2.a figura:
f 5 1358 1 908 5 2258
g 5 458 1 458 5 908
h 5 i 5 j 5 908 1 458 5 1358
1. Um reto e dois agudos.
2.
a) 4 retos.
b) 2 agudos e 2 obtusos.
c) 2 retos, 1 agudo e 1 obtuso.
d) 2 agudos e 2 obtusos.
3. a 1 b 5 1808
17x 2 168 1 7x 1 48 5 1808
17x 1 7x 5 1808 1 168 2 48
24x 5 1928
x 5 88
 a 5 17 ? 88 2 168 5 1368 2 168 5 1208
e b 5 7 ? 88 1 48 5 568 1 48 5 608
4. 408 1 x 5 908 ⇒ x 5 908 2 408 ⇒ x 5 508
2y 1 158 1 408 1 508 1 y 5 1808 ⇒
⇒ 2y 1 y 5 1808 2 158 2 408 2 508 ⇒
⇒ 3y 5 758 ⇒ y 5 258
5.
a) 208 1 x 1 408 5 908
x 5 908 2 208 2 408
x 5 308
b) x 1 68 1 x 5 908
x 1 x 5 908 2 68
2x 5 848
x 5 428
arte
de A
Editoria ⇒ 4 cm B
C
3. Por dois pontos distintos de um plano
passa uma única reta.
4. Concorrentes (se a intersecção for com
um único ponto) ou coincidentes (se a
intersecção for com todos os pontos).
5.
a) 5 b) 6 c) 4
6.
a) 12 b) 9
7. med MN
x y
( )5
1
2
8. 6 segmentos (AB, AC, AD, BC, BD,CD)
9.
a) C externo a AB: med (AC) 5 11 1 7 5 18 ⇒
⇒ 18 cm
b) C interno a AB: med (AC) 5 11 2 7 5 4 ⇒

260
c) 4x 1 4x 1 x 1 908 5 3608
4x 1 4x 1 x 5 3608 2 908
9x 5 2708
x 5 308
d) 608 1 x 1 808 5 1808
x 5 1808 2 608 2 808
x 5 408
e) 12x 1 108 1 5x 5 1808
12x 1 5x 5 1808 2 108
17x 5 1708
x 5 108
f) x
x x o
2
1 13 590
x 1 x 1
x o 5
2 6
2
180
2
9x 5 1808
x 5 208
g) x 1 x 1 1008 1 2x 1 x 1 1108 5 3608
x 1 x 1 2x 1 x 5 3608 2 1008 2 1108
5x 5 1508
x 5 308
h) x 1 1268 1 2x 5 1808
x 1 2x 5 1808 2 1268
3x 5 548
x 5 188
6. (2x 1 208) 1 (x 1 408) 1 (2x 2 508) 1
1 (3x 2 908) 5 3608
2x 1 x 1 2x 1 3x 5
5 3608 2 208 2 408 1 508 1 908
8x 5 4408
x 5 558
 Os ângulos medem:
(2x 1 208)5 (2  55 1 208) 5 1308
(x 1 408) 5 (55 1 408) 5 958
(2x 1 508) 5 (2  558 2 508) 5 608
(3x 2 908) 5 (3  558 2 908) 5 758
Respostas em aberto. O aluno pode traçar
o ângulo em qualquer posição.
1. x
o o
50
2
70
2
o o o 5 1 5 1 5
25 35 60

2. OB
é bissetriz de AÔC ⇒ y 5 238
 208 1 x 1 238 1 238 5 1808 ⇒
⇒ x 5 1808 2 208 2 238 2 238 ⇒
⇒ x 5 1148

3. OM
é bissetriz de CÔD ⇒ x 5 388
 y 1 388 1 388 1 y 2 308 5 1808 ⇒
⇒ y 1 y 5 180o 2 38o 2 38o 1 30o
2y 5 1348
y 5 678

4. PN
é bissetriz de BPC ⇒ x 5 8y

PM
é bissetriz de APB⇒MPB5y
 8y 1 x 1 y 1 y 5 180o ⇒
⇒ x 1 10y 5 1808
x 5 8y
x 1 10y 5 1808 ⇒ 8y 1 10y 5 1808 ⇒
⇒ 18y 5 1808
y 5 108
x 5 8y ⇒ x 5 8  108 5 808
1. 508 1 x 5 908
x 5 908 2 508
x 5 408
2. x 1 508 5 1808 ⇒ x 5 1308
y 1 1008 5 1808 ⇒ y 5 808
3.
a) 908 2 358 5 558
b) 908 2 428 5 488
c) 908 2 228 30’ 5 678 30’
d) 908 2 698 40’ 5 208 20’
4.
a) 1808 2 758 5 1058
b) 1808 2 828 30’ 5 978 30’
c) 1808 2 1358 5 458
d) 1808 2 1298 50’ 5 508 10’
5. x 5 (908 2 x) 1 708
x 1 x 5 908 1 708
2x 5 1608
x 5 808
6. x
o x x o x
5
180 2
2
5
3
3
3
180
3
⇒
3x 1 x 5 1808
4x 5 1808
x 5 458
7. x 5 4  (908 2 x)
x 5 3608 2 4x
x 1 4x 5 3608
5x 5 3608
x 5 728
8. 3x 5 2  (1808 2 x)
3x 5 3608 2 2x
3x 1 2x 5 3608
5x 5 3608
x 5 728
9. 1808 2 x 5 4  (908 2 x)
1808 2 x 5 3608 2 4x

261
2x 1 4x 5 3608 2 1808
3x 5 1808
x 5 608
10.
 

x y
x y
o
o
90
1 5
5 1
2 30
⇒⇒
 

x y
x y
x
x
o
o
1 5
2 5
o
o
1
5
5
90
2 30
3 120
40
408 1 y 5 908 ⇒ y 5 908 2 408 ⇒ y 5 508
11.
x y
x y x y
x y
x y
o
1 5 o
5 5
1 5 ?
2 5
180
7 5
5
35
7
35
180 7
⇒ 5 7

 
 
⇒ ( )
0
 

⇒
⇒
 

x y
x y
x
x
7 1 7 5
1 260
5 2 7 5
0
12 1 260
105
o
o
o
1
5
5
1058 1 y 5 1808
y 5 1808 2 1058 ⇒ y 5 758
1. Latitude: 218 40’ a 218 43’ Sul
Longitude: 438 52’ a 438 54’ Oeste
2. 90
270 90 270 270
5 5 5 53 t
90
t
t t
⇒ ⇒t horas
3.
b) x 5 y
x 1 408 5 1808
x 5 1808 2 408
x 5 1408
 x 5 y 5 1408
Distância (em km) do
Parque Estadual de Ibitipoca
Brasília
Vitória
São Paulo
Belo Horizonte
Rio de Janeiro
Juiz de Fora
0
200 400 600 800 1000 1200
4. A maior altitude é 1 784 m.
5. 218 40’ 2 208 19’ 5 18 21’ Sul
438 52’ 2 418 43’ 5 28 9’ Oeste
6. É o terceiro pico mais alto do país.
1.
a) x 5 808
y 1 808 5 1808
y 5 1808 2 808
y 5 1008
2. x 5 z
y 5 408
x 1 408 5 1808
x 5 1808 2 408
x 5 1408
x 5 z 5 1408
y 5 408
3.
a) 2x 2 1008 5 x 1 308
2x 2 x 5 308 1 1008
x 5 1308
1308 1 308 1 y 5 1808
y 5 1808 2 1308 2 308
y 5 208
b)
x y
x y
x
x
o
o
o
1 5
2 5
o
1
5
5
100
80
2 180
90

 
 
908 1 y 5 1008
y 5 1008 2 908
y 5 108

4. OM
bissetriz de AÔB ⇒ med (AÔB) 5 2x
2x 5 488
x 5 248
5. x
x o
1 5180
x x o 1
3
5
3
3
540
3
4x 5 5408
x 5 1358
135
3
o
 med (AMD) 5 458
med (AMC)5135o
med (BMC)545o
med (BMD)5135o
1. di 60 – fr 25 – di 50 – fr 18 – es 120 – fr 20 –
– di 130 – fr 60
2. Possível resposta: di 30 – fr 80 – di 120 –
– fr 80 – di 120 – fr 80.
c) x 5 708
708 1 y 5 1808
y 5 1808 2 708
y 5 1108
Editoria de arte

262
ÂNGULOS FORMADOS POR DUAS RETAS
PARALELAS COM UMA reta TRANSVERSAL
30 – Reta transversal
a) 3ˆ , 4ˆ , 5ˆ e 6ˆ
b) 1ˆ, 2ˆ , 7ˆ e 8ˆ
c) 1ˆ, 4ˆ , 5ˆ e 8ˆ ou 2ˆ , 3ˆ , 6ˆ e 7ˆ
d) 1ˆ e 5ˆ ou 2ˆ e 6ˆ
e) 3ˆ e 7ˆ ou 4ˆ e 8ˆ
31 – Ângulos correspondentes
32 – Ângulos alternos
33 – Ângulos colaterais
1.
a) o.p.v.: mˆ e nˆ ou pˆ e qˆ .
b) adjacentes suplementares:
pˆ e oˆ ou oˆ e qˆ .
c) correspondentes: mˆ e pˆ ou nˆ e qˆ .
d) alternos internos: nˆ e pˆ .
e) alternos externos: mˆ e qˆ .
f) colaterais internos: nˆ e oˆ .
2.
a) o.p.v.
b) adjacentes suplementares
c) correspondentes
d) correspondentes
e) alternos internos
f) colaterais internos
3.
a) 3x 5 1358
x 5 458
b) x 1 258 5 758
x 5 758 2 258
x 5 508
c) 3x 2 458 5 x 1 458
3x 2 x 5 458 1 458
2x 5 908
x 5 458
d) (x 2 1008) 1 (x 1 408) 5 1808
x 1 x 5 1808 1 1008 2 408
2x 5 2408
x 5 1208
4. a 5 758 (alternos internos)
c 5 558 (alternos internos)
758 1 b 1 558 5 1808 ⇒
⇒ b 5 1808 2 758 2 558 ⇒ b 5 508
5.
a) 708 1 a 5 1808
a 5 1808 2 708
a 5 1108
b) 1528 1 a 5 1808
a 5 1808 2 1528
a 5 288
6. 5x 1 208 5 2x 1 508
5x 2 2x 5 508 2 208
3x 5 308
x 5 108
7. 2
3
15
x
x o 5 2
x x o
2
3
3 45
3
5
2
2x 2 3x 5 2458
2x 5 2458
x 5 458
b x o
o
2
3
2
3
o 5 5  5 5
45
90
3
30
x 2 158 1 a 5 1808
458 2 158 1 a 5 1808
a 5 1808 2 458 1 158
a 5 1508
8. x
y
5 x y z
o
5
o
o
1 1 5
60
40
180
 

⇒
9.
a) a 5 558
b 5 558
c 5 1808 2 558 5 1258
b) a 5 1808 2 1408 5 408
b 5 1408
c 5 408

263
c) a 5 1808 2 1308 5 508
c 5 708
508 1 b 1 708 5 1808
b 5 1808 2 508 2 708
b 5 608
d) a 5 1808 2 1058 5 758
b 5 408
c 5 408
10.
a) a 5 1208
b 5 1808 2 1208 5 608
d 5 1808 2 1308 5 508
e 5 508
608 1 c 1 508 5 1808 ⇒
⇒ c 5 1808 2 608 2 508 ⇒ c 5 708
b) a 5 1808 2 1358 5 458
b 5 608
c 5 1358
458 1 d 1 608 5 1808 ⇒
⇒ d 5 1808 2 458 2 608 ⇒ d 5 758
e 5 758
11. (3x 2 508) 1 (2x 2 108) 5 1808
3x 1 2x 5 1808 1 508 1 108
5x 5 2408
x 5 488
3x 2 508 5 3  488 2 508 5 1448 2 508 5 948
2x 2 108 5 2  488 2 108 5 968 2 108 5 868
Os ângulos medem 948 e 868.
12. 4 ângulos medem 558 e 4 ângulos medem
1258.
13. x 5 308
y 5 1808 2 1308 5 508
 x 1 y 5 308 1 508 5 808
14. x 5 (1808 2 1608) 1 708
x 5 208 1 708
x 5 908
15.
a) m 5 (1808 2 1408) 1 (1808 2 1508)
m 5 408 1 308
m 5 708
b) m 5 408 1 (1808 2 1388)
m 5 408 1 428
m 5 828
16. (2m 1 308) 5 (3m 2 208)
2m 2 3m 5 2208 2 308
2m 5 2508
m 5 508
17.
x y
x y
x
x
1 5 8
2 5 8
1
5 8
5 8
180
20
2 200
100



 
1008 1 y 5 1808
y 5 1808 2 1008
y 5 808
18. Cada ângulo agudo mede 1928  4 5 488.
 x 5 y 5 180 2 488 5 1328
1.
a) a 5 e
b 5 f
 b 1 d 5 1808 ⇒
⇒ 3x 1 108 1 9x 2 108 5 1808
3x 1 9x 5 1808 2 108 1 108
12x 5 1808
x 5 158
b) a 5 2x 1 58 5 2  158 1 58 5 308 1 58 5 358
b 5 3x 1 108 5 3  158 1 108 5 458 1 108 5 558
c)
a e
b f
5 a 1 b 1 c 5 e 1 f 1 c 5
o
5

⇒ 180
2. BÂC – agudo; ABˆ C – agudo; ACˆ B – reto
3. Complementares.
1. b 5 c 5 328
 a 5 908 2 328 5 588
Alternativa a.
2.
1
2
x 2x 135o 180o 1 1 5
x x o o 1 1
5
4 270
2
360
2
x 1 4x 5 3608 2 2708
5x 5 908
x 5 188
Alternativa d.
3. 3x 2 118 5 2x 1 68
3x 2 2x 5 68 1 118
x 5 178
y 1 (2x 1 68) 5 1808
y 1 (2  178 1 68) 5 1808
y 1 408 5 1808
y 5 1808 2 408
y 5 1408
Alternativa c.

264
4.
o 1 5
5
x y
x y
180
3

⇒
⇒ 3y 1 y 5 1808
4y 5 1808
y 5 458
x 5 3  458
x 5 1358
x 2 y 5 1358 2 458 5 908
Alternativa a.
5. y 5 1808 2 1258 5 558
x 1 558 5 908
x 5 908 2 558 5 358
 y 2 x 5 558 2 358 5 208
Alternativa e.
6. z 5 1808 2 1278 5 538
x 5 y 5 428
 x 1 y 1 z 5 428 1 428 1 538 5 1378
Alternativa c.
7. 2x 1 4x 5 1208
6x 5 1208
x 5 208
4x 1 y 51808
4  20 1 y 5 1808
y 5 1808 2 808
y 5 1008
Alternativa a.
8. x 1 z 5 1808
y 1 508 1 z 5 1808 ⇒ y 1 z 5 1808 2 508 ⇒
⇒ y 1 z 5 1308
Somando (x 1 z) 1 (y 1 z) 5 1808 1 1308 ⇒
⇒ x 1 y 1 2z 5 3108
x 1 2 1 2 z
5 340
8
x 1 y 1 2 z
5 310 8 ? ( 2
1)

⇒
⇒
 

2 2 340
x y z
x y z
1 1 5
2 2 2 5
y
o
o
o
1
5
2 310
30
Alternativa a.
9. 3ˆ 51ˆ 12ˆ ⇒(med Bˆ )545o155o5100o
Alternativa c.
10. Se med (DÂC) 5 x, então med (BÂC) 5 2x.
med (DÂC) 1 med (BÂC) 5 908 ⇒
⇒ x 1 2x 5 908 ⇒ 3x 5 908 ⇒
⇒ x 5 308
 a 5 608 e b 5 308
Logo: a 2 b 5 608 2 308 5 308.
Alternativa c.

265
34 – O polígono e seus elementos
1.
Quadriláteros
N de peças do tangram Triângulos Quadrados Retângulos Paralelogramos Trapézios
4 peças
5 peças
6 peças não é possível não é possível o retângulo ao lado
7 peças
POLÍGONOS
2.
pentágono hexágonos
3.
1.
a) Retângulos e trapézios.
b) Retângulos: 9; trapézio: 1.
c) Um deles tem 5 lados e o outro tem
6 lados.
2. Barsotti: triângulos e losango.
Sued: retângulos e trapézios.
4. Sugestões para pesquisa: Aluísio Carvão,
Hélio Oiticica, Lygia Clark, Lygia Pape,
Frans Weissmann, Willys de Castro, entre
outros.
35 – Perímetro de um polígono
1. P  2  1,3  1,3  2  1,3  1,3  9,2 ⇒
⇒ 9,2 cm
2. P  8x
8x  180 ⇒ x  22,5 ⇒ 22,5 cm
3. P  12,5 cm  8,5 cm  9 cm
P  30 cm
4. P  6,70  3,80  4,50  5,00  20 ⇒ 20 m
Custo: 20  2,50  50
Deverei gastar: R$ 50,00.
1. 2.
36 – Diagonais de um polígono
1.
a) Triângulo.
b) Quadrilátero.
2. n  3  15 ⇒ n  18
O polígono tem 18 lados.
3.
Número de lados do polígono 8 15 20 28
Número de diagonais d1 d2 d3 d4
d1
 ( )
8  8 
3
2
8 5
2
 
20

d2
 ( )
15  15 
3
2
15 12
2
 
90

d3
 ( )
20  20 
3
2
20 17
2
 
170

d4
 ( )
28  28 
3
2
28 25
2
 
350

Editoria de arte
Editoria de arte
Editoria de arte
Hexágono

266
60
6
10⇒10
4. n5 5 lados
35 35 ( ) ⇒
? 2
d5 5
diagonais
?
5
10 10 3
2
10 7
2
5.
a)
n ( n
2 3
) n ( n 3
) 5
n
⇒ 2
2
n
2
5
⇒
2
2
⇒n223n52n
n (n23)52n
n2352
n55
 Pentágono
b)
n ( n
2 3
) n ( n 3
) 5
4
n
⇒ 2
8
n
5
⇒
2
2
2
⇒n2358
n511
 Undecágono
6. n 5 9
d5
( 2
)
?
5
5 5
27 9 9 3
2
9 6
2
54
2
 n ? d 5 9 ? 27 5 243
37 – Ângulos de um polígono
convexo
1.
a) m 1 c 5 1808
b) a 1 b 1 c 5 1808
2.
a) x 1 608 1 608 5 1808
x 5 1808 2 608 2 608
x 5 608
b) 2x 1 x 1 908 5 1808
3x 5 1808 2 908
3x 5 908
x 5 308
c) x 1 108 1 x 1 208 1 x 1 308 5 1808
x 1 x 1 x 5 1808 2 108 2 208 2 308
3x 5 1208
x 5 408
d) x 1 x 1 1508 5 1808
2x 5 1808 2 1508
2x 5 308
x 5 158
e) 4x 1 5x 1 3x 5 1808
12x 5 1808
x 5 158
f) x o x o o o 126 1 1(180 2110 )5180
x x o o o o 1 5 180 226 2180 1110
2x 84o 5
x o 542
3. 818 1 288 1 x 5 1808
x 5 1808 2 818 2 288
x 5 718
4. b 5 1808 2 1358 5 458
c 5 1808 2 1588 5 228
a 1 458 1 228 5 1808
a 5 1808 2 458 2 228
a 5 1138
5. c 1 608 1 568 5 1808
c 5 1808 2 608 2 568
c 5 648
b 5 c
 b 5 648
a 5 568
6. med (Mˆ )5100o
med (Pˆ )5180o2125o555o
x 1 1008 1 558 5 1808
x 5 1808 2 1008 2 558
x 5 258
7. a 5 2b 5 2 ? (3c) 5 6c
b 5 3c
 6c 1 3c 1 c 5 1808
10c 5 1808
c 5 188
8. x 5 288 1 468 5 748 ou a 1 x 1 b 5 1808
Onde 908 1 468 1 a 5 1808
 a 5 1808 2 908 2 468 ⇒ a 5 448
e 908 1 288 1 b 5 1808
b 5 1808 2 908 2 288 ⇒ b 5 628
448 1 x 1 628 5 1808
x 5 1808 2 448 2 628
x 5 748
9. 348 1 a 1 x 5 1808
a 5 1808 2 348 2 x
a 5 1468 2 x
638 1 b 1 y 5 1808
b 5 1808 2 638 2 y
b 5 1178 2 y
Como a 5 b:
1178 2 y 5 1468 2 x
x 2 y 5 1468 2 1178
x 2 y 5 298

o
o 22 ?180 51 440 225 2 5 5
( ) ⇒ ⇒ 2 8⇒ 10
o
o 22 ?180 51 800 225 2 5 5
( ) ⇒ ⇒ 2 10⇒ 12
o
o 22 ?180 52160 225 2 5 5
( ) ⇒ ⇒ 2 12⇒ 14
o
o 22 ?180 52 340 225 2 5 5
( ) ⇒ ⇒ 2 13⇒ 15
o o o o
n o
o 15 15
267
10.
x y
z w
o o
1 1 5
1 1 5
o o
1
20 180
30 180
 

x1y1z1w120o130o5180o1180o
x y z w o o o o 1 1 1 5180 1180 220 230
x y z w o 1 1 1 5310
11. c 5 458
b 1 958 5 1808 ⇒ b 5 1808 2 958 ⇒ b 5 858
 b 2 c 5 858 2 458 5 408
12.
x y
x y
o o
90 180
18
1 1 5
2 5
o
 

⇒
⇒
 

x y
x y
x
x
90
90
1 5 8
2 5 8
1
2 108
5 8
5 8
54
54o1y590o
y o o 590 254
y o 536
Polígono No de lados
No de triângulos na
decomposição
Soma dos ângulos
internos
o
22 ?180 51 440 225 2 5 5
o ( ) ⇒ ⇒ 2 8⇒ 10
Quadrilátero 4 2 3608
Pentágono 5 3 5408
Hexágono 6 4 7208
Heptágono 7 5 9008
Octógono 8 6 1 0808
Eneágono 9 7 1 2608
o
o 22 ?180 51 800 225 2 5 5
( ) ⇒ ⇒ 2 10⇒ 12
o
o 22 ?180 52160 225 2 5 5
( ) ⇒ ⇒ 2 12⇒ 14
1. n 2 2 5 8 ⇒ n 5 8 1 2 5 10 ⇒ 10 lados
Decágono
2.
o
o 22 ?180 52 340 225 2 5 5
( ) ⇒ ⇒ 2 13⇒ 15
Polígono Pentágono Eneágono Icoságono
Soma das medidas
dos ângulos internos
S1 S2 S3
o o o o
n o
S1 5 (5 2 2) ? 1808 5 3 ? 1808 5 5408
S2 5 (9 2 2) ? 1808 5 7 ? 1808 5 1 2608
S3 5 (20 2 2) ? 1808 5 18 ? 1808 5 3 2408
3. n o o ( 22)?180 51 620
180o ?n2360o51 620o
180on51 620o1360o
180on51 980o
n
o
o 5
1 980
180
n511⇒11lados
Undecágono
4. Si Se o 1 51 080
Si o o 51 080 2360
Si o 5720
n o o ( 22)?180 5720
n
o
o 225
720
180
n2254⇒n56⇒6 lados
Hexágono
5. S5 5 5408
 2x 1 3x 1 1508 1 1358 1 1208 5 5408
2x 1 3x 5 5408 2 1508 2 1358 2 1208
5x 5 1358
x 5 278
med (EAˆ B)52x52?27o554o
med (ABˆ C)53x53?27o581o
6.
Soma das medidas
dos ângulos
internos
1 4408 1 8008 2 1608 2 3408
Número de lados
do polígono
10 12 14 15
1 440
180
n o o n n n
1 440
180
n o o n n n
1 800
180
n o o n n n
1 800
180
n o o n n n
2160
180
n o o n n n
2160
180
n o o n n n
2 340
180
n o o n n n
2 340
180
n o o n n n
7. 24
360 24 360 360
24
n
n n
5 ⇒ 5 ⇒n5 ⇒n5 ⇒ lados
24
360 24 360 360
o 15 15
24
n
n n
5 ⇒ 5 ⇒n5 ⇒n5 ⇒ lados
90 90 ( ) ⇒
? 2
d5 5
diagonais
?
5 5
15 15 3
2
15 12
2
180
2
90 90 ( ) ⇒
? 2
d5 5
diagonais
?
5 5
15 15 3
2
15 12
2
180
2
38 – Ângulos de um polígono
regular
Resposta em aberto.

268
1.
a) Si 5 (8 2 2) ? 1808 5 6 ? 1808 5 1 0808
o
b) Ai
1 080
8
360
o 5 5
135
c) Se 5 3608
d) Ae
o
360
8
o 5 5
45
2.
36 ⇒36 360 ⇒ 10⇒10  Decágono regular
a) Si 5 (6 2 2) ? 1808 5 4 ? 1808 5 7208
b) Se 5 3608
c) Ai 5
720
6
8
5 8
120
d) Ae
5 ⇒ 5 360 ⇒ 5 o
Se
n
o
Ae Ae
6
60
3. Triângulo: Ai 5 608 ⇒ Ae 5 1808 2 608 5 1208
Octógono: Ai 5 1358 ⇒ Ae 5 1808 2 1358 5 458
 x 5 1208 1 458 5 1658
4. n 2 3 5 5 ⇒ n 5 8
a) Si 5 (8 2 2) ? 1808 5 6 ? 1808 5 1 0808
o
b) Ai
1080
8
o 5 5
135
5. Si o o o 5(522)?180 53?180 5540
o
540
5
o o 5 5 5
Ai y
108  108
x 1 x 1 1088 51808
2x 5 1808 2 1088
2x 5 728
x 5 368
 y 2 x 5 1088 2 368 5 728
6. (n ) o o 22 ?180 54 ?360
(n ) o o 22 ?180 51 440
n
o
o 225
1 440
180
n2258
n510
 Decágono
7. Ângulo interno do pentágono: Ai 5 1088.
No triângulo:
x 1 (1808 2 1088) 1 (1808 2 1088) 5 1808
x 1 728 1 728 5 1808
x 5 1808 2 728 2 728
x 5 368
8. Ângulo externo do hexágono: Ae
o
360
6
o 5 5
60
Ae
o
360
6
o 5 5
60
Ângulo externo do octógono: Ae
o
360
8
o 5 5
45
 x 5 608 1 458 5 1058
1. Ae
360
n
36 ⇒36 360 ⇒ 10⇒10
n n lados
o
o o o 5 5 5 5
Ae
n
n n lados
o
o o o 5 5 5 5
2. Caminhou: 10 ? 120 m 5 1 200 m ou 1,2 km.
3. 1200
8
?115150?1151650 ⇒1650 passos
1.
a) Maior produção: março de 2007.
Maior quantidade vendida: dezembro
de 2006.
b) Dezembro de 2006 a janeiro de 2007.
c) Junho a julho de 2006 e outubro a
dezembro de 2006.
2.
a) Área de desmatamento (km2)
10 000
km2
Estados
8 000
6 000
4 000
2 000
0
Acre Amazonas Pará Mato
Grosso
Rondônia
2006 2007
b) Pará
Aumento: 5 400 – 2 700 5 2 700
Taxa de aumento:
2700
2700
5 1 5
100
100
5 100%
c) Acre
Redução: 400 – 200 5 200
Taxa de redução:
200
400
5 0,50 5
5
0 50 100
100
50
100
, ?
5 5 50%
1. P 5 3,9 cm 1 5,3 cm 1 5,0 cm 1 x 1 x 5 22,6 cm
x 1 x 5 22,6 cm 2 3,9 cm 2 5,3 cm 2 5 cm
2x 5 8,4 cm
x 5 4,2 cm
Alternativa d.
2. P 5 4 ? 62 cm 1 4 ? 40 cm 5
5 248 cm 1 160 cm 5 408 cm
 P 5 4,08 m
Alternativa a.
3. n 2 3 5 9 ⇒ n 5 9 1 3 ⇒ n 5 12 ⇒ 12 lados
Alternativa c.
4. d5
54 ( ) ⇒ 54
? 2
5
?
5 5
12 12 3
2
12 9
2
108
2
diagonais
Alternativa a.
Editoria de arte

⇒ 2 12⇒ 12 2⇒ 14
⇒ ⇒ 15⇒15
360 60 360 360
⇒ ⇒ ⇒ 6 Ae
269
5. d5
44 ( ) ⇒ 44
? 2
5
?
5 5
11 11 3
2
11 8
2
88
2
diagonais
Alternativa c.
6. d5
9 ( ) ⇒ 9 diagonais
? 2
5
?
5
6 6 3
2
6 3
2
Total: diagonais 1 lados 5 9 1 6 5 15
 Serão 15 estradas.
Alternativa b.
7. 3x 1 x 1 6x 5 1808
10x 5 1808
x 5 188
Maior ângulo: 6x 5 6 ? 188 5 1088
Alternativa e.
8. 50
2
3
o1x1 x5180o
150 3 2
o1 x1 x o
3
540
3
5
3x 2x 540o 150o 1 5 2
5x 390o 5
x o 578
Alternativa d.
o
o 225 2 5 5 1 5
2160
180
9. x 1 (1808 2 1008) 1 (1808 2 1108) 5 1808
x 1 808 1 708 5 1808
x 5 1808 2 808 2 708
x 5 308
Alternativa c.
10. a 1 a 1 508 5 1808
360
a 1 a 5 1808 2 508
2a 5 1308
a 5 658
b 5 1808 2 658
b 5 1158
 b 2 a 5 1158 2 658 5 508
Alternativa e.
11. x 5 418 1 748
x 5 1158
x 1 y 5 1808
y 5 1808 2 1158
y 5 658
 x 2 y 5 1158 2 658
x 2 y 5 508
Alternativa e.
12. 858 5 458 1 x ⇒ x 5 858 2 458 5 408
Alternativa a.
13.
x 1 y 5
4
m
y 1 m 5 m y 5 m 2 m y 5
m
2 5 ⇒ 5 2 ⇒ 3

Substituindo na 1.a equação, temos:
x 1 3m 5 4m
x 5 4m 2 3m
x 5 m
Alternativa d.
14. (n ) o o 22 ?180 52160
o
o 225 2 5 5 1 5
2160
180
n n n n
⇒ 2 12⇒ 12 2⇒ 14 ⇒ 14 lados
n n n n
Alternativa a.
15. S6 5 (6 2 2) ? 1808 5 4 ? 1808 5 7208
x 1 x 1 1608 1 x 1 x 1 1608 5 7208
x 1 x 1 x 1 x 5 7208 2 1608 2 1608
4x 5 4008
x 5 1008
Alternativa b.
16. A
o
o
360
24
360 24 360
n n
o o o
n
n
n lados e
o 5 5 5 5 5
24
A
o
o
24
360 24 360
⇒ ⇒ 15⇒15
n n
o o o
n
n
n lados e
o 5 5 5 5 5
24
d5
? 2
5
?
5 5
15 15 3
2
15 12
2
180
2
90
( )
⇒ 90
diagonais
Alternativa a.
17. ai 5 1208 ⇒ ae 5 608
Ae
n o
360
60
n n
n
n n
o
o o o o
o 5 5 5 5 5
60
360
⇒ 60
⇒ ⇒ 6 ⇒6 os
360 60 360 360
n n
n
n n
n lad
o
o
o o o o
o 5 5 5 5 5
60
Alternativa b.
18. S o o o
5(622)?180 54 6 ?180 5720
o
Ai
720
6
o 5 5
120
x o o o 5120 290 530
Alternativa d.

270
Estudando os triângulos
39 – Elementos de um triângulo
1. Triângulo.
2.
a) 1 d) 2
b) 2, 3 e 4 e) 4
c) 5
3.
400
m2
a) A1 5 A2 5 5
2
200 m2
600
m2
B1 5 B2 5 5
2
300 m2
500
m2
C1 5 C2 5 5
2
250 m2
b) Forma triangular.
40 – Condição de existência
de um triângulo
2.
a) Sim, nos itens b e c.
b) Poderá ter medidas que variam de 2 a
8 cm, ou seja, 2, 3, 4, 5, 6, 7 ou 8 cm.
1.
a) Sim. d) Não (7 5 5 1 2).
b) Sim. e) Não (15 8 1 6).
c) Sim. f) Sim.
2.
a) BC b) AB c) ˆB
3. Não é possível, pois 120 cm 70 cm 1 48 cm.
4. As possíveis medidas do 3.o lado são 8 cm
ou 9 cm.
5. A medida mínima para o 3.o lado deve ser
4 cm.
6. Como as medidas de dois lados são 7 cm
e 4 cm, a medida do terceiro lado deve ser
um valor entre 4 cm e 10 cm.
7. O maior lado pode medir 10 cm ou 11 cm.
Mínima: 24 km (maior que 55 2 32 5 23).
Máxima: 86 km (menor que 55 1 32 5 87).
41 – Os ângulos no triângulo
1. a 1 b 5 180° (externo e interno são
suplementares).
a 5 c 1 d (externo é a soma dos internos
não adjacentes).
b 1 c 1 d 5 180° (soma dos internos de um
triângulo qualquer).
2.
a) BC b) PN
3. med(Pˆ )5med(Mˆ )1med(Nˆ )
117° 5 72° 1 med N ( ˆ )
117° 2 72° 5 med N ( ˆ )
 med N ( ˆ ) 5 45°
4.
x
x o o
2
1 278 5135
x 1 x 2
o o 5
2 156
2
270
2
x 1 2x 5 270° 1 156°
3x 5 426°
x 5 142°
 med B
x o
142
2
( ˆ )5 2
5 5 71
o 5.
a) x 1 x 5 130°
2x 5 130°
x 5 65°
b) x 1 90° 5 160°
x 5 160° 2 90°
x 5 70°
6. x 1 x 2 20° 5 116°
x 1 x 5 116° 1 20°
2x 5 136°
x 5 68°
med (Aˆ )5180o2116o564o
med(Bˆ )5x568o
med(Cˆ )5x220o568o220o548o

271
7. x  60°  2x  10°
x  2x  10°  60°
x  50°
x  50°
8. (180°  a)  (180°  b)  (180°  70°)  180°
ab 180o 180o 180o180o70o
a  b  290° ( 1)
a  b  290°
a  b

10
o

a  b

290
o
 

2a  300°
a  150°
150°  b  290°
b  290°  150°
b  140°
42 – Classificação dos triângulos
a) Retângulo, escaleno.
b) Acutângulo, equilátero.
c) Acutângulo, isósceles.
d) Obtusângulo, isósceles.
e) Obtusângulo, escaleno.
1.
a) Escaleno.
b) Isósceles.
c) Equilátero.
d) Isósceles.
2.
a) Obtusângulo.
b) Retângulo.
c) Acutângulo.
3. x  x  x  18 cm ⇒ 3x  18 cm ⇒ x  6 cm
Os lados medem 6 cm.
4.
a) Equilátero e acutângulo.
b) Escaleno e retângulo.
c) Isósceles e acutângulo.
d) Isósceles e obtusângulo.
5.
a) Se o triângulo é isósceles, o 3.o lado
deve medir 5 cm ou 7 cm.
b) Se o 3.o lado for 5 cm:
P  5 cm  5 cm  7 cm  17 cm
Se o 3.o lado for 7 cm:
P  5 cm  7 cm  7 cm  19 cm
6. (x  3)  (x  3)  x  15,6
x  x  x  15,6  3  3
3x  9,6
x  3,2 ⇒ 3,2 cm
7. x  y, pois ambos são ângulos da base.
Alternativa d.
1.
2. 16 pequenos
7 médios
3 grandes
1 maior
Total: 27 triângulos
43 – Altura, mediana e bissetriz
de um triângulo
1. med(AB)3,5cm
2. Todos os triângulos traçados têm a
mesma altura relativa ao lado AB: 6,1 cm.
3.
a) Menor perímetro: AFB.
b) Maior perímetro: ACB e AIB.
1.
• O ângulo será de 90.
•
O
2.
•
C
• Sim.
Editoria de arte
Editoria de arte Editoria de arte

272
o o
1y1 5 o
A
x
60° 20°
B C
H
3.
•
6. No ABC, temos:
x 1 60° 1 40° 5 180°
x 5 180° 2 60° 2 40°
x 5 80°
No triângulo que contém y, temos:
60
40
180
2
2
30° 1 y 1 20° 5 180°
y 5 180° 2 30° 2 20°
y 5 130°
7. No triângulo que contém a, temos:
35° 1 a 1 30° 5 180°
a 5 180° 2 35° 2 30°
a 5 115°
a e c são suplementares:
115° 1 c 5 180°
c 5 180° 2 115°
c 5 65°
No triângulo que contém b, temos:
35° 1 b 1 65° 5 180°
b 5 180° 2 35° 2 65°
b 5 80°
8.
G
I
• A razão é
1
2 .
4.
• a e b.
• Sim.
1.
a) Mediana.
b) Altura.
c) Mediana.
d) Bissetriz.
e) Altura.
f) Altura, bissetriz e mediana.
2. P 5 6 cm 1 8 cm 1 4 cm 1 4 cm 5 22 cm
3. x 1 70° 5 90°
x 5 90° 2 70°
x 5 20°
y 1 40° 5 90°
y 5 90° 2 40°
y 5 50°
4. 35o145o1med(Mˆ )5180o
med(Mˆ )5180o235o245o
med(Mˆ )5100o
o
 med PMA
100
2
( ˆ )5 5 50
o
5. a 1 60° 1 90° 5 180°
a 5 180° 2 60° 2 908
a 5 30°
b 5 a 5 30°
b 1 c 1 90° 5 180°
30° 1 c 1 90° 5180°
c 5 180° 2 30° 2 90°
c 5 60°
med (Aˆ )5180o260o220o5100o
med(BAˆH)5180o290o260o530o
med ( A
ˆ )
 x
5 2med ( BAH
ˆ )
2
x
o
100
2
o o o o 5 2 5 2 5
30 50 30 20
9. ABM:
o med A o ( ˆ )
med B
( ˆ )
190 1 5
2
180
med B o
o
80
2
( ˆ )190 1 5 180
o
med(Bˆ )5180o290o240o
med (Bˆ )550o
O mesmo se aplica para med C ( ˆ ).
med(Cˆ )550o
10. AD é altura: a 5 90°.
45° 1 358 1 med A ( ˆ ) 5 180°
med A ( ˆ ) 5 180° 2 45° 2 35°
med A ( ˆ ) 5 100°
Editoria de arte
Editoria de arte
Editoria de arte

273
b
med A
5
( ˆ )
2
b
o
100
2
o 5 5
50
No ACD, temos:
50° 1 35° 1 c 5 180°
c 5 180° 2 50° 2 35°
c 5 95°
11. 40° 1 50° 1 med A ( ˆ ) 5 180°
med A ( ˆ ) 5 180° 2 40° 2 50°
med A ( ˆ ) 5 90°
 med(BAˆ S) 5 45° (bissetriz)
No AHB (retângulo), temos:
40° 1 90° 1 med(BAˆH) 5 180°
med(BAˆH) 5 180° 2 40° 2 90°
med(BAˆH) 5 50°
x 5 med(BAˆH) 2 med(BAˆ S) 5 50° 2 45° 5 5°
12. x 1 628 5 908
x 5 908 2 628
x 5 288
y 1 288 5 908
y 5 908 2 288
y 5 628
1. Escala e rosa dos ventos (simplificada).
2. 1 : 37 000 000, ou seja, cada centímetro no
mapa corresponde a 37 000 000 cm
(370 km) no real.
3. Aproximadamente: 3,1 cm, 3,5 cm e 3,5 cm.
4. Medidas reais:
3,1 ? 370 km 5 1 147 km
3,5 ? 370 km 5 1 295 km
 P 5 1 147 km 1 1 295 km 1 1 295 km 5
5 3 737 km
44 – Congruência de triângulos
1. Caso LAL; x 5 608; y 5 308.
2. x 5 4 cm; y 5 5 cm
3. ABBC, med(ABˆD)5med(CBˆD)5120o , BD
é comum.
ADBCDB
4. Se ACMN, Cˆ Nˆ e Aˆ Mˆ (90o). Então,
pelo caso ALA os triângulos ABC e MPN
são congruentes, logo ABPM.
5. a, b e c: Como ABAC, BDDC e AD é
lado comum, os triângulos ABD e ACD são
congruentes (LLL).
Logo: x 5 y, Bˆ Cˆ e AD é altura, bissetriz e
mediana relativa ao lado BC.
6. Alternativa b.
(ABAC; Bˆ Cˆ e BDEC 2 LAL)
7. Aˆ Bˆ , AMMB, AMˆ CBMˆ D (opv) 2 ALA
 AMCBMD
Logo, CMMD ou M é ponto médio de CD.
8. ABCD é um retângulo; logo, O é ponto
médio das diagonais. Daí: OBOD,
AOˆ BCOˆ D (o.p.v.), OCOA. Pelo caso
LAL, os triângulos AOB e COD são
congruentes.
9. a) LLL
b) x 5 y 5 908 (pois x 5 y e x 1 y 5 1808)
10.
BM MC
B C
CD BA
Pelo caso LAL
temos DMC AM




ˆ ˆ ,
:

 
 
  B.
 AMDM e o AMD é isósceles.
11. Alternativa a. (caso LAAo)
12. Alternativa c. (VAMOe LAAO)
45 – Propriedades do triângulo
isósceles e do triângulo
equilátero
Resposta em aberto.
1. Triângulo retângulo isósceles: um ângulo
reto e dois agudos iguais (458).
2. 378 1 378 1 x 5 1808
x 5 1808 2 378 2 378
x 5 1068
 Os ângulos são: 378, 378 e 1068, e o
triângulo é obtusângulo.
3. Se MNP é equilátero, MNP, e mede
608 cada um.
 x 5 608 e y
( ˆ )
2
med M o
60
2
o 5 5 5
30
4. Se ABBC, o triângulo é isósceles; logo,
x 5 678.
y 1 x 1 678 5 1808
y 1 678 1 678 5 1808
y 5 1808 2 678 2 678
y 5 468

274
5. ABBC  o ABC é isósceles.
508 1 x 1 x 5 1808
x 1 x 5 1808 2 508
2x 5 1308
x 5 658
6. x 1 x 1 1358 5 1808
2x 5 1808 2 1358
2x 5 458
x 5 228 30’
7. ABC é isósceles.
c 5 b 5 1808 2 1108 5 708
x 1 708 1 708 5 1808
x 5 1808 2 708 2 708
x 5 408
8. ABC isósceles med(Cˆ )5med(Aˆ )540o
BM é mediana, altura e bissetriz.
 408 1 408 1 2x 5 1808
2x 5 1808 2 408 2 408
2x 5 1008
x 5 508
9. x 5 608 med (Bˆ )560o  Seu suplemento é
1208.
Como ABD também é isósceles, temos:
1208 1 y 1 y 5 1808
y 1 y 5 1808 2 1208
2y 5 608
y 5 308
10. AB // CD ⇒ a 5 208 (alternos internos)
a a b
(180 ) 180
1 1 2 5
1 1 2 5
2 5 2
20 20 180 b
180
b
o o
o o o o
o o
180 20 22 2
b
b
208 1 1108 1 c 5 1808
c 5 1808 2 208 2 1108
c 5 508
2 52
5
20 180
40
40
o o
o
o
11. x 5 608 (ABE é equilátero.)
x 1 y 5 908
608 1 y 5 908
y 5 908 2 608
y 5 308
Como ADZ é isósceles, então:
308 1 z 1 z 5 1808
z 1 z 5 1808 2 308
2z 5 1508
z 5 758
12. S
( 5 2 )
180 3 180 540
5 5 2  5  5
A
med A
o o o
i
o
o
540
5
108
5 5
 ( ˆ ) 5
108o
Como AEAB, o ABE é isósceles.
 x 1 x 1 1088 5 1808
x 1 x 5 1808 2 1088
2x 5 728
x 5 368
1. Acre R 2 triângulos retângulos e
escalenos.
Minas Gerais R um triângulo acutângulo e
equilátero.
Pará R 2 triângulos retângulos e escalenos.
Rio Grande do Sul R 2 triângulos
retângulos e escalenos.
Mato Grosso do Sul R um triângulo
retângulo e isósceles.
2. Sim.
3. Acre e Pará – região Norte.
Minas Gerais – região Sudeste.
Rio Grande do Sul – região Sul.
Mato Grosso do Sul – região Centro-Oeste.
4. Todas as bandeiras são retângulos. Além
disso:
Acre – decágono (estrelinha);
Pará – hexágono e decágono;
Rio Grande do Sul – paralelogramo ou
quadrilátero;
Mato Grosso do Sul – trapézios (um
isósceles e um retângulo) e decágono.
5. Bahia, Paraná, Rondônia, Roraima e
Tocantins.
1. Os lados são 3 cm e 11 cm; portanto, o 3.o
lado pode ser 9 cm, 10 cm, 11 cm, 12 cm
ou 13 cm.
Alternativa c.
2. 18
3
4
18 13 5
13 ,
5
2
cm;  5 , cm; 5 6 ,
75
Sim, Caio pode construir um triângulo.
3. Alternativa d.
4. Alternativa a.
5. x 1 x 1 2 (x 1 x) 5 1808
x 1 x 1 4x 5 1808

275
6x 5 1808
x 5 308
 A 5 2 ? (308 1 308) 5 1208
Alternativa e.
( ˆ )
( ˆ) ( )
6. med C
o o o
180 155 25
25 
5 2 5
5
o
med A ABC isósceles
med(Bˆ )52x
2x 1 258 1 258 5 1808
2x 5 1808 2 258 2 258
2x 5 1308
x 5 658
Alternativa c.
7. BDC é equilátero; logo, cada ângulo
interno tem 608.
med B
med C
o o o
20 60 80
15 60 75
5 1 5
5 1 5
o o o
80 75 x
5
5 2 2
5
( ˆ )
( ˆ )
o o
1 1
o
180
o o o
180 80 75
25
x
x
o
Alternativa d.
8. y 1 1208 5 1408
y 5 1408 2 1208
y 5 208
x 1 908 1 208 5 1808
x 5 1808 2 908 2 208
x 5 708
 x 2 y 5 708 2 208 5 508
Alternativa b.
9. Como ABC é isósceles, PQ é bissetriz e
altura
med(Cˆ )5y
No ABP, temos:
208 1 z 1 z 5 1808
2z 5 1808 2 208
2z 5 1608
x 5 808
Em P:
z 1 2x 5 1808
808 1 2x 5 1808
2x 5 1808 2 808
2x 5 1008
x 5 508
No ABC, temos:
2x 1 y 1 y 5 1808
1008 1 y 1 y 5 1808
2y 5 1808 2 1008
2y 5 808
y 5 408
 x 1 y 5 508 1 408 5 908
Alternativa a.
10. Se o ABC é retângulo e isósceles, Bˆ e Cˆ
medem 458.
No ABC, temos:
45 ( ˆ) 22 30 ’
180
o o o
1 1 5
( ˆ) o o o
’
med P
180 45 22 30
med P
m
5 2 2
( ˆ) ’
( ˆ ) ’
ed P
med BPC
o
o
5
112 30
 5
112 30
Alternativa d.
11.
a) O MNP também é equilátero, e cada
ângulo interno tem 608.
b) Equilátero.
12. Alternativa a.
13. CDEF; Cˆ Fˆ ; Dˆ Eˆ
 CDG ≅ FEG
 med DG cm med CG cm e
med CD cm
med A
( ) , ; ( ) ,
( ) ,
(
4 5 5 1
3 9
5 5
5
1
3
C cm
cm
cm
) ,
5 ,
1
5 1
5 ? 5 5
3
med AG cm cm
,
( ) , ,
5 1 5
1 7
5 1 1 7
⇒
⇒ 6,8 cm
5 1
cm
4 5
cm
5
⇒
6 8
cm
BG
⇒ 5 1 6 8 4 5
⇒
⇒ 5 1
?? 5
,
,
,
, , ,
,
cm ? BG 5 cm ?
cm
cm
BG
⇒
⇒
med BG 5
cm
∴ cm
med BD 5 ? cm
5 5
c
m
5 1
6 8
30 6
6
1
6
4
6
4
1 5
,
( )
( ) ,
4 5
cm
cm
cm
AB
5
⇒
⇒ 5 1 3 9 6 8
⇒
⇒ 5 1
?? 5
,
,
,
, , ,
,
cm ? AB 5 cm ?
cm
cm
AB cm
med AB 5
cm
26 ,
52
5 2
( ) ,
⇒
⇒
Perímetro de ABCD: P 5 5,2 cm 1 1,5 cm 1
1 3,9 cm 1 1,7 cm 5 12,3 cm
Alternativa b.
14. a 1 x 5 1808
5x 1 x 5 1808
6x 5 1808
x 5 308
 a 5 5 ? 308 5 1508
Alternativa e.
15. No quadrilátero ABCO, temos:
x 1 x 1 20° 1 30° 1 90° 5 360° R
R 2x 5 220° R x 5 110°
Alternativa c.

276
Estudando os quadriláteros
46 – O quadrilátero e
seus elementos
1. Quadrilátero.
2.
a) Fig. 1, Fig. 2, Fig. 3.
b) Fig. 1, Fig. 2, Fig. 3, Fig. 4.
c) Fig. 1, Fig. 2, Fig. 3.
d) Fig. 4.
e) Nenhuma.
f) Fig. 1.
1.
a) P 
b) PS
c) PR eQS
2. x 1 2x 1 34 cm 1 24 cm 5 103 cm
x 1 2x 5 103 cm 2 34 cm 2 24 cm
3x 5 45 cm
x 5 15 cm
med(AB)5AB5x515cm
med(BC)2BC52x52?15cm530 cm
3. 3x 1 1 1 2x 1 7 1 4x 2 3 1 3x 2 2 5 51
3x 1 2x 1 4x 1 3x 5 51 2 1 2 7 1 3 1 2
12x 5 48
x 5 4 ⇒ x 5 4 cm
Lados:
3x 1 1 5 3 ? 4 1 1 5 13 ⇒ 13 cm
2x 1 7 5 2 ? 4 1 7 5 15 ⇒ 15 cm
4x 2 3 5 4 ? 4 2 3 5 13 ⇒ 13 cm
3x 2 2 5 3 ? 4 2 2 5 10 ⇒ 10 cm
4. 738 1 1028 1 988 1 x 5 3608
x 5 3608 2 738 2 1028 2 988
x 5 878
O quarto ângulo mede 878.
5. x 1 5x 1 2x 1 4x 5 3608
12x 5 3608
x 5 308
Os ângulos medem 308, 1508, 608 e 1208.
x o o 1 1 1 5 2
6. x x
75 360
x x x o o 1 1 1
2 2 150
2
720
2
5
2x 2x x 720o 150o 1 1 5 2
5x 570o 5
x o 5114
Os ângulos são 1148, 1148 e 578.
7. 2x 1 358 1 x 1 258 1 3x 1 x 1 208 5 3608
2x 1 x 1 3x 1 x 5 3608 2 358 2 258 2 208
7x 5 2808
x 5 408
Ângulos:
2x 1 358 5 2 ? 408 1 358 5 1158
x 1 258 5 408 1 258 5 658
3x 5 3 ? 408 5 1208
x 1 208 5 408 1 208 5 608
8. b 5 c 5 3a e d 5 2a
a 1 3a 1 3a 1 2a 5 3608
9a 5 3608
a 5 408
Assim:
a 5 408
b 5 c 5 1208
d 5 808
9. 3x22481x1681x11281x212853608
3x1x1x1x536081248268 2128 1128
6x53788
x 5638
Ângulos:
3x 2 248 5 3 ? 638 2 248 5 1658
x 1 68 5 638 1 68 5 698
x 1 128 5 638 1 128 5 758
x 2 128 5 638 2 128 5 518
10.
y 2
x
y 1
x
y
y
5 8
5 8
8
8
1
5
5
80
180
2 260
130
 

13081x51808
x5180821308
x 5508
Os ângulos são: 508, 908, 908 e 1308.

277
47 – Os paralelogramos
1. 758, 1058 e 1058.
2. 4x 1 18 5 6x 2 218
4x 2 6x 5 2218 2 18
22x 5 2228
2x 5 228
x 5 118
Ângulos:
4 ? 118 1 18 5 458
458
1808 2 458 5 1358
1358
3. med(Dˆ )5med(Bˆ )5808
 80817081x51808
x5180828082708
x 5308
4. O ângulo interno do pentágono vale 1088
⇒
S S
i
A A
o
(5 2) 180 540
540
5 2 ? 5
i
o
i
o
i
o
5 5
5
108
⇒
O menor ângulo do paralelogramo vale
1808 2 1088 5 728.
 Os ângulos medem: 728, 728, 1088 e 1088.
5. x o o o o 135 1(180 282 )5180
x o o o o 5 180 235 2180 182
x 5478
6.
a) x 5 21 cm y 5 35 cm
b) P 5 21 cm 1 35 cm 1 50 cm
P 5 106 cm
7. x
med ( BD )
cm
5 5 5 ,
cm
2
21
2
10 5
y
med ( AC )
cm
5 5 5 ,
cm
2
15
2
7 5
8.
x 2
y
x y
5
2 5
4

⇒
⇒2y2y54
y54 ⇒y54 cm
x 5 2 ? 4
x 5 8 cm
AC 5 16 cm
BD 5 8 cm
9.
 

x y
x y
2 10
1 5
2 5 ?
2 4 ( 2)
⇒
⇒
 

x y
x y
1 5
2 5
1
2 10
4 2 8
5x518
x53,6⇒x53,6 cm
3,6 1 2y 5 10
2y 5 10 2 3,6
2y 5 6,4
y 5 3,2 ⇒ y 5 3,2 cm
1.
a) V
b) F
c) V
d) F
e) V
f) V
2.
a) P 5 2 ? (3x 1 2y) 1 2 ? (2x 1 y) 5
5 6x 1 4y 1 4x 1 2y
P 5 10x 1 6y
b) A 5 (3x 1 2y) ? (2x 1 y) 5
5 6x2 1 3xy 1 4xy 1 2y2
A 5 6x2 1 7xy 1 2y2
3.
a) P 5 4 ? (5x 2 y) 5 20x 2 4y
b) A 5 (5x 2 y)2 5 25x2 2 10xy 1 y2
4. AC 5 2 ? (5x 1 3y) 5 10x 1 6y
5. APPB⇒5x228552
5x552128
5x580
x516⇒x516 cm
6.
a) x 5 16 e y 5 12
b) PAMB 5 12 1 16 1 20 5 48
ABC 5 20 1 20 1 24 5 64
P
ABD 5 20 1 20 1 32 5 72
P
7.
2 11
2 5
4 16
x y
x y
x
x
1 5
2 5
4
1
5
5
 

2? 41y511
81y511
y51128
y 53
8. x 5 908, y 5 458
9. x 1 x 1 (1808 2 1258) 5 1808
x 1 x 5 1808 2 1808 1 1258

278
2x 5 1258
x 5 628 30’
y 1 628 30’ 5 908
y 5 908 2 628 30’
y 5 278 30’
10. x 1 408 5 908
x 5 908 2 408
x 5 508
y 1 x 1 908 5 1808
y 1 508 1 908 5 1808
y 5 1808 2 508 2 908
y 5 408
11. 398 1 908 1 x 5 1808
x 5 1808 2 398 2 908
x 5 518
12. Os ângulos que a diagonal menor forma
com os lados medem
110
2
55
o
o 5 .
O 3.o ângulo é:
558 1 558 1 x 5 1808
x 5 1808 2 558 2 558
x 5 708
 Os ângulos são: 558, 558, 708.
13. x 1 x 1 1148 5 1808
x 1 x 5 1808 2 1148
2x 5 668
x 5 338
y 1 y 1 668 5 1808
y 1 y 51808 2 668
2y 5 1148
y 5 578
17. (2x 1 58) 1 (x 1 408) 1 (2x 1 58) 1 (x 1 408) 5 3608
2x 1 x 1 2x 1 x 5 3608 2 58 2 408 2 58 2 408
6x 5 2708
x 5 458
2x 1 58 5 2 ? 458 1 58 5 958
x 1 408 5 458 1 408 5 858
Os ângulos são 958, 958, 858 e 858.
18. O ângulo interno do hexágono mede 1208
(ex. 2 – p. 261).
 x 5 608 (suplemento de 1208)
x 1 x 1 y 1 y 5 3608
608 1 608 1 y 1 y 5 3608
y 1 y 5 3608 2 608 2 608
2y 5 2408
y 5 1208
48 – Os trapézios
1. 3608
2. 788 1 1028 1 988 1 x 5 3608
x 5 3608 2 788 2 1028 2 988
x 5 828
3. Dois valem 748; os outros dois valem:
x 1 x 1 748 1 748 5 3608
x 1 x 5 3608 2 748 2 748
2x 5 2128
x 5 1068
 Os ângulos são 748, 748, 1068 e 1068.
4.
x y
x y
o
62
90 90 360
2 5
1 1 1 5
o o o
 

⇒
⇒
 

x y
x y
o
o
2 5
1 5
1
62
180
2x 242o 5
x o 5121
1218 2 y 5 628
2y 5 628 2 1218
2y 5 2598
y 5 598
5. x 1 1188 1 908 1 908 5 3608
x 5 3608 2 1188 2 908 2 908
x 5 628
6. x 1 308 1 708 5 1808
x 5 1808 2 308 2 708
x 5 808
x
114
66
x
y
y
14. a 1 y 5 908
a 1 x 1 908 5 1808 (no AMB)
a 1 x 5 1808 2 908
a 1 x 5 908
 a1y5a1x⇒y5 a 1x 2a ⇒y5x
15. 608, 608, 1208, 1208
16. b é ângulo externo do ABD (isósceles).
Portanto:
a1a5b (soma dos ângulos internos não
adjacentes)
2a 5 b
b
a
5 2
Editoria de arte

279
x 1 y 1 508 5 1808
808 1 y 1 508 5 1808
y 5 1808 2 808 2 508
y 5 508
4
5
4
5
7. x 1 x 1 x 1 x 5
360
o x x x x o 1 1 1
5 5 4 4
5
1800
5
5
18x 1800o 5
x o 5100
4
5
o
400
5
o 5 5
x 80
Os ângulos são 1008, 1008, 808 e 808.
8. Chamando de y os ângulos da base,
teremos:
1068 1 1068 1 y 1 y 5 3608
y 1 y 5 3608 2 1068 2 1068
2y 5 1488
y 5 748
Como AM é bissetriz de ˆA
, , ,
, os ângulos da
base do AMB valem
74
2
37 8
5 8. Logo:
x 1 378 1 378 5 1808
x 5 1808 2 378 2 378
x 5 1068
9.
med MN
cm 1
cm cm
( )5 5 5
, cm
21 12
2
33
2
16 5
b) med MN
, , ,
cm 1
cm cm
( ) 5 5 5
,
cm
9 36 592
2
15 28
2
7 64
med MN
cm 1
cm cm
( ) 5 5 5
,
cm
9 36 592
2
15 28
2
7 64
13. 2
x110524
3
2 30
3
72
3
x 1
5
2x572230
2x542
x521⇒x521 cm
14. 16 7
12 9
2
,
,
5
x1
33 4
2
, ,
12 9
2
5
x1
33,4212,95x⇒x520,5⇒x520,5cm
15. 25
1
5 50
2
1 5
x y
⇒x y
x y
x y
x
x
1 5
2 5
1
5
5
50
14
2 64
32
 

321y550
y550232
y 518
16.
a) Sim; caso LAAo.
b) BE
c) FE 5 16 cm
d) AF
cm 2
cm cm
5 5 5
cm
28 16
2
12
2
6
1. Triângulos, quadriláteros (retângulos,
quadrados, losangos e trapézios) e ainda
algumas figuras irregulares.
2.
a) Os acutângulos:
?
A5 5 5
m
1 15 090
2
1 035
2
0 5175 0 5175 2 , , ,
, ⇒ ,
?
A5 5 5
m
1 15 090
2
1 035
2
0 5175 0 5175 2 , , ,
, ⇒ ,
Os obtusângulos:
1 8 ?
0 575
A5 5 5
m
2
1 035
2
0 5175 0 5175 2 , , ,
, ⇒ ,
?
1
A5 5 5
m
1 8 0 575
2
1 035
2
0 5175 0 5175 2 , , ,
, ⇒ ,
37
37
x
x 1 908 1 908 1 748 5 3608
x 5 3608 2 908 2 908 2 748
x 5 1068
 Os ângulos são 1068, 908, 908 e 748.
10. a 1 228 1 908 5 1808
a 5 1808 2 908 2 228
a 5 688  b 5 688
c 5 908 1 228
c 5 1128
11. ABC é retângulo e isósceles, logo os
ângulos da base AC medem 458. Como
o ACD também é isósceles, os ângulos
da base também valem 458, portanto
med(Dˆ )5458.
Sendo ˆ ˆ A B  com 908, o ângulo ˆC mede
1358.
12. Sendo MN a base média, temos:
a) med MN
cm cm cm
( )5 5 5
, cm
21 12
2
33
2
16 5
Editoria de arte

280
b) São iguais.
c) 4 triângulos e 12 trapézios.
3.
a) Jogo de dados (Geraldo de Barros).
b) Losangos; cubos.
4. Não.
5. Perímetro:
P 5 2,96 m 1 4,85 m 1 2,96 m 1 4,85 m 5 15,62 m
Área: A 5 2,96 m ? 4,85 m 5 14,356 m2
6. Projeto para uma paixão sem fim:
A 5 1,80 ? 1,15 5 2,07 m2
Sem título: A 5 2,96 m ? 4,85 m 5 14,356 m2
Raios de sol: A 5 4,40 m ? 4,00 m 5 17,6 m2
Jogo de dados: A 5 2,63 m ? 21,70 m 5 57,071 m2
Base média 5
15 25
2
40
2
20
m m m
1
5 5
m Área 5 A520m?24m5480m2
Valor total: 480 ? 50 5 24 000
O valor total do terreno é R$ 24 000,00.
Tratando a informação, páginas 321 a 323.
1.
a) Resposta em aberto. Espera-se que se
observe o seguinte: na faixa de 0 a
14 anos os homens apresentam maior
porcentagem da população brasileira.
b) De 30 a 34 anos; a mais para as
mulheres (0,48%).
2.
a) De 0 a 5 anos de idade e de 20 a
25 anos de idade.
b) Resposta em aberto. Espera-se que
seja percebido o envelhecimento da
população brasileira e, pela projeção de
2050, o aumento da expectativa de vida.
3.
a) Homens; de 0 a 4 anos.
b) Homens.
1
cm 56 34
1
cm 56 34
1. 60% de 15: 0,6 ? 15 5 9
Os lados do retângulo são 9 e 15 cm,
portanto seu perímetro será:
P 5 9 cm 1 15 cm 1 9 cm 1 15 cm 5 48 cm.
Se o quadrado tem o mesmo perímetro,
seus lados medem 12 cm.
Alternativa b.
2. x 5 3 cm ⇒ x 1 y 5 3 cm 1 2 cm 5 5 cm
y 5 2 cm
Alternativa a.
3.
a b
a b
a b
o
1 5 o
5
5 2
160
3 7
160

⇒
3(160o2b)57b⇒480o23b57b⇒480o57b13b⇒
3(160o2b)57b⇒480o23b57b⇒480o57b13b⇒
3(160o2b)57b⇒480o23b57b⇒480o57b13b⇒
⇒10b 480o⇒b 48o 5 5
a o o o 5160 248 5112
b c o o c o o o c c o 2 522 ⇒48 2 522 ⇒48 222 5 ⇒ 526
b c o o c o o o c c o 2 522 ⇒48 2 522 ⇒48 222 5 ⇒ 526
a 1 b 1 c 1 d 5 3608
1128 1 488 1 268 1 d 5 3608
d 5 3608 2 1128 2 488 2 268
d 5 1748
Alternativa c.
4.
x y
x y
3 40
1 5
1 5 2
30 ( 1)

⇒
x y
x y
3 40
1 5
2 2 5 2
y
y
1
5
5
30
2 10
5
 

x 1 5 5 30
x 5 30 2 5
x 5 25
 x 2 y 5 25 2 5 5 20
Alternativa c.
5. P 5 (x 2 3) 1 (2x 1 1) 1 (x 2 3) 1 (2x 1 1) 5 6x 2 4
Alternativa a.
6. x
cm 1
cm cm
5 5 5
cm
40 28
2
68
2
34
28
cm y cm cm 5 2
28
34
2
56
2
34
2
cm x y
cm
1
5
1
5
1
⇒ ⇒ 28
2
28
34
2
56
2
34
2
x y
cm
cm y cm cm y
5 5
y cm c
1
5
1
⇒ ⇒ ⇒ 5 2 m522 cm
28
2
28
34
2
56
2
34
2
x y
cm
cm y cm cm y
5 5
y cm c
1
5
1
⇒ ⇒ ⇒ 5 2 m522 cm
 x 2 y 5 34 cm 2 22 cm 5 12 cm
Alternativa c.
7. r // s
Portanto, o ângulo externo a ˆB
vale 1158.
Como AD BC // , o ângulo ˆA
também mede
1158 (correspondente).
Alternativa e.

281
8. No quadrilátero, temos:
x
x
3
x 1 1 2
x
1 5 360
o 2
2
x x x x o 1 1 1
2 4 3
2
720
2
5
10x 720o 5
x o B o o 572  ˆ 5272 5144
No BMN, temos:
1448 1 y 1 y 5 1808
y 1 y 5 1808 2 1448
2y 5 368
y 5 188
Alternativa d.
9. No ABD, temos:
728 1 (218 1 y) 1 (218 1 y) 5 1808
(CBD – isósceles)
y 1 y 5 1808 2 728 2 218 2 218
2y 5 668
y 5 338
Alternativa c.
10. AB // CD  No CDE, temos med(Dˆ )582o.
No trapézio:
82o1(180o282o)1118o1y5360o
y o o o o o 5360 282 2180 182 2118
y o 562
No CDE, temos:
(180o2118o)182o1(180o2x)5180o
62o182o1180o2x5180o
2x5 180o 262o282o 2180o
2x52144o
x o 5144
 x 1 y 5 1448 1 628 5 2068
Alternativa a.
11. No paralelogramo ABCF, temos
med (C 
) 5 55°, portanto o valor de x é 55°.
Alternativa c.

Estudando a circunferência E o Círculo
282
49 – A circunferência
1. Círculo.
2.
a) Em linha reta, até o bebedouro.
b) Todos percorrerão a mesma distância.
3. Em linha reta, na direção de Gílson.
4. Sim, 10 metros.
1.
a) OA eOB
b) AB
c) Não.
d) Sim, pois OAOB.
2.
a) d 5 2 ? 15 cm 5 30 cm
b) d 5 2 ? 0,75 cm 5 1,50 cm
c) d52? cm5 cm
1
4
1
2
3
2
d) d5 2 ? cm5 3
cm
3.
a) r
54
2
cm
5 5 27
cm
b) r
11
2
cm
5 5 5,5
cm
4. AB 5 PB 2 PA
AB 5 72 cm 2 38 cm 5 34 cm (diâmetro)
r
34
2
cm
5 5 17
cm
5.
a) r 5 10,5 cm ⇒ , 5 2 ? 10,5 cm 5 21 cm
b) , 5 61 cm ⇒ r5 cm5 cm
61
2
30,5
6. Média mínima: 2 ? 6 cm 5 12 cm
1. São iguais.
2. Sim.
3.
A
B
C
50 – O círculo
Editoria de arte
1.
a) x . 10 (externo)
b) x , 10 (interno)
c) x 5 10 (na circunferência)
2. 3x 1 5 5 20
3x 5 20 2 5
3x 5 15
x 5 5 ⇒ x 5 5 cm
3. 7x 1 33 . 75
7x . 75 2 33
7x . 42
x . 6
Portanto, o menor valor inteiro será x 5 7.
a) z 5 8 600 1 16 800 5 25 400 eleitores
b) Total 5 2 ? 25 400 5 50 800 eleitores
1. O raio é 4 metros.
2. 2 1
10
3
(x ) x
x
2 2 5
1
6 1 3
3
10
3
(x2 )2 x x
5
1
6x 2 6 2 3x 5 x 1 10
6x 2 3x 2 x 5 10 1 6
2x 5 16
x 5 8
 O diâmetro mede 8 m.
C 5 2 ? p ? r ⇒ C 5 2 ? 3,14 ? 4 m 5 25,12 m
3. Curitiba: raio é 4 m.
Garanhuns: raio é 2 m, logo o diâmetro é 4 m.

283
4. Resposta em aberto. Uma das respostas
possíveis: 6 horas.
5.
a) Poços de Caldas (MG), Blumenau (SC) e
Aparecida do Norte (SP).
b)
Cidades brasileiras com relógios de flores
Cidade Estado Ano Diâmetro
Curitiba PR 1972 8 m
Petrópolis RJ 1972 8 m
Garanhuns PE 1979 4 m
Poços de Caldas MG 1972 2 m
Blumenau SC 2000 4 m
Aparecida do Norte SP 2003 9 m
6.
6.
a) 5
x11054x13
3
5 x1 30
x
3
12 9
3
5
1
5x 2 12x 5 9 2 30
27x 5 221
7x 5 21
x 5 3 ⇒ x 5 3 cm
b) PA 5 4 ? 3 1 3 5 12 1 3 5 15 ⇒ 15 cm
c) PB 5 PA 5 15 cm
d) P 5 15 cm 1 15 cm 1 7 cm 1 7 cm
P 5 44 cm
7. P 5 x 1 x 1 y 5 2x 1 y
8.
a) a 5 11 cm
b 5 25 cm (CPCN)
c 5 31 cm (BNBM)
b) P 5 (11 1 31) cm 1 (11 1 25) cm 1
1 (25 1 31) cm
P 5 42 cm 1 36 cm 1 56 cm
P 5 134 cm
9.
a) x 5 12 cm 1 8 cm 5 20 cm
(BMBP e CMCN)
b) AN 5 AP 5 y
Perímetro:
P 5 (12 1 y) 1 20 1 (8 1 y) 5 46
y 1 y 5 46 2 12 2 20 2 8
2y 5 6
y 5 3 ⇒ y 5 3 cm
 AN 5 3 cm
10.
a) BMBP  BM 1 r 5 8
6 1 r 5 8  r 5 2
b) P 5 4 ? 2 5 8
c) P 5 8 1 (6 1 a) 1 (a 1 2) 5 2a 1 16
d) P 5 6 1 2 1 2 1 6 5 16
52 – Posições relativas de
duas circunferências
1.
a) Externas.
b) Secantes.
c) Tangentes internamente.
d) Tangentes externamente.
11
10
9
8
7
6
5
4
3
2
1
0
Diâmetro (em cm)
Cidades
Curitiba
Cidades brasileiras com relógios
de flores e os respectivos raios
Petrópolis
Garanhuns
Poços
de Caldas
Aparecida
do Norte
Blumenau
51 – Posições relativas de uma
reta e uma circunferência
1.
a) r e x
b) s e t
c) Não.
d) C é ponto de tangência.
e) Reta t.
f) OC
2.
a) Lado: 16 cm
b) P 5 4 ? 16 cm 5 64 cm
c) A 5 (16)2 5 256 ⇒ 256 cm2
d) r 5 8 cm
3. O maior valor inteiro é 9 cm (r , 10).
4. Se r é tangente e AO é raio, então x 5 908.
x 1 y 1 308 5 1808
908 1 y 1 308 5 1808
y 5 1808 2 908 2 308
y 5 608
5. x 5 y
Editoria de arte

284
2.
a) Uma é interna à outra.
b) Tangentes externamente.
d) Secantes.
e) Externas.
3. x 5 14 cm 1 20 cm 5 34 cm
4. 18 cm 1 37 cm 1 r 5 65 cm
r 5 65 cm 2 18 cm 2 37 cm
r 5 10 cm
5. P 5 (13 1 7) cm 1 (7 1 9) cm 1 (13 1 9) cm
P 5 20 cm 1 16 cm 1 22 cm
P 5 58 cm
6.
a) Externas.
b) Tangentes externamente.
7. x 5 OB 2 OA 5 10,0 cm 2 6,5 cm 5 3,5 cm
8.
a) O1O2 5 O1A 1 AB 1 BO2 5 4 cm 1 7 cm 1
1 4 cm 5 15 cm
P 5 4 ? 15 cm 5 60 cm
b) A 5 (15)2 5 225 ⇒ 225 cm2
c) P 5 15 cm 1 7 cm 1 15 cm 1 7 cm 5
5 44 cm
9. Distância: d 5 x 1 y 1 x 5 2x 1 y
10.
a) Tangentes externamente (26 5 10 1 16).
b) Externas (30 . 16 1 10).
c) Tangentes internamente (6 5 16 2 10).
53 – Arco de circunferência e
ângulo central
1.
a) O arco AB mede 75º.
O arco ACB mede 285º (360º 2 75º).
b) O arco AB mede 90º.
O arco ACB mede 270º (360º 2 90º).
2. O arco DE mede 90º.
O arco BC mede 45º
(360º 2 90º 2 20º 2 135º 2 70º 5 45º).
3. med(AB)5120o (180o260o)
med(CD)560o (90o230o)
med(FA)560o (AOˆ F e BOˆ C são o.p.v.)
med(EF)530o (90o260o)
4.
a) x 5 1208
b) x 5 458
5. x 1 358 1 358 5 1808
x 5 1808 2 358 2 358
x 5 1108
y 5 x 5 1108
6. a b c med AB med BC med CA
o
o 5 5 5 ()5 ()5 ()5 5 360
3
120
a b c med AB med B C med CA
o
o 5 5 5 ()5 ()5 ()5 5 360
3
120
7. Se ABC é equilátero, cada ângulo
interno mede 608.
 med(AB)560o
8. x 5 1808 2 1358 5 458
9. med(BC)580o⇒x580o
y o o o 5180 280 5100
10.
a) São congruentes pelo caso LLL.
b) x 5 y, são o.p.v.
c) Sim; ABRS.
11. 2x 1 2x 1 208 1 2x 1 408 5 3608
2x 1 2x 1 2x 5 3608 2 208 2 408
6x 5 3008
x 5 508
 a 5 2 ? 508 5 1008
b 5 2 ? 508 1 208 5 1008 1 208 5 1208
c 5 2 ? 508 1 408 5 1008 1 408 5 1408
1. Vôlei: 0,45 ? 3608 5 1628
Basquete: 0,20 ? 3608 5 728
Futebol: 0,35 ? 3608 5 1268
2.
a) Por que os carros param
63%
12%
17,5%
7,5%
Falha mecânica
Pneu furado
Falta de combustível
Pane elétrica
b) Falha mecânica.
Editoria de arte

285
54 – Ângulo inscrito
1. p – inscrito
t – central
t
p
5 2
2.
a) x
o
134
2
o 5 5
67
b) x 5 2 ? 438 5 868
3. x
o
92
2
o 5 5
46
y 5 928
4.
a) Inscritos: ABS e RCD.
b) Centrais: ROˆ De COˆ D.
c) RCˆ D
1
5
5. med AB o o x
o
()5 ? 60 5 72
5 5 o
72
2
 36
1
6
med CD o o y
o
()5 ? 360 5 60
5 5 o
60
2
 30
6. a
o o o
1
5
5 5
o 60 48
2
108
2
54
b
o o o
1
5
5 5
o 60 142
2
202
2
101
c
o o o
1
5
5 5
o 110 142
2
252
2
126
d
o o o
1
5
5 5
o 48 110
2
158
2
79
7. med(AOˆ B)560o
med APB
o
60
2
( ˆ )5 5 30
o
8. a 5 1408
Como ROS é isósceles, b 5 c.
a 1 b 1 c 5 1808 ⇒ 1408 1 b 1 b 5 1808
b 1 b 5 1808 2 1408
2b 5 408
b 5 c 5 208
x 5 1808 2 1408 5 408
9. 7
10 48
2
x
x o
5
1
x x o
14
2
10 48
2
5
1
14x 2 10x 5 48º
4x 5 48º
x 5 12º
 O ângulo central (10x 1 488) mede 1688, e
o inscrito (7x) mede 848.
10. s 5 2 ? 528 5 1048
BOC é isósceles:
1048 1 t 1 t 5 1808
t 1 t 5 1808 2 1048
2t 5 768
t 5 388
11. med(BAC)5med(BDC)
5x 5 25º
x 5 5º
12. x
o x
o
1 2
1 5
62
2
x o x o 1
2 4
2
62
2
5
1
2x 2 x 5 62º 2 4º
x 5 58º
 O ângulo inscrito (x 1 28) mede 608.
13. BOˆ C – central
BAˆ D – inscrito
AD / / OC⇒med(BAˆ D)5x
med ( BOD
)
med ( BAD
ˆ )
5

2
x
x o
5
145
2
2x 5 x 1 45º
2x 2 x 5 45º
x 5 45º
2
5
14. Arco o
o
: 360
o
720
5
? 5 5144
a) Central: 1448
b) Inscrito
o
144
2
: 572
o
15. 2x 1 3x 1 x 1 308 1 x 1 508 5 3608
2x 1 3x 1 x 1 x 5 3608 2 308 2 508
7x 5 2808
x 5 408
med(AB)580o,med(BC)5120o,
med(CD)570o,med(DA)590o
o
a) med BAC
120
2
( ˆ )5 5 60
o
b) med BCD
o o o
1
( ˆ )5 5 5
o
90 80
2
170
2
85

() () 1
2 2 2 2 2
() () 2
2 2 2 2 2
286
1.
a) med(BC)5180o
o
b) a
180
2
o 5 5
90
c) Triângulo retângulo.
2.
a) med(EF)5180o
o
b) d
180
2
o 5 5
90
c) Triângulo retângulo.
55 – Ângulos cujos vértices não
pertencem à circunferência
1.
a) x
() () 1
2 2 2 2 2
med AB med CD t s t s
5 1 5 1 5
1 5 1 5
b) x
() () 2
2 2 2 2 2
5 2 5 2 5
2 5 2 5
2. a
o o o o o
2
5 2 5
5 5
o 125
2
65
2
125 65
2
60
2
30
b
o o o o o
1
5 1 5
5 5
o 125
2
65
2
125 65
2
190
2
95
c o o o 5185 295 585
3.
a) x
o o
86
2
28
2
o o o 5 2 5 1 5
43 14 57
b) x
o o
92
2
56
2
o o o 5 2 5 2 5
46 28 18
4. 35
157
2 2
o
o med CD
5
()
2 ()
o o med CD
5
70
2
157
2
70o2157o52med(CD)
med(CD)587o
1. Gráfico de setores.
2.
a) Homens: 54%, mulheres: 16%.
b) Não, homens: 11% e mulheres: 38%.
c) 8%.
d) Maior para as mulheres, pois a
porcentagem é maior.
e) Mulheres: não, pois 16% é bem inferior
a 50% (1808).
Homens: correta, pois 54% é maior que
50%.
1. 3x 1 5x 2 2 1 2x 1 6 5 24
3x 1 5x 1 2x 5 24 1 2 2 6
10x 5 20
x 5 2
Diâmetro:
2x 1 6 5 2 ? 2 1 6 5 10 ⇒ 10 cm
 O raio é 5 cm.
Alternativa e.
2. 1
2
2 3
x52 1x
3
3 1 9
3
x 2 1 x
2 3
3
2
5
29x 2 3x 5 22 2 1
212x 5 23
12x 5 3
x5 5 5 m
3
12
1
4
0,25⇒0,25
Se a medida do raio é 0,25 m, o diâmetro
será 0,5 m (2 ? 0,25 m).
Alternativa c.
3. Diâmetro: 40 cm ⇒ raio: 20 cm
4
3
11
1
2
x1 5 x126
8 66
6
3 156
6
x1 x
5
1
8x 2 3x 5 156 2 66
5x 5 90
x 5 18
AD 5 20 cm
AB 5 20 cm
CD5 ? 1 5 cm
4
3
18 11 35⇒35
1
2
18 26 35⇒35
BC5 ? 1 5 cm
P 5 20 cm 1 20 cm 1 35 cm 1 35 cm 5 110 cm
Alternativa a.
4. P 5 AB 1 AC 1 BC 5 (a 1 b) 1 (a 1 b) 1
1 (b 1 b) 5 2a 1 4b
Alternativa c.

287
5.
x 1 y
5
17
1
x 2 y
5
3
2 x 5 20 x 5 10 x 5
10
cm
 

⇒ ⇒
Alternativa a.
6.
3 2 29
6 5
5 2 29
6 5 2
x y x y
x y
x y
x y
1 1 1 5
2 5
1 5
, 2 5 , (? )

⇒

5 x 1 2 y
5
29
2 x 2 2 y
5
13
7 x 42 x
6
1
5 5
 

⇒
Como x 2 y 5 6,5 ⇒
⇒ y 5 6 2 6,5 ⇒
⇒ y 5 20,5.
Alternativa e.
7. med(Oˆ )575o
 75o190o190o1med(OTˆ B)5360o
med(OTˆ B)5360o275o290o290o
med(OTˆ B)5105o
Alternativa b.
8. x
y y x y
114
2
⇒ ⇒2 x y
120
o o o
2
5 2 5
5
o 2
1 5
120
2 2
120
2
2
2
120
2
y y x y
⇒ ⇒2 x y
120
o o
2
2 5
5
o 2
1 5
2
120
2
2
2
120
2
o o o
y 1
y o o
⇒ ⇒ 2 5 ⇒
o 200 120
100
120
2 2
200
2
120
5 1 5 y
2
200
2
120
1
2
⇒ 200 2 120
5 ⇒ y 5 80º
Substituindo, temos:
2x 1 808 5 1208
2x 5 408
x 5 208
o o
y o o
5 y
 A razão
x
y
o
o 5 5
20
80
0,25
Alternativa c.
9. ADB é isósceles:
208 1 y 1 208 5 1808
y 5 1808 2 208 2 208 (y – ângulo do vértice)
y 5 1408
x5 5
° 70°
140
2
Alternativa b.
10. 120
2
5
2
o x x
5 1
120
5
2
o x 1
x
5
120
6
2
o x
5
120º 5 3x
x 5 40º
med(AC)55x55? 40o5200o
Alternativa d.
11. x 5 2y; Cˆ mede
o
120 o
2
560 .
 x 1 y 1 608 5 1808
2y 1 y 1 608 5 1808
2y 1 y 5 1808 2 608
3y 5 1208
y 5 408  x 5 808
x 2 y 5 808 2 408 5 408
Alternativa b.
12. DAC é isósceles:
1148 1 y 1 y 5 1808
y 1 y 5 1808 2 1148
2y 5 668
y 5 338
o
x
5 5
57
o  x 2 y 5 578 2 338 5 248
Alternativa a.
13. No ABP, os ângulos internos são:
ˆ o , ˆ o (sup o
)
ˆ (
Bcom Pcom lementar de e
Acom
85 60 120
35 o
180o 2 85o 2 60o ).
med(BC)52?35o570o
 x
o
70
2
o 5 5
35
Alternativa e.
14. y 5 2x (inscritos)
x 1 y 1 908 5 1808 (pois o triângulo é
retângulo)
x 1 y 5 1808 2 908
x 1 y 5 908

2
y 5
x
x 1 y 5 o x 1 x 5 o x 5 o x 5
o
90 ⇒ 2 90 ⇒3 90 ⇒ 30

Como y 5 2x, temos: y 5 2 ? 308 5 608.
Alternativa c.
15. Como Rˆ é inscrito,med(PQ)52?65851308.
ComoMOˆ N é central,med(MN)5628.
o o
x
130
2
62
2
o o o 5 2 5 2 5
65 31 34
Alternativa d.

288
1. Conservação.
2. Segurança e informações sobre cuidados
no uso.
4. Praticidade no abrir e resistência no
guardar.
5. Que não estragam por ação do tempo.
6.
a) Reciclável.
b) Frágil.
c) Não expor à luz.
d) Inflamável.
e) Manter fora do alcance de crianças.
f) Desaconselhável para crianças de 0 a
3 anos.
g) Para cima.
h) Não molhar.
7. 8 caixas.

SUMÁRIO
9o . ano
Noções elementares de estatística...................................................................... 291
Estudando as potências e suas propriedades....................................................... 296
Calculando com radicais................................................................................... 304
Equações do 2o. grau.......................................................................................... 338
Função polinomial do 1o. grau............................................................................ 388
Função polinomial do 2o. grau (ou função quadrática)....................................... 397
Segmentos proporcionais.................................................................................... 411
Semelhança....................................................................................................... 419
Estudando as relações trigonométricas no triângulo retângulo....................... 430
Estudando as relações trigonométricas nos triângulos..................................... 442
Estudando as áreas das figuras geométricas planas........................................... 453
Estudando a circunferência e o círculo............................................................. 465

291
Noções elementares de Estatística
• Quer saber a média de anos de estudo que os brasileiros têm?
Média de anos de estudo dos brasileiros com 7 ou mais anos de idade:
0,2 0,9 1,7 2,4 3,2 4,0 4,7 5,4 6,1 6,7 7,2 7
M
5
1 1 1 1 1 1 1 1 1 1 1 ,818,118,216,1
5 15
4,8
M 5 4,8 anos.
Logo, os brasileiros com 7 anos ou mais de idade têm 4,8 anos de estudo em média.
• Mate a curiosidade: Quais são os países mais populosos do mundo?
Observando o gráfico, nos três anos (1980, 1991 e 2000), o país mais populoso do mundo é a
China, seguido da Índia.
• Qual o número médio de pessoas nas famílias brasileiras?
O número médio de pessoas nas famílias brasileiras é dado por:
4 3 1 3 9 1
3 3
N 5
5
3
3 83 38
, , ,
, → N  , pessoas.
1 2 Organizando os dados
2.
Lançamento de dados
Faces Frequência Porcentagem
1 2 10%
2 5 25%
3 2 10%
4 2 10%
5 5 25%
6 4 20%
Total 20 100%
3.
Aproveitamento dos alunos
na prova de matemática
Notas Quatidade de alunos Porcentagem
1 1 3,8%
2 2 7,7%
3 4 15,4%
4 4 15,4%
5 4 15,4%
6 2 7,7%
7 5 19,2%
8 2 7,7%
9 2 7,7%
Total 26 100%
a) n 5 R n 5 1 1 2 1 4 1 4 5 11
11 alunos obtiveram notas menores
que 5.
b) n 5 R n 5 4 1 2 1 5 1 2 1 2 5 15
15
26
 0,5769 → 57,7%
p5 p
c) Observando a tabela, a nota com
maior frequência é 7 (5 alunos), que
corresponde a 19,2%.
4.
IDADES DOS ALUNOS
Idades Número de alunos Porcentagem
11 2 5%
12 6 15%
13 8 20%
14 12 30%
15 10 25%
16 2 5%
Total 40 100%
5.
ALTURAs DOS alunos
Alturas Quantidade de atletas Porcentagem
Menos de 1,80 m 11 27,5%
De 1,80 m até
22 55%
menos de 2,00 m
2,00 m ou mais 7 17,5%
Total 40 100%
2 2 Estudando gráficos
1.
a) Analisando o gráfico, temos que
os fogões elétricos são os mais

292
eficientes, alcançando uma eficiência
de 60%. Os fogões a lenha são os
menos eficientes.
b) Fogões a gás e elétricos.
2.
a) Observando o gráfico, temos que em
julho/agosto foram vendidas 40 000
unidades do produto B.
b) A venda do produto A foi de 20 000
unidades em novembro/dezembro.
c) O índice de vendas mais baixo do
produto B ocorreu em janeiro/fevereiro
e foi de 10 000 unidades.
d) Não; o número de unidades vendidas
de A foi igual ao de B num dado
momento entre agosto e setembro,
mas não perdurou em nenhum dos
bimestres especificados.
3.
a) 1 aluno R 19 anos; 2 alunos R 20 anos;
5 alunos R 21 anos
Total 5 1 1 2 1 5 5 8
Logo, 8 alunos têm no mínimo 19 anos.
b) 4 alunos R 16 anos; 5 alunos R 17 anos;
3 alunos R 18 anos;
8 alunos R 19 anos ou mais
Total 5 4 1 5 1 3 1 8 5 20
Logo, no curso de inglês há 20 alunos.
4.
a) O setor que só mostrou crescimento
ao longo das décadas indicadas é o
representado no gráfico pelas barras
azuis (Comércio e serviços).
b) O setor que teve queda contínua
ao longo das décadas indicadas é o
representado no gráfico pelas barras
verdes (Agropecuária).
5.
Construção da casa R 25%
Pomar R 50%
Horta R 20%
Jardim R 100% 2 ( 25% 1 50% 1 20% ) 5 5%
O gráfico que representa essa divisão é o
da alternativa d:
pomar
horta
casa
jardim
6. Total de empregados R 180
a) 40% preferiram o café.
40% de 180 5 72
Logo, 72 empregados preferiram o café.
b) 30% preferiram o chá.
30% de 180 5 54
Logo, 54 empregados preferiram o chá.
c) A bebida que teve a menor preferência
foi o leite (10%).
d) 20% dos funcionários não
manifestaram preferência por
qualquer bebida.
20% de 180 5 36
Logo, 36 funcionários não manifestaram
preferência por qualquer bebida.
7.
a) 6 ex-alunas R sem filhos
8 ex-alunas R 1 filho
4 ex-alunas R 2 filhos
2 ex-alunas R 3 filhos
2 ex-alunas R 4 filhos ou mais
Total 5 6 1 8 1 4 1 2 1 2 5 22
Logo, 22 ex-alunas participaram do
encontro.
b) Pela análise do gráfico, 8 ex-alunas têm
apenas um filho.
c) 6 ex-alunas R sem filhos
Total R 22 ex-alunas
p5 5 p
6
22
0,2727→ 27,3%
Logo, aproximadamente 27,3% não têm
filhos.
8. Para 1 200 n 1 300, observando o
gráfico, temos:
Fevereiro R 1 200 ligações
Março R 1 250 ligações
Abril R 1 300 ligações
Junho R 1 220 ligações
Julho R 1 200 ligações
Setembro R 1 220 ligações
Outubro R 1 200 ligações
Novembro R 1 300 ligações
Total R 8 meses
Editoria de arte

293
O número de ligações foi maior ou igual a
1 200 e menor ou igual a 1 300 em 8 meses.
9. Possível resposta.
Idade Número de alunos
14 4
15 12
16 8
17 1
correspondente ao arco de uma volta
(3608) equivale a 100%, calculamos
as medidas dos ângulos centrais dos
respectivos setores:
Voleibol R 50% de 3608 5 1808
Basquetebol R 17% de 36085 61,28  618
Futebol R 8% de 3608 5 28,88  298
Natação R 4% de 3608 5 14,48  148
Outros R 21% de 3608 5 75,68  768
arte
de Editoria 17
Ilustrações: O total de alunos é dado por:
600 1 200 1 100 1 50 1 250 5 1 200 R
R 1 200 alunos
Determinando as taxas percentuais,
temos:
Voleibol R 600 de 1 200 5 50%
Basquetebol R 200 de 1 200 5 16,7%  17%
Futebol R 100 de 1 200 5 8,3%  8%
Natação R 50 de 1 200 5 4,2%  4%
Outros R 250 de 1 200 5 20,8%  21%
Lembrando que o ângulo central Idade (em anos)
Idade dos alunos do coral
Número de alunos
16
15
14
0 1 2 3 4 5 6 7 8 9 10 11 12 13
Mulheres matriculadas no curso de informática
Ano Número de matrículas
2002 10
2003 15
2004 30
2005 40
2006 60
voleibol; 50%
Atividade esportiva na escola
(preferência dos alunos)
outros; 21%
natação; 4%
futebol; 8%
basquetebol; 17%
Usando legendas, temos:
Atividade esportiva na escola
50%
(preferência dos alunos)
21%
4%
8%
17%
Outros
Voleibol
Basquetebol
Futebol
Natação
1. a) 2000 R 11 milhões de dólares
2001 R 13 milhões de dólares
Logo, o aumento foi de:
13 2 11 5 2 R 2 milhões de dólares
b) Para 2007, analisando o gráfico, a
meta a ser atingida é de 40 milhões de
dólares.
2. Participação feminina brasileira nos
Jogos Olímpicos
2008 - Pequim 133
22
35
Ano/
local
51
66
94
122
2004 - Atenas
2000 - Sydney
1996 - Atlanta
1992 - Barcelona
1988 - Seul
1984 - Los Angeles
N° de participantes
Mulheres matriculadas no
no de curso de informática
matrículas
2002 2003 2004 2005 2006
60
50
40
30
20
10
anos
Atividade esportiva na escola (preferência dos alunos)
Atividade esportiva Número de alunos
Voleibol 600
Basquetebol 200
Futebol 100
Natação 50
Outros 250

294
3. a) 3. 3 3 20 5 60 R 60 reais
Santo Domingo/2003
Número de medalhas brasileiras
em Jogos Pan-americanos
Indianópolis/1987
Havana/1991
Mar del Plata/1995
Winnipeg/1999
Santo Domingo/2003
Rio de Janeiro/2007
61
79
82
101
161
123
170
160
150
140
130
120
110
100
90
80
70
60
50
40
30
10
0
1987
Indianópolis/Havana/1991
Mar del Plata/1995
Winnipeg/1999
Rio de Janeiro/2007
20
Número total de medalhas
Local/ano
Número de medalhas brasileiras
em Jogos Pan-americanos
2 3 15 5 30 R 30 reais
M5
1
1
5 5
60 30
3 2
90
5
18
Em média, Karina pagou 18 reais por
caneta.
4. M5
1 1 1 1
5 5
1 98 202 2 08 192 1 95
5
9 95
5
1 99
, , , , , ,
,
M5
1 1 1 1
5 5
1 98 202 2 08 192 1 95
5
9 95
5
1 99
, , , , , ,
,
A média de altura dos jogadores dessa
equipe é de 1,99 m.
5. 3 500 3 30 5 105 000 R 105 000 reais
8 500 3 24 5 204 000 R 204 000 reais
M5
1
1
5 5
105 000 204 000
3 500 8 500
309 000
12 000
25,75
O preço médio por unidade desse produto
foi R$ 25,75.
6.
Número de funcionários Salário Soma
12 800 9 600
5 1 200 6 000
3 2 000 6 000
M5
1 1
1 1
5 5
9 600 6 000 6 000
12 5 3
21 600
20
1 080
M5
1 1
1 1
5 5
9 600 6 000 6 000
12 5 3
21 600
20
1 080
O salário médio dos empregados dessa
empresa é R$ 1 080,00.
7. M5
1 1 1 1 1 1 1
5 5
26 28 34 40 28 30 38 32
8
256
8
32
M5
1 1 1 1 1 1 1
5 5
26 28 34 40 28 30 38 32
8
256
8
32
A idade média dos professores desse
colégio é 32 anos.
8. 8 3 80 5 640
2 3 130 5 260
M5
1
1
5 5
640 260
8 2
900
10
90
O custo de cada copo é de 90 centavos.
9. M5
 1 
1
5
1
5 5
22 4 8 13 4
22 13
1056 52
35
157 6
35
4 5028 4
, , ,
,  ,5
M5
22  4,8 1 13  4
22 1 13 5
105,6 1 52
35 5
157,6
35 5 4,5028  4,5
A nota média da classe foi,
aproximadamente, 4,5.
b)
3 2 Estudando médias
1.
2a feira 3a feira 4a feira 5a feira 6a feira Sábado
13 23 22 27 22 25
M5
1 1 1 1 1
5 5
13 23 22 27 22 25
6
132
6
22
A média diária durante a semana foi de
22 livros vendidos.
2. M5
1 1 1
5 5
104 96 117 103
4
420
4
105
105 pontos foi a média de pontos
marcados por essa equipe.

40 40 110 5
295
10. 0 507
0 551 0 402
3
,
, ,
5
1 1x
3 3 0,507 5 0,551 1 0,402 1 x
x 5 1,521 2 0,551 2 0,402
x 5 0,568
O índice de educação dessa região é 0,568.
Alternativa b.
M5
5 ? 20 1 15 ? 30 1 30 ? 40 1 40 ? 50 1 6 ? 60 1 3 ? 70 1 1 ?
80
5 1 15 1 30 1
40 6 3 1
100 450 1 200 2 000 360 210 80
100
4 400
1 1 1
5
5
1 1 1 1 1 1
5 100
544
A velocidade média dos veículos que trafegam nessa avenida é 44 km/h.
2. M5
1 1 1 1
5 5
27 29 30 38 46
5
170
5
34
A idade média dessa equipe é 34 anos.
3. a) M1
8 4 4 8 5 11 3 15
8 4 5 3
32 32 55 45
20
5
? 1 ? 1 ? 1 ?
1 1 1
5
1 1 1
5 M 1
8 ? 4 1 4 ? 8 1 5 ? 11 1 3 ?
15
32 1 32 1 55 1
45
164
5
8 5
1 4 1 5 1
3
20
20 5 558,2
b) M2
10 ? 4 1 5 ? 8 1 10 ? 11 1 12 ?
15
10 1 5 1 10 1
12
5
1 1 1
37
M 2
10 4 5 8 10 11 12 15
10 5 10 12
40 40 110 180
5
? 1 ? 1 ? 1 ?
1 1 1
5
1 1 1
37
370
37
5 510
c)
M
M
1
2
8 2
10
5 5
0 82
,
,
4. M5
? 1 ? 1 ?
1 1
5
1 1
5 5
2 3 3 4 1 6
2 3 1
6 12 6
6
24
6
4
A massa média desses objetos é de 4 kg.
5.
Idade dos frequentadores
Número de pessoas Idade(anos)
11 14
30 27
26 35
5 42
Total 5 72
Lembrando que o ângulo central é o arco
de uma volta (3608), que corresponde a 72
pessoas, calculamos a medida do ângulo
central correspondente ao setor 14 anos e
11 pessoas assim:
72 R 3608
11 R a
a 5
?
5
11 360
72
55
Logo, a 5 558.
1. Mantendo o ritmo de crescimento de 1980
a 1990, a altura do homem brasileiro no
ano 2000 é 0,02 m a mais, ou seja, 1,77 m.
2. Considerando o casal com a média de
idades de 30 anos, temos:
h 1
5
1 5 1 5
1 82 168
2
0 10 175 0 10 185
, ,
, , , ,
Assim, a provável altura do filho na idade
adulta é 1,85 m.
3. Considerando o casal com média de
idades de 20 anos, temos:
h 1
5
2 5 2 5
1 78 164
2
0 03 171 0 03 168
, ,
, , , ,
Então, a provável altura de Juliana aos 18
anos é 1,68 m.
4. Considerando a mesma proporção, em 25
anos, teremos:
41,5 2 39 5 2,5 R 2,5 cm
Logo, em 2015, o número médio será:
41,5 1 2,5 5 44
O número médio do calçado masculino
em 2015 será 44.
1.
PREFERÊNCIA POR ESPORTE
Esporte Número de pessoas Porcentagem
Voleibol 5 25%
Futebol 12 60%
Basquetebol 3 15%
Total 20 100%

296
Estudando as potências
e suas propriedades
• Pra pensar, sem se cansar: E se você lançar 3 moedas ao mesmo tempo, quantos serão os
resultados?
Chamando a face cara de C e a face coroa de K, se lançarmos três moedas ao mesmo tempo,
teremos as seguintes possibilidades:
1a moeda 2a moeda 3a moeda
C CCC
C
K CCK
C
C CKC
K
K CKK
C KCC
C
K KCK
K
C KKC
K
K KKK
Logo, lançando 3 moedas ao mesmo tempo, teremos 8 resultados possíveis:
CCC, CCK, CKC, CKK, KCC, KCK, KKC e KKK.
• Tantas dobras, quantas partes?
E se fosse possível dobrar ao meio 10 vezes consecutivas, em quantas partes ela estaria
dividida?
1 vez R 2 partes 5 21
2 vezes R 4 partes 5 22
[...]
10 vezes R 210 5 1 024 partes
Se a folha fosse dobrada ao meio por 10 vezes consecutivas estaria dividida em
1 024 partes.
• Qual número é o maior? Qual é o menor?
1
0 0000001
, 5 2
7 10 000 000
5 5 Esses números são todos iguais.
1
10
10 7
4 – Potência de um número real
com expoente natural
1.
No de dobras ao
meio
No de partes de
mesmo tamanho
obtidas
Potências de 2
1 2 21
2 4 22
3 8 23
4 16 24
2. 6 dobras R 26 5 64 partes
3. n dobras R 2n partes
1.
a) 72 5 7 ? 7 5 49
b) (211)2 5 (211) ? (211) 5 121
c) (25)3 5 (25 ) ? (25 ) ? (25 ) 5 2125
d) 2 5 2 ? 2 5
2
5
2
5
2
5
4
25
2  
 
 
 
 
 
1 ( ) 5
e) 3 3

297
1
2
f) 2 5 2 ? 2 ?
? 2 ? 2
1
2
1
2
1
2
1
2
5  
 
 
 
 
 
 
 


 
 
 
1
2
? 2 5 2
1
32
g) (22,3)2 5 (22,3) ? (22,3) 5 5,29
h) 262 5 2 6 ? 6 5 236
i) 35 5 3 ? 3 ? 3 ? 3 ? 3 5 243
j) (20,6)3 5 (20,6) ? (20,6) ? (20,6) 5 20,216
2.
(22)3 2 (21)2 1 (23)2 2 (22)5 5
5 (22) ? (22) ? (22) 2 (21) ? (21) 1 (23) ?
? (23) 2 (22) ? (22) ? (22) ? (22) ? (22) 5
5 28 2 1 1 9 2 (232 ) 5
5 32
1
2 2

 3. ( 2
) ( )
2 2 2 1 1 2 5
( ) ( )
5 2 ? 2 2 2
3
1
6
2 2
1
2
2
2
 
 
 
;
2
1
2
3 3
1
6
? 2
1
6
 
 
 
 
 
 
 
 
? 1 2 ? 2
;
;( ) ( ) 5
4
1
4
9
1
36
1
36
1
36
5 2 1 5 2 1 5
5
4
; 4
4. d
n n
5
2 2 3
2
a) Polígono de 6 lados R n 5 6
d 5
2 ?
5
2
5
6 3 6
2
36 18
2
9
2
O polígono de 6 lados possui 9 diagonais.
b) Polígono de 10 lados R n 5 10
d 5
2 ?
5
2
5
10 3 10
2
100 30
2
35
2
O polígono de 10 lados possui 35
diagonais.
5. x 5 [(21)3 2 (21)5 ? (21)4] 1 (21)7
x 5 [(21) 2 (21) ? (1)] 1 (21)
x 5 [21 1 1] 2 1
x 5 21
y 5 (22)4 ; 23 2 42 ; (22)2
y 5 (22) ? (22) ? (22) ? (22) ; 8 2 16 ; 4
y 5 16 ; 8 2 16 ; 4
y 5 2 2 4
y 5 22
xy 5 (21 ) ? (22 ) 5 2
6. n 5 x2 2 x
n 5 202 2 20
n 5 400 2 20
n 5 380
Logo, esse campeonato tem 380 jogos.
7. Substituindo 2
1
3
na equação, temos:
3
1
3
2
1
3
1 0
3
 
1
9
2
3
1 0
1
3
2
3
1
2
 
? 2 2 ? 2 2 5
? 1 2 5
1 2 5
 
 
0
3
3
→ 2150
Logo, 2
1
3
é raiz da equação.
8.
a) 72 5 49 e (27)2 5 (27) ? (27) 5 49
Logo, 72 5 (27)2.
b) 292 5 281 e (29)2 5 81
Logo, 292  (29)2.
c) (22)5 5 (22) ? (22) ? (22) ? (22) ? (22) 5
5 232 e 225 5 2 2 ? 2 ? 2 ? 2 ? 2 5 232
Logo, (22)5 5 225.
d) (24)3 5 (24) ? (24) ? (24) 5 264 e 243 5
5 2 4 ? 4 ? 4 5 264
Logo, (24)3 5 243.
1. 112 5 121
113 5 1 331
114 5 14 641
2. 115 5 161 051
116 5 1 771 561
Logo, o fato não se repete para esses
números.
1.
a) 29 ? 25 5 29 1 5 5 214
b) 310 ; 37 5 310 – 7 5 33
c) (1,4)6 ? (1,4)4 5 (1,4)6 1 4 5 (1,4)10
d) (2,7)5 ; (2,7) 5 (2,7)5 – 1 5 (2,7)4
e) 58 ? 5 ? 54 5 58 1 1 1 4 5 513
f) 1
7 1
5 1
7 5 1
2 2
2
2
2

  
 
 
 
 
 
 
2
; 5 5
g) (0,1)10 ? (0,1)8 ? (0,1)2 5 (0,1)10 1 8 1 2 5
5 (0,1)20
h) (53)7 5 53 ? 7 5 521
i) [(1,3)4]5 5 (1,3)4 ? 5 5 (1,3)20
j) [(26)2]2 5 26 ? 2 ? 2 5 224
2.
a) (x ? y)3 5 x3y3
b) (a ? b2)2 5 a1 ? 2 ? b2 ? 2 5 a2b4

298
c) (x3 ? y2)4 5 x3 ? 4 ? y2 ? 4 5 x12y8
d) (a2 ? b5 ? c3)2 5 a2 ? 2 ? b5 ? 2 ? c3 ? 2 5 a4b10c6
3.
a) x2 ? x ? x8 ? x3 (x  0) 5 x2 1 1 1 8 1 3 5 x14
b) x12 ; x9 (x  0) 5 x12 2 9 5 x3
c) (x5)4 (x  0) 5 x5 ? 4 5 x20
d) a ? a7 ? a2 (a  0) 5 a1 1 7 1 2 5 a10
e) p4 ; p3 (p  0) 5 p4 2 3 5 p
f) x10 ? x7 ? x8 (x  0) 5 x10 1 7 1 8 5 x25
g) [(x5)2]4 (x  0) 5 x5 ? 2 ? 4 5 x40
4.
a) a 5 (32)3 ? (33 ; 32)4 5 32 ? 3 ? (33 2 2)4 5
5 36 ? (31)4 5 36 1 4 5 310
b 5 (39)2 ; (34 ? 32)2 5 39 ? 2 ; (34 ? 2 ? 32 ? 2) 5
5 318 ; (38 ? 34 )5 318 2 12 5 36
a ; b 5 310 ; 36 5 310 2 6 5 34 5 81
b) [(25)3]2 5 25 ? 3 ? 2 5 230
[(25)2]3 5 25 ? 3 ? 2 5 230
c)
2
2
2 2
10
10 1 9 5 5 2
1.
a) 50 5 1
b) 250 5 21
c) (25)0 5 1
d) 2(25)0 5 21
2.
a) 250 1 30 2 (24)0 5 21 1 1 2 1 5 21
b) 1
25
0 17
1
5
1
6
5
1( , )0 5 1 5
3.
2 1
2
1
4
2
1 1
2
1
4
1
3
2
3
4
3
2
 ; ?? 2 5 2 4
3
4
3
2
0
0
1
2
5
1
2
5
2
 
 
5 2 5  
2  
3
 
1 1
2
1
4
1
3
2
3
4
  4.
3
2
3
4
3
2
1
2
5
2
 
 
 
5 2 5  
2  
; ?? 2 5 2 4
3
a) A 5 (20 1 21 1 22 1 23 1 24) cm2
b) A 5 (20 1 21 1 22 1 23 1 24 1 25 1 26 1 27) cm2
c) A10 5 (20 1 21 1 22 1 23 1 24 1 25 1
1 26 1 27 1 28 1 29) cm2
A9 5 (20 1 21 1 22 1 23 1 24 1 25 1
1 26 1 27 1 28) cm2
Então, calculamos A10 2 A9:
(20 1 21 1 22 1 23 1 24 1 25 1 26 1 27 1
1 28 1 29) 2 (20 1 21 1 22 1 23 1 24 1
1 25 1 26 1 27 1 28) 5 29 5 512 cm2
5. 3
1
3
1
5 5
3 (2x 1 )0
1.
Nº de moedas lançadas Nº de resultados possíveis
1 moeda 2 5 21
2 moedas 4 5 22
3 moedas 8 5 23
4 moedas 16 5 24
5 moedas 32 5 25
6 moedas 64 5 26
7 moedas 128 5 27
8 moedas 256 5 28
9 moedas 512 5 29
10 moedas 1 024 5 210
a) Para 100 moedas, n 5 2100.
b) Para n moedas, n 5 2n.
5 – Potência de um número real
com expoente inteiro negativo
1.
a) 34 5 3 ? 3 ? 3 ? 3 5 81
b) 33 5 3 ? 3 ? 3 5 27
c) 32 5 3 ? 3 5 9
d) 31 5 3
e) 30 5 1
f) 321 5
1
3
g) 3
1
3
1
3
1
3
1
9
2
2
 
 
 
 
 
 
2 5 5 ? 5
h) 3
1
3
1
3
1
3
1
3
1
27
3
3
 
 
 
 
 
 
 
 
2 5 5 ? ? 5
2.
a) 2
1
2
21 5
1
2
b) 2255 5
1
32
 
 
5
1
2
c) (2 ) 5 2 5 2 2
1
4
2
2  
 
1
2
d) 2 5 5 2 2 2
1
16
4
4  
 
1
4
1
64
e) 2 2 5 2 2 52 2 5 2 ( ) 4
1
64
3
3  
 
 
 
1
10
f) 2 2 5 22 5 2 ( 10)
1
10
1  
 

5  
299
1
10
g) 103 
1
1 000
 
 
3
1
7
h)      ( ) 7
1
49
2
2
−  
 
3.
a) 1
2
2
1  
 


b) 1
2
2 4
2
 

2  
 
 1
3
 
c)   
3 9
2
 
( )
2  1
4
d)   
4 4
1  
 
( )
e) 2
3
3
2
1  
 


 2
5
5
2
f)    
25
4
2 2  
 
 
 
 5
3
3
5
g)    
27
125
3 3  
 
 
 
 1
6
h)      
6 6
1  
 
( )
1
3
 
−
i)      
3 9
2
 
( )
2  3
2
2
3
8
27
5  
j)        
1
4
8
27
3 3  
 
 
 
 
 
4.
a) 1
10 2
10
2  
b) 1
7 3
7
3  
c) 1
5 6
5
6  
d) 1
2 7
2
7  
e) 1
6 4
6
4  
f) 1
10 8
10
8  
5.
a) 1
2
4
2 16 4
  
b) 2
4
2
2 4 2 16 32 2
     
c) 2 7
1
2
7
7
8
3
3
 
 
   

d) 2
5
5
2
25
8
3
2
2
3

  
e) 3
2
1 2 32
0
5
5
   
f) 9 3
1
9
27
27
81
1
3
2 3
2
 
 
     
1
4
6. (40  4  1)  (40  4  1)  1   1
  
 1
4
5
4
3
4
 
 
 
4
4
3
 1
5 4

 (40  4  1)  (40  4  1)  1   1
  
 1
4
5
4
3
4
 
 
 
4
4
5
 3

3 (40  4  1)  (40  4  1)  1   1
  
 1
4
5
4
3
4
 
 
 
4
4
5
 3

3 7.
a) (2 2) 3
3
1
2x
x   
1
2 8x6
 
 
b) (3 )
2 2 2
9
2 1 2
4 a x
a
  

  
1
3a
1
x
1
x x
4
2 9a

 

 
c) ab
c
1
c
a
1
b
1
2
1
2





 

 

 
 
 
 
 




b
ac2
 
 
d) (x y )
y
x
4 2 3
6
12
1
   
x
1
y
4
2
3
 
 






 2 3 1 ( )  
e) a b 

 

 






1
1
a
b
a
2 b
3
2
3
f)
x
a b
x
   
a
b
bx
a

 


2
1
2
2
1
1

 

 
8.
1
3
 
a) ( 3 )  ( 1
)    ( 1
)    1
3
1
4
3
1 3 3  
1
3
( 3 )  ( 1
)    ( 1
)    1
3
1
4
3
1 3 3   
b) 2 2
1
2
4
1
16
4
63
16
4 2
4
 
 
      
c) (4 2 )
1
4
1
2
1
4
1
8
1 3 1
3 1 1
  


 
 

 

 
 
 
     
3
8
8
3
1  
 


(4 2 )
1
4
1
2
1
4
1
8
1 3 1
3 1 1
  


 
 

 

 
 
 
     
3
8
8
3
1  
 


d) (6 3 )
1
6
2 1 1

9
9
36
 
 

 
 
2 2 1 4
 


 
 
    
9.
1
y
1
x
a) (xy ) (x y)      2 3  x 
y
2 3  
 

 

 
 
 

 

 

 

 
 
 

 
  x
y
y
x
2 3 

? ;
 
 
300
1
y
1
x
y
2 3  
 

 
 
 

 

 

3 4
5 5 ? 5
 

 
 
 

; 3
 

 

 

 
x
y
y
x
x
y
x
y
x
2 3 2 y
2 2 2 2 1
b) (a b )
a
b
2 2
a
b
b
a
a
b
2 1 2
1
2
 
 
 
 

? 5 ? 5
 

 

 

 
2 2
2
? 5 ? 5
4
3
5
b
a
b
a
b
a
b
a
a
b
b
a
a
b
1
2
2 2 1
2 2

5 ? 5
 

 

 

 
2 2
2
? 5 ? 5
4
3
5
b
a
b
a
b
a
b
a
10. 2 2 4 2 1 16
1
16
0 4 2 3 8 1 1 8 10 1 2 ? 2 2 5 1 ? 2 2 5 1 1 5 2 ( ) ( ) ( )
2 4 2 1 16
1
16
4 2 3 8 1 1 8 10 2 ? 2 2 5 1 ? 2 2 5 1 1 5 2 ) ( ) ( )
11. a
b
a 2 2 1 5 1 5 1 1 ab ba 2ab
b
12.
2 1
2 1 2 1
5
2 1
2 1 1
5
2
5 2
2
2
1
3
2 3 4
4 3
16 9 1
5
6
5
6
2
2
4 2 0
2
 
 
( )
5
2 1
2 1 1
5
2
5 2
4 3
16 9 1
5
6
5
6
2
13. x y
x y
x
y
x
y
xy
y
xy
y
xy
xy
1
2
5
1
2
5
1
2
5
1
2
1
1
2
2
1
1
1
1
1
1
Para x 5 y 5 3, temos:
9 1
1
10
5
9 5 2
1
8
5
4
1.
a) 79 ? 726 5 79 2 6 5 73
b) 1029 ? 10 ? 105 5 1029 1 1 1 5 5 1023
c) 83 ? 826 5 83 2 6 5 823
d) x3 ? x25 ? x4 5 x3 2 5 1 4 5 x2
e) a8 ? a28 ? a21 5 a8 2 8 2 1 5 a21
2.
a) 64 ; 65 5 6 4 2 5 5 621
b) 27 ; 222 5 27 2 (22) 5 27 1 2 5 29
c) 724 ; 721 5 724 2 (21) 5 724 1 1 5 723
d) 10
10
10 10 10
3
5
3 5 3 5 2
2
2
2 2 2 2 1 5 5 5 ( )
e) x
x
x x x
6
2
6 2 6 2 8
2
2 2 1 5 5 5 ( )
f) a
a
a a
9
11
9 11 2 5 5 2 2
3.
a) (621)4 5 621 ? 4 5 624
b) (106)22 5 106 ? (22) 5 10212
c) (521)23 5 5(21) ? (23) 5 53
d) (x6)22 5 x6 ? (22) 5 x212
4.
a) (5 ? 11)22 5 522 ? 1122
b) (3 ? 102)21 5 321 ? 1022
c) (224 ? 54)22 5 2(24) ? (22) ? 54 ? (22) 5 28 ? 528
d) (721 ? x)23 5 7(21) ? (23) ? x23 5 73 ? x23
5.
a) (8 ; 3)22 5 822 ; 322
b) (3 ; 8)22 5 322 ; 822
c) (622 ; 5)24 5 6(22) ? (24) ; 524 5 68 ; 524
d) (722 ; 221)23 5 7(22) ? (23) ; 2(21) ? (23) 5 76 ; 23
6.
a) (25 ? 75) 5 (2 ? 7)5 R Verdadeira.
b) x ; x2 5 x1 2 2 5 x21 R Verdadeira.
c) x5 ? y10 5 (x ? y2)5 R Falsa.
d) xy21 5 (x21 ? y)21 R Verdadeira.
7. a 5 1027; b 5 1011; c 5 1024
a) a ? b 5 1027 ? 1011 5 1027 1 11 5 104
b) a ? c 5 1027 ? 1024 5 10(27) 1 (24) 5 10211
c) b ? c 5 1011 ? 1024 5 10(11) 1 (24) 5 107
d) a ? b ? c 5 1027 ? 1011 ? 1024 5 1027 1 11 2 4 5
5 100 5 1
8. a2n 2 1 ? an 1 1 5 a(2n 2 1) 1 (n 1 1) 5 a3n
9.
a) (5 )
1
5
1
5
1
5
5 2
5 2 10
10
 
 

2 5 5 5
 

 
 
 
b) 2 2 2 2
1
2
1
2
3 5 3 5 2
2
 
2 ? 5 5 5 5 2 2 2  
c) 5
5
5 5
1
5
1
5
2
4
2 4 2
2
 
2 5 5 5 5 2 2  
d) (10 ) 10 10
1
10
2 3 2 3 6
6
2 ? 2 2 5 5 5 ( )
e) 1 1
x y 2 5 5
1 2 2
2 2
(xy)
xy
 
 
f) 6 6 6 6
1
6
24 3 24 13 21 ? 5 5 5
2 2 2
g) 3 3
3
3
3
3
3
5
2
1 5
2
4
2
?
5 5
5 324 2 2 5 326 5
1
36
h) (221)25 ? (23)22 5 25 ? 226 5 221 5
1
2
10.
a) 2x ? 23 5 2x 1 3
b) 7x ; 73 5 7x 2 3
c) (5x)3 5 53x
d) 83x ? 822x 5 83x 2 2x 5 8x
e) 103x ; 1022x 5 103x 2 (22x) 5 103x 1 2x 5 105x
f) 7x ? 7x 1 3 5 7x 1 x 1 3 5 72x 1 3
g) 2
2
1 1 1
2 2 2 1
n
n
n n n n
2
2 2 2 1 5 5 5 ( )
h) (22)x 2 1 5 22 ? (x 2 1) 5 22x 2 2
i) 3x 1 1 ? 3x 2 1 5 3x 1 1 1 x 2 1 5 32x
j) 10
10
10 10
3
3 3
x
x
x x
1
1 2 5 5

, 5 ? , 5 59 ? 10 6 2
5
5
301
11.
a) x
x
x x x
2
3
2
2 32 5 2 10
2
2 2 5 5 5

 

 
( ( )) ( )
b) (x23 ? x)21 5 ( x23 1 1)21 5 ( x22 ) 21 5 x22 ? (21) 5 x2
c) (xn1 2 2 (xn1 1 2 2 2 2 ? 5 5 5 5 1 2 2 1 2 2 3 2 6
1
6
x x x
x
n) n) ( )
2 2 (xn1 1 2 2 2 2 5 5 5 5 2 1 2 2 3 2 6
1
6
x x
x
n) n) ( )
12. n 5 21
6 – Transformando e
, 5 ? , 5 59 ? 10 6 2
simplificando uma expressão
1.
a) Decompondo 64 em fatores primos,
temos: 64 5 26.
3 4 7 3
6 ? ?
?
? 2
( ) ( )
b) Decompondo 128 em fatores primos,
temos: 128 5 27.
Logo:
1
128
1
2
7 5 5 2
2 7
c) Decompondo 512 em fatores primos,
temos: 512 5 29.
Então:
1
512
1
2
9 5 5 2
2 9
6 3 5 5
2 3 7
18 ?
?
? 2
( ) ( )
d) Decompondo 2 048 em fatores primos,
temos: 2 048 5 211.
2. Decompondo 729 em fatores primos,
temos: 729 5 36.
Então é possível escrever 729 na forma de
potência de 3: 729 5 36
temos: 625 5 54.
Logo:
1
625
1
5
4 5 5 2
5 4
4.
a) 100 000 000 5 108
b) 1
0 00001
, 5 5 5 = 2
100 000
1
10
10 5
7 , 5 5 5
c) 0 0000001
1
10 000 000
1
10
2
10 7
d) 1 000 5 103
( 2
) 2 1 1
temos: 81 5 34.
Então: (81) ( ) 2 2 2 5 5 5 2 4 2 8
1
3
8 3 3
6.
? 2 2 2
?
a) 700 5 7 ? 100 5 7 ? 102
b) 0 06 6 0 01 6
1
100
, 5 ? , 5 56 ? 10 2 2
, 5 ? , 5 ? 57 ? 10 5 2
c) 0 00007 7 000001 7
1
100 000
d) 0 002 2 0001 2
1
1 000
, 5 ? , 5 ? 52 ? 10 3 2
e) 0 000009 9 0000001 9
1
1 000 000
0 000009 9 0 0000 01 9
1
1 000 000
f) 0 5 5 01 5
1
10
, 5 ? , 5 ? 55 ? 10 1 2
7. Decompondo 9, 27 e 243 em fatores
primos, temos:
9 5 32 27 5 33 243 5 35
Então: 9 27 3
3 4 7 3
6 ? ?
?
3 243
? 2
( ) ( )
3 3 3
3 3
1 2
2 3 3 4 7
1 52
5
? ?
?
5
2
2
2
( )
3 3
3 3
3
3
12 7
1 10
11
9
? ?
5 2
2
9 27 3
3 243
3 3 3
3 3
1 2
2 3 3 4 7
1 52
5
? ?
?
5
2
2
2
( )
3 3
3 3
3
3
3 3
12 7
1 10
11
9
? 5 5 11 9 5
2
?
2
2
2
8. Decompondo 125 e 25 em fatores primos,
temos:
25 5 52 125 5 53
Então: 125 25
6 3 5 5
2 3 7
18 ?
?
? 2
5 25
3 6 2 3
6 27
( ) ( )
5 5
5 5
5
?
?
5
2
2
2 ( )
( )
2
2
2
?
5 5 5
6
6 14
12
8
8 5 5
512 125 25
5 3 6 ?
5
2 2
3
2
6
5
12
5
5
5 5 512 2
8 5
5
4
( 5 )
2
25
5 2 6 ?
( 5
27
)
5 2
6 ?
5
14
5
8
9. Decompondo 16, 64 e 1 024 em fatores
primos, temos:
16 5 24 64 5 26 1 024 5 210
Então: (162 ? 643) ; 1 0242 5
5 (24)2 ? (26)3 ; (210)2 5 28 ? 218 ; 220 5
5 28 1 18 2 20 5 26
10. a
b ? c
a 5 1626 b 5 823 c 5 4210
Decompondo 4, 8 e 16 em fatores primos,
temos:
4 5 22 8 5 23 16 5 24
a
( 2
) 2 1 1
b 5
? c
?
5
?
5
2
2 2
2
2 2
( 2 ) ( 2
)
2
2 2
2
4 6
3 3 2 10
24
9 20
24 9 20 525 532
a
b ? c
5
?
5
?
5
2
2 2
2
2 2
( 2 ) ( 2
)
2
2 2
2
4 6
3 3 2 10
24
9 20
24 9 20 525 532
11.
a) ( )
x ? y 2 2 2
(
x ?
y
( )
x y
x y
2 2
2 2
2
2
5
?
?
5 ?
2 5
3 2 4
10 5
12 8 x10 12 y 5 2 2 5 ? 5 8 2 3
3
2
) x y
y
x
( )
( )
x y x y
(
x y
x y
2 2
2 2
2
2
5
?
?
5 ?
2 5
3 2 4
10 5
12 8 x10 12 y 5 2 2 5 ? 5 8 2 3
3
2
) x y
y
x

2 2 1 2(2 1 ) 2 1
3 4 8 1 4 2
302
b) ( )
x y
x y
( )
x y
x y
x y
6 25
7 43
30 10
21 12
? 5
30 21 10
?
?
?
5 ?
2
2
2
2
2 2 22 2 5 ( 12) x9y2
)
)
y
y
x y
x y
x y
25
43
30 10
21 12
? 5
30 21 10
?
?
?
5 ?
2
2
2
2
2 2 22 2 5 ( 12) x9y2
12. 6 10 10 10
? ? ? 3 4 8 1 4 2
6 10 10
10 10
3 4 8
1 4
? ?
5 5 5
2 2
2
2 2 1 2(2 1 ) 2 1
102
10 10
5 5
102
1. E 5 2 800 km 5 2 800 000 m 5
5 28 ? 105 m 5 280 ? 104 m
2. A 5 641 000 km2 5 641 000 000 000 m2 5
5 641 ? 109 m2
3. L 5 4 ? 1 m3 5 4 m3 5 4 000 000 cm3 5
5 4 ? 106 cm3 5 40 ? 105 cm3 5 400 ? 104 cm3
4. V 5 240 m3 5 240 000 dm3 5 240 000 , 5
5 24 ? 104 , 5 240 ? 103 ,
1. 1 5 12
1 1 3 5 4 5 22
1 1 3 1 5 5 9 5 32
1 1 3 1 5 1 7 5 16 5 42
A soma dos 20 primeiros números
ímpares naturais é dada por:
S 5 1 1 3 1 5 1 7 1 ... 5 202 5 400
2. A soma dos 100 primeiros números
ímpares naturais é dada por:
S 5 1 1 3 1 5 1 ... 5 1002 5 10 000
3. A soma dos n primeiros números ímpares
naturais é dada por:
S 5 n2
4. S 5 900 5 n2
Logo: n 5 900 530
900 é a soma dos 30 primeiros números
ímpares naturais.
1.
a) 1 000 000 5 1 ? 106
b) 23 000 000 000 000 000 000 000 5
5 2,3 ? 1022
c) 1 500 000 000 5 1,5 ? 109
d) 6 800 5 6,8 ? 103
205 000 000 5 2,05 ? 108
e) 0,0000000106 5 1,06 ? 1028
f) 300 000 5 3 ? 105
g) 32 000 000 5 3,2 ? 107
h) 0,01 5 1 ? 1022
Resposta em aberto.
1. Resposta em aberto. Resposta possível:
A notícia quer dizer que, em 2006, os
investimentos do Brasil no exterior
foram maiores do que os aplicados pelos
estrangeiros no país.
2. Os investimentos estrangeiros aplicados
no Brasil foram maiores em 2000: 33
bilhões de dólares contra 2,3 bilhões de
dólares, ou seja, 30,7 bilhões de dólares a
mais do que o aplicado pelos brasileiros.
3. Observando o gráfico, podemos
calcular, ano a ano, a diferença entre os
investimentos:
2003 R diferença de 9,9 bilhões de dólares;
2004 R diferença de 8,3 bilhões de dólares;
2005 R diferença de 12,6 bilhões de dólares.
Logo, em 2004, os investimentos
brasileiros no exterior se aproximaram
mais dos investimentos estrangeiros no
Brasil.
4.
INVESTIMENTOS
Ano
Investimento estrangeiro
no Brasil (em dólares)
Investimento brasileiro
no exterior (em dólares)
2000 3,3 ? 1010 2,3 ? 109
2001 2,24 ? 1010 2,3 ? 109
2002 1,66 ? 1010 2,5 ? 109
2003 1,01 ? 1010 2,0 ? 108
2004 1,81 ? 1010 9,8 ? 109
2005 1,51 ? 1010 2,5 ? 109
2006 1,55 ? 1010 2,6 ? 1010
1. Alternativa c.
4
3
A 5 r
3
Para π 5 3,14 e r 5 13, temos:
A5 ? ? 5
4
3
3,14 33 113,04
2. Alternativa a.
(x2)3 ? (x4)5 ? (x3)27 5 x6 ? x20 ? x221 5
5 x6 1 20 2 21 5 x5

a b a b
5 513,5
6
6 6 6 ( )
5 1 1 5 1 1 y 5 y 1 ? y 1 2 2 2 2
5 1 2
303
3. Alternativa d.
?  2
3 4 2 7 ?
0 001 100 ( ) ( )
9 2
2
10 2 2
3 3
3 2
10 8 4
2
3 2 1
2 1 1 2
5
2
2 1 1
5
2 2
( )

 

 

 

 
 

? 5 ? 5 ? 2
 
3
58
3 2
10 8 4
2
1
3
2
2 1 1
5
2

 
 

 
3
58
4. Alternativa b.
2 1 2 4 1 2 2
( ) ( ) 2
? 2 2 2
− 2 2 2
, ( , ) 1 1 3 1
0 1 0 001 10
10 0 0001
10 10 10
2 2 1 1
10 10
? ?
?
( , )
5
? ?
?
5
3
10
10
2 1 2 4 1 2 2
( ) ( ) 2
? 2 2 2
2 2 1 1
10 5 3 2
10
2 1 2 5 5 5 5 5 4
2
2
2
10 10 0 01
1
100
,
1 3 1
? ?
2 2 2
10 10 10
10 ?
10
5
3
10 5 3 2
10
2 1 2 5 5 5 5 5 4
2
2
2
10 10 0 01
1
100
,
5. Alternativa e.
2
x
2
2
1
5 ? ( ) 2
( )
1 2
1
2
1
2
2
2
2
?
2
1 1
5
?
2 ?
5
2
5 ?
2
5
2
2 2
y x
x
y x
x
x y
xy
x
xy
x y
y
x 22y
1
2
2
2
2
2
5
2
5 ?
2
5
x
x
x y
xy
x
xy
x y
y
x 22y
6. Alternativa a.
6
5 1 1 5 1 1 y 5 y 1 ? y 1 y 5 2 2 2 2
a 5 (22)3 5 26
b 5 82 5 (23)2 5 26
c 5 1623 5 (24)23 5 2212
a ? b ? c 5 26 ? 26 ? 2212 5 26 1 6 2 12 5 20 5 1
7. Alternativa b.
1
3
4
2 2  
 
A5 (9 2 ? 3 2 )
2 ? 2 5 9 ? 3
? 5 1
3
1 3 1 3
3
4
 
 
8. Alternativa d.
?  2
( , )
3 4 2 7 ?
0 001 100 ( ) ( )
( , )
10
0 01
10 10
10
4 7
5
3
? 5
 

 
5
2 3
2 2  
12 14
5
10
10
5 ? ( ) 2
( )
5 513,5
 

10 6 3
? 5 ? 5 ? 2
1
3

10 10 10

 

 



  2 1
2 2 ( ) 22 2 5 6 10 9
3 4 2 7 ?
100 ( ) ( )
( , )
10
0 01
10 10
10
4 7
5
3
? 5
? 2

 
5
2 3
12 14
5
10
10
1
10 6 3
? 5 ? 5 ? 2
10 10 10

 

 

 

 
2 1
2 2 ( ) 22 2 5 6 10 9
( , )
( , )
10
0 01
10 10
10
4 7
5
3
? 5
 

 
5
2 3
12 14
5
10 6 3
10 10 10

 

 

 

 
2 1
2 2 ( ) 22 2 5 6 10 9
9. Alternativa b.
a b a b a b
a b a b a b
? ? ? ? ? a b
? ? ? ? ?
5
2
−
?? ? ? ?
? ? ? ? ?
5
2 2
2 2
a b a b a b
a a 4 8 2 2
2 2 1 1
a b a b a b
a b a b a b
? ? ? ? ? a b
? ? ? ? ?
5
2
−
?? ? ? ?
? ? ? ? ?
5
?
?
5
2 2
2 2
2
2 a b a b
a b a b a b
a b
a b
a
4 8 2 2
2 2 1 1
1 4
3
4b3
10. Alternativa e.
3 4
6 12
3 2
2 3 2 3
3 2
3 2
3 2
8 4
4
8 24
2 4
8 8
5 9
? 5
3
?
?
? ? ?
5
?
?
1 27
2
3 4
6 12
3 2
2 3 2 3
3 2
3 2
3 2
8 4
4
8 24
2 4
8 8
5 9
? 5
3
?
?
? ? ?
5
?
?
1 27
2
11. Alternativa c.
A
y y
y
y y
1 2
8
1 2
8 2 6 2 3
6 6
A
y y
y
y y
1 2
8
1 2
8 2 8 11 6 2 3
6 6
6 6 6 6
( )
y6
12. Alternativa b.
x 57 y 5 z5
2
8 87
1
3
2
2 744
1
6
3
2
3
2
x
y
z 1 5 ? 1 5 1
 

 
 
 
2
2 744 62 8 8 7
1
3
2
2 744
1
6
3
2
3
2
x
y
z 1 5 ? 1 5 1
 

 
 
 
2
5 1 5
2
2 744 62 2 780
13. Alternativa d.
s
t
t
s ts
1
1 1 5 s ? t 1 t ? s 1 1 ? ts 5 3
st 2 1 2 1 2 1
( )
s
t
t
s ts
1 1 5 s ? t 1 t ? s 1 1 ? ts 5 3
st 2 1 2 1 2 1
( )

304
Calculando com radicais
7 – Raiz enésima de um número real
1.
a) 3 28 , 10 1 , 5 32 , 49 , 3 2125 , 7 21 , 8 256
b) 4 216 , 21
2.
a) 49 → É definida em IR.
b) 121 → É definida em IR.
c) 225 → Não é definida em IR.
d) 64 → É definida em IR.
e) 10 → É definida em IR.
f) 29 → Não é definida em IR.
3. Para a 5 10, b 5 21 e c 5 23, temos:
b224ac 5 (21)224 ?10? (23) 5 11120 5 121 511
Assim, verifica-se que para esses valores de a, b e c a expressão dada representa um número real.
4. Para x 5 5 e y 5 4, temos:
x21y2 5 52242 5 25216 5 9 53
Logo, a expressão dada é definida em IR.
5.
a) 25 55
b) (26)2 5 36 56
c) 5 232
Decompondo, temos: 32 5 25.
Lembrando que (22)5 5 232, fazemos:
5 232 5 5 (225) 55 (22)5 522
 
, 5 ( ) 5 5 5 , 2  
d) 0 01 10
1
10
1
10
2
2 0 1
e ) 24 81
Decompondo: 81 5 34.
Substituindo:24 81 524 34 523 .
f) 23 28
Decompondo: 8 5 23.
Lembrando que (22)3 5 28, calculamos:
23 28 52 22 52 22 52 3 ( )3 ( )

305
g) 6 64
Substituindo: 6 64 6 26 2 5 5 .
h) 2 (22)2 522
i) 121 511
j) 23 2125
Lembrando que (25)3 5 2125, substituímos:
23 2125 523 (25)3 55
6.
a) 4 16 23 28 54 24 23 (22)3 522(22)521254
b) 3 2125 24 1 1 (23)2 53 (25)3 241352524135252413526
c) 5 32 23 227 16 1 55 25 23 2(3)3 1152131156
d) 7 21 2 16 23 264 521242(24)521
e) 5 2 3 6 8 5 8 9 36 64 5 1 10
1
2
( 3 32 2 );( 21 2 )5( 3 2 ); 1 5 (2 ); 52
f) (24)21(23)2 23 252117 5 1619 23 225117 552(22)57
7. a5 36 1 64 5618514 b5 36164 5 100 510
Logo, a ≠ b.
8. x 5
2 2 2 2
2
5
2 2 2
2
5
2
2
51
2 ( 2) 27 ( )
2 2
4 3
1 2
1
1
1
2 3
0
9. x2 y2 xy ? 5
1.
a) 169 513 e 961 531
Logo, o fato se repete com esse par de números.
b) 12544 5112 e 44521 5211
c) 12769 5113 e 96721 5311
d) 14884 5122 e 48841 5221
2. Trabalho em grupo.

306
8 – Radical aritmético e suas propriedades
1.
a) 102 10 5
b) 5 35 3 5
c) 9 29 2 5
d) 3 73 7 5
e) 6 (2x)6 52x
f) 7 (2?5)7 52 ? 5510
g) (5a2)2 55a2
h) 4 (x2y)4 x2y 5
2.
a) 49 5 72
Logo, 49 72 7 5 5 .
b) 729 5 36
Logo, 6 729 6 36 3 5 5 .
c) 625 5 54
Logo, 4 625 4 54 5 5 5 .
d) 1 024 5 210
Logo, 10 1024 10 210 2 5 5 .
e) 81 5 34
Logo, 4 81 4 34 3 5 5 .
f) 343 5 73
Logo, 3 343 3 73 7 5 5 .
3.
a) 15 25 515 ; 5 25 ;
5 53 2 b) 14 37 14 7 5 ; 37 ;
7 5 3
c) 16 104 516 4 104 4 54 10 ; ;
d) 9 x6 9 3 x6 3 3 x2 5 5 ; ;
e) 10 58 10 2 58 2 5 54 5 5 ; ;
f) 20 a12 20 4 a12 4 5 a3 5 5 ; ;
g) 8 y4 58 4 y4 4 5 y ; ;
h) 21 614 21 7 614 7 3 62 5 5 ; ;

307
4.
a) 14 28 24 5 x → O expoente do 2 deve ser 4.
14;2 28;2 7 24 24 5 5x
Logo, x 5 7.
b) 15 105 3 10 5 x → O índice deve ser 3.
15;5 105;5 3 10 3 10 5 5 x
Logo, x 5 1.
c) 8 54 5 5 x → O índice deve ser 2.
8;4 54;4 2 5 5 5 5 x
Logo, x 5 1.
d) 10 6x 5 6 5 → O índice deve ser 5.
10;2 6x;2 5 6x;2 5 6 5 5
x : 2 5 1 → x 5 1  2 → x 5 2
5.
a) 32 5 25
10 32 10 2 5 10 ; 5 5 5 2 5 ;
5
5 2 b) 27 5 33
9 27 59 33 59 3 33 3 53 3 ; ;
c) 81 5 34
16 81 516 34 516 4 34 4 54 3 ; ;
d) 16 5 24
6 16 6 24 6 2 24 2 3 22 5 5 5 ; ;
e) 64 5 26
8 64 8 26 8 2 26 2 4 23 5 5 5 ; ;
f) 1 024 5 210
12 1024 12 210 12 2 210 2 6 25 5 5 5 ; ;
6.
a) 5 x 510 x
b) 6 54 6
c) 4 3 a 512 a
d) 3 3 2 59 2
e) 8 10 516 10
f) 2 58 2
7.
a) 4 3 64 5 12 26 12 ; 6 5 26 ;
6 5 2
b) 5 243 10 5 5 10 35 5 ; 35 ;
5 5 3

308
8.
a) 4 x 58 x
b) 6 2x 512 2x
c) 3 x 512 x
d) 7 3 x5 21 x5 5
9.
a) x 6 10 524 10
6x 10 524 10 →6? x524→x54
b) 5 x 3 515 3
5x 3 515 3 →5? x515→x53
10.
a) 5?7 5 5 ? 7
b) 3 ax 53 a ? 3 x
c) 7 32 ?11 57 32 ? 7 11
d) 6 x ? y 56 x ? 6 y
e) 2ab 5 2 ? a ? b
f) 3 x2y 53 x2 ? 3 y
11.
a) 10 5 2  5
10 5 2?5 5 2 ? 5
b) 21 5 3  7
6 21 56 3?7 56 3 ? 6 7
c) 35 5 5  7
9 35 59 5?7 = 9 5 ? 9 7
d) 30 5 2  3  5
7 30 57 2?3?5 57 2 ? 7 3 ? 7 5
e) 15 5 3  5
10 15 510 3?5 510 3 ? 10 5
f) 154 5 2  7  11
3 154 53 2?7?11 53 2 ? 3 7 ? 3 11
12.
a) 3 ? 5 5 3?5 5 15
b) 3 2 ? 3 7 53 2?7 53 14
c) 6 3 ? 6 13 56 3?13 56 39
d) 2 ? 5 ? 7 5 2?5?7 5 70

309
13.
a) 12 x5 12 x 12 x5 x 12 x6 12  6      x6 
6  x
b) 20 y3  20 y 20 y3  y 20 y4 20 4 y4 4 5 y  
c) 15 x4y2  15 xy3 15 x5  y5 15 (x  y)5 15 5 (x  y)5 5 3 xy  
d) 14 y3  14 y3  14 y 14 y3  y3  y 14 y7 14 7 y7 7  y  
14.
a)
11
6
11
6

b)
7
5
7
5
3
3
3 
c) 3
11
3
11
8
8
8 
d) 13
2
13
2

e)
2
13
2
13
6
6
6 
f)
4
5
4
5
7
7
7

15. 6 a3 6 3   a3 
3  a
12 b6 12 6   b6 
6  b
a  b  ab
1. 1234321 1111
2. a) 123454321 11111
b) 12345654321 111111
9 – Simplificando radicais: extração de fatores do radicando
1.
a) 2 72 2 72 7 2    
b) 5 35 11 5 35  5 11 3 5 11
c) 3 23 353 3 23  3 3  3 53 25 3 3 103 3
d) 103 102 10 102 10 10 10     
e) 27 2 22 22 22 2 2 2 2 8 2         
f) 3 23 54 3 23  3 53 5 3 23  3 53  3 5 25 3 5 103 5

310
2.
a) x5 x2 x2 x x2 x2 x x x x x2 x 5   5   5   5
b) 3 y4 53 y3  y 53 y3  3 y 5y 3 y
c) x9 x2 x2 x2 x2 x x x x x x x4 x 5     5     5
d) 5 y12 55 y5  y5  y2 5y  y  5 y2 5y2 5 y2
e) x2y3 x2 y2 y x2 y2 y xy y 5   5   5
f) 5 x5y7 55 x5  y5  y2 55 x5  5 y5  5 y2 5xy 5 y2
g) 9 y10 59 y9  y 5y 9 y
h) 10 x13 10 x10 x3 10 x10 10 x3 x10 x3 5  5  5
3.
a) 75 5 3  52
75 3 52 3 52 5 3 5  5  5
b) 700 5 22  52  7
700 22 52 7 22 52 7 2 5 7 10 7 5   5   5   5
c) 250 5 2  53
3 250 53 253 53 53  3 2 55 3 2
d) 192 5 26  3
5 192 55 26 3 55 25 23 55 25  5 23 52 5 6
e) 176 5 24  11
4 176 54 24 11 54 24  4 11 52 4 11
f) 800 5 25  52
800 25 52 22 22 2 52 22 22 2 52 2 2 5 2 20 2 5  5    5    5    5
g) 1800 5 23  32  52
1800 22 2 32 52 22 2 32 52 2 3 5 2 30 2 5    5    5    5
h) 375 5 3  53
3 375 53 353 53 3  3 53 55 3 3
i) 2 700 5 22  33  52
2700 22 32 3 52 22 32 3 52 2 3 5 3 30 3 5    5    5    5
j) 640 5 27  5
6 640 56 26 25 56 26  6 10 52 6 10
4. x 5 5184
5 184 5 26  34
5184 26 34 22 22 22 32 32 22 22 22 32 32 2 2 2 5  5     5     5   33572
Logo, x 5 72.
5. 2 51,41; 3 51,73; 5 52,23; 6 52,44
a) 50 2 52 2 5 5 1 41 7 05 5  5  5  , 5 ,
b) 27 32 3 3 3 1 73 3 5 19 5  5  5 ,  5 ,

311
c) 80 24 5 22 22 5 2 2 5 4 2 23 8 92 5 ? 5 ? ? 5 ? ? 5 ? , 5 ,
d) 150 2 3 52 6 5 5 2 44 12 2 5 ? ? 5 ? 5 ? , 5 ,
e) 200 22 2 52 2 5 2 10 1 41 14 1 5 ? ? 5 ? ? 5 ? , 5 ,
f) 500 22 52 5 2 5 5 10 2 23 22 3 5 ? ? 5 ? ? 5 ? , 5 ,
g) 294 2 3 72 7 6 7 2 44 17 08 5 ? ? 5 ? 5 ? , 5 ,
h) 675 32 3 52 3 5 3 15 1 73 25 95 5 ? ? 5 ? ? 5 ? , 5 ,
6.
a) 9a3 5 32 ?a2 ?a 53?a? a 53a a
b) b? 20b2 b? 22 ?5? b2 2? b? b? 5 2b2 5 5 5 5
c) ab 3 27a4 5a? b? 3 33 ?a3 ?a 5a? b?3?a? 3 a 53a2b 3 a
d) ab a2b5 a b a2 b5 a b a2 b2 b2 b a b a b b b a2b 5 ? ? ? 5 ? ? ? ? ? 5 ? ? ? ? ? 5 3 b
e) 1
2
176
1
2
2 2 11
1
2
a4 5 2 ? 2 ? ?a2 ?a2 5 ?2?2?a?a? 11 52a2 11
f)
1
12
1
5 ? 2 ? 3
? ? ? ? 5 ? ?a?a? b? b 5 a 3b
1
4 3 2 2 2 2 2 3 2
ab
a b
ab
a a b b
ab
g) 1
a
50
1
5 ? ? ? ? ? 5 ? ?a?a?a? a 5 a a
2 5
1
7
5 2 5 2 2
2
2 2 2 2
a a
2
a a a a
a
h) 1
4
48
1
4
2 2 3
1
4
a2b a2b4 5 a2b 2 ? 2 ? ?a2 ? b2 ? b2 5 a2 ? b?2?2?a? b? b? 3 a3b3 3 5
7.
a5 4096 b54 1296 c53 3375
4 096 5 212 → a5 4096 2 2 212 2 26 64 5 5 5 ; ;
1 296 5 24  34 → b54 1296 54 24 ?34 52?356
3 375 5 3353 → c53 3375 53 33 ?53 53?5515
a 1 b 1 c 5 64 1 6 1 15 5 85
8.
6 729 15 1024 23 125
729 5 36 → 6 36 3 5
1 024 5 210 → 5 1024 55 25 ?25 52?254
125 5 53 → 3 125 3 53 5 5 5
6 729 15 1024 23 125 53142552
9.
A
A 53 1728 B
56 64 5?
B 1 728 5 23  23  33 → A53 1728 53 23 ?23 ?33 52?2?3512
64 5 26 → B56 64 5 6 26 5
2 A
12
B 5 2
5
6

312
10.
3 51,73 e 10 53,16
1000 2 27 5?
1 000 5 23  53 → 1000 22 2 52 5 2 5 2 5 10 10 10 3 16 31 6 5 ? ? ? 5 ? ? ? 5 5 ? , 5 ,
27 5 33 → 27 32 3 3 3 3 1 73 5 19 5 ? 5 ? 5 ? , 5 ,
1000 2 27 531,625,19526,41
11.
a)
5 1
50
50 5 2 ? 5 2
5 2 ?
5 5
5 2
5 5 2 5 1 2
( )
1 5 ? 1
b)
3 2
18
18 5 2 ? 3 2
5
3 2
3 3 2 3 1 2
2 5 ? ( 2 )
c)
10 2
8
8 5 2 2
?
2 5
2 2
10 2 2 2 5 2
5 ( )
2 ? 2
d)
10 1
200
200 5 2 2 ? 2 ? 5 2
5 2 ? 5 ?
2 5
10 2
10 10 2 10 1 2
5 ( )
1 ? 1
12. 1728
64
1728
64
27 3 3
6
6
6 6 6 3 3 3
5 5 5 5 ; ;
13. A59800m2 2 1 41 5 ,
3 2 2
9800 2 5 7
2 2 2
9800 2 2 5 7 2 5 7 2 2 5
5 ? ?
A5,2 →,5 5 ? ? ? 5 ? ? ? 5 ? ??7?1,41598,7
Logo, , 5 98,7 m.
14.
E ab c
a 40; b 25; c 200
E
5
1
5 5 5
40 25 200 1200 24 3 52 5 22 22 3 52 2 2 5 3 20 3 ? ? ? 5 ? ? ? 5
5 5 5
? 1 ? ?
15.
A5 5
32 ? 0 0004 ?
25000 5 223
5 2
5 5
32 2 00004
4
10000
5
( , ) ; ,
; ,
2
4 4 2 4
3 5
5
2 5
1
2 5
25000 2 5
0 0004 25000 2
? ?
5 ?
? ? ?
5
5
;
32 ( , )
1
2 5
3 5 6
2 5 2 5
2 4
6 2 2 2
?
? ? ?
2 ? 5 2 ? 2 ? 2 ? 5 2 ? 2 ? 2 ?
5 8 5
5
A5 5 5 5 58?2,23517,84

313
16.
a) 3 4096 12 4096 12 1212 2 5 5 5
b) 10000 54 10000 54 24 ?54 52?5510
1. 1,2 milhão de quilômetros quadrados 5 1 200 000 km2
70% de 1 200 000 5 0,7  1 200 000 5 840 000
Logo, aproximadamente 840 000 km2 do Aquífero Guarani estendem-se
pelo Brasil.
2.
Porcentagem ocupada pelo Aquífero Guarani
Argentina
19%
Brasil
70%
Uruguai
5%
Paraguai
6%
3.
a) 45 000 000 000 000 000 5 45  1015
Notação científica 5 4,5  1016 litros de água.
b) 45  105 5 32  5  105 (Não é um quadrado perfeito.)
22 500 5 22  32  52  52 (É um quadrado perfeito.)
22 500 22 32 52 52 2 3 5 5 150 5 ? ? ? 5 ? ? ? 5
c) Menores números: 50 e 1 800.
50 2 52 2 5 5 2 5 ? 5 ? 5
1 800 22 2 32 52 22 2 32 52 2 3 5 2 30 2 5 ? ? ? 5 ? ? ? 5 ? ? ? 5
10 – Introduzindo um fator externo no radicando
1.
a) 9 2 92 2 162 5 ? 5
Editoria de arte

314
b) 2 7 22 7 28   
c) 10 5 102 5 500   
d) 53 2 3 532 3 250
e) 25 2 5 252 5 64
f) 8 a  82a  64a
g) 2a a  22a2a  4a3
h) x10 x3 10 x10 x3 10 x13   
i) 6b3 2b 3 63  b3 2 b 3 432b4
2.
a) 6 x 3 x2 6 3 x3 x2 18 x5   
b) x 5 x2y3  5 x5  x2  y3 10 x7y3
3. a
b
a
b
a
b
a
b
a
b
a
b
3
2
3
3
6
3
 
 
 
 
 
 
   
 
 
3
63 
a
b
4. 3 3 3 3 32 3 34 33 4 34 33 8 37      
5. x
y
y
x
x
y
y
x
x
y
x x
y
x
x
y
3 32 5
4
4

   4 
4

 

 
11 – Adicionando algebricamente dois ou mais radicais
1.
a) 7  7 2 7 → Verdadeira.
b) 6  5  11 → Falsa.
c) 1 2  3 → Falsa.
d) 10  10  10 3 10 → Verdadeira.
2.
a) 9 10 5 10 4 10
b) 2 5 7 5 16 5 7 5
c) 6  6  6 3 6
d) 6 3 2 10 3 2 4 3 2
e) 2 x 2 x 2 x 2 x 8 x
f) 4 3 74 3 11 4 3 2 4 3 214 3
g) 5a 10 7a 10 9a 10 3a 10
h) 27 6 2 6 119 6
i) 2 7 2 7 3 7 2 7 1

315
j) 2 5 18 2 26 2 18 5 22 2 510 5
3.
a) 12 1 75 29 3 1 27 1 48
12 5 22  3
Logo: 12 22 3 2 3 5 ? 5 .
75 5 3  52
Logo: 75 3 52 5 3 5 ? 5 .
27 5 33
Logo: 27 32 3 3 3 5 ? 5 .
48 5 24  3
Logo: 48 22 22 3 4 3 5 ? ? 5 .
Agora, calculamos:
12 1 75 29 3 1 27 1 48 52 3 15 3 29 3 13 3 14 3 55 3
b) 4 125 13 45 230 5
125 5 53
Logo: 125 52 5 5 5 5 ? 5 .
45 5 32  5
Logo: 45 32 5 3 5 5 ? 5 .
Agora, calculamos:
4 125 3 45 30 5 4 5 5 3 3 5 30 5
20 5 9 5 30 5 5
1 2 5 ? 1 ? 2 5
5 1 2 52
c) 54 1 6 2 150 12 24
54 5 2  33
Logo: 54 2 32 3 3 6 5 ? ? 5 .
150 5 2  3  52
Logo: 150 2 3 52 5 6 5 ? ? 5 .
24 5 23  3
Logo: 24 22 2 3 2 6 5 ? ? 5 .
Agora, calculamos:
54 6 150 2 24 36 6 5 6 2 2 6
8 6 5 6 3 6
1 2 1 5 1 2 1 ? 5
5 2 5
4.p5 28 1 112 1 175
28 5 22  7
Logo: 28 22 7 2 7 5 ? 5 .
112 5 24  7
Logo: 112 22 22 7 4 7 5 ? ? 5 .
175 5 52  7
Logo: 175 52 7 5 7 5 ? 5 .

316
Então:
p5 28 1 112 1 175 52 7 14 7 15 7 511 7
5. A5 18 13 50 1 98 ; 2 51,41
18 5 2  32
Logo: 18 2 32 3 2 5 ? 5 .
50 5 2  52
Logo: 50 2 52 5 2 5 ? 5 .
98 5 2  72
98 2 72 7 2 5 ? 5
A5 18 13 50 1 98 53 2 13?5 2 17 2 53 2 115 2 17 2 525 2
Como é dado 2 51,41, fazemos:
A525 2 525?1,41535,25
6.
a) 16x 1 9x 2 36x
2 2
16 2 2 4
9 3 3
36 2 3 6
16 9 36
x x x
x x x
x x x
x x
5 ? ? 5
5 2
? 5
5 2 ? 2
? 5
1 2 x 54 x 13 x 26 x 5 x
b) 8a3 1 72a3 2 18a3
3 3 3 2 2
8 2 2 2 2 2
72 2 3 2 2 3
a a a a a a
a a a
5 ? 5 ? ? ? 5
3 5 3 ? 2 ? 3 5 2 ? ? 2
? 2
3 2 2
3 3 3
6 2
18 2 3 3 2
8 72 18 2 2
? 5
5 ? ? ? 5
1 2 5 1
a a a
a a a a a
a a a a a 6a 2a 23a 2a 55a 2a
c) 3x x2y 22 x4y 16x2 y 53x ? x y 22x ? x y 16x2 y 57x2 y
d) 3 3 7 3
4
a ab 2 ba b 1 ab ab
5
3 a a b 2 b 7 b a 2 a b ab 2
2
a b
5 ? ? 2 ? ? 1 ? ? 5
53ab ab 27ab ab 12ab ab 522ab ab
1
4
1
2
7. x5 48
1 243
2
2 2
5 ? ? 5
5 ? ? 5
5
1
6
12
48 2 2 3 4 3
243 3 2 3 2
3 9 3
12
2 3 2 3
1
4
48
1
2
243
1
6
12
1
4
4 3
1
2
9 3
1
6
2 3
3
2 ? 5
5 1 2
5 ? 1 ? 2 ? 5
x
x
5
11 2 5
1 2
5
9
2
3
1
3
3
6 3 27 3 2 3
6
31 3
6
8. p54 486 14 96 15 216
5 2 2
486 5 2 ? 3 5 2 ? 3 ? 3 ? 3 5
9 6
96 5 2 5 ? 3 5 2 2 ? 2 2
? 2 ? 3 5
4 6
216 5 2
3
?? 3 5 2 ? ? 2
? 5
3 2 2 3 3 6 6
p 6
4 486 4 96 5 216 36 6 16 6 30 6 82
5 1 1 5 1 1 5

317
5 2 2
486  2  3  2  3  3  3 
9 6
96  2 5  3  2 2  2 2
 2  3 
4 6
216  2
3
 3  2   2
 
3 2 2 3 3 6 6
4 486 4 96 5 216 36 6 16 6 30 6 82
p       
6
9. 28 
175
63
28  2  7 
2 7
175  5  7 
5 7
63  3  7 
3 7
28 
175
63
2 7 5 7
3 7
2
2
2


7 7
3 7
 
7
3
10. p2 250 2 40
2
250  2  5  5 
5 10
40  2 2
 2  5 
2 10
2 5 10 2 2 10 10 10 4
p      10 14 10
14 10

p cm
11. x3 250 3 16 3 54 3 2
3 3 3 3
250  2  5 
5 2
16  2  2  2 
2 2
54  2  3 
3 2
3 3 4 3 3 3
3 3 3 3
3 3 3 3
x 2
50  16  54 
2
3 3 3 3 3
x    
5 2 2 2 3 2 2 5 2
12. 50 
18
200
50 2 5 5 2
18 2 3 3 2
200 2 5 2 2 5 10 2
50 18
  
  
     

00
2
2
2
3 2 2 2
5 2 3 2
10 2
2 2
10 2
1
5


 
13. 3 20  80 
2 45
8
2
20  2  5 
2 5
80  2 4  5  2 2  2 2
 5 
4 5
45  3 2
 5 
3 5
3 20  80  2 4
5
8
6 5 4 5 6 5
8
5
2

 

14. x 2 ; y 98  32  8
2
98  2  7 
7 2
32  2 5  2 2  2 2
 2 
4 2
8  2 3  2 2
 2 
2 2
xy 2  7 2
4 2 2 2 2 2

318
15. a5 2 ; b5 1 ;
c5 2
1 27 1 75 2 108
27 5 3 3 5 3 2
? 3 5
3 3
75 5 3 ? 5 2
5
5 3
108
55 22 ?33 52 ?3 3 56 3
a) a1b1c5123 3 1115 3 1226 3 5424 3
b) a2b2c5(123 3 )2(115 3 )2(226 3 )5
5123 3 2125 3 2216 3 52222 3
16. 5 52,23; 2 51,41
x5 1 1 1
5000 500 50 5
3 4
5000 5 2 ? 5 5 2 ? 5 ? 5 ? 2 5
50 2
500 5 2 2 ? 5
3 5
2 5 5 10 5
2
? ? 5
50 5 2 ? 5 5
5 2
x
5 5000 1 500 1 50 1
5
x 5 50 2 1 10 5 1
5 2
11 5 1
5 ? 1 ?
5 1 5
5 55 2 11 5
55 1 41 11 2 23
77 55 24 53 102 0
x
x
, ,
, , , 8
17. A5 2 B5 2
243 162 300 50
2 2
243 5 3 ? 3 ? 3 5
9 3
162 5 2 ? 3 4
5
9 2
300
5
;
2 2
2 ? 3 ? 5 5
10 3
2
50 5 2 ? 5 5
5 2
9 3 9 2 10 3 5 2
A ;
B
A B
5 2 5 2
1 5 2
(( 9 3 9 2
)1(10 3 25 2 )519 3 214 2
18. 3 17 , ; 2 1 ,
4
5 5
2 1 1
5 ? 5
5 ? 5
4 3 7 18 5 48 200
18 2 3 2
3 2
48 2 4
3 4 3
20
0 5 23 ? 52 5
10 2 4 3 7 18 5 48 200
4 3 21 2 20 3 10 2
24 3 11 2
24 1 7
2 1 1 5
5 2 1 1 5
5 2 5
5 ? , 22 11 ? 1 ,
4
5
5 2 5
408 , 15 , 4 25 ,
4
12 – Multiplicando expressões com radicais de mesmo índice
1.
a) 5 ? 7 5 5?7 5 35
b) 5 2a ? 5 7a 55 2a?7a 55 14a2

319
c) 3? 2 ?9 3 527? 2?3 527 6
d) 3 xy ? 3 xy 53 xy ? xy 53 x2y2
2.
a) 6 3 18 2 32 3 2 ? 5 5 ? 5
b) 28 21 588 22 3 72 2 7 3 14 3 ? 5 5 ? ? 5 ? ? 5
c) 10 20 200 23 52 2 5 2 10 2 ? 5 5 ? 5 ? ? 5
d) 2 21 5 2 7 10 294 10 2 3 72 70 6 ? ? 5 ? 5 ? ? 5
3.
a) p52?9 2 12?5 2 518 2 110 2 528 2
p528 2 cm
b) A59 2 ?5 2 545? 2?2 590
A 5 90 cm2
( ) 2
2
4 A5 9 5 59 5 ?9 5 581? 5 581?55405
A 5 405 unidades de área.
5. A
b h
5
?
2
A
A
5
5 6 ?
3 2
5 5
?
5
? ?
5
2
5 5 ?
15 12
2
15 2 3
2
15 2 3
2
15 3
15 3 15 1 73
2
, 525,95
A 5 25,95 cm2
6. A
B b h
5
( 1 )?
2
A5
+
?
?
?
5
5
5 5
12 5 ( )
,
3 5 2 5 5
2
5 5 5
2
5 5
2
25
2
7. V 5 a  b  c
V
V
3 3
12 6 3 12 6 3 216 2 3 2 3 6 6 6
6 6 6 2 45 14
5 ? ? 5 ? ? 5 5 ? 5 ? 5
5 5 ? 5
, ,7
V 5 14,7 cm3
8.
a) 3 x2 ? 3 x2 53 x2 ? x2 53 x4 5x 3 x
b) 6 a5 ? 6 a3 ? 6 a5 56 a5 ?a3 ?a5 56 a13 56 a6 ?a6 ?a 5a?a 6 a 5a2 6 a
c) 4 st3 ? 4 t 54 st4 5t 4 s
d) 5 a4b 5 ab6 5 a5b7 ab 5 b2 ? 5 5
e) a
x
ab
x
2
2
a b
x
a
x
? 5 5 b
f) 8 x3y7 ? 8 2x5y 58 2x8y8 5xy 8 2
g) 2 2
2 2
ax
? 3
? 5
n 3
2 2
3
2 2
3
3 2 2
2
a
n
x ax
n
a x
n
a x
n
? ?
?
5
? ?
5

320
1.
a) 2 6 3 2 6 2 3 12 6 22 3 6 2 3 6  (  )5    5  5   5 
b) 7  ( 7  2 )5 7  7  7  2 5 49  14 57 14
c) 10  (5 2 3 10 )5 10 5 2 3 10  10 55 20 3 100 5
55 22 5 310510 5 30
d) 5  (7 5 )57 5  5  5 57 5 5
e) 15 3 5 15 3 15 5 45 75 32 5 3 52  (  )5    5  5    5
53 5 5 3
f) 8 2 6 2 8 8 6 2 23 48 4 2 24 3 4 2 4 3  (  )5    5   5   5 
2.
( ) ( )
a) 2 6 2 26 2 2 2 2 6 6 2 2 6 6
   5        5
2 2 12 12 2 6
5     5
5
10 12 10 22 3 10 2 3  5   5 
( )( )( ) 2
   5 5  5
b) 5 7 5 7 52 7 25 7 18
( ) ( )
c) 3 5 2 5 3 3 5 5 9 5 2 5 6
   5     5
3 5 7 5 6 9 7 5
5    5 
( )( )( ) 2
   5 5  5
d) 4 13 4 13 42 13 16 13 3
( ) ( )
3. A5 6 2  1  2 3  6 5 12  6  6  12
5
2 12 2 22 3 4 3
5 5   5
( ) ( )
4. x5    5     5
3 2 3 1 3 3 3 3 2 3 2 3 3
3 3 6 3 3
5   5 
5.
a) p52 (5 5 )2 (6 5 )5102 5 122 5 522
p 5 22 cm
b) A5(5 5 ) (6 5 )5305 5 6 5 5525 5
A5(25 5 )cm2
6.
(  ) 2
5 2
   ( ) 5
512 5 5562 5
a) 1 5 1 2 1 5 5
2
( ) 2
 5    ( ) 5
544 3 3574 3
b) 2 3 2 2
2 2 3 3
2
( ) 2 5( ) 2 ( ) 2
    5
552 15 3582 15
c) 5 3 5 2 5 3 3
( ) 2 5( ) 2 ( ) 2
    5
572 14 2592 14
d) 7 2 7 2 7 2 2

321
2
1 ? 2 5 ( 1 )? ( 2 ) 5 2( ) 5 2 5
7. 7 5 7 5 7 5 7 5 72 5 49 5
5 44 5 22 ?11 52 11
8. 10 10 10 10 10 10 10 10 10 10 100 10
9
2
2
1 ? 2 5 1 ? 2 5 2 5 2 5
5
( ) ( ) ( )
0 2 32 5 3 10 5 ? ? 5
( ) ( )
9. 2 1 ? 1 2 52 2 1 1 2 5
5 2 7 4 7 37 20 5 7 8 7 14 3 7
6 3 7 37 6
52 1 2 52
( ) ( )
10. 4 2 3 2 1 4 2 2 4 2 3 2 3
1 ? 2 5 ? 2 1 2 5
8 2 3 5 2
5 2 2 5 2
Considerando 2 51,41, temos:
52 2 5521,4153,59
11.
( 4 2 ) ( 4 2
)
4 2
16 2
( 3 3 ) ( 3 3
)
3 3
9 3
5 1
2
2
2
2
1 ? 2
1 ? 2
5
2
2
5
2
2
( )
( )
4
6
7
3 5
12.
a)
2 6 24
2 144
2 2 3
2 4 3
? x
5 ?
x
5
x
5 4 ?
2
x
5 ?
12
x
5
2
x
5
6
b)
9 x
13 10 13 10
9 x
13 10
( ) ( )
( ) ( )
? 5 2 ? 1
2 2
5 2
9 13 10
3
9
1
3
x
x
x
5 2
5
5
2 ( ) ( ) ( )  
 
( )
13. V59? 62 2 ? 61 2 59? 622 2 59? 3622 5306
V 5 306 cm3
13 – Dividindo expressões com radicais de mesmo índice
1.
a) 15 3
15
3
; 5 5 5

322
b) 21 7
21
7
4  4 4 4 3
c) 162 3
162
3
54 2 33 3 6      
d) 240 6
240
6
40 22 2 5 2 10       
e) 90 5
90
5
18 2 32 3 2      
 5 5 6 5 5   5
f) x x
9
3
x
x
5 9 5 3 x x x x x
g) a a
8
3
a
a
3 8 3 3 a a a a a
3 3 5 3 3 2 3 2      
 4 4 4  4
h) a b ab
5 2
a b
ab
4 5 2 4 a b a b
2. 8 20
2

8  2  2  2 
2 2
20  2  5 
2 5
8 
20
2
2 2 2 5
2
4 5
3 2
2



3.
a) 40
5
40
5
8 23 22 2 2 2      
b) 54
3
54
3
18 2 32 3 2     
c) 486
3
486
3
162 2 34 9 2     
d) 150
3
150
3
50 2 52 5 2     
e) x
x
x
x
x x x x x
7 11
7 3
11
3
7 7 8 7 7   7
f) 972
3
972
3
324 2 3 2 3 18
6
3
6
3
x x
3 2 4 3 2
x
x
  x    x    x x  x x
3 3
a 2 2 2
a
g) 225
5
225
5
45 3 5 3 5
a
a
  a   a  a
h) 192
3
192
3
64 2 2 2
5 7
5 2
7
2
b b
 5  5 b 5  5 6  b 5  b
5
b
b
4. 2 3
2 6
6 2
2 3
3
( 2 3 )
3
 3
2 6
6 2
( 2 6
)) (  )









 


 

 
 

 



  


6 2
2 3 3
2 6 4 6 2 6
3 2 3
2

323
14 – Multiplicando e dividindo expressões com radicais de índices diferentes
1.
a) 3 2 , 3
m.m.c.(3, 2) 5 6
Logo: 6 22 , 6 33 .
b) 7 a3 , 3 b2
m.m.c.(7, 3) 5 21
Logo: 21 a9 , 21 b14 .
c) 5 32 , 4 33
m.m.c.(5, 4) 5 20
Logo: 20 38 , 20 315 .
d) 14 25 , 21 29
m.m.c.(14, 21) 5 42
Logo: 42 215 , 42 218 .
e) 10 32 , 6 2 , 15 24
m.m.c.(10, 6, 15) 5 30
Logo: 30 36 , 30 25 , 30 28 .
f) 5 34 , 10 6 , 2
m.m.c.(5, 10, 2) 5 10
Logo: 10 38 , 10 6 , 10 25 .
2.
a) 10 2 e 15 22
m.m.c.(10, 15) 5 30
30 23 e 30 24
30 23 30 24 10 2 15 22  → 
b) 12 310 e 18 311
m.m.c.(12, 18) 5 36
36 3 30 36 3
22
3 3 3 3
e
. → .
36 30 36 22 12 10 18 11
c) 6 25 e 9 27
m.m.c.(6, 9) 5 18
18 2 15 18 2
14
2 2 2 2
e
. → .
18 15 18 14 6 5 9 7
d) 8 23 e 6 23
m.m.c.(8, 6) 5 24
24 2 9 24 2
12
2 2 2 2
e
 → 
24 9 24 12 8 3 6 3

324
1.
a) 3 10 ? 5 10
m.m.c.(3, 5) 5 15
15 105 15 103 15 105 103 15 108 ? 5 ? 5
b) 7 ; 5 7
m.m.c.(2, 5) 5 10
10 75 10 72 10 75 72 10 73 ; 5 ; 5
c) 4 3 ? 3
m.m.c.(4, 2) 5 4
4 3 4 32 4 33 ? 5
d) 2 20 27 ;
m.m.c.(2, 20) 5 20
20 210 20 27 20 23 ; 5
e) 6 52 10 53 ;
m.m.c.(6, 10) 5 30
30 510 ;30 59 530 5
f) 6 75 3 72 ;
m.m.c.(6, 3) 5 6
6 75 ; 6 74 56 7
g) 4 23 5 24 10 27 ? ?
m.m.c.(4, 5, 10) 5 20
20 215 20 216 20 214 20 245 20 220 220 25 2 220 25 4 2 ? ? 5 5 ? ? 5 ? 5 4
h) 8 65 12 62 ;
m.m.c.(8, 12) 5 24
24 615 24 64 24 611 ; 5
2.
a) 8 a5b3 6 ab2 ;
m.m.c.(8, 6) 5 24
24 a15b9 24 a4b8 24 a11b ; 5
b) 9 a7b6 6 a3b2 ;
m.m.c.(9, 6) 5 36
36 a28b24 36 a18b12 36 2 a10 2b12 2 18 a5b6 ; 5 5 : : :
c) a
b
b
a
3
3
a
b
b
a
a
b
b
a
a
b
a
b
a
b
; 3 6
; ;
2
2
6
3
3
2
2
6
3
3
2
2
6
5
5
5 5 5 ? 5 6
d) a b a b a b a b
15 9
10 9
a b
a b
4 5 3 12 10 9 12 15 9 12 10 9 a
12 12 5 ; 5 ; 5 5
e)
(ab)
ab
a b
a b
a b
a b
a b
6 5
4 3
12 10 10
12 3 9
10 10
3 9
12 12 7 5 5 5

325
15 – Potenciação de uma expressão com radicais
1.
2
( ) 5 ? 5 2 5
a) 17 17 17 17 17
4
( ) 53 ? 3 ? 3 ? 3 53 4 53 3 ? 5 3
b) 3 2 2 2 2 2 2 2 2 2 2
2
( ) 5 ? 5 ? ? 5 ? 2 5 ? 5
c) 6 2 6 2 6 2 36 2 2 36 2 36 2 72
d) 1
2
10
1
2
10
1
2
10
1
4
10 10
1
4
10
2  
 
 
 
 
 
5 ? 5 ? 5 ? 5
5
2
2.
2
a) (a b ) 5 (a b ) ? (a b ) 5 a 2 ? b 2 5
a 2 b ( ) 4
5( 3 )? ( 3 )? ( 3 )? ( 3 )5 4 ? 3 4 5 4 ? 3 3 ? 5ab4 3 a
b) b3 a b a b a b a b a b a b a a
( ) 4
5( 3 )? ( 3 )? ( 3 )? ( 3 )5 4 ? 4 ? 3 4 5 4b5 3 b
c) ab3 b ab b ab b ab b ab b a b b a
d) a
b
ab
2 2
a
b
2 2 5 ? 5 5
ab
a
b
ab
a
b
a b
a a
b
 
 
 
 
 
 
2
?
?
a b
? ? 5
b
3
a
b
2( ) 3
5 3 2 3 5 3 5 2 ? 5 ? ? 5
3. 4 8 2 42 2 3 2 3 2 2 3 2 2 6 2
4. x52 3 ; y53 2
x2 y2
( ) ( )
2 2
2 3 3 2 2 3 2 3 3 2 3 2 36 3 3 2 2
? 5 ? 5 ? ? ? 5 ? ? ? ? 5
5 ? ?
36 3
3 ? 2?2 536?3?25216
5. a5 10 e b52 5
2 1105( 10 ) 2(2 5 ) 110510222 ? 52 11052022050
a2 b2
2 2
6.
( ) 2 5( ) 2 1 1 ? ? 1( ) 2
5 1 1 5 1
a) 3 2 3 2 3 2 2 3 2 6 2 5 2 6
( 2 ) 2
5 2
2 ? ? 1( ) 2
5 2 1 5 2
b) 1 7 1 2 1 7 7 1 2 7 7 8 2 7
( )( )5( ) 2
1 2 2 2 5 ? 2 2 5 2 5
c) 4 2 5 4 2 5 4 2 5 16 2 25 32 25 7
( 1 ) 2
5 2
1 ? ? 1( ) 2
5 1 1 5 1
d) 2 10 2 2 2 10 10 4 4 10 10 14 4 10
( 1 )( 2 )5( ) 2 2( ) 2
5 2 5
e) 11 7 11 7 11 7 11 7 4
( ) 2 5( ) 2 1( ) 2
1 1 ? ? 5
5(9?3)16 6 1252916 6
f) 3 3 2 33 23 3 2 2
( 1 )( 2 )5 2( ) 2
5 2 5
g) 7 19 7 19 72 19 49 19 30
( )( ) ( ) 2
2
h) 23 5 11 23 5 21 5 23 5 21 54521544
( ) 2 5( ) 2 1( ) 2
1 1 ? ? 5
5(4 ?7)112 35 1(9?5)528112 35 145573112 35
i) 2 7 3 5 2 7 2 2 7 3 5 3 5

326
7.
( ) 2
( )
2 2
a) A 3 3 3 23 3  3 96 3 3126 3
A126 3
( ) 2
( )
2 2
b) A 5 7 5 25 7  7 2510 7 73210 7
A3210 7
8. a 5  3
a2
( 5  3 ) 2 ( 5 ) 2 2 5  3 ( ) 2
3 52 15 382 15
9. x3 2
6 2 (3 2 ) 6 2 
3223 2  2 6 2 96 2 26 2 11
a) x2
2
2 ( )
4 4(3 2 ) 4(3 2 )4
b) x2 x
2
2
2 ( )
3 2 3 2 2 12 4 2 4
9 6 2 2 12 4 2 4 5 2 2
        
       
10. x24x20, se x2 2
( ) 2
( ) 2
( )
2
2 2 4 2 2 2 2 2 2 2 2 8 4 2 2
4 4 2 2 8
            
    
4 2 2884 2 4 2 0
Portanto, a igualdade é verdadeira.
11.
a 8 6 eb 8 6
a b (8 6 ) (8 )
   
     
2 2 2 2
2 8 2
2
( )  
 
6
64    16 
6  6  
140 ( )  
8 6 8 28 6
        
64 16 6 6
   
2
6 2 6
12.

 ( 21 13 ) ( 21 13 ) ( 10 7 ) ( 10 7
)
( ) ( )        
 ( ) ( )  
2 2
21 13
 

 



2 2
 10  7  2113  10 7 835
13.
( )
2
3 2 5 720 18
3 2 3 2 5 2 5 2 2 3

2
( )   
2
2 2 2
   
        
5 18
 
             

1
9 12 5 4 5 2 2 3 5 18 29 12 5 12 5 18 1
14.
(  
2
7 5 ) ( 7 5 )( 7 5
)
( ) ( )     
 
( ) (( )  
2 2 2
7 2 7 5 5 7 5
      
 




2
7 2 35 5 7 5 10 2 35

      

327
15.
( 6 2
)
( 7 3 ) ( 7 3
)
6 2 6 2 2
7 3
6 2
2 2 2
2 2
1
1 ? 2
5
1 ? ? 1
2
5
5
1
( ) ( )
( ) ( )
12 2
7 3
8 2 2 3
4
8 4 3
4
2 3
2 1
2
5
1 ?
5
1
5 1
1.
a)
3 6 0
3 6
3 36
x x
2
x
x
x
12
2
5
5
5
5
(  )
( )
Verificação:
x 5 12 (Satisfaz a condição x0.)
3 6
3 12 6
6 6 12
x 5
? 5
5 →Logo, x5 vale como solução:S5{12}.
b)
3 2 5 3 2 0
3 2 5
3 2 25
3 25 2
x x
x
x
x
x
2 5 2
27
3
2
9
2
2 5
2 5
5 1
5 5
(  )
( )
Verificação:
3 x
2 9
2 5
? 2
2
9 2 0
27 2 0
25 0 9
x 5
s




0,parax :
3
→ atisfaz a condição 0.
Logo, x 9 vale
3 2
3 2 5
3 9 2 5
25 5
5 5
x
x
2
2 5
? 2 5
5
5 5

→ como solução:S5{9}.
c)
2 1 3 2 1 0
2 1 3
2 1 9
2 8
x x
x
x
x
x
1 52 1
4
2 2
1 52
1 5
5
5
(  )
( ) ( )

328
Verificação:
2 x 1 1 
0
, para x
5
4:
2 ? 4 1
1 
0
9 
0 x 5
4 s
2
→ atisfaz a condição x
x
1
1 52
? 1 52
52
52 5
1 0
2 1 3
2 4 1 3
9 3
3 3
 .
→ Logo, x 4 não vale como solução:S5 .
d)
2 4 0
2 4
4 16
x x
2
x
x
x
4
2
5
5
5
5
(  )
( )
Verificação:
x
5
4
(Satisfazacondiçãox 0.)
2 x
5
4
2 4 5
4
2 ? 2 5
4
4 5
4
Logo

→ , x54 vale como solução:S5{4}.
e)
3 12 0
3 12
9 144
x x
2
x
x
x
16
2
5
5
5
5
(  )
( )
(Satisfaz a condição x0.)
Verificação:
3 x 5
12
3 16 5
12
3 4 12
12 12
? 5
f)
2
x 1 x 2 5
x
x x x
x x x
x
x
( 2
)
2
2
3 9
3 9
3 9
1 2 5
2 2
1 2 5
5
5
3 9
3
Verificação:
x2 x x
1 2 5
2
1 ? 2 5
1 2 5
5
3 9
3 3 3 9 3
9 9 9 3
9 3
3 3

329
g)
2 5 8
2 5 8
2 5 8
2 8 5
x 1 5 x
1
x x
x x
x x
x
( ) ( )
3
2 2
1 5 1
1 5 1
2 5 2
5
Verificação:
2 5 8
2 3 5 3 8
11 11
x1 5 x1
? 1 5 1
h)
3 2 6
( 3 2 )
6
9 2 36
18 36
2
2
2
x
x
x
x
x
5
5
? 5
5
5
Verificação:
3 2 x
6
3 2 2 6
3 2 6
6 6
S
5
? 5
? 5
5 →Logo, x52 vale como solução: 5{2}.
2. x x
2 1
2
2 2 1
1 5 1
( ) (x 1)
x
x x x
1 5 1 1
x
2 52
x
2
2
2 2
1 5 1
2 2
2 1
1
2
5
Verificação:
x2 x
2 1
1 5 1
2
1
2
2
1
2
1
1
4
2
3
2
9
4
3
2
3
2
3
2
1 5 1
1 5
5
5
 
 
1
2 { }.
1
2 5 5
→ Logo, x valecomo solução:S
3. 5 2 6 9
x 1 5 2 1
x
x x
( ) ( )
5x 2 6 9x
5x 9x 6 2
22 52
5
2 2
5 1 2 5 2 6 1
9
1 52 1
2 52 2
4x 8
x 2

330
Verificação:
5 x 2 6 9
x
5 2 2 6 9 2
12 12 2
1 5 2 1
? 1 5 2 1 ?
5 → Logox , 5 valecomo
solução:S5{2}.
4. x
x
5
2 5
x
x
x
x
2
5
2
2 5
2
2 5
2
3
5
5
3
5
5
9
5
2
2
( − ) 
 

 
(x 5) 2
9
x
2 10x 1 25 2 9 5
0
x 2
10x 16 0
(x 8) (x 2) 0
x 8oux 2
2 1 5
2 ? 2 5
5 5
Verificação:
Para x 5 8 → x
5 ? 5 5
x
2 5
2
2 5
2
3
5
8 5
3
8 5
→ → 3 3 3→3 3
Logo, x 5 8 vale como solução.
Para 5 2 → x
x
2 5
2
2 5
2
2 5
2
5
3
5
2 5
3
2 5
3
3
3
→ →
Não existe 23 em IR; logo, x 5 2 não vale como solução.
Portanto, S 5 {8}.
16 – Racionalizando denominadores de uma expressão fracionária
1.
a) 2
10
2
10
10
10
2 10
10
2 10
10
10
5 ? 5 5 5
2 5
b)
6
6
6
6
6
6
6 6
6
6
5 ? 5 5
2
c)
9
3
9
3
3
3
9 3
3
3 3
5 ? 5 5
2
d)
5
2
5
2
2
2
10
2
10
5 ? 5 5
2 2
e)
20
2 5
20
2 5
5
5
10 5
5
2 5
5 ? 5 5
2
f)
3
6
3
6
6
6
3 6
6
6
5 ? 5 5
2 2
g)
20
3 10
20
3 10
10
10
20 10
3 10
20 10
3 10
2 10
2 3
5 ? 5
?
5
?
5
h) 1
7
7
7 5 ? 5
1
7
7
7

331
i) 2 3
5 2
2 3
5 2
2
2
2 6
5 2
6
5 ? 5 5
2 5
j) 7 3
2 7
7 3
2 7
7
7
7 21
2 7
21
5 ? 5 5
2 2
2.
a) 1 3
3
( 1 3
) 2
3
3
3
3 3 3
3 3
3 3
3
2
5
2
? 5
2 ?
?
5
b) 3 2
2
3 2
2
2
2
3 2 2 2
2 2
3 2 2
2
− ( 2
) 5
? 5
2 ?
?
5
2
c) 5 2
5
( 5 2
)
1 5
5
5
5 5 2 5
5 5
5 10
5
1
5
1
? 5
? 1 ?
?
5
d) 3 2
3
3 2 3
( ) 2
3 3
9 6
3
3 6
3
2
5
2 ?
?
5
2
5
e) 2 2
2 1 1
2
2 2 2
2 2
2 2 4
2
2 2 2
2
5
1 ?
?
5
1
5
1
5 1
( )
f) 1 2
5
1 2 5
( ) 1
5 5
5 10
5
1
5
1 ?
?
5
3.
a) x
x
x
x
x
x
x x
x
5 ? 5 5 x
b)
x
y
x
y
y
y
x y
y
x y
5 ? 5 5
2 2 2 2 2y
c) xy
x
xy
x
x
x
xy x
5 ? 5 5 5
x
xy x
x
y x
5 5 5 2 5 5
d) x y
y x
xy
y 5 ? 5 5 5
x y
y x
x
x
x xy
y x
x xy
yx
2
4.
a) 3
10
3
10
10
10
30
10
30
5 ? 5 5
2 10
b) 5
3
5
3
3
3
5 3
3
15
2 3
5 ? 5
?
5
c) 1
2
1
2
2
2
2
2
2
5 ? 5 5
2 2
d)
1
8
1
2 2
1
2 2
2
2
2
2 2
2
2 2 4
5
?
5 ? 5 5
e) 0 9
9
10
9
10
3
10
10
10
3 10
10
3 10
, 5 5 5 ? 5 5
2 10
f) 5
8
5
2 2
5
2 2
2
2
10
2 2
10
2 2 4
5
?
5 ? 5 5
5. 6 52,449; 2 51,414; 10 53,162
a) 3
2
3
2
2
2
6
2
6
2
2 449
2
1 224
5 ? 5 5 5 5
2
,
,
b) 2
5
2
5
5
5
10
5
10
5
3 162
5
0 632
5 ? 5 5 5 5
2
,
,

332
c) 1
2
1
2
2
2
2
2
2
2
1 414
2
0 707
5 ? 5 5 5 5
2
,
,
d) 2
3
2
3
2 3
3 3
6
3
2 449
3
?
?
,
5 5 5 5 5
0 ,
816
6.
a) 1
6
1
6
5 2
6
6
6
6
6
5 3 5 3 5 2
6
5 2
5 5
5 2
5 ? 5 5
b) 15
3 5 3 3
5
15
5
5
5
15 5
5
15 5
5
3 2
3 2
3 2
3 3
3 2
3 2 5 ? 5 5 5
c) 2
2
2
2
2
2
2 2
2
2 2
2
2
9 7 9 7
9 2
9 2
9 2
9 9
9 2
9 2 5 ? 5 5 5
d) 6
3
6
3
3
3
6 3
3
6 3
3
2 3
10 5 10 5
10 5
10 5
10 5
10 10
10 5
10 5 5 ? 5 5 5
e) 4
8
4
8
8
8
4
4 8
8
4 8
8
8
4
4
4 3 4 3 4 4
2
4 4
5 ? 5 5 5
f) 20
10
20
10
10
10
20 10
10
20 10
11 8 11 8
11 3
11 3
11 3
11 11
1 3
5 ? 5 5
1
11 3
10
52 10
7.
a) 1
3 6
1
3 6
3 6
3 6
3 6
3 6
3 6
2 9 6
5
2
2
2 ?
1
1
5
1
2
5
1
2
5

 

 

 

 
( )
3 1
6
3
b) 2
5 3
2
5 3
5 3
5 3
2 5 3
5 3
5 3 ( )
2 5
5
1
1
2 2 ?
2
2
5
2
2
5

 

 

 

 
( )
( ) ( )
2
2
5 2
3
5 3
c) 1
4 5
 1
1
4 5
4 5
4 5
4 5
4 5
4 5
2 11
5
2
2
2 ?
1
1
5
1
2
5
 

 

 

 
( )
d) 11
2 3 1
 1
11
2 3 1
2 3 1
2 3 1
112 3 1
5
( )
2 2
2 3
?
1
1
5
 

 

 

 
( )
2
12
112 3 1
11
2 3 1
2
5
1
5 1
( )
e) 2 2
3 2
2 2
3 2
3 2
3 2
6 2 2 32 2
3 2
2
2
2
1
5
2
1
?
2
2
5
2 2 1
2

 

 

 

 
(( )2
8 2
5 2
7 5
 1 2 2
2 2
2
f) 2 2 2
2 2
2 2 2
2 2
2 2
2 2
4 2 2 4 2 2 2
2
5
2
2
?
1
1
5
 

 

 

 
2
( )
52 2
2
4 2 2 4
4 2
2
2
5
2 2
2
g)
1 5
3 5
1 5
3 5
3 5
3 5
3 5 15 5
3
2
2
1
1
5
1
1
?
2
2
5
2 1 2
2

 

 
 

 
( ) 5
3 5 15 5
3 5
5 3 5 15
2
2 ( ) 5
5
2 1 2
2
5
2 1 2
h)
3 2
3 2
 2 ? 1
3 2
3 2
3 2
3 2
2 2
3 2 3 2 2
3
2
2
1
5
2
1
?
2
2
5
 

 

 

 
( ) 2
5
5
1 2
2
5 2
2
3 2 2 6
3 2
5 2 6
2 ( )

333
17 – Simplificando expressões com radicais
1.
1
5 ( )( ) ( )
2 2
3 3
1
3 3
3 3 3 3
3 3 3 3
6
3 3
6
9 3
1
2
1
1
5
1 1 2
2 1
5
2
5
2
 2
2. 2 3 3
2
2 3 3
2
2 3 3
2
4 27
2
23
2
2
2
2
1
?
2
5
2
5
2
5
 

 

 

 
( )
( ) ( ) ( )
2 ? 1 ? 2 5 ? 1 2 5 ? 1 2 5
3. 10 2 2 2 2 2 10 2 2 2 2 10 2 2 2 2
10 2 2 2
5 ? 5
0
4. 1
2 3
1
2 3
( 2 3 ) ( 2 3
)
4
4
5 5 5 ( 2 3 ) ( 2 3
) 2 2 − ( 3
) 4 −
3
1
1
2
2 5
2 1 1
1 ? 2
4
5. 2
3
2
3
2
2
3
2
2
3
2
2
3
3
3
2 6
3
2 6
1 5 5 5 ? 5 5
2 3
6. A5 2 5 2 5
2
?
5
2
5 ? 5
3
2
2
3
3
2
2
3
3 2
2 3
3 2
6
1
6
6
6
6
6
2 2
7. 3
2
3 1
1
3 1
? 2 1
2
5

 

 
5 ? 2 1
 −
2
?
1
1

5 ? 2 1
1
2
3
2
3 1
1
3 1
3 1
3 1
3
2
3 1
3 1
2
3 1
2
( )
( )

 

 
( )





3 2 1 1
2
 

 

 

5
5 ? 2 1
1
5 ?
3 1
3 1
3 1
3
2
2 3 2 3 1
2  

 

 
5 ?
2
5
5
2
3
2
3 3 1
2
9 3
4
8. 3
2
2 3
3
2 3
3 2 3 2 2 3 3 2 3
2 3
2
2
1
2
1
1
5
? 2 1 ? 1 1 ? 2
2 ?
( ) 

( ) ( )
( ) 2 3
3 1 4 2 3 23 3
2 3
3 4 4 3 3
4 3
5 3 1
1
2
2
2
1
5
5
? 1 1 1 2
2
5
1 1 2
2
5
1
( )
( ) 555 3 11
18 – Potências com expoente racional
1.
a) 7 23 2
3
5 7
b) 5 104 10
4
5 5
c) 3 72 7
2
5 3
d) 25 2
5
5 2
e) 6 2 2
1
5 6
f) 9 5 5
1
5 9
g) 11 11
1
5 2
h) 4 23 2
3
5 4

334
2.
2
3 3 2 5
a) 5 5
5
7 7 5 5
b) 3 3
3
4 4 3 5
c) 10 10
1
2 5
d) 7 7
4
3 3 4 5
e) 6 6
5
7 7 5 5
f) 8 8
3
2 3 5
g) 6 6
4
9 9 4 5
h) 7 7
1
2
1
1
+
1
5
 3
5 2
3
5 6 5
6 5 3. x x x x x
4.
( 1
) 1
2 1
1
3
5 5
6 a) 3 3 3
3
1
2

2
3
1
6
2
3
1
6
− +
b) 3 3 3 3
5
 6
5 5
5( ) 5 5 2
1
6 3
1
6
3
6
c) 27 3 3 3
1
5( ) 5 5 2
5
4 2
5
4
10
4
d) 9 3 3 3
5
( ) ( ) 

4 ( ) 

3
1
6
3
6
1
2
1
2 1
5. 10 5 10 5 10 5
10
6.
1
4 4
1
4 4
1
4 8
1
( x y ) 5( ) (x ) (y )4 5 xy2
a) 16 4 8 2 2
1
2 2
1
2 6
1
2 10
1
( a b ) 5( ) (a ) (b )2 5 a3b5
b) 4 6 10 2 2
1
1
.( ) 2 2
2 2 5  ( )( )
c) t t t t + ( ) − 

+ ( ) 

− ( ) 

1 1 1 1 2 2
1
2 1 1 2 1 5 t t2 5t 2
d) 256 2 2 4 4
8
1
4 8
1
4 4
1
4
8
1
4
2
2 2
x
y
x
y
x
y
x
y

 

 
( ) ( )
( )
5 5 5
7.
4
3 4 5( ) 5 5
4
3 3
a) 8 2 2 16
25
100 8
1
, 4 2 5( ) 5( ) 5 5
b) 2560 25 28 2 2 4
3
2 9 5( ) 5 5
3
2 6
c) 64 2 2 512
8. 625 5 5
1
5
1
25
05 4
1
2 2
2
2 2 5 5 5 5 , ( )  
 
−
1. Maior temperatura registrada: 9,4 °C.
Menor temperatura registrada: 3,6 °C.
T 5 9,4 °C 2 36 °C 5 5,8 °C.
Logo, a variação entre as temperaturas foi de 5,8 °C.

335
2. Analisando a tabela, verificamos que a maior temperatura ocorreu no bairro Consolação, e a
menor temperatura ocorreu em Parelheiros.
3. M5
, 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1
, 71,3
5
9 4 8 5 8 2 7 9 7 7 7 3 6 9 6 6 5 2 3 6
10
10
57,13
A temperatura média foi de 7,13º
4. A temperatura mais próxima da temperatura média ocorreu na Freguesia do Ó (7,3 °C).
5.
a)
Bairro Temperatura (em °C) Desvio
Consolação 9,4 9,4 2 7,13 5 2,27
Ermelino
8,5 8,5 2 7,13 5 1,37
Matarazzo
Capela do
Socorro
8,2 8,2 2 7,13 5 1,07
Itaquera 7,9 7,9 2 7,13 5 0,77
Campo Limpo 7,7 7,7 2 7,13 5 0,57
Freguesia do Ó 7,3 7,3 2 7,13 5 0,17
Butantã 6,9 6,9 2 7,13 5 20,23
Santana 6,6 6,6 2 7,13 5 20,53
Perus 5,2 5,2 2 7,13 5 21,93
Parelheiros 3,6 3,6 2 7,13 5 23,53
b) Considerando o valor absoluto, o maior afastamento foi em Parelheiros (3,53 °C),
e o menor foi na Freguesia do Ó (0,17 °C).
6.
Bairro Temperatura Desvio Quadrado do desvio
Consolação 9,4 2,27 5,1529
Ermelino
8,5 1,37 1,8769
Matarazzo
Capela do
Socorro
8,2 1,07 1,1449
Itaquera 7,9 0,77 0,5929
Campo Limpo 7,7 0,57 0,3249
Freguesia do Ó 7,3 0,17 0,0289
Butantã 6,9 20,23 0,0529
Santana 6,6 20,53 0,2809
Perus 5,2 21, 93 3,7249
Parelheiros 3,6 23,53 12,4609
Md 5
5,152911,876911,144910,592910,324910,028910,0529 0 2809 3 7249 12 4609
10
25 641
10
2 5641
1 1 1
5 5
, , ,
,
M , d
Desvio padrão: 2,5641 .1,6 .
1. Alternativa c.
5 5 5 5 5 5 5 5 5 5 5 52 5
2
? 1 ? 2 5 ? 1 ? 2 5 ? 2 ( ) ( ) ( ) ( ) 

( ) 


5
5 5 ? 20 5 5 ? 22 ?5 5 5 ?2? 5 52 52 52?5510
2. Alternativa a.
5 6 5 6 5 6
31 10 83 4 31 10 83 2 31 10 81
31 10 9
1 2 2 5 1 2 2 5 1 2 5
5 5 1 6
2 555 3116 1 55 3111 55 32 52

336
3. Alternativa e.
1
2
1
 5 5( 4
) + ( )5 5 2 5
1
2 5
1
81 32 3 2 3 2 11
4. Alternativa b.
a
a
a a
a a
a a
a
a a
a


5 5
a a

5

5 5
2
4
5. Alternativa d.
2 x 42 3 y
5 6
4 2 2 32
;
→
 5  5
5  5
x x
5 6
y → 6
y 5
→
y
3
3
x y
5 2
5 5 5
3 2
 5 
5 2 58 2
6. Alternativa c.
a
b
a b
3 2
24 2 3 2 2 3 2 6
36 2 3 6 6
2 6
5 5  5   5
5 4 5 4 2  2 42 5 22
5
 5
 6 52 62 526512
7. Alternativa e.
( 5
5
10 5
5 9
3 6 ) ( 6 3 ( ) ( 1
) 1 29  2 9
) 5 ( 18 2 9
)  ( 18 2 9
) 5 2 18
5
2
2
0
525532
8. Alternativa a.
( )
3
32  4 8  50  2
5
2 5 4 2 2 2 2 5 2 2 2
2
4 2 4 2 2 5 2
5        5
5    
 5
5
2 2
5 2
9. Alternativa b.
125
100 4
5
, ( ) ( )4 5
a 5 16 e b 5 1,25 → ab5161 255 24 5 2 52 532
10. Alternativa d.
x y
x
1 3 1 3
5  5 
2
5  5     5   5 
2 1 3 1 2
2 1 3 3 1 2 3 3 4 2 3
2
;
( ) ( )
2
( ) ( ) ( ) ( )
25(42 3 )(42 3 )542 3 42 3 50
y
x y
2 2 2
2
5 1 3 5 1 2 1  3  3 512 3 3542 3

11. Alternativa a.
x y
12 3 15
2 2 5 5
2 2 2 2 2 12 6
5 5 5
;
→ → →
→ 3 155 3 15 5
5 5
5 5 5 5
5
x x
12 2 12
y
3 15
x x
y y y
6 5 1
x y
5 5 5
 5  5
→ →
12. Alternativa b.
p q
2 2 10 0 0001 25
2 2 2 2
; , ;
r
→ → p → p
18
36
2
36
1
2
36
5 5 5
36
2
p p
5 5 5 5
 , → → →
q q q q
10 0 0001 10
1
10000
10 10 4
5 5 5 5
25
4
1
2
1
( )2 → r
→ 5 5
r r
5 5
2
18 4 5 19
p q r
5
  5   5

337
p q
2 2 10 0 0001 25
2 2 2 2
; , ;
r
→ → p → p
18
36
2
36
1
2
36
5 5 5
36
2
p p
5 5 5 5
2 , → → →
q q q q
10 0 0001 10
1
10000
10 10 4
5 5 5 52
25
4
1
2
1
( )2 → r
→ 5 5
r r
5 5
2
18 4 5 19
p q r
5
1 1 5 2 1 5
13. Alternativa c.
2 1 2 4 2 2 2 2
( )
1 2 x xy y
( ) (
x y xy
x y
x xy y xy
x y
2
5
1 1 2
2
5
2 2
2 4
2
2
2 x y
x y
x y
x y
x y
2
5
2
2
5
2
2
5
)
( )
( )
( )
( )
2
2
2
1
2
14. Alternativa d.
3 10
10
10 3
3 10
( ) 1
10 10 3
10 3 10 3
3 10
10 3 1
2
2
5 2
 1
2  1
5 2
( ) ( )
0
10 9
3 10 10 3 10 10
2
5
5 2 2 52
15. Alternativa c.
A
A
A
1
3
1
4 2
8 16 2 8
2 2 4 2
2
5 1 2 2 1
5 1 2 1
5
4
3
3
1
3 4
1
4 3
4
3
( )
( ) ( ) ( )
11224124516
16. Alternativa a.
E
x x
x
E
 2
x x
x
x
x
x x x x x
x
5
2
1
5
2
1

2
2
5
2 2 1
1
1
1
1
 

 

 

 
( ) ( ) 2 2 1
2
1
2
2 2 2 2 2
2
2
5
2 1
2
5
5
2  1
2
x x x x
x
Quandox temos
E
, :
1
53 2 24
17. Alternativa e.
75
1
3
2 3
3
1 1 5
3 5
1
3
3
3
2 3
3
5 3
3
3
2 3
3
153 3 2 3
3
2
5  1  1 5
5 1 1 5
1 1
5
18 3
3
56 3
18. Alternativa d.
3
3 1
1
3
2
1 3
3 3 1
3 1 3 1
( )  2
1 3
3 3
2 1 3
2 1
2 1
1
5
 1
2  1
2

1
( )( )
( )
( 11  2
5
5
1
2 1
2
2
5
1
2 2
2
5
5
1 2
3 1 3
9 3
2
3
3
2 2 3
2
3 3
2
3
3
2 2 3
2
9 3 3
) ( )
2 3 6 6 3
6
7 3 3
6
2 1
5
1
19. Alternativa b.
320,2 1 270,5 2
(108)
2
1
2
1 (0,0016)0,25 5 (25)0,2 1 (33)0,5 2
2 3
(2 3 )
2
1
 2 1 [(0,2)4]0,25 5
5 2 1 31,5 2
15  ,
2 3
2
1 0,2 5 2 1 31,5 2 31,5 1 0,2 5 2,2

338
Equações do 2.O grau
• Pra você pensar!: Qual o valor de dois
números inteiros, sabendo-se a soma e o
produto deles?
Exemplo: soma 5 e produto 6.
Se pensarmos em dois números naturais,
temos três possibilidades para que a soma
seja 5: 0 e 5; 1 e 4 ou 2 e 3.
Como queremos o produto igual a 6,
podemos dizer que 2 e 3 são os números
cuja soma é 5 e o produto é 6.
19 – Equação do 2.o grau
com uma incógnita
a) Área do quadrado: x2.
Área do retângulo: 3x.
x2 2 3x 5 4
b)
x x2 2 3x 5 4
2 22 2 3 ? 2 5 22 (Não satisfaz.)
5 52 2 3 ? 5 5 10 (Não satisfaz.)
9 92 2 3 ? 9 5 54 (Não satisfaz.)
6 62 2 3 ? 6 5 18 (Não satisfaz.)
4 42 2 3 ? 4 5 4 (Satisfaz.)
8 82 2 3 ? 8 5 40 (Não satisfaz.)
7 72 2 3 ? 7 5 28 (Não satisfaz.)
10 102 2 3 ? 10 5 70 (Não satisfaz.)
12 122 2 3 ? 12 5 108 (Não satisfaz.)
Logo, o valor que satisfaz a equação é o
número 4.
• Resposta em aberto.
1.
a) 3x2 2 5x 1 1 5 0 é uma equação do
2.o grau.
b) 10x4 2 3x2 1 1 5 0 não é uma equação
do 2.o grau, pois existe um termo x4.
c) 2x 2 3 5 0 não é uma equação do
2.o grau, pois não existe o termo x2.
d) 2x2 2 3x 1 2 5 0 é uma equação do
2.o grau.
e) 4x2 2 x 5 0 é uma equação incompleta
do 2.o grau.
f) 9x2 2 1 5 0 é uma equação incompleta
do 2.o grau.
g) 2x4 1 5 5 0 não é uma equação do 2.o
grau, pois existe o termo x4.
h) 0x2 2 5x 1 6 5 0 não é uma equação
do 2.o grau, pois não existe o termo x2.
Logo, as equações dos itens a, d, e, f são do
2.o grau com uma incógnita.
2.
a) x2 2 7x 1 10 5 0 R Completa.
b) 22x2 1 3x 2 1 5 0 R Completa.
c) 24x2 1 6x 5 0 R Incompleta.
d) x2 2 x 2 12 5 0 R Completa.
e) 9x2 2 4 5 00 R Incompleta.
f) 7x2 1 14x 5 0 R Incompleta.
3.
a) 10x2 1 3x 2 1 5 0
a 5 10; b 5 3;c 5 21
b) x2 1 2x 2 8 5 0
a 5 1; b 5 2; c 5 28
c) y2 2 3y 2 4 5 0
a 5 1; b 5 23; c 5 24
d) 7p2 1 10p 1 3 5 0
a 5 7; b 5 10; c 5 3
e) 24x2 1 6x 5 0
a 5 24; b 5 6; c 5 0
f) r2 2 16 5 0
a 5 1; b 5 0; c 5 216
g) 26x2 1 x 1 1 5 0
a 5 26; b 5 1; c 5 1
h) 5m2 2 10m 5 0
a 5 5; b 5 210; c 5 0
4.
a) a 5 1; b 5 6; c 5 9
x2 1 6x 1 9 5 0
b) a 5 4; b 5 26; c 5 2
4x2 2 6x 1 2 5 0
c) a 5 4; b 5 0; c 5 225
4x2 2 25 5 0
d) a 5 221; b 5 7; c 5 0
221x2 1 7x 5 0
1.
x2 1 3x 5 x 1 35
x2 1 3x 2 x 2 35 5 0
x2 1 2x 2 35 5 0
A equação reduzida que se pode formar
com os dados é: x2 1 2x 2 35 5 0.

339
2.
a) x2 2 7 5 x 1 5
x2 2 x 2 7 2 5 5 0
x2 2 x 2 12 5 0
b) x2 1 11x 5 16x 2 6
x2 1 11x 216x 1 6 5 0
x2 2 5x 1 6 5 0
c) x(x 2 6) 1 x2 5 (x 2 5 )(x 1 2)
x2 2 6x 1 x2 5 x2 2 3x 2 10
x2 2 3x 1 10 5 0
d) (x 2 10)2 1 x( x 1 17) 5 104
x2 2 20x 1 100 1 x2 1 17x 2 104 5 0
2x2 2 3x 2 4 5 0
1 1
2
3
6
e) x x
2 2
x x
6 2
2
→ 5 → 2 5
2 2 x
2 5 5 2 0
6 6
1 1
2
3
6
x x
2 2
x x
6 2
2
→ 5 → 2 5
2 2 x
2 5 5 2 0
6 6
f) x x x x x x
5
x x
2 2 2 2
2
4
1
10 5 2
5 2
20
4 10
( 3
)
2
( )
2
1 5 1 10 2 0
20
1
5
1
→ → 2 1 5
x x x x x
x x
2 2 2 2
2
4
1
10 5 2
5 2
20
4 10
1 5 1 10 2 0
20
1
5
1
→ → 2 1 5
g) x
x
x
x
1 5
2 1
x x
( )( )
x
( )

x
x
2
5
2
−
x 1 x 2 5
x
6
4
2
2
2 6
2
4
2
2 4 12 4
→
→ →
x221250
h) x
x x
x x
x
( , )
x x
x
x x
2
x x
x
2
1
1
5
2
2
2
2
1
1
5
2
1
1
1
1
3
1
1 1
1
1
1
3
2
2
(
 
x
1 1
x x x
x x
1 1
1 1
2
x x
x x
3
1 1
2
)( )
( )
( )( ) ( )( )
x
2
1 1 2
1 2
5
2
1 2
1x 1 x 2 1 5 x 2
3
x
x x
4 1 2 1 5
0
2
2
3. , 5 (3x 2 1) cm
A 5 64 cm2
,2 5 A
(3x 2 1)2 5 64
9x2 2 6x 1 1 5 64
9x2 2 6x 2 63 5 0
3x2 2 2x 2 21 5 0
4. (x 2 3)2 5 5x 2 1
x2 2 6x 1 9 5 5x 21
x2 2 11x 1 10 5 0
5. A 5 54 m2
c 5 (x 1 1) cm
, 5 (x 2 2) cm
c ? , 5 A
(x 1 1)(x 2 2) 5 54
x2 2 x 2 2 5 54
x2 2 x 2 56 5 0
6. d
n n
n n
n n
n n
2
5
2
5 2
2 2 5
10
3
2
20 3
3 20 0
2
20 – Resolvendo equações
incompletas do 2.o grau
1.
a) x2 2 12x 5 0
x(x 2 12) 5 0
x 5 0 ou
x 2 12 5 0
x 5 12
S 5 {0, 12}
b) x
2
2 5
56 56
5 2
2
1 0
→
x x
S
1 1
1 1
{ , }
c) x
x
x
x
S
2
2 5
5
56
56
5{2 , }
2
16 0
16
16
4
4 4
x2 x
x x
x ou
x x
S
d) 5 3 0
2 5
2 5
5
5 3 0
0
5 3 0
3
5
( )
→
{ }
2 5 5
0
3
5
5
,
e) x2 1 x 5 0
x(x 1 1) 5 0
x 5 0 ou
x 1 1 5 0 R x 5 21
S 5 {21, 0}
f ) x
x
x
x
S
2
2 5
5
56
56
5 2{ , }
2
64 0
64
64
8
8 8

340
g) x
x
x
S
2
1 5
52
5 2
5
2
16 0
16
16 16
Nãoexiste emIR.
{ }
( − )

x2 x
x x
x ou
x x
h) 7 0
7 1 0
0
7 1 0
1
7
( )
→
{ 1
0
}
7
S
2 5
2 5
5
2 5 5
5
,
i) 9 25
25
9
25
9
5
3
5
3
5
3
2
x
x
2
x x
S
5
5
5 5
5 2
→
{ , }
j) 24x2 1 28x 5 0
4x(2x 1 7) 5 0
4x 5 0 R x 5 0 ou
2x 1 7 5 0 R x 5 7
S 5 {0, 7}
k) x
2
2 5
5
5 5  5
5 2
2
x
x 2
x
S
20 0
20
→
20 2 5 2 5
2 5 2 5
{ , }
l) 2 2 5
x2 x
x x
x x ou
x x
15 5 0
5 3 1 0
5 0 0
3 1 0
2 1 5
2 5 5
1 5 52
5 2
1
3
S
( )
→
→
1
3
{ , 0}
2.
a) (x 1 5)(x 2 6) 5 51 2 x
x2 2 x 2 30 2 51 1 x 5 0
x2 2 81 5 0
x2 5 81
x 5 81
x 59
S 5 {29, 9}
b) x2 1 3x(x 2 12) 5 0
x2 1 3x2 2 36x 5 0
4x2 2 36x 5 0
4x(x 2 9) 5 0
4x 5 0 R x 5 0 ou
x 2 9 5 0 R x 5 9
S 5 {0, 9}
c) (x 2 5)2 5 25 2 9x
x2 2 10x 1 25 5 25 2 9x
x2 2 10x 1 9x 5 0
x2 2 x 5 0
x(x 2 1) 5 0
x 5 0 ou
x 2 1 5 0 R x 5 1
S 5 {0, 1}
d) 2x(x 1 1) 2 x(x 1 5) 5 3(12 2 x)
2x2 1 2x 2 x2 2 5x 5 36 2 3x
x2 2 36 5 0
x2 5 36
x 5 36
x 56
S 5 {26, 6}
e) (x 1 2)(x 2 16) 1 (x 1 7)2 5 89
x2 2 14x 2 32 1 x2 1 14x 1 49 2 89 5 0
2x2 2 72 5 0
2x2 5 72
x2 5 36
x 5 36
x 56
S 5 {26, 6}
f) (x 2 4)2 1 5x(x 2 1) 5 16
x2 2 8x 1 16 1 5x2 – 5x – 16 5 0
6x2 2 13x 5 0
x(6x 2 13) 5 0
x 5 0 ou
6 13 0
13
6
x x
0
13
6
S
2 5 5
5
→
{ , }
3.
a) 3
1
3
(  )
0 0
x
9 1
3
0
9 1 3
1
9
1
9
1
3
2
2
2
x
x
x
x
x x
x
→
x x
S
2 5
2
5
2 5
5
5 5
1
3
{ , }
55 2
1
3
b) x
4
x
2
2
5
2
1
10
4
4
4
2 52
2
5
2
x2 2 6 5 0
x2 5 6
x 5 6
S5{2 6 , 6 }

341
x2 x x
c) 11
10
3
5 2
2 5
x22 x x
11 6
10
5
10
5
11x2 2 11x 5 0
11x(x 2 1) 5 0
11x 5 0 R x 5 0 ou
x 2 1 5 0 R x 5 1
S 5 {0, 1}
d)
x
x
x
x
1
5 1
2
x 2
x
x x
5
1 2
x x x
5
1 2 1
1
8
3 1
3 ( 1
)
3 11
8 11 3
( )( )
( )( ) (x
x x
1
1 2
1
3 11
)
( )( )
3x 2 3x2 5 8(x 2 x2 1 1 2 x) 1 3x2 1 3x
26x2 5 28x2 1 8 R 2x2 5 8
x2 5 4 R x 56 4 R x 5 62
S 5 {22, 2}
e) x
3
4
2
2
1
1 5
x x
x
1
2
2
2
3
1
x 2 2 x 1
2
x
x x x
1 5
2
2 1 2 1
1
2
3 2 2
2
( )( )
( )( )
x
5
1
2
(x 2 2 )(x 1 2 ) ( x 2 2 )( x
1
2
)
x 2 3 1 x2 2 4 5 x 1 2
x2 2 9 5 0
x2 5 9
x56 9 →x563
S 5 {23, 3}
f) 3
5
1
5
10
2
25
2
1
1
3 5 1 5
5 5
10
x x 2
x
x
x x
x x
5
2
1 1 2
2 1
5
2
−
( ) ( )
( )( )
x
x x
2
( 25)( 15)
3x 1 15 1 x 2 5 5 10 2 x2
x2 1 4x 5 0
x(x 1 4) 5 0
x 5 0 ou
x 1 4 5 0 R x 5 24
S 5 {24, 0}
2 x x2
2 3
4. x x
x
2
5 2
2
(x22x) x (x x2)
3
6
6 2
6
5
2 2
3x2 2 3x 5 6x 2 2x 1 2x2
x2 2 7x 5 0 R x(x 2 7) 5 0
x 5 0 ou x 2 7 5 0 R x 5 7
Como o problema pede o número real
positivo, a resposta é 7.
5. A 5 L, R A 5 899 m2
899 5 (x 1 1)(x 2 1)
899 5 x2 2 1
x2 5 900
x 56 900
x 5630
Como a área é um número positivo,
x 5 30.
, 5 x 2 1 R , 5 30 2 1 R , 5 29
L 5 x 1 1 R L 5 30 1 1 R L 5 31
As medidas dos lados são: L 5 31 m e , 5 29 m.
6. V k
h
2
5 1
5 5
24 2
V ek
h
5
24 2 2
5 ? 1
5
2
2
120 5 20 1 h2
h2 5 100
h56 100
h5610
h 5 10 ou h 5 210
7. x2 ? y 5 90
a) x 5 50% de 8 R x 5 4
x2 ? y 5 90
42 ? y 5 90
y 5 5,625
b) y 5 10
x2 ? y 5 90
x2 ? 10 5 90
x2 5 9
x 56 9 R x 563
x 5 23 ou x 5 3
8. x2 5 81
x56 81 →x569
Como o número é positivo, então x 5 9.
5y 5 y2
y2 2 5y 5 0
y(y 2 5) 5 0
y 5 0 ou y 5 5.
Como y é real e positivo, y 5 5.
Logo, x 1 y 5 9 1 5 5 14.
c) IMC
m
h
81
2
h
25
2
h
h
5
5
5
2
81
25
81
25
56 56
9
5

342
IMC
m
h
81
2
h
25
2
h
h
5
5
5
2
81
25
81
25
56 56
9
5
Como a altura é positiva,
h5 5 m
9
5
1,80 .
Logo, a altura da pessoa é 1,80 m.
21 – Resolvendo uma equação
completa do 2.o grau com
uma incógnita
a) Mariana precisará de 4 quadradinhos
(cada um com 1 cm de lado) para
formar o novo quadrado.
b) Cada um desses quadradinhos terá a
área dada por: A 5 ,2 5 (1 cm)2 5 1 cm2.
c) O novo quadrado terá lado igual a:
L 5 3 cm 1 1 cm 1 1 cm 5 5 cm
Logo, a área do novo quadrado será:
A 5 ,2 5 52 5 25 cm2
a) x2 1 8x 5 x2 1 2 ? (4x)
d) x2 2 12x
Para se ter um trinômio quadrado
perfeito, devemos acrescentar um
quadrado de área 62 5 36.
x2 2 2 ? 6x 1 36 5 (x 2 6)2
e) x2 1 9x
quadrado de área
9
2
81
4
2  
 
5 .
9
2 1 1 5 1
x2 x x
2
9
81
4
 
 
f) x2 2 5x
quadrado de área
5
2
25
4
2  
 
5 .
5
2 2 1 5 2
x2 x x
2
5
25
4
 
 
a) x2 1 2x 2 15 5 0
x2 1 2x 5 15
x2 1 2x 1 1 5 15 1 1
(x 1 1)2 5 16
x1156 16
x 1 1 5 64
x 1 1 5 4 R x 5 3 ou
x 1 1 5 24 R x 5 25
S 5 {25, 3}
b) x2 1 4x 2 12 5 0
x2 1 2 ? 2x 5 12
x2 1 4x 1 4 5 12 1 4
(x 1 2)2 5 16
x1256 16
x12564
x 1 2 5 4 R x 5 2 ou
x 1 2 5 24 R x 5 26
S 5 {26, 2}
c) x2 1 12x 1 32 5 0
x2 1 2 ? 6x 1 62 5 232 1 36
(x 1 6)2 5 4
x1656 4
x 1 6 5 62
x 1 6 5 2 R x 5 24 ou
x 1 6 5 22 R x 5 28
S 5 {28, 24}
x
x2 4x
4x
x
4
4
Editoria de arte
x2 1 8x 1 42 5 (x 1 4)2
b) x2 2 10x
x2 2 2 ? 5x 1 25 5 (x 2 5)2
c) x2 1 2x
x2 1 2 ? x 1 1 5 (x 1 1)2

343
d) x2 1 6x 2 7 5 0
x2 1 2 ? 3x 1 9 5 7 1 9
(x 1 3)2 5 16
x1356 16
x13564
x 1 3 5 4 R x 5 1 ou
x 1 3 5 24 R x 5 27
S 5 {27, 1}
e) x2 1 3x 2 10 5 0
9
4 1 ? 1 5 1
x2 x
2
2
3
2
3
2
10
 
 
3
2
x1 5
49
4
2  
 
3
2
x1 5 6
49
4
3
2
x1 56
7
2
3
2
7
2
x 1 5 x 5
2
ou
x x
3
2
7
2
1 52 52
5
→
→
S 5 {25, 2}
f) x2 1 2x 1 1 5 0
x2 1 2x 5 21
x2 1 2x 1 1 5 21 1 1
(x 1 1)2 5 0
x 1 1 5 0
x 5 21
S 5 {21}
Chegou a sua vez! página 112.
2
x x
x 2
x
10 9 0
10 9
2 1 5
2 52
10 2 5
5
2 2 2
x x
x
2 5 5 9 5
5
2 ? 1 52 1
2
2
;
16
( )5
2 56
2 56
5 1 5
52 1 5
5
x
5 16
x
5 4
x 4 5 →
x 9
ou
x 4 5 →
x
1
S
{ 1 , 9
}
2
b) x x
2
x x
2
x x
2
6 0
6
1 2
1
2
2
1
2
1
2
6
1
2
1 2 5
1 5
5
1 ? 1 5 1
;
 
 
 

 
 
 
→ 
 
2
2 2 1
2
x x
6
1
4
1
2
25
4
1
2
25
4
x
x
1 5 1 1 5
1 56
1
1
2
5
2
5
2
56
1
2
x 5 2 x 5
2
ou
5
1
x x
2
2
S
3
52 2 52
5 2
3 2
→
→
{ , }
c) x x
2
2
4 5 0
4 5
1 2 5
1 5
5
1 ? ? 1 5 1
1 5
1
x x
4 2 2
2 2 2
x x
x
x
2 2 2 5 2
2 2
9
;
( )
2 56
9
2 3
2 3 1
2 3 5
5 1
x
1 56
x 1 5 →
x 5
ou
x 1 52 →
x
52
S
5 { 2
, }
2
d) x 10x 24 0
2
2 1 5
2 52
x 10x 24
10
;2 5
5
x2 2 2 ? 5x 1 52 52 24 1
52
(x
2 5 )2
5
1
x
2 5 56
1
x 2 5 51 1 →
x 5
6
ou
x 2 5 52 1 →
x
5
4
S
5
{ 4 , 6
}
22 1 5
e) 2x 9x 4 0
Dividindo todos os termos por 2, tem
os:
9
2
x22 1 5
2 52
5
2 0
9
2
2
9
2
2
9
4
9
9
2
x
x x
;
2 2
9
4 785 mm2
x 32
x
Editoria de arte
x(x 1 32) 5 4 785
x2 1 2 ? 16x 1 162 5 4 785 1 162
(x 1 16)2 5 4 785 1 256
(x 1 16)2 5 5 041
x11656 5041
x1165671
x 1 16 5 71 R x 5 55 ou
x 1 16 5 271 R x 5 287 (Não convém.)
As medidas dos lados do cartão são:
55 mm e 87 mm.
2
a) x x
2
10 9 0
10 9
2 1 5
2 52
x x
10 2 5
5
2 2 2
x x
x
2 5 5 9 5
5
2 ? 1 52 1
2
2
;
( )5
2 56
16
5 16
x

344
22 1 5
2x 9x 4 0
Dividindo todos os termos por 2, tem
os:
9
2
x22 1 5
2 0
9
2
2 52
5
2
;
2 ? 1
9
2
2
9
4
2
9
4
9
4
2
2
x
x x
x x
 
 
2 2
9
52 2
1
4  
 
9
4
49
16
x x
2 5 2 56
x
2 56
x 5 1 x 5
o
9
4
49
16
9
4
7
4
7
4
9
4
4
2  
 
→
→ u
x x
S
52 1 5
5
7
4
9
4
1
2
1
2
4
→
{ , }
2
f) x 8x 16 0
2
1 1 5
1 52
5
1 ? 1 52 1
1
x 8x 16
8
;2 4
x2 x 2 2
x( )
2 4 4 16 4
4
2 5 0 52
4
4
{ }
5 2
→ x
S
1.
• x2 2 3x 2 4 5 0
a 5 1; b 5 23; c 5 24
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (24)
D 5 9 + 16 5 25
D . 0
• x2 2 7x + 15 5 0
a 5 1; b 5 27; c 5 15
D 5 b2 2 4ac
D 5 (27)2 2 4 ? 1 ? 15
D 5 49 2 60 5 211
D , 0
• 5x2 + 4x 2 1 5 0
a 5 5; b 5 4; c 5 21
D 5 b2 2 4ac
D 5 42 2 4 ? 5 ? (21)
D 5 16 + 20 5 36
D . 0
• x2 + 8x + 16 5 0
a 5 1; b 5 8; c 5 16
D 5 b2 2 4ac
D 5 82 2 4 ? 1 ? 16
D 5 64 2 64 5 0
D 5 0
• 12x2 2 x 2 1 5 0
a 5 12; b 5 21; c 5 21
D 5 b2 2 4ac
D (21)2 2 4 ? 12 ? (21)
D 5 1 + 48 5 49
D . 0
• 9x2 2 6x + 1 5 0
a 5 9; b 5 26; c 5 1
D 5 b2 2 4ac
D 5 (26)2 2 4 ? 9 ? 1
D 5 36 2 36 5 0
D 5 0
a) Três dessas equações têm raízes reais
diferentes (D . 0 ):
x2 2 3x 2 4 5 0; 5x2 1 4x 2 1 5 0;
12x2 2x 2 1 5 0
b) Duas dessas equações têm uma única
raiz real (D 5 0 ):
x2 1 8x 1 16 5 0; 9x2 2 6x 1 1 5 0
2.
a) x2 2 7x 1 6 5 0
a 5 1; b 5 27; c 5 6
D 5 b2 2 4ac R
R D 5 (27)2 2 4 ? 1 ? 6 5 49 2 24 5 25
Como D é positivo (D . 0), a equação
tem duas raízes reais distintas:
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
b
a
x
x
x
2
7 25
2 1
7 5
2
7 5
2
6
7 5
2
→ →

 
 
’
”
x5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
b
a
x
x
x
2
7 25
2 1
7 5
2
7 5
2
6
7 5
2
1
→ →

 
 
’
”
S 5 {1, 6}
b) x2 2 x 2 12 5 0
a 5 1; b 5 21; c 5 212
D 5 b2 2 4ac R
R D 5 (21)2 2 4 ? 1 ? (212) 5 1 + 48 5 49
Como D é positivo (D . 0), a equação
tem duas raízes reais distintas:
x 5
2 6 D
5
6
?
5
’
 ”
6 5
1
5
5
2
52
b
a
x
x
x
2
1 49
2 1
1 7
2
1 7
2
4
1 7
2
→ →

 

x5
2 6 D
5
6
?
5
’
 ”
6 5
1
5
5
2
52
b
a
x
x
x
2
1 49
2 1
1 7
2
1 7
2
4
1 7
2
3
→ →

 

S 5 {23, 4}

345
c) x2 2 3x 2 28 5 0
a 5 1; b 5 23; c 5 228
D 5 b2 2 4ac R D 5 (23)2 2 4 ? 1 ? (228) 5 9 + 112 5 121
Como D é positivo (D . 0), a equação tem duas raízes reais distintas:
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
b
a
x
x
x
2
3 121
2 1
3 11
2
3 11
2
7
3 11
2
4
→ →
’
”

 
 
S 5 {24, 7}
d) x2 1 12x 1 36 5 0
a 5 1; b 5 12; c 5 36
D 5 b2 2 4ac R D 5 122 2 4 ? 1 ? 36 5 144 2 144 5 0
Como D 5 0, a equação tem uma única raiz real:
x 2
5
5
2
?
52
b
a
x
2
12
2 1
→ 6
S 5 {26}
e) 6x2 2 x 2 1 5 0
a 5 6; b 5 21; c 5 21
D 5 b2 2 4ac R D 5 (21)2 2 4 ? 6 ? (21) 5 1 + 24 5 25
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
b
a
x
x
x
2
1 25
2 6
1 5
12
1 5
12
1
2
1 5
12
1
→ →
’
”
3
1
3
1
2

 
 
S5{2 , }
f) 9x2 1 2x 1 1 5 0
a 5 9; b 5 2; c 5 1
D 5 b2 2 4ac R D 5 22 2 4 ? 9 ? 1 5 232
Como D é número negativo (D , 0), não há valores reais para x: S 5 .
g) 3x2 2 7x 1 2 5 0
a 5 3; b 5 27; c 5 2
D 5 b2 2 4ac R D 5 (27)2 2 4 ? 3 ? 2 5 49 2 24 5 25
x 5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
b
a
x
x
x
2
7 25
2 3
7 5
6
7 5
6
12
6
2
7 5
6
2
6
→ →
’
” 5
5
1
3
1
3
2

 
 
S { , }
h) 25x2 2 10x 1 1 5 0
a 5 25; b 5 210; c 5 1
D 5 b2 2 4ac R D 5 (210)2 2 4 ? 25 ? 1 5 100 2 100 5 0
x 2
2 2
5
5
?
5 5
5
b
a
x
S
2
10
2 25
10
50
1
5
1
5
( )→
{ }

346
3.
a) x2 2 2x 5 2x 2 4 R x2 2 4x 1 4 5 0
a 5 1; b 5 24; c 5 4
D 5 b2 2 4ac R D 5 (24)2 2 4 ? 1 ? 4 5 16 2 16 5 0
x 2
2 2
5
5
?
5 5
b
a
x
2
4
2 1
4
2
2
( ) →
S = {2}
b) x2 2 2x 5 x 1 4 R x2 2 3x 2 4 5 0
a 5 1; b 5 23; c 5 24
D 5 b2 2 4ac R D 5 (23)2 2 4 ? 1 ? (24) 5 9 1 16 5 25
x 5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
b
a
x
x
x
2
3 25
2 1
3 5
2
3 5
2
8
2
4
3 5
2
2
2
→ →
’
” 5521

 
 
S 5 {21, 4}
c) x2 1 10 5 9x 2 10 R x2 2 9x 1 20 5 0
a 5 1; b 5 29; c 5 20
D 5 b2 2 4ac R D 5 (29)2 2 4 ? 1 ? 20 5 81 2 80 5 1
x 5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
b
a
x
x
x
2
9 1
2 1
9 1
2
9 1
2
10
2
5
9 1
2
8
2
→ →
’
” 4

 
 
S 5 {4, 5}
d) 6x2 1 3x 5 1 1 2x R 6x2 1 x 2 1 5 0
a 5 6; b 5 1; c 5 21
D 5 b2 2 4ac R D 5 12 2 4 ? 6 ? (21) 5 1 1 24 5 25
x 5
2 6 D
5
2 6
?
5
2 6 5
2 1
5
5
2 2
b
a
x
x
x
2
1 25
2 6
1 5
12
1 5
12
1
3
1 5
1
→ →
’
”
2
1
2
1
2
1
3
52
5 2

 
 
S { , }
e) 9x2 1 3x 1 1 5 4x2 R 5x2 1 3x 1 1 5 0
a 5 5; b 5 3; c 5 1
D 5 b2 2 4ac R D 5 32 2 4 ? 5 ? 1 5 9 2 20 5 211
Como D é um número negativo (D , 0), não há valores reais para x: S 5 .
f) 9x2 2 1 5 3x 2 x2 R 10x2 2 3x 2 1 5 0
a 5 10; b 5 23; c 5 21
D 5 b2 2 4ac R D 5 (23)2 2 4 ? 10 ? (21) 5 9 1 40 5 49
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
b
a
x
x
x
2
3 49
2 10
3 7
20
3 7
20
1
2
3 7
20
→ →
’
”
1
5
1
5
1
2

 
 
→ 

S5 2 ,

347
4. x2 2 2x 2 15 5 0
a 5 1; b 5 22; c 5 215
D 5 b2 2 4ac R D 5 (22)2 2 4 ? 1 ? (215) 5 4 1 60 5 64
x 5
2 6 D
5
6
?
5
’
 ”
6 5
1
5
5
2
52
b
a
x
x
x
2
2 64
2 1
2 8
2
2 8
2
5
2 8
2
3
→ →

 

S 5 {23, 5}
As raízes são –3 e 5.
Os inteiros entre elas são: 22, 21, 0, 1, 2, 3 e 4.
Logo, existem 7 números entre as raízes.
5.
• x2 2 12x 5 85 R x2 2 12x 2 85 5 0
a 5 1; b 5 212; c 5 285
D 5 b2 2 4ac R D 5 (212)2 2 4 ? 1 ? (285) 5 144 1 340 5 484
x
b
2 a
2
x
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
12 484
2 1
12 22
2
12 22
2
17
12 2
→ →
’
”
2
2
525

 
 
S 5 {25, 17}
• x2 1 51 5 20x R x2 2 20x 1 51 5 0
a 5 1; b 5 220; c 5 51
D 5 b2 2 4ac R D 5 (220)2 2 4 ? 1 ? 51 5 400 2 204 5 196
x
b
2 a
2
x
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
20 196
2 1
20 14
2
20 14
2
17
20 1
→ →
’
”
4
2
53

 
 
S 5 {3, 17}
A raiz comum é 17; logo, a soma das raízes não comuns é 25 1 3 5 22.
6. 4x2 2 21x 1 20 5 0
a 5 4; b 5 221; c 5 20
D 5 b2 2 4ac R D 5 (221)2 2 4 ? 4 ? 20 5 441 2 320 5 121
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
b
a
x
x
x
2
21 121
2 4
21 11
8
21 11
8
4
21 11
→ →
’
”
8
10
5
5 8
5
4 
 
 
A raiz fracionária é
5
4 ; logo, a soma de seus termos é: 5 1 4 5 9.
7. x2 2 7x 1 10 5 0
a 5 1; b 5 27; c 5 10
D 5 b2 2 4ac R D 5 (27)2 2 4 ? 1 ? 10 5 49 2 40 5 9
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
1
b
a
p
q
pq qp
2
7 9
2 1
7 3
2
7 3
2
5
7 3
2
2
→

 
 
2 5→p q
55 1 1 5 1
1 5
5 2 25 32
57
p q
q p
q p

348
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
1
b
a
p
q
pq qp
2
7 9
2 1
7 3
2
7 3
2
5
7 3
2
2
→

 
 
2 5→p q
55 1 1 5 1
1 5
5 2 25 32
57
p q
q p
q p
8.
2 x 2 x 2 x
b c
a) ( )
x x x 4 0 x 0
a
2 0 4 5 4
1 5 4
1 1 5 1 1 1 5 1 1 5
5 ; 5 ;
5
D 5
→ →
b2 4ac 52 4 1 4 25 16 9
2 D5 2 ? ? 5 2 5
D D
0
→
Como é positivo ( . ),a equação temduas raízes reaisdistintas:
x 5
b 2
2a
2 6 D
5
56
?
5
x
x
2 6 5
2 1
52
5
2 2
52
5 2 2
9
2 1
5 3
2
5 3
2
1
5 3
2
4
4
→

 
 
S
’
”
{ , 1}
→ →
b) 3x2 2 3x2 2
2 (x 1 ) 3 2 (x 2 x 1 )
3
5 2 1 5 2 1 1
→ 3 x 2 5 2 x 2
2 4 x
1 2 1
3
→x x
b c
b ac
2
a ; ;
5 5 52
D 5 2 D5 2 ? ? 2 5
→ ( ) 11 5
2 2
4 5 0
1 4 5
1 2 5
4 4 4 1 5 16
D D
20 36
Como é positivo ( .0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
2 6
?
5
2 6 5
2
b
a
x
x
2
4 36
2 1
4 6
2 → →
’
4 6
2
1
4 6
2
5
5 1
1
5
5
2 2
52
5 2
x
S
”
{ , }

 
 
111 12 121 50→ 2111 12 1425 → 2113 1425
55 5 5
D 5 2 D5 2 ? ? 5 2 5
c) x(x ) (x ) x x x 0 x x 0
a
; b ;c
b ac →
1 13 42
2 4 132 4 1 42 169 168 1
Como D é positivo (D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
2 6
?
5
2 6 5
2 1
b 52
a
x
x
2
13 1
2 1
13 1
2
13 1
2
6
→
’
” 5
2 2
52
5 2 2
13 1
2
7
7 6

 
  S { , }
( 2 ) 2 2 2
d) 6 x x x
2 2 5 1 2 2 2 2 5
2 2 5
x
a
2
1 14 5 6 6 14 5 0
20 0
5
x x x
x
→ →
→
1 1 20
; b ;c
b ac
52 52
D5 2 2 4 →D5(2 2 1 ) 2 4 ? 1 ? (2 20 )5 1 1 80 5
81
Como D é positivo (D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
’ 5
6 5
1
b 5 5
a
x
x
2
1 81
2 1
1 9
2
1 9
2
10
→ → 2
1 9
2
8
2
4
4 5
x
S
”
{ , }
5
2
52 52
5 2

 
 
9. 32 2 [8x 1 (8 2 2x) ? (4 2 x)] 5 8
32 2 [8x 1 (32 2 8x 2 8x 1 2x2)] 5 8
32 2 [8x 1 32 2 16x 1 2x2] 5 8
32 2 8x 2 32 1 16x 2 2x2 2 8 5 0

349
22x2 1 8x 2 8 5 0
2x2 1 4x 2 4 5 0
a 5 21; b 5 4; c 5 24
D 5 b2 2 4ac
D 5 42 2 4 ? (21) ? (24)
D 5 16 2 16 5 0
x 2
5
5
2
? 2
5
b
2a
4
2 1
2
( )
( )
Logo, para que o valor numérico dessa expressão seja 8, x deve ser 2.
10.
x2 x 3 x 2
5
3
2
2
2 4
( ) ( )
2 2
→ 5
→
2
4
3
6
x
→ →
2 2
2 5 2 2
3
6
2 8 3 9 2 3
x x x x
1 0
11 5
2 b 3 c
1
b ac →
mo D é positivo(D.0),a equação temduas raízes reaisdistintas:
5 52 5
D 5 2 D5 2 2 ? ? 5 2 5
2 4 3 2 4 2 1 9 8 1
a
Co
; ;
( )
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
b
a
x
x
2
3 1
2 2
3 1
4
3 1
4
1
3 1
4
→
’
”
1
2

 
 
A maior das raízes é 1, portanto não podemos afirmar que a maior raiz é um número
primo.
11.
4
5
a) x x
x
2 5
x
→
a
2
2
2
1
5
5 4
→ →
5
1
5
5 4 1 0
5 4 1
2
5
2 2 5
5 52 52
D
x
x
; b ;c
b2 4ac→ ( 4)2 4 5 ( 1) 16 20 36
55 2 D 5 2 2 ? ? 2 5 1 5
Como D
é positivo ,aequação temduas raízes reais distintas:
x
D
5
2
( .0)
b
a
x
x
x
6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
4 36
2 5
4 6
10
4 6
10
10
10
1
4 6
10
→ →
’
” 22 52
5 2
2
10
1
5
1
5
1

 
 
S { , }
b) x
2 2
4
5
x x x
2
2
→ →
x x 6 0
a
1
1
5
1 1
5
1 2 5
b c
5 5 52
D
5 4
5
10
5
5
1 5 6
→
; ;
b2 4ac→ 52 4 1 ( 6) 25 24 49
55 2 D 5 2 ? ? 2 5 1 5
Como D é positivo( D
.0),a equação temduas raízes reaisdistintas:
x 5
2b6 D
2
5 49
2 1
5 7
2
5 7
2
1
5 7
2
6
a
x
x
S
5
2 6
?
5
2 6 5
2 1
5
5
2 2
52
5
→

 
 
’
”
{26,1}

350
2 2
x
c) x x
2
→ x
2
→
2
12
3
x
2
3 2 12
→ →
6
12
6
1
5
3 2 24 12
2 1
5
2 2 5
x x
x x
( )
2
3 14 24 0
3 14 24
2 2
x
4 14 4
a
2 2 5
5 52 52
D 5 2 D5 2 2
x
; b ;
c
b ac
→ ( ) ?? ? 2 5 1 5
D D
3 24 196 288 484
0
( )
Como é positivo( . ),a equação temduas raízes reaisdistintas:
x 5
b 6
2a
2 6 D
5
14 484
2?
5
x
’
 ”
6 5
1
5 5
5
2
52 52
3
14 22
6
14 22
6
36
6
6
14 22
6
8
6
4
3
→

 

x
S5{4
2 ,6
}
3
d)
x(x1 ) x ( x ) 3x(x ) x ( x )
1 2
2
4
2
5
→ 10 2 1 12
2 1
2
2
5
5
12
5 2 1
6
1
12
5
12
2 2
3 3 5 20 10 3 18 15 0
3 18
→
→ x x x x → x x
1 2 1 5 2 2 1 5
a5 ; b 52 ; c
515
b ac → ( )
2 4 18 2 4 3 15 324 180 144
D 5 2 D5 2 2 ? ? 5 2 5
Como D
é positivo (D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
6 5
1
5
5
2
b
a
x
x
2
18 144
2 3
18 12
6
18 12
6
5
18 1
→
’
”
2
6
1
1 5
5
5

 
 
S { , }
12.
a) x
x
( Comx  IR e x
 .)
x
x
1 52
1
52 1 1 5
10
9
0
10
10 9
2
2
x x 9
x
x 0
a
→
1 10 9
; b ;c
b ac →
55 5 5
D 5 2 D5 2 ? ? 5 2 5
2 4 102 4 1 9 100 36 64
Como D
é positivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
2 6
?
5
2 6 5
2 1
52
5
b
a
x
x
2
10 64
2 1
10 8
2
10 8
2
1
→
’
” 22 2
52
5 2 2
10 8
2
9
9 1

 
 
S { , }
b) 6 5
3 5
1
( .)
1
6 1 5 1
1
3
x
x
x
Comx IR e x
x x x
x
x
1 5
1
2
2 1 2
2
5
1
( ) ( )
 
5
1
6 6 5 5 3 5 6 4 10 0
6 4 1
2 2
x
x x x x
b c
2
2 1 2 5 1 2 2 5
5 52 52
→ x → x
a ; ; 0
b ac → ( ) ( )
2 4 4 2 4 6 10 16 240 256 D 5 2 D5 2 2 ? ? 2 5 1 5
Como D
é positivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
’
6 5
1
b 5 5
a
x
x
2
4 256
2 6
4 16
12
4 16
12
20
12
5
→ 3
” 5
2
52
5 2
4 16
12
1
1
5
3

 
 
S { , }

351
c) 1 3
2
1
1
( , 0 1
.)
2 1
2 1
3
x x
Comx IRx ex
x
x x
x x
5 2
2
2
2
5
2
( )
( )
(
  
1 2
2 1
2 2 3 3 2 3 7 2 0
3
) 2 2
( )
;
2
2
2 5 2 2 2 1 2 5
52 5
x
x x
x x x x x
b
→ → x
a 7 ;
2
2 4 72 4 ( 3 ) ( 2 )
49 24 25
c
b ac
52
D 5 2 D5 2 ? 2 ? 2 5 2 5
D
→
Como é positivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
2 6
? 2
5
2 6
2
5
2 1
2
5
2
b 2
a
x
2
7 25
2 3
7 5
6
7 5
6
2
6
( ) →
’ 5
5
2 2
2
5
2
2
5
5
1
3
7 5
6
12
6
2
1
3
2
x
S
”
,

 
 
{ }
d) x
x x x x
Comx IRx ex
2
x x
2
2
5
2 2
2
2 2
3
1
3
2 1
1 2
1 3
( )( )
( , .)
( )
  
( x
)
x x x x 2
( x 2 )( x 2
) ( x )( x
)
5
2 2
2 2 1 5 2 1
2
2 1
3
2 1
→ 2 3 6 3→x2 4 3 0
1 4 3
2 4 4 2 4 1 3 16 12 4
5
5 52 5
a
D 5 2 D5 2 2 ? ? 5 2 5
C
; b ;c
b ac → ( )
omo D é positivo (D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
4 6
4
2 ?
1
5
4 6
2
2
5
1
5 5
5
b
a
x
’
2 x
4 2
2
6
2
3
4 →
” 2
5 5
2
2
2
2
1
(Não convém,pois, pelas
condições, x 1 e x 2
.)
Logo, S = {3}.

 
 
e) x
x x
Comx IRx ex
2
2
4
1
x x x
x
1
2
5
2 1 2
2
5 1 2
1 4 2
2
( , .)
( ) ( )
( )
  
( )
5 2 1
( )( )
( )( )
(
x
x x
x x
x x x x
2
5
2 2
2 2
1
2 1
2 1 2 5 2 1 → 2 4 8 5 x2 3 2
2 3 8 5 2 15 10 4 2 18 18 0 2 2 9 9
) →
→x 1 x2 5 x 2 x1 →2 x 1 x2 5 → x 2 x1 50
; b ;
c
b ac →
o D é positivo(D.0),a equação temduas raízes reaisdistintas:
2 9 9
5 52 5
2 4 9 2 4 2 9 81 72 9
a
D 5 2 D5 2 2 ? ? 5 2 5
Com
( )
x 5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
b
a
x
x
2
9 9
2 2
9 3
4
9 3
4
12
4
3
9
→
’
”
3
4
6
4
3
2
3
2
3
5 5
5

 
 
S { , }

352
f) 2
1
2
1
1 1
2
1 1
2
x2
x
x
Comx IRx ex
x x
x
x
2
2 5
2
2
2 1
2 5
( , .)
( )
  
( ) 2
2 1
2
( x 2 )( x
1
)
( x 2 )( x
1
)
5
x ( x
1
)
x 2
)( )
1
2
1 1
2 1 1
1 1
1
( x )( x ) (
1
2 2
( )
x
x x x
x x x
x x
x
1
2 2 5 1
2 1 2 2 5
2 2 1 5
1
2 2 1
2 2 2 2 2
0
3 2
4 0
3
2
4 0
1 2 5
5 5 52
D 5 2 D5 2 ? ? 2 5 1
a 3; b 1;c 4
2 2
4 1 4 3 4 1 4
x
b ac
→ ( ) 8 49
0
5
Como D é positivo(D. ),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
2 6
?
’ 55 5
2 6 5
2 1
b
a
x
2
1 49
2 3
7 7
6
1 7
→ → 6
5
2 2
5
2
(Não convém.)
52
6
6
1
1 7
6
8
6
4
3
x
Logo
”
,

 
 
4
3 { }.
S5 2
g) 3
2
3
4
2 2 2
1
3
2
3
2
2
x
x x
Comx IRx ex
2
2
x
x x
5 2
1
2
1
( , .)
( ) ( )(
  
x
→ ( )( 2
x x
x x x x
x x
2
5
2
1 2
2
1 2
5
1 2
2
2
3 2
2 2
3
2 2
2 2
)
( )
( )( ) ( )( )
2 2
3 2 6 3 2 2 4 3 2 6 3 2 2 8
)
( )( )
( )
x x
x x x x
1 2
2 2 5 2 2 2 2 1 5
→
→ x → x 0 6 5 0
1 6 5
a ; ;
4 6 4 1 5
2
2 2
→
→
x x
b c
b ac
2 1 5
5 52 5
D 5 2 D5 2 2 ? ? 5
( ) 16
Como D é positivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
’ 5
6 5
1
b 5 5
a
x
2
6 16
2 1
6 4
2
6 4
2
10
→ 2
6 4
2
2
2
1
1 5
x
S
”
{ , }
5
2
5 5
5

 
 
h) 1
2 5
x 3
x
1
2
1
2
2 3
2
2 2
2 3 2
Comx IRx ex
x
x x
2
2
2 2
( , .)
( )
( )( )
  
2
2 2
2 2
5
2
2 2
2
( )( )
( )( )
( )
( )( )
x x
x x
x
x x
x
3 2
2 3 2
2 3
2 3 2
2 4
→
→ 22 (x 2 2 x 1 ) 5 x 2 x 2 2 x 2
1 x 2 2 x
1 5
2
x x
5 6 2 6 2 4 5 6 2 6 0
5 4
2 1 2 5
→ →
→ 0 5 4 0
1 5 4
2
→
a ; ;
b c
b ac
5 52 5
D 5 2 D5 2 2 ? ? 5
→
x x
2 2
2 1 5
4 5 4 1 4
( ) 9
Como D é positivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
6 5
1
b 5 5
a
x
x
2
5 9
2 1
5 3
2
5 3
2
8
2
4
→
’
” 5
2
5 5
5
5 3
2
2
2
1
1 4

 
 
S { , }

353
13. x
x
x
( Comx
 .)
→
1
1 5
2
8
2 8 2 2 8 0
x x x x x
0
1 5 2 1 2 5
5 5 52
a 1; b 2;c 8
→ ( )
b2 4ac 22 4 1 8 36
D 5 2 D5 2 ? ? 2 5
Como é positivo
D D
0
( . ),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
b
2a
22 6
?
5
2 6 5
2 1
5 5
5
2 2
5
2
52
2 36
2 1
2 6
2
2 6
2
4
2
2
2 6
2
8
2
4
→
x
x
’
”
 
 
S1 5{24,2}
9
2
4
2
3
2
1 2
9 2
2 2
8
2
2
1
2
5 2
2 2
2
1
x
x
x Com x
x x
x x
( )(  .)
( )( )
( ) ( 2
5
x x
3 1 2
( 2 )( 2
)
x
2 2
( 2
)
2
)
9 x 2 18 2 x 2 1 2 x 1 8 5 3 (
x 2 2 3 x
1
2
→
→ ) →
→ 11 x 2 10 2 x 2 2 3 x 2 1 9 x 2 6 5 0 → 2 4
x 2
1 20 x
2 16 5
0
→
→
x 2
2 5 x
1
4
5
a 1; b 5;c
5 52 5
D 5 2 D5 2 2 ? ? 5
b ac → ( )
D
0
4
2 4 5 2 4 1 4 9
Como é p
ositivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
b
a
x
x
2
5 9
2 1
5 3
2
5 3
2
8
2
4
5 3
2
2
→
’
”
2
1
1 4
4 2 1 4 3
2
1 2
5
5
1 52 1 1 1 5

 
 
S
S S
{ , }
14. y
6
3 4
5 1 2 5
x
x se y
x
x
x x
x
x
x
1 2 5
x x
1 2
5
2 1 5
6
3 4
6 3 4
7 6 0
2
2
( )
→ →
→
a 1; b 7;c
5 52 5
D 5 2 D5 2 2 ? ? 5
Como D
é po
6
b2 4ac→ ( 7)2 4 1 6 25
sitivo(D.0),a equação temduas raízes reaisdistintas:
x 5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
b
a
x
x
2
7 25
2 1
7 5
2
7 5
2
12
2
6
7 5
2
→
’
”
2
2
51

 
 
Os valores de x são 1 ou 6.
22 – Resolvendo problemas
1. x 5 número procurado
x2 5 7x 2 6
x2 2 7x 1 6 5 0
a 5 1; b 5 27; c 5 6

354
D 5 b2 2 4ac
D 5 (27)2 2 4 ? 1 ? 6
D 5 25
Como D é positivo, a equação tem duas raízes reais:
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
7 25
2 1
7 5
2
7 5
2
12
2
6
7 5
2
2
2
1
→
’
”

 
 
O número é 1 ou 6.
2. (x 2 3)2 5 5x 2 1
x2 2 6x 1 9 2 5x 1 1 5 0
x2 2 11x 1 10 5 0
a 5 1; b 5 211; c 5 10
D 5 b2 2 4ac
D 5 (211)2 2 4 ? 1 ? 10
D 5 81
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
2 2
5
11 81
2 1
11 9
2
11 9
2
20
2
10
11 9
2
→
’
” 55 5
2
2
1

 
 
O número é 1 ou 10.
3. x2 2 7 1 6x 5 6x 1 13 2 x
x2 1 x 2 20 5 0
a 5 1; b 5 1 e c 5 220
D 5 b2 2 4ac
D 5 12 2 4 ? 1 ? (220)
D 5 81
x
b
a
x
x
5
2 D
5
2 6
?
5
2 6 5
2 1
5 5
5
2 2
5
2
± 1 81
1 9
→ 2
2 1
2
1 9
2
8
2
4
1 9
2
’
”
10
2
525

 
  Os números são 4 e 25.
4. p 5 x(x 2 1)
p 5 380
x2 2 x 5 380
x2 2 x 2 380 5 0
a 5 1; b 5 21 e c 5 2380
D 5 b2 2 4ac
D 5 (21)2 2 4 ? 1 ? (2380)
D 5 1 521
x
b
2 a
2
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
1 1521
2 1
1 39
2
1 39
2
40
2
20
1 39
→
’
”
2
38
2
2
5 19
52 (Não convém.)

 
 
Logo, 20 equipes participam do torneio.

355
5. x3 1 6x2 2 x 2 6 x 1 1
2x3 2 x2 x2 1 5x 2 6 5 Q(x)
5x2 2 x 2 6
25x2 2 5x
26x 2 6
6x 1 6
0
Q(x) 5 x2 1 5x 2 6 5 0
x2 1 5x 2 6 5 0
a 5 1; b 5 5; c 5 26
D 5 b2 2 4ac
D 5 52 2 4 ? 1 ? (26)
D 5 25 1 24
D 5 49
x
b
a
x
x
5
2 6 D
5
2 6
?
5
2 6 5
2 1
5
5
2 2
52
2
5 49
2 1
5 7
2
5 7
2
1
5 7
2
6
→


’
”

 
Os valores reais de x que tornam Q(x) 5 0 são: 26 e 1.
6. Seja x o número de crianças e y o número de balas:
x ? y 5 240
x ? (y 2 1) 5 x ? x
Logo, y 5 1 1 x.
x(1 1 x) 5 240
x2 1 x 2 240 5 0
a 5 1; b 5 1 e c 5 2240
D 5 b2 2 4ac
D 5 12 2 4 ? 1 ? (2240)
D 5 961
x
b
2 a
2
x
x
5
2 6 D
5
2 6
?
5
2 6 5
2 1
5 5
5
1 961
2 1
1 31
2
1 31
2
30
2
15
1
→
’
” 2
5
2
52
31
2
32
2
16 (Não convém.)

 
 
Logo x 5 15.
1
10
7. T x
2
( )
12 10
52 2 1
5
T C
x
9 6
2
52 2 1
9 6
1
10
12 10
, º
, ( )
96 5 2(x2 2 24x 1 144) 1 100
96 2 100 1 x2 2 24x 1 144 5 0
x2 2 24x 1 140 5 0
a 5 1; b 5 224; c 5 140
D 5 b2 2 4ac
D 5 (224)2 2 4 ? 1 ? (140)
D 5 576 2 560 5 16

356
x
b
2 a
2
x
x
5
2  D
5

?
5
 5
1
5 5
5
24 16
2 1
24 4
2
24 4
2
28
2
14
24 4
2
→
’
” 55 5
20
2
10

 
 
Como o enunciado pede a hora do período da tarde, temos 14 h.
1.
(I) x2 2 8 100 5 0
x2 5 8 100
x5 8 100 590
Como 290 não convém, são 90 km de praias protegidas.
(II) 2x2 2 46x 5 0
2x(x 2 23) 5 0
x 5 0 (Não convém.)
x 2 23 5 0 R x 5 23
Logo, Santa Cruz de Cabrália está a 23 km de Porto Seguro.
(III) x2 2 15x 2 16 5 0
a 5 1; b 5 215; c 5 216
D 5 b2 2 4ac
D 5 (215)2 2 4 ? 1 ? (216)
D 5 225 1 64 5 289
x
b
a
x
x
5
2  D
5

?
5
 5
1
5 5
5
2
15 289
2 1
15 17
2
15 17
2
32
2
16
15
→
’
” 2
5
2
52
17
2
2
2
1

 
 
Logo, cerca de 16 km de praias paradisíacas desenham a paisagem de Arraial D’Ajuda.
(IV) e (V) x2 2 50x 1 624 5 0
a 5 1; b 5 250; c 5 624
D 5 b2 2 4ac
D 5 (250)2 2 4 ? 1 ? 624
D 5 2 500 2 2 496 5 4
x
b
a
x
x
5
2  D
5

?
5
 5
1
5 5
5
2
5
2
50 4
2 1
50 2
2
50 2
2
52
2
26
50 2
2
→
’
”
48
2
524

 
 
Logo, Trancoso fica a 24 km de Arraial D’Ajuda e a 26 km de Porto Seguro.
2.

V
300
 
  ( ) x x
x
V
300
x
5
40
1 5
x x
x
2
1 5
2
2 1
2
300
40
300
2
300 2 40
x x
x
x x
( 2
)
( 2
) ( )
5
2
2
2
300
2

357
300x 2 600 1 40x2 2 80x 5 300x
40x2 2 80x 2 600 5 0
x2 2 2x 2 15 5 0
a 5 1; b 5 22; c 5 215
D 5 b2 2 4ac
D 5 (22)2 2 4 ? 1 ? (215)
D 5 64
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
5
2
2 64
2 1
2 8
2
2 8
2
10
2
5
2 8
2
6
2
→
’
” 23(Nãoconvém.)

 
 
O tempo é de 5 horas.
a) D
t
t
5 ?
D
t
t
t
t
1
1
2
5
1
1
2 5
1
1
5
4
7
1
1
0
7
1
1 0
7
1
2
2
2

 

 

 

 
1
t2 1 1 5 t 1 7
t2 2 t 2 6 5 0
a 5 1; b 5 21; c 5 26
D 5 b2 2 4ac
D 5 (21)2 2 4 ? 1 ? (26)
D 5 25
t
b
a
’
” (Não convém.)
t
t
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
52
2
1 25
2 1
1 5
2
1 5
2
6
2
3
1 5
2
4
2
2

 
 
Logo, o carro levou 3 horas para percorrer a distância de A até B.
b) V
D
s
5
D
t Como o carro percorreu 240 km em 3 horas, temos:
V5 5
240
3
80 R V 5 80 km/h
1.
1 100 m2
x 28
x
A 5 x(x 2 28)
1 100 5 x(x 2 28)
x2 2 28x 2 1 100 5 0
a 5 1; b 5 228; c 5 21 100

358
D 5 b2 2 4ac
D 5 (228)2 2 4 ? 1 ? (21 100)
D 5 784 1 4 400 5 5 184
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5 5
5
2
52
2
28 5184
2 1
28 72
2
100
2
50
44
2
2
→
’
” 2(Nãoconvém.)

 
 
Como x 5 50 e x 2 28 5 22, as dimensões do terreno são: 50 m e 22 m.
2.
V 5 a ? b ? c
30 5 3 ? x ? (x 1 3)
3x2 1 9x 2 30 5 0
x2 1 3x 2 10 5 0
a 5 1; b 5 3; c 5 210
D 5 b2 2 4ac
D 5 32 2 4 ? 1 ? (210)
D 5 49
x
b
a
x
x
5
2 6 D
5
2 6
?
5
2 6 5 5
5
2
52
2
3 49
2 1
3 7
2
4
2
2
10
2
5
→
’
” (Nãoconvém.)

 
 
Logo, x 5 2.
3. d
n n
5
( 23)
2
a) 9
n(n2 3
)
2 5
18 5 n2 2 3n
n2 2 3n 2 18 5 0
a 5 1; b 5 23; c 5 218
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (218)
D 5 81
n
b
a
n
n
5
2 6 D
5
6
?
5
6 5 5
5
2
52
2
3 81
2 1
3 9
2
12
2
6
6
2
3
→
’
” (Nãoconvém.)

 
 
Logo, o polígono que tem 9 diagonais é o hexágono (n 5 6).
b) 20
n(n2 3
)
2 5
40 5 n2 2 3n
n2 2 3n 2 40 5 0
a 5 1; b 5 23; c 5 240
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (240)
D 5 169

359
n
b
a
n
n
5
2 6 D
5
6
?
5
6 5 5
5
2
52
2
3 169
2 1
3 13
2
16
2
8
10
2
5
→
’
” (Nãoconvém.)

 
 
Logo, o polígono que tem 20 diagonais é o octógono (n 5 8).
4.
a)
2 m S
5 m
2 x 7s
5 x
(2 1 x)(5 1 x) 5 7 ? 2 ? 5
x2 1 7x 1 10 2 70 5 0
x2 1 7x 2 60 5 0
a 5 1; b 5 7; c 5 260
D 5 b2 2 4ac
D 5 72 2 4 ? 1 ? (260)
D 5 289
x
b
a
x
x
5
2 6 D
5
2 6
?
5
2 6 5 5
5
2
52
2
7 289
2 1
7 17
2
10
2
5
24
2
12
→
’
” (Não convém.)

 
 
Logo, as dimensões do novo retângulo são:
7 m (2 m 1 5 m) e 10 m (5 m 1 5 m)
b) Perímetro 5 7 1 7 1 10 1 10 5 34
Logo, o perímetro é 34 m.
5. (x 1 2)(x 1 6) 5 140
x2 1 8x 1 12 5 140
x2 1 8x 2 128 5 0
a 5 1; b 5 8; c 5 2128
D 5 b2 2 4ac
D 5 82 2 4 ? 1 ? (2128) R D 5 576
x
b
a
x
x
5
2 6 D
5
2 6
?
5
2 6 5 5
5
2
52
2
8 576
2 1
8 24
2
16
2
8
32
2
16
→
’
” (Não convém.)

 
 
Logo, as medidas são: 10 m (8 m 1 2 m) e 14 m (8 m 1 6 m).
6. AC 5 x; AB 5 10; BC 5 10 2 x; 5 52,23
AC2 5 AB ? BC
x2 5 10(10 2 x)
x2 1 10x 2 100 5 0
a 5 1; b 5 10; c 5 2100
D 5 b2 2 4ac
D 5 102 2 4 ? 1 ? (2100)
D 5 500

360
x
b
a
x
x
5
2 6 D
5
2 6
?
5
2 6 5
2 1
5
2
10 500
2 1
10 10 5
2
10 10 5
2
6 15
→
’ ,
” 5
2 2
52
10 10 5
2
16,15(Não convém.)

 
 
Logo, a medida de x é 6,15.
7. x ? x 5 16(x 1 5)
x2 5 16x 1 80
x2 2 16x 2 80 5 0
a 5 1; b 5 216 e c 5 280
D 5 b2 2 4ac
D 5 (216)2 2 4 ? 1 ? (280)
D 5 256 1 320 5 576
x
b
a
’
” (Não convém.)
x
x
5
2 6
5
6
?
5
6 5 5
5 52
Δ
2
16 576
2 1
16 24
2
40
2
20
8
2
4
→
−

 
 
a) O lado do quadrado mede 20, e seu perímetro é 4 ? 20 5 80.
b) Os lados do retângulo são 16 e 25 (20 1 5); logo, seu perímetro será:
16 1 16 1 25 1 25 5 82
8. 1 000 5 (50 2 2x)(80 2 2x)
1 000 5 4 000 2 100x 2 160x 1 4x2
4x2 2 260x 1 3 000 5 0
x2 2 65x 1 750 5 0
a 5 1; b 5 265; c 5 750
D 5 b2 2 4ac
D 5 (265)2 – 4 ? 1 ? 750
D 5 4 225 2 3 000 5 1 225
x
b
a
x
5
2 6 D
5
6
?
5
6 5 5
2
65 1 225
2 1
65 35
2
100
2
50
→
’ (Nãoconvém.)
x”5 5
30
2
15

   
Logo, o recuo é de 15 m.
9. 2 400 5 (30 1 2x)(50 1 2x)
2 400 5 1 500 1 60x 1 100x 1 4x2
4x2 1 160x 2 900 5 0
x2 1 40x 2 225 5 0
a 5 1; b 5 40; c 5 2225
D 5 b2 2 4ac
D 5 402 2 4 ? 1 ? (2225)
D 5 1 600 1 900 5 2 500
x
b
a
x
x
5
2 6
5
2 6
?
5
2 6 5 5
5
2
52
Δ
2
40 2 500
2 1
40 50
2
10
2
5
90
2
4
→
’
” 5(Nãoconvém.)

 
 
Logo, x 5 5 cm.

361
23 – Estudando as raízes de uma
equação do 2.o grau
1. x2 2 2x 2 8 5 0
x 5 22 R
R (22)2 2 2 ? (22) 2 8 5 4 1 4 2 8 5 0
Logo, 22 é raiz da equação.
x 5 0 R 0 2 0 2 8 5 28 ≠ 0
Logo, 0 não é raiz da equação.
x 5 1 R 12 2 2 ? 1 2 8 5 29 ≠ 0
Logo, 1 não é raiz da equação.
x 5 4 R 42 2 2 ? 4 2 8 5 0
Logo, 4 é raiz da equação.
Então, apenas os números 22 e 4 são
raízes da equação dada.
2. x2 2 4x 2 2 5 0
( ) 2
( )
2 1 6 2 4 2 1 6 2 2 5
0
4 1 4 6 1 6 2 8 2 4 6 2 2 5
0
10 2 10 5
0
(Verdadeiro.)
Logo, 21 6 é raiz da equação dada.
3. 2x2 1 kx 2 1 5 0
Para k 5 1, temos:
2x2 1 x 2 1 5 0
a 5 2; b 5 1; c 5 21
D 5 b2 2 4ac
D 5 12 2 4 ? 2 ? (21) 5 9
Como D é positivo, a equação tem duas
raízes reais:
b
x
a
x
x
5
2 6 D
5
2 6
?
5
2 6
5
2 1
5 5
5
2 2
5
2
1 9
2 2
1 3
4
1 3
4
2
4
1
2
1 3
4
→
→
’
” 2
52
4
4
1

 
 
Logo, a menor raiz da equação é o número
inteiro 21.
4. x2 2 7x 2 2c 5 0
x 5 23 R (23)2 2 7 ? (23) 2 2c 5 0
9 1 21 2 2c 5 0
2c 5 30
c 5 15
Logo, c 5 15.
5. 2x2 2 bx 1 10 5 0
x 5 5 R 2 ? 52 2 b ? 5 1 10 5 0
50 1 10 5 5b
5b 5 60
b 5 12
Logo, b 5 12.
6. 9x2 2 6x 1 2m 5 0 (Raízes reais R D 0.)
a 5 9; b 5 26; c 5 2m
D 5 b2 2 4ac 0
(26)2 2 4 ? 9 ? 2m 0
36 2 72m 0
72m 236
72m 36
m
1
2
O valor real de m é m
1
2 .
7. 9x2 1 9x 1 k 5 0 (Nenhuma raiz
real R D , 0.)
a 5 9; b 5 9; c 5 k
D 5 b2 2 4ac
D 5 92 2 4 ? 9 ? k , 0
81 2 36k , 0
236k , 281
k .
81
36
k .
9
4
Para que a equação dada não tenha raízes
reais, k .
9
4 .
8. 2x2 1 bx 1 8 5 0 (Uma única raiz
real R D 5 0.)
D 5 b2 2 4ac
D 5 b2 2 4 ? 2 ? 8 5 0
b2 5 64
b5 ± 64
b568
Para b 5 8 ou b 5 28, a equação terá uma
única raiz real.
9. 4x2 2 4x 1 2p 2 1 5 0 (Raízes reais e
diferentes R D . 0.)
a 5 4; b 5 24; c 5 2p 2 1
D 5 b2 2 4ac
(24)2 2 4 ? 4(2p 2 1) . 0
16 2 32p 1 16 . 0
232p . 232
32p , 32
p , 1
Para p , 1, a equação dada terá duas
raízes reais e diferentes.
10. x2 1 (m 2 1)x 1 m 2 2 5 0 (Uma única
raiz real R D 5 0.)
a 5 1; b 5 m; c 5 m 2 2

362
D 5 b2 2 4ac
D 5 (m 2 1)2 2 4 ? 1 ? (m 2 2) 5 0
m2 2 2m 1 1 2 4m 1 8 5 0
m2 2 6m 1 9 5 0
D5(26)224 ?1?953623650
m
2 b
 D
a 5
5
6 
0
2 ?
1
6
2
5 5 2
3
Para m 5 3, a equação dada terá uma
única raiz real.
11. (k 2 2)x2 2 6x 2 3 5 0 (Nenhuma raiz
real R D , 0.)
a 5 k 2 2; b 5 26; c 5 23
D 5 b2 2 4ac
(26)2 2 4 ? (k 2 2)(23) , 0
36 1 12(k 2 2) , 0
36 1 12k 2 24 , 0
12k , 212
k , 21
Para k , 21, a equação dada não possui
raízes reais.
24 – Relacionando as raízes
e os coeficientes da equação
ax 2 1 bx 1 c 5 0
1.
a) x2 2 x 2 20 5 0
S x x
b
a
5 1 5
P x x
2
c
a
52
2
5
5 ? 5 5
2
52
’ ”
( )
’ ”
1
1
1
20
1
20
b) 16x2 1 8x 1 1 5 0
’ ”
S x x
b
a
5 1 5
P x x
2
c
a
52 52
’ ”
5 ? 5 5
8
16
1
2
1
16
c) 6x2 2 4x 2 3 5 0
S x x
b
a
5 1 5
P x x
2
c
a
5
( )
2 2
5
5 ? 5 5
2
52
’ ”
’ ”
4
6
2
3
3
6
1
2
d) 10x2 1 3x 2 4 5 0
S x x
b
a
5 1 5
P x x
2
c
a
52
5 ? 5 5
2
52
’ ”
’ ”
3
10
4
10
2
5
2. x2 2 6x 2 16 5 0
a) x x
b
a
’ ”
( )
1 5
2
52
2
5
6
1
6
b) x x
c
a
’? ”5 5
2
52
16
1
16
c) 1 1 6
16
3
x ” 1
x
’
1 5
” ?
’ x ’ x ” x x
8
5
2
52
3. 1 1
1
5
x 1
x 5
1
6 6 1 6
6 1
5 1
6 1
( )
( )
( )
( )
x x
x x
x x
x x
1 1
1
5
1
1
6x 1 6 1 6x 5 5x2 1 5x
5x2 2 7x 2 6 5 0
S x x
b
a
’ ”
5 1 5
P x x
c
a
S eP
2
5
2
5
5 ? 5 5
2
5 52
( )
’ ”
.
− 7
5
7
5
6
5
7
5
6
5
4. x2 2 11x 1 28 5 0
’ ”
S x x
b
a
5 1 5
P x x
c
a
S P
2
52
( 2
)
5
’ ”
5 ? 5 5 5
2 5 2
11
1
11
28
1
28
11 285217
5. x2 2 0,8x 2 1,6 5 0
S x x
b
a
5 1 5
P x x
c
a
S
P
2
5
2 2
5
5 ? 5 5
2
52
’ ”
( , )
,
’ ”
,
,
0 8
1
0 8
1 6
1
1 6
5
2
5
2
52 5
0 8
1 6
8
16
1
2
0 5
,
,
− ,
6. x224 2 x1350
S x x
b
a
1
’ ”
5 1 5
P x x
2
c
a
1
2
x x
4 2
1
4 2
3
1
3
2 3
52
2
5
5 ? 5 5 5
2 2 5
( )
’ ”
0
2
1
2
3
1
3
’ ”
S x x
4 2 2
2
2
b
a
P x x
c
a
S
5 1 5
2
52
2
5
5 ? 5 5
2
52
5 1
( )
’ ”
5
5 ? 2 52
5 2
P 3 ( 3) 9
7. 10x2 2 7x 1 c 5 0
P x x
c
a
c
c
’ ”
5 ? 5 5 5
5 5
,
10
1
8
10
8
1 25

363
8. 4x2 2 3px 1 p 2 4 5 0
S 5 P
x’ 1 x” 5 x’ ? x”
2
5
2 2
5
2
b
a
c
a
( 3p) p
4
4
4
3p 5 p 2 4
2p 5 24
p 5 22
9. x2 2 3mx 1 m 5 0
S
b
a
S
m
5
2
5
5
2 2
5
15
3
1
15
( )
3m 5 15
m 5 5
P
c
a
m
5 5 1
Como m 5 5, P 5 5.
10. x2 2 2mx 1 m 5 0
P 5 4
P
c
a
m
5 5 5 1
4 R m 5 4
S
b
a
m
2 2
5 5 S 5
m
− ( 2 ) →
1
2
Como m 5 4:
S 5 2m R S 5 2 ? 4 R S 5 8
11. x2 2 mx 2 5 5 0
(x’ 1 x”) 1 (x’ ? x”) 5 1
2
1 5
b
a
c
a
1
2 2
1
2
5
( m) ( 5
)
1
1
1
m 2 5 5 1
m 5 6
O valor real de m que satisfaz a condição
dada é m 5 6.
12. 2x215x1h2550
Se x
1
, então: x’ ? x” 5 1.
x
’
” 5
x x
c
a
’? ”5
c
a
h
5
5
2
1
1
5
2
h 2 5 5 2
h 5 7
13. 4x2 2 2(k 2 1)x 2 1 5 0
Se x’ 5 2x”, então: x’ 1 x” 5 0.
x x
b
a
k
’ ”
1 5
k
2
( )
5

2 1
4
2 2
0
2 2 4 0
2 1 5 ?

2k 2 2 5 0
k 5 1
a) x2 2 5x 1 6 5 0
S 5 5 e P 5 6
S 5 2 1 3 5 5
P 5 2 ? 3 5 6
As raízes são 2 e 3.
b) x2 2 7x 1 10 5 0
S 5 7 e P 5 10
S 5 2 1 5 5 7
P 5 2 ? 5 5 10
c) x2 2 10x 1 24 5 0
S 5 10 e P 5 24
S 5 4 1 6 5 10
P 5 4 ? 6 5 24
d) x2 2 8x 1 7 5 0
S 5 8 e P 5 7
S 5 1 1 7 5 8
P 5 1 ? 7 5 7
e) x2 2 4x 2 12 5 0
S 5 4 e P 5 212
S 5 6 1 (22) 5 4
P 5 6 ? (22) 5 212
25 – Escrevendo uma equação do
2.o grau quando conhecemos
as duas raízes
1.
a) 5 e 7
S 5 5 1 7 5 12
P 5 5 ? 7 5 35
x2 2 Sx 1 P 5 0
x2 2 12x 1 35 5 0

364
b) 6 e 6
S 5 6 1 6 5 12
P 5 6 ? 6 5 36
x2 2 Sx 1 P 5 0
x2 2 12x 1 36 5 0
c) 22 e 11
S 5 22 1 11 5 9
P 5 (22) ? 11 5 222
x2 2 Sx 1 P 5 0
x2 2 9x 2 22 5 0
d) 28 e 25
S 5 28 2 5 5 213
P 5 (28) ? (25) 5 40
x2 2 Sx 1 P 5 0
x2 2 (213)x 1 40 5 0
x2 1 13x 1 40 5 0
e) 28 e 8
S 5 28 1 8 5 0
P 5 (28) ? 8 5 264
x2 2 Sx 1 P 5 0
x2 2 0x 2 64 5 0
x2 2 64 5 0
f) 29 e 0
S 5 29 1 0 5 29
P 5 (29) ? 0 5 0
x2 2 Sx 1 P 5 0
x2 2 (29)x 1 0 5 0
x2 1 9x 5 0
g) 1
2
e24
1
2
S5 2 4
52
7
2
1
2
P5 ? 2 52
( 4) 2
x2 2 Sx 1 P 5 0
x2 7 x
1 2250
2
2x2 1 7x 2 4 5 0
h) 3
4
3
4
e
3
4
3
4
6
4
S5 1 5 5
3
2
3
4
3
4
P5 ? 5
9
16
x2 2 Sx 1 P 5 0
x2 3 x
2
9
16
2 1 50
16x2 2 24x 1 9 5 0
i) 41 2 e 42 2
S
P
4 2 4 2 8
4 2 4 2
42 2 2 16 2 14
5 1 1 2 5
5 ( 1 )( ? 2 )
5
5 2 5 2 5
( )
x2 2 Sx 1 P 5 0
x2 2 8x 1 14 5 0
j) 211 10 e212 10
S
P
( )
1 10 1 10 2
1 10 1 10
1 2 10 2
52 1 12 2 52
5 2 1 2 2 5
5 2 2
( )( )
( ) ( ) 551210529
x2 2 Sx 1 P 5 0
x2 2 (22)x 1 (29) 5 0
x2 1 2x 2 9 5 0
2.
a) S 5 11 e P 5 18
x2 2 Sx 1 P 5 0
x2 2 11x 1 18 5 0
b) S 5 25 e P 5 284
x2 2 Sx 1 P 5 0
x2 2 (25)x 1 (284) 5 0
x2 1 5x 2 84 5 0
1
3
c) S5 e P52
1
3
2
x Sx P
x 2
x
x x
2 1 5
2 2 5
2 2 5
2
0
1
3
1
3
0
3 1 0
26 – Equações biquadradas
1.
a) x4 2 8x2 2 9 5 0
Fazendo x2 5 p, temos:
p2 2 8p 2 9 5 0
D 5 b2 2 4ac
D 5 (28)2 2 4 ? 1 ? (29)
D 5 64 1 36 5 100

365
p
b
a
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
8 100
2 1
8 10
2
8 10
2
18
2
9
8 10
2
→
’
” 2
52
2
2
1

 
 
Para p 5 9, temos:
x2 5 p R x2 5 9 R x 5 63
Para p 5 21 temos:
x2 5 p R x2 5 21 R x 56 21 (Não existe em IR.)
Logo, S 5 {23, 3}.
b) x4 2 4 5 3x2 R x4 2 3x2 2 4 5 0
p2 2 3p 2 4 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (24)
D 5 9 1 16 5 25
p
b
a
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
52
2
3 25
2 1
3 5
2
3 5
2
8
2
4
3 5
2
2
2
→
’
” 1

 
 
Para p 5 4, temos:
x2 5 p R x2 5 4 R x 5 62
Para p 5 21, temos:
Logo, S 5 {22, 2}.
c) x4 2 16x2 5 0
x x
x ou
x
2 2
2
2 16 0
0
16 0
( 2 )5
5
2 5
→
 

Para x2 5 0, temos: x 5 0.
Para x2 2 16 5 0, temos:
x2 5 16 R x56 16 →x564
Logo, S 5 {24, 0, 4}.
d) x4 2 8x2 1 16 5 0
p2 2 8p 1 16 5 0
D 5 b2 2 4ac
D 5 (28)2 2 4 ? 1 ? 16
D 5 0
p
2
b
5
a 8
2
5 5 2
4
Para p 5 4, temos:
x2 5 p R x2 5 4 R x 562
Logo, S 5 { 22, 2}.
2. 11x4 2 6x2 5 x2 1 4 R 11x4 2 7x2 2 4 5 0
11p2 2 7p 2 4 5 0

366
D 5 b2 2 4ac
D 5 (27)2 2 4 ? 11 ? (24)
D 5 49 1 176 5 225
p
b
2 a
2
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
7 225
2 11
7 15
22
7 15
22
22
22
1
7
→
’
”
15
22
2
8
4
5
22
52
11 
 
 
Para p 5 1, temos:
x2 5 p R x2 5 1 R x56 1 561
Para p52
4
11
, temos:
x2 5 p R x2 4
11 52 R x 56 2
4
11
(Não existe em IR.)
As expressões dadas apresentam valores numéricos iguais para
x 5 21 e x 5 1.
3.
a) (x2 2 1)(x2 2 12) 1 24 5 0 R x4 2 13x2 1 12 1 24 5 0 R x4 2 13x2 1 36 5 0
p2 2 13p 1 36 5 0
D 5 b2 2 4ac
D 5 (213)2 2 4 ? 1 ? 36
D 5 169 2 144 5 25
p
b
a
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
13 25
2 1
13 5
2
13 5
2
18
2
9
13 5
2
→
’
”
8
2
54

 
 
Para p 5 9, temos:
x2 5 p R x2 5 9 Rx56 9 563
Para p 5 4, temos:
x2 5 p R x2 5 4 Rx56 4 562
S 5 {23, 22, 2, 3}
b) (x2 1 2)2 5 2(x2 1 6) R x4 1 4x2 1 4 5 2x2 1 12 R x4 1 2x2 2 8 5 0
p2 1 2p 2 8 5 0
D 5 b2 2 4ac
D 5 22 2 4 ? 1 ? (28)
D 5 4 1 32 5 36
p
b
2 a
2
p
p
5
2 6 D
5
2 6
?
5
2 6 5
2 1
5 5
5
2 2
5
2 36
2 1
2 6
2
2 6
2
4
2
2
2 6
2
→
’
”
8
2
524

 
 
Para p 5 2, temos:
x2 5 p R x2 5 2 R x 56 2
Para p 5 24, temos:
S5{2 2 , 2 }

367
c) (x 1 2)(x 2 2)(x 1 1)(x 2 1) 1 5x2 5 20
(x2 2 4)(x2 2 1) 1 5x2 2 20 5 0
x4 2 5x2 1 4 1 5x2 2 20 5 0
x4 2 16 5 0
p2 5 16
p56 16 →p564
Para p 5 4, temos:
x2 5 p R x2 5 4 R x 5 62
Para p 5 24, temos:
S 5 {22, 2}
d) x2(x2 2 9) 5 220 R x4 2 9x2 1 20 5 0
Fazendo x2 5 p:
p2 2 9p 1 20 5 0
D 5 b2 2 4ac
D 5 (29)2 2 4 ? 1 ? 20 5 1
p
b
a
p
’
p
 ” 
5
2 6 D
5
6
5
6 5
1
5 5
5
2
5 5
2
9 1
2
9 1
2
9 1
2
10
2
5
9 1
2
8
2
4
→

 
Para p 5 5, temos:
x2 5 p R x2 5 5 R x 56 5
Para p 5 4, temos:
x2 5 p R x2 5 4 R x56 4 →x562
S5{2 5 ,22,2, 5 }
4. x4 2 26x2 1 25 5 0
p2 2 26p 1 25 5 0
D 5 b2 2 4ac
D 5 (226)2 2 4 ? 1 ? 25
D 5 676 2 100 5 576
p
b
a
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
26 576
2 1
26 24
2
26 24
2
50
2
25
26
→
’
” 2
5 5
24
2
2
2
1

 
 
Para p 5 25, temos:
x2 5 p R x2 5 25 R x56 25 →x565
Para p 5 1, temos:
x2 5 p R x2 5 1 R x56 1 →x561
As raízes reais positivas da equação dada são 5 e 1; logo, a soma dessas raízes é 6 (S 5 5 1 1 R S 5 6).
5. x
x
2
2 2
6
1
2 5
2
(Com x ≠ 1 e x ≠ 21.)
2 2
(x 2 ) (x 1
)
2 2
x 1
x
6
1
2 2
2
5
2
(x2 2 2)(x2 2 1) 5 6 R x4 2 3x2 1 2 2 6 5 0 R x4 2 3x2 2 4 5 0

368
p2 2 3p 2 4 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (24)
D 5 9 1 16 5 25
p
b
a
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
52
2
3 25
2 1
3 5
2
3 5
2
8
2
4
3 5
2
2
2
→
’
” 1

 
 
Para p 5 4, temos:
x2 5 p R x2 5 4 R x56 4 →x562
Para p 5 21, temos:
Logo, a equação dada tem duas raízes reais: 22 e 2.
6. x
2
2 Com x
1 53( 0.)
x
2
x
4
12 3
x
2
5
x
2
x
2
x4 2 3x2 1 2 5 0
p2 2 3p 1 2 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? 2 5 1
p
b
a
p
p
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
3 1
2 1
3 1
2
3 1
2
4
2
2
3 1
2
2
2
1
→


’
”

 
Para p 5 2, temos:
x2 5 p R x2 5 2 R x 56 2
Para p 5 1, temos:
x2 5 p R x2 5 1 R x56 1 →x561
Todas as raízes da equação dada (2 2 ,21, 2 e 1) são números reais; logo, a afirmação é
correta.
27 – Equações irracionais
1. x x
1 3
1 3
2 5 2
( 2 x 2 ) 5 ( 2
x
)
x 2 1 5 9 2 6x 1 x2
x2 2 7x 1 10 5 0
D 5 b2 2 4ac
D 5 (27)2 2 4 ? 1 ? 10
D 5 49 2 40 5 9

369
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
7 9
2 1
7 3
2
7 3
2
10
2
5
7 3
2
4
2
2
→
 ’
”
 
 
Verificação
• Para x 5 5, temos:
x21 532x
521 5325
2 5 22 (Falso.)
Portanto, x 5 5 não é solução.
x21 532x
221 5322
1 5 1 (Verdadeiro.)
Portanto, x 5 2 é solução.
Logo, S 5 {2}.
2. x226x116 52 2
( ) 2 5()
2
x2 26 x
116 2 2 x2 2 6x 1 16 5 4 ? 2
x2 2 6x 1 8 5 0
D 5 b2 2 4ac
D 5 (26)2 2 4 ? 1 ? 8
D 5 36 2 32 5 4
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
6 4
2 1
6 2
2
6 2
2
8
2
4
6 2
2
4
2
2
→


’
”

 
Verificação
x226x116 52 2
42 6 4 16 2 2 2 ? 1 5
16224116 52 2
8 52 2
2 2 52 2 (Verdadeiro.)
x226x116 52 2
2 6 2 16 2 2
4 12 16 2 2
22 ? 1 5
2 1 5
8 52 2
2 2 52 2 (Verdadeiro.)
Logo, S 5 {2, 4}.

370
3. 42x5 x12
2
(4 2x )2 5( x1 2
)
16 2 8x 1 x2 5 x 1 2
x2 2 9x 1 14 5 0
D 5 b2 2 4ac
D 5 (29)2 2 4 ? 1 ? 14 5 81 2 56 5 25
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
9 25
2 1
9 5
2
9 5
2
14
2
7
9 5
2
4
2
2
→
’
”

 
 
Verificação
42x5 x12
4275 712
23 5 3 (Falso.)
42x5 x12
4225 212
2 5 2 (Verdadeiro.)
Logo, S 5 {2}.
4. x229 5 x111
( 2 x2 29 ) 5( 2
x
111 )
x2 2 9 5 x 1 11
x2 2 x 2 20 5 0
D 5 b2 2 4ac
D 5 (21)2 – 4 ? 1 ? (220) 5 81
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
52 5
2
1 81
2 1
1 9
2
1 9
2
10
2
5
1 9
2
8
2
→
’
” 24

   
Verificação
x229 5 x111
2529 5 5111
x229 5 x111
1629 5 24111
7 5 7 (Verdadeiro.)
Logo, para x 5 24 ou x 5 5 as expressões dadas apresentam o mesmo valor.

371
5. 7x23 215x
7x23 5x11
7 3 1
( ) 2
x2 5(x1 )2
7x 2 3 5 x2 1 2x 1 1
x2 2 5x 1 4 5 0
D 5 b2 2 4ac
D 5 (25)2 2 4 ? 1 ? 4 5 25 2 16 5 9
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
5 9
2 1
5 3
2
5 3
2
8
2
4
5 3
2
2
2
1
→


’
”

 
Verificação
7 x2 3 2 1
5x
7 ? 4 2 3 2 1 5
4
2823 2154
25 2154
4 5 4 (Verdadeiro.)
7 x2 3 2 1
5x
7 ? 1 2 3 2 1 5
1
4 2 1 5
1
1 5 1 (Verdadeiro.)
Logo, S 5 {1, 4}.
2
6. x x
2 1 5
( x 2
2 x
1 ) 5
x2 2 x 1 4 5 16
x2 2 x 2 12 5 0
D 5 b2 2 4ac
D 5 (21)2 2 4 ? 1 ? (212) 5 1 1 48 5 49
4 4
2
4 4
2
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
52 52
2
1 49
2 1
1 7
2
1 7
2
8
2
4
1 7
2
6
2
→
’
” 3

 
 
Verificação
x22x14 54
162414 54
16 54
4 5 4 (Verdadeiro.)

372
x22x14 54
91314 54
16 54
4 5 4 (Verdadeiro.)
Logo, o valor real x é x 5 4 ou x 5 23.
→( ) 2 ( ) 2
→
7. x1 x21 5 7 x1 x21 5 7
→x1 x21 57→ x21 572x→
→( 2
x21 ) 5 ( 72x
)2
x 2 1 5 49 2 14x 1 x2
x2 2 15x 1 50 5 0
D 5 b2 2 4ac
D 5 (215)2 2 4 ? 1 ? 50 5 225 2 200 5 25
x
b
2 a
2
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
15 25
2 1
15 5
2
15 5
2
20
2
10
15 5
2
→
’
” 55 5
10
2
5

 
 
Verificação
x1 x21 5 7
101 9 5 7
13 5 7 (Falso.)
x1 x21 5 7
51 4 5 7
7 5 7 (Verdadeiro.)
Logo, o número real é x 5 5.
8. x
x
x
Comx
4
4
2
4
2
5
2 (  .)
 2
x
x
2 2
x
4
4
2
2
5
 

 

 

 
x
x
x
4
4
5
2
2 2
2x 5 (4 2 x)2
2x 5 16 2 8x 1 x2
x2 2 10x 1 16 5 0
D 5 b2 2 4ac
D 5 (210)2 2 4 ? 1 ? 16 5 100 2 64 5 36

373
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
10 36
2 1
10 6
2
10 6
2
16
2
8
10 6
2
→
’
”
4
2
52

 
 
Verificação
• Para x 58 , temos:
x
x
x
4
4
5
2
2 2
8
4 8
4 8
5
2
2 2
22 5 22 (Não existe.)
x
x
x
4
4
5
2
2 2
2
4 2
4 2
5
2
2 2
1 5 1 (Verdadeiro.)
Logo, S 5 {2}.
9. x 522x
( x ) x 2
5(22 )2
x 5 4 2 4x 1 x2
x2 2 5x 1 4 5 0
D 5 b2 2 4ac
D 5 (25)2 2 4 ? 1 ? 4 5 9
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
5 9
2 1
5 3
2
5 3
2
8
2
4
5 3
2
2
2
1
→


’
”

  Verificação
x54→ x 522x
4 5224
2 5 22 (Falso.)
x 522x
1 5221
1 5 1 (Verdadeiro.)
Logo, x 5 1.

374
10. x1 x12 510
x12 5102x
x12 5 102x
( ) 2
( )2
x 1 2 5 100 2 20x 1 x2
x2 2 21x 1 98 5 0
D 5 b2 2 4ac
D 5 (221)2 2 4 ? 1 ? 98 5 441 2 392 5 49
x
b
2 a
2
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
21 49
2 1
21 7
2
21 7
2
28
2
14
21 7
2
→
’
” 55 5
14
2
7

 
 
Verificação
x1 x12 510
141 16 510
18 5 10 (Falso.)
x1 x12 510
71 9 510
Logo, x 5 7.
28 – Resolvendo sistemas de equações do 2.o grau
1.
a)
x y
x y
2
2 35
5
1 5

Substituindo x 5 2y na segunda equação, temos:
2y 1 y2 5 35
y2 1 2y 2 35 5 0
D 5 b2 2 4ac
D 5 22 2 4 ? 1 ? (235) 5 4 1 140 5 144
y
b
2 a
2 2
y
y
5
2 6 D
5
2 6
?
5
2 6 5
2 1
5 5
5
2 144
2 1
2 12
2
2 12
2
10
2
5
2
→
’
”
12
2
14
2
2
5 52
7

 
 
• Se y 5 27, temos:
x 5 2y R x 5 2 ? 27 R x 5 214
Então, (214, 27) é solução.
x 5 2y R x 5 2 ? 5 R x 5 10
Logo, S 5 {(214, 27); (10, 5)}

375
b)
x y
xy
1 5
5
9
14

Da primeira equação, temos: y 5 9 2 x.
Substituindo y 5 9 2 x na segunda equação:
x(9 2 x) 5 14
9x 2 x2 5 14
x2 2 9x 1 14 5 0
D 5 b2 2 4ac
D 5 (29)2 2 4 ? 1 ? 14 5 81 2 56 5 25
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
9 25
2 1
9 5
2
9 5
2
14
2
7
9 5
2
4
2
2
→
’
”

 
 
• Se x 5 7, temos:
y 5 9 2 x R y 5 9 2 7 R y 5 2
y 5 9 2 x R y 5 9 2 2 R y 5 7
Logo, S 5 {(7, 2); (2, 7)}.
c)
x 5 5 2
2
y
y 2 2 7 52
3
x

Substituindo x 5 5 2 2y na segunda equação, temos:
y2 2 7 5 23(5 2 2y)
y2 2 7 5 215 1 6y
y2 2 6y 1 8 5 0
D 5 b2 2 4ac
D 5 (26)2 2 4 ? 1 ? 8 5 36 2 32 5 4
y
b
a
y
y
5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
2
6 4
2 1
6 2
2
6 2
2
4
6 2
2
2
→

 
 
’
”
x 5 5 2 2y R x 5 5 2 2 ? 4 R x 5 23
x 5 5 2 2y R x 5 5 2 2 ? 2 R x 5 1
Logo, S 5 {(23, 4); (1, 2)}.
d)
x y
x xy
4
1 5
2 5
2 6

Da primeira equação, temos: y 5 4 2 x.
Substituindo y 5 4 2 x na segunda equação:
x2 2 x(4 2 x) 5 6
x2 2 4x 1 x2 2 6 5 0
2x2 2 4x 2 6 5 0

376
x2 2 2x 2 3 5 0
D 5 b2 2 4ac
D 5 (22)2 2 4 ? 1 ? (23) 5 4 1 12 5 16
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
2
2 16
2 1
2 4
2
2 4
2
3
2 4
2
1
→

 
 
’
”
y 5 4 2 x R y 5 4 2 3 R y 5 1
y 5 4 2 x R y 5 4 2 (21) R y 5 5
Logo, S 5 {(3, 1); (21, 5)}.
2.
y 3
x
x y x
5 2
1 2 5
2 (4 ) 7

Substituindo os valores da primeira equação na segunda, temos:
x2 1 (3 2 x)(4 2 x) 5 7
x2 1 12 2 7x 1 x2 2 7 5 0
2x2 2 7x 1 5 5 0
D 5 b2 2 4ac
D 5 (27)2 2 4 ? 2 ? 5 5 49 2 40 5 9
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
7 9
2 2
7 3
4
7 3
4
10
4
5
2
7 3
4
4
4
1
→
’
”

 
 
• Se x 5
5
2
, temos:
→ 5
→
1
2
2 y532x y532 y5
Então,
5
2
1
2
,  
 
é solução.
y 5 3 2 x R y 5 3 2 1 R y 5 2
5
2
a) x x 11 25 1 5 1
7
2
5
2 1 5 1 5
b) y y 1 2
1
2
2
3.
2 5 3
y x x
y x
1 2 5
1 52
2

Da segunda equação, temos: y 5 22 1 x.
Substituindo y 5 22 1 x na primeira equação, temos:
22 1 x 1 x2 2 5x 2 3 5 0
x2 2 4x 2 5 5 0
D 5 b2 2 4ac
D 5 (24)2 2 4 ? 1 ? (25) 5 16 1 20 5 36

377
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
2
4 36
2 1
4 6
2
4 6
2
5
4 6
2
1
→

 
 
’
”
y 5 22 1 x R y 5 22 1 5 R y 5 3
y 5 22 1 x R y 5 22 2 1 R y 5 23
Logo, S 5 {(5, 3); (21, 23)}.
Agora, podemos calcular a soma:
x1 1 y1 1 x2 1 y2
5 5 1 3 2 1 2 3 5 4
4.
xy
x y
140
5
2 5
4

Da segunda equação, temos: y 5 x 2 4.
Substituindo y 5 x 2 4 na primeira equação, temos:
x(x 2 4) 5 140
x2 2 4x 2 140 5 0
D 5 b2 2 4ac
D 5 (24)2 2 4 ? 1 ? (2140) 5 16 1 560 5 576
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
2
4 576
2 1
4 24
2
4 24
2
14
4 24
2
10
→
’
”

 
 
Como o problema pede números inteiros e positivos, consideramos apenas x 5 14.
Se x 5 14 R y 5 14 2 4 5 10
Logo, os números são 14 e 10.
5.
2 2 52
x y
y x
1 5
5 2
2

Substituindo a segunda equação na primeira, temos:
x2 1 (x 2 2)2 5 52
x2 1 x2 2 4x 1 4 2 52 5 0
2x2 2 4x 2 48 5 0
x2 2 2x 2 24 5 0
D 5 b2 2 4ac
D 5 (22)2 2 4 ? 1 ? (224) 5 4 1 96 5 100
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
2
52
2
2 100
2 1
2 10
2
2 10
2
6
2 10
2
4
→
’
” (Não convém.)

 
 
Se x 5 6 R y 5 6 2 2 R y 5 4
Para x 5 6 e y 5 4, temos:
A1 5 x2 5 62 5 36 R A1 5 36 cm2
A2 5 y2 5 42 5 16 R A2 5 16 cm2

378
6.
x
y
5
y x
3
2 5 1
10

 
 
Da primeira equação, temos: x 5 3y.
Substituindo x 5 3y na segunda equação, temos:
y2 5 3y 1 10
y2 2 3y 2 10 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (210) 5 9 1 40 5 49
y
b
a
y
y
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
5
2
3 49
2 1
3 7
2
3 7
2
10
2
5
3 7
2
2
2
→
’
” 21(Nãoconvém.)

 
 
Se y 5 5 R x 5 3y R x 5 3 ? 5 R x 5 15
Logo, os números são x 5 15 e y 5 5.
7.

xy
15
x y
5
1 1 5
( 4)( 2) 45
xy
xy x y
15
2 4 8 45 0
5
1 1 1 2 5

Da primeira equação, temos: y
15
x 5
.
Substituindo y
15
x 5
na segunda equação, temos:
15 2 4
15
1 x1 ? 23750
x
2
60
x 22 0
x 1 2 5
2x2 1 60 2 22x 5 0
x2 2 11x 1 30 5 0
D 5 b2 2 4ac
D 5 (211)2 2 4 ? 1 ? 30 5 121 2 120 5 1
x
b
a
’
 ”
x
x
5
2 6 D
5
6
?
5
6 5
1
5
5
2
5
2
11 1
2 1
11 1
2
11 1
2
6
11 1
2
5
→

 

15
6
→ 2,5
Se x56 y5 5
15
5
Se x 5 5 R y5 5
3
Há duas possibilidades para x e y: se x 5 6 cm, y 5 2,5 cm;
se x 5 5 cm, y 5 3 cm.
8. Se x é o comprimento, e y é a largura do galpão, escrevemos:

xy
96
x y
5
1 1 5
( 3)( 2) 150
R
xy
xy x y
96
2 3 6 150 0
5
1 1 1 2 5

Da primeira equação, temos y
96
x 5
.

379
Substituindo y
96
x 5
96 2 3
96
1 x1 ? 214450
x
2
288
x 48 0
x 1 2 5
2x2 1 288 2 48x 5 0
x2 2 24x 1 144 5 0
D 5 b2 2 4ac
D 5 (224)2 2 4 ? 1 ? 144 5 576 2 576 5 0
x
2
b
5
a 24
2
5 5 2
12
96
12
→ 8
Se x512 y5 5
Logo, as dimensões originais são 12 m e 8 m.
9.

xy
54
x y
5
1 1 5
( 2)( 2) 88
xy
xy x y
54
2 2 4 88
5
1 1 1 5

Da primeira equação, temos: y
54
x 5
.
Substituindo y
54
x 5
54 2 2
54
1 x1 ? 28450
x
2
108
x 30 0
x 1 2 5
2x2 2 30x 1 108 5 0
x2 2 15x 1 54 5 0
D 5 b2 2 4ac
D 5 (215)2 2 4 ? 1 ? 54 5 225 2 216 5 9
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
15 9
2 1
15 3
2
15 3
2
18
2
9
15 3
2
1
→
’
”
2
2
56

 
 
54
9
→ 6
Se x59 y5 5
54
6
→ 9
Se x56 y5 5
O lado menor do retângulo deve ser 6 cm, e o maior, 9 cm.
1.
a) x
x
2
4
25 12450
x2 2 20x 1 96 5 0
D 5 b2 2 4ac
D 5 (220)2 2 4 ? 1 ? 96 5 400 2 384 5 16

380
x
b
a
x
x
5
2  D
5

?
5
 5 5
5 5
2
20 16
2 1
20 4
2
24
2
12
16
2
8
→

 
 
’
”
A 5 8 e B 5 12.
b) • A 5 8% de 160 000 000
0,08 ? 160 000 000 5 12 800 000
12 800 000 brasileiros com mais de 60 anos.
• B 5 12% de 200 000 000
0,12 ? 200 000 000 5 24 000 000
24 000 000 brasileiros com mais de 60 anos.
• 42% 2 24,3% 5 17,7%
• 24,3% de 200 000 000
0,243 ? 200 000 000 5 48 600 000 R 48 600 000 jovens.
2.
a) D 5 b2 2 4ac
D 5 (0,4)2 2 4 ? 1 ? (23,2) 5 0,16 1 12,8 5 12,96
x
b
a
, ,
, , , , x
’ 1
5
2  D
5
2 
?
5
2  5
2 1
5
2
0 4 12 96
2 1
0 4 3 6
2
0 4 3 6
2
→
,
2 2
x ”
5 2
, ,
6
0 4 3 6
2
52 (Não convém.)

 
 
Portanto, a taxa é de 1,6.
b) Analisando o gráfico, temos que o maior crescimento populacional ocorreu de 1940 a
1950.
c) Analisando o gráfico, temos que a maior queda no crescimento populacional ocorreu de
1980 a 1990.
1. 5 4
1
7
x 1
x 5
1
12 60 1 48
12 1
7 1
12 1
( )
( )
( )
( )
x x
x x
x x
x x
1 1
1
5
1
1
60x 1 60 1 48x 5 7x2 1 7x
7x2 2 101x 2 60 5 0
D 5 b2 2 4ac
D 5 (2101)2 2 4 ? 7 ? (260) 5 10 201 1 1 680 5 11 881
x
b
2 a
2
x
x
5
2  D
5

?
5
 5 5
5
101 11881
2 7
101 109
14
210
14
15
→
’
”
8
14
4
7 5
2 (Não convém.)

 
 
Logo, o tempo é de 15 minutos.

381
1. Alternativa d.
5 9 5
1
x
x 1 5 1
5x2 1 9x 5 5x 1 1
5x2 1 4x 2 1 5 0
D 5 b2 2 4ac
D 5 42 2 4 ? 5 ? (21) 5 16 1 20 5 36
x
b
a
x
x
5
2 6 D
5
2 6
?
5
2 6 5
2 1
5
5
2 2
5
2
4 36
2 5
4 6
10
4 6
10
1
5
4 6
10
→
’
” 2
52
10
10
1

 
 
Logo, a menor raiz da equação é 21.
2. Alternativa a.
x(4x 2 1) 5 3(x 1 1)
4x2 2 x 5 3x 1 3
4x2 2 4x 2 3 5 0
D 5 b2 2 4ac
D 5 (24)2 2 4 ? 4 ? (23) 5 16 1 48 5 64
x
b
2 a
2
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5 5
5
4 64
2 4
4 8
8
4 8
8
12
8
3
2
1 5
4 8
8
→
’ ,
” 5
2
52 52
4
8
1
2
0,5

 
 
3. Alternativa c.
x
12
2 5 x
x
1( 0)
x2 2 12 5 x
x2 2 x 2 12 5 0
D 5 b2 2 4ac
D 5 (21)2 2 4 ? 1 ? (212) 5 49
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
52
2
1 49
2 1
1 7
2
1 7
2
8
2
4
1 7
2
6
2
→
’
” 3

 
 
(x’ 2 x”)2 5 [4 2 (23)]2 5 72 5 49
4. Alternativa e.
x
1 5
x 1 5
2
(x deve ser inteiro e diferente de zero.)
2 2
2
5
2
x2
x
x
x
1
5
2x2 2 5x 1 2 5 0
D 5 b2 2 4ac
D 5 (25)2 2 4 ? 2 ? 2 5 25 2 16 5 9

382
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
5 9
2 2
5 3
4
5 3
4
8
4
2
5 3
4
2
4
1
2
→
’
” (Nãoconvém.)

 
 
Considerando a raiz inteira (x 5 2), temos:
x
63
8 2 5 2 5 2 5
x
3
3
3
3
1
2
1
2
8
1
8
5. Alternativa b.
x2 1 11 5 12x
x2 2 12x 1 11 5 0
D 5 b2 2 4ac
D 5 (212)2 2 4 ? 1 ? 11 5 144 2 44 5 100
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
12 100
2 1
12 10
2
12 10
2
22
2
11
12
→
’
” 2
5 5
10
2
2
2
1

 
 
Agora, calculamos a média aritmética das raízes encontradas:
x x
M
1
1
5
5
5
’ ”
2
11 1
2
6
6. Alternativa e.
5x2 1 6 5 31x R 5x2 2 31x 1 6 5 0
D 5 b2 2 4ac
D 5 (231)2 2 4 ? 5 ? 6 5 961 2 120 5 841
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
31 841
2 5
31 29
10
31 29
10
60
10
6
→
’
”
31 29
10
2
10
1
5
2
5 5

 
 
Soma dos termos da raiz expressa pela fração
1
5
:11556.
7. Alternativa a.
V k
h
V ek
h
2
5 1 5 5
5 ? 1
h
5 1
5
25 2 5
25 2 25
5
25 5
5
2
2
2
( ,.)
,
125 5 25 1 h2
h2 5 100
h 5 610
8. Alternativa d.
y
4
52 1x2 y5
x
1 ( 2)
2
4
52 1 x
21 x
2x 5 24 1 x2 2 x

383
x2 2 3x 2 4 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (24) 5 9 1 16 5 25
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
52
2
3 25
2 1
3 5
2
3 5
2
8
2
4
3 5
2
2
2
→
’
” 1

 
 
Logo, o menor valor que verifica a igualdade nas condições dadas é x 5 21.
9. Alternativa c.
ax2 2 4x 2 16 5 0
x 5 4 é raiz.
a ? 42 2 4 ? 4 2 16 5 0
16 ? a 5 32
a 5 2
2x2 2 4x 2 16 5 0
D 5 b2 2 4ac
D 5 (24)2 2 4 ? 2 ? (216) 5 16 1 128 5 144
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
4 144
2 2
4 12
4
4 12
4
16
4
4
4 12
4
→
’
” 2
52
8
4
2

 
 
Logo, a outra raiz da equação dada é 22.
10. Alternativa b.
x2 1 (2m 2 3)x 1 m2 1 3 5 0 (Duas raízes diferentes R D . 0.)
D 5 b2 2 4ac
D 5 (2m 2 3)2 – 4 ? 1 ? (m2 1 3)
4m2 2 12m 1 9 2 4m2 2 12 . 0
212m 2 3 . 0
12m 1 3 , 0
12m , 23
m2
1
4
11. Alternativa e.
px2 2 2(q 2 1)x 1 6 5 0
S 5 23
P 5 3
S
2
b
q
5
a
5
p 2
52
2 1
3
( )
P
c
6
a p
3→ 2
5 5 5 p5
2 1
3
(q 2
)
p
52
2(q 2 1) 5 2(23)
2q 2 2 5 26
2q 5 24
q 5 22

384
12. Alternativa a.
2x2 1 5x 2 3 5 0
S
2
b
5
a 52
5
2
P
c
a 5 5
23
2
S
P 5
2
2
5
5
2
3
2
5
3
13. Alternativa c.
2x224x19 52x23
2 2 4 9 2 3
2 2 ( x 2 x1 ) 5( x2 )
2x2 2 4x 1 9 5 4x2 2 12x 1 9
2x2 2 8x 5 0
2x(x 2 4) 5 0
x 5 0 ou x 5 4
Verificação
2x224x19 52x23
02019 5023
3 5 23 (Falso.)
2x224x19 52x23
2?1621619 5823
25 55
5 5 5 (Verdadeiro.)
Logo, o valor de x que satisfaz a equação dada (x 5 4) está entre 3 e 5.
14. Alternativa b.
x2352 x
(x − 3)2 (2 x )
2
5
x2 2 6x 1 9 5 4x
x2 2 10x 1 9 5 0
D 5 b2 2 4ac
D 5 (210)2 2 4 ? 1 ? 9 5 100 2 36 5 64
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
10 64
2 1
10 8
2
10 8
2
18
2
9
10 8
2
→
’
”
2
2
51

 
 
Verificação
x2352 x
9 – 3 5 2 9
6 5 6 (Verdadeiro.)

385
x 2 3 5 2 x
1 2 3 5 2 ? 1
22 5 2 (Falso.)
15. Alternativa d.
20
3
4
2
1
5 1
x
1 5
y

 
 
x y
Da segunda equação, temos: y 5 2 2 x.
Substituindo y 5 2 2 x na primeira equação, temos:
20
5 4 1 2
2 x
3
1
x
20
3
6
1
5 2 x
x
(3 1 x)(6 2 x) 5 20
18 1 3x 2 x2 2 20 5 0
x2 2 3x 1 2 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? 2 5 9 2 8 5 1
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5 5
2
3 1
2 1
3 1
2
3 1
2
4
2
2
3 1
2
2
2
1
→


’
”

 
y 5 2 2 x R y 5 2 2 2 5 0
y 5 2 2 x R y 5 2 2 1 5 1
16. Alternativa a.
2 3 0
x xy
x y
1 5
2 5
2

Da segunda equação, temos: y 5 x 2 2.
Substituindo y 5 x 2 2 na primeira equação, temos:
x2 1 3x(x 2 2) 5 0
x2 1 3x2 2 6x 5 0
4x2 2 6x 5 0
2x(2x 2 3) 5 0
x 5 0 ou x 5
3
2
x1 5 0 R y1 5 22
x y 2
3 5 → 2
3
1
5 2 2
2
2
52
2 y y 2
1 2 1
1
4 1
5
1 52 1 2 2
2 2
2
52 2 2
5
2
52
2  
 

386
17. Alternativa b.

a 2 b
4
a b
2 5
2 2 1 52
2( 3) 3( 1) 2
Da primeira equação, temos: a 5 4 1 2b.
Substituindo a 5 4 1 2b na segunda equação, temos:
2(4 1 2b 2 3) 2 3b 2 3 5 22
8 1 4b 2 6 2 3b 2 3 5 22
b 5 21
a 5 2
Agora, verificamos se (2, 21) é solução de:
a) x2 2 x 1 2 5 0
x 5 2 R 4 2 2 1 2 5 4 (Não é raiz.)
Logo (2, 21) não é solução de x2 2 x 1 2 5 0.
b) x2 2 x 2 2 5 0
x 5 2 R 4 2 2 2 2 5 0 (É raiz.)
x 5 21 R 1 1 1 2 2 5 0 (É raiz.)
Logo (2, 21) é solução de x2 2 x 2 2 5 0.
18. Alternativa d.
V 5 3(3 2 2x)(3 2 x) (V 5 15)
15 5 3(9 2 9x 1 2x2)
5 5 2x2 2 9x 1 9
2x2 2 9x 1 4 5 0
D 5 b2 2 4ac
D 5 (29)2 2 4 ? 2 ? 4 5 81 2 32 5 49
x
b
a
x
5
2 6 D
5
6
?
5
6 5
1
5 5
2
9 49
2 2
9 7
4
9 7
4
16
4
4
→
’ (Nãoconvém.)
x”2
5 5 5 5
,
9 7
4
2
4
1
2
0 5

 
 
Logo, as dimensões são 3 cm, 2 cm e 2,5 cm, e a soma das três dimensões é dada por:
S 5 3 cm 1 2 cm 1 2,5 cm 5 7,5 cm
19. Alternativa c.
x y
x y
1
2 5
1 5
2 2 8,5

Da primeira equação, temos: y 5 x 2 1.
Substituindo y 5 x 2 1 na segunda equação, temos:
x2 1 (x 2 1)2 5 8,5
x2 1 x2 2 2x 1 1 2 8,5 5 0
2x2 2 2x 2 7,5 5 0
D 5 b2 2 4ac
D 5 (22)2 2 4 ? 2 ? (27,5) 5 4 1 60 5 64
x
b
2 a
2
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2 64
2 2
2 8
4
2 8
4
10
4
5
2
2 8
4
6
4
→
’
” 552
3
2
(Não convém.)

 
 

387
Parax 5
temos
y x y y 2
5 2 5 2 5
y
5
5
2
1
5
2
1
5 2
2
3
2
, :
→ → →
Logo, x 1 y vale:
5
3
8
54
2
1 2
5 2
20. Alternativa a.
x3 2 2x2 2 21x 2 18 x 1 1
2x3 2 x2 x2 2 3x 218 5 Q(x)
2 3x2 2 21x 2 18
3x2 1 3x
2 18x 2 18
18x 1 18
0
Q(x) 5 x2 2 3x 2 18 5 0
D 5 b2 2 4ac
D 5 (23)2 2 4 ? 1 ? (218) 5 9 1 72 5 81
x
b
a
x
x
5
2 6 D
5
6
?
5
6 5
1
5 5
5
2
5
2
5
2
3 81
2 1
3 9
2
3 9
2
12
2
6
3 9
2
6
2
→
’
” 23

 
 
Logo, a razão
x
x
’
”
vale:
x
x
’
” 5
2
52
6
3
2

Função polinomial do 1.o grau
388
29 – Sistema de coordenadas
cartesianas
1.
a) (H, 9) e (I, 9).
b) (H, 6).
2.
a) Casa.
b) Posto de gasolina.
c) Árvore.
1. 3.a fila horizontal: (2, 3); (4, 3); (6, 3) e (8, 3).
4.a fila horizontal: (1, 4); (3, 4); (5, 4) e (7, 4).
2. 5.a fila horizontal: (1, 5); (3, 5); (5, 5) e ( 7, 5).
6.a fila horizontal: (2, 6); (4, 6); (6, 6) e (8, 6).
3. Se a soma dos números de um par
ordenado for ímpar, a casa será preta; se
for par, a casa será branca.
4. Se a soma dos quatro números que
aparecem nos dois pares ordenados for
um número ímpar, as casas terão cores
diferentes; se a soma for um número par,
as casas terão a mesma cor.
1.
a) (5, 3)
b) (3, 2)
c) (4, 4)
2.
A (5, 4); B (24, 3); C (22,22); D (6, 23);
M (25, 0); N (0, 24); P (2, 0)
3.
a) (E, 7)
b) (F, 6)
4.
a) P (4, 2)
b) A (6, 0)
c) D (0, 22)
5.
a) A (22, 22); B (2, 22) ; C (2, 2) e D (22, 2)
b) Cada lado tem 4 uc.
6.
a) A (1, 1); B (5, 1) e C (1, 3)
b) O triângulo é retângulo, pois possui um
ângulo reto.
c) O cateto AB tem 4 uc.
d) O cateto AC tem 2 uc.
7.
a) O (4, 3)
b) O raio tem 3 uc.
c) O eixo tangente à circunferência é o
eixo x.
8. A (2, 5) B (23, 6) C (4, 24)
D (21, 21) E (0, 3) F (29, 23)
6
5
3
y
0 2 4
1
9 3 x 1
3
4
B (3, 6)
D (1, 1)
C (4, 4)
F (9, 3)
A (2, 5)
E (0, 3)
9.
a) A (5, 2) e B (21, 4)
b) P (22, 22) e R (3, 24)
1
1
4
1
2
4
2 3
2
A (5, 2)
5
y
x
B (1, 4)
P (2, 2)
R (3, 4)
10.
4
3
2
1
21
y
1 x
a) Sim, o triângulo RST é retângulo em R.
b) O triângulo RST é isósceles, pois
RT 5 SR 5 2 uc.
5
S (5, 3)
R (5, 1)
T (3, 1)
2 3 4
Ilustracões: Editoria de arte

389
11. 30 – A noção de função
1. Área: y Lado: x
Lei de formação que relaciona essas
grandezas: y 5 x2.
2. A lei de formação da função estabelecida
entre as grandezas y (ganho mensal) e x
(total de vendas do mês), se y 5 0,15x, é
dada por: y5 x
15
100
.
3. Valor a pagar: y.
Número de dúzias de laranjas compradas: x.
Preço da dúzia de laranjas: 3 reais.
Lei de formação que relaciona as
grandezas: y 5 3x.
4. Taxa fixa de visita: 25 reais.
O valor cobrado pela mão de obra (por
hora): 10 reais.
O preço total do conserto: y.
Horas de mão de obra empregadas: x.
Lei de formação que define uma função
entre as grandezas: y 5 25 1 10x.
5. Preço pago aos professores por aula dada:
15 reais.
Abono mensal fixo: 200 reais.
Valor que o professor recebe por mês: y.
Total de aulas dadas no mês: x.
grandezas: y 5 200 1 15x.
6. Quantidade de peças produzidas por
hora: 1 200 peças.
Produção diária de peças: y.
Número de horas que a máquina trabalha
durante o dia: x.
Lei de formação: y 5 1 200x
7.
a) y 5 3x
b) y 5 2x 2 10
1
c) y
x 5
d) y 5 x2 2 4
x
e) y
5 1 2
5
8.
a) y 5 2,50x
b) Se x 5 3, então:
y 5 2,50 ? 3 5 7,50
Logo, na compra de 3 sorvetes,
gastam-se R$ 7,50.
y
arte
5
A (0, 5)
de 4
Editoria 3
2
1
Ilustracões: C (3, 0)
B (0, 0)
1 2 3 4
5
x
Perímetro: 4 ? 7 5 28
Área: ,2 5 72 5 49 O triângulo é retângulo em B.
12.
4 A (4, 4)
2
4 2
a) O comprimento de cada lado desse
quadrado é de 8 uc.
b) Perímetro 5 4 ? 8 5 32 R 32 uc
y
1 x
1
21
2
4
3
3
3
3
4
D (4, 4)
B (4, 4)
C (4, 4)
y
1 x
5
2
1
4 21
2
2
4
3
3
3
3
4 5
4
C (5, 4)
C (2, 3)
a) Para formar um quadrado, a abscissa
do B deve ser a mesma do C; a
ordenada deve ser a mesma do A; e a
abscissa do D
deve ser a mesma do A. Logo: B (5, 23)
e D (22, 4).
b)
y
4 C (5, 4)
1 x
2
1
D (2, 4)
4 21
2
2
3
3
3
3
4 5
A (2, 3) B (5, 3)
c) Medida do lado: 7

390
c) y 5 2,50x
y 5 12,50
12,50 5 2,50x
x5 5
12 50
2 50
5
,
,
Logo, pagando R$ 12,50, compram-se
5 sorvetes.
9.
12.
Idade dos filhos Camping do Sol Camping dos Pássaros
x , 5 2 ? 15 ? 7 1 2 ? 14 ? 7 5 406 2 ? 14 ? 14 1 2 ? 12 ? 14 5 728
y , 5 e 5 x , 15 3 ? 15 ? 7 1 3 ? 14 ? 7 5 609 2 ? 14 ? 14 1 2 ? 12 ? 14 5 728
y , 5 e x 15 3 ? 15 ? 7 1 3 ? 14 ? 7 5 609 3 ? 14 ? 14 1 1 ? 12 ? 14 5 756
y 5 e x , 15 4 ? 15 ? 7 1 4 ? 14 ? 7 5 812 2 ? 14 ? 14 1 2 ? 12 ? 14 5 728
5 y , 15 e x 15 4 ? 15 ? 7 1 4 ? 14 ? 7 5 812 3 ? 14 ? 14 1 1 ? 12 ? 14 5 756
y 15 4 ? 15 ? 7 1 4 ? 14 ? 7 5 812 4 ? 14 ? 14 5 784
1. Se x 5 50, temos:
9
5
y5 x1
32
9
5
y5 ? 1
50 32
y 5 122
9
5
2. F5 C1
32
86
9
5
5 C132
9
C554
5
?
C5 5
C
54 5
9
30→30 º
31 – A função polinomial
do 1.o grau
1. y 5 5x 1 3
Para x 5 22, temos:
y 5 5(22) 1 3
y 5 27
2. y 5 28x 1 4
Para y 5 0, temos:
0 5 28x 1 4
8x 5 4
x 5
4
8
x 5
1
2
3.
a)
x y 5 4x
5 cm 20 cm
7,2 cm 28,8 cm
11 cm 44 cm
20,5 cm 82 cm
10 3 cm 40 3 cm
x
50
a) Área: y.
Editoria de arte
Largura: x.
Comprimento do retângulo:
50 unidades.
grandezas: y 5 50x.
b) Se x 5 16,5, a área do retângulo será:
y 5 50 ? x R y 5 50 ? 16,5 R
R y 5 825 unidades de área.
c) Se y 5 1 800 unidades de área,
a largura do retângulo será:
y 5 50x R 1 800 5 50 ? x R
R x5 x5 unidades
1800
50
→ 36→36 .
10. y 5 51x 1 17
Distâncias percorridas:
• x 5 1 hora R y 5 51 ? 1 1 17 5 68 R 68 km
• x 5 2 horas R y 5 51 ? 2 1 17 5 119 R 119 km
• x 5 3 horas R y 5 51 ? 3 1 17 5 170 R 170 km
• x 5 4 horas R y 5 51 ? 4 1 17 5 221 R 221 km
11. y 5 100 2 0,5x R 5 yx
4 800 5 (100 2 0,5x)x R
R 4800 100
2
2
1 x2
x
R
R 9 600 5 200x 2 x2 R
R x2 2 200x 1 9 600 5 0
Δ 5 b2 2 4ac
Δ 5 (2200)2 2 4 ? 1 ? 9 600 5
5 40 000 2 38 400 5 1 600
x
b
a
x
5
2 
5

?
5
5
 5
1
5 5
Δ
2
200 1600
2 1
200 40
2
200 40
2
240
2
1
→
’ 20
200 2
40
2
160
2
x”5 5 5
80

 
 
Nas condições enunciadas, o preço cobrado
por unidade de produto vendida é:
x” 5 R$ 120,00 ou x’ 5 R$ 80,00.

391
b) A imagem de 10 3 é 40 3 .
c) O número real cuja imagem é 44 é
x 5 11.
4. Quantidade de mercadorias vendidas na
semana: y.
Número de comerciais de televisão
durante a semana: x.
Lei de formação da função: y5 x1
3
2
150.
a) Quando x 5 42, o número de
mercadorias y foi:
y5 x1
3
2
150
3
2
y5 ? 1
42 150 R y 5 213 R 213
mercadorias.
b) Para y 5 240, temos:
3
2
y5 x1
150
240
3
2
5 x1150
3
2
x590
x 5
?
5
90 2
3
60
Portanto, o comercial apareceu
60 vezes na televisão.
5.
1
4
a) x 5 0 R y5 x2 2
y5 ? 2 y52
1
4
→ 0 2→ 2
1
4
→ 0 2→ 2
x2 y5 ? 2 y52
2
1
4
b) x54 y5 x2 2
y5 ? 2 y52
1
4
→ → 4 2→ 1
1
4
→ 4 2→ 1
x2 y5 ? 2 y52
2
1
4
c) x528 y5 x2 2
y5 2 2 y52
1
4
→ → ( 8) 2→ 4
1
4
→ ( 8) 2→ 4
y5 2 2 y52
2
6.
a) y 5 19 R y 5 1 2 9x R 19 5 1 2 9x R
R 18 5 29x R x 5 22
b) y 5 0,1 R y 5 1 2 9x R 0,1 5 1 2 9x R
R 20,9 5 29x R x 5 0,1
7.
a) x 5 102
y 5 2x 1 144 R y 5 2 ? 102 1 144 R
R y 5 348
Logo, o perímetro é 348 cm.
b) y 5 402
y 5 2x 1 144 R 402 5 2x 1 144 R
R 2x 5 258 R x 5 129
Logo, o comprimento será 129 cm.
Este é um bom momento para mostrar que
numa função do 1.o grau do tipo
y 5 ax 1 b as grandezas não são
proporcionais como na função do tipo
y 5 ax.
1. Quantidade de minutos de uma ligação
no plano PASSO: x.
Valor pago por uma ligação nesse plano: y.
a) y 5 0,15 1 0,04x
b) É uma função polinomial do 1.o grau,
pois é do tipo y 5 ax 1 b,
com a 5 0,04  0 e b 5 0,15.
2. 7 telefonemas 5 7y
x 5 8 minutos
y 5 0,15 1 0,04x
y 5 0,15 1 0,04 ? 8 5 0,47
7y 5 7 ? 0,47 5 3,29
As ligações custariam R$ 3,29.
3.
Minutos
Valor (em R$)
y 5 0,15 1 0,04x
5 0,35
10 0,55
15 0,75
20 0,95
25 1,15
30 1,35
60 2,55
90 3,75
4. y 5 0,15 1 0,04x
0,83 5 0,15 1 0,04x
0,04x 5 0,68
x 5 17
Logo, a ligação durou 17 minutos.
5.
a) 0,55 2 0,35 5 0,20
A cada 5 minutos, o valor cobrado
aumenta R$ 0,20.
b) 2,55 2 1,35 5 1,20
A cada 30 minutos, o valor cobrado
aumenta R$ 1,20.
c) x 5 2 horas 5 120 minutos
y 5 0,15 1 0,04x
y 5 0,15 1 4,8 5 4,95

392
O valor cobrado será menor que o
dobro, pois a função é do tipo
y 5 ax 1 b; Esse valor seria o dobro se
a função fosse do tipo y 5 ax; O valor
cobrado é de R$ 4,95.
d) De acordo com o item anterior, fica
mais barato fazer uma ligação de
3 horas do que fazer 3 ligações de
1 hora. Resposta em aberto.
32 – Gráfico da função
polinomial do 1.o grau no
plano cartesiano
1.
a) y 5 x 1 1
f) y 5 3x 1 1
1
2
1
0
y
x
b) y 5 x
x y
0 1
1 2
2
2
y
x
0
x y
0 0
2 2
c) y 5 2x 1 4
1 2
3 4
2
1
0
y
x
x y
0 4
2 2
d) y 5 1 2 2x
x y
0 1
1 21
1
1
2
0
1
2
3
y
x
e) y 5 24x
1
0
4
y
x
x y
0 0
1 24
1
4
3
2
1
y
0 x
1
2
g) y5 x1
2
x y
0 1
1 4
1 2
3
2
1
1
y
0 x
x y
0 2
2 3
h) y 5 2 2 3x
1
2
1
1
y
0 x
x y
0 2
1 21
2.
y 5 3x 2 2
x y
0 22
2 4
y 5 2x 2 1
x y
0 21
2 3
4
3
2
y 3x 2
O ponto de intersecção das retas é (1, 1).
3.
y 5 x 1 3
x y
0 3
1 4
1
y
0 x
1
1
y 2x 1
(1, 1)
2 3 4
2
y 5 x 2 2
x y
0 22
2 2
y
y x 2
x
5
4
3
2
1
0 1
6 5 4 3 2 1 2 3 4 5 6
1
2
3
4
5
y x 3
As retas não se encontram, ou seja, são
retas paralelas.

393
4. y 5 2x 1 1
y é a posição, em metros,
e x é o tempo, em segundos.
x y
0 1
1 3
2 5
3.
1 2 3
6
5
4
3
2
1
y
0 x
5. y 5 6 2 x
x y
0 22
6 4
y 5 x 2 2
x y
0 2
6 4
arte
de Editoria 7
6
Ilustracões: 5
4
3
2
1
2 1 0 1
2 3 4 5 6 7
O ponto de encontro é (4, 2).
1.
Quantidade de
Concentração de álcool
latas de cerveja
no sangue (g/,)
1 0,30
2 0,60
3 0,90
4 1,20
5 1,50
6 1,80
7 2,10
8 2,40
9 2,70
10 3,00
2.
2x 1 10 5 0 R x 5 10
Logo, o zero da função é dado por
x 5 10. y
x
1
2
3
4
5
y x 2
(4, 2)
y 6 x
1 2 3 4 5 6 7 8 9 10
Quantidade de latas de cerveja
g/l
3,5
3
2,5
2
1,5
0,5
0
1
Concentração de álcool no sangue
1 2 3 4 5 6 7 8 9 10
Quantidade de latas de cerveja
g/l
3,5
3
2,5
2
1,5
0,5
0
1
Concentração de álcool no sangue
O gráfico de linhas permite uma melhor
visualização da situação, mas nele não são
considerados valores intermediários.
4. Sendo y a concentração de álcool no
sangue e x a quantidade de latas de
cerveja ingeridas, temos y 5 0,30x.
5. Uma pessoa que tomou 5 latas de cerveja
tem uma concentração de álcool no
sangue correspondente a 1,50 g/,
(5 ? 0,30). Pela tabela dos efeitos, temos
os seguintes efeitos para esse valor:
instabilidade emocional; decréscimo da
inibição; perda do julgamento crítico;
enfraquecimento da memória e da
compreensão.
6. Como a lei de formação da função que
relaciona essas grandezas é
y 5 0,30x, temos:
0,30 ? x . 3,5
x . 11,6
Logo, a pessoa deve tomar mais de 11 latas
de cerveja seguidamente.
Se cada lata de cerveja contém 350 m,
cada uma, a pessoa consumiria:
11 ? 350 m, 5 3 850 m, 5 4 ,
33 – Zero da função polinomial
do 1.o grau
1.
a) y 5 x 2 6
x 2 6 5 0 R x 5 6
x 5 6.
b) y 5 2x 2 4
2x 2 4 5 0 R x 5 24
x 5 24.
c) y 5 2x 1 10

394
d) y 5 2x 2 3
2 3 0
3
2
x2 5 →x5
x 5
3
2
e) y 5 1 2 5x
1
1 2 5 x5 0
→x5
5 Logo, o zero da função é dado por
x 5
1
5
.
1
2
f) y5 x1
3
1
2
x1350→x526
Logo, o zero da função é dado por x 5 26.
2.
a) y 5 x 1 1
• y 5 0 para x 5 6.
• y . 0 para x . 6.
• y , 0 para x , 6.
b) y 5 x 1 7
a 5 1 R a . 0 (Função crescente.)
y 5 0 R x1750→x527
y
x
3
2
1
0 1
2 1 2 3
1
2
b) y 5 2x 1 3
y
x
3
2
1
0 1
2 1 2 3
1
2
c) y 5 2 2 x
y
x
3
2
1
0 1
2 1 2 3
1
2
y . 0
y 5 0
y , 0
6
27
y . 0
y 5 0
y , 0
• y 5 0 para x 5 27.
• y . 0 para x . 27.
• y , 0 para x , 27.
c) y 5 2x 2 1
a 5 21 R a , 0 (Função decrescente.)
y 5 0 R 2x 2 1 5 0 R x 5 21
y . 0
• y 5 0 para x 5 21.
• y . 0 para x , 21.
• y , 0 para x . 21.
d) y 5 6x 2 6
y 5 0 R 6x2650→x51
1
y . 0
y 5 0
y , 0
3
2
y . 0
y 5 0
y , 0
21
y 5 0
y , 0
• y 5 0 para x 5 1.
• y . 0 para x . 1.
• y , 0 para x , 1.
e) y 5 2x 2 3
y 5 0 R 2 3 0
3
2
x2 5 →x5
• y 5 0 para x 5
3
2
.
• y . 0 para x .
3
2
.
• y , 0 para x ,
3
2
.
O zero da função
é x 5 21.
O zero da função
é x 5 3.
O zero da função
é x 5 2.
34 – Analisando o gráfico de uma
função polinomial do 1.o grau
a) y 5 x 2 6
y 5 0 R x2650→x56

395
f) y 5 10 2 2x
y 5 0 R 10 2 2x 5 0 R x 5 5
2.
y . 0
5
y 5 0
y , 0
• y 5 0 para x 5 5.
• y . 0 para x , 5.
• y , 0 para x . 5.
y . 0
24
y 5 0
y , 0
g) y 5 23x 2 12
y 5 0 R 23x 2 12 5 0 R x 5 24
• y 5 0 para x 5 24.
• y . 0 para x , 24.
• y , 0 para x . 24.
1
2
h) y5 x2
3
a5
1
2
R a . 0 (Função crescente.)
y 5 0 R
1
2
x2350→x56
6
y . 0
y 5 0
y , 0
• y 5 0 para x 5 6.
• y . 0 para x . 6.
• y , 0 para x , 6.
1.
a) M (22, 5)
b) N (24, 21)
c) P (5, 24)
d) Q (7, 0)
y
x
M (2, 5)
N (4, 1)
Q (7, 0)
P (5, 4)
y
x
A (4, 1)
B (4, 2)
D (2, 1)
C (2, 2)
a) Um retângulo.
b) Lado maior: 4 1 2 5 6
Lado menor: 2 1 1 5 3
Área 5 3 ? 6 5 18
3. y
S (4, 4)
P (0, 2) R (8, 2)
x
Q (4, 0)
O quadrilátero desenhado é um losango.
4.
y
x
A (3, 3)
B (0, 3)
C (0, 0) D (3, 0)
O lado do quadrado tem 3 unidades de
comprimento; logo, o perímetro é dado por:
P5 4 ? , 5 4 ? 3 5 12 uc
5.
y 5 1 2 7x
a) Para x 5 23, temos:
y 5 1 2 7 ? (23) 5 1 1 21 5 22
Logo, y 5 22.
b) Para x 5 0,2, temos:
y 5 1 2 7 ? 0,2 5 20,4
Logo, y 5 20,4.
c) Para y 5 241, temos:
241 5 1 2 7x R x 5 6
Logo, x 5 6.
6. y 5 2 1 0,53x
a) Se x 5 16 R y 5 2 1 0,53 ? 16 R
R y 5 2 1 8,48 R y 5 10,48
Logo, a corrida custará R$ 10,48.
b) Se y 5 8,36 R 8,36 5 2 1 0,53x R
R 6,36 5 0,53x R x 5 12
Bruno percorreu 12 km.
7. y 5 x 2 3
Analisando o gráfico, temos:
a) y 5 0 para x 5 3.
b) y . 0 para x . 3.
c) y , 0 para x , 3.

396
8. y 5 2x 1 2
Analisando o gráfico, temos:
a) y 5 0 para x 5 2.
b) y . 0 para x , 2.
c) y , 0 para x . 2.
9.
a) y 5 x 2 7
x 2 7 5 0
x 5 7
b) y 5 4 1 8x
4 1 8x 5 0
8x 5 24
x 52
1
2
c) y 5 3x 2 2
3x 2 2 5 0
x 5
2
3
1
2
d) y5 x1
5
1
2
x1550
x 5 210
10.
a) y 5 x 2 9
y 5 0 R x2950→x59
b) y 5 25x 1 20
y 5 0 R 25x 1 20 5 0 R x 5 4
y . 0
4
y 5 0
y , 0
y . 0
3
y 5 0
y , 0
9
y . 0
y 5 0
y , 0
28
y . 0
y 5 0
y , 0
• y 5 0 para x 5 9.
• y . 0 para x . 9.
• y , 0 para x , 9.
• y 5 0 para x 5 4.
• y . 0 para x , 4.
• y , 0 para x . 4.
1
4
c) y5 x1
2
a5
1
4
R a . 0 (Função crescente.)
y 5 0 R
1
4
x1250→x528
• y 5 0 para x 5 28.
• y . 0 para x . 28.
• y , 0 para x , 28.
d) y 5 22x 1 6
y 5 0 R 22x 1 6 5 0 R x 5 3
• y 5 0 para x 5 3.
• y . 0 para x , 3.
• y , 0 para x . 3.

397
Função polinomial do 2.o grau
(ou função quadrática)
35 – Função polinomial do 2.o grau
(ou função quadrática)
1. V 5 1  x  (x 1 1)
y 5 x2 1 x
2. A 5 (x 1 2)(x 1 6)
y 5 x2 1 8x 1 12
3. A área da figura é a área do quadrado de
lado 5 menos a área do retângulo de lados
x e (5 2 x):
A 5 52 2 x(5 2 x)
y 5 25 2 5x 1 x2
4. y 5 x2 2 15x 1 26
Para x 5 10, temos:
y 5 102
2 15  10 1 26 R y 5 224
Logo, a imagem é 224.
5. y 5 6x2 2 x 2 3
Para x 5
1
2
, temos:
1
2
1
2
y56? 2 2
3
2  
 
R y 5 22
Logo, a imagem é 22.
6.
a) y
2
2 2
x x
5 1
Se x 5 1 000, temos:
y5 1
1000
2
1000
2
2
1 000 000
y5 1
2
500
y 5 500 000 1 500
y 5 500 500
b) y
2
2 2
x x
5 1
Para y 5 66, temos:
x 2
x 66
5 1
R
2 2
R 132 5 x2 1 x R x2 1 x 2 132 5 0
Δ 5 b2 2 4ac
Δ 5 12 2 4  1  (2132)
Δ 5 1 1 528 5 529
x
b
a
x
x
5
2 6
5
2 6
?
5
2 6 5
2 1
5
2 2
D
2
1 529
2 1
1 23
2
1 23
2
1 23
2
→
’
” 
 
 
x
b
a
x
x
5
2 6
5
2 6
?
5
2 6 5
2 1
5
5
2 2
D
2
1 529
2 1
1 23
2
1 23
2
11
1 23
2
→
’
” 55212

 
 
Como o problema pede um número
inteiro positivo, consideramos apenas
x’ 5 11.
7. y 5 x2
a) x 5 100
y 5 1002 5 10 000
ímpares positivos é 10 000.
b) y 5 256
256 5 x2
x 5 6 256
x 5 ± 16
Como queremos os primeiros números
positivos, consideramos apenas
x 5 16
c) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25,
27, 29, 31.
Logo, a maior parcela é 31.
1.
Figura 1 2 3 4 5 6 7 8
Total de quadradinhos 1 4 9 16 25 36 49 64
Quadradinhos roxos 1 2 3 4 5 6 7 8
Quadradinhos azuis 0 2 6 12 20 30 42 56
2. Observando a tabela do exercício 1,
temos:
a) A figura n tem n2 quadradinhos.
b) A figura n tem n quadradinhos roxos.
c) A figura n tem n2 2 n quadradinhos
azuis.
3. A figura n tem n2 2 n quadradinhos azuis;
logo, y 5 n2 2 n.

3
4
9
4
→ → 5
398
36 – Gráfico da função quadrática
1.
a) y 5 x2 1 6x 1 8
x
b
2
2
v5 a
2

R x x v5 v
52
6
2 1
→ 3
yv 5 (23)2 1 6  (23) 1 8 R
R yv 5 9 2 18 1 8 R yv 5 21
Logo, V (23, 21).
b) y 5 x2 2 2x 2 8
x
b
a
2
→ → 1 ( )
x x v5 v v
2
5
5 2 2

2
2 1
yv 5 12 2 2  1 2 8 R yv 5 29
Logo, V (1, 29).
c) y 5 2x2 1 8x 2 15
x
b
a
2
8
→ → 4 ( )
v5 x x v 5
v
2
2
2
2 1
5 yv 5 2(4)2 1 8  4 2 15 5 R yv 5 1
Logo, V (4, 1).
d) y 5 24x2 1 6x
x
b
a
2
→ 6
→ 3
( )
4 v5 x x v 5
v
2
2
2
2 4
5 3
4
2
→ → 5 ( )
10
2 1
5 2
2
→ → 1 ( )
5 2
2
1
4 → ( ) →
( )
1
4
2
→ → 5 ( )
y v524 1 6
 y v52  1 y v52 1 y v
3
4
4
9
16
18
4
9
4
18
4
2  
 
→ → → 5
9
4
v524 1 6
 y v52  1 y v52 1 y v
3
4
4
9
16
18
4
9
4
18
4
2  
 
→ → → 5
9
4
18
4
y y v52 1 v
9
4
Logo, V
3
4
9
4
,  
 
.
e) y 5 x2 1 6x 1 11
x
b
a
2
6
2 1
→ → 3
v5 x x v 5
v
2

52 2
yv 5 (23)2 1 6  (23) 1 11 R yv 5 2
Logo, V (23, 2).
f) y 5 2x2 1 36
x
b
a
2
0
→ → 0 ( )
v5 x x v 5
v
2
2
2
2 1
5 yv 5 202 1 36 R yv 5 36
Logo, V (0, 36).
g) y 5 2x2 1 7x 2 10
x
b
a
2
→ ( 7
) →
7
( )
2 v5 x x v 5
v
2
2
2
2 1
5 7
2
7
7
2
10
y y v52 1  2 v5
9
4
2  
 
→
V
7
2
9
4
,  
 
h) y 5 x2 2 10x 1 24
x
b
a
v5 x x v 5
v
2 2

yv 5 52 2 10  5 1 24 R yv 5 21
Logo, V (5, 21).
i) y 5 2x2 2 4x 2 1
x
b
a
v5 x x v 5
v
2 2

4
2 2
yv 5 2  12 2 4  1 2 1 R yv 5 23
Logo, V (1, 23).
j) y 5 24x2 2 2x
x
b
a
2
v5 x x v 5
v
2 2
2
2
2 4
52 y v524 2 2 2
2 y v5
1
4
1
4
2  
 
 
 
→
Logo, V 2
1
4
1
4
,  
 
.
2. y 5 22x2 1 20x 1 150
a) O valor máximo é dado pelo x do
vértice:
x
b
a
20
2 2
v5 x x v 5
v
2
2
5 2
Logo, a venda atingiu o valor máximo
depois de 5 dias.
b) As vendas se reduzem a zero quando
y 5 0. Então, fazemos:
22x2 1 20x 1 150 5 0
 5 b2 2 4ac
 5 202 2 4  (22)  150
 5 400 1 1 200
 5 1 600
x
b
a

x
5
2 
 52
5
2 
 2
5
2 
2
2
20 1600
2 2
20 40
4
5
( )
’
→
(x” 515
x
b
a

x
5
2 
 52
5
2 
 2
5
2 
2
2
20 1600
2 2
20 40
4
5
( )
’
→
(Não convém.)
x” 515
Logo, as vendas se reduziram a zero
em 15 dias.
a) y 5 x2 2 1
• Determinamos as coordenadas do
vértice:
x
b
a
0
2 1
x x
5
2
5
2 2
V v v v
y y
v v
2

5
5 2 52
0
0 1 1
0 1
2
→ →
→

 
 
( , )

399
• Organizamos a tabela:
x y
22 3
21 0
0 21
1 0
2 3
• Marcamos os pontos:
21 2
x
y
3
0
1
1
2
1
• Construímos o gráfico:
21 2
x
y
3
0
1
1
2
1
b) y 5 2x2
vértice:
x
b
a
x x
5
2
v 2
v v
V y y
v v
5
2
? 2
5
52 5
0
2 1
0
0 0
0 0
2
→ →
→

 
 
( ) ( , )
• Organizamos a tabela
x y
22 24
21 21
0 0
1 21
2 24
1 1 2
x
y
2 0
1
2
3
4
1 1 2
x
y
2 0
1
2
3
4
c) y 5 x2 1 2x 2 8
vértice:
x
b
a
→ →
x x
5
v v v
y
v
y
( ) ( ) →
v
2
5
2
?
52
2
2
5 2 1 ? 2 2
5 2
2
2 1
1
1 2 1 8
1 2
→ 2 52
2 2
8 9
1 9
→





y
V
v
( , )
x y
23 25
22 28
21 29
0 28
1 25
y
32 0
1 2 1
1
2
3
4
5
6
7
8
9
x
y
32 0
1 2 1
1
2
3
4
5
6
7
8
9
x
d) y 5 x2 2 2x
vértice:
x
b
a
2
2 2
x x
5
2
5
2
2 1
V v v v
y y
v v
?
5
5 2 ? 52
1
1 2 1 1
1
2
→ →
→

 
 
( )
( ,21)
x y
21 3
0 0
1 21
2 0
3 3

400
y
arte
de Editoria 3
2
1
Ilustracões: 1 0
1 2
3 x
1
y
3
2
1
1 0
1 2
3 x
1
e) y 5 x2 2 2x 1 4
vértice:
2
b
2 ( 2
2
) 
x
5
→ x 5
→
x
1
v 2
a
v 2 ?
1
v 5
V
1
y v 5 1 2
2 2 ? 1 1 4 →
y
v
5
3
’
”  
 
( ,3)
x y
21 7
0 4
1 3
2 4
3 7
y
7
6
4
3
2
1
0
1 1 2 3
x
5
y
7
6
4
3
2
1
0
1 1 2 3
x
5
f) y 5 2x2 1 6x 2 9
vértice:
x
b
a
→ →
x x
5
v v v
y
v
y
v
2
5
2
? 2
5
2
2
52 1 ? 2
52 1
6
2 1
3
3 63 9
9 1
→
→
( )
( )
8 9 0
3 0
2 → 5

 
 
( )
y
V
v
,
x y
1 24
2 21
3 0
4 21
5 24
1 2 3 4 5
y
0
1
2
3
4
x
1 2 3 4 5
y
0
1
2
3
4
x
37 – Zeros da função polinomial
do 2.o grau
1.
a) y 5 x2 2 25
 5 b2 2 4ac
 5 0 2 4  1  (225) 5 100
b
x
a
x
x
5
2 6
?
5
2 6 5 5
5
2
52
Δ
2
0 100
2
10
2
5
10
2
5
→

 
 
’
”
x
b
a
x
x
5
2 6
?
5
2 6 5 5
5
2
52
Δ
2
0 100
2
10
2
5
10
2
5
→

 
 
’
”
Os zeros dessa função são: 25 e 5.
b) y 5 x2 2 10x 1 21
 5 b2 2 4ac
 5 (210)2 2 4  1  21 5 100 2 84 5 16
b
x
a
x
x
5
2 6
?
5
6
?
5
6 5 5
5 5
Δ
2
10 16
2 1
10 4
2
14
2
7
6
2
3
→

 
 

401
a
x
x
6
?
5
6
?
5
6 5 5
5 5
Δ
10 16
2 1
10 4
2
14
2
7
6
2
3
→

 
 
’
”
c) y 5 2x2 1 6x
 5 b2 2 4ac
 5 62 2 4  (21)  0 5 36
x
b
a
’
”

x
x
5
2 6
?
5
2 6
? 2
5
2 1
2
5
5
2 2
2
5
Δ
2
6 36
2 1
6 6
2
0
6 6
2
→
 
 
( ) 6
a
’
”

x
x
6
5
2 6
? 2
5
2 1
2
5
5
2 2
2
5
Δ
6 36
2 1
6 6
2
0
6 6
2
→
 
 
( ) 6
Os zeros da função são: 0 e 6.
d) y 5 x2 1 4x 1 8
 5 b2 2 4ac
 5 42 2 4  1  8 5 16 2 32 5 216
Como   0, essa função não tem zeros
reais.
e) y 5 2x2 1 x 1 6
 5 b2 2 4ac
 5 12 2 4  (21)  6 5 25
x
b
a
x
x
5
2 6
?
5
2 6
? 2
5
2 1
2
52
5
2 2
2
5
Δ
2
1 25
2 1
1 5
2
2
1 5
2
3
( )
’
”
→

 

 
a
x
x
6
?
5
2 6
? 2
5
2 1
2
52
5
2 2
2
5
Δ
1 25
2 1
1 5
2
2
1 5
2
3
( )
’
”
→

 

 
f) y 5 9x2 2 1
 5 b2 2 4ac
 5 0 2 4  9  (21) 5 36
x
b
a
x
x
5
2 6
?
5
6
?
5 5
5
2
52
Δ
2
0 36
2 9
6
18
1
3
6
18
1
3
→

   
’
”
a
x
x
6
?
5
6
?
5 5
5
2
52
Δ
2
0 36
2 9
6
18
1
3
6
18
1
3
→

 
 
’
”
Os zeros dessa função são:2
1
3
1
3
e .
g) y 5 24x2 1 4x 2 1
 5 b2 2 4ac
 5 42 2 4  (24)  (21) 5 16 2 16 5 0
x
2
b
5
a 5
4
2
? 2
2
2 4
5 1
( ) 2
Como  5 0, essa função tem um único
zero real: o número 1
2
.
h) y 5 6x2 1 6x
 5 b2 2 4ac
 5 62 2 4  6  0 5 36
b
x
a
x
x
5
2 6
?
5
2 6
?
5
2 1
5
5
2 2
52
Δ
2
6 36
2 6
6 6
12
0
6 6
12
1
→

 
 
’
”
x
b
a
x
x
5
2 6
?
5
2 6
?
5
2 1
5
5
2 2
52
Δ
2
6 36
2 6
6 6
12
0
6 6
12
1
→

 
 
’
”
2.
a) y 5 x2 2 2x 2 24
 5 b2 2 4ac
 5 (22)2 2 4  1  (224) 5 4 1 96 5 100
Como  . 0, a parábola corta o eixo x
em dois pontos:
b
x
a
x
x
5
2 6
?
5
6
?
5
6 5 5
5
2
52
Δ
2
2 100
2 1
2 10
2
12
2
6
8
2
4
→

 
 
’
”
x
b
a
x
x
5
2 6
?
5
6
?
5
6 5 5
5
2
52
Δ
2
2 100
2 1
2 10
2
12
2
6
8
2
4
→

 
 
’
”
A parábola corta o eixo x nos pontos
(6, 0) e (24, 0).
b) y 5 x2 2 6x 1 9
 5 b2 2 4ac
 5 (26)2 2 4  1  9 5 0
Como  5 0, a parábola tem apenas
um ponto em comum com o eixo x:
x
2
b
5
a 6
2
5 5 2
3
A parábola corta o eixo x no ponto (3, 0).
c) y 5 2x2 1 9x 2 14
 5 b2 2 4ac
 5 92 2 4  (21)  (214) 5 81 2 56 5 25
Como  . 0, a parábola corta o eixo x
em dois pontos:
x
b
a
x
x
5
2 6
?
5
2 6
? 2
5
2 1
2
5
5
2 2
2
5
Δ
2
9 25
2 1
9 5
2
2
9 5
2
7
( )
’
”
→

 
 
(2, 0) e (7, 0).
d) y 5 x2 2 7x 1 13
 5 b2 2 4ac
 5 (27)2 2 4  1  13 5 49 2 52 5 23
Como   0, a parábola não corta o eixo x.
3.
a) y 5 x2 2 16
em que y 5 0:

402
x2 2 16 5 0
x2 5 16
x56 16 564
x 5 4 ou x 5 24
Logo, as coordenadas são (24, 0) e (4, 0).
b) y 5 2x2 1 12x 2 36
em que y 5 0:
2x2 1 12x 2 36 5 0
 5 b2 2 4ac
 5 122 2 4  (21)  (236) 5 144 2 144 5 0
Como  5 0, a parábola tem apenas
um ponto em comum com o eixo x:
x
2
b
5
a 5
2
12
2 2
1
5 2
6
( )
Logo, as coordenadas desse ponto são
(6, 0).
c) y 5 3x2 2 21x
em que y 5 0:
3x2 2 21x 5 0
3x(x 2 7) 5 0
x 5 0 ou x 5 7
Logo, as coordenadas são (0, 0) e (7, 0).
38 – Estudando a concavidade
da parábola
1.
a) y 5 x2 2 7x 1 10
a 5 1 . 0 R A parábola tem a
concavidade voltada para cima.
b) y 5 3x2 2 7x 1 4
c) y 5 2x2 1 25
a 5 21  0 R A parábola tem a
concavidade voltada para baixo.
d) y 5 26x2 1 x 1 1
e) y 5 2x2 2 14x 2 49
f) y 5 7x2 2 2x
2.
a) A parábola está com a concavidade
voltada para cima e não corta o eixo
x; logo, a . 0 e   0.
b) A parábola está cortando o eixo x num
único ponto, e a concavidade está
voltada para cima; logo, a . 0 e  5 0.
c) A parábola está com a concavidade
voltada para baixo e não corta o eixo x;
logo, a  0 e   0.
d) A parábola está com a concavidade
voltada para baixo e corta o eixo x em
dois pontos; logo, a  0 e  . 0.
e) A parábola está com a concavidade
voltada para cima e corta o eixo x em
dois pontos; logo, a . 0 e  . 0.
f) A parábola está com a concavidade
voltada para baixo e corta o eixo x em
um único ponto; logo, a  0 e  5 0.
39 – Ponto de mínimo e ponto
de máximo
1.
a) y 5 x2 2 8x 1 6
a 5 1 . 0 R A concavidade da parábola
está voltada para cima; logo, a função
tem ponto de mínimo.
b
x
8
2
v52 a 5 5 2
4
yv 5 42 2 8  4 1 6 5 210
Logo, essa função tem ponto de
mínimo: (4, 210).
b) y 5 2x2 1 4x 1 5
a 5 21  0 R A concavidade da
parábola está voltada para baixo; logo,
a função tem ponto de máximo.
b
x
v52 a 5
4
2
2
2
5 2
2
yv 5 24 1 4  2 1 5 5 9
máximo: (2, 9).
c) y 5 26x2 1 6x
b
x
v52 a 5
6
2
? 2
2
2 6
5 1
( ) 2
1
2
yv526? 1 6
? 5
1
2
3
2
2  
 

403
máximo: 1
2
3
2
,  
 
.
d) y 5 x2 2 16
b
x
v5 a 5
2
0
2 ?
1
5 2
0
yv 5 216
mínimo: (0, 216).
e) y 5 x2 2 4x 2 45
b
x
v52 a 5 2
2
yv 5 4 2 8 2 45 5 249
mínimo: (2, 249).
f) y 5 3x2 1 6x
b
x
v52 a 5
2
6
2 ?
3
52 2
1
yv 5 3 2 6 5 23
mínimo: (21, 23).
g) y 5 x2 1 9
b
x
v52 a 5
0
2 1
2
5 2
0
( )
yv 5 9
máximo: (0, 9).
h) y 5 5x2 2 8x 1 3
x
b
a
y
v
v
52 5
8
2 ?
5
5
2
4
5
5
4
5
8
4
5
3 5
16
25
5 ? 2 ? 1 5 ? 2
32
5
2  
 
11352
1
5
b
a
52 5
8
2 ?
5
5
2
4
5
? 2 ? 1 5 ? 2
5
4
5
8
4
5
3 5
16
25
32
5
2  
 
11352
1
5
mínimo: 4
5
1
5
, 2
 
 
.
2. y 5 3x2 2 6x 2 2
x
b
2
v5 a
5
1 ( )
2 2
2
5 ?
6
2 3
yv 5 3  1 2 6 2 2 5 25
As coordenadas desse ponto são (1, 25).
3. y 5 2x2 1 4x
A altura máxima é o ponto de máximo da
função:
b
x
v52 a 5
4
2
2
2
2 1
5 2
( )
yv 5 24 1 8 5 4
As coordenadas são (2, 4).
40 – Analisando a função
y 5 ax2 1 bx 1 c
quanto ao sinal
1. y 5 x2 2 x 2 6
está voltada para cima; logo, a função tem
ponto de mínimo.
a) y 5 0
x2 2 x 2 6 5 0
 5 b2 2 4ac
 5 (21)2 2 4  1  (26) 5 25
Como  0, a função possui dois zeros:
b
x
a
x
x
5
2 6
?
5
6
5
6 5
52
Δ
2
1 25
2
1 5
2
3
2
→

’
”
x
b
a
x
x
5
2 6
?
5
6
5
6 5
52
Δ
2
1 25
2
1 5
2
3
2
→

’
”
Logo, a função é nula para x 5 3 ou
x 5 22.
b) Esboçando o gráfico, temos:
y  0 y  0
2 2 y  0 3
Então, y . 0 para x  22 ou x . 3.
c) y  0 para 22  x  3.
2. y 5 9x2 2 8x 2 1
está voltada para cima; logo, a função tem
ponto de mínimo.
a) y 5 0
9x2 2 8x 2 1 5 0
 5 b2 2 4ac
 5 (28)2 2 4  9  (21) 5 100
Editoria de arte

404
Como  . 0, a função possui dois zeros:
b
x
a
x
x
5
2 

5


5

5
52
Δ
2
8 100
2 9
8 10
18
1
1
9
→

 
 
’
”
a
x
x


5


5

5
52
Δ
8 100
2 9
8 10
18
1
1
9
→

 
 
’
”
A função é nula para x51 ou2
1
9 .
Então, y . 0 para x  2
1
9
ou x . 1.
c) y  0 para2
1
9  x  1.
3. y 5 2x2 1 5x
a 5 21  0 R A concavidade da parábola
está voltada para baixo; logo, a
função tem ponto de máximo.
a) y 5 0
2x2 1 5x 5 0
 5 b2 2 4ac
 5 52 2 4  (21)  0 5 25
x
b
a
’
”

x
x
5
2 

5
2 
2
5
2 
2
5
5
Δ
2
5 25
2 1
5 5
2
0
→
( ) 5
a
’
”

x
x


5
2 
2
5
2 
2
5
5
Δ
5 25
2 1
5 5
2
0
→
( ) 5
A função é nula para x 5 0 ou x 5 5.
0 5
Então, y . 0 para 0  x  5.
c) y . 0 para x , 0 ou x . 5.
4. y 5 2x2 1 10x 2 25
está voltada para baixo; logo, a função tem
ponto de máximo.
a) y 5 0
2x2 1 10x 2 25 5 0
 5 b2 2 4ac
 5 102 2 4  (21)  (225) 5 0
Como  5 0, a função possui um único
zero:
x
2 b

2
b
5
a
5


a 5
2
 2
5
Δ
2 2
10
2 1
( ) 5
A função é nula (y 5 0) para x 5 5.
5
Analisando o gráfico, vemos que y
nunca será maior que zero.
c) y  0 para x  5 ou x . 5 ou qualquer
x ≠ 5.
5. y 5 x2 2 6x 1 15
está voltada para cima.
 5 b2 2 4ac
 5 (26)2 2 4  1  15 5 224
  0 R A parábola não corta o eixo x.
Fazendo um esboço do gráfico, temos:
Logo, a função será positiva para qualquer
valor real de x.
6. y 5 x2 2 9x 2 10
 5 b2 2 4ac
 5 (29)2 2 4  1  (210) 5 121
b
x
a
x
x
5
2 

5


5
 5
52
Δ
2
9 121
2 1
9 11
2
10
1
→

’
”
Esboçando o gráfico, temos:
Logo, y . 0 para x  21 ou x . 10.
7. x2 2 8x 1 16  0
a 5 1 0 R A concavidade da parábola
 5 b2 2 4ac
 5 (28)2 2 4  1  16 5 0
Como  5 0, a função possui um único
zero, e a parábola tangencia o
eixo x:
2 b
x

5

a 5 5
Δ
2
8
2
4
Logo, a função nunca será menor que zero,
ou seja, não há valores reais x para que
y  0, pois ou a função será positiva ou
igual a zero (quando x 5 4).
1
y  0 y  0
21 y  0 10
y  0
y  0 y  0
y  0 y  0
y  0 y  0
y  0 y  0
4
y  0 y  0
y  0 2 __19

405
8. y 5 2x2 2 x 1 3
 5 b2 2 4ac
 5 (21)2 2 4  2  3 5 223
Como   0, a parábola não corta o eixo x:
y  0 y  0
Para qualquer valor real de x, a função é
sempre positiva.
9. x2 1 3x  0
 5 b2 2 4ac
 5 32 2 4  1  0 5 9
b
x
a
x
x
5
2 6
?
5
2 6
?
5
2 6 5
52
Δ
2
3 9
2 1
3 3
2
0
3
→

’
”
Como a inequação pede y  0,
consideramos 23  x  0.
Logo, S 5 {x  IR 23  x  0}.
10.
(x 2 1)2 1 x . 3
x2 2 2x 1 1 1 x 2 3 0
x2 2 x 2 2 . 0
 5 b2 2 4ac
 5 (21)2 2 4  1  (22) 5 9
b
x
a
x
x
5
2 6
?
5
6
?
5
6 5
52
Δ
2
1 9
2 1
1 3
2
2
1
→

’
”
A inequação pede y . 0; logo, x  21 ou
x . 2.
Então: S 5 {x  IR  x  21 ou x . 2}.
11. x3 2 1  x3 2 x2 1 5x 2 5
21 1 x2 2 5x 1 5  0
x2 2 5x 1 4  0
 5 b2 2 4ac
 5 (25)2 2 4  1  4 5 9
x
b
a
x
x
5
2 6
?
5
6
?
5
6 5
5
Δ
2
5 9
2 1
5 3
2
4
1
→

´
´´
Logo, y  0 para 1  x  4.
12.
(3x 2 1)(x 2 2) . 2(x2 2 2)
3x2 2 6x 2 x 1 2 2 2x2 1 4 . 0
x2 2 7x 1 6 . 0
 5 b2 2 4ac
 5 (27)2 2 4  1  6 5 25
b
x
a
x
x
5
2 6
?
5
6
?
5
6 5
5
Δ
2
7 25
2 1
7 5
2
6
1
→

’
”
Então: S 5 {x  IR  x  1 ou x . 6}.
Portanto, o menor inteiro positivo que
verifica a inequação é x 5 7.
13. x2 2 5x 2 36  0
 5 b2 2 4ac
 5 (25)2 2 4  1  (236) 5 169
b
x
a
x
x
5
2 6
?
5
6
?
5
6 5
52
Δ
2
5 169
2 1
5 13
2
9
4
→

’
”
Esboçando o gráfico:
Temos y  0 para 24  x  9.
Logo, o menor e o maior inteiro que
satisfazem a inequação são 23 e 8,
respectivamente.
14.
y 5 x2 2 10x 1 21  0
 5 b2 2 4ac
y  0 y  0
2 3 y  0 0
y  0 y  0
1 y  0 4
y  0 y  0
1 y  0 6
y  0 y  0
24 y  0 9
y  0 y  0
2 1 y  0 2

406
 5 (210)2 2 4  1  21 5 16
b
x
a
x
x
5
2 

5


5
 5
5
Δ
2
10 16
2 1
10 4
2
7
3
→

’
”
Esboçando o gráfico, temos
Logo, a função é negativa (y  0) para
3  x  7.
15. 4x2 2 3  12(x 2 1)
4x2 2 3 2 12x 1 12  0
4x2 2 12x 1 9  0
 5 b2 2 4ac
 5 (212)2 2 4  4  9 5 0
Como  5 0, a função possui um única
raiz:
2 b
x

5

a 5

5
Δ
2
12
2 4
3
2
Logo, não há x real que satisfaça y  0.
16. 8(x2 2 3) 1 1  5(x2 2 1) 2 6
8x2 2 24 1 1  5x2 2 5 2 6
3x2 2 12  0
 5 b2 2 4ac
 5 0 2 4  3  (212) 5 144
b
x
a
x
x
5
2 

5

5
 5
52
Δ
2
144
6
12
6
2
2
→

’
”
Então, y  0 para 22  x  2.
Portanto: S 5 { x  IR  22  x  2}.
17. Área 5 (x 1 6)(x 2 2) . 9
x2 1 4x 2 12 2 9 . 0
x2 1 4x 2 21 . 0
 5 b2 2 4ac
 5 42 2 4  1(221) 5 100
Como  . 0, a função possui duas raízes
reais:
b
x
a
x
x
5
2 

5
2 

5
2  5
52
Δ
2
4 100
2 1
4 10
2
3
7
→

´
´´
x
b
a
x
x
5
2 

5
2 

5
2  5
52
Δ
2
4 100
2 1
4 10
2
3
7
→

´
´´
Então, y . 0 para x  27 (não convém) ou
x . 3.
Logo, a área do retângulo é maior que 9
para x . 3.
Chegou a sua vez, páginas 193 e 194.
1.
a) R 5 αD2 1 βD
Para D 5 1, temos: R 5 α 1 β.
Para D 5 2, temos: R 5 4α 1 2β.
b) α 5 1 e β 5 3
Para D 5 1, temos:
R 5 α 1 β R R5 1 1 3 R R5 4
1 1 Para D 5 2, temos:
R 5 4α 1 2β R R5 4 1 6 R R5 10
2 2 O valor do aumento é dado por:
R2 R5 10 2 4 5 6
2 1 Aumento porcentual 5
valor doaumento
5
valor inicial 100
6
4
Aumento porcentual 5  5
100 150
Portanto, o aumento foi de 150%.
2. Alternativa a.
R 5 αD2 1 βD
D 5 1 R R5 α 1 β (Valor inicial.)
1 D 5 2 R R5 4α 1 2β
2 Valor do aumento é dado por:
R2 R5 (4α 1 2β) 2 (α 1 β) 5 3α 1 β
2 1 Aumento porcentual 5
valor doaumento
5
valor inicial 100
Aumento porcentual 5
5
α β 100 3
α β
(3 ) ( )
1
1
 5
1
1
100
α β
α β
3. Alternativa d.
R 5 1,5D2 1 D
D 5 1 R R1 5 2,5
D 5 2 R R2 5 8
y  0 y  0
3 y  0 7
y  0 y  0
2 2 y  0 2
y  0 y  0
27 y  0 3
y  0 y  0
3
2

407
Valor do aumento 5 8 2 2,5 5 5,5
Aumento porcentual 5
5 5100
2 5
220
,
,
→ %
1. De acordo com a tabela, a maior fonte de
energia é o carvão, e a menor fonte é o
petróleo.
2.
Geradores de energia elétrica no mundo
40
16
15
18
11
0 10 20 30 40
Fonte de
energia
Nuclear
Gás
Petróleo
Hidroelétrica
Carvão
Porcentagem (%)
Fonte: Brasil, MCT.
1
2
1
2
2
1. y5 x 1 x
a) Se x 5 40, temos:
1
2
y5  40
1  y5
1
2
2 40→ 820
inteiros positivos é 820.
b) Quando y 5 210, temos:
210
1
2
1
2
2 5 x 1 x
420 5 x2 1 x
x2 1 x 2 420 5 0
 5 b2 2 4ac
 5 1 2 4  1  (2420) 5 1 681
b
x
a
x
x
5
2 

5
2 

5
2  5
52
Δ
2
1 1681
2 1
1 41
2
20
21
→
y
9
8
7
6
4
3
2
1
0
y
9
8
7
6
4
3
2
1
0
25
4 2  
’
” (Nãoconvém.)

x
x
5
2 

5
2  5
52
Δ
1 1681
2 1
1 41
2
20
21
→
’
” (Nãoconvém.)

Logo, 210 é a soma dos 20 primeiros
números inteiros positivos.
2. a) y 5 2x2 1 9
vértice:
x
b
a
y

 
 
v V
v
5
2
5
2
2
5
5
2
0
2 1
0
9
( )
( ) 0,9
x y
22 5
21 8
0 9
1 8
2 5
21 1 2
x
5
21 1 2
x
5
b) y 5 x2 2 5x
vértice:
x
b
a
y
V
v
v
5
2
5
5 2  52
2
2
5
2
5
2
5
5
2
25
4
5
2
 

 
 
,  
 
x y
0 0
1 24
2 26
5
2
2
25
4
3 26
5 0
1 2 3 4
y
0
1
3
4
5
6
x
2
5

408
1 2 3 4
y
0
1
3
4
5
6
x
2
5
c) y 5 x2 2 4x 2 5
vértice:
x
b
a
y
5
2
4
2
5 5
2
v V
v
2 2
4 8 5 9
5 2 2 52
2 9

 
 
( , )
x y
0 25
1 28
2 29
3 28
4 25
1 2 3 4
y
0
1
2
6
7
8
9
x
3
4
5
1 2 3 4
y
0
1
2
6
7
8
9
x
3
4
5
d) y5x 1x1 2 1
4
vértice:
x
b
a
y
V
v
v
5
2
5
2
?
52
5 2 1 5
2
2
1
2 1
1
2
1
4
1
2
1
4
0
1
2
0

 
 
 
 
,
x y
22
9
4
21
1
4
2
1
2
0
0
1
4
1
9
4
y
6
4
3
2
1
0
3 21 1 2
x
5
y
6
4
3
2
1
0
3 21 1 2
x
5
3. y 5 (k 2 3)x2 1 x
A parábola tem a concavidade voltada para
cima se a . 0, então fazemos:
k 2 3 . 0
k . 3
Logo, a parábola tem a concavidade
voltada para cima quando k . 3.
4.
a) y 5 x2 2 25
a 5 1 . 0 R A concavidade está voltada
para cima; logo, há ponto de mínimo.
x
2
b
0
2 1
0
v5 a 5
5
?
V
5
2 2
0 25
y 25 v

 
 
( , )
b) y 5 2x2 1 25
a 5 21  0 R A concavidade está
voltada para baixo; logo, há ponto de
máximo.
x
b
a
y

 
 
v V
v
5
2
5
2
? 2
5
5
2
0
2 1
0
25
( ) (0, 25)

409
c) y 5 2x2 1 10x
a 5 21  0 R A concavidade está
voltada para baixo; logo, há ponto de
máximo.
x
b
a
y

 
 
v V
v
5
2
5
2
? 2
5
5
2
10
2 1
5
25
( ) (5, 25)
d) y 5 4x2 1 4x 1 1
a 5 4 . 0 R A concavidade está voltada
para cima; logo, há ponto de mínimo.
x
b
a
y
4
2 4
v V
v
5
2
5
2
?
52
2 2
5 2 1 5
1
2
1 2 1 0
1
2
0

 
 
 
 
,
5. y 5 2 x2 1 9
está voltada para baixo; logo, a função tem
ponto de máximo.
a) 2x2 1 9 5 0
 5 b2 2 4ac
 5 0 2 4  (21)  9 5 36
b
x
a
x
x
5
2 6
?
5
6
2
52
5
Δ
2
0 6
2
3
3
→

’
”
23 3
A função é nula para x 5 23 e x 5 3.
b) y . 0 para 23  x  3.
c) y  0 para x  23 ou x . 3.
6. x2 1 3x 2 10  0
 5 b2 2 4ac
 5 32 2 4  1  (210) 5 49
b
x
a
x
x
5
2 6
?
5
2 6
?
5
2 6 5
52
Δ
2
3 49
2 1
3 7
2
2
5
→

´
´´
Então, y  0 para 2 5  x  2.
Logo, o menor inteiro negativo que satisfaz
a inequação é 24.
7.
1
3
7
3
2 2
y52 x 1 x2
a52
1
3
0 R A concavidade da
parábola está voltada para baixo.
 5 b2 2 4ac
Δ5 2 ? 2 ? 2 5
49
9
4
1
3
2
25
9
 
 
( )
x
b
a
x
x
5
2 6
?
5
2 6
?
2
5
2 6
2
5
5
Δ
2
7
3
25
9
2 1
3
7
3
5
3
2
3
1
6
→

’
”
x
b
a
x
x
5
2 6
?
5
2 6
?
2
5
2 6
2
5
5
Δ
2
7
3
25
9
2 1
3
7
3
5
3
2
3
1
6
→

’
”
1 6
a) O míssil voa fora da água no intervalo
1  x  6.
b) A posição da pedra é o ponto (6, 0).
8. x2 2 36  0
 5 b2 2 4ac
 5 0 2 4  1  (236) 5 144
x
b
a
x
x
5
2 6
?
5
6
?
56
5
52
Δ
2
0 144
2 1
12
2
6
6
→

’
”
S 5 {x  IR 26  x  6}
9.
y 5 x2 2 2x 1 8 0
 5 b2 2 4ac
 5 (22)2 2 4  1  8 5 228
Como   0, a parábola não corta o eixo x.
Então, y . 0 para qualquer x; logo,
a afirmação é verdadeira.
y  0 y  0
25 y  0 2
y  0 y  0
2 6 y  0 6
y  0
y  0 y  0
y  0
y  0 y  0
y  0

410
10.
2 x2 1 13x 2 22 . 0
está voltada para baixo.
 5 b2 2 4ac
 5 132 2 4  (21)  (222) 5 81
x
b
a
’
”

x
x
5
2 6
?
5
2 6
? 2
5
2 6
2
5
5
Δ
2
13 81
2 1
13 9
2
2
→
( ) 11
’
”

x
x
5
2 6
? 2
5
2 6
2
5
5
13 81
2 1
13 9
2
2
→
( ) 11
2 11
Então, para y . 0 temos 2  x  11.
Logo, o maior inteiro positivo que satisfaz a
inequação é 10.
11.
V 5 2  x  (x 1 3) . 20
2x2 1 6x 2 20 . 0
x2 1 3x 2 10 . 0
 5 b2 2 4ac
 5 32 2 4  1  (210) 5 49
x
b
a
x
x
5
2 6
?
5
2 6
?
5
2 6 5
52
Δ
2
3 49
2 1
3 7
2
2
5
→

’
”
y  0 y  0
25 y  0 2
Então, y . 0 para x  25 (não convém) ou
x . 2.
Logo, o volume do paralelepípedo
retângulo é maior que 20 para x . 2.
y  0
y  0 y  0

411
Segmentos proporcionais
41 – Razão e proporção
1.
14
20
7
10
a) r5 5 5
0,7
35
50
7
10
b) r5 5 5
0,7
2. Sim, a razão entre 14 e 20 é igual à razão
entre 35 e 50.
3. Sim, os números 14, 20, 35 e 50.
4. Sim, 14
20
35
50 5 .
42 – Segmentos proporcionais
1. AB
8
20
2
5
CD 5 5 5
0,4
2. 2 m 5 200 cm
200
80
5
2
r5 5 5
2,5
3. r 5 0,4
8 cm 5 0,08 m
r
4
x
10 0 08
50 ,
45 5
,
10  x 5 4  0,08
x 5 0,032 m
4. x2 2 24x 1 135 5 0
 5 b2 2 4  a  c
 5 (−24)2 2 4  1  135 5 576 2 540 5 36
x
b
a
x
x
5
2 
5


5
 5
5
Δ
2
24 36
2 1
24 6
2
15
9
→

’
”
Logo, a 5 9 e b 5 15.
Agora, podemos calcular a razão de
AB para BC :
r5 5 5
9
15
3
5
0,6
1.
a) Primeira: Salvador; segunda: Rio de
Janeiro.
b) e
21 2
1060
cm
km
cm
21 2
5 106000000
cm 5
1
5000000
, = ,
A escala é de 1 : 5 000 000.
c)
1
5 5
10000000 1310
1
10000000
131000000
5
x cm
km
x cm
cm
→
→
131000000
10000000
→ x5 5
13,10
A distância entre as duas cidades no
mapa é de 13,1 cm.
Resposta em aberto.
2.
a) Vamos verificar se a razão entre a
largura e o comprimento é 14
20
7
10 5 .
1 75
2 5
175
100
25
10
175
250
r5 5 5 5
7
10
,
,
Logo, pode-se confeccionar uma
bandeira com essas dimensões.
b) r
7
x
10 30
5 5
x 5 21
Se o comprimento for de 30 m, a largura
deverá ser de 21 m.
c)
r
7
x
10 55
7 55
10
x
5 5
5

5
38,5
A bandeira deverá ter 38,5 m de largura.
1. AB 5 20 cm; BC 5 50 cm; CD 5 80 cm e
DE 5 200 cm.
AB
BC
CD
DE
→ AB
=
CD
2
BC
DE
5 20
50
5 5
2
5
80
200
2
5
5 5 5
Os segmentos são proporcionais.

412
2. AB 5 4 cm
CD 5 6 cm
MN 5 8 cm
PQ 5 12 cm
AB
CD
MN
PQ
→
AB
MN
2
CD
PQ
3 4
6
5 5
2
3
8
12
2
3
5 5 5 5
Logo, os segmentos são proporcionais.
3. MN , RS ,
PTe XY
MN
RS
PT
XY
x
x ,
cm
PT mede
5
5
5
?
5
12
15 8
12 8
15
6 4
6,4 cm.
43 – Feixe de retas paralelas
44 – Teorema de Tales
1.
arte
r
de x
2x 1 4
Editoria s
Ilustrações: x 1 2
25
t
Pelo teorema de Tales, temos:
x
2 x
1
4
x
5
1
2
25
Pela propriedade fundamental da
proporção, temos:
25x 5 (x 1 2)(2x 1 4)
25x 5 2x2 1 8x 1 8
2x2 2 17x 1 8 5 0
 5 b2 2 4ac
 5 (−17)2 2 4 ? 2 ? 8 5 225
Δ

2 b
6
17 6
225
17 6
15
x
5
8
x
5
→
2
a
5
2 5
?
2
4
1
x
5 2
5
0 5
x 1 y 5 2,5 1 4,4 5 6,9  
 
’
” ,
x
x
5
6
?
5
6
5
5 5
17 225
2 2
17 15
4
8
1
2
0 5
→

 
 
’
” ,
2.
a)
a
40 32
100 x
b
c
40
32
100
5
32 100
40
80
80
5
?
5
5
x
x
x
b)
a
5,4 4,5
3
x
b c
4 5
3
5 4
5
3 5 4
4 5
3 6
3 6
,
,
,
,
,
,
5
?
5
5
x
x
x
3.
5
a
b
c
x 2,75
8 4 y
5
2 5
8 4
5
8
x
2 75
4 4
x
5 5
5 5
y
y
→
→
,
,
,

413
4. Se AC 5 42 e AB 5 14, temos BC 5 28 e
DF 5 x 1 18.
arte
A
D
a
de Editoria B 14 18
E
b
Ilustrações: 28 x
C
F
c
14
18
28
5 x
x 5 36
DF 5 36 1 18 5 54
5.
A
M
a
5
B
x
N
b
36
13 y
C
P
c
y 5 36 2 x
Aplicando o teorema de Tales, temos:
5
x
5
 5(36 2 x) 5
13 36 2
x
5 13x  180 2 5x 5 13x  18x 5
5 180  x 5 10
y 5 36 2 x  y 5 36 2 10  y 5 26
y 2 x 5 26 2 10 5 16
6.
a b c d
x
y
z 4
8 10
10
x 5 4 1 z
4 8
z
5 →z5
5
10
x 5 4 1 z  x 5 5 1 4  x 5 9
Ainda pelo teorema de Tales, temos:
x(x 1 1) 5 12
y
10
→ y
520
x2 1 x 2 12 5 0
8
5 4
 5 b2 2 4ac
Logo, x 5 9 e y 5 20.
 5 12 2 4 ? 1 ? (−12) 5 49 45 – Aplicações do teorema de Tales
1.
a) MP / / BC
A
7 8
M P
21 x
B C
Pelo teorema de Tales aplicado nos
triângulos, temos:
7
8
21
5 x
7x 5 8 ? 21
x 5 24
b) PQ / / AB
A
B C
Q
P
5
x
3 x 2 1
triângulos, temos:
x x
2
1
5
5
3 3x 5 5(x 2 1)
3x 5 5x 2 5
22x 5 25
x 5 2,5
c) DE / / BC
x
A
E
B
C
D
3
x 1 1 4
triângulos, temos:
x
x
1
5
1
4
3

414
x
b
a
x
x
5
2 6
5
2 6
?
5
2 6 5
52
Δ
2
1 49
2 1
1 7
2
3
4
→

’
 ” (Não convém.)
x
x
5
2 6
?
5
2 6 5
52
Δ
1 49
2 1
1 7
2
3
4
→

’
Então, x 5 3.
d) AB // MP
M
arte
de Editoria 4x 1 2
A
Ilustrações: 3x 2 1
P
6
B
N
4
triângulos, temos:
3 x
2
1
4
4 x
1
2
5
6
6(3x 2 1) 5 4(4x 1 2)
18x 2 6 5 16x 1 8
2x 5 14
x 5 7
2. AB 5 x 2 1 1 3 5 x 1 2 e AC 5
5 x 1 4 1 x 5 2x 1 4
A
x 1 x 2 1 4
D E
3
x
B
C
14
triângulos, temos:
x 2
1 x
1
4
3
5
x
x(x 2 1) 5 3(x 1 4)
x2 2 x 5 3x 1 12
x2 2 4x 2 12 5 0
 5 b2 2 4ac
 5 (−4)2 2 4 ? 1 ? (−12) 5 64
60x 5 100(120 2 x)
2 b
6
Δ
4 6
64
4 6 8
x
5
6
60x 12 000 100x
x
5 2 5
2
a
5
→
2 ?
1
5
2
x
52
2
160x 5 12 000
x 5 75
y 5 120 2 75  y 5 45
Perímetro do lote 1:
30 1 100 1 (120 2 45) 5 205  205 m
Perímetro do lote 2:
30 1 50 1 60 1 45 5 185  185 m 
100
60
’
” (Nãoconvém.)
x
x
5
6
?
5
6 5
52
Δ
4 64
2 1
4 8
2
6
2
→

’
” (Nãoconvém.)
AB 5 x 1 2  AB 5 6 1 2 5 8  AB 5 8 cm
AC 5 2x 1 4  AC 5 12 1 4 5 16  AC 5
5 16 cm
Perímetro 5 8 1 16 1 14 5 38  38 cm
3. BC 5 32 cm e y 5 32 2 x
A
10
6
E
B C
x D y
triângulos, temos:
x
32 x
10
5
2 6
6x 5 10(32 2 x)
6x 2 320 1 10x 5 0
16x 5 320
x 5 20
y 5 32 2 x  y 5 32 2 20  y 5 12
x 2 y 5 20 2 12 5 8.
Logo, x 5 20 cm; y 5 12 cm e x 2 y 5 8 cm.
4. y 5 120 2 x
60
50
Lote 2
30
Lote 1
B
100
A
C
D
E
120
x
y
triângulos, temos:
x
y
x
x
5
2
5
120
100
60

415
5. Fazendo um esboço do triângulo, temos:
A
D
18
E
x
9
y 3
B C
12
y 5 18 2 x
triângulos, temos:
x
y
5
x
2
x
5
9
3
18
9
3
3x 5 9(18 2 x)
12x 5 162
x 5 13,5
y 5 18 2 x  y 5 18 2 13,5  y 5 4,5
Logo, AD 5 13,5 cm e DB 5 4,5 cm.
6.
A
50 m 80 m
6. Usando o teorema de Tales, temos:
50
80
36
5
x2
x
50x 5 80x – 2 880
30x 5 2 880
x 5 96
x 2 36 5 96 – 36 5 60
Portanto, as medidas dos quarteirões da
segunda avenida são 60 m e 96 m.
7.
5 m 4 m
x 4 m
triângulos, temos:
4
x
5 5
4 16
5
x5 5
3,2
A distância procurada é 3,2 m.
1.
a) Pelo teorema da bissetriz interna,
temos:
4
10
2
5
20
4
5
5 5
5
5
x
x
x
b) Pelo teorema da bissetriz interna,
temos:
x
11
x
4
4
44
4
11
5
5 5
c) Pelo teorema da bissetriz interna,
temos:
4 3
2
8
3
x
x
5
5
d) Pelo teorema da bissetriz interna,
temos:
6
4
1
x
x
2
+ x 5
6x 5 (x 2 1)(x 1 4)
6x 5 x2 1 3x 2 4
x2 2 3x 2 4 5 0
 5 b2 2 4ac
 5 (−3)2 2 4 ? 1 ? (24) 5 25
x
b
a
x
x
5
2 
5

5
 5
52
Δ
2
3 25
2
3 5
2
4
1
→

’
” (Nãoconvém.)
x
b
a
x
x
5
2 
5

5
 5
52
Δ
2
3 25
2
3 5
2
4
1
→

’
” (Nãoconvém.)
Logo, x 5 4.

416
2.
A
arte
de Editoria 7,5 cm
10 cm
Ilustrações: B x 2 2 D x
C
Pelo teorema da bissetriz interna, temos:
7 , 5
x2
2
10
5
x
7,5x 5 10(x 2 2)
2,5x 5 20
x 5 8
BC 5 x 2 2 1 x 5 2x 2 2 5 8 ? 2 2 2 5 14
Logo, BC 5 14 cm.
3.
A
8 cm 12 cm
B x D y
C
15 cm
8
x
12
5
y
8
x
12 5
15
2
x
12x 5 8(15 2 x)
12x 1 8x 5 120
20x 5 120
x 5 6
y 5 15 2 x  y 5 15 2 6  y 5 9
Sabendo que x 5 6 cm e y 5 9 cm,
calculamos:
y 2 x 5 9 cm 2 6 cm 5 3 cm
4.
Perímetro 5 6 1 9 1 5 5 20 A
B
C
4 cm 6 cm
x D y
5 cm
4
6
5
5
4
6 5
5 2
5
2
x
y
Comoy xfazemos
x
x
, :
6x 5 4(5 2 x)
10x 5 20
x 5 2
Logo, AD 5 2 cm e DC 5 3 cm.
5.
A
6 x
z 3
P M
2 3
B C
D
4 y
a) Pelo teorema de Tales aplicado nos
triângulos, temos:
6
x
2 5
3 x 5 9
Pelo teorema da bissetriz interna no
triângulo APM, temos:
6
z
x 5
3
Como x 5 9, já podemos obter z:
6
z
9 5
3 z 5 2
Pelo teorema da bissetriz interna no
triângulo ABC, temos:
6 2
x 3
y
4
8
12
4
1
1
5
5
y
y 5 6
Agora, calculamos:
x 1 y 1 z 5 9 1 6 1 2
x 1 y 1 z 5 17
b) AB 5 8; AC 5 12 e BC 5 10
Perímetro 5 8 1 12 1 10 5 30
c) AP 5 6; AM 5 9 e PM 5 5

417
1. Alternativa a.
, 5 3 cm
d 5
3 2
cm
d
r
3 2
3
2 1414
5 5 5 5
,
,
2. Alternativa e.
AB 5 32 cm
AB
8
BC 5
3
A B C
32 8
3
8 32 3
96
8
12
BC
5 → ?BC5 ? →BC5 →BC5
Logo, BC 5 12 cm.
3. Alternativa c.
A x 84 x
P B
84 cm
PA
PB
x
5
x
2
2
5
5
84
2
5
5x 5 2(84 2 x)
7x 5 168
x 5 24
PA 5 24 cm e PB 5 60 cm
Agora, calculamos:
PB 2 PA 5 60 cm 2 24 cm 5 36 cm
4. Alternativa a.
Base maior (M) 5 10 u
Base menor (m) 5 6 u
r
m
6
5 M 5 10
5
0,6
5. Alternativa c.
a
x
a
5 30 5
x 5 6, independente do valor de a.
6. Alternativa d.
2
5
4
5 x
x 5 10
2
10
5
5 y
y 5 25
y 2 x 5 25 2 10 5 15
7. Alternativa c.
x
5
18
5
15 x 5 6
y
10
x 5
5
Como x 5 6, para obter y, fazemos:
y
10
6
5
5 y 5 12
Agora, calculamos:
AB 5 18 1 x 1 y
AB 518 1 6 1 12 5 36
8. Alternativa a.
triângulos, temos:
80
60
90
5 x
x 5 67,5
Logo, o comprimento do outro quarteirão é
67,5 m.
9. Alternativa e.
triângulos, temos:
1 , 5
1
6
5 h
h 5 4
A altura da antena é 4 m.
10. Alternativa c.
triângulos, temos:
10
x
20 5
y
Se AE 5 42, então y 5 42 2 x.
10
x
20 5
42 2
x
20x 5 10(42 2 x)
30x 5 420
x 5 14
y 5 42 2 x 5 42 2 14 5 28
Logo, y 5 28 m.

418
11. Alternativa b.
triângulos, temos:
25
5
30
x
5
x 2 x
10
1
1
25(x 1 10) 5 (x 2 5)(x 1 30)
25x 1 250 5 x2 1 25x 2 150
x2 5 400
x 5 20 ou x 5 220 (Não convém.)
Perímetro do triângulo ABC:
P 5 25 1 x 2 5 1 x 1 30 1 x 1 10 1 70
P 5 130 1 3x
P 5 130 1 3  20
P 5 190
12. Alternativa a.
x 2 y 5 3; então, y 5 x 2 3.
A
arte
de Editoria x y
Ilustrações: B 6 cm 5 cm
C
x
6
y
5
5
x
6
x
2
3
5
5
5x 5 6(x 2 3)
5x 5 6x 2 18
x 5 18 cm R x 5 18 cm
18 6
y 5
5 6y 5 18  5
6y 5 90
y 5 90
6
y 5 R 15 y 5 15 cm
Perímetro do triângulo ABC:
P 5 x 1 y 1 6 1 5
P 5 18 1 15 1 11
P 5 44 R P 5 44 cm
13. Alternativa c.
4x 1 10 5 5x
4x 2 5x 5 2 10
x 5 10 A
6 cm y
D
B
C
3 cm
2 cm
6 3
y 2 5
y 5 4 R y 5 4 cm
Perímetro do triângulo:
P 5 6 cm 1 4 cm 1 5 cm
P 5 15 cm
14. Alternativa d.
B D C
A
9 cm 6 cm
y
x
Se o perímetro é 45 cm, temos:
x 1 y 5 45 2 9 2 6 R x 1 y 5 30
Logo, y 5 30 2 x.
x
y
5
x
2
x
5
9
6
30
9
6
6x 5 9(30 2 x)
6x 5 270 2 9x
15x 5 270
x 5 18
AC 5 30 2 18 5 12
Logo, AB 5 18 cm e AC 5 12 cm.
15. Alternativa c.
Pelo teorema de Tales aplicado no
triângulo ADE, temos:
x
12
36
5
10 x 5 43,2
Aplicando o teorema de Tales,
encontramos y:
10 36
y 18 5
y 5 5
Agora, calculamos:
x 2 y 5 43,2 2 5
x 2 y 5 38,2
16. Alternativa e.
triângulos, temos:
35
2 x
1
5
1
70
5
5
x
5
2

419
46 – Figuras semelhantes
a) r
6
9
c5 5
r
5 5
2
3
4
6
2
 3
b) As razões são iguais.
1. Resposta em aberto. O aluno deve
multiplicar por 3 as medidas do
retângulo original, formando o novo
retângulo.
2.
a) Sendo 30 m a distância correspondente
aos braços abertos do Cristo, temos:
r
1
x
3 30
→ 10→ 10
5 5 x5 x5 m
A distância correspondente aos braços
abertos do Cristo deve ser 10 m.
b) Sendo 30 m a altura da estátua, temos:
r
1
1
cm
m
1
100
cm
cm
5 5 5
x
5
x x
5 5 5
1
100
1
100 30
30
100
0,30→ 0,30m530 cm
O Cristo terá 30 cm de altura no
desenho.
47 – Polígonos semelhantes
1.
a) c 5 30 cm e , 5 20 cm
r
24
30
c5 5
r
5 5
4
5
15
20
3
, 4
Os retângulos não são semelhantes
4
3
5

4  
 
.
b) c 5 40 cm e , 5 25 cm
r
24
40
c5 5
r
5 5
3
5
15
25
3
 5
Os retângulos são semelhantes
3
3
5
5
5  
 
.
2. Pelas propriedades dos paralelogramos
Â 5 708 e ˆC
5 708; então, ˆD
5180°70°5110°
e ˆB
5 1108, e o mesmo acontece com os
ângulos Â’, Bˆ ’, Cˆ ’ e Dˆ ’. Concluímos, então,
que os ângulos correspondentes são
congruentes.
r5 5
3
5
6
10
(Verdadeiro.)
Logo, os paralelogramos são semelhantes.
3.
a) Não. Dois retângulos nem sempre são
semelhantes, pois os lados podem não
ser proporcionais.
b) Sim. Dois quadrados são sempre
semelhantes, pois os ângulos
são congruentes, e os lados são
proporcionais.
c) Não. Dois triângulos só serão
semelhantes se dois ângulos forem
congruentes, e os lados homólogos
forem semelhantes.
d) Sim. Dois triângulos equiláteros são
sempre semelhantes, pois todos os
ângulos medem 608, e os lados são
proporcionais.
e) Sim. Polígonos regulares sempre são
semelhantes, pois possuem os lados
e os ângulos congruentes, e os lados
homólogos proporcionais.
4.
20
15
a) r5 5
4
3
b) Quando dois polígonos são
semelhantes, os perímetros desses
polígonos são proporcionais às
medidas de dois lados correspondentes
quaisquer, portanto a razão entre os
perímetros H1 e H2 é dada por:
r5 5
20
15
4
3
Semelhança

420
c) Os ângulos dos polígonos regulares são
congruentes; logo, os ângulos dos dois
polígonos são todos congruentes.
5.
12 m
A B
D C
x
8 m
M N
y
Q P
r
1
4
1
4
12
12 4
48→ 48
5
x
5 ?
5 5
5
x
x x m
1
4
8
5
y
y
5 4 ?
8
y 5 32 →y 5
32
m
As dimensões do retângulo MNPQ são
48 m 3 32 m.
6. Se os trapézios são semelhantes, os lados
homólogos são proporcionais.
a) r5 5
24
12
2
A razão de semelhança é 2.
b) r
30 40 62
x y z 525 5 5
x 5 15; y 5 20 e z 5 31.
c) Quando dois polígonos são
semelhantes, os perímetros desses
polígonos são proporcionais às
medidas de dois lados correspondentes
quaisquer; logo, r 5 2.
7.
r
x
5
2
5
5
2
5
5
25
2
x5 5
12,5
O lado do outro quadrado mede 12,5 cm.
Logo, o perímetro do outro quadrado é
dado por:
P 5 12,5 ? 4 5 50 R P 5 50 cm
8. Perímetro do retângulo dado:
P 5 2 ? 15 1 2 ? 10 5 50 R P 5 50 cm
Quando dois polígonos são semelhantes,
os perímetros desses polígonos são
proporcionais às medidas de dois lados
correspondentes quaisquer; logo:
r
90
50
9
x
5 10
90
5
→ → 18→ 18
x x x cm
5 5
9
5
5 5 5 5
9
5 15
y
→y →y →y cm
135
5
5 5 527 527
As medidas dos lados do retângulo ABCD
são 27 cm e 18 cm.
9.
a)
r 5
3
2
b)
r
2 ,
1
x
4 ,
2
3
5
3
2
5
3
2
, → ,
1 4 1 4
x 5 5 x 5
cm
c) Como os pentágonos são semelhantes
Dˆ 5Dˆ ’5105°.
10. PI 5 28 1 34 1 26 1 60 5 148
PII 5 37
R
P
P
I
II
148
37
5 5 5
4
correspondentes quaisquer; logo, a razão
entre os lados também é 4:
28 34 60 26
r
z y x w 545 5 5 5
Então, z 5 7 cm; y 5 8,5 cm; x 5 15 cm
e w 5 6,5 cm.
11.
13
52
r
5 5
P 5
cm
1
4
245 Ilustrações: Editoria de arte

421
correspondentes quaisquer; logo:
p
1
P
4
1
p
4 245
→4 245→ 61,25→ 61,25
p p p cm
5
5 5 5 5
12. O terreno maior tem 50 m de frente, e seu
contorno é de 400 m.
Conhecendo essas medidas, podemos
calcular a medida do fundo do terreno
maior:
P 5 2A 1 2B
400 5 2 ? 50 1 2B
400 5 100 1 2B
B 5 150
O terreno maior tem 150 m de fundo.
a)
r 5
2
5
2
5 50
x
→ x →x
5 5 5100 520
Logo, o terreno menor tem 20 m de
frente.
2
y
5 → 5 y 5300 →y
560
5 150
Logo, o terreno menor tem 60 m de
fundo.
Portanto, as dimensões do terreno
menor são 20 m por 60 m.
b)
p52a12b
p 5 2 ? 20 1 2 ? 60
p 5 160
O contorno do terreno menor mede
160 m.
13.
r 5
3
4
3
4
27
→ 3 x 27 4
→x →x
108
3
5 5 ? 5 536 x
O perímetro do segundo polígono é 36 cm.
14.
r 5
1
200
a)
1
200
5
→x →x
5 5200?5 51000 x
Então, x 5 1 000 510 m.
1
6
200
→y →y
5 56?200 51200 y
Então, y 5 1 200 cm 5 12 m.
Logo, as dimensões reais da sala são
10 m por 12 m.
b) Área na planta:
A 5 5 cm ? 6 cm R A 5 30 cm2
c) Área real:
A 5 10 m ? 12 m R A 5 120 m2
48 – Triângulos semelhantes
1.
a) Sim, pois possuem dois ângulos
congruentes.
b) Não, pois os ângulos não são
congruentes.
c) Sim, pois possuem dois ângulos
congruentes.
d) Sim, pois possuem os ângulos
congruentes. No primeiro triângulo,
o ângulo que falta indicar é 40º, e no
segundo, 30º.
2.
a) Sim; os dois triângulos são retângulos;
logo, possuem os três ângulos
congruentes.
b)
BCeDE; ABe EF e ACeDF.
3. Se os triângulos são semelhantes, os lados
homólogos são proporcionais:
AC
AB
BC
MN
5 PM
5
PN Substituindo os valores, temos:
x
y
5 R x2 5 y ? z
z
x Portanto, é correto escrever x2 5 y ? z.
4. Como os triângulos são semelhantes, os
lados homólogos são proporcionais.
a)
AB
A B
BC
B C
AC
’ ’ 5 ’ ’ 5
A’C’ 18 12
x
y 5 9 5
18
Da primeira igualdade, temos:
y ?
5
5
18 9
12
13,5

422
Da segunda igualdade, temos:
x ?
5
5
12 18
9
24
b)
AE
CD
EB
AB
5 BD
5
BC 2
4
3
x
8 5 5 y
y ?
5
5
3 4
2
6
x ?658?3 x5 5
24
6
→ 4
c)
AB
EF
BC
AC
5 DE
5
DF 6 9
3
10
y 5 5
x Da primeira igualdade, temos:
y ?
5
5
6 3
9
2
x ?
5
5
10 3
9
10
3
5. Os lados homólogos são proporcionais;
logo, podemos escrever:
AB
BC
AC
DE
5 DF
5
EF Substituindo os valores dados na primeira
igualdade, temos:
1
2
x x
1 5
3
x 5 3(1 − x)
x 5 3 − 3x
4x 5 3
x 5
3
4
x 5 0,75
6.
a) Sim, pois os ângulos são congruentes.
b) ACeDE; ABeDF e BCe EF
c) x
9
5
4 x
x
x
x
x
2 36
36
6
6
5
56
5
52
→

’
” (Nãoconvém.)
Logo, x 5 6.
7.
20 12
A 30 C
E
B
D
Nos triângulos ABC e CDE, se AB // CD,
então, Â  ˆC
2; se BC // DE, ˆC
1  Ê. Logo,
os triângulos são semelhantes, e os lados
homólogos são proporcionais:
BC
AC
DE
5
CE 20
12
30
5 x
x 5 18
8. Os lados homólogos são proporcionais
AB
DE
AC
DF
BC
EF
6 x y
1
4
y
5 5
5
1
5
6
6
4
4(x 1 6) 5 36
x 1 6 5 9
x 5 3
Igualando a primeira e a terceira razão,
temos:
6
y1
4
4
5
y
6y 5 4(y 1 4)
6y 5 4y 1 16
2y 5 16
y 5 8
Logo, x 5 3 e y 5 8.
9. Os triângulos ABC e DEF são semelhantes,
pois têm os ângulos congruentes
e, portanto, os lados homólogos
proporcionais.
AB
BC
AC
DE
EF
DF
x
y
5 5
10
4
5 5 4 8
16
,
4x510? 4,8→x512
10y516? 4→y56,4
Portanto:
x 1 y 5 12 1 6,4 5 18,4
Editoria de arte

423
10.
A
arte
de Editoria Ilustrações: 4,80 m x
2,05x 5 x(x 1 0,80)
x2 1 0,80x – 2,05x 5 0 obelisco
pessoa
2,10 m
A’
B C B’ C’
Os triângulos são semelhantes; logo, os
AB
BC
A ’ B
’ 5
B ’ C
’
5
5 ?
5
x
,
x
x
,
, ,
,
14
2 10
4 80
14 4 80 210
0 72
A sombra projetada tem 72 m.
11.
A
x
prédio
ripa
3,5 m
A’
B C B’ C’
14 m 0,70 m
AB
BC
A B
B C
x
x
5
’ ’ ’ ’
5
, ,
,
,
5
?
3 5
14
0 70
3 5 14
0 70
x 5 70
A altura do prédio é 70 m.
12.
A
x
6 m 1,20 m
mastro
pessoa
1,80 m
A’
B C B’ C’
AB
BC
A B
’ ’ B’C’ 5
x
1 80
x
6
1 20
5
, ,
6 180
,
1 ,
20
5
?
x 5 9
O mastro tem 9 m de altura.
13.
x
x 0,80 x
Caio
fã
2,05 m
2,05 x
1
0,80
x
5
x

424
x2 − 1,25x 5 0
’
” , ( ) → ( )
x x
x
x
2 5
5
5
1 25 0
0
1 25
,
 

Não convém.
A altura da fã é 1,25 m.
14. Os triângulos são semelhantes; logo, os
AB
AC
BC
DF
5 DE
5
FE Da primeira igualdade, temos:
8
14
4
5
y
14 4
8
5
?
y
y 5 7
Da figura, temos que 2x 1 y 5 14.
Substituindo y 5 7 na expressão:
2x 1 y 5 14
2x 1 7 5 14
2x 5 7
x 5 3,5
Portanto, x 5 3,5 e y 5 7.
15. Os triângulos PQR e PSR possuem um
ângulo em comum ( ) e um ângulo
congruente; logo, são semelhantes, e os
PQ
QR
PR
PR
5 RS
ˆP
5
PS Da primeira igualdade, temos:
10
8
4
5
SR
4 8
10
5
?
SR
SR 5 3,2
Usando a primeira e a terceira razão,
temos:
10
4
4
5 PS
PS5
4 ? 4
10
PS 5 1,6
Então, RS 5 3,2 e PS 5 1,6.
16. Os triângulos ABC e AMN são
semelhantes, pois possuem um ângulo
em comum (Â) e um ângulo de 308. Então,
os lados homólogos são proporcionais.
AC
BC
AB
AM
5 MN
5
AN Da primeira igualdade, temos:
100 80
40
100 40
80
AM
AM
5
5
?
AM 5 50
80
60
40
AN
40 60
80
5
5
?
AN
AN 5 30
Perímetro 5 AM 1 AN 1 NM
Perímetro 5 50 1 30 1 40 5 120
O perímetro do triângulo AMN é 120 m.
Desafio, página 235.
A
12,3 m
1,5 m
x
C
4 m
B
E
D
Toda reta que é paralela a um lado de
um triângulo e encontra os outros dois
lados em pontos distintos determina com
esses lados um triângulo semelhante ao
primeiro; logo,  ABC   ADE.
AC
AE
BC
ED
x
5
1
,
, 5
,
12 3
12 3
4
1 5
(12,3 1 x)1,5 5 4 ? 12,3
18,45 1 1,5x 5 49,2
1,5x 5 30,75
x 5 20,5
A pessoa deve caminhar 20,5 m para
atingir o ponto mais alto da rampa.
1. Sendo MN // BC, usando o teorema
fundamental da semelhança de
triângulos, temos:
 ABC  AMN
AB
AC
BC
AM
5 AN
5
MN Usando a primeira igualdade, temos:
x
1
x
9 9115
5
9
24x 5 9(x 1 9)
24x 5 9x 1 81
Editoria de arte

425
15x 5 81
x 5 5,4
Usando a segunda igualdade, temos:
24
y
9 5
6
24 6
9
5
?
y
y 5 16
Logo, x 5 5,4 e y 5 16.
2. Usando o teorema fundamental da
semelhança de triângulos, temos:
 ABC   CMN
AB
BC
MN
5
CN 9
6 5
x1y
y
9y 5 6(x 1 y)
9y 5 6x 1 6y
3y 5 6x
y 5 2x
Logo, a relação y 5 2x é válida.
3. A área do trapézio é dada por A
B bh
5
( 1 )
2
.
No trapézio ABED, temos B 5 15 e h 5 8 .
Vamos, então, determinar b (o lado DE ),
usando o teorema fundamental da
semelhança de triângulos:  ABC   CDE
AC
AB
CD
DE
DE
DE
5
2
5
5
( )
? 2
20
20 8
15
15 20 8
20
DE 5 b 5 9
Agora, calculamos a área:
( B bh
) ( )
A
1
1 5
5
2
15 9 8
2
A área do trapézio é 96.
 ABC  AMN
AC
AB
BC
AN
5 AM
5
MN Usando a primeira igualdade, temos:
x1 1 x
3 6 4
1
6
5
4
4(x 1 9) 5 6(4 1 x)
4x 1 36 5 24 1 6x
2x 5 12
x 5 6
4 1
6
7 ,
5
4
5
4 1 6 5 4 ?
75
,
10 5
30
y
y y
y
y 5 3
Agora, calculamos:
x 1 y 5 6 1 3
x 1 y 5 9
A
50 cm
x 75 cm
136 cm
B
C
D
E
 ABE   EDC
AB
CD
AE
CE
x
5
136 1
50
5
75
75
50(x 1 75) 5 10 200
x 1 75 5 204 5 AE
Logo, AE 5 204 cm.
Observe que não foi necessário determinar
x para encontrar a medida de AE ; mas,
caso haja necessidade, pode-se também
primeiro determinar x 5 129 para, depois,
somar 75 e obter AE .
 ADE   ABC
AD
AE
DE
AB
5 AC
5
CB Usando a primeira igualdade, temos:
42 70
70
50
50
1
5
x1
112 ? 50 5 70(x 1 50)
5 600 5 70x 1 3 500
2 100 5 70x
x 5 30 R EC 5 30
Editoria de arte

426
50 1
30
5
DE
50 40
DE 5 64
Logo, EC 5 30 e DE 5 64.
7.
A
y m 56 m
Lote 1
arte
de Editoria E D
48 m
Ilustrações: 16 m Lote 2
x m
B C
60 m
Usando o teorema fundamental da
 ABC  ADE
AB
BC
AC
AE
5 ED
5
AD Usando a primeira igualdade, temos:
y
1
16 60
y
5
48
48(y 1 16) 5 60y
48y 1 768 5 60y
12y 5 768
y 5 64
60
56
1x
48
5
56 40x 5 25(x 1 30)
40x 5 25x 1 750
15x 5 750
x 5 50
A distância do observador em O até o
ponto P é de 50 m. 60 ? 56 5 48(56 1 x)
70 5 56 1 x
x 5 14
Perímetro do lote 1 (triângulo ADE):
P1 5 y 1 56 1 48
P1 5 64 1 56 1 48
P1 5 168
Logo, o perímetro do triângulo ADE é 168 m.
Perímetro do lote 2 (trapézio BCDE):
P2 5 16 1 48 1 x 1 60
P2 5 16 1 48 1 14 1 60
P2 5 138
Logo, o perímetro do trapézio BCDE é 138 m.
 PDC   PAB
PC
PA
DC
AB
x
200
80 100
x
x
5
5
5
5
20000
80
250
A largura do lago é 250 m.
 ABC   BPN
AC
AB
PN
5
BP
8 6
5
x 2
y
6
8(6 − y) 5 6x
48 − 8y 5 6x
8y 5 48 − 6x
y562 x
3
4
10.
P
A
rio
O
x m
25 m
30 m
B C
40 m
 PBC   POA
PB
BC
PO
AO
5
1
x
x
30 40
5
25

427
1.
a) A B
3
1
’ ’
’ ’ ,
AB
B C
BC
D C
DC
AD
AD
4 5
1 5
,
’ ’ ,
7 5
2 ,
5
’ ’
5 5
3
5 5
3
5 5
3
6
2
55 5
3
As razões são todas iguais a 3.
b)
OA
OA
OB
OB
OC
OC
OD
OD
’
’
’
9
3
5 5
12
4
12
4
’ ,
4 5
1 ,
5
5
3
3
5 5
3
5 5
3
=
As razões são todas iguais a 3.
c) 3
Tratando a informação, páginas 239 a 241.
1. Para encontrar a mediana no gráfico,
devemos separar os pontos do gráfico,
traçando uma reta paralela ao eixo das
pedras, deixando metade dos pontos menos
um acima da reta e metade dos pontos
menos um abaixo dessa reta. Nesse caso,
R$ 30,00 é a mediana dos pontos que
indicam os preços das pedras no gráfico:
50% dos preços são maiores que R$ 30,00;
50% dos preços são menores que R$ 30,00.
2. Significa que 50% dos preços de venda
das gemas são menores ou iguais a
R$ 35,00, e os outros 50% dos preços são
maiores ou iguais a R$ 35,00.
1. Alternativa d.
prédio
A
arte
de x
poste
Editoria A’
2 m
B C B’ C’
y 5 3,5
40 m 5 m
x 5 12 − y
x 5 12 − 3,5
x 5 8,5 Os triângulos são semelhantes; logo, os
AB
A B
BC
B C
x
2
x
x
’ ’ ’ ’ 5
5
5
5
40
5
80
5
16
A altura do prédio é 16 m.
2. Alternativa b.
r
x
x
x
5
5
5

5
14
3
14
3 09
14 0 9
3
4 2
,
,
,
O comprimento do carro do pai de Caio é
4,2 m.
3. Alternativa c.
30
4 5
5
5 30
4
37 5
5

5
h
h
h ,
A altura da árvore é 37,5 m.
4. Alternativa a.
r
x
x
x
5
5
5
5
5
2
5
2
6
12
5
2,4
A altura da porta é 2,4 m.
5. Alternativa e.
BC
AC
EC
CD
14 12
y
5
5
3

428
6. Alternativa b.
1,80 m
A C
2,70 m 6,30 m
H
B
D
 ABC  ADE
AC
BC
AE
DE
H
2 70 630
H
5
1
5
, ,
5
2 , 70 180
,
6
A altura do poste é 6 m.
7. Alternativa b.
O losango é um paralelogramo com os
4 lados congruentes.
A
P
M
20 cm
x
x
x
B 5 cm D C
x
 ABC  AMP
AB
AM
BC
MP
x x
5
2
5
20
20
5
20x 5 5(20 − x)
20x 5 100 − 5x
25x 5 100
x 5 4
Agora, calculamos o perímetro do losango:
P54 ? x→P54 ? 4→P516
Logo, o perímetro do losango é 16 cm.
8. Alternativa a.
Os triângulos são semelhantes, e os lados
 ABC   CDE
AC
AB
EC
ED
x
x
5
5
5
?
36
300
60
60 300
36
x 5 500
A largura do lago é 500 m.
9. Alternativa c.
1,60 m
10 m 2,50 m
H
Observe que os triângulos que
representam as projeções das sombras
no esquema são semelhantes, e os lados
homólogos são proporcionais. Vamos,
então, calcular H:
2 , 50
1,60
10
5 H
H 5 6,4
Logo, a árvore tem 6,4 m de altura.
10. Alternativa e.
Sejam x, y e z as medidas dos lados do
triângulo XYZ.
AB
BC
AC
x
5 y
5
z
15 18 27
5 5
x y z
Pela propriedade das proporções, fazemos:
15118127 15 18 27
x y 5 5 5 1 1
z x y z
Como x 1 y 1 z 5 20, temos:
60
27
20
5 z
z 5 9
Portanto, XZ 5 9 cm.

429
11. Alternativa c.
Os triângulos são semelhantes, e os lados
 ABD   CAD
AB
AD
BD
AC
5 DC
5
AD Usando a primeira igualdade, temos:
6
x
8 5
64 ,
x 5 4,8
Usando a primeira razão com a terceira,
temos:
6
y
8 5
48 ,
y 5 3,6
Agora, calculamos:
x 1 y 5 4,8 1 3,6
x 1 y 5 8,4
12. Alternativa d.
Os triângulos possuem um ângulo comum
e outro congruente; logo, são semelhantes.
AB
BC
BD
AB
4 10
x
5
5
4
x 5 1,6
Logo, BD 5 1,6 cm.
13. Alternativa b.
 ABC   APQ
AC
BC
AQ
5
PQ
x
5
7
3
10,5
x 5 4,5
Perímetro do trapézio:
P 5 4,5 1 6,5 1 10,5 1 4
P 5 25,5
14. Alternativa c.
 AEC  ADB
EC
AE
DB
AD
t
t
5
2
2
5
2
2
500 100
400 100
5
2
21 7
21
4
3
14
21
21 − t 5 10,5
t 5 21 − 10,5
t 5 10,5
15. Alternativa e.
Seja x o lado do paralelogramo.
DE 5 36 − x e como DF 5 8 cm,
CF 5 10 cm
B
18
x
x
8
10
1
2
36 2 x
C
F
A D E
BCF  FDE, pois BC // DE e
F F(o.p.v.)
1 2 BC
CF
DE
5
FD
x
x
36
5 2
10
8
8x 5 360 − 10x
18x 5 360
x 5 20
Logo, AD 5 20 cm.
16. Alternativa a.
20
25
10
r
45
r
20 5
10
10 45
20
5
?
r
r 5 22,5 R r 5 22,5 cm

430
Estudando as relações trigonométricas
no triângulo retângulo
• Pra pensar, sem se cansar: Quantos
ângulos retos há no triângulo retângulo?
Num triângulo retângulo, há um ângulo
reto e outros dois ângulos, que juntos
devem somar 908, já que a soma dos
ângulos internos de um triângulo é sempre
1808.
49 – O teorema de Pitágoras
1. A1 5 52 5 25
2. A2 5 42 5 16
3. A3 5 32 5 9
4. A1 5 A2 1 A3, pois 25 5 16 1 9.
5. Sim.
1.
a) x2 5 212 1 282
x2 5 441 1 784
x2 5 1 225
x 5 35
b) 252 5 x2 1 242
x2 5 625 2 576
x2 5 49
x 5 7
c) 112 5 x2 1 52
x2 5 121 2 25
x2 5 96
x2 5 25 ? 3
x 5 4 6
d)
x
x
x
x
x
2
( ) ( )
2 2
5 1
5 1
5
5 5 ?
5
2
2
10 10
10 10
20
20 2 2
5
2 5
( ) 2
5 21x2
x2 5 29 2 25
e) 29 5
x2 5 4
x 5 2
f) x2 5 242 1 322
x2 5 576 1 1 024
x2 5 1 600
x 5 1600
x 5 40
2. O maior lado é 26, então fazemos:
262 5 102 1 242
676 5 100 1 576
676 5 676
Como 262 5 102 1 242, podemos dizer que o
triângulo é retângulo.
3.
a) Aplicando o teorema de Pitágoras,
temos:
6 2
36 2 2
( ) 2
5 1
? 5
5
5
36
6
2 2
2
2
x x
x
x
x
b) Como AB BC, um lado do retângulo
mede 6; e se F é ponto médio de BE,
então BE 5 12.
Conhecendo esses valores, calculamos
a área do retângulo BCDE:
A 5 b ? h
A 5 12 ? 6
A 5 72
4. Os triângulos QMR, QRP e PRN são
retângulos; logo, aplicando o teorema
de Pitágoras, determinamos os valores
solicitados.
a) No triângulo QMR, temos:
a2 5 22 1 42
a2 5 4 1 16
a2 5 20
a5 20
a52 5
b) No triângulo PRN, temos:
b2 5 82 1 42
b2 5 64 1 16

431
b2 5 80
b
b
b
80
2 5
4 5
5
5 4
?
5
c) No triângulo QRP, temos:
c2 5 a2 1 b2
c
2
c
c
c
c
c
( ) ( )
2 2
2
2
2
2 5 4 5
4 5 16 5
20 80
100
100
1
5 1
5 ? 1 ?
5 1
5
5
5
0
d) O perímetro do trapézio MNPQ é dado
por:
P 5 2 1 4 1 4 1 8 1 c
P 5 18 1 10
P 5 28
5. Aplicando o teorema de Pitágoras, temos:
Q1 5 Q2 1 Q3
900 5 Q2 1 324
Q2 5 576 unidades
6. Seja x o lado BD do triângulo BCD.
Aplicando o teorema de Pitágoras no
triângulo ADB, temos:
x2 5 92 1 122
x2 5 81 1 144
x2 5 225
x 5 225
x 5 15
Ou seja, BD 5 15.
a) Calculamos, então, o perímetro do
triângulo BCD:
P 5 3 ? 15
P 5 45
b) Calculamos o perímetro do
quadrilátero ABCD:
P 5 9 1 12 1 15 1 15
P 5 51
7.
a) O triângulo ABC é retângulo em C;
logo, aplicando o teorema de Pitágoras,
encontramos a medida de AB:
x2 5 122 1 162
x2 5 144 1 256
x2 5 400
x 5 400
x 5 20 R AB 5 20
b) Como AB 5 BD, DC 5 20 1 16 5 36.
O triângulo ADC é retângulo em C,
de catetos 12 e 36; logo, aplicando o
teorema de Pitágoras, encontramos a
hipotenusa:
y2 5 362 1 122
y2 51 296 1 144
y2 5 1 440
y
5
1440
y
5 2 5 ? 3 2
?
5
y
5
12 10
Logo, AD512 10 .
8. O triângulo PRQ é retângulo em P;
logo, aplicando o teorema de Pitágoras,
determinamos x:
3 41 10 12
( ) 2
5( 1x)21 2
369 5 100 1 20x 1 x2 1 144
125 2 20x 2 x2 5 0
x2 1 20x 2 125 5 0
Δ5b224ac
D 5 400 2 4 ? 1 ? (2125)
D 5 900
b
x
a
x
x
5
2 6
5
2 6
?
5
2 6 5
52
Δ
2
20 900
2 1
20 30
2
5
25
→
’
” (Nãoconvém.)

x
b
a
x
x
5
2 6
5
2 6
?
5
2 6 5
52
Δ
2
20 900
2 1
20 30
2
5
25
→
’
” (Nãoconvém.)

O triângulo SQP é retângulo em P;
portanto, aplicando o teorema de
Pitágoras, determinamos y:
y2 5 x2 1 122
y2 5 52 1 144
y2 5 169
y 5 13
Logo, x 5 5 e y 5 13.
9. O triângulo EFG é retângulo em G; logo,
aplicando o teorema de Pitágoras, temos:
102 5 62 1 x2
x2 5 100 2 36
x2 5 64
x 5 8
a) O perímetro do quadrado ABGF é:
4 ? x 5 4 ? 8 5 32.
b) O lado do quadrado BCDE é:
6 1 x 5 6 1 8 5 14.
Então, o perímetro do quadrado BCDE
é: 4 ? 14 5 56.
c) O perímetro do polígono ACDEF é dado
por:

432
P 5 x 1 x 1 y 1 y 1 y 1 10
P 5 16 1 42 1 10
P 5 68
10. Fazendo um esquema da situação, temos:
A
arte
de x
160 m
Editoria Ilustrações: B
C
120 m
x2 5 1602 1 1202
x2 5 25 600 1 14 400
x2 5 40 000
x
5
40000
x
5
200
Logo, a pessoa andará 200 m, se for pelo
terreno baldio.
11.
A
30
h
25
B C
D
11 x
O triângulo ADC é retângulo em C.
Aplicando o teorema de Pitágoras, temos:
x2 1 h2 5 252 (I)
O triângulo ABC é retângulo em C.
302 5 (11 1 x)2 1 h2
900 5 121 1 22x 1 x2 1 h2 (II)
900 5 121 1 22x 1 252
900 2 121 2 625 5 22x
154 5 22x
x 5 7
Substituindo x 5 7 em (I), temos:
x2 1 h2 5 252
72 1 h2 5 625
h2 5 576
h 5 24
Então, x 5 10 cm. 12. Se a base BC mede 48 cm, HC mede
24 cm, e o triângulo AHC é retângulo
em H. Aplicando o teorema de Pitágoras,
temos:
AC2 5 h2 1 HC2
402 5 h2 1 242
h2 5 1 600 2 576
h2 5 1 024
h 5 32
Logo, h 5 32 cm.
13. O triângulo ABC é retângulo em C.
d2 5 272 1 362
d2 5 729 1 1 296
d2 5 2 025
d5 2025
d 5 45 R d 5 45 cm
14.
a)
PM
MQ
80
2
5 5
40
18
2
5 5
9
Aplicando o teorema de Pitágoras,
temos:
x2 5 402 1 92
x2 5 1 600 1 81
x2 5 1 681
x 5 41 R x 5 41 cm
b) O perímetro do losango é:
4 ? 41 cm 5 164 cm.
15.
A D
C
x
y
E
B
6
7
15
a) AB 5 15 cm e AE 5 7 cm; logo,
EB 5 8 cm e EC 5 6 cm.
O triângulo BCE é retângulo em E.
temos:
x2 5 62 1 82
x2 5 36 1 64
x
x
x
2 100
10
10
5
5
52
→

’
” (Nãoconvém.)

433
b) O triângulo ABD é retângulo. Aplicando
o teorema de Pitágoras, temos:
y2 5 62 1 152
y2 5 36 1 225
y2 5 261
y
5
261
y
5 3 2
?
29
y 5 3 29 y 5
329
cm
→
16.
12 m
16 m
x
x2 5 122 1 162
x2 5 144 1 256
x2 5 400
x 5 20
O terceiro lado do terreno mede 20 m.
17.
4 m
3 m
x
x2 5 32 1 42
x2 5 9 1 16
x2 5 25
x 5 5
A trave de madeira mede 5 m.
18.
30
x
C
10 3
A B
x2 530 2
1(10 3 )
x2 5 900 1 300
x2 5 1 200
x
x
x
2
1200
2 3 5
20 3
5
5 ? ?
5
4 2
Logo, AC 5 20 3 km.
19.
20
D
A
B
C
20
x
y
12
O triângulo ABD é retângulo em A.
202 5 x2 1 122
x2 5 400 2 144
x2 5 256
x 5 16 R x 5 16 m
O triângulo BCD é retângulo em D.
y2 5 202 1 202
y2 5 800
y
5
800
y
5 2 5 ?
5
2
y 5 202 y 5
20 2
m
→
O perímetro desse terreno é dado por:
P 5 x 1 12 1 y 1 20
P 5 16 1 12 1 20 ? 1,4 1 20
P 5 76 R P 5 76 m
20.
V
e
f
 

e V t
e V t
5
5 ?
5 1
1
→ ( 7
)
2 V t
(V 7)t
13
Depois de 1 hora, t 5 1.
132 5 (V 1 7)2 1 V2
169 5 V2 1 14V 1 49 1 V2
2V2 1 14V 2 120 5 0
V2 1 7V 2 60 5 0
V
V
V
V
5
2 6 2 2
5
2 6 5
52
7 7 4 60
2
7 289
2
5
12
2 ( )
’
”
→
(Não convém.)


434
Se V 5 5 milhas/hora, então:
V 1 7 5 12 milhas/hora.
Logo, as velocidades são: 5 milhas/hora e
12 milhas/hora.
x
1 m
10 m
6 m
102 5 x2 1 62
x2 5 100 2 36
x2 5 64
x 5 8 R x 5 8 m
Em relação ao chão, a altura desse
apartamento é de 8 m 1 1 m 5 9 m.
30 cm
x
30 cm
90 cm
5 24 cm
x2 5 902 1 1202
x2 5 8 100 1 14 400
x2 5 22 500
x 5 150
O comprimento todo do corrimão é dado
por:
30 1 150 1 30 5 210 R 210 cm 5 2,10 m
Logo, o corrimão mede 2,10 m.
x
8 m
6 m
x2 5 62 1 82
x2 5 36 1 64
x2 5 100
x 5 10
São necessários 10 m de fio.
x 9 x
8 m
(9 2 x )2 5 x2 1 32
81 2 18x 1 x2 5 x2 1 9
18x 5 72
x 5 4
A altura do tronco que restou em pé é de 4 m.
A matemática Chinesa e Bhaskara, página 254.
Fazendo um esquema da situação, temos:
16
x
32 2 x
(32 2 x )2 5 x2 1 162
1 024 2 64x 1 x2 5 x2 1 256
64x 5 768
x 5 12
O bambu foi quebrado a 12 cúbitos do
chão.
y2 5 x2 1 x2
y2 5 2x2
y5x 2
x
y
x
x
x
y
x
x
x
y
5 ?
5
5
2
2
2
2
2
2

435
1.
a) d 5  2 5 4 2 R d 5 4 2 cm
b)
arte
de Editoria d

Ilustrações:
temos:
d2 5 2 1 2
d2 5 22
d 5  2 R d 5  2 cm R d 5 4 2 cm
2.
a) , 3
12 3
h5 5 5 6 3 → h5 6 3
cm
2
2
b)
h
12
6
temos:
122 5 h2 1 62
h2 5 144 2 36
h2 5 108
h
5
108
h
5 2 2 ?
3
3
h 5 6 3 →
h 5
6 3
cm
3.
11 2 x
x
( ) 2
11 2
5x21x2
242 5 2x2
x 5 11
Perímetro 5 4 ? 11 5 44
A medida do lado é 11 cm, e o perímetro
é 44 cm.
Área 5 200 R Área 5 200 cm2 4.
h
cm
5
,
3
2
,
5
5 ?
3 3
3 2 3 3
2 3 3
5
?
3
2
3
6 → 6
5 5
,
,
, ,
Perímetro 5 3 ? 6 cm 5 18 cm
5.
A 5 2 5 225 R 2 5 225 cm2
 5 225
 5 15 R 15 cm
d
5
, 2
d
5
15 2
d 5 21,15 R d 5 21,15 cm
6. A
h
5
, ?
2
 5 4 cm
h
5
→
→
h 5 5 h 5
cm
A 5
A cm
?
5 5
, 3
2
4 3
2
2 3 2 3
4 2 3
2
4 3 4 3 2
A 5 6,92 cm2
7.
P
Q A
D
B
x
10
C
10
a) x2 5 102 1 102
x2 5 200
x5 200 5 2 ?5 510 2 3 2
, 510 2 cm
b)
Perímetro54 ?10 2 540 2 →Perímetro540 2 cm
Perímetro54 ?10 2 540 2 →Perímetro540 2 cm
c)
Área
Área
Área
,2
5
5
5 ?
( )
2
10 2
100 2

436
8. t 5 dq
dq5 2 56 2 →6 2 cm
q 5 dR 56 2 cm
t q t  3
ht t
5 2
?
h t5 5 h cm t
5
6 2 3
2
3 6 → 3 6
arte
de Editoria 1
Ilustrações: 1
BC 5 54 e BD 5 48
CD 5 54 2 48 5 6
Com esses valores, podemos calcular h:
h2 5 m ? n
h2 5 6 ? 48
h2 5 288
h 5 288
2 5 ?
3 2 h 5 h 5 12 2 1
1 1
1
1
1
2
4 2 3
5
6
7
8
1.
4 3 2 1 0 1 2 3 4
2 8
2. 8 23 2 2 5 5
Sim; 8 é o dobro de 2 .
3.
12 22 3 2 3 5 ? 5
Logo, para determinar 12 na reta,
basta dobrar o valor de 3 e, usando o
compasso, transportá-lo para a direita a
partir da origem.
50 – As relações métricas no
triângulo retângulo
1.
C
A
H
B
x
y
z
p
r
s
x2 5 y2 1 z2
z2 5 x ? s
y2 5 x ? r
p2 5 r ? s
x 5 r 1 s
px 5 y ? z
2.
t
x y
t2 5 x ? y
3.
m n
8
A
t
C B
16
b2 5 a ? m
82 5 16 ? m
16m 5 64
m 5 4
m 1 n 5 16
n 5 16 2 4 5 12
Logo, m 5 4 e n 5 12.
4.
C
h
54
48
b
A B

437
Agora calculamos b:
2
b
2 5 6 2
1
( 12 2
)
b
2
5 36 1 144 ?
2
b
2
5
324
b
5
324
b
5
18
5.
a
n 9
15
h2 5 m ? n
152 5 9 ? n
n5 5
225
9
25
a 5 n 1 9
a 5 25 1 9 5 34
Logo, n 5 25 e a 5 34.
6.
36
h
64
c
A
b
B a C
h2 5 m ? n
h2 5 36 ? 64
h 5 6 ? 8
h 5 48 R h 5 48 mm
a 5 36 1 64
a 5 100 R a 5 100 mm
c2 5 a ? n
c2 5 100 ? 36
c2 5 3 600
c 5 3600
c 5 60 R c 5 60 mm
b2 5 a ? m
b2 5 100 ? 64
b2 5 6 400
b5 6400
b 5 80 R b 5 80 mm
Portanto, a 5 100 mm; b 5 80 mm;
c 5 60 mm e h 5 48 mm.
7.
A
7 24
B C
a
h
a) a2 5 72 1 242
a2 5 49 1 576
a2 5 625
a 5 625
a 5 25 R a 5 25 cm
b) ah 5 bc
25 ? h 5 7 ? 24
h 5 6,72 R h 5 6,72 cm
8.
10 b
5
A
B C
a
h
a) c2 5 a ? n
102 5 a ? 5
a 5 20 R a 5 20 cm
b) a2 5 b2 1 102
202 5 b2 1 102
b2 5 400 2 100
b2 5 300
b
5
300
b
5 22 ? 52 ?
3
b 5 10 3 R b 5 10 3 cm
c) a ? h 5 b ? c
20 ? 5 10 3 ?
10
100 3
20
5
h
h
h55 3 →h55 3 cm
9. Se BD 5 9 cm e raio 5 8 cm, então
OD 5 1 cm e DC 5 7 cm.
A
x
8 1 7
9
B C
O
h
D

438
h2 5 m ? n
h2 5 9 ? 7
h 5 63
x2 5 h2 1 92
x2 5 63 1 81
x 5 144
x 5 12 R x 5 12 cm
10. A
arte
de y z
x
Editoria 4 9
B C
Ilustrações: H O
x2 5 4 ? 9
x 5 36
x 5 6 R x 5 6 cm
y2 5 x2 1 42
y2 5 62 1 42
y2 5 36 1 16
y
5
52
y
5 2 2
?
13
y 5 2 13 →
y 5
213
cm
z2 5 x2 1 92
z2 5 36 1 81
z
5
117
z
5 32 ?
13
z53 13 →z53 13 cm
11.
A
80
x
b
m n
B C
100
c2 5 a ? n
802 5 100 ? m
m 5 64
Se m 5 64 km, então n 5 36 km. Daí, temos:
x2 5 m ? n
x2 5 36 ? 64
x 5 6 ? 8
x 5 48 R x 5 48 km
Logo, a estrada terá 48 km de
Logo, a hipotenusa do triângulo ABC mede
comprimento.
25 cm. 12.
36
64
y
h
x
h2 5 m ? n
h2 5 36 ? 64
h 5 6 ? 8
h 5 48 R h 5 48 cm
x2 5 642 1 h2
x2 5 4 096 1 2 304
x 5 6400
x 5 80 R x 5 80 cm
y2 5 362 1 h2
y2 5 1 296 1 2 304
y 5 3600
y 5 60 R y 5 60 cm
Agora, calculamos o perímetro do
retângulo:
P 5 2x 1 2y
P52?8012?60
P 5 160 1 120
P 5 280 R P 5 280 cm
13.
A
b
B C
H
15
16
b2 5 am
b2 5 a ? 16
a2 5 b2 1 152
a2 5 (16 ? a) 1 225
a2 2 16a 2 225 5 0
a5
( 16 ) 256 4 1 ( 225
)
2 2 6 2 ? ? 2
2 ?
1
a
a
a
5
6
5
6 5
52
16 1156
2
16 34
2
25
9
→

’
” (Nãoconvém.)
a
a
a
5
6
5
6 5
52
16 1156
2
16 34
2
25
9
→

’
” (Nãoconvém.)

439
a) A torre possui 6 triângulos isósceles de
lados x e 2.
1 m 1 m
x
2 m
1 m
x2 5 12 1 12
x 5 2 m
Perímetro de um triângulo:
P 5 2 1 2x 5
5 2 1 2 ? 1,41  2 1 2,82  4,82
Como são 6 faces, temos:
P 5 6 ? 4,82m  28,92 m
b) Cada quadrado tem aproximadamente
m  
1,66 m 10
6
 
de lado.
Cada uma das diagonais mede:
d5 2 51,66? 2 2,34→d2,34m
Como são 6 quadrados, temos 12
diagonais:
2,34 ? 12 528,08 R 28,08 m
Somando os lados dos quadrados,
temos:
20 1 7 ? 1,66 1 6 ? 1,66 5 41,58 R 41,58 m
Temos mais duas diagonais nos
quadrados do extremo, logo:
2 ? 2,34 5 4,68 R 4,68 m
Total de ripas:
28,08 1 41,58 1 4,68 5 74,34
Logo, foram usados 74,34 m de ripa.
Supondo que cada metro de ripa tenha
custado R$ 20,00, o construtor teria
gastado:
74,34 ? 20 5 1 486,80 R R$ 1 486,80
1. Alternativa a.
II 5 I 1 III
100 5 36 1 III
III 5 64
2. Alternativa d.
y2 5 h2 1 62 (I)
72 5 h2 1 x2 (II)
De (I), temos: h2 5 y2 2 62.
Substituindo h2 5 y2 2 62 em (II), temos:
72 5 (y2 2 62) 1 x2
49 2 36 2 5y 2 1x
x2 1 y2 5 49 1 36
x2 1 y2 5 85
3. Alternativa b.
A B
E F
C O D
16 5
4
5 5
4 5 →4 5 cm

2
Como COOD5 5 cm
2 5 .
triângulo ODB, temos:
r2 5 OD2 1 DB2
r
( ) ( )
r
r
r
r
r
2
2 2
2
2
2 5 4 5
20 80
100
100
10
10
5 1
5 1
5
5
5
52
→
’
” (Não convém.)
 Logo, r 5 10.
4. Alternativa c.
24 cm
7 cm
x
2
x
2
x
2
x2 5 72 1 242
x2 5 49 1 576
x2 5 625
x
x
x
2 625
25
25
5
5
52
→

’
” (Nãoconvém.)
Logo, x 5 25 cm.
A medida da mediana é dada por:
x
25
5 512,5R 12,5 cm
2
2
5. Alternativa c.
AC2 5 AB2 2 BC2
AC2 5 502 2 402
AC2 5 2 500 2 1 600
AC2 5 900
AC 5 30

2 →
21 4 1 108 6
2 1
440
6. Alternativa a.
O h é perpendicular à corda AB; logo, H é
ponto médio da corda AB.
O triângulo OHB é retângulo em H.
HB
16
2
cm
5 5 8 cmeOH5 6
cm
r2 5 OH2 1 HB2
r2 5 62 1 82
r2 5 36 1 64
r2 5 100
r
r
r
5
5
52
100
10
10
→

’
” (Nãoconvém.)
Logo r 5 10, e o diâmetro mede:
d
5 2 ?
10
d
5
20
7. Alternativa b.
AB2 1 BC2 5 AC2
AB2 5 AC2 2 BC2
AB2 5 10,252 2 2,252
AB2 5 105,0625 2 5,0625
AB2 5 100
AB
AB
AB
5
5
52
100
10
10
→

’
” (Nãoconvém.)
AB 5 10 R AB 5 10 m
8. Alternativa d.
x2 2 21x 1 108 5 0
x 5
( 21 ) 21 2 4 1 108 6
→
2 2 6 2 ? ?
?
5
6 2
5
6
5
2 1
21 441 432
2
21 9
2
21 3
2

x
x
’
”
12
9
5
5
2 ? ?
?
5
6 2
5
6
5
21 441 432
2
21 9
2
21 3
2

x
x
’
”
12
9
5
5
5
6
5
6
432
21 9
2
21 3
2
→

x
x
’
”
12
9
5
5
arte
de Editoria 9 12
Ilustrações: h
triângulo CDB, temos:
BD2 5 122 1 162
x
BD2 5 144 1 256
BD2 5 400
x2 5 92 1 122
BD2 5 400
x2 5 81 1 144
BD 5 20
x2 5 225
15
triângulo ABD, temos:
x 5 225
→
15
AD2 5 BD2 1 AB2
AD2 5 202 1 152 
x
x
´
´´
5
52 (Não convém.)
Pelas relações métricas no triângulo
retângulo, temos:
a ? h 5 b ? c
15 ? h 5 9 ? 12
h 5 7,2
9. Alternativa c.
Se ABCD é um paralelogramo,
AD 5 BC 5 15 cm.
No triângulo retângulo KBC denominamos
x o lado KB.
CD 5 11 1 x
A 11 cm
12 cm 15 cm
16 cm
K x B
C
M
D
triângulo KBC, temos:
152 5 x2 1 122
x2 5 225 2 144
x2 5 81
x
x
x
5
5
52
81
9
9
→

’
” (Nãoconvém.)
Logo, AB 5 11 1 9 5 20 cm e CD 5 20 cm.
triângulo CDM, temos:
CD2 5 CM2 1 DM2
202 5 CM2 1 162
CM2 5 400 2 256
CM2 5 144
CM 5 144
CM 5 12 R CM 5 12 cm
O perímetro do quadrilátero ABMD é dado
por:
P 5 16 1 15 1 20 1 15 1 12
P 5 78 R P 5 78 cm
10. Alternativa a.

441
AD2 5 400 1 225
AD2 5 625
AD 5 625
AD 5 25
11. Alternativa c.
x y
24 cm
a
retângulo, temos:
a ? h 5 b ? c
a ? 24 5 x ? y (I)
x2 1 y2 5 a2 (II)
É dado que x 1 y 5 70, elevando os dois
membros ao quadrado, temos:
(x 1 y)2 5 702
x2 1 2 ? x ? y 1 y2 5 4 900 (III)
Substituindo (I) e (II) em (III), temos:
a2 1 2 ? (a ? 24) 5 4 900
a2 1 48 ? a 2 4 900 5 0
a
2 ( ) a
’
5
48 48 4 1 4900 2 6
2 6 2 ? ? 2
?
5
2 6
5
2 1
48 21904
2
48 148
2
→ 5
50
a” 52
98(Não convém.)

( ) a
’
4 1 4900 2 6
2 1
2 ? ? 2
?
5
2 6
5
48 21904
2
48 148
2
→ 5
50
a” 52
98(Não convém.)

a
2 6
5
2 6
48 21904
2
48 148
2
’
→ 5
50
a” 52
98(Não convém.)

Calculamos o perímetro do triângulo:
P 5 a 1 (x 1 y)
P 5 50 1 70
P 5 120 R P 5 120 cm
12. Alternativa c.
Fazendo um esquema da situação, temos:
x
2 m
1,5 m
x2 5 1,52 1 22
x2 5 2,25 1 4
x2 5 6,25
x5 6,25
x 5 2,5 R x 5 2,5 m
13. Alternativa e.
Fazendo um esquema do trajeto, temos:
300 km
6 cm
y
200 km
800 km
300 km
12 cm
A
C
D
x
B
E
triângulo ACD, temos:
x2 5 2002 1 8002
x2 5 40 000 1 640 000
x2 5 680 000
x 5 680000
x 5 824,62 R x 5 824,62 km
triângulo CBE, temos:
y2 5 3002 1 3002
y2 5 90 000 1 90 000
y2 5 180 000
y 5 180000
y 5 424,26 R y 5 424,26 km
x 1 y 5 824,62 1 424,26
x 1 y 5 1 248,88 R x 1 y 5 1 248,88 km
O valor mais próximo é 1 250 km.
14. Alternativa a.
CB2 5 AB2 1 AC2
102 5 AB2 1 82
AB2 5 100 2 64
AB2 5 36
AB 5 6 R AB 5 6 cm
retângulo, temos:
a ? h 5 b ? c
10 ? h 5 6 ? 8
h 5 4,8 R h 5 4,8 cm

442
Estudando as relações trigonométricas
nos triângulos
51 – Relações trigonométricas no
triângulo retângulo
a) São iguais.
b) São iguais.
c) São iguais.
1.
sen
medida do cateto oposto a
medida da hipotenusa
se
β β
5
n
β
5 5 5
β medida do cateto adjacentea
β
5
5
3
2 23
3
0 74
,
,
cos
cos β 5 5
,
tg
β
medida do cate
5
2
3
0 66
to oposto a
medida do cateto adjacentea
tg
β
β
5
2
β5 5
2,23
2
51,11
sen  5 0,74; cos  5 0,66 e tg  5 1,11.
2.
sen
medida da hipotenu
45
45
º 5
°
sa
sen
medida do cateto adj
45
2 2
2
2
2
2
45
º
cos º
5 5  5
5




acente a
45
45




2 2
2
2
º
cos º5 5  5
2
2
45
45
tg
medida do cateto
º
º
5 adjacentea
tg


5 5
sen etg
45
45 1
45
2
2
45
2
2
4
º
º
º ;cos º
5 5
5º51.
3.
sen
medida da hipotenu
45
35
º
º
5 sa
sen
medida do cateto adjacen
35
3 4
6
0 56
35
º
,
,
cos º
5 5
5
te a
me
35
35
5
6
0 83
º
cos º 5 5
,
dida do cateto oposto a
35º
sen
medida da hipotenu
45
35
º
º
5 sa
sen
medida do cateto adjacen
35
3 4
6
0 56
35
º
,
,
cos º
5 5
5
te a
tg
me
35
35
5
6
0 83
35
º
cos º ,
º
5 5
5
dida do cateto oposto a
35º
35
35
3 4
5
0 68
º
º
,
tg 5 5 ,
sen 358 5 0,56; cos 358 5 0,83 e
tg 358 5 0,68.
4.
h5
 3
2
No triângulo AHC, temos:
sen
medida da hipotenu
60
60
º
º
5 sa
sen
medida do cateto ad
60
3
2 3
2
1 3
2
60
º
cos º
5 5  5
5




jacentea
60

60 2
2
1
º
cos º5 5  5



1
2
60
60
tg
medida do cateto
º
º
5 adjacentea
tg
sen
60
60
3
2
2
3
2
2
3
5 5  5
60
3
2
º
º
º 5
;cos




60
1
2
º5 e tg 60º5 3 .
5.
sen
medida da hipotenu
30
30
º
º
5 sa
sen
30 2
2
1 1
2
medida do cateto adja
30
º
cos º
5 5  5
5




centea
30
30
3
2 3
2
1
º

cos º5 5  5



3
2

443
tg
30
30
º
º
5 acente a
tg
sen
30
30 2
5 5 ? 5 ? 5
3
2
2
2
3
1
3
3
3
3
3
30
1
2
º
º
º
5
,
,
,
,
3
3
5 e tg 2
5
3 ;cos 30º 30
º .
6.
sen
se
β β
5
n
β
5 5
β medida do cateto adjacentea
β
medida
5
6
10
0,6
cos
da hipotenusa
cos β 5 5
,
tg
β
medida do cateto opos
5
8
10
0 8
to a
tg
β
β
6
8
β5 5
0,75
sen  5 0,6; cos  5 0,8 e tg  5 0,75.
1.
a)
sen
medida da hipotenu
65
65
º
º
5 sa
sen
x
x
x
º
65
9
0 91
9
8 19
,
,
5
5
5
cos º
º
65
65
5
y
5
y
cos º
,
65
9
0 42
9
5
y 5 3,78
Logo, x 5 8,19 e y 5 3,78.
b)
sen
medida da hipotenu
30
30
º
º
5 sa
sen
a
a
a
30
10
1
2
10
20
30
º
cos º
5
5
5
5
acente a
c
a
c
c
30
30
3
2 20
1
º
cos º5
5
5 0 3
a
a
1
2
10
5
5
20
30
cos º
5
acente a
c
a
c
c
30
30
3
2 20
1
º
cos º5
5
5 0 3
Assim,a520 e c510 3 .
2.
sen
medida da hipotenu
40
40
º
º
5 sa
sen
x
x
x
medida do cateto a
40
7
0 64
7
º
4 48
40
,
,
cos º
5
5
5
5
djacente a
y
y
40
40
7
0 77
7
º
cos º
,
5
5
y 5 5,39
Agora, calculamos x 1 y:
x 1 y 5 4,48 1 5,39
x 1 y 5 9,87
3.
sen
medida da hipotenu
60
60
º
º
5 sa
a
3
2
12 3
5
a 5 24
cos º
º
60
60
5
1 b
2
b
→ 1
5 a
2 5
24 b 5 12
Agora calculamos a razão enunciada:
b
12
a
5
24
b
1
a
5
2
4.
x
y
50 cm
37o
Editoria de arte

444
sen
medida da hipotenu
37
37
º
º
5 sa
x
0 60
, 5
50
x 5 30 R x 5 30 cm
cos º
º
37
37
5
y
0 , 80
5
50
y 5 40 R y 5 40 cm
Logo, os catetos desse triângulo medem
30 cm e 40 cm.
5.
sen
se
α α
5
n
α
5 5
α medida do cateto adjacentea
α
medida
5
6
10
0,6
cos
da hipotenusa
cos α 5 5
,
tg
α
medida do cateto opos
5
8
10
0 8
to a
tg
α
α
6
8
α5 5
0,75
a)
cos sen
cos sen
, ,
, ,
α 1
α
α 2
α
5
1
2
5
0 8 0 6
0 8 0 6
7
b)
2
1 1
2 075
1 075 1 075
?
1 ? 2
5
?
1 ? 2
tg
tg tg
Faz
α
( α) ( α)
,
( , ) ( , )
3
4
, 5 , :
endo 0 75 temos
2 3
4
7
4
1
4
24
7
?
?
5
6.
sen
medida da hipotenu
18
18
º
º
5 sa
y
0 , 31
5
10
y 5 3,1 R y 5 3,1 cm
cos º
º
18
18
5
x
0 , 95
5
10
x 5 9,5 R x 5 9,5 cm
O perímetro do retângulo é dado por:
P 5 2x 1 2y
P 5 2 (3,1 1 9,5)
P 5 25,2
Logo, o perímetro do retângulo é 25,2 cm.
7.
a) No triângulo ABC, temos:
tg
x
x
º 5
30
300
3
3 5
300
x5100 3 →x5100 3 cm
b) No triângulo DCB, temos:
tg
x
y
y
60
3
º 5
100 3
5
y 5 100 R y 5 100 cm
c) AD 5 300 2 y
AD 5 300 2 100
AD 5 200 R AD 5 200 cm
8. ˆB
5 30°, ˆC
5 60°, pois o triângulo ABC é
retângulo em A.
O triângulo AHC é retângulo em H; logo:
sen
medida da hipotenu
60
60
º
º
5 sa
3 x
2 20 5
x 5 10 3 5 17,3
cos º
º
60
60
5
1 y
2 20 5
y 5 10
Assim, calculamos x 1 y:
x 1 y 5 17,3 1 10
x 1 y 5 27,3
9.
tg
x
x
2
2
( x
)
x
º 5
30
1
3
3
3
1
3
5
3 3 5 3 ? 2
1
3 5 3 3 1
3
x 5 3 1 1
x 5 1,73 1 1
x 5 2,73 R x 5 2,73 m

445
10. tg 60° 5 3
tg 60° 5
x
1,2
x
1 2
3
,
5 R x 5 1,2 ? 3 R x 5 1,2 ? 1,70
R x 5 2,04
A altura do muro é 2,04 m.
11.
sen
h
h
37
10
0 602
10
º
,
5
5
h 5 6,02
Logo, h 5 6,02 m.
12. Seja x a distância AB.
sen
medida da hipotenu
30
30
º
º
5 sa
x
1
2
120
5
x 5 240 R x 5 240 m
Arco 2 x 5 376,8 m 2 240 m 5 136,8 m
13. Fazendo um esquema, temos:
x
36°
40 m
30,4 m
tg
x
x
36
30 4
40
0 72
30 4
40
º
,
,
,
5
2
5
2
30,4 2 x 5 28,8
x 5 30,4 2 28,8
x 5 1,6 R x 5 1,6 m
14.
x
posto
casa
18 km
A supermercado
30°
B y C
sen
medida da hipotenu
30
30
º
º
5 sa
x
x x km
1
2 18
5 → 59→ 59
cos º
º
30
30
5
y
y y y km
3
2 18
5 → 59 3 → 59?1,7→ 515,3
Indo por AB e BC, Carolina percorre:
d 5 15,3 km 1 9 km 5 24,3 km
Indo por AC, Carolina percorre 18 km.
Logo, indo por AB e BC ela vai percorrer a
mais:
24,3 km 2 18 km 5 6,3 km
15.
a)
sen
3
3
º
º
5
0 05
30
, 5 x
x 5 600 R x 5 600 m
b)
t
d
v
5
600
240
2,5→ 2,5min
t 5 5 t 5
utos
16.
x
100 m
y
A
a
a
2
B C
â
â
1 5 2
90º
2â 1 â 5 180°
3â 5 180°
a
a 560 e
5
º 30º
2

446
O lado menor está oposto ao ângulo de 308.
sen
medida da hipotenu
30
30
º
º
5 sa
1 x
2 100 5
x 5 50 R x 5 50 m
17. Vamos determinar a altura do avião:
sen
medida do cateto ad
25
25
º
º
5 jacentea
h
25
0 47
2000
º
, 5
h 5 940 R h 5 940 m
Como o ponto D está a 600 m, fazemos:
x 5 940 m 2 600 m 5 340 m
18.
tg
28
28
º
º
5 acente a
h
28
0 53
12
º
, 5
h 5 6,36 R h 5 6,36 km
19.
30°
60°
y
B
C
F
D
x
18 km
30 km
3 km
No triângulo BCE, temos:
sen
medida da hipotenu
30
30
º
º
5 sa
x
1
2
18
5
x 5 36 R x 5 36 km
No triângulo ADF, temos:
sen
medida da hipotenu
60
60
º
º
5 sa
y
y
3
2
30
60
3
60
3
3
3
20 3 20 17 34
5
5 5 ? 5 5 ? , 5
d 5 36 1 3 1 34
d 5 73 R d 5 73 km
20. Fazendo um esquema do problema,
temos:
N
y x
60O
A B
1 200 m
a)
tg
60
60
º
º
5 acentea
x
x x
60
3
º
1200
1 200 3 1200 1 ,
73 2076 2076
5
5 5 ? 5 → 5 m
b)
cos º
º
60
60
5
y
1
2
1 200
5
y 5 2 400 R y 5 2 400 m
21.
sen
h
h
70
30
0 94
30
º
,
5
5
h 5 28,2 R h 5 28,2 m
Em relação ao solo, a escada pode
alcançar:
28,20 m 1 2 m 5 30,20 m
52 – Estudando as relações
trigonométricas em um
triângulo qualquer
1. Aplicando a lei dos senos, temos:
x
sen45º sen º
x
x
5 2
30
2
2
5 2
1
2
1
2
5 2
2
2
5
5
? 5 ?

447
x
sen45º sen º
x
x
5 2
30
2
2
5 2
1
2
1
2
5 2
2
2
5
5
? 5 ?
x 5 10
20
b a
sen30º 5 sen80º 5
sen70º Da primeira igualdade, temos:
20 sen 80
º
b
sen
b
5
?
5
?
30
20 0 98
0 5
º
,
,
b 5 39,2 R b 5 39,2 cm
Igualando a primeira com a terceira razão,
temos:
20
30 5
70
20 70
sen º sen º
sen º
sen 30
º
20 0 ,
94
0 ,
5
5
?
5
?
a
a
a
a 5 37,6 R a 5 37,6 cm
Logo, temos a 5 37,6 cm e b 5 39,2 cm.
3.
30°
16 cm
x
B
A
C
20 3 cm
Aplicando a lei dos cossenos, temos:
x
x
2 2
( ) 2
cos º
2
16 20 3 216 203 30
5 1 2 ? ?
256 1 200 2 16 20
5 1 2 ? ?
?? 3 ?
3
2
x2 5 1 200 1 256 2 960
x2 496
5
5 8
x5 496 5 24 ?31 54 31 →x54 31 cm
4. Aplicando a lei dos cossenos, temos:
c2 5 a2 1 b2 2 2 ? a ? b ? cos 458
c2 2
2
2
5 8 1( 6 2 ) 2 2 ? 8 ? 6 2
?
2 c2 5 64 1 72 2 96
c2 5 136 2 96
c2 5 40
c 5 40
c52 10 →c52 10 cm
ˆN
ˆN
52 5 82 1 72 2 2 ? 8 ? 7 ? cos 25 5 64 1 49 2 112 ? cos 112 cos 5 64 1 49 2 25
ˆN
112 cos ˆN
5 88
cos ˆ
cos ˆ
N
N
5
5
88
112
11
14
72 5 x2 1 52 2 2 ? x ? 5 ? cos ˆD
49 5 x2 1 25 2 2 ? x ? 5 ? 1
x2 2 2x 2 24 5 0 5
x
x
x
5
2 2 6 2 2 ? ?
5
6 5
52
2 2 4 1 24
2
2 10
2
6
4
2 ( ) ( ) →
’
” (Nãoconvém.)

x
x
x
5
2 2 6 2 2 ? ?
5
6 5
52
2 2 4 1 24
2
2 10
2
6
4
2 ( ) ( ) →
’
” (Nãoconvém.)

Logo, x 5 6.
x2 5 502 1 802 2 2 ? 50 ? 80 ? cos 60°
x2 5 2 500 1 6 400 2 2 ? 50 ? 80 ? 1
2
x2 5 8 900 2 4 000
x2 5 4 900
x 5 70 km
A distância é de 70 km.
12
30 5
8
45
12 45
30
12
2
2
1
2
12
2
2
sen sen
sen º
sen º
8
5
?
5
?
5 ?
x
x ??2512 2 512?1,4516,8→12
30 45
12 45
30
12
2
2
1
2
12
2
2
sen sen
sen º
sen º
8
5
?
5
?
5 ?
x
x ??2512 2 512?1,4516,8→x516,8 cm
Como 1 cm equivale a 0,1 km,
16,8 equivalem a:
x 5 16,8 ? 0,1 5 1,68 R 1,68 km
A distância entre as ilhas é de 1,68 km.
Editoria de arte

448
9. Fazendo um esquema do brinquedo,
temos:
A
2 m 2 m
B x
C
120°
x2 5 22 1 22 2 2 ? 2 ? 2 ? cos 120°
x2 4 4 8
 
1
2 5 1 2 ? 2
 
x2 5 8 1 4
x2 5 12
x 5 12
x 5 22 3 ?
x 5 2 3 5 2?1,7353,46→ x 5 3,46 m
A distância é 3,46 m.
10.
24 cm x
60°
C
A B
30 cm
x2 5 242 1 302 2 2 ? 24 ? 30 ? cos 608
x2 5 576 1 900 2 2 ? 24 ? 30 ? 1
2
x2 5 1 476 2 720
x2 5 756
x
x
x
x
756
2 3 21
6 21
6 458 27 48
5
5 2 ? 2
?
5
5 ? 5
, ,
BC 5 27,48 cm
11.
33°
x
5 km
12°
S
F
T
a) Aplicando a lei dos senos, temos:
x
5
12 33
5
0 208 0 545
sen º sen º
5 0545
0 208
13 1
, ,
,
,
,
5
5
5
?
5
x
x 0
5
x
12 33
5
0 208 0 545
sen º sen º
5 0545
0 208
13 1
, ,
,
,
,
5
5
5
?
5
x
x 0
A distância é 13,10 km.
b)
v
e
t
5
530minutos50,5
v5 5 v5
t h
13 10
0 5
26 20 26 20
,
,
, → , km/h
12.
30°
72°
78°
50 m
transformador
galpão
casa
y
x
Aplicando a lei dos senos, temos:
50
x y
sen 30º 5 sen 78º 5
sen 72º Usando as duas primeiras igualdades,
temos:
50
0 , 5 5
0 ,
98
49
0 5
98 98
5
,
5 5
x
x
x →x m
Usando a primeira e a última razão, temos:
50
30 5
72
50
0 5 0 95
sen º sen º
, ,
50 0 ,
95
0 ,
5
95 9
5
5
?
5 5
y
y
y
y →y 5m
Logo, x 5 98 m e y 5 95 m.
13. No triângulo ABO, temos:
tg
r
AB
r
5 → r
5
15
0 27
5
10 3
2 7 3
º
, ,

449
Sendo BC 5 x e aplicando a lei dos
cossenos no triângulo OBC, temos:
x2 5 r2 1 r2 2 2 ? r ? r ? cos 708
x2 5 2r2 2 2r2 ? cos 708
x2 5 2r2 (1 2 cos 708)
x2 52 ? (2,7 3 )2 ? (120,34)
x2 5 2 ? 21,8 ? 0,66
x2 5 28,8
x 5 5,36
1.
sen 30° 5
1
2
1
2 16
sen 30° 5
5
x
1
x
5
2 16
R 2x 5 16 R x 5 8
Eleva-se 8 m.
2.
1,80 m
1
B
C
2 D
A
20 m
30
No triângulo ACD, temos:
CD 5 8 2 1,80 5 6,2
tg ˆ ,
2 ,
6 2
20
5 50 31
De acordo com a tabela dada, 2ˆ 517°.
tg
( 1 ˆ ˆ ) 30
1
CD 30 2 1
6 ,
2
1 5 5
5
1 ,
81
20
20
De acordo com a tabela, (1ˆ 12ˆ) 5 618.
Logo, 561821785448.
3.
Altura total: 710 1 8 1 30 5 748 R 748 m
tg 30° 5
3
3
tg 30° 5
748
d
3
3
748
5 3 ?
d
→ d 5 3 ? 748
1,73d 5 2 244 R d 5
2244
1,73 R d . 1 297
A distância será de aproximadamente
1 297 m.
4.
540 km
360 km
N
x
R
F
30o
x2 5 3602 1 5402 2 2 ? 360 ? 540 ? cos 308
x2 5 129 600 1 291 600 2 2 ? 360 ? 540 ? 3
2
x2 5 421 200 2 194 400 3
x2 5 421 200 2 336 312
x2 5 84 888
x  291 R 291 km
A distância entre Natal e Recife é de,
aproximadamente, 291 km.
1. Alternativa d.
sen
medida da hipotenu
15
15
º
º
5 sa
x
0 26
, 5
10
x 5 2,6 R x 5 2,6 m
2. Alternativa b.
4 cm 5 cm
B C
6 cm
A

450
Num triângulo, ao maior lado, opõe-se
o maior ângulo; logo, o maior ângulo do
triângulo dado é o Â.
62 5 42 1 52 2 2 ? 4 ? 5 ? cos Â
36 5 16 1 25 2 40 cos Â
25 5 240 cos Â
cos Â 5 5
40
1
8 5
3. Alternativa a.
O triângulo ABD é retângulo em Â. Como
ˆB
5 458, ABD é isósceles; logo,
AD 5 2. Aplicando o teorema de Pitágoras,
temos:
DB2 5 22 1 22
DB2 5 8
DB52 2
No triângulo BCD, temos:
x
sen
5
x
x
y
y
cos º
y
y
º
30
2 2
1
2 2 2
2
30
2 2
3
2 2 2
2 2 3
2
3 2
5
5
5
5
5
?
5 ?
y 5 6
4. Alternativa c.
tg
m
º
53
? 5
5

50
1 32

50
 →
66 66
,
5 5
5. Alternativa e.
18
a b
sen 64º 5 sen 76º 5
sen 40º Usando as duas primeiras igualdades,
temos:
18
0 90 097
18 0 97
0 90
194 19 4
, ,
,
,
, ,
5
5
?
5 5
a
a →a cm
Usando a primeira e a última razão, temos:
18
0 90 064
18 0 64
0 90
128 12 8
, ,
,
,
, ,
5
5
?
5 5
b
b → b cm
Agora, calculamos a 1 b:
a 1 b 5 19,4 1 12,8 5 32,2 R 32,2 cm
6. Alternativa b.
2,50 m
60o
x
tg
60
60
º
º
5 acente a
x
x
60
3
2 50
2 50
3
1 47
º
,
,
,
5
5 5
A sombra mede 1,47 m.
7. Alternativa c.
Fazendo o esquema do exercício, temos:
h
12 m
30o
sen
medida da hipotenu
30
30
º
º
5 sa
1 h
2 12 5
h 5 6
A altura de cada andar é 6 m.

451
arte
de Editoria Ilustrações: 20°
h 5 1,5x (II) A
B
2 m
h
C
8. Alternativa a.
100
sen 45 º 5
sen 120
º 100
2
2
3
2
5
d
d
d5
?
5 ? 5 ? 5 5 ? 5
100
3
2
2
2
100 3
2
2
2
200 3
2 2
2
2
200 6
4
50 2,44 122→d5122m
100 3
5 ? 5 ? 5 5 ? 5
2
2
2
200 3
2 2
2
2
200 6
4
50 2,44 122→d5122m
5 ? 5
200 6
4
50 2,44 122→d5122m
9. Alternativa e.
A bissetriz divide o ângulo em dois ângulos
de 308; então, temos o triângulo:
O
2,8 cm P
30°
30°
x
sen
medida da hipotenu
30
30
º
º
5 sa
1 x
2 28 5 ,
x 5 1,4
10. Alternativa b.
11. Alternativa d.
O triângulo ABC está inscrito na
semicircunferência; logo, é retângulo em C,
e AB é o diâmetro da circunferência.
sen
medida da hipotenu
30
30
º
º
5 sa
d
1
2
12
5
d 5 24 R d 5 24 cm
Logo, r 5 24
2
R r 5 12 R r 5 12 cm.
12. Alternativa b.
d2 5 122 1 152 2 2 ? 12 ? 15 ? cos 608
d2 5 144 1 225 2 2 ?180 ? 1
d2 5 369 2 180 2
d2 5189
d  13,74 R d  13,74 milhas
13. Alternativa c.
sen
medida da hipotenu
20
20
º
º
5 sa
h
0 34
, 5
2
h 5 0,68 R h 5 0,68 m
14. Alternativa e.
tg
medida do cateto adjacen α α
5 te a
tg
h
d x
h
x
α
α 5
1
5
1
0 5
40
,
h 5 0,5(40 1 x)
h 5 20 1 0,5x (I)
tg
medida do cateto adjacen β β
5 te a
tg
h
x
β
β 5
1,55
h
x
B
6 cm 6 cm
A
x C
6 cm 6 cm
D
120°
Aplicando a lei dos cossenos no triângulo
ABD, temos:
x2 5 62 1 62 2 2 ? 6 ? 6 ? cos 1208
x2 5 36 1 36 2 2 ? 36 ? 2
1
2
 
 
x2 5 72 1 36
x5 108 5 22 ?33 56 3 →x56 3 cm

452
Igualando (I) e (II), temos:
20 1 0,5x 5 1,5x
x 5 20
Substituindo x 5 20 em (I), temos:
h 5 20 1 0,5x
h 5 20 1 0,5 ? 20
h 5 30
Como x 5 20 cm e h 5 30 cm, temos:
h 1 x 5 20 1 30
h 1 x 5 50 R h 1 x 5 50 cm
15. Alternativa c.
No triângulo retângulo CDE, temos:
tg
30
30
º
º
5 acente a
60
CE
30
3
3
180
3
3
3
º
CE CE m
60 3 102 102
5
5 ? 5 ? 5 → 5
ABDE é um quadrado de área:
A5 602
q A5 3 600
q Área do triângulo CDE:
60 ?
102
At 5
5
2
3 060
Área total do terreno:
A 5 Aq 1 At
A 5 3 600 1 3 060
A 5 6 660
Logo, o terreno tem 6 660 m2.
16. Alternativa d.
Se o móvel caminha a uma velocidade
constante de 50 km/h, em 3 horas,
caminhou 150 km.
30°
C
x
A B
sen
medida da hipotenu
30
30
º
º
5 sa
1 x
2 150 5
x 5 75
Logo, o móvel se encontra a 75 km da
semirreta.
17. Alternativa a.
10 km
A B
30°
60°
P x D d C
No triângulo PAD, temos:
tg
60
60
º
º
5 acente a 60º
3
10
10
3
3
5
5
x
x (I)
tg
30
30
º
º
5 acente a
x d
30
3
3
10
º
5
1
305 3 ? (x1d) (II)
30 3 10
3
3

5 1
 
30 5 10 1
3
20
3
3
3
5 ?
20 3
3
5
d
d
d
d km

 
18. Alternativa e.
Seja x o lado procurado.
72 5 x2 1 32 2 2 ? 3 ? x ? cos 608
49 5 x2 1 9 2 6 ? x ? 1
x2 2 3x 2 40 5 0 2
x
x
x
5
6 2 ? ? 2
?
5
6 5
52
3 9 4 1 40
2 1
3 13
2
8
5
( ) ’»
”
→
(Não convém.)

x
x
x
5
6 2 ? ? 2
?
5
6 5
52
3 9 4 1 40
2 1
3 13
2
8
5
( ) ’»
”
→
(Não convém.)

Logo, x 5 8 cm.
19. Alternativa b.
Aplicando a lei dos cossenos no triângulo
ABD, temos:
x2 5 52 1 82 2 2 ? 5 ? 8 ? cos 608
x2 5 25 1 64 2 2 ? 5 ? 8 ? 1
x2 5 89 2 40 2
x2 5 49
x 5 7
Logo, x 5 7.

Estudando as áreas das
figuras geométricas planas
453
• Esta é fácil!: Qual das figuras você acha
que ocupa a maior área?
As 4 figuras ocupam a mesma área, uma
vez que todas são formadas por peças
iguais, todas são formadas pelas sete peças
do tangram.
53 – Calculando as áreas de
algumas figuras geométricas
1. Seja o quadrado de 1 cm2 o quadrado-
-padrão. O tangram é construído por 16
desses quadrados.
a) O triângulo maior possui quatro desses
quadrados de 1 cm2 de área cada um;
logo:
A 5 4 ? 1 cm2 5 4 cm2
b) O quadrado do tangram (colorido de
azul no desenho) possui dois desses
quadrados de 1 cm2 de área cada um;
logo:
A 5 2 ? 1 cm2 5 2 cm2
c) O triângulo médio possui dois desses
quadrados; logo:
A 5 2 ? 1 cm2 5 2 cm2
d) O triângulo menor possui um
quadrado-padrão; logo:
A 5 1 cm2
e) O paralelogramo possui dois desses
quadrados-padrão; logo:
A 5 b ? h 5 2 ? 1 cm2 5 2 cm2
2. Pelos resultados do exercício anterior,
calculamos:
a) A 5 4 cm2 1 4 cm2 5 8 cm2
b) Triângulo médio:
Améd. 5 2 cm2
Triângulo menor:
Amenor 5 1 cm2
Atotal 5 2 ? 1 cm2 1 2 cm2 5 4 cm2
3.
a) A 5 4 cm2 1 4 cm2 5 8 cm2
b) A 5 4 cm2 1 4 cm2 5 8 cm2
c) A 5 2 cm2 1 1 cm2 1 2 cm2 1 2 cm2 1
1 1 cm2 5 8 cm2
d) A 5 4 cm2 1 1 cm2 1 2 cm2 1 2 cm2 1
1 2 cm2 1 1 cm2 1 4 cm2 5 16 cm2
e) A 5 4 cm2 1 4 cm2 1 2 cm2 1 2 cm2 1
1 1 cm2 1 1 cm2 1 2 cm2 5 16 cm2
O triângulo, o paralelogramo e o
retângulo, respectivamente dos itens a,
b, e c, têm a mesma área (8 cm2);
o trapézio e o hexágono,
respectivamente dos itens d e e, têm a
mesma área (16 cm2).
1.
a) O lote (I) é um retângulo de lados 90 m
e 110 m, e sua área é dada por:
AI 5 90 ? 110 5 9 900 R AI 5 9 900 m2
O lote (II) é um retângulo de lados
30 m e 122 m, e sua área é dada por:
AII 5 30 ? 122 5 3 660 R AII 5 3 660 m2
b) A área total do terreno é dada por:
At 5 AI 1 AII
At 5 9 900 1 3 660 5 13 560 R
R At 5 13 560 m2
2. Podemos dividir a figura que representa o
terreno em dois retângulos:
40 m
30 m
60 m
60 m A1
A2
Primeiro, calculamos a área de cada
retângulo:
A1 5 40 ? 60 5 2 400 R A1 5 2 400 m2
A2 5 30 ? 60 5 1 800 R A2 5 1 800 m2
Agora, calculamos a área total do terreno:
At 5 A1 1 A2
At 5 2 400 1 1 800 5 4 200 R At 5 4 200 m2
3. Área da lona:
AL 5 500 ? 1,40 5 700 R AL 5 700 m2
Editoria de arte

454
Comissão pelos metros vendidos:
C 5 700 ? 0,50 5 350 R C 5 R$ 350,00
Nesse caso, o salário do vendedor seria:
S 5 300 1 350 5 650 R S 5 R$ 650,00
4. tg
37
37
º
º
5 acente a
x
x
37
0 754
5
0 754 5
º
,
,
5
5 ?
x 5 3,77 R x 5 3,77 cm
A 5 b ? h
A 5 5 ? 3,77
A 5 18,85 R A 5 18,85 cm2
( ) 2
3 5 5x21 3
2
45 5 x2 1 9
x2 5 36
x 5 6 R x 5 6 cm
A 5 b ? h
A 5 6 ? 3
A 5 18 R A 5 18 cm2
área total
6. Como as raízes da equação dada são as
medidas dos lados da região retangular,
a área dessa região será igual ao produto
das raízes da equação:
A 5 P
P 5 x’ ? x”
P
c
a
P
P
5
5
5
26
1
26
Logo, A 5 26 cm2.
7.
Agora, já podemos calcular a área do
retângulo:
A 5 b ? h 5 80 ? 60
A 5 4 800 R A 5 4 800 cm2
8.
D
M
2 ( ) ’ 23
C
m
a
b 64 cm
A B
c
36 cm
DB a
n
h
No triângulo ABD, temos: a 5 100 cm;
n 5 64 cm e m 5 36 cm.
Com esses valores, calculamos:
b2 5 a ? m
b2 5 100 ? 36
b 5 60 R b 5 60 cm
c2 5 a ? n
c2 5 100 ? 64
c 5 80 R c 5 80 cm
18,25 m
1,25 m
0,75 m
Área total a ser ladrilhada:
A 5 18,25 ? (1,25 1 0,75)
A 5 36,5 R A 5 36,5 m2
área total
Número de ladrilhos 5 5 5
área de um ladrilho
36 5
0 0625
584
,
,
5 5 5
área de um ladrilho
36 5
0 0625
584
,
,
Logo, serão colocados no muro
584 ladrilhos.
9. (x 1 4) ? (x 2 1) 5 594
x2 1 3x 2 4 5 594
x2 1 3x 2 598 5 0
x
5
2 ( ) →
2 6 3 2 6 2 ? ? 2
?
5
2 6
5
3 4 1 598
2 1
3 2401
2
3 49
2

x
x
x
5
2 6 2 ? ? 2
?
5
2 6
5
2 6 5
52
3 3 4 1 598
2 1
3 2401
2
3 49
2
”
→
26 (Não convém.)

Se x 5 23, os lados do terreno medem:
x 1 4 5 23 1 4 5 27 R 27 m
x 2 1 5 23 2 1 5 22 R 22 m
Como a plantação deverá iniciar a uma
distância de 1 m das extremidades do
terreno, o terreno para plantio terá:
25 m 3 20 m.
O espaçamento é de 2,5 m; logo,
25
2 5
10
espaços que correspondem a
, 5 11 eucaliptos no comprimento, e
20
2 5
5 8
espaços que correspondem a
, 9 eucaliptos na largura.
1. Aplicando o teorema de Pitágoras,
calculamos o lado x do quadrado:
x2 5 12 1 72
x5 50 →x5 50 cm
Agora, calculamos a área do quadrado:
A 5 ,2
A5 50
2 ( )
A 5 50 R A 5 50 cm2

455
2. Para 20 fileiras de azulejo, cada um com
15 cm de lado, calculamos a largura da
parede:
L 5 20 ? 15 5 300 R L 5 300 cm 5 3 m
Para 40 desses azulejos, calculamos
o comprimento da parede
revestida:
C 5 40 ? 15 5 600 R C 5 600 cm 5 6 m
5.
arte
6 m
de Editoria Ilustrações: 3 m
Agora, calculamos a área revestida:
A 5 L ? C
A 5 6 ? 3 5 18 R A 5 18 m2
3. x 5 x2 2 20
x2 2 x 2 20 5 0
1 6 81
x
5
x
5
→
5
2
x
52
4
triângulo ABC, determinamos x:
172 5 82 1 x2
x2 5 289 2 64 
’
” (Nãoconvém.)
x 5 5
Se x 5 ,, então , 5 5; logo:
A 5 ,2
A 5 52
A 5 25
4.
x
x 1
2 5 A2 A1
A 5 ,2
A1
5(2 5 )
2
A 5 20 R A1 5 20 cm2
Como A1 5 A2 e A2 5 x ? (x 1 1), fazemos:
x ? (x 1 1) 5 20
x2 1 x 2 20 5 0
x
x
x
5
2 6 5
52
1 81
2
4
5
→
 ’
” (Nãoconvém.)
Se um lado do retângulo é x 5 4 cm, o
outro lado é x 1 1 5 5 cm.
Logo, o perímetro do retângulo é dado por:
P 5 2 ? 4 1 2 ? 5
P 5 18 R P 5 18 cm
15 cm
3 m 15 cm
Como a área foi totalmente coberta, temos:
3 m 5 300 cm
300
520 15
R 20 quadrados na lateral
Total de quadrados 5 1 200
1200
20
560 R 60 quadrados de comprimento
60 ? 15 5 900 R 900 cm de comprimento
900 cm 5 9 m
Logo, o maior lado da região retangular
mede 9 m.
6. A
D
M
x2
x
10
x
C B
x
triângulo BCM, temos:
10
2
100
4
2 2
2
2
2
x
5 1
5 1
x
x
x
 
 
400 5 4x2 1 x2
x2 5 80
x
x
x
56 56 ? 56
5
52
80 2 5 4 5
4 5
4 5
4 →
 

’
” (Nãoconvém.)
x
x
x
56 56 ? 56
5
52
80 2 5 4 5
4 5
4 5
4 →
 

’
” (Nãoconvém.)
x
x
x
4 5
4 223
8 92
5
5 ?
5
,
,
Agora, calculamos o perímetro:
P 5 4 ? x
P5 4 ? 8,92
P 5 35,68
Por fim, determinamos a área:
A 5 x2
A 5 (8,92)2
A 5 79,5664
7. Aplicando o teorema de Pitágoras no

456
x2 5 225
x 5 15
A 5 x2
A 5 152
A 5 225 R A 5 225 cm2
8. Chamando a medida do lado do quadrado
verde de x, temos:
(9 1 x) ? (3 1 x) 5 91
27 1 12x 1 x2 5 91
x2 1 12x 2 64 5 0
x
x
x
5
2 1 1
5
2 6 5
52
12 144 256
2
12 20
2
4
16
→

’
x
x
5
2 6 5
52
256
12 20
2
4
16
→

’
Então, a medida do lado do quadrado é
4 cm, e a área desse quadrado é:
A 5 ,2
A 5 42
A 5 16 R A 5 16 cm2
9. De 1 m2 são aproveitados 9 quadrados de
lado 30 cm.
1 m2 5 10 000 cm2
9 ? 302 5 9 ? 900 5 8 100 R 8 100 cm2
Logo, são reaproveitados
10 000 cm2 2 8 100 cm2 5 1 900 cm2.
10. Alternativa a.
A área de uma face do cubo tem:
Af 5 ,2
Af 5 22
Af 5 4 R Af 5 4 m2
Como o cubo possui 6 faces, a área total da
superfície desse cubo é:
A 5 6 ? Af
A 5 6 ? 4 5 24 R A 5 24 m2
11. Cada peça tem área ,2. Como são
400 peças, então:
a) A 5 36 5 400 ? ,2
,2 5
36
400
,2 5 0,09
Logo, 0,09 m2 é a área de cada peça.
b) a 5 0,09 5 ,2
,5 0,09 R , 5 0,3
Perímetro 5 4 ? ,
Perímetro 5 4 ? 0,3 5 1,2
Logo, cada peça tem 1,2 m de
perímetro.
1.
a) A 5 110 ? 75 5 8 250 R A 5 8 250 m2
b) A 5 106 ? 76 5 8 056 R A 5 8 056 m2
c) A 5 16,5 ? (16,5 1 7,3 1 16,5)
A 5 40,3 ? 16,5
A 5 664,95 R A 5 664,95 m2
2.
a) Região Norte:
3853327
8514876
545,25%
Região Centro-Oeste:
1606372
8514876
518,87%
Região Nordeste:
1554257
8514876
518,25%
Região Sudeste:
924511
8514876
510,86%
Região Sul:
576409
8514876
56,77%
1. Alternativa d.
A área de um quadrado é ,2, então:
,2 5 0,4
, 5 0,6324 R , 5 0,6324 km 5 632,4 m
Logo, a medida dos lados está entre 632 m
e 633 m.
2.
a) Área do retângulo inicial:
35 ? 75 5 2 625 R 2 625 cm2
b) Retirando-se os quatro cantos de área
x2, temos:
2 625 2 4x2 5 1 725
4x2 5 900
2 900
x
x
4
30
2
5
5
x 5 15 R x 5 15 cm
3. Alternativa a.
1
1
1
1
1
1
2
2
2
2
1
1
Editoria de arte

457
Examinando uma pétala do mosaico,
temos, na parte clara, 4 triângulos de lados
2 e 1 e dois quadrados de lado 1.
Aclara5 ?
2 ?
1
2
2 12
4 1 ?
Aclara 5 4 1 2 5 6
Aescura 5 32 2 Aclara
Aescura 5 9 2 6 5 3
A figura é composta de 16 partes iguais a
essa; logo:
Aescura 5 16 ? 3 5 48
Aclara 5 16 ? 6 5 96
A
A
escura
clara
48
96
5 5
1
2
132 5 52 1 x2
x2 5 169 2 25
x2 5 144
x 5 12 R x 5 12 cm
Considerando um cateto como base e
outro como altura, temos:
A
b h
5
?
2
12 5
2
30→ 30 2
A
5
A A cm
?
5 5
2. Sendo o triângulo isósceles, D é ponto
médio; logo, BD 5 DC 5 12 cm.
3. A
b h
5
?
2
16 8 2
,
A
5
A A cm
?
2
, → ,
656 65 6 2
5 5
172 5 x2 1 (x 1 7)2
289 5 x2 1 x2 1 14x 1 49
2x2 1 14x 2 240 5 0
x2 1 7x 2 120 5 0
x
x
x
5
2 6 1
5
2 6 5
52
7 49 480
2
7 23
2
8
15
→

’
” (Nãoconvém.)
x
x
x
5
2 6 1
5
2 6 5
52
7 49 480
2
7 23
2
8
15
→

’
” (Nãoconvém.)
Se x 5 8, os catetos do triângulo medem
8 cm e 15 cm (x 1 7).
A
b h
5
?
2
8 15
2
60→ 60 2
A
5
A A cm
?
5 5
5. Sendo o triângulo equilátero, D é ponto
médio de BC.
arte
A
de Editoria 20 cm 20 cm
h
Ilustrações: B C
12 cm D 12 cm
triângulo ADC, temos:
202 5 h2 1 122
h2 5 400 2 144
h2 5 256
h 5 16 R h 5 16 cm
b A
?
h
5
, → , 2
24 16
2
192→ 192 2
A
5
A A cm
?
5 5
A
12 cm 12 cm
h
B D C
6 cm 6 cm
triângulo ADC, temos:
122 5 h2 1 62
h2 5 144 2 36
h2 5 108
h
5
108
h 5 6 3 →
h 5
6 3
cm
h
5 6 ?
173
,
h 5 10 , 38 h 5
10 ,
38
cm
→
A
b h
5
?
2
12 10 38
,
A
5
A A cm
?
2
62 28 62 28 2
5 5

458
6. ADB e CDB são triângulos de base 100 e
altura 60.
h 5 4,5 R h 5 4,5 cm
b A
?
h
5
2
13 4 5
,
A
5
A A cm
?
2
, → ,
29 25 29 25 2
5 5
9. Seja G a projeção de D sobre o eixo OE.
A 5 A1 A1 AABOF CDFG DGE
ABOF é um retângulo de lados 1 e 2; logo:
A5 1 ? 2 5 2 R A5 2 cm2
ABOF ABOF CDFG é um quadrado de lado 3; logo:
A5 32 5 9 R A5 9 cm2
CDFG CDFG DGE é um triângulo de base 2 e altura 3;
logo:
A ?
DGE5 5 A cm DGE
5
2 3
2
3→ 3 2
A 5 AABOF 1 ACDFG 1 ADGE
A 5 2 1 9 1 3 5 14 R A 5 14 cm2
10. A 5 AT 2 At
A
b h
, , 2
,
125 12 5
A km
A
5
?
5
5 ?
5
2
5 5
2
T T
b h
A
5
?
5
?
5
t t
2
1 1
2
0 5
→
→ 50,5m2
A 5 AT 2 At
A 5 12,5 2 0,5
A 5 12 R A 5 12 km2
a) 300 ? 0,001 5 0,3 R 0,3 km2 por dia
12
0 3
5 40 → 40
dias
, b) 20 ? 0,06 5 1,2 R 1,2 km2 por dia
12
1 2
5 10 → 10
dias
, 11. O terreno é formado por dois triângulos
de base comum igual a 120 m, e alturas
são 50 m e 30 m respectivamente.
A 5 A1 A1 2
b h
A
A m
1 1
A
b h
2
2
2
120 50
2
3000 3000
2
120 30
2
1
5
?
5
?
5 5
5
?
5
?
5
→
→A 5 m2
800 1800 2
A 5 A1 1 A2
A 5 3 000 1 1 800
A 5 4 800 R A 5 4 800 m2
A
80 E 20
D B
C
60
60
A
b h
A cm
b h
A
ADB
ADB
CDB
5
?
5
?
5
5
5
?
5
2
100 60
2
3000
3000
2
1
2
→
→
00 60
2
3000
3000 2
?
5
5
→
→A cm CDB
A área do quadrilátero será dada por:
AQ 5 AADB 1 ACDB
AQ 5 3 000 1 3 000 5 6 000 R
R AQ 5 6 000 cm2
7. No triângulo ABC, o ângulo ˆC
5 60° (o.p.v.).
sen
medida da hipotenu
60
60
º
º
5 sa
3 x
2 2 5
x 5 3 R x 5 3 cm
cos º
º
60
60
5
1
2 2 5
y
y 5 1 R y 5 1 cm
b h
A
A
ABC
ABC
5
?
5
2
3 ?
1
2
3
2
A 5 A 5
cm
ABC ABC
3
2
→ 2
8. O triângulo ADC é retângulo.
A
B C
D
30°
9 cm
13 cm
h
sen
medida da hipotenu
30
30
º
º
5 sa
1 h
2 9 5

459
1. A5 p(p2a)(p2b)(p2c)
a) 40 cm, 30 cm e 20 cm.
p
p
A
A
5
40 1 30 1
20
2
45
45 45 40 45 30 45 20
45 5
5
5 2 2 2
5 ? ?
( )( )( )
15 25
A
84375
A
3 3 5
5
A 75 15 →A 75 15
cm
2
?
5
5 ?
5 5
b) 40 cm, 50 cm e 60 cm.
p
p
A
A
5
40 1 50 1
60
2
75
75 75 40 75 50 75 60
75 35
5
5 2 2 2
5 ?
( )( )( )
25 15
?? ?
2 6
A
5 3 ? 5 ?
7
A 5 375 7 →A 5
375 7
cm
2
2.
1. A 5 b ? h
A 5 60 ? 43
A 5 2 580 R A 5 2 580 cm2
2.
arte
de Editoria A
Ilustrações: 2
75 50
2
1875 → 1875 2 B
C
D
E
J
H
G F
I
A área da região verde é a soma das áreas:
A 5 A1 A1 A1 A1 A1 A1 AAHI AHB BHC CED CHEJ EJF GHF
3 ?
1
3
A
AHI
5
2
5
2
3 2
A
?
5
5
3
AHB
2
1 A
?
2
BHC
5
1
2
5
1 2
1
A
?
CED
5
2
5
2
A
CHEJ
EJF
A
A
A
GHF
1 1 1
1 1
2
5 ? 5
5
?
5
5
1 ?
1
2
1
2
5
1
3
2
3 1
1
2
5 1 1 1 1
111 1 5
5
1
2
1 85
8 5
,
,
→
→A unidadesde área
A
N
B
C
D
x
x
60 cm
40 cm
a) x2 1 x2 5 402
2x2 5 1 600
x2 5 800
x
x
x
800
20 2
20 1,41
5
5
5 ?
x 5 28,2 R x 5 28,2 cm
b) A 5 b ? h
A 5 60 ? 28,2
A 5 1 692 R A 5 1 692 cm2
c) A
x
2
2
A cm AND5 5 5 AND5
2
800
2
400→ 400
d) ABCND 5 1 692 2 400 5 1 292 R
R ABCND 5 1 292 cm2
1. No triângulo retângulo, temos:
102 5 x2 1 (2x)2
100 5 x2 1 4x2
5x2 5 100
x2 5 20
x
d x d d
D x D D
2 5
2 22 5 4 5
4 42 5 8 5
5
5 5 ? 5
5 5 ? 5
→ →
→ →
A
D d
A
A
5
?
5
?
5
2
8 5 4 5
2
80
2. A
D d
5
?
A
5
A A cm
?
5 5

460
3. x520 3 →x520 3 cm
d 5 2y R d52?20→d540→d540 cm
D x D
→ →
→ →
D D cm
D d
A
A
A
5 5 ?
5 5
5
?
5
?
5
2 220 3
403 40 3
2
40 3 40
2
800
3 →A5800 3 cm2
7. x2 2 13x 1 40 5 0
x
x
x
5
6 2
5
6 5
5
13 169 160
2
13 3
2
8
5
→

’
”
d 5 5 e D 5 8
D d
A
?
5
2
8 5
2
20→ 20 á
A
5
A A unidades de rea
?
5 5
8.
a) No triângulo AHO, temos:
sen
medida da hipotenu
30
30
º
º
5 sa
2
4 4
5
x
5 → 5
No triângulo HBO, temos:
sen
1
2
x x cm
medida da hipotenu
60
60
º
º
5 sa
2
y
3
2
5
4 3
3
4 3
3
5 → 5
y y cm
→ →
b) d y d
2 2
5 5 ?
4 3
3
8 3
3
d 5 d 5
cm
8 3
3
→ →
D 5 2x →D52? 4→D58→D58 cm
D d
A
A
A
A
5
?
5
2
8 8 3
?
5
3
2
64 3
3
2
64 3
3
5 ?
1
2
32 3
3
A 5 A 5
cm
32 3
3
→ 2
A
30 cm 30 cm
x
24 cm
B C
24 cm
30 cm 30 cm
302 5 x2 1 242
x2 5 900 2 576
x2 5 324
x
x x cm
324
18→ 18
5
5 5
d 5 2x R d 5 2 ? 18 R d 5 36 R d 5 36 cm
D 5 48 cm
D A
?
d
5
2
48 36
2
864→ 864 2
A
5
A A cm
?
5 5
4. A
D d
5
?
2
110 35
A
5
A A cm
?
2
1925→ 1925 2
5 5
5.

x y
x y
31
1 5
2 5
5 11
Resolvendo o sistema por adição, temos:
6x 5 42
x 5 7 e y 5 24
d 5 7 e D 5 24
D A
?
d
5
2
24 7
2
84→ 84 unidades de área
A
5
A A
?
5 5
6. sen
medida da hipotenu
30
30
º
º
5 sa
1 y
2 40 5
y 5 20 R y 5 20 cm
cos º
º
30
30
5
3
2 40 = x
Editoria de arte

Logo, poderão participar do evento no
máximo 1 125 pessoas. Ilustrações: Editoria de arte
→ → 90→ trapézio trapézio (B b)h ( )
461
1. A
( B bh
)
( , , )
5
1
2
115 55 6
A
5
A A cm
1
2
51→ 51 2
5 5
2. A
( B bh
)
( )
5
1
2
13 10 7
A
5
A A cm
1
2
80 , 5→ 80 ,
5 2
5 5
3.
5.
10
13
15
5
A
E
D
B C
h
A
B bh
5
( 1 )
2
B 5 15 cm; b 5 10 cm
triângulo CDE, temos:
132 5 h2 1 52
h2 5 169 2 25
h2 5 144
h 5 12 R h 5 12 cm
(15 10)12
A
1
5
2
A
A A cm
300
2
150→ 150 2
5
5 5
4. Agramado 5 Atrapézio 2 Aretângulo
A
( B bh
)
( )
A
trap é
zio
trap é
zio
5
1
5
2
35 1
24 22
2
→ → 90→ trapézio trapézio trapézio590m2
Atrapézio 5 649 R Atrapézio 5 649 m2
Aretângulo 5 b ? h
Aretângulo 5 10,5 ? 6
Aretângulo 5 63 R Aretângulo 5 63 m2
Agramado 5 Atrapézio 2 Aretângulo
Agramado 5 649 2 63
Agramado 5 586 R Agramado 5 586 m2
40 m
A B
C
D
36 m
E
40 m
30 m
x
ABDE é um trapézio de bases b 5 36 m;
B 5 x m e altura h 5 40 m.
BCD é um triângulo retângulo de catetos
40 m e 30 m.
Logo: A5 A1 Aterreno ABDE BCD
triângulo BCD, temos:
x2 5 402 1 302
x2 5 1 600 1 900
x2 5 2 500
x 5 50 R x 5 50 m
( B bh
)
A
A
ABDE 5
1
5
( 1
)
2
36 50 40
2
A5 1 720 R A5 1 720 m2
ABDE ABDE b h
A
A
BCD 5
?
5
?
2
40 30
2
ABCD 5 600 R ABCD 5 600 m2
Aterreno 5 AABDE 1 ABCD
Aterreno 5 1 720 1 600
Aterreno 5 2 320 R Aterreno 5 2 320 m2
6. Adisponível 5 Aretângulo 2 Atrapézio
Aretângulo 5 b ? h R Aretângulo 5 18 ? 30 R
R Aretângulo 5 540 R Aretângulo 5 540 m2
Atrapézio 5
(B b)h ( )
18 12 6
1
A 1
5
A 2
2
5 18 12 6
1
A 1
5
A A 2
2
5 Adisponível 5 Aretângulo 2 Atrapézio R
R Adisponível 5 540 m2 2 90 m2 5 450 m2
A concentração é de 5 pessoas a cada
2 m2; logo:
Participantes 5 5
2
5 450
2
2250
2
?
? 5 5 5
1125
Adisponível
5
2
5 450
2
2250
2
?
? 5 5 5
1125
Adisponível

462
triângulo retângulo, temos:
152 5 122 1 x2
x2 5 225 2 144
x2 5 81
x 5 9 R x 5 9 unidades de comprimento
A
B bh
A
A
trap é
zio
trap é
zio
trap é
zio
5
1
5
1
5
( )
2
( )
29 20 12
2
294→A 294 unidadesde rea trapézio 5 á
8. O triângulo BCE é retângulo em B.
a) x2 1 x2 5 202
2x2 5 400
x2 5 200
x 5 10 2 R x 5 10 2 cm
b) A
B bh
trapézio5
( 1 )
2
B56 2 110 2 →B516 2 → B516 2 cm
110 2 →B516 2 →B516 2 cm
b56 2 cm
h5x510 2 cm
Atrapézio5
(16 2 16 2 )10 2
2
Atrapézio 5 220 R Atrapézio 5 220 cm2
54 – Usando a malha quadriculada
para calcular a área de uma
figura plana qualquer
A5 21 u
1 A5 41 u 1 21 u 5 62 u
2 21 u 1
62
u
A
5 5
u
2
41,5
A 5 41,5 ? 150
A 5 6 225 R A 5 6 225 km2
1.
Espera-se que o aluno perceba que o
estado representado pelo retângulo mais
comprido (Pará) é aquele que tem maior
frequência, ou seja, é o estado modal.
b) Resposta em aberto. Espera-se que o aluno
perceba que o estado modal é aquele
representado pelo maior setor (Pará).
Número de municípios dos estados da região Norte
Acre; 22
Amapá; 16
Tocantins; 139
Roraima; 15
c) Não; considerada a distribuição por
número de municípios, o estado
modal é o que tem maior número de
municípios, ou seja, o estado do Pará,
com 143 municípios. O estado que tem
menor área é o Acre e não é o que tem
menor número de municípios, que é
Roraima.
2.
a) Santa Catarina.
b) Rio Grande do Sul.
c) Paraná; mulas e burros.
1. Alternativa c.
Área 5 3,45 ? 4,2 5 14,49
Área de cada ladrilho 5 0,302 5 0,09
N5 5
14 49
0 09
161
,
,
São necessários 161 ladrilhos.
2. Alternativa b.
A
D d
losango 5
x
?
5
5
?
2
20
20
5
2
5x 5 40
x 5 8 R x 5 8 m
3. Alternativa a.
Seja x a medida do lado do quadrado
menor.
A medida do lado do quadrado maior mede
x 1 2.
(x 1 2)2 5 25
x2 1 4x 1 4 2 25 5 0
x2 1 4x 2 21 5 0
x
x
x
5
2  1
5
2  5
52
4 16 84
2
4 10
2
3
7
→

’
” (Não convém.)
x
x
x
5
2  1
5
2  5
52
4 16 84
2
4 10
2
3
7
→

’
” (Não convém.)
Amazonas; 62
Pará; 143
Rondônia; 52
Editoria de arte

463
Logo, no quadrado menor, , 5 3 m.
No quadrado maior, , 5 3 m 1 2 m 5 5 m.
Aazul 5 Amaior 2 Amenor
Aazul 5 52 2 32
Aazul 5 25 2 9
Aazul 5 16 R Aazul 5 16 m2
4. Alternativa c.
O telhado é formado por dois retângulos de
dimensões 10 m 3 4 m; logo, a
área que será coberta é dada por:
A 5 2 ? 10 ? 4
A 5 80 R A 5 80 m2
Então, para cobrir todo o telhado são
necessárias:
80 ? 20 5 1 600 R 1 600 telhas.
5. Alternativa b.
A caixa de papelão possui:
dois retângulos de 17 cm 3 24 cm;
dois retângulos de 24 cm 3 5 cm e dois
retângulos de 17 cm 3 5 cm.
Logo, o papelão necessário para montar
essa embalagem terá:
A 5 2(17 ? 24 1 24 ? 5 1 17 ? 5)
A 5 2(408 1 120 1 85)
A 5 1 226 R A 5 1 226 cm2
6. Alternativa e.
ABCD é um trapézio:
→
h 5 2 3 h 5
2 3
cm
( B bh
) ( )
A
1
1
5
5
2
→
A 5 A 5
cm
6 22 3
2
8 3 8 3
7. Alternativa d.
C
60° 60°
A
D
h h
E F
6 cm
4 cm
x x
B
A
( ) ( 1 )
B bh AB DC h
5
1
5
2 2
AB 5 6 cm
Os triângulos ADE e CFB são retângulos e
congruentes.
x
cos 60º
4 5
1
2 4 5
x
x 5 2 R x 5 2 cm
DC 5 6 cm 2 2 cm 2 2 cm 5 2 cm
h
sen
º 5
h
60
4
3
2 5
4
a
A a M
x
x
x
x
U
T
S
R
C
N
B
O
D
P
a2
a2
Área do quadrado maior: a2
Seja x o lado do quadrado menor.
2 2
DN a
a
5 1
DN a
a
DN
5 1
a
DN
a
DN a
2
2 2
2
2
2
2
2
4
5
4
5
4
5
2
5
5
5
 
 
nDNC  nDSC
DC
DN
DS
DC
a
DS
a
a
a DS a
DS
a
a
DS a a
a
DS
5
5
5 ?
5
5 ? ?
5
5
2
5
2
5
2
2
5
2
2
2 a
5
5
a
DS
a
x
2
a
a
a
x
2
x a
2 5
5
5
5
5
5

464
Logo, x
2
5 5
2 a
Ou seja,
1
5
do quadrado ABCD.
8. Alternativa b.
11. Alternativa a.
Aquadrado 5 802 5 6 400 R Aquadrado 5 6 400 cm2
Averde5 ?
B 1
bh →
2 5 1 5
2
80 50 30 3900
( )
( )
R Averde 5 3900 cm2
Arestante 5 Aquadrado 2 Averde
Arestante 5 6 400 2 3 900 5 2 500 R
R Arestante 5 2 500 cm2
12. Alternativa c.
Aregião 5 20 ? 12 5 240 R Aregião 5 240 km2
d 5 240 ? 72 5 17 280 R
R d 5 17 280 habitantes
13. Alternativa d.
10
2
2 2
a
5 1
100
5
4
2
2
5
a
a
 
 
15 cm
8 cm
A1 5 15 ? 8 5 120 R A1 5 120 cm2
50% de 15 5 0,5 ? 15 5 7,5
15 1 7,5 5 22,5 R 22,5 cm
50% de 8 5 0,5 ? 8 5 4 R 4 cm
8 cm 1 4 cm 5 12 cm
Logo, o novo retângulo terá as seguintes
medidas:
22,5 cm
12 cm
A2 5 22,5 ? 12 5 270 R A2 5 270 cm2
A
A
2
1
270
9
5 120
5
4 9. Alternativa e.
h
18 cm 32 cm
h2 5 m ? n
h2 5 18 ? 32 5 576
h 5 24 R h 5 24 cm
b h
A
?
5
2
18 32 24
( )
A
5
A
A A cm
1 ?
5
50 ?
24
2
600 600 2
2
→
5 5
10. Alternativa b.
Afaixa 5 7 ? 1,05 5 7,35 R Afaixa 5 7,35 m2
Aquadrado 5 (0,35)2 5 0,1225 R Aquadrado 5
5 0,1225 m2
N5 5
7 35
0 1225
60
,
,
Logo, serão obtidos 60 quadrados.
D C
10 cm
a
A B
M
a2
a2 5 80
a54 5 →a54 5 cm
B bH
A
trapézio5
( 1 )
2
A
a
a
a a
a
trap é
zio
A
5
trap é
z
1
5
?
5
?
5
2
2
3
2
2
3 80
4
60
 
 
→
→ io 560 cm2
14. Alternativa d.
Medidas da folha A4:
1189
4
. 297 R 297 mm R 29,7 cm
e
841
4
. 210 R 210 mm R 21 cm
Área da folha: 29,7 ? 21 5 623,7 R 623,7 cm2

465
Estudando a circunferência e o círculo
55 – Calculando o comprimento de
uma circunferência
1. r 5 5,25 cm
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 5,25
C 5 32,97 R C 5 32,97 cm
2.
12 cm
9 cm
x
Aplicando o teorema de Pitágoras nesse
triângulo, temos:
x2 5 92 1 122
x2 5 81 1 144
x2 5 225
x 5 15 R x 5 15 cm
Logo, r 5 15 cm.
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 15
C 5 94,2 R C 5 94,2 cm
3. C 5 50,24 cm
a) C 5 2 ?  ? r
50,24 5 2 ? 3,14 ? r
r 5
50 ,
24
6 ,
28
r 5 8 R r 5 8 cm
b) • Quadrado inscrito:
8 cm
8 cm

temos:
2 5 82 1 82
2 5 168
 5 8 2 R  5 8 2 cm
• Hexágono regular inscrito:
r

r
A circunferência possui ângulo central
de 360°, e cada triângulo com centro
em O será um triângulo equilátero.
Logo, o lado do hexágono é
 5 r 5 8 cm.
• Triângulo equilátero inscrito:

r
A
O
B C
D
r
r
2

2
Se o triângulo está inscrito na
circunferência, o centro será o
baricentro do triângulo e divide a
altura AD na razão 1 para 3; logo,
r
OD
5 2
, OC 5 r e CD 5 2
.

466
triângulo ODC, temos:
r
r
 
 
5 1
 
2 2
r
r
5 2
4 4
r
r
2
2 2
2
2
2
2 2
4
3
4
3
5
5 5
 
→



  8 3 cm
4. x2 2 10x 2 24 5 0
x
x
x
5
6 1
5
6 5
52
10 100 96
2
10 14
2
12
2
→

’
” (Nãoconvém.)
x
x
6 1
5
6 5
52
10 100 96
2
10 14
2
12
2
→

’
” (Nãoconvém.)
Logo, r 5 12 cm.
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 12
C 5 75,36 R C 5 75,36 cm
5. Se o quadrado tem 80 cm de lado, o raio
da circunferência é dado por:
r
r r cm
80
2
40→ 40
5
5 5
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 40
C 5 251,20 R C 5 251,20 cm
6. 1 volta R C 5 2 ?  ? r
C 5 2 ? 3,14 ? 25
C 5 157 R C 5 157 m
20 voltas R 20 ? 157 m 5 3 140 m
7. 1 volta R 6280
2000
53,14→1 volta53,14m
C 5 2 ? 3,14 ? r
3,14 5 2 ? 3,14 ? r
r 5 0,5 R r 5 0,5 m
8. Rodas dianteiras:
D 5 0,70 cm
r 5 0,35 cm
Rodas traseiras:
D 5 1,40 cm
R 5 0,70 cm
Cdianteira 5 2 ? 3,14 ? 0,35 5
5 2,198 R Cdianteira 5 2,198 cm
Ctraseira 5 2 ? 3,14 ? 0,70 5
5 4,396 R Ctraseira 5 4,396 cm
a) Ndianteira 5
10990
2 198
5000 5000
,
5 → voltas.
b) Ntraseira 5
10990
4 396
2500 2500
,
5 → voltas.
9. D 5 0,90 m
r 5 0,45 m
a) C 5 2 ?  ? r
C 5 2 ? 3,14 ? 0,45
C 5 2,826 R C 5 2,826 m
9891
2 826
b) N5 5 3500 N5 3500
voltas
,
→ .
10. C 5 2 ?  ? r
10 ? C 5 2 198
10 ? 2 ? 3,14 ? r 5 2 198
628 5
2198
2 198
62 8
35 35
,
,
r
r
r r m
5
5 → 5
D r
D
D D m
2
2 35
70→ 70
5
5 ?
5 5
Logo, o diâmetro desse jardim mede 70 m.
11. • 1.a possibilidade: trajeto em linha reta.
triângulo do esquema dado, temos:
AB2 5 602 1 602
AB2 5 3 600 1 3 600
AB2 5 7 200
AB 5 84,6 R AB 5 84,6 km
Custo desse trajeto:
Custo 5 84,6 ? 2 700
Custo 5 228 420,00 R
R Custo 5 R$ 228 420,00
• 2.a possibilidade: trajeto em arco.
r
r
5
5
84 ,
6
2
42 ,
3
C
r
? ?
5 5
C km
? ?
5 5
2 3
2
2 3 42 3
2
126 9 126 9
,
, → ,
C
r
? ?
5 5
C km
? ?
5 5
2 3
2
2 3 42 3
2
126 9 126 9
,
, → ,
Custo 5 126,9 ? 1 600
Custo 5 203 040,00 R Custo 5
5 R$ 203 040,00
Logo, o custo do trajeto em arco é o
mais barato, pois
R$ 203 040,00  R$ 228 420,00.

467
12. D 5 3 cm
r 5 1,5 cm
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 1,5
C 5 9,42
Em cada volta, a moeda percorre 9,42 cm.
A moeda rolou por 489,84 cm, então:
N5 5 N5 voltas
489 84
9 42
52 52
,
,
→ .
13. 360° 2 ?  ? r
120° x
x
r
x
C
5
? ? ?
5
120 2
360
3
º
º
p
Logo, o comprimento x do arco será:
r 5 30 cm
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 30
C 5 188,4 R C 5 188,4 cm
C
x
5 3
x5 5 x5 cm
188 4
3
628 62 8
,
, → ,
14. 3608 2 45° 5 315°
315° 5 7 ? 45°
Logo, o comprimento do arco do come-
-come é:
c360° 2 c45° 5 7c45°
r 5 2 cm
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 2
C 5 12,56 R C 5 12,56 cm
c45° 5 C
8
5 12 56
, 5 1,57 R c45° 5 1,57 cm
8
7c45° 5 7 ? 1,57 5 10,99 R 7c45° 5 10,99 cm
Logo, o comprimento do arco é 10,99 cm.
15. 360° 2 ? 3,14 ? r
30° 6,28
r5 r cm
º ?
,
→
º ?
, 5 5
360 6 28
30 6 28
12 12
16. O carro percorreu 3608 2 608 5 3008.
3608 2 ? 3 ? 20
3008 c
c 5
300 ?120
360
º
º → c 5 100
Portanto, o veículo percorreu 100 m.
a) D 5 30 polegadas.
Se cada polegada equivale a 2,54 cm,
temos:
30 polegadas 5 30 ? 2,54 5 76,2 R
R 30 polegadas 5 76,2 cm
D 5 76,2 cm
r 5 38,1 cm
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 38,1  239 R C  239 cm
b) 4 km 5 400 000 cm
Se cada volta corresponde a 239 cm,
temos:
N5 N voltas
400000
239
.1673→ .1673 .
c) 1 volta R 239 cm
Se dá 2 000 voltas, ida e volta, então:
1 000 voltas 5 distância casa-clube
distância casa-clube 5 1 000 ? 239 cm 5
5 239 000 cm 5 2 390 m 5 2,39 km
56 – Relações métricas na
circunferência
1.
a) 4 ? x 5 3 ? 8
x 5 6
b) 5(x 1 2) 5 6x
5x 1 10 5 6x
x 5 10
c) (6 1 2)6 5 (x 1 4)4
48 5 4x 1 16
4x 5 32
x 5 8
d) (8 1 10)10 5 (x 1 11)x
180 5 x2 1 11x
x2 1 11x 2 180 5 0
x
x
x
5
2 6 1
5
2 6 5
52
11 121 720
2
11 29
2
9
20
→

’
x
x
x
5
2 6 1
5
2 6 5
52
11 121 720
2
11 29
2
9
20
→

’
Logo, x 5 9.
e) x2 5 (8,1 1 1,9)8,1
x2 5 81
x 5 9
2. x2 5 (10 1 8)8
x2 5 144
x 5 12
(9 1 y)9 5 (10 1 8)8

468
81 1 9y 5 144
9y 5 63
y 5 7
3. 182 5 3r ? r
324 5 3r2
r2 5 108
r 56 3
4.
P
A
3x
4x 1
x
x 1
D
C
B
a) 3x(x 1 1) 5 x(4x 2 1)
3x2 1 3x 5 4x2 2 x
x2 2 4x 5 0
x(x 2 4) 5 0 →

x
x
’
”
0
4
5
5
(Não convém.)
Logo, x 5 4.
b) AB 5 3x 1 x 1 1
AB 5 4x 1 1
AB 5 4 ? 4 1 1
AB 5 17
CD 5 x 1 4x 2 1
CD 5 5x 2 1
CD 5 5 ? 4 2 1
CD 5 19
Logo, AB 5 17 e CD 5 19.
P
A
6 cm
8 cm
x
T
B
x2 5 (8 1 6 1 6)8
x2 5 160
x54 10 →x54 10 cm
6. D
A 18 y
2x
x
y
C
B
x 1 2x 5 12
3x 5 12
x 5 4 R 2x 5 8
D
A 18 y
8
4
y
C
B
4 ? 8 5 y(18 2 y)
32 5 18y 2 y2
y2 2 18y 1 32 5 0
y
y
y
5
6 2
5
6 5
5
18 324 128
2
18 14
2
16
2
→

’
”
Logo, AB fica determinado por segmentos
de 2 cm e 16 cm.
P
A
8 cm
12 cm
12 cm
6 cm
x
18 cm
B
(x 1 8)x 5 (6 1 12 1 12)6
x2 1 8x 5 180
x2 1 8x 2 180 5 0
x
x
x
5
2 6 1
5
2 6 5
52
8 64 720
2
8 28
2
10
18
→

’
” (Nãoconvém.)
x
x
x
5
2 6 1
5
2 6 5
52
8 64 720
2
8 28
2
10
18
→

’
” (Nãoconvém.)
Logo, x 5 10 cm.
a) Comprimento do segmento:
C 5 x 1 8
C 5 10 1 8
C 5 18 R C 5 18 cm
b) Comprimento da parte externa:
x 5 10 cm
P
r
C 9 cm
r
3 cm
92 5 (3 1 2r)3
81 5 9 1 6r Ilustrações: Editoria de arte

469
72 5 6r
r 5 12 R r 5 12 cm
B
A
5 cm 2 cm
M x
O
arte
4 cm
de Editoria 6 cm
5x 5 2(4 1 6)
5x 5 20
x 5 4 R x 5 4 cm
57 – Polígonos regulares inscritos
na circunferência
1.
a) Triângulo equilátero:
a
8
5
→ a 8
c n
c 5
→
a
c
a
 5 r
 5 40 cm x
x →x cm
( n
) ( ) → ? 8
→ → n
a
i i
5 8
5
2 ? 8
5
2
360 360
3
120
2 180 3 2
5
8
5
60 ?
25
150
1500
150
5
5
48
60
4 3
60 4 3
48
5 3 → 5 3
5
x
5
5 8
180
3
180
3
a a 60 i i
a
( ) → ? 8
a
→ → c
8
i
5 8
→
5
2
360
3
120
3 2
5
8
5 8
180
3
180
3
a a 60 i i
b) Quadrado:
a
n
8
→ →
a a
5
8
5
c c c
a
( n
) → ( )?? 8
n
a
i i
5 8
5
2 ? 8
5
2
360 360
4
90
2 180 4 2
5
? 8
28 ,
28
39 ,
592 7
28 28 7
39 592
5 5
,
,
→
5
10→ 10
8
5 8
180
4
2 180
4
5
360
4
5
→a →a →a 90 i i i
a
→ ( )?? a
8
c
8
i
5 8
→
5
2
360
4
90
4 2
5
? 8
5
8
5 8
180
4
2 180
4
360
4
→a →a →a 90 i i i
c) Hexágono regular:
a
n
8
→ →
a a
5
8
5
c c c
a
( n
) → ( )?? 8
n
a
i i
5 8
5
2 ? 8
5
2
360 360
6
60
2 180 6 2
5
? 8
28 ,
28
39 , 592 3 ,
5
28 28 3 5
39 592
2 5 2
, ,
,
, → ,5cm
5
8
5 8
180
6
4 180
6
5
720
6
→a →a →a 120 i i i
a
→ ( )?? a
8
c
8
i
5 8
→
5
2
360
6
60
6 2
5
? 8
5
8
5 8
180
6
4 180
6
720
6
→a →a →a 120 i i i
d) Octógono regular:
a
n
8
→ →
a a
5
8
5
c c c
a
( n
) → ( )?? 8
n
a
i i
5 8
5
2 ? 8
5
2
360 360
8
45
2 180 8 2
5
? 8
r
5
8
5 8
180
8
6 180
8
1080
8
→a →a →a 135 i i i
a
→ ( )?? a
8
c
8
i
5 8
→
5
2
360
8
45
8 2
5
? 8
5
8
5 8
180
8
6 180
8
1080
8
→a →a →a 135 i i i
2. R
r
P
p
x
5
5 25
60
150
x
x 5 5 x 5
cm
3. P
p
A
a
x
x
5
x x cm
?
5 5
4. 2
5 20 2
2 20 2
5
8 2 8 2
5
?
5 5
5. P
p
R
r
r
r
5
r r cm
?
5 5
P
p
A
a
a
a
5
a a
?
5 5
1. r 5 40 cm
a) Quadrado:

 
5
5 5
cm
2
40 2 → 40 2
b) Hexágono regular:

470
c) Triângulo equilátero:
r

 
5
5 5
cm
3
40 3 → 40 3
2. r 5 15 cm
a) Quadrado:
a 5
r
2
2
15
2
2
a
5
a 5 a 5
cm
10,575→ 10,575
b) Hexágono regular:
a r
a
5
5
3
2
15
3
2
a 5 12,975 R a 5 12,975 cm
c) Triângulo equilátero:
a
r
a
5
5
2
15
2
a 5 7,5 R a 5 7,5 cm
3.
arte
A B
de Editoria 32 cm
O
Ilustrações: D C
triângulo BCD, temos:
642 5 2 1 2
22 5 4 096
2 5 2 048
532 2 →532 2 cm
Conhecendo o valor de , calculamos o
perímetro do quadrado:
P
5 4 ?
32 2
P 5 128 2 → P 5
128 2
cm
2
2
20 2
2
10 2 → 10 2 Podemos determinar também a área:
A
5
,2
2
A
5
( 32 2
)
A
5 1024 ?
2
A 5 2048 A 5
2048
cm
2
→
4. a
r
r
5
2
5
,
6 25
2
,
, → ,
6 25 2
125 12 5
r
5 ?
r 5 r 5
cm
5.
9 cm
M
R
S
T
O
a) RÔS é o ângulo interno do triângulo
RST; logo:
a a i5 i5
360
3
º
→ 120
º
b) RS é a medida do lado do triângulo;
logo:

r
 
5
5 5
cm
3
9 3 → 9 3
c) OM é a medida do apótema do
triângulo; logo:
r
a
5
29
a
5
a 5 a 5
cm
2
4,5→ 4,5
d) SM é a altura do triângulo RST; logo:
h
5
 3
2
9 3 3
h
5
h
h h cm
?
2
27
2
13,5→ 13,5
5
5 5
6.  5
2
202 5
2
r
r
20→ 20
r 5 r 5
cm
a
r
5
a
5
a 5 a 5
cm

471
7.
a)
a
r
r
5
2
15
5
5 5
2
30→ 30
r r cm
b)
r



 
5
5
5 ?
5 5
cm
3
30 3
30 1 73
519 51 9
,
, → ,
8.
A
arte
G H
de Editoria F B
R
Ilustrações: E C
J I
D
O lado do hexágono é o raio da
circunferência; então, r 5 50 cm.

r
2
4
5

5
50 2
4

50 1 ,
41
4
5 ?
 5 705 , → 4 
4
5
70 ,
5
cm
9. r 5 3 cm
a) 5 3 cm
6 AB 5 3 cm
b)

4
5
r
2

5
3 2
4

3 1 ,
4
4
5 ?
 5 4 , 2 → 
5
4 ,
2
cm
4 4
c) d 5 d1 dAB BC
d 5 3 1 4,2
5r 3
d 5 7,2 R d 5 7,2 cm
3 5 3 3
3 10.  5r 3
53?1,73
3 510 3 →510 3 cm
5 5,19 R 5 5,19 cm
3 3 r
a
5 2
2 5 5,19 2 4,23
3 4 10
2 5 0,96
a5
3 4 2
Logo, a diferença entre as medidas das
a 5 5 R a 5 5 cm
cordas é 0,96 cm. Logo, um dos catetos mede10 3 cm, e o
outro mede 5 cm.
Aplicando o teorema de Pitágoras nesse
triângulo, temos:
x2
5() 2
10 3 152
x2 5 300 1 25
x 5 325
x55 13 →x55 13 cm
11.
4 cm
a)  4 5r 2
4 4 54 2 → 54 2 cm
b) L4 5 2 ? 4
L4 5 8 R L4 5 8 cm
c)  4
4
4 2
8
2
L 2 5 5
12. C 5 2 ?  ? r
6 5 2 ?  ? r
r 5 3 R r 5 3 cm
B
A
C
D
 4 5r 2


 
3 2
3 1 41
4 23 423
5
5 ?
5 5
4
4
4 4
,
, → , cm

472
1.  5 8 cm
tg

36º5 2
a
0 73
4
, 5 a
a . 5,47 R a . 5,47 cm
Conhecendo a, calculamos a área do
pentágono:
A
a
? 5
5 ?
2

A.5
8 ? 5 ,
47
2 ?
, → Semiperímetro Semi
A . 109,40 R A . 109,40 cm2
2.  5 80 cm
perímetro
80 6
2
10 ?
6 2
, → ro531cm
c) Área 5 semiperímetro ? apótema
a) Semiperímetro 5 5
cm
?
5 2
240→240
cm
perímetro
5
80 ?
6
2
5 2
240→240
b) a5  3
2
a5
80 3
2
a 5 40 3 cm →a540?1,73→ a 5
5 69,2 R a 5 69,2 cm
c) Área 5 semiperímetro ? apótema
Área 5 240 ? 69,2
Área 5 16 608 R Área 5 16 608 cm2
3.
a) r 5 
 5 18 cm
b) perímetro
2
6 ?
18
2
5 → cm
5 54 54
c)
a
r
3
2
18 3
2
9 3 → 9 3
5
a
5
a 5 a 5
cm
d) Área 5 semiperímetro ? apótema
Área554 ?9 3
Área 5 486 3 R Área 5 486 3 cm2
4. r 5 10 cm
a) sen
cateto oposto
hipotenusa
18º 5
0 31 2
10
, 5


2
53,1
 5 6,2 R  5 6,2 cm
cos º
,
18
0 95
5
10
5
cateto adjacente
hipotenusa
a
a 5 9,5 R a 5 9,5 cm
perímetro
10 ?
6 2
b) Semiperímetro Semi
5 5 perímet
2
2
5 31
perímetro
5 5 perímet
2
2
5 31
Área 5 31 ? 9,5
Área 5 294,5 R Área 5 294,5 cm2
58 – Área de regiões circulares
Área do retângulo 5  ? r ? r 5  ? r2
1. A 5  ? r2
2 ( )
A5π ? 6 2
A 5 3,14 ? 36 ? 2
A 5 226,08 R A 5 226,08 cm2
2. d 5 80 cm
r 5 40 cm
A 5  ? r2
A 5  ? 402
A 5 5 024 R A 5 5 024 cm2
3. Perímetro do hexágono: 60 cm
60
6
→ 510→ 510 cm
6 5 6 6
r 5 6
A 5  ? r2
A 5 3,14 ? 102
A 5 314 R A 5 314 cm2
4.
a) A região colorida de azul corresponde a
1
4
do círculo, pois o ângulo central é 90°.

473
b) A
A
azul
5 círculo
4
A
r
azul 5
p ? 2
4
Aazul 5
, 2
3 14 ?8
4
Aazul 5 50,24 R Aazul 5 50,24 cm2
48
4
5 → 512→ 512 cm
5. 4 4 4
12
2
6→ 6
r5 5 r5 cm
A 5  ? r2
A 5 3,14 ? 62
A 5 113,04 R A 5 113,04 cm2
6. 360°  ? r2
60° A
A5
º 2
60 ? ?6
360
º
p
A 5 6 ?  R A 5 6 ?  cm2 . 18,84 cm2
7. Pizza grande: d 5 44 cm e r 5 22 cm.
A 5  ? r2
A 5 3,14 ? 222
A 5 1 519,76 R A 5 1 519,76 cm2
Pizza média: d 5 30 cm e r 5 15 cm.
A 5  ? r2
A 5 3,14 ? 152
A 5 706,5 R A 5 706,5 cm2
Como são duas pizzas médias, temos:
2A 5 2 ? 706,5 R A 5 1 413 R A 5 1 413 cm2
Logo, a família que pede a pizza grande
come mais, pois 1 519,76 cm2  1 413 cm2.
8.
2
x
x 3 13
1 1 5
2
4
2
x1x 5 13 2 3
5
x
5
10
2
x 5 4
a) Raio do círculo de centro em A R 2x R
2 ? 4 5 8 R 8 cm
Área : π ? 82 5 π ? 16 . 3,14 ? 64 5 200,96
R 200,96 cm2
b) Raio do círculo de centro em B R x
2
1 3 R
4
2
1 3 5 5 R 5 cm
Área: p ? 52 5 p ? 25 . 3,14 ? 25 5 78,50 R
78,50 cm2
9. Acoroa 5 AR 2 Ar
AR 5  ? R2
AR 5 3,14 ? 112
AR 5 379,94 R AR 5 379,94 cm2
Ar 5  ? r2
Ar 5 3,14 ? 72
Ar 5 153,86 R Ar 5 153,86 cm2
Acoroa 5 AR 2 Ar
Acoroa 5 379,94 2 153,86
Acoroa 5 226,08 R Acoroa 5 226,08 cm2
triângulo da figura, temos:
x2 5 152 1 82
x2 5 225 1 64
x2 5 289
x 5 17 R x 5 17 cm
r5 5 r5 cm
17
2
8,5→ 8,5
A
A5 círculo
2
A
r
5
p ? 2
2
A5
, , 2
3 14 ?8 5
2
A 5 113,43 R A 5 113,43 cm2
11. R 5 35 km
d
hab
km
5
.
2
A 5  ? R2
A 5 3 ? 352
A 5 3 675 R A 5 3 675 km2
d5
700000
3675 → d 5 190,47 hab./km2
12. C 5 282,6 cm
C 5 2 ? r
282,6 5 2 ? 3,14 ? r
r 5 45 R r 5 45 cm
A 5  ? r2
A 5 3,14 ? 452
A 5 6 358,50 R A 5 6 358,50 cm2
13. sen
cateto oposto
hipotenusa
30º 5

474
1
x
2 5
16 x 5 8
r 5 4
cos 30º5
cateto adjacente
hipotenusa
3
y
2 5
16 y 5 8 3 →y58? 3 →y513,84
A 5 Atriângulo 1 Asemicírculo
Atriângulo5
x ? y
2
Atriângulo5
8?13 84
2
,
Atriângulo 5 55,36
Asemicírculo5
 ? r2
2
Asemicírculo5
, 2
3 14 ? 4
2
Asemicírculo 5 25,12
A 5 Atriângulo 1 Asemicírculo
A 5 55,36 1 25,12
A 5 80,48 cm2
14. A 5 Aretângulo 2 Acírculo
Aretângulo 5 b ? h
Aretângulo 5 48 ? 28
Aretângulo 5 1 344 R Aretângulo 5 1 344 m2
Acírculo 5  ? r2
Acírculo 5 3,14 ? 82
Acírculo 5 200,96 R Acírculo 5 200,96 m2
A 5 Aretângulo 2 Acírculo
A 5 1 344 2 200,96
A 5 1 143,04 R A 5 1 143,04 m2
1
2
15. AC5CB5 AB5 16
cm
1
2
16
2
DB5 AC5 5 8
cm
A área da figura é a soma das áreas
do semicírculo de raio 16 cm (A1) e do
semicírculo de raio 8 cm (A2).
A
R
1
 ?
2
5
2 A1
3 , 14 ?
162
2 5
A5 401,92 R A5 401,92 cm2
1 1 r
A
2
 ?
2
5
2 A2
3 , 14 ?
82
2 5
A2 5 100,48 R A2 5 100,48 cm2
A 5 A1 1 A2
A 5 401,92 1 100,48
A 5 502,40 R A 5 502,40 cm2
16. r
t
5 5
a) t 5 4
r 5
4
5
r 5 0,4 R r 5 0,4 m
b) A 5  ? r2
A 5 3,14 ? 0,42
A 5 0,5024 R A 5 0,5024 m2
Alternativa e.
• Tampa grande:
r 5 1 m
Q1 5 Aquadrado 2 Acírculo
Q1 5 22 2  ? r2
Q1 5 4 2 3,14 ? 12
Q1 5 0,86 R Q1 5 0,86 m2
• Tampa média:
r 5 0,5 m
Q2 5 Aquadrado 2 4 ? Acírculo
Q2 5 22 2 4 ?  ? r2
Q2 5 4 2 4 ? 3,14 ? 0,52
Q2 5 4 2 3,14
Q2 5 0,86 R Q2 5 0,86 m2
• Tampa pequena:
R 5 0,25 m
Q3 5 Aquadrado 2 16 ? Acírculo
Q3 5 22 2 16 ?  ? r2
Q3 5 4 2 16 ? 3,14 ? 0,252
Q3 5 4 2 3,14
Q3 5 0,86 R Q3 5 0,86 m2
Q1 5 Q2 5 Q3 5 0,86 m2
Logo, as três entidades recebem iguais
quantidades de material.

475
1.
a) 14
20
70
5 x
x 5
20?70
14
x 5 100 R x 5 100 cm
b) 20 módulos 100 cm
3,5 módulos x cm
3 5?100
x 5
20
,
x 5 17,5 R x 5 17,5 cm
c) A 5  ? r2
A 5 3,14 ? 17,52
A 5 961,625 R A 5 961,625 cm2
2.
a) Averde 5 Aretângulo 2 Alosango
Aretângulo 5 2 ? 1,40
Aretângulo 5 2,80 R Aretângulo 5 2,80 m2
2 m
1,40 m
17 cm
17 cm 17 cm
17 cm
Losango:
D 5 2 2 2 ? 0,17
D 5 1,66 R D 5 1,66 m
d 5 1,40 2 2 ? 0,17
d 5 1,06 R d 5 1,06 m
Alosango5
D ?
d ?
2
5
1 , 66 1 ,
06
2
Alosango 5 0,8798 R Alosango 5 0,8798 m2
Averde 5 Aretângulo 2 Alosango
Averde 5 2,80 2 0,8798
Averde 5 1,9202 R Averde 5 1,9202 m2 5
5 1 9202 cm2
b) Aamarelo 5 Alosango 2 Acírculo
Alosango 5 0,8798 m2
R 5 35 cm 5 0,35 m
Acírculo 5  ? r2
Acírculo5 ?
22
7
0,352
Acírculo 5 0,385 R Acírculo 5 0,385 m2
Aamarelo 5 Alosango 2 Acírculo
Aamarelo 5 0,8798 2 0,385
Aamarelo 5 0,4948 m2
P5 5 5
0 4948
2 80
0 1768 17 67
,
,
, , %
A parte amarela corresponde a 17,67%
da área do retângulo da bandeira.
3. r 5 35 cm
A 5  ? r2
A 5  ? 352
A 5 3 850 R A 5 3 850 cm2
4. Ceará, Mato Grosso, Paraná, Pernambuco, Rio
de Janeiro, Rio Grande do Sul e São Paulo.
1. O gráfico trata da distribuição percentual
da produção brasileira de cereais,
leguminosas e oleaginosas no ano 2006.
2. É um gráfico de setores (pizza).
3. 44% ______ 52 464 640
100% ______ T
52 464 640 T5 ?
100
5
toneladas
44
119237818,2 .
A produção total foi de aproximadamente
119 237 818 toneladas.
4. Soja:
360° 100%
x 44%
x 5
8 ?
5 8
360 44
100
158
Milho:
360° 100%
x 36%
x 5
?
5
360 36
100
130
º
º
Arroz:
360° 100%
x 10%
x 5 36°
Feijão:
3608 100%
x 3%
x 5
?
5
360 3
100
11
º
º
Editoria de arte

476
Trigo:
3608 100%
x 2%
x 5
?
5
360 2
100
7
º
º
Demais produtos:
3608 100%
x 5%
x 5
?
5
360 5
100
18
º
º
5. Área do círculo 5  ? r2
A 5 3,14 ? 52
A 5 78,5 R A 5 78,5 cm2
Soja:
100% 78,5 cm2
44% x
x5 ?
5 x 5
cm
44 78 5
100
34 54 34 54 2 ,
, → ,
Milho:
100% 78,5 cm2
36% x
x5 ?
5 x 5
cm
36 78 5
100
28 26 28 26 2 ,
, → ,
Arroz:
100% 78,5 cm2
10% x
x5 ?
5 x 5
cm
10 78 5
100
7 85 7 85 2 ,
, → ,
1. Alternativa d.
B
A
C
15 x
P
D
x
9 cm
4 cm
PA ? PB 5 CP ? PD
36 5 x(15 2 x)
36 5 15x 2 x2
x2 2 15x 1 36 5 0
x
x
x
5
 2
5
 5
5
15 225 144
2
15 9
2
12
3
→

’
”
Como se pede a medida do maior
segmento, consideramos x 5 12 cm.
2. Alternativa a.
AB 5 6
6 5 R 5 10 cm
BC 5 4
 4 2 10 2
R cm
5 5
5 1
5 1
D AB BC
D
10 10 2
D 5 10 1 10 ? 1,41
D 5 24,1 R D 5 24,1 cm
3. Alternativa a.
6 5 R
6 5 8 cm
a6

3
5
6 2 a54 3 56,8→a 5 6,8 cm
4. Alternativa b.
B
D
O C 2 cm
x
x
x
x
P
A
PA ? PB 5 PC ? PD
x ? 2x 5 2(2 1 2x)
2x2 5 4 1 4x
x2 2 2x 2 2 5 0
x
x
x
5
 1
5 
5 1 5 1 5
5 2 5 2 52
2 4 8
2
1 3
1 3 1 173 2 73
1 3 1 173 0
→
’ , ,
” , ,73( 

x
x
x
5
 1
5 
5 1 5 1 5
5 2 5 2 52
2 4 8
2
1 3
1 3 1 173 2 73
1 3 1 173 0
→
’ , ,
” , ,73(Nãoconvém.)
 

Logo, x 5 2,73 cm.
5. Alternativa c.
O quadrado de maior tamanho possível é o
quadrado inscrito nesse círculo.

4
   
r
2
20 2 20 14 28 28
5
5 5 ? 5 5
→ , → → cm
4 4 4 4
6. Alternativa d.
r 5 4 3
6 5 r
6 5 4 3 cm
a6

3
5
6 2 4 3 ?
3
5 5 → 5
a a cm 6 6
2
12
2
5 6 6

477
7. Alternativa b.
T
arte
de x
Editoria 5 cm
B P
Ilustrações: A
8 cm
(PT)2 5 PA ? PB
x2 5 8(8 1 10)
x2 5 144
x 5 12 R x 5 12 cm
8. Alternativa b.
PQ é lado de um quadrado inscrito na
circunferência; logo:

5
r
2
4
4 5
r
2
r 5 2 2 →
r 5
2 2
cm

r
3
3
5
 5 2 2 ? 3 5 2 6 →
3 
2 6
cm
3
5
Perímetro 53?2 6 56 6 →Perímetro56 6 cm
Portanto, a pessoa percorre o contorno de 4 6 →Perímetro56 6 cm
9. Alternativa d.
D 5 50 cm
r 5 25 cm
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 25
C 5 157 R C 5 157 cm
78,5 m 5 7 850 cm
n5 5
7850
157
50
Logo, foram dadas 50 voltas pelas rodas
desse carro.
10. Alternativa b.
De 12 h às 17 h, o ponteiro deu 5 voltas
completas.
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 1,5
C 5 9,42 R C 5 9,42 cm
Como foram dadas 5 voltas, fazemos:
C 5 5 ? 9,42
C 5 47,10 R C 5 47,10 cm
11. Alternativa c.
Se os centros estão a 50 cm de distância,
temos o esquema:
10 cm 10 cm
30 cm
O comprimento da correia é 50 1 50 1 C,
em que C é o comprimento da
circunferência de raio 10 cm. Logo, temos:
C 5 2 ?  ? r
C 5 2 ? 3,14 ? 10
C 5 62,8 R C 5 62,8 cm
Ccorreia 5 50 1 50 1 62,8
Ccorreia 5 162,8 R Ccorreia 5 162,8 cm
12. Alternativa e.
2x 1 1 1 x 2 3 5 19
3x 5 21
x 5 7
R1 5 2 ? 7 1 1
R1 5 15 R R1 5 15 m
R2 5 7 2 3
R2 5 4 R R2 5 4 m
Saindo de P, contornando as duas
circunferências e voltando a P percorre-se
o comprimento das duas circunferências,
ou seja:
C 5 C1 1 C2
C 5 2 ?  ? R1 1 2 ?  ? R2
C 5 2 ?  (R1 1 R2)
C 5 2 ? 3,14 ? 19
C 5 119,32 R C 5 119,32 m
13. Alternativa a.
30
360
12
º
º
5
O comprimento do arco é 1
12
do
comprimento da circunferência de raio AO.
C 5 2 ?  ? r
C 5 2 ? 3 ? 5
C 5 30 R C 5 30 cm
C C cm arco5 5 arco5
30
12
2,5→ 2,5
14. Alternativa c.
A diagonal do quadrado é 6 2 .
Como d54 tem 2 , os:6 2 2 54
4 5 6
Logo, o raio da circunferência é: r5 5 4
2
3

, , , , , , ’ ,
5 5720→ Carco 5 720 m
478
semicircunferências, o que equivale a
2 circunferências:
D 5 2 ? 2 ?  ? r
D 5 4 ? 3,14 ? 3
D 5 37,68 R D 5 37,68 unidades de
comprimento.
15. Alternativa d.
120
360
3
º
º
5
Logo, o arco correspondente a
120
circunferência
º5 .
3
Ccircunferência 5 2 ?  ? r
Ccircunferência 5 2 ? 3 ? 360
Ccircunferência 5 2 160 R Ccircunferência 5 2 160 m
Carco 5 circunferência
3
2160
3
5 5720→
circunferência
2160
3
16. Alternativa d.
Caminho 1:
2
2
p ?
r
5
942 94 2 , → , m
Caminho 2:
Arco de 30° 1 Arco de 60° 1 CD 5
5 Arco 90° 1 CD
Arco
p r
→
2
4
?
90 º5 5
47,1 47,1
m
O triângulo COD é retângulo em O,
portanto, aplicando o teorema de Pitágoras
nele, obtemos:
CD2 5 302 1 302
CD2 5 1 800
CD
5
1 800
CD
5 3 ? 2 ?
5 2
CD
5
30 2
CD
5 30 ?
1 4
CD 5 42 CD 5
42
m
,
→
Logo, o caminho 2 é:
47,1 m 1 42 m 5 89,1 m
Calculamos, então, a diferença:
Caminho 2 2 Caminho 1 5
5 94,2 m 2 89,1 m 5 5,1 m
Portanto, o caminho 1 é 5,1 m mais longo
que o caminho 2.
17. Alternativa b.
0 5
0 5
,
,
x
5 1x
x2 1 0,5x 2 0,5 5 0
x
, , , , , , x
’ x
”
5
2 6 0 5 0 25 2
2 6 1
5
2 6
5
2
0 5 2 25
2
0 5 1 5
2
→

x
x
x
5
2 6 1
5
2 6
5
2 6 5
52
0 5 0 25 2
2
0 5 2 25
2
0 5 1 5
2
0 5
2
”
→
(Não convém.)

Considerando x 5 0,5 cm, calculamos a
área do círculo:
A 5  ? r2
A 5 3,14 ? 0,25
A 5 0,785 R A 5 0,785 cm2
18. Alternativa a.
At 5 2 ? AB 1 Aretângulo
AB 5  ? r2
AB 5 3,1 ? 52
AB 5 77,5 R AB 5 77,5 cm2
Como o comprimento do retângulo é o
comprimento da circunferência de raio
5 cm, a área do retângulo é dada por:
Aretângulo 5 2 ?  ? r ? h
Aretângulo 5 2 ? 3,1 ? 5 ? 10
Aretângulo 5 310 R Aretângulo 5 310 cm2
Agora, calculamos a área total da
superfície:
At 5 2 ? AB 1 Aretângulo
At 5 2 ? 77,5 1 310
At 5 465 R At 5 465 cm2
19. Alternativa c.
A área da figura é a soma das áreas de dois
quadrados de lado 2 e um quarto de um
círculo de raio 2:
A5 ? ?
2
4
2 2
2
? p 2
A 5 8 1 3,14
A 5 11,14
20. Alternativa d.
A área ocupada pelos jardins corresponde
a quatro vezes o setor de 308, ou seja, a um
setor de 1208.
A
A
120
5 360
º
º 3
r 5 d
2
60
2
5 530→ r 5 30 m
A120
302
3
p ?
5 → A1208 5 942 m2
942 º 5

479
21. Alternativa d.
r 5 10 cm
5r 3
35 10 ? 1,7
3 5 17 R 5 17 cm
3 3 r
a
→ 5
5 a5 cm 2
h 5 5 1 10
h 5 15 R h 5 15 cm
b ?
h
A
5
5
17 ?
15
2
5 2
127,5R A 5 127,5 cm2
22. Alternativa b.
A área da região colorida de roxo é a área
do semicírculo mais a área do triângulo
retângulo de catetos 6 cm e 8 cm.
BC2 5 62 1 82
BC2 5 36 1 64
BC 5 10 R BC 5 10 cm
r 5 5 cm
A
 ?
r
semicírculo5 5
A semicírculo
?
5 5
2 3 14 5
2
2
2
39 25
,
⇒ ⇒ ⇒ 6 6
, → 39 25
?
 ?
semicírculo5 2
A semicírculo
6 8
2
24 24
2 2
, cm2
A
b h
r
triângulo5 5
A c triângulo
?
5 → 5 m2
r
A semicírculo
 ?
5
?
5 5
2 3 14 5
2
2
2
39 25
,
, → 39 25
2
6 8
2
A
24 24
, cm2
h
A c triângulo
5
?
5
5 → 5 m2
?
5 5
2 3 14 5
2
2
2
39 25
,
, → 39 25
?
2
6 8
2
24 24
, cm2
A
b h
triângulo5 5
A c triângulo
?
5 → 5 m2
A 5 Asemicírculo 1 Atriângulo 5
5 39,25 cm2 1 24 cm2 5 63,25 cm2
23. Alternativa c.
Podemos perceber que a área da parte
procurada (S) corresponde a
1
3
da
diferença entre a área do círculo (A1) e a
área do triângulo ABC (A2)
S 5
1
3
(A1 2 A2)
Vamos determinar A1:
A r
2 3 2 3
5 ? 5 ? 5  ? ? 5
A m
1
2 2 2 2
1
2
3 1 4 3 37 2
5 ? ?
( ) ( )
, →  ,
Vamos determinar A2:
No triângulo equilátero ABC, vemos ter:
OC 5
2 3
m
OM 5
3
m apótema
AM 5
3 3
m altura
( )
( )
triângulo retângulo OCM, temos:
(2 3 ) ( 3 )
 
 
 
⇒ ⇒
5 1 ? 5 1
2
2 3 3
4
4
9 36
2
3
2
2
2
5 5 5

 
3 3
2
3 3
2
ou 
não convém

52
9 3 15 3 2 2
2
A 5
A m
?
5
?
5
( )
,
6 ⇒ 
Assim, temos:
S5 A 2 A 5
2 5 ? 5
1
3
1
3
372 15 3
1
3
219 73
1 2 ( )
( , , ) , ,
Logo, a área da parte sombreada é 7,3 m2.
Projeto
1. Tales mediu a altura das grandes
pirâmides por meio da proporção entre
as sombras da pirâmide e usando uma
estaca fincada perpendicularmente ao
chão.
c
S b
B
H
H
B S
c
5
1 b
2. Exemplo: cálculo da altura de um poste.
h
c
a b
H
a
c
b 5
3. Com o auxílio de um astrolábio,
determina-se o ângulo de elevação da
árvore. Em seguida, aplica-se a fórmula
conveniente (seno, cosseno ou tangente
de um ângulo) para o cálculo da altura
correspondente. Resposta em aberto.
Ilustrações: Editoria de arte M
C
A
B
O
2

Impresso no Parque Gráfico da Editora FTD
Avenida Antonio Bardella, 300
Fone: (0-XX-11) 3545-8600 e Fax: (0-XX-11) 2412-5375
07220-020 GUARULHOS (SP)

A conquista da matematica

Mais conteúdo relacionado

Mais procurados

Semelhante a A conquista da matematica

Último

A conquista da matematica