Equilíbrio, Estática, Física

1. Versão preliminar
19 de setembro de 2002
Notas de Aula de Física
13. EQUILÍBRIO ................................................................................................................. 2
CONDIÇÕES PARA O EQUILÍBRIO ........................................................................................... 2
SOLUÇÃO DE ALGUNS PROBLEMAS ....................................................................................... 3
10 .................................................................................................................................. 3
15 .................................................................................................................................. 3
19 .................................................................................................................................. 4
25 .................................................................................................................................. 5
27 .................................................................................................................................. 6
34 .................................................................................................................................. 7
35 .................................................................................................................................. 8
39 .................................................................................................................................. 8

2. Prof. Romero Tavares da Silva
13. Equilíbrio
Condições para o equilíbrio
Diz-se que um corpo está em equilíbrio quando o seu momento linear e o seu momento angular são constantes, ou seja:
!
P = cons tan te

!
 L = cons tan te

Quando as constantes mencionadas acima são nulas, diz-se que o corpo está em
equilíbrio estático. Nessa situação ele não está em movimento de translação e também
não está em movimento de rotação.
As condições expostas nas equações anteriores implicam que:
!
!
 dP
= F EXT = 0

 dt
 !
 dL ! EXT
=τ
=0

 dt
ou seja, para que um corpo esteja em equilíbrio estático devemos ter as seguintes condições satisfeitas:
!
F EXT = 0


!
τ EXT = 0

Cap13
romero@fisica.ufpb.br
2

3. Prof. Romero Tavares da Silva
Solução de alguns problemas
Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
10 Uma esfera uniforme de peso P e raio r é mantida no lugar por uma corda presa a
uma parede, sem atrito, situada a uma distância L acima do centro da esfera, conforme a figura a seguir.
a) Encontre a tensão na corda.
Como a esfera está em repouso,
temos que:
! ! !
T +P +N =0
y
θ
!
T
!
N
ou seja:
!
T
L
!
N
T cos θ − P = 0


T sen θ − N = 0

!
P
!
P
Logo
T cos θ = P
⇒ T =
 L2 + r 2
∴ T =

L

P
cos θ

P


onde
cos θ =
L
L +r2
2
b) Encontre a força exercida pela parede sobre a esfera.
N T sen θ
=
P T cos θ
⇒
N = P tan θ
r 
∴ N =  P
L
onde
tan θ =
r
L
Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
15 Uma viga é transportada por três homens, estando um homem em uma das extremidades e os outros dois sustentando a viga por meio de uma trave transversal, colocada de modo que a carga esteja igualmente dividida entre os três homens. Em que
posição está colocada a trave transversal? (Despreze a massa dessa trave.)
Por exigência do enunciado, temos que:
F1 = F2 = F3 = F
Cap13
romero@fisica.ufpb.br
!
F1
!
P
Eixo
x
!
!
F2 + F3
3

4. Prof. Romero Tavares da Silva
Como o corpo está em repouso a resultante de forças é nula, logo:
F1 + F2 + F3 - P = 0
!
P
!
F1
O torque resultante também é nulo. Vamos considerar o torque em relação a
uma eixo que passa ao longo da trave
transversal. Desse modo:
!
F2
x
!
F3
Eixo
L

F1 (L − x ) − P  − x  = 0
2

Da primeira equação encontramos que P = 3 F , e usando esse resultado na segunda equação:
3L 
L

L

F (L − x ) − 3F  − x  = 0 ⇒  L −
 + (3 x − x ) = 0 ∴ x =
2 
4
2


Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
19 Duas esferas idênticas, uniformes e sem atrito, cada uma de peso P , estão em repouso conforme mostra a figura à seguir.
a) Encontre, em termos de P , as forças que atuam sobre as esferas devido às superfícies do recipiente.
θ = 450
F12 = F21 = F
P1 = P2 = P
!
N1
Os dois corpos estão em repouso, logo
a resultante das forças que atuam em
cada um deles é nula.
 F sen θ − P = 0


F cos θ − T = 0
2

Das equações acima encontramos que:
T1 = T2 = F cosθ
Cap13
romero@fisica.ufpb.br
!
T2
!
F21
N 1 − P − F sen θ = 0

e

 T − F cos θ = 0
1

!
F12
!
T1
!
P2
!
P1
!
N1
θ
!
F21
!
T1
!
P1
!
F12
θ
!
T2
!
P2
4

5. Prof. Romero Tavares da Silva
e
N1 - P - P = 0
F=
⇒
N1 = 2 P
P
=P 2
sen θ
T = F cos θ = P cot anθ
⇒ T =P
b) Encontre, em termos de P , as forças que atuam sobre as esferas devido uma à
outra, se a linha que une os centros das esferas faz um ângulo de 450 com a
horizontal.
F=
P
=P 2
sen θ
Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
25 Uma placa quadrada uniforme, pesando 50,0kg e tendo 2,0m de lado, está pendurada em uma haste de 3,0m de comprimento e massa desprezível. Um cabo está
preso à extremidade da haste e a um ponto na parede situado 4,0m acima do ponto
onde a haste é fixada na parede, conforme mostra a figura a seguir.
a) Qual é a tensão no cabo?
L2 = 2,0m
L3 = 3,0m
M = 50kg
L1 = 4,0m
Vamos considerar apenas as forças
que atuam na haste horizontal.
!
T
Como a placa é uniforme as forças P1
e P2 são tais que:
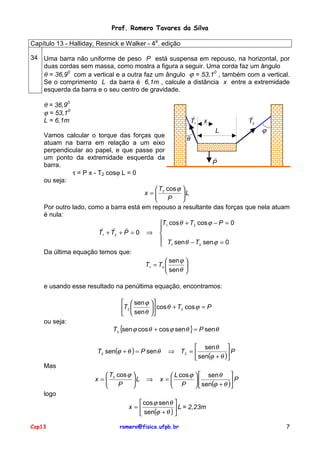
P1 = P2 = P / 2 = M g / 2
θ
!
FV
!
FH
!
P2
L1
!
P1
L2
Vamos considerar o torque das forças
que atuam na haste, em relação a um
eixo perpendicular ao papel e que pasL3
se no ponto onde a haste está presa na
parede.
T senθ L3 - P2 L3 - P1 ( L3 - L2 ) = 0
T sen θ L3 =
P

[L3 + (L3 − L2 )] ⇒ T =  2L3 − L2
 2L sen θ
2
 3
Mas
sen θ =
Cap13
L1
L2 + L2
1
3
 (2L3 − L2 ) L2 + L2
1
3
⇒ T =
2L1L3


romero@fisica.ufpb.br

P



 P = 408,34N


5

6. Prof. Romero Tavares da Silva
b) Qual é a componente vertical da força exercida pela parede sobre a haste?
Vamos considerar o torque das forças que atuam na haste, em relação a um eixo
perpendicular ao papel e que passe no ponto onde o cabo suspende a haste.
P1 L2 - FV L3 = 0
FV =
P1L2 PL2
=
= 163,34N
L3
2L3
c) Qual é a componente horizontal da força exercida pela parede sobre a haste?
Como a placa está em repouso, a resultante das forças que atuam nela é zero,
Segundo um eixo horizontal, as forças que atuam são tais que:
T cos θ − FH = 0
⇒

L3
FH = T cos θ = T 
 L2 + L2
3
 1




Usando o resultado para T deduzido anteriormente, temos que:
 2L − L2
FH =  3
 2L
1


 P = 245N


Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
!
27 Na figura a seguir, qual a magnitude da força F , aplicada horizontalmente no eixo
da roda, necessária para fazer a roda ultrapassar um obstáculo de altura h ? Considere r como sendo o raio da roda e P o seu peso.
Na iminência da ultrapassagem do obstáculo, a roda perdeu o contato com o solo,
e as forças que atuam nela estão mostradas na figura ao lado. Como ainda não
existe movimento, a resultante é nula.
Logo:
F - N cosθ = 0
!
N
θ
r
r-h
h
!
P
P - N senθ = 0
P N sen θ
=
= tan θ
F N cos θ
!
F
⇒
F=
P
tan θ
Mas
tan θ =
Cap13
r −h
r 2 − (r − h )
2
=
r −h
2rh − h 2
romero@fisica.ufpb.br
⇒
 2rh − h 2
F=
 r −h


P


6

7. Prof. Romero Tavares da Silva
Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
34 Uma barra não uniforme de peso P está suspensa em repouso, na horizontal, por
duas cordas sem massa, como mostra a figura a seguir. Uma corda faz um ângulo
θ = 36,90 com a vertical e a outra faz um ângulo ϕ = 53,10 , também com a vertical.
Se o comprimento L da barra é 6,1m , calcule a distância x entre a extremidade
esquerda da barra e o seu centro de gravidade.
θ = 36,90
ϕ = 53,10
L = 6,1m
!
T1
x
!
T2
ϕ
L
Vamos calcular o torque das forças que
θ
atuam na barra em relação a um eixo
perpendicular ao papel, e que passe por
!
um ponto da extremidade esquerda da
P
barra.
τ = P x - T2 cosϕ L = 0
ou seja:
 T cos ϕ 
x= 2
L
P


Por outro lado, como a barra está em repouso a resultante das forças que nela atuam
é nula:
T1 cos θ + T2 cos ϕ − P = 0
! !
!

T1 + T2 + P = 0 ⇒ 
 T sen θ − T sen ϕ = 0
2
 1
Da última equação temos que:
 sen ϕ 
T1 = T2 

 sen θ 
e usando esse resultado na penúltima equação, encontramos:
  sen ϕ 
T2  sen θ  cos θ + T2 cos ϕ = P

 
ou seja:
T2 {sen ϕ cos θ + cos ϕ sen θ } = P sen θ
T2 sen(ϕ + θ ) = P sen θ
 sen θ 
⇒ T2 = 
P
 sen(ϕ + θ )
Mas
 T cos ϕ 
x= 2
L
P


⇒
 L cos ϕ   sen θ 
x=

P
 P   sen(ϕ + θ )
logo
 cos ϕ sen θ 
x=
 L = 2,23m
 sen(ϕ + θ ) 
Cap13
romero@fisica.ufpb.br
7

8. Prof. Romero Tavares da Silva
Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
35 Na figura a seguir, uma barra horizontal fina AB , de massa desprezível e comprimento L , é presa a uma dobradiça em uma parede vertical no ponto A e sustentada em B , por um fio fino BC , que faz um ângulo θ com a horizontal. Um peso P
pode ser movido para qualquer posição ao longo da barra, sendo a sua posição definida pela distância x desde a parede até o seu centro de massa.
a) Encontre a tensão no fio.
Iremos considerar apenas as forças que atuam na barra.
Vamos calcular o torque em relação a um eixo perpendicular à folha de
papel e que passe pelo ponto onde a
barra está presa á parede pela dobradiça (ponto A)
Como a barra está em repouso o
torque em relação a qualquer eixo é
nulo, logo:
T senθ L - P x = 0
C
!
T
B
!
FV
!
FH
θ
A
!
P
x
L
 x 
T =
P
 L sen θ 
b) Encontre a componente horizontal da força exercida sobre a barra pelo pino da
dobradiça em A .
Como a barra está em repouso a resultante das forças que nela atuam é nula. A
componente horizontal da resultante é:
 x 
∴ FH = 
P
 L tan θ 
c) Encontre a componente vertical da força exercida sobre a barra pelo pino da dobradiça em A .
T cos θ − FH = 0
⇒
FH = T cos θ
Vamos considerar, agora, o torque das forças em relação a um eixo perpendicular à folha de papel e que passe pelo ponto onde o fio está preso na barra (ponto
B).
x
L − x

P (L − x ) − FV L = 0 ⇒ FV = 
 P ∴ FV = 1 −  P
L
 x 

Capítulo 13 - Halliday, Resnick e Walker - 4a. edição
39 Uma tábua uniforme de comprimento L = 6,1m e peso P = 444,8N está em repouso no chão, encostada numa quina sem atrito, situada no alto de uma parede de altura h = 3,0m conforme a figura a seguir. A tábua permanece em equilíbrio para qualquer valor do ângulo θ ≥ 700 , mas escorrega para θ < 700 . Encontre o coeficiente
de atrito entre a tábua e o chão.
Cap13
romero@fisica.ufpb.br
8

9. Prof. Romero Tavares da Silva
θ é o ângulo limite para o deslizamento, e
isso significa que para esse ângulo a força
de atrito estático é máxima, logo
!
T
α
Fa = µE N
α
!
N
Pode-se perceber que os ângulos α e θ
são complementares, logo:
α = π/2 - θ
h
θ
!
P
!
Fa
A força da quina na tábua é perpendicular à
tábua pois não existe atrito entre as duas.
d
Como o corpo está em equilíbrio, a resultante de forças é nula e o torque resultante
também é nulo.
O torque em relação a um eixo que passe pelo ponto de apoio da escada no chão e
que seja perpendicular à folha de papel tem a forma:
-(T cosα ) h - (P senα) L/2 = 0
T =
PL sen α
2h cos α
A resultante de forças tem a forma:
T sen α − P + N = 0
! ! ! !

T + P + N + FaE = 0 ∴ 
 − T cos α + F = 0
aE

ou seja:
FaE
µ N
T cos α
=
= E
N
P − T sen α
N
∴ µE =
T cos α
P − T sen α
e usando o resultado anterior para T , encontramos:
 PL sen α 

 cos α
 2h cos α 
µE =
 PL sen α 
P −
 sen α
 2h cos α 
Cap13
L
sen α
2h
∴ µE =
= 0,3981
L sen 2 α
1−
2h cos α
romero@fisica.ufpb.br
9