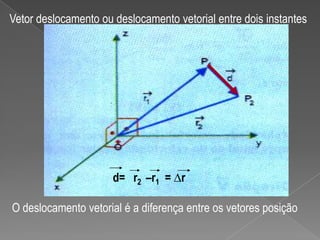
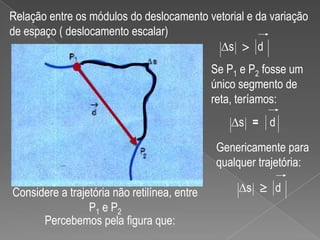
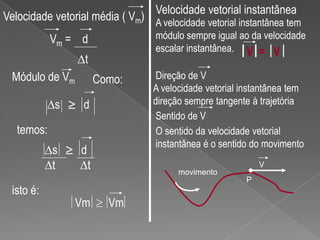
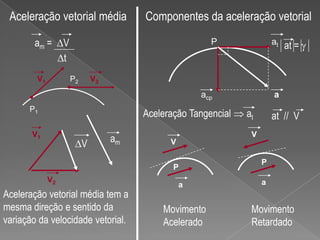
1) O documento discute conceitos de cinemática vetorial como deslocamento vetorial, velocidade vetorial instantânea e média, aceleração vetorial e seus componentes. 2) É explicado que a velocidade vetorial instantânea tem módulo igual à velocidade escalar e direção tangente à trajetória, enquanto a aceleração vetorial média tem a mesma direção e sentido da variação da velocidade vetorial. 3) São apresentados exemplos de aceleração para movimentos retilíneos uniformes e unifor

1. Cinemática Vetorial Conceitos de definições Prof. João Batista

2. d= r2 –r1 = ∆r Vetor deslocamento ou deslocamento vetorial entre dois instantes O deslocamento vetorial é a diferença entre os vetores posição

3. ∆s  d ∆s =d ∆s  d Relação entre os módulos do deslocamento vetorial e da variação de espaço ( deslocamento escalar) Se P1 e P2 fosse um único segmento de reta, teríamos: Genericamente para qualquer trajetória: Considere a trajetória não retilínea, entre P1 e P2 Percebemos pela figura que:

4. Velocidade vetorial instantânea Velocidade vetorial média ( Vm) Vm = d V=V ∆t Direção de V Módulo de Vm Sentido de V ∆s  d V ∆t ∆t movimento P Vm  Vm ∆s  d A velocidade vetorial instantânea tem módulo sempre igual ao da velocidade escalar instantânea. Como: A velocidade vetorial instantânea tem direção sempre tangente à trajetória temos: O sentido da velocidade vetorial instantânea é o sentido do movimento isto é:

5. at am = ∆V ∆t V1 P2 V2 acp a Aceleração Tangencial  at P1 at // V am at =  V1 ∆V P P V2 a a V V Aceleração vetorial média Componentes da aceleração vetorial P Aceleração vetorial média tem a mesma direção e sentido da variação da velocidade vetorial. Movimento Acelerado Movimento Retardado

6. Aceleração Centrípeta  acp Varia a direção da velocidade vetorial V : isto é , faz curva. = 0  at = 0 acp = V² R Direção de acp Retilínea  acp = 0 Retilínea  acp = 0 a = 0  ≠ 0  at ≠ 0 Sentido de acp a = at Aceleração Vetorial para Movimentos importantes MRU Movimento Retilíneo Uniforme Tem direção normal à reta tangente à trajetória, isto é, é perpendicular à velocidade vetorial. MRUVMovimento retilíneo Uniformemente Variado É sempre dirigida para dentro da curva descrita.

8. b) para o centro de Júpiter.

9. c) para o centro da Terra.

10. d) para o centro de Ganimedes.