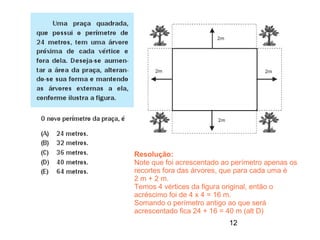
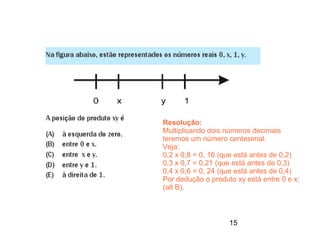
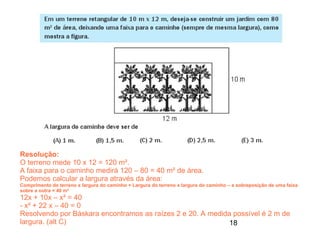
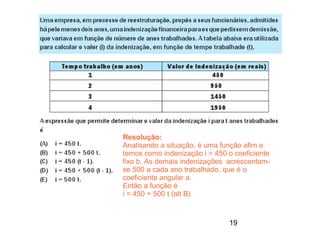
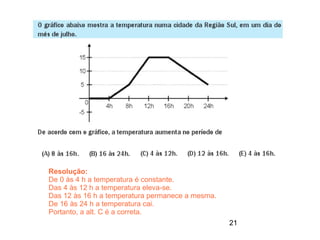
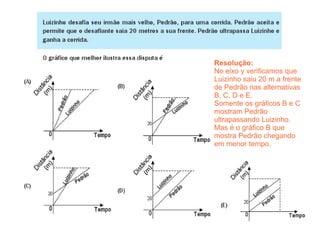
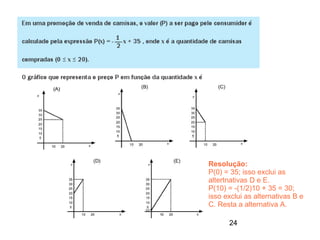
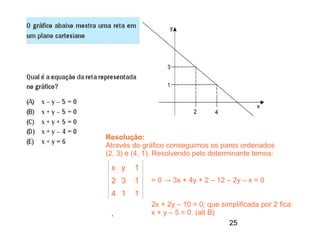
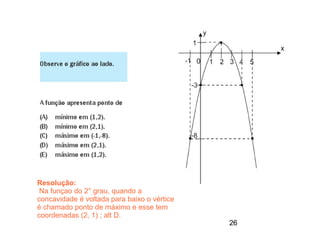
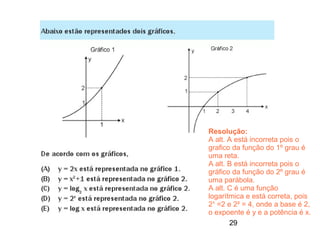
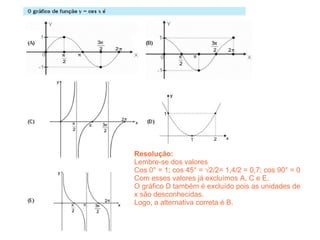
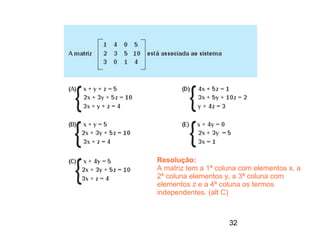
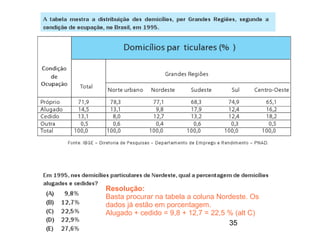
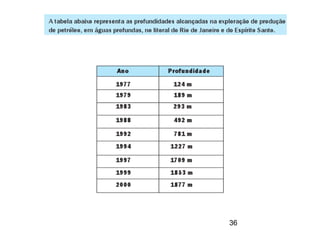
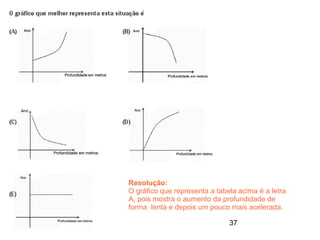
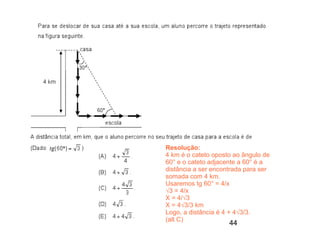
Este documento contém resoluções de questões de matemática do 3o ano do ensino médio. As questões abordam tópicos como geometria plana e espacial, funções, porcentagem, estatística e probabilidade. As resoluções variam de uma a três frases e fornecem as etapas essenciais para chegar à resposta correta de cada questão.

1. Questões resolvidas para
preparação SIMAVE/PROEB
2011
Matemática do 3º ano Ensino Médio
Prof. Idelma
23/11/2011

2. Resolução:
Pelo teorema de Tales temos o
triângulo BGE ≈ CGD.
Então, fazemos: x/8 = 10/10
x = 8 (alt D)
2

3. Resolução:
Temos a fórmula d² = a² + b² + c²
Então fica d² = 6² + 3² + 4²
d² = 36 + 9 + 16
d² = 61
d = √61 (alt E) 3

4. Resolução:
Duas bases iguais é prisma.
Como as bases são hexagonais,
é um prisma de base hexagonal
(alt B)
4

5. Resolução:
Pela relação de Euler encontramos o
número de vértices:
F+V=A+2
7 + V = 15 + 2
V = 10
Como são 3 parafusos em cada vértice,
então são 3 x 10 = 30 (alt D)
5

6. Resolução:
Para o ângulo de 15° temos x como o cateto oposto e 24 como o
cateto adjacente.
Portanto usaremos a fórmula da tangente:
Tg 15° = x/24
0,26 = x/24
x = 0,26 x 24
x = 6,24
(alt A)
6

7. Resolução:
Todo par ordenado é do tipo (x,y). Então a
A tem coordenadas (3,4) : (alt C)
7

8. Resolução:
Para uma reta ser paralela aos eixos x ou y, é necessário faltar y ou x,
respectivamente. Portanto as alternativas A e B estão descartadas.
O coeficiente angular (a) é do tipo y = ax + b. Então:
2y = - x
y = - x/2
a = -1/2 : (alt C)
8

9. Resolução:
Uma forma prática de encontrar a equação
é pelo determinante, que é igual a ZERO.
Faz-se:
x y 1
D=
3 5 1
4 -2 1
5 x + 4 y – 6 – 20 – 3y + 2 x = 0
7x + y – 26 = 0
y = - 7x + 26
(alt A)
9

10. Resolução:
Resolvendo o sistema de equações pelo
Para encontrar o
método da substituição vem:
x vamos
Eq. I: x+3y–1=0
substituir o valor
Isolando o x temos: x = 1 - 3y
de y na eq. I:
Substituindo a x por 1 – 3y na eq. II temos:
X = 1 – 3.1
1–3y–y+3=0
X=1–3
-4y+4=0
X = -2
y=-4/-4
y=1
Logo, P(-2, 1)
A única alternativa que tem y = 1 é a B.
10

11. Resolução:
A equação da circunferência é do tipo:
r² = (x – a)² + (y – b)², que desenvolvida fica assim:
r² = x² – 2ax + a² + y² – 2by + b²
x² + y² – 2ax – 2by + a² + b² – r² = 0
Por análise, descartamos as alternativas B, D e E, visto
que temos nelas o oposto de y². E na alternativa C
temos o r² = -16, que é impossível de resolver no
conjunto dos reais. Logo,a alternativa correta é (A).
Desenvolvendo a alternativa A por comparação, temos:
x² – 2x + 1 + y² – 25 = 0
-2 x = -2ax ↔ a = 1
b=0
E a² + b² – r² = - 25
1² + 0² – r² = - 25
- r² = - 25
r² = 25
r=5.
11

12. Resolução:
Note que foi acrescentado ao perímetro apenas os
recortes fora das árvores, que para cada uma é
2 m + 2 m.
Temos 4 vértices da figura original, então o
acréscimo foi de 4 x 4 = 16 m.
Somando o perímetro antigo ao que será
acrescentado fica 24 + 16 = 40 m (alt D)
12

13. Resolução:
Vou calcular a área cinza excluindo as partes
brancas da área total.
AT = 40 x 40 = 1600 cm²
Área dos triângulos brancos:
A = 4. b. h/2
A = 4x20x20/2 = 4x200 = 800
Área dos 4 arcos (formam um círculo):
A = π . r² = 3,14 x 10² = 3,14 x 100 = 314 cm²
Área cinza = 1600 – 800 – 314 = 486 (alt C)
13

14. Resolução:
Se o pote tem 12 cm de altura e foi colocado água até
a altura de 8 cm, sobra 4 cm, que é a altura ocupada
pelas bolas de gude.
Seu volume será:
V = π . 4². 4 = π 16 . 4 = 64 π
(alt C)
14

15. Resolução:
Multiplicando dois números decimais
teremos um número centesimal.
Veja:
0,2 x 0,8 = 0, 16 (que está antes de 0,2)
0,3 x 0,7 = 0,21 (que está antes de 0,3)
0,4 x 0,6 = 0, 24 (que está antes de 0,4)
Por dedução o produto xy está entre 0 e x:
(alt B).
15

16. Resolução:
Podemos assim resolver:
7 partes + 11 partes = 18 partes
180 / 18 = 10 reais por cada parte.
Então o filho mais novo recebe 7 x 10 = 70 reais e o
mais velho 11 x 10 = 110 reais. (alt A)
16

17. Resolução:
70% de 1000 = 0,7 x 1000 = 700 pessoas que bebem café.
44% de 700 = 0,44 x 700 = 308 mulheres bebem café.
Logo, são 700 – 308 = 392 homens que bebem café. (alt C)
17

18. Resolução:
O terreno mede 10 x 12 = 120 m².
A faixa para o caminho medirá 120 – 80 = 40 m² de área.
Podemos calcular a largura através da área:
Comprimento do terreno x largura do caminho + Largura do terreno x largura do caminho – a sobreposição de uma faixa
sobre a outra = 40 m²
12x + 10x – x² = 40
- x² + 22 x – 40 = 0
Resolvendo por Báskara encontramos as raízes 2 e 20. A medida possível é 2 m de
largura. (alt C) 18

19. Resolução:
Analisando a situação, é uma função afim e
temos como indenização i = 450 o coeficiente
fixo b. As demais indenizações acrescentam-
se 500 a cada ano trabalhado, que é o
coeficiente angular a.
Então a função é
i = 450 + 500 t (alt B)
19

20. Resolução:
Montando a função onde C é o custo e x o nº de peças fabricadas, temos:
C = 1500 + 10x
Substituindo C por 3200:
3200 = 1500 + 10x
3200 – 1500 = 10x
10x = 1700
x = 170 (alt D)
20

21. Resolução:
De 0 às 4 h a temperatura é constante.
Das 4 às 12 h a temperatura eleva-se.
Das 12 às 16 h a temperatura permanece a mesma.
De 16 às 24 h a temperatura cai.
Portanto, a alt. C é a correta.
21

22. Resolução:
No eixo y verificamos que
Luizinho saiu 20 m a frente
de Pedrão nas alternativas
B, C, D e E.
Somente os gráficos B e C
mostram Pedrão
ultrapassando Luizinho.
Mas é o gráfico B que
mostra Pedrão chegando
em menor tempo.
22

23. Resolução:
Como o problema já forneceu a fórmula da quantia poupada, é só
substituir os valores nela.
a12 = 30 + (12-1) . 5
a12 = 30 + 11.5
A12 = 30 + 55 = 85 (alt E)
23

24. Resolução:
P(0) = 35; isso exclui as
altertnativas D e E.
P(10) = -(1/2)10 + 35 = 30;
isso exclui as alternativas B e
C. Resta a alternativa A.
24

25. Resolução:
Através do gráfico conseguimos os pares ordenados
(2, 3) e (4, 1). Resolvendo pelo determinante temos:
x y 1
2 3 1 = 0 → 3x + 4y + 2 – 12 – 2y – x = 0
4 1 1
2x + 2y – 10 = 0; que simplificada por 2 fica:
. x + y – 5 = 0. (alt B)
25

26. Resolução:
Na funçao do 2° grau, quando a
concavidade é voltada para baixo o vértice
é chamado ponto de máximo e esse tem
coordenadas (2, 1) ; alt D.
26

27. Resolução:
Podemos efetuar a multiplicação distributiva e resolver
a equação do 2° grau ou simplesmente fazer
x–3=0→x=3
x + 1 = 0 → x = -1
Logo, as raízes são 3 e -1. (alt B)
27

28. Resolução:
A função exponencial tem o
expoente variável (x).
Faça
(0,1)0 = 1 e (0,1)¹ = 0,1 perceba
que os valores de x aumentaram e
y diminuiram.
100 = 1 e 10¹ = 10 verifique que os
valores de x e de y aumentaram
(alt D)
28

29. Resolução:
A alt. A está incorreta pois o
grafico da função do 1º grau é
uma reta.
A alt. B está incorreta pois o
gráfico da função do 2º grau é
uma parábola.
A alt. C é uma função
logarítmica e está correta, pois
2¹ =2 e 2² = 4, onde a base é 2,
o expoente é y e a potência é x.
29

30. Resolução:
400 = 25. 2 t
400/25 = 2 t
2 t = 16
2t = 24
t= 4 horas
(alt C)
30

31. Resolução:
Lembre-se dos valores
Cos 0° = 1; cos 45° = √2/2= 1,4/2 = 0,7; cos 90° = 0
Com esses valores já excluímos A, C e E.
O gráfico D também é excluído pois as unidades de
x são desconhecidas.
Logo, a alternativa correta é B.
31

32. Resolução:
A matriz tem a 1ª coluna com elementos x, a
2ª coluna elementos y, a 3ª coluna com
elementos z e a 4ª coluna os termos
independentes. (alt C)
32

33. Resolução:
Em análise combinatória, essa situação é arranjo, pois a ordem das
premiações faz diferença.
A maneira prática de calcular é multiplicar tantos fatores que for o p
(neste caso é 3) em ordem decrescente, partindo do n (que é 7). Veja:
A7,3 = 7 x 6 x 5 = 210 possibilidades. (alt D)
33

34. Resolução:
O número do elementos do espaço amostral é 6, pois o dado tem 6
faces.
O número de elementos do evento é 2, pois o evento tem apenas os
números 4 e 6.
p = 2/6
p = 1/3 (alt B)
34

35. Resolução:
Basta procurar na tabela a coluna Nordeste. Os
dados já estão em porcentagem.
Alugado + cedido = 9,8 + 12,7 = 22,5 % (alt C)
35

36. 36

37. Resolução:
O gráfico que representa a tabela acima é a letra
A, pois mostra o aumento da profundidade de
forma lenta e depois um pouco mais acelerada.
37

38. Resolução:
Total de estudantes: 400 + 800 = 1200
Sexo feminino: 800
p = 800/1200
p = 8/12
p = 2/3 (alt E)
38

39. Resolução:
Volume do cilindro = π. R² . h
Como as alturas são iguais e o π também,
podemos simplificar a razão V2/V1 assim:
6²/3³ = 36/6 = 4 vezes maior. (alt C)
39

40. Resolução:
Observando os pontos cardeais, podemos
perceber que a direção Sul e a Leste são
ortogonais (formam entre si um ângulo de
90°).
Portanto podemos formar um triângulo
retângulo, onde a distância é a hipotenusa e
vamos utilizar o Teorema de Pitágoras:
D² = 12² + 5²
D² = 144 + 25
D² = 169
D² = 13²
D = 13 m
(alt B)
40

41. Resolução:
Em análise combinatória, esse é um caso de
arranjo.
A 6, 2 = 6.5 = 30 maneiras. (alt D)
41

42. Ao passar sua mão direita por todos os vértices e arestas de um poliedro, somente uma
vez, um deficiente visual percebe que passou por 8 vértices e 12 arestas.
Conclui-se que o número de faces desse poliedro é igual a
(A) 20.
(B) 12. Resolução:
(C) 8. Usando a Relação de Euler, temos
(D) 6. V+F=A+2
(E) 4. 8 + F = 12 + 2
F = 14 – 8
F = 6. (alt D)
42

43. Resolução:
Simplificando o polinômio por 5 temos:
X² + x – 6 = 0
Resolvendo a equação do 2º grau
encontramos as raízes -3 e 2.
Fazemos
x = -3
x+3=0e
x =2
x– 2 = 0
Então representamos o polinômio por
5(x + 3)(x – 2), que é alt. B
.
43

44. Resolução:
4 km é o cateto oposto ao ângulo de
60° e o cateto adjacente a 60° é a
distância a ser encontrada para ser
somada com 4 km.
Usaremos tg 60° = 4/x
√3 = 4/x
X = 4/√3
X = 4√3/3 km
Logo, a distância é 4 + 4√3/3.
(alt C)
44

45. Resolução:
Usando dois pontos, escolhi (10, 55) e
(20, 60).
Resolvendo pelo determinante cheguei a
55q + 600 = 20C – 60q – 1100 – 10C = 0
-5q – 500 + 10C = 0
Dividindo por 10 fica:
-1/2 q – 50 + C = 0
C = ½ q + 50, que é a alt. D
45

46. Resolução:
Basta observar a reta numerada. A equipe masculina
fica em -55 e a feminina em + 45. (alt D)
46

47. Resolução:
Basta fazer t =0 e
encontramos V = 0. O
único gráfico que
corresponde a isso é o
da alt. C.
47

48. Resolução:
A única alternativa com base
circular é a D.
48

49. (A) y = − cos x .
Resolução: Notamos nesta tabela, que não
(B) y = cos .x/2.
pertence ao problema, que os valores de
(C) y = sen ( − x ) . seno são opostos aos do gráfico, então a
(D) y = sen 2 x . função é y = sen(-x).
(alt C)
(E) y = 2 sen x . .
49

50. Resolução:
Às 23 horas ele está na
toca. Portanto, às 18 h ele
está mais longe. (alt A)
50