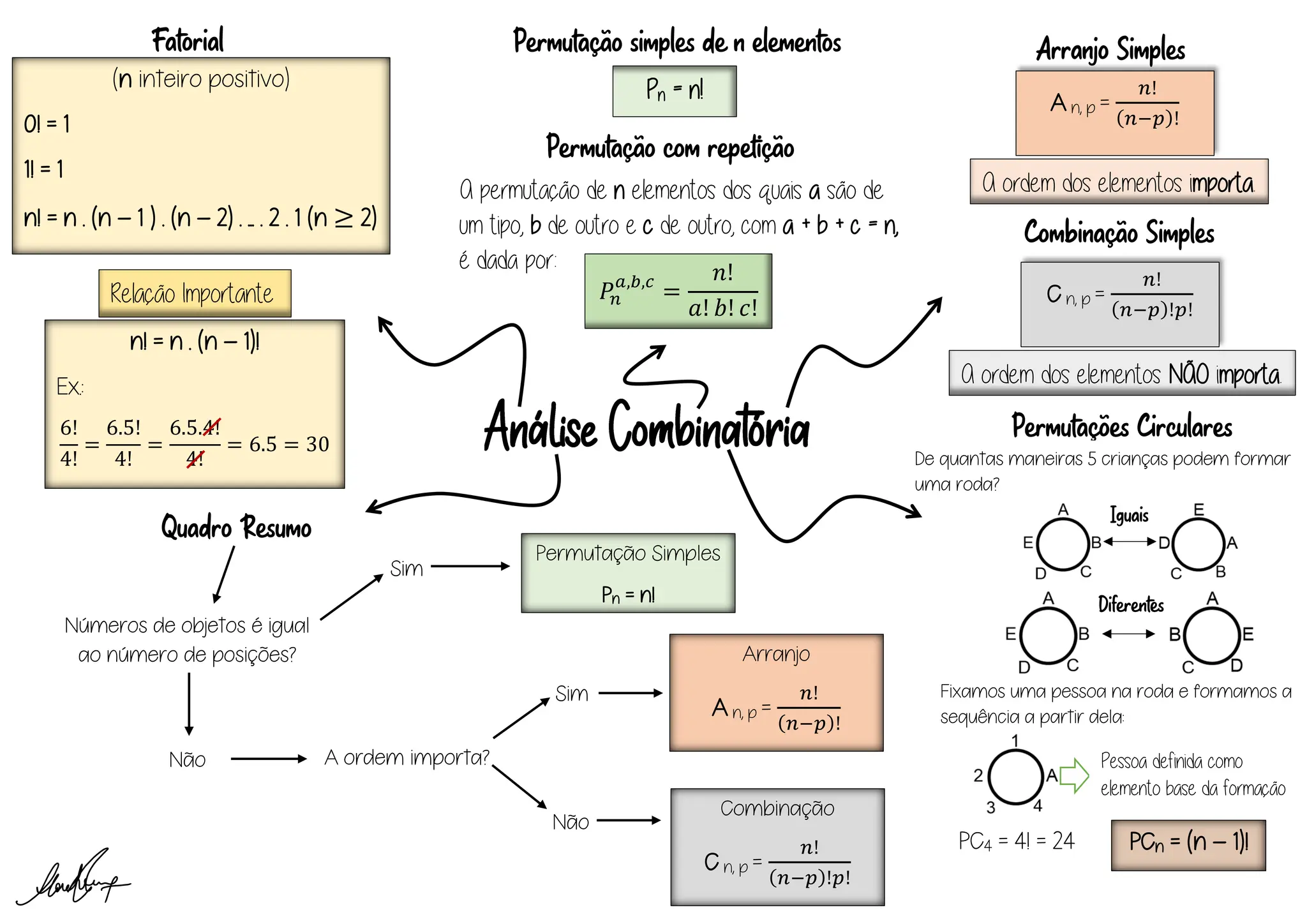
1) O documento apresenta fórmulas para cálculo de fatorial, permutação, arranjo e combinação. 2) É explicado que a permutação conta a ordem dos elementos, enquanto a combinação não leva em conta a ordem. 3) São mostrados exemplos de como aplicar as fórmulas para diferentes situações, como permutação com repetição de elementos.

1. Fatorial
(n inteiro positivo)
0! = 1
1! = 1
n! = n . (n – 1 ) . (n – 2) . ... . 2 . 1 (n ≥ 2)
Relação Importante
n! = n . (n – 1)!
Ex.:
6!
4!
=
6.5!
4!
=
6.5.4!
4!
= 6.5 = 30
Permutação simples de n elementos
Pn = n!
Permutação com repetição
A permutação de n elementos dos quais a são de
um tipo, b de outro e c de outro, com a + b + c = n,
é dada por:
𝑃𝑛
𝑎,𝑏,𝑐
=
𝑛!
𝑎! 𝑏! 𝑐!
Arranjo Simples
A n, p =
𝑛!
ሺ𝑛−𝑝ሻ!
A ordem dos elementos importa.
Combinação Simples
C n, p =
𝑛!
ሺ𝑛−𝑝ሻ!𝑝!
A ordem dos elementos NÃO importa.
Permutações Circulares
Pessoa definida como
elemento base da formação
Fixamos uma pessoa na roda e formamos a
sequência a partir dela:
De quantas maneiras 5 crianças podem formar
uma roda?
PC4 = 4! = 24 PCn = (n – 1)!
Iguais
Diferentes
Números de objetos é igual
ao número de posições?
Sim
Permutação Simples
Pn = n!
Não A ordem importa?
Sim
Arranjo
A n, p =
𝑛!
ሺ𝑛−𝑝ሻ!
Não
Combinação
C n, p =
𝑛!
ሺ𝑛−𝑝ሻ!𝑝!
Quadro Resumo