Este documento apresenta uma lista de revisão de Matemática com exercícios de nível básico, intermediário e avançado sobre funções e trigonometria. Os exercícios abordam tópicos como funções injetoras, sobrejetoras e bijetoras; gráficos de funções; equações do 1o e 2o grau; trigonometria; e números complexos. O documento fornece instruções sobre a realização e entrega da lista de exercícios.
![LISTA DE REVISÃO 01 – MATEMÁTICA E
FUNÇÕES E TRIGONOMETRIA
Considerações iniciais:
Esta lista deverá ser feita em folha a parte devidamente identificada e entregue em aula na data combinada;
Alguns exercícios desta lista foram ou serão resolvidos em sala de aula, mas isto não exclui a necessidade deles
constarem na resolução pessoal de vocês;
Será atribuída uma nota simbólica, de 0 a 10, para que possa haver uma medida para o desempenho pessoal de
cada um;
As questões estão divididas em níveis de dificuldade, entre básico, intermediário e avançado, contendo questões
de vestibulares passados, livros didáticos e outros processos que envolvam em sua avaliação questões de
matemática;
Qualquer dúvida vocês podem entrar em contato comigo pelo facebook ou em aula!!!
Bons estudos!!
Felipe.
“Suba o primeiro degrau com fé. Não é necessário que você veja toda a escada. Apenas dê o primeiro passo .”
(Martin Luther King)
d) R4 = {(x,y) / x+y=4}
Nível Básico: 05. Considere a tabela que relaciona o preço com
01. Seja a função f(x) = x2+2x+1. Qual a imagem de f combustível com a quilometragem de um automóvel:
quando x = 2? Preço gasto (R$) Quilometragem (km)
0,00 4,00
02. Qual o domínio da função f(x) = √ ? 0,50 7,50
0,65 7,65
03. Determinar o conjunto imagem, o domínio e o 1,00 8,00
contradomínio da função f= que manifesta a curva 5,00 12,00
9,00 16,00
abaixo.
9,625 16,625
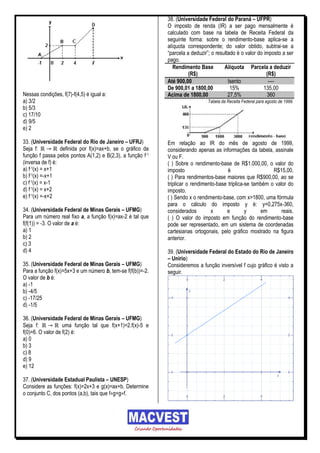
Sabendo que a função modelada pelos dados acima é
linear, determine uma lei para a função ( ) ,
onde p é dado em R$ e q em km. Esboce um gráfico,
para esta função, representando seu plano cartesiano.
06. Uma equação biquadrada é denominada equação
redutível a uma equação do 2º grau através de uma troca
de variáveis. Sabendo que f(x) = :
a) Determine os pontos em que a função f intercepta o
eixo das abcissas.
b) Determine os pontos em que a função f intercepta o
eixo das ordenadas.
c) Determine a imagem de f no ponto de abcissa 1.
d) A função no intervalo ] é crescente ou
decrescente? Justifique.
e) A função no intervalo é crescente ou
04. Verifique se as relações binárias abaixo são ou não decrescente? Justifique.
são funções. Se a relação for uma função, determinar o
seu domínio, contradomínio e o conjunto imagem. 07. A função f(x) = é injetora, sobrejetora ou
a) R1 = {(0,1); (0,2); (0,3); (1,1); (1,2); (1,3)} bijetora? Justifique.
b) R2 = {(0,1); (1,1); (2,1); (3,1); (4,1); (5,1)}
c) R3 = {(1,1); (2,2); (3,3); (4,4); (5,5); (6,6); ...; (n,n)}, com
n .](https://image.slidesharecdn.com/listadereviso01-121026201605-phpapp01/75/Lista-de-revisao-01-1-2048.jpg)

![Nível Intermediário 29. (Pontifícia Universidade Católica – PUC)
25. Sendo A={2,3,4} e B={5,6,7,9,12}, qual o conjunto Com base no gráfico da função y = f(x), o valor de f(f(f(1)))
imagem da função de A em B, tal que é:
f={(x,y) AxB|y=3x}?
26. (Universidade Federal do Pernambuco – UFPE)
Dentre as curvas a seguir, qual pode ser o gráfico de uma
função injetora y=f(x)?
a) -8/3
b) -5/3
c) 8/3
d) 5/3
e) 5
27. (Pontifícia Universidade Católica – PUC)
Seja f a função de em , dada pelo gráfico a seguir: 30. (Universidade Estadual de Londrina – UEL)
Se a função f, do primeiro grau, é tal que f(1)=190 e
f(50)=2052, então f(20) é igual a:
a) 901
b) 909
c) 912
d) 937
e) 981
31. (Universidade Federal de Santa Maria – UFSM)
A figura representa o gráfico de uma função do primeiro
é correto afirmar que: grau que passa pelos pontos A e B, onde a≠2.
a) f é sobrejetora e não injetora.
b) f é bijetora.
c) f(x)=f(-x) para todo x real.
d) f(x)>0 para todo x real.
e) o conjunto imagem de f é ]-∞;2].
28. (Universidade Federal Rural do Rio de Janeiro –
UFRRJ)
No gráfico a seguir, a imagem do intervalo[-1,2[ é:
O ponto de intersecção da reta ̅̅̅̅ com o eixo x tem
abcissa igual a:
a) 1-a
b) a-2
c) ( )
d) 4-a
e) 12-3ª
a) [1/2; 1[ U ]-2; 1]
b) [1/2; 1] U [-2; 1] 32. (Universidade Estadual Paulista – UNESP)
c) [-1/2; 1] U ]1; 2] A poligonal ABCD da figura adiante é o gráfico da função f
d) [-1; 1/2] U ]1; 2[ cujo domínio é o intervalo -1≤x≤7. Sabe-se que ̅̅̅̅ é
e) [-1; 1/2] U [1; 2] paralelo a ̅̅̅̅ e ̅̅̅̅ é paralelo ao eixo do x.](https://image.slidesharecdn.com/listadereviso01-121026201605-phpapp01/85/Lista-de-revisao-01-3-320.jpg)

![52. (Universidade de Taubaté – UNITAU) 57. (Universidade Presbiteriana Mackenzie)
( | |) Para qualquer valor real de x,
O domínio da função ( ) √[ ] é: ( ( ) ( )) (( ( ) ( ))
a) 0 ≤ x ≤ 2 É igual a:
b) x ≥ 2 a) -1
c) x ≤ 0 b) 0
d) x < 0 c) 1
e) x > 0 d) 2
e) 2.sen(2x)
53. Determinar as raízes da equação:
| | | ||| 58. (Instituto Tecnológico da Aeronáutica – ITA)
Sejam a, b e c elementos dos números reais (excetuando-
se o zero) com . Se x, y e z satisfazem o
54. (Fundação Universitária para o Vestibular – sistema:
FUVEST) ( ) ( )
O ângulo agudo formado pelos ponteiros de um relógio a
{ ( ) ( )
1 hora e 12 minutos é:
a) 27° ( ) ( )
b) 30° Então, cos(x)+cos(y)+cos(z) é igual a:
c) 36° a)
d) 42°
e) 72° b)
55. (Fundação Universitária para o Vestibular – c)
FUVEST)
A figura a seguir mostra parte do gráfico da função: d)
e)
59. (Fundação Universitária para o Vestibular –
FUVEST)
Calcule:
a) sen(15°)
b) a área do polígono regular de 24 lados inscrito no
círculo de raio 1.
60. (Fundação Universitária para o Vestibular –
FUVEST)
O valor de (sen(22°30’) + cos(22°30’))² é:
a) 3/2
√
b)
a) sen(x)
√
b)2.sen(x/2) c)
c) 2.sen(x) d) 1
d) 2.sen(2x) e) 2
e) sen(2x)
Observação da questão 60: a notação “ ‘ “ indica uma
Observação da questão 55: admita que a imagem da subdivisão do grau, o minuto. Dizer que determinado
função descrita no gráfico é [-2,2] e que seu período é de ângulo possui 34° 30’ é equivalente a falar sobre o ângulo
4π. 34,5°. Deve-se atentar ao fato de cada grau possuir 60
minutos.
56. Achar os valores de x que verifiquem
simultaneamente as igualdades: 61. Transforme o produto cos(2x).cos(4x) em uma soma
( ) ( ) . equivalente.](https://image.slidesharecdn.com/listadereviso01-121026201605-phpapp01/85/Lista-de-revisao-01-6-320.jpg)
![62. (Universidade Estadual Paulista – UNESP)
Determinar os valores de θ, 0≤ θ≤2π, de maneira que o
determinante | | seja nulo.
63. (Instituto Tecnológico da Aeronáutica – ITA)
A soma das raízes da equação
√ ( ) √ ( ) ( )
Que pertencem ao intervalo [0; 2π] é:
a) 17π/4
b) 16π/3
c) 15π/4
d) 14π/3
e) 13π/4
64. (Cesgranrio)
Resolva a equação ( ) .
Nível Avançado:
65. (Fundação Universitária para o Vestibular – FUVEST)
Seja ( ) , em que a, b e c são números reais. A imagem de f é a semirreta ]-1, ∞[ e o gráfico de f intercepta
os eixos coordenados nos pontos (1, 0) e (0-, ). Então, o produto abc vale:
a) 4
b) 2
c) 0
d) -2
e) -4
66. (Instituto Tecnológico da Aeronáutica – ITA)
( ) ( )
Se a e b são ângulos complementares, 0 < b < π/2 e √ , então ( ) ( ) é igual:
( ) ( )
a) √
√
b)
c) √
√
d)
e) 1](https://image.slidesharecdn.com/listadereviso01-121026201605-phpapp01/85/Lista-de-revisao-01-7-320.jpg)