1) O documento apresenta os conceitos fundamentais da geometria plana, incluindo noções primitivas como ponto, reta e plano, além de proposições como postulados da existência e determinação da reta. 2) São definidos ainda conceitos como retas paralelas, equação geral de uma reta e postulado da determinação do plano. 3) Os capítulos subsequentes abordam temas como ângulos, triângulos, circunferência, funções trigonométricas e introdução a cônicas.

1. Índice.
Capitulo 1. (Noções e proposições primitivas)
Ponto, Reta e Plano ............................................................................ 02
Proposições primitivas ............................................................................ 03
Postulado da existência. ............................................................................ 03
Postulado da determinação Da reta ............................................................................ 04
Equação geral de uma reta ............................................................................ 05
Postulado da determinação do plano ............................................................................ 05
Plano cartesiano. ............................................................................ 06
Ponto médio ............................................................................ 07
Distancia entre dois pontos ............................................................................ 07
Capitulo 2. (Ângulos).
Ângulos ............................................................................ 09
Ângulos consecutivos ............................................................................ 09
Ângulos adjacentes ............................................................................ 09
Ângulos Opostos Pelo Vértice (O.P.V.). ............................................................................ 10
Bissetriz de um ângulo ............................................................................ 10
Ângulo reto, agudo, obtuso ............................................................................ 10
Unidade de medida de um ângulo ............................................................................ 11
Ângulos complementares e ângulos
............................................................................ 11
suplementares
Condição para que duas retas sejam paralelas ............................................................................ 13
Capitulo 3. (Triângulos).
Triângulos. (definição). ............................................................................ 14
Elementos. (Vértice, lados e ângulos.) ............................................................................ 14
Classificação. (Quanto aos lados.) ............................................................................ 14
Classificação. (Quanto aos ângulos.) ............................................................................ 14
Congruência de triângulos. ............................................................................ 15
Mediana de um triângulo ............................................................................ 15
Bissetriz interna de um triângulo. ............................................................................ 16
A soma dos ângulos de um triângulo ............................................................................ 16
Teorema de tales ............................................................................ 18
Casos de semelhança ............................................................................ 19
1° caso: AA (Ângulo – Ângulo) ............................................................................ 20
2° caso: LAL (Lado – Ângulo – Lado) ............................................................................ 20
3 caso: LLL (Lado – Lado – Lado) ........................................................................ 21
Teorema de Pitágoras ............................................................................ 21
O enunciado do teorema de Pitágoras ............................................................................ 22
A Demonstração clássica. ............................................................................ 22
A Demonstração de Perigal. ............................................................................ 24

2. Recíproco do teorema de Pitágoras. ............................................................................ 24
Aplicações do Teorema de Pitágoras. ............................................................................ 26
Terno Pitagórico ou triângulos Pitagóricos. ............................................................................ 27
Capitulo 4. (Circunferência).
Circunferência (definição) ............................................................................ 31
Corda e diâmetro ............................................................................ 31
Posição de ponto e circunferência. ............................................................................ 31
Círculo.
............................................................................ 32
Partes do círculo.
Semicírculo, Secante ............................................................................ 33
Tangente
............................................................................ 34
Posições relativas de duas circunferências.
Circunferências Concêntricas
Circunferências secantes ............................................................................ 35
Segmentos Tangentes.
Arcos de uma Circunferência
Ângulo Central. ............................................................................ 36
Medida de um Arco
Medida do ângulo inscrito em uma
circunferência. ............................................................................ 37
Medida do ângulo inscrito
Radiano.
Comprimento da Circunferência. ............................................................................ 39
Quadratura do círculo.
Capitulo 5.(Razões trigonométricas)
Razões trigonométricas ............................................................................ 41
Seno de um ângulo ‫ܣ‬መ
መ
Cosseno de um ângulo ‫.ܣ‬ ............................................................................ 42
Tangente de um ângulo ‫ܣ‬ መ
Razões inversas. ............................................................................ 43
Relações entre razões trigonométricas ............................................................................ 44
Razões trigonométricas de ângulos
............................................................................ 45
fundamentais
Seno, cosseno e tangente de ângulos quaisquer ............................................................................ 46
Capitulo 6.( Funções trigonométricas)
Ciclo trigonométrico – determinações
............................................................................ 50
Arco trigonométrico
Conjunto das determinações de um arco ............................................................................ 51
Funções Trigonométricas
............................................................................ 52
Definição da função seno
Variação da função seno. ............................................................................ 53

3. Gráfico da função seno. ............................................................................ 54
Função cosseno ............................................................................ 55
Variação da função cosseno ............................................................................ 56
Gráfico da função cosseno. ............................................................................ 57
Função tangente ............................................................................ 60
Variação da função tangente. ............................................................................ 60
Gráfico da função tangente. ............................................................................ 61
Capitulo 7.(Derivada e a reta tangente.)
Derivada e a reta tangente ............................................................................ 62
Informações dadas pela primeira derivada
............................................................................ 64
Crescimento e decrescimento de funções
Máximos e mínimos relativos ............................................................................ 66
Pontos críticos e números críticos.
............................................................................ 67
Sobre o teste da primeira derivada
Capitulo 8.(Progressões)
Sequências.
Representação de uma sequência. ............................................................................ 69
Representação genérica de uma sequência.
Progressão Aritmética ............................................................................ 70
Notações especiais:
............................................................................ 71
Termo Geral de uma P.A.
Soma de termos de uma P.A. ............................................................................ 72
Teorema 1.
A soma dos n primeiros inteiros positivos
............................................................................ 73
Teorema 2
Teorema 3
Progressões Geométricas. (P.G) ............................................................................ 74
Termo geral de uma PG. ............................................................................ 75
Soma dos termos de uma ܲ‫ ܩ‬finita. ............................................................................ 77
Limite da soma dos termos de uma PG. ............................................................................ 79
Capitulo 9.(Introdução a cônicas.)
Parábola.
Considerações
............................................................................ 83
Definição.
Elementos da parábola
Equação da parábola de vértice na origem. ............................................................................ 84
Gráfico de uma função.
f (x ) = ax 2 + bx + c, a ≠ 0 f : R → R .
............................................................................ 85
Elipse.
Considerações. ............................................................................ 87
Definição

4. Elementos da elipse
Equação da elipse com centro na origem. ............................................................................ 88
Hipérbole.
Considerações
............................................................................ 91
Definição.
Elementos da Hipérbole.
Equação da Hipérbole com centro na origem ............................................................................ 92

5. Capitulo 1.
Noções e proposições primitivas
As noções (conceitos, termos, entes) geométricas são estabelecidas por meio de definição.
Mas é importante resultar que, os conceitos primitivos (noções primitivas) da geometria, não
possuem definição.
Adotaremos sem definir as noções de:
Ponto, Reta e Plano.
O conhecimento que temos de ponto, reta e plano. É intuitivo decorrente da experiência e da
observação e não por definição.
Ponto:
Pode ser dado como exemplo: Uma marca de giz no quadro negro, a marca da ponta de um
lápis ou caneta, mas tudo sempre no mundo das idéias de ponto em geometria. E o ponto não tem
dimensões (tamanho).
Reta:
Exemplo: as linhas de marcação de uma quadra, um fio esticado, as linhas do seu caderno.
Dão a idéia de reta em geometria, com a diferença que: a reta não tem começo e nem fim, logo não
pode ser medida.
Plano:
Exemplo: o chão ou as paredes de uma sala, uma quadra, uma folha de papel, sugerem a
idéia de plano em geometria.
Notação de ponto, reto e plano.
a) Com letras
Ponto _ letras maiúsculas latinas: A, B, C, ...

6. Reta _ letras minúsculas latinas: a, b, c, ...
Plano _ letras gregas minúsculas: α , β, ϒ, ...
b) Notações gráficas.
O ponto ࡼ A reta ࢘
O plano ∝
Proposições primitivas.
As proposições (propriedades, afirmações) geométricas são aceitas mediante
demonstrações. Mas em particular as proposições primitivas ou postulados ou axiomas são
aceitos sem demonstração. Iniciaremos a Geometria Plana com alguns postulados
relacionando o ponto, a reta e o plano.
Postulado da existência.
a) Numa reta, bem como fora dela, há infinitos pontos.
b) Num plano, bem como fora dele, há infinitos pontos.
A expressão “infinitos pontos” tem o significado de “tantos pontos quantos quisermos”.
A figura ao lado indica uma reta r e os pontos A, B, P, R, S e M, sendo que:
A, B e P estão em r ou a reta r passa por A, B e P, ou ainda
A Є r, B Є r, P Є r;
R, S e M não estão em r ou r não passa por R, S e M, ou ainda R ∉ r, S ∉ r, M ∉ r.
Pontos colineares são pontos que pertencem a uma mesma reta.

7. Os pontos A, B e C são colineares. Os pontos R, S, e T não são colineares.
Postulado da determinação da reta.
Dois pontos distintos determinam uma única (uma, e uma só) reta que passa por eles. Os
pontos A e B distintos determinam a reta que indicamos por AB.
ሺ‫ݎ ∈ ܤ ,ݎ ∈ ܣ ,ܤ ് ܣ‬ሻ
A expressão duas retas coincidentes é equivalente a uma única reta.
Retas concorrentes.
Definição
Duas retas são concorrentes se, e somente se, elas têm um
único ponto comum.
‫ ݏ ∩ ݎ‬ൌ ሼܲሽ
Retas paralelas
Definição.
Duas retas são paralelas (símbolo: //) se, e somente se,
são coincidentes (iguais).
Ou
São coplanares e não tem nenhum ponto em comum.
ሺܽ ⊂ ߙ, ܾ ⊂ ߙ, ܽ ∩ ܾ ൌ ∅ሻ → ܽ//ܾ
Exercícios:
Demonstre que num plano existem infinitas retas.
Solução: Consideremos um plano ߙ e nele dois pontos
distintos A e B, estes pontos determinam uma reta r, que esta contida
em ߙ, pois tem dois pontos distintos em ߙ. Consideremos em ߙ e fora
de r um ponto C. Os pontos A e C determinam uma reta ‫ ,ݏ‬que esta em
ߙ. Os pontos B e C determinam uma reta ‫ ݐ‬que esta em ߙ. Desse
modo podemos construir em ߙ “tantas” retas quantas quisermos isto é “infinitas” retas.
Se duas retas são paralelas e distintas, todo plano que contem uma delas e um ponto da
outra, contém a outra.

8. Solução: Sejam r e s as duas retas, P um ponto de S e ߙ o plano (r, P). As retas r e s
determinam um plano ߙ′. Temos, então:
ሺߙ ᇱ ൌ ሺ‫ݏ ,ݎ‬ሻ, ܲ ∈ ‫ݏ‬ሻ ⟹ ߙ ᇱ ൌ ߙ. Se ߙ ൌ ߙ′ contem S, então o plano ߙ contem a reta s.
Equação geral de uma reta
Seja os pontos ‫ܪ‬ሺ0, 2ሻ, ‫ܫ‬ሺ3, 0ሻ e ‫ܬ‬ሺെ3, 4ሻ, pertencentes à mesma reta ‫.ݎ‬
Se ܲሺ‫ݕ ,ݔ‬ሻ é um ponto pertencente a reta ‫ ,ݎ‬temos:
‫ݔ‬ ‫ݕ‬ 1
ܲ, ‫ ܫ ݁ ܪ‬são colineares ⇒ อ0 2 1อ ൌ 0 ⇒ 2‫ ݔ‬൅ 3‫ ݕ‬െ 6 ൌ 0 ሺ1ሻ
3 0 1
‫ݔ‬ ‫ݕ‬ 1
ܲ, ‫ ܬ ݁ ܪ‬são colineares ⇒ อ 0 2 1อ ൌ 0 ⇒ െ2‫ ݔ‬െ 3‫ ݕ‬൅ 6 ൌ 0 ሺ2ሻ
െ3 4 1
‫ݔ‬ ‫ݕ‬ 1
ܲ, ‫ ܬ ݁ ܫ‬são colineares ⇒ อ 3 0 1อ ൌ 0 ⇒ െ4‫ ݔ‬െ 6‫ ݕ‬൅ 12 ൌ 0 ሺ3ሻ
െ3 4 1
As equações (1), (2) e (3) são equivalentes entre si. Podemos, então, associar qualquer uma
dessas equações à reta ‫.ݎ‬
Generalizando, seja r uma reta qualquer determinada pelos pontos ‫ܣ‬ሺ‫ݔ‬஺ , ‫ݕ‬஺ ሻ e ‫ܤ‬ሺ‫ݔ‬஻ െ ‫ݕ‬஻ ሻ
distindos (‫ݔ‬஺ ് ‫ݔ‬஻ ou ‫ݕ‬஺ ് ‫ݕ‬஻ ሻ e ܲሺ‫ݕ ,ݔ‬ሻ um ponto qualquer de ‫ .ݎ‬Pela condição de alinhamento
de ܲ, ‫ ܣ‬e ‫ ,ܤ‬vem:
‫ݔ‬ ‫ݕ‬ 1
อ ‫ݔ‬஺ ‫ݕ‬஺ 1อ ൌ 0 ⇒ ሺ‫ݕ‬஺ െ ‫ݕ‬஻ ሻ‫ ݔ‬൅ ሺ‫ݔ‬஻ െ ‫ݔ‬஺ ሻ‫ ݕ‬൅ ‫ݔ‬஺ ‫ݕ‬஻ െ ‫ݔ‬஻ ‫ݕ‬஺ ൌ 0
‫ݔ‬஻ ‫ݕ‬஻ 1
Fazendo ‫ݕ‬஺ െ ‫ݕ‬஻ ൌ ܽ, ‫ݔ‬஻ െ ‫ݔ‬஺ ൌ ܾ e ‫ݔ‬஺ ‫ݕ‬஻ െ ‫ݔ‬஻ ‫ݕ‬஺ ൌ ܿ, temos:
ܽ‫ ݔ‬൅ ܾ‫ ݕ‬൅ ܿ ൌ 0, onde ܽ ് 0 ‫ ,0 ് ܾ ݑ݋‬e ሺ‫ݕ ,ݔ‬ሻ são as coordenadas de um ponto qualquer da reta r.
Postulado da determinação do plano.
Três pontos não colineares determinam um único plano que passa por
eles. Os pontos ‫ ܤ , ܣ‬e ‫ ܥ‬não colineares determinam um plano ߙ que
indicamos por (‫ .)ܥ ,ܤ ,ܣ‬O plano ߙ é o único plano que passa por ‫ ܤ ,ܣ‬e ‫.ܥ‬
Postulado da inclusão.

9. Se uma reta tem dois pontos distintos num plano, então a reta está contida nesse mesmo
plano.
ሺ‫ ݎ ,ܤ ് ܣ‬ൌ ‫ߙ ∈ ܤ ,ߙ ∈ ܣ ,ܤܣ‬ሻ ⟶ ‫.ߙ ⊂ ݎ‬
Dados dois pontos distintos A e B de um plano, a reta r = AB tem todos os pontos no plano.
Plano cartesiano
No inicio do século XVII, a geometria ainda era a base que
sustentava a matemática da época e o livro Os Elementos, de
Euclides já não atendia as necessidades da matemática da época. O
que se buscava na época era uma maneira de se unir a recém-criada
álgebra linear e a geometria grega da época, nesta tarefa se destaca o
Frances René Descartes (1596 - 1650).
Em 1617, formado em direito, entrou para a carreira militar, a
serviço do príncipe Mauricio de Nassau. O ato mais conhecida dos
René Descartes em pintura de
seus quase 12 anos de carreira militar foi o sonho que teve o revelo a Frans Hals.
inutilidade de como estava sua vida de induzi-lo a abraçar a filosofia.
A grande obra de Descartes foi o Discurso do método (1637), um trabalho de filosofia da
ciência universal. Em relação ao conhecimento ele entendia que o se humano é dotado de duas
faculdades essenciais: a intuição, que proporciona conhecimentos simples, claros e validos (para ele
os sentimentos não eram confiáveis, pois podiam induzir a erros) e a dedução, com a qual se pode
estabelecer verdades ordenadas racionalmente. Ele
escolheu a Matemática para adotar como o método de
verdade por seu um método dedutivo pela forma
segura de se estabelecer a verdade. Mas estranhamente
na parte do Discurso dedicada à matemática, que
intitulou A Geometria, que é uma das obras
matemáticas mais influentes de todos os tempos.
Nesse trabalho podemos conhecer o poderoso
método matemático que veio a se tornar a geometria
analítica que conhecemos nos dias de hoje.

10. Basicamente consiste em estabelecer a correspondência entre pontos de um plano e pares ordenados
de números reais associados univocamente a uma equação de duas variáveis a uma curva desse
plano, e vice-versa. Para isso é utilizado como referencia um par de eixos, em geral ortogonais.
O plano cartesiano é um sistema formado por dois eixos perpendiculares entre si com o
ponto ܱ em comum entre eles.
0ܺ – eixo das abscissas
0ܻ – eixo das ordenadas
Cada ponto pertencente ao plano possui uma abscissa ܺ‫ ݌‬e uma ordenada ܻ‫ ,݌‬que indicamos
pelo par ordenado ሺܺ‫݌ܻ ,݌‬ሻ e chamamos de coordenadas cartesianas de ܲ.
O plano dividido pelos eixos da origem a quatro regiões ou quadrantes.
Os pontos pertencentes ao 1° quadrante tem abscissa e ordenadas positivas;
Os pontos pertencentes ao 2º quadrante tem abscissa negativa e ordenada positiva.
Os pontos pertencentes ao 3º quadrante tem abscissa e ordenada negativas.
Os pontos pertencentes ao 4º quadrante tem abscissa positiva e ordenada negativa.
Ponto médio
Dados dois pontos ‫ܧ‬ሺ‫ݔ‬ா , ‫ݕ‬ா ሻ e ‫ܨ‬ሺ‫ݔ‬ி , ‫ݕ‬ி ሻ, para obter as coordenadas do ponto médio do
segmento തതതത .
‫ܨܧ‬
Seja ‫ܯ‬ሺ‫ݔ‬ெ , ‫ݕ‬ெ ሻ o ponto médio de തതതത . Temos que
‫ܨܧ‬
abscissa ‫ݔ‬ெ é igual a media aritmética de ‫ݔ‬ா ݁ ‫ݔ‬ி . O mesmo
raciocínio pode ser aplicado a ‫ݕ‬ெ . Assim;
‫ݔ‬ா ൅ ‫ݔ‬ி
‫ݔ‬ெ ൌ
2
‫ݕ‬ா ൅ ‫ݕ‬ி
‫ݕ‬ெ ൌ
2
Distancia entre dois pontos
Sejam os pontos ‫ܧ‬ሺ‫ݔ‬ா , ‫ݕ‬ா ሻ e ‫ܨ‬ሺ‫ݔ‬ி , ‫ݕ‬ி ሻ representados no gráfico ao lado.
Como podemos calcular a distancia entre ‫ ܧ‬e ‫?ܨ‬
Vamos supor que ‫ݔ‬ா ് ‫ݔ‬ி e ‫ݕ‬ா ് ‫ݕ‬ி . O segmento തതതത mede |‫ݔ‬ி െ ‫ݔ‬ா | e o segmento ‫ܥܨ‬
‫ܥܧ‬ തതതത
mede |‫ݕ‬ி െ ‫ݕ‬ா |.
A distância entre ‫ ܧ‬e ‫ ܨ‬é igual à medida da hipotenusa do triangulo ‫ ,ܥܨܧ‬retângulo em ‫.ܥ‬
Para calcular essa medida, aplicamos o teorema de Pitágoras:

11. ሺ‫ܨܧ‬ሻଶ ൌ ሺ‫ܥܧ‬ሻଶ ൅ ሺ‫ܥܨ‬ሻଶ ou ሺ‫ܨܧ‬ሻଶ ൌ ሺ‫ݔ‬ி െ ‫ݔ‬ா ሻଶ ൅ ሺ‫ݕ‬ி െ ‫ݕ‬ா ሻଶ
Temos que:
݀ாி ൌ ඥሺ‫ݔ‬ி െ ‫ݔ‬ா ሻଶ ൅ ሺ‫ݕ‬ி െ ‫ݕ‬ா ሻଶ

12. Ângulos
Definição:
Chama-se ângulo à reunião interna ou externa compreendida entre duas semi-retas de
mesma origem, não contidas numa mesma reta (não colineares).
෠ തതതത തതതതത
‫ ܤܱܣ‬ൌ ‫ ܤܱ ∪ ܱܣ‬
O ponto O é o vértice do ângulo.
As semiretas AO e OB são os lados do ângulo.
Os ângulos também podem ser representados por letras gregas tais
como: ߙ, ߚ, ߛ, ߠ, ߮ ou simplesmente com o acento circunflexo na letra: Â, Ê, Ĉ, Ĥ, Ô.
Ângulos consecutivos
Dois ângulos são consecutivos se, e somente se, um lado de um deles é também lado do
outro (um lado de um deles coincide com um lado do outro).
AÔB e AÔC são consecutivos
. AÔC e BÔC são consecutivos
(OA é o lado comum) (OC é o lado comum)
AÔB e AÔC são consecutivos
(OA é o lado comum)
Ângulos adjacentes.
Dois ângulos consecutivos são adjacentes se, e somente se, não
tem pontos internos em comuns.
‫ܣ‬Ô‫ ܤ‬e ‫ܤ‬Ô‫ ܥ‬são ângulos adjacentes.

13. Ângulos Opostos Pelo Vértice (O.P.V.)
Dois ângulos são opostos pelo vértice se, e somente se, os
lados de um deles são as respectivas semi-retas opostas aos lados
do outro.
തതതത ݁ ܱ‫ݏ݋ݐݏ݋݌݋ ܥ‬
ܱ‫ ܣ‬തതതതത ෠ ෠
ൠ → ‫ݏ ܦܱܣ ݁ ܤܱܣ‬ã‫ݒ ݋݈݁݌ ݏ݋ݐݏ݋݌݋ ݋‬é‫.݁ܿ݅ݐݎ‬
തതതത തതതത
ܱ‫ݏ݋ݐݏ݋݌݋ ܦܱ ݁ ܤ‬
Notemos que duas retas concorrentes determinam dois pares de ângulos opostos pelo
vértice.
Bissetriz de um ângulo.
Definição
෠ ෠
Uma semi-reta ܱ‫ ܥ‬interna a um ângulo ‫ ܥܱܣ‬é bissetriz do ângulo ‫ ܤܱܣ‬se, e somente se:
෠ ෠
‫ܥܱܤ ≡ ܥܱܣ‬
A bissetriz de um ângulo é uma semi-reta interna ao ângulo,
com origem no vértice do ângulo e que divide em dois ângulos
congruentes.
Ângulo reto, agudo, obtuso.
Ângulo reto é todo ângulo que mede 90˚. Que é congruente a seu suplementar adjacente. É o
ângulo de 360˚ dividido em 4 partes iguais. É representado por:
Ângulo agudo é um ângulo menor que um ângulo reto (90˚).
Ângulo obtuso é um ângulo maior que um ângulo reto

14. Unidade de medida de um ângulo.
Um ângulo não tem comprimento, nem largura nem espessura. Ele só tem uma medida
chamada amplitude e sua unidade de medida é o graus representado pelo sinal ° Ex. 30° (trinta
graus).
O instrumento usado para medir um ângulo é o
transferidor. Observe o desenho do transferidor e veja como
se faz para medir um ângulo.
O transferidor é dividido em unidades de medidas
denominadas GRAUS, no intervalo de 0˚ à 180˚ (meia
circunferência) ou de 0˚ à 360˚ (uma circunferência).
Esta região, em destaque, esta marcando um ângulo de 40˚
Ângulo de um grau (1º) é o ângulo submúltiplo
segundo 90(noventa) de um ângulo reto.
â௡௚௨௟௢ ௥௘௧௢
Ângulo de: Um grau ൌ
ଽ଴°
.
Um ângulo reto tem 90 graus (90˚).
A medida de um ângulo agudo é menor que 90˚ (um ângulo agudo tem menos que 90 graus).
A medida de um ângulo obtuso é maior que 90˚ (um ângulo obtuso tem mais de 90 graus).
A medida α de um ângulo é tal que:
0° ൏ α ൏ 180°
Ângulo de um minuto (1’) é o ângulo submúltiplo segundo 60 (sessenta) do ângulo de um
grau.
1°
1ᇱ ൌ
60
Um grau tem 60 minutos (60’).
Ângulos complementares e ângulos suplementares.
Ângulos complementares
Dois ângulos são complementares se, e somente se, a soma de suas medidas é 90˚. Um deles
é o complementar do outro.
Exemplo:

15. Se você juntar os dois ângulo terá um ângulo de 90˚.
Calcule o complementar do ângulo de 35˚
Solução:
Sendo X a medida do complemento de 35˚ você tem:
ܺ ൅ 35° ൌ 90°
ܺ ൌ 90° െ 35°
ܺ ൌ 55°(complementar de 35˚)
Ângulos suplementares
Dois ângulos são suplementares se, e somente se, a soma de suas medidas é 180˚. Um deles
é o suplementar do outro.
Exemplo1:
Os ângulos de 55˚ e 125˚ são suplementares pois a suma deles é 180˚, o que também pode
ser observado sobrepondo os ângulos
Sejam a e b duas retas distintas, paralelas ou não, e t uma reta concorrente com a e b, logo
t é uma transversal de a e b.
Dos oito ângulos determinados por essas retas, indicados nas figuras acima, chamam-se
ângulos:
Alternos: 1 e 7, 2 e 8, 3 e 5, 4 e 6. Correspondentes: 1 e 5, 2 e 6, 3 e 7, 4 e 8.

16. Colaterais: 1 e 8, 2 e 7, 3 e 6, 4 e 5.
Observações:
i) Com mais detalhes podemos ter:
alternos internos : 3 e 5, 4 e 6
 ˆ ˆ ˆ ˆ Colaterais internos : 3 e 6, 4 e 5
 ˆ ˆ ˆ ˆ
alternos externos : 1 e 7, 2 e 8 Colaterais externos : 1 e 8, 2 e 7
Alternos  Colaterais 
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
 
ˆ ˆ
i) A congruência de dois ângulos alternos de um dos pares. Exemplo, 1 ≡ 7 . Então
podemos dizer que:
a) a congruência dos ângulos de todos os pares de ângulos alternos “ 2 ≡ 8 , 3 ≡ 5 , 4 ≡ 6 ”;
ˆ ˆ ˆ ˆ ˆ ˆ
b) a congruência dos ângulos de todos os pares de ângulos correspondentes
"1 ≡ 5 , 2 ≡ 6 , 3 ≡ 7 e 4 ≡ 8" ;
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
c) a suplementar idade dos ângulos de todos os pares de colaterais
"1 + 8 = 2 + 7 = 3 + 6 = 4 + 5 = 180 °" ;
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
Condição para que duas retas sejam paralelas.
Uma condição necessária e suficiente para duas retas
distintas sejam paralelas e formarem com uma transversal, ângulos
alternos, ou ângulos correspondentes, congruentes.
a // b ⇔ o ≡ u
ˆ ˆ
Da condição acima podemos retirar outras considerações;
1° Dois ângulos de lados respectivamente paralelos são congruentes ou suplementares.
Analisando a ilustração, conclui-se:
Como os ângulos alternos formados
com a transversal t, são congruentes.
( )
Exemplo 2: Seja a//b Pode-se concluir que:
Como a reta ‘a’ é paralela a reta
‘b’, logo os ângulos ‘û’ e ‘ô’, são
congruentes.
(

17. Capitulo 3.
Triângulos
Definição
Dados três pontos ‫ ܤ ,ܣ‬e ‫ ܥ‬não colineares, à
തതതത തതതത തതതത
reunião dos segmentos ‫ ܥܣ , ܤܣ‬e ‫ ܥܤ‬chama-se
triângulo ‫.ܥܤܣ‬
Indicação: Triangulo ‫ ܥܤܣ‬ൎ ‫ܥܤܣ‬
തതതത തതതത തതതത
‫ܥܤ ∪ ܥܣ ∪ ܤܣ = ܥܤܣ‬
Elementos.
Vértices: os pontos ‫ ܤ ,ܣ‬e ‫ ܥ‬são os vértices do ‫.ܥܤܣ‬
Lados: os segmentos AB (de medida C), ‫( ܥܣ‬de medida b) e ‫( ܥܤ‬de medida a) são os lados
do triangulo.
Ângulos: os ângulos BÂC ou Â, ‫ ܥܤܣ‬ou B e ‫ ܤܥܣ‬ou Ĉ são os ângulos do
̂ ‫( ܥܤܣ‬ou
ângulos internos do ‫.)ܥܤܣ‬
͞ ͞ ͞ ̂
Diz-se que os lados BC, AC e AB e os ângulos Â, B e Ĉ são, respectivamente, opostos.
Classificação.
Quanto aos lados, os triângulos de classificam em:
Equilátero se, e somente se, têm os três lados congruentes (tem a mesma medida).
Isósceles se, e somente se, têm dois lados congruentes (mesma medida) e um diferente.
Escalenos se, e somente se, não possui lados congruentes (os 3 lados são diferentes).
Um triângulo com dois lados congruentes é isóscele; o outro lado é chamado base e o
ângulo oposto à base é o ângulo do vértice. Notemos que todo triângulos equiláteros é também
triangulo isósceles.
Quando aos ângulos, os triângulos se classificam em:
Retângulos: se, e somente se, têm um ângulo reto ሺ90˚ሻ.

18. Acutângulos: se, e somente se, têm ângulos agudos, ou seja, os três ângulos com medida
menores do que 90˚.
Obtusângulos: se, e somente se, têm um ângulo obtuso (tem um ângulo com medida maior
que 90˚).
O lado oposto ao angula reto de um triangulo retângulo é sua hipotenusa e os outros dois são
os catetos do triângulo.
Congruência de triângulos.
Definição
Um triângulo é congruente (símbolo ≡) a outro se, e somente se, é possível estabelecer uma
correspondência entre seus vértices de modo que:
Seus lados são ordenadamente congruentes aos lados do outro e Seus ângulos são
ordenadamente congruentes aos ângulos do outro.
‫ `ܣ ≡ ܣ → `ܤ`ܣ ≡ ܤܣ‬
‫≡ ܥܤܣ‬ ‫ `ܥ`ܤ`ܣ‬൝‫`ܤ ≡ ܤ → `ܥ`ܣ ≡ ܥܣ‬
‫`ܥ ≡ ܥ → `ܥ`ܤ ≡ ܥܤ‬
Mediana de um triângulo.
Mediana de um triângulo é um segmento com extremidades num vértice e no ponto médio
do lado oposto.
‫ܯ‬ଵ é o ponto médio do lado ‫.ܥܤ‬

19. ‫ܯܣ‬ଵ é a mediana relativa ao lado ‫.ܥܤ‬
‫ܯܣ‬ଵ é a mediana relativa ao vértice ‫.ܣ‬
Bissetriz interna de um triângulo.
Bissetriz interna de um triângulo é o segmento, com
extremidades num vértice e no lado oposto, que divide o
ângulo desse vértice em dois ângulos congruentes.
ܵଵ ∈ ‫,ܥܤ‬ ܵଵ ‫ܵ ≡ ܤܣ‬ଵ ‫ܥܣ‬
‫ܵܣ‬ଵ é a bissetriz relativa ao lado ‫.ܥܤ‬
‫ܵܣ‬ଵ é a bissetriz relativa ao vértice ‫.ܣ‬
A soma dos ângulos de um triângulo.
Somando os ângulos internos de um triângulo qualquer, obteremos sempre 180º.
Para demonstração realizaremos a seguinte experiência.
WWW...Você pode ainda verificar a demonstração interativa dessa
propriedade.(http://www.aevouzela.net/moodle/file.php/2/geogebra/triangulo1.html)

20. Tales.
Tales é considerado um importante filósofo e matemático, nasceu na Grécia antiga, mais
precisamente na cidade de Mileto (620-549 a.C).
Pouco se sabe sobre a sua vida. Parece que começou como
mercador, dono de uma inteligência notável, logo obteve grande
ascensão econômica, para depois, se dedicar à busca do saber – o
que ele mais valorizava. Na época e Tales a Grécia não era a grande
potencia cultural que se tornaria mais tarde, e possível que tenha
ido estudar matemática nos centros mais avançados, como o Egito e
a Mesopotâmia. Retornando a sua cidade natal, ganhou o merecido
respeito de seus conterrâneos como estadista filosofo, matemático e
astrônomo.
Existem muitas lendas e histórias sobre ele. Certa vez com base nos seus conhecimentos
sobre o tempo ele pode prever que a safra seguinte de azeitona seria muito abundante. Assim obteve
a o monopólio de todas as prensas da região. Confirmada a previsão alugou todas as prensas e
obteve grande lucro. Outra história contada e a de que Tales previu o eclipse solar do ano de 580
a.C., mas há serias duvidas sobre isso. De fato e muito improvável naquela época, mesmo entre os
babilônicos, tabelas astronômicas que permitissem fazer tal previsão.
Diz-se que, ao ser interrogado sobre o que era difícil Tales respondeu: “Conhecer a si
mesmo”. O que era fácil: “Ser dirigido por outro”. Agradável: “Seguir a própria vontade”. Divino:
“Aquilo que não tem começo nem fim”.
O filosofo utilizava boa parte do tempo para viajes, comum aos homens importantes daquela
época. Em uma de suas visitas ao Egito,
começou a ser muito admirado por,
supostamente, ter medido a altura de uma
pirâmide sem precisar escalá-la.
Para realizar esta façanha, Tales
posicionou uma estaca verticalmente no chão.
Comparando a medida da estaca com a medida de sua sombra projetada verificou que em certo
momento a medida da sombra era a mesma da estaca. Relacionou então a medida da estaca com a
medida da pirâmide no mesmo instante. Observe a ilustração a seguir.

21. Sistematizando a ideia de tales.
Utilizando de algumas ideias Tales conseguiu
calcular a altura da pirâmide.
Entre estas ideias estavam:
Se dois triângulos internos possuem ângulos
congruentes, então os seus lados satisfazem a seguinte
relação:
a b c
= =
x z y
Tales observou também que os raios solares eram
paralelos, logo os ângulos de incidência dos raios solares
num mesmo instante tinham a mesma medida.
Assim, é possível escrever a seguinte relação:
H ൌ Altura da pirâmide.
H B h ൌ Altura da estaca
=
h b B ൌ Metade da base ൅ sombra.
b ൌ Sombra da estaca.
Essa relação utilizada por Tales facilitou muito a medida de distâncias que aparentemente
não conseguimos alcançar, e mais essa relação de Tales e utilizada até hoje para medir tamanhos de
montanhas, rios arvores...
Teorema de tales.
Se duas retas transversais interceptam um feixe de retas paralelas, então a razão entre dois
segmentos quaisquer de uma reta é equivalente à razão dos segmentos correspondentes da outra.
Observe a ilustração abaixo:

22. No feixe de paralelas e duas transversais, ‫ ݌‬e ‫ .ݍ‬Suponha que exista um segmento ‫ ݑ‬de
஺஻
modo que ‫ ܤܣ‬ൌ ݉‫ ݑ‬e ‫ ܦܥ‬ൌ ݊‫ ݑ‬ሺ݉, ݊ ∈ Գሻ. Assim na razão
஼஽
temos:
஺஻ ௠௨ ௠
ൌ ൌ
஼஽ ௡௨ ௡
തതതത
Analisando os pontos que dividem ‫ ܤܣ‬e
തതതത em ݉ e ݊ partes congruentes ao segmento de
‫ܦܥ‬
medida ‫ ݑ‬são traçadas retas paralelas ao feixe.
Assim os segmentos തതതതതത e തതതതതത ficam divididos
‫`ܦ`ܥ `ܤ`ܣ‬
em ݉ e ݊ partes iguais a ‫ `ܤ`ܣ . ݑ‬ൌ ݉‫ ݑ‬e
‫ `ܦ`ܥ‬ൌ ݊‫.ݑ‬
‫ܤܣ ݉ ݑ݉ `ܤ`ܣ‬
ൌ ൌ ൌ
‫ݑ݊ `ܦ`ܥ‬ ݊ ‫ܦܥ‬
Assim concluímos que:
‫ܤܣ `ܤ`ܣ‬ ‫`ܦ`ܥ `ܤ`ܣ‬ ‫ܤܣ‬ ‫ܦܥ‬
ൌ ‫ ݑ݋‬ ൌ ‫ ݑ݋‬ ൌ
‫ܦܥ `ܦ`ܥ‬ ‫ܤܣ‬ ‫ܦܥ‬ ‫`ܦ`ܥ `ܤ`ܣ‬
A principal ideia e perceber que o segmento ‫“ ݑ‬cabe” ݉ vezes em ‫ ܤܣ‬e ݊ vezes em തതതത .
തതതത ‫ܦܥ‬
Consequentemente ‫“ ݑ‬cabe” ݉ vezes em തതതതതത e ݊ vezes em തതതതതത.
‫`ܤ`ܣ‬ ‫`ܦ`ܥ‬
Exemplo.
Um quadrado ܴܲܳܵ inscrito num triângulo ‫ .ܥܤܣ‬Sendo ‫ ܥܤ‬ൌ 48 ܿ݉ e a altura relativa à base
igual a 32 ܿ݉, Qual a medida do lado desse quadrado?
Primeiramente observemos que o lado ܲܳ é
paralelo ao lado ‫ ܥܤ‬do ∆‫ .ܥܤܣ‬Logo ∆‫ ܳܲܣ‬é semelhante
௫ ଵ଺ି௫
a ∆‫ ,ܥܤܣ‬então: ଶସ
ൌ
ଵ଺
→ ‫ ݔ‬ൌ 4,8
Casos de semelhança
Já sabemos que se dois triângulos internos possuem ângulos congruentes, então os seus
lados são ordenadamente proporcionais.

23. Matematicamente falando:
ܽ ܾ ܿ
ൌ ൌ ො ො, ෠
݁ ܽ ≡ ‫ݕ ≡ ̂ܿ ݁ ̂ݖ ≡ ܾ ݔ‬
ᇣᇧᇧᇧᇧᇧᇤᇧᇧᇧᇧᇧᇥ ො
ᇣᇧ ‫ ݖ‬ᇧᇥ
‫ ݔ‬ᇧᇤᇧ ‫ݕ‬
஼௢௡௚௥௨ê௡௖௜௔
௉௥௢௣௢௥௖௜௢௡௔௟௜ௗ௔ௗ௘
௘௡௧௥௘ ௢௦ â௡௚௨௟௢௦.
௘௡௧௥௘ ௢௦ ௟௔ௗ௢௦.
No entanto essas exigências podem ser reduzidas. Os casos de semelhança que
verificaremos a seguir mostram quais são as condições mínimas para dois triângulos serem
semelhantes.
1° caso: AA (Ângulo – Ângulo)
Definição:
Se dois triângulos (∆) possuem dois ângulos ordenadamente congruentes, então eles são
semelhantes (≈ ) .
ˆ ˆ ˆ
 ≡ A ` e B ≡ B `⇒ ∆ ABC ≈ ∆ A `B `C `
2° caso: LAL (Lado – Ângulo – Lado)
Definição:
Se dois lados de um triângulo são proporcionais aos homólogos de outro triangulo é os
ângulos compreendidos são congruentes, então os
triângulos são semelhantes.

24. ࢉ ࢈
ൌ ൌࡷ
.ࢉ´ ࢈´ ቋ → ∆࡭࡮࡯ ൎ ∆࡭`࡮`࡯` →
෡ ෡
࡭≡࡭
ܽ
→ ቀ ෠ ෠ መ መ
ൌ ‫` ܥ ≡ ܥ ,`ܤ ≡ ܤ ,ܭ‬ቁ
ܽ´
3 caso: LLL (Lado – Lado – Lado)
Definição:
Se dois lados de um triângulo têm os lados homólogos proporcionais, então eles são
semelhantes.
a b c
= = ⇒ ∆ABC ≈ ∆A´B´C´
a´ b´ c´
Teorema de Pitágoras.
Pitágoras nasceu na ilha de Samos, no mar Egeu, por volta de 572 a.C, perto de Mileto onde
há 50 anos nascerá Tales. Foi a partir das ideias desses dois grandes personagens que a matemática
se inicia como ciência e pôde se desenvolver enormemente nos séculos seguintes.
Pitágoras viajou bastante. Esteve no Egito na babilônia,
talvez tenha ido até a índia, ele sempre observava os conceitos
matemáticos e as ideias religiosas de cada região. Voltando a
Grécia, fundou Crotana (Sudeste da Itália, hoje) uma escola na
verdade uma sociedade secreta, dedicada ao estudo da matemática
e da filosofia. A maior parte dos documentos daquela época se
perdeu, logo grande parte das informações que temos daquele
período são de referencias de outros autores que vieram séculos
depois. Por isso que podemos dizer que a figura de Pitágoras é um
tanto obscura na historia da matemática e, para dificultar ainda
mais as coisas, a sua escola, além de secreta era comunitária, ou seja, todas as descobertas e todos
os conhecimentos eram comuns, pertenciam a todos. Assim é difícil saber se o próprio Pitágoras

25. que descobriu o teorema que leva o seu nome, pois era comum naquela época dar todo credito de
uma descoberta ao mestre. Não é conhecido também qual foi a demonstração original, mas
historiadores acreditam que deve ter sido alguma usando áreas.
O teorema de Pitágoras é um dos mais belos é importantes teoremas da matemática de todos
os tempos e ocupa uma posição especial na historia do conhecimento matemático. Desde o século 5
a.C. até o século 20 d.C. inúmeras demonstrações apareceram. Em 1940, o matemático americano
E. S. Loomis publicou 370 demonstrações, mas ainda há mais demonstrações.
O enunciado do teorema de Pitágoras.
Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à
soma das áreas dos quadrados que têm como lados cada um dos catetos.
Sejam ࢇ e ࢈ as medidas dos catetos e ࢉ a medida da hipotenusa o enunciando do teorema de
Pitágoras equivale a afirmar que: A soma dos quadrados dos catetos é igual ao quadrado da
hipotenusa
Expressando matematicamente temos:
ܽଶ ൌ ܾ ଶ ൅ ܿ ଶ
A Demonstração clássica
Para tal demonstração utilizaremos a seguinte identidade algébrica:
ሺܽ ൅ ܾሻଶ ൌ ܽଶ ൅ 2ܾܽ ൅ ܾ ଶ
Primeiro, observe que essa identidade pode ser demonstrada pelo diagrama a seguir.
Note que (a + b ) ² é a área do quadrado de lado a + b que está dividido em dois quadrados
de lados a e b em quatro triângulos retângulos agrupados dois a dois retângulos de lados a e b .

26. ௔௕
ଶ
A área de cada um dos quatro triângulos é . Assim, a área do quadrado maior é igual à
soma das áreas dos dois quadrados menores com a área dos quatro triângulos.
ܾܽ
ሺܽ ൅ ܾሻଶ ൌ ܽଶ ൅ ܾ ଶ ൅ 4 ൬ ൰ ൌ ܽଶ ൅ 2ܾܽ ൅ ܾ ଶ ሺ݅ሻ
2
Agora, um novo arranjo dos triângulos dentro do quadrado maior revela em seu interior um
quadrado de lado c, a hipotenusa do triângulo retângulo de catetos a e b .
Assim temos a seguinte ilustração:
Da mesma forma, a ilustração permite a seguinte interpretação:
ሺܽ ൅ ܾሻଶ ൌ 2ܾܽ
ต ൅ ܿଶ
ณ ሺ݅݅ሻ
á௥௘௔ ௗ௢௦ ௧௥௜â௡௚௨௟௢௦ á௥௘௔ ௗ௢ ௤௨௔ௗ௥௔ௗ௢ ௠௘௡௢௥
Fazendo ሺ݅ሻ ൌ ሺ݅݅ሻ, ‫:ݏ݋݉݁ݐ‬
2ܾܽ ൅ ܿ ଶ ൌ ܽଶ ൅ 2ܾܽ ൅ ܾ ଶ
ܿ ଶ ൌ ܽଶ ൅ ܾ ଶ
Sua Vez...
Você já sabe que existem inúmeras maneiras Uma dica interessante pode ser observada
de demonstrar o teorema de Pitágoras. Apresente uma em:“http://www.youtube.com/watch?v=bFzv6
demonstração diferente das abordadas neste fascículo haSSYg&feature=related”

27. A Demonstração de Perigal.
A demonstração de feita por Perigal é sem dúvida uma das mais elegantes e evidentes da
veracidade do teorema de Pitágoras. Consiste em mostrar que as áreas dos quadrados construídos
sobre os catetos preenchem o quadrado construído sobre a hipotenusa.
Perigal usa o quadrado de lados iguais a hipotenusa do triangulo. Projeta duas retas passando
pelo centro, onde a primeira reta e paralela a hipotenusa do triangulo e a segunda reta é
perpendicular a primeira.
Recíproco do teorema de Pitágoras.
Se num triangulo o quadrado de um lado é igual à soma dos quadrados dos outros dois,
então o triangulo é retângulo.

28. Demonstração:
Suponha um triangulo ‫ ܥܤܣ‬de lados ܽ, ܾ ݁ ܿ, onde ‫ ܤܣ‬ൌ ܿ BC = a e AC = b .
ˆ
Suponha que b < 90 ° .
Faremos a projeção do ponto C sobe o lado AB, o qual
denominaremos de ponto P . Ainda definiremos a distância de AP = x ,
logo a distância de PB = x − c . Note que neste caso P estará contido
no segmento ‫.ܤܣ‬
Assim no triângulo ‫ ܥܲܣ‬retângulo em P , temos as seguintes relações:
b² = x² + h²
h² = b² − x²
Assim no triângulo BPC retângulo em P , temos as seguintes relações:
a ² = h ² + (c − x )²
a ² = b ² − x ² + c ² − 2 cx + x ²
a ² = b ² + c ² − 2 cx
Ou seja, concluímos que se, b < 90 ° , então: ࢇ૛ ൏ ࢈૛ ൅ ࢉ૛
ˆ
Suponha, que no próximo triângulo ˆ
b > 90º .
Faremos a projeção do ponto C sobre o lado AB, denominaremos de ponto P.
Ainda definiremos a distância de AP = x , logo a distância de PB = x − c . Note
que neste caso o ponto P não está contido no ponto no segmento AB , mas
sim em seu prolongamento.
Assim no triângulo CPB retângulo em P, temos as seguintes
relações:

29. ܾ ଶ ൌ ‫ ݔ‬ଶ ൅ ݄ଶ
݄ଶ ൌ ܾ ଶ െ ‫ ݔ‬ଶ
Assim no triângulo ‫ ܥܲܣ‬retângulo em ܲ, temos as seguintes relações:
ܽଶ ൌ ሺ‫ ݔ‬൅ ܿሻଶ ൅ ݄ଶ
ܽଶ ൌ ሺ‫ ݔ‬൅ ܿሻଶ ൅ ܾ ଶ െ ‫ ݔ‬ଶ
ܽଶ ൌ ‫ ݔ‬ଶ ൅ 2‫ ܿݔ‬൅ ܿ ଶ ൅ ܾ ଶ െ ‫ ݔ‬ଶ
ܽ² ൌ ܾ² ൅ ܿ² ൅ 2‫ܿݔ‬
෠
Ou seja, concluímos que se, ܾ ൐ 90°, então: ܽ² ൐ ܾ² ൅ ܿ².
Interpretação dos dados:
Analisando as situações chegamos à seguinte conclusão:
Podemos escrever a seguinte relação entre os lados, e o ângulo em questão.
෠
(i) Se o ângulo ܾ ൏ 90° → ܽ² ൏ ܾ² ൅ ܿ². ෠
(ii) Se o ângulo ܾ ൐ 90° → ܽ² ൐ ܾ² ൅ ܿ².
Então, por exclusão podemos concluir que, para qualquer triângulo ABC de lados a , b e c
tem se que:
෠ ෠
ሺ݅ሻ ܾ ൏ 90° → ܽଶ ൏ ܾ ଶ ൅ ܿ ଶ ሺ݅݅ሻ ܾ ൐ 90° → ܽଶ ൐ ܾ ଶ ൅ ܿ ଶ
෠
ሺ݅݅݅ሻ ܾ ൌ 90° → ܽଶ ൌ ܾ ଶ ൅ ܿ ଶ
Portanto se um triângulo de lados a, b e c é tal que ܽଶ ൌ ܾ ଶ ൅ ܿ ଶ , então esse triângulo é
retângulo no vértice A. Esse resultado é conhecido como a recíproca do Teorema de Pitágoras.
Aplicações do Teorema de Pitágoras.
Diagonal do quadrado.
Em um quadrado de lado ܽ calcule o a diagonal ݀ Como mostra a
figura, ao lado, temos um quadrado de lado a formado pelos vértices
‫ ,ܦܥܤܣ‬sua diagonal e o segmento que une os vértices ‫.ܦܤ‬
Usando o teorema de Pitágoras temos:

30. d ² = a² + a²
Sua Vez... Qual o valor dos
d ² = 2a ²
ângulos? Particionados pela diagonal?
d = 2a ² ⇒ d= a 2 Construa sua resposta baseada em
argumentos matemáticos.
Altura do triângulo equilátero.
Em um triângulo equilátero de lado a calcule o a altura h . Observando a figura, ao lado,
temos um triângulo de lado a formado pelos vértices ABC,
sua altura e a projeção do ponto A no segmento BC.
Usando o teorema de Pitágoras temos:
2
a
a ² =   + h²
2
a²
h² = a ² −
4
3a ² a 3
h= ⇒ h=
4 2
Raio da circunferência
Raio da circunferência circunscrita a um triangulo isósceles de base 8
e altura 10. ‘O’ é o centro da circunferência circunscrita ao triangulo ‫. ܥܤܣ‬
É de fácil verificação que ‫ ܲܤ‬ൌ ܲ‫ , ܥ‬Logo AP divide o segmento ‫ܥܤ‬
em duas partes iguais, ou seja, nesse caso a altura do triângulo esta
localizada sobre a mediatriz de ‫. ܥܤ‬
a² + b² = c²
4² + (10 − R )² = R²
R = 5,8
Sua vez... Diagonal de um paralelepípedo de base retangular. Mostre que a
diagonal do paralelepípedo e representado pela equação abaixo.
ࢊ² ൌ ࢇ² ൅ ࢈² ൅ ࢉ²
Terno Pitagórico ou triângulos Pitagóricos.
Definição: Sendo a, b e c inteiros positivos com ܽ ൐ ܾ e ܽ ൐ ܿ dizemos que ሺܾ, ܿ, ܽሻ é um
terno pitagórico se ܽ² ൌ ܾ² ൅ ܿ².

31. Um terno pitagórico é dito primitivo, quando b e c são primos entre si, ou seja, ݉݀ܿሺܾ, ܿሻ ൌ
1. Logo ሺ3, 4, 5ሻ é um terno pitagórico primitivo. Atenção, todo terno escrito da seguinte maneira
ሺ3݇, 4݇, 5݇ሻ com ݇ maior que 1 é pitagórico, mas não primitivo.
Nesse momento entenderemos melhor como obter triângulos retângulos cujos lados são
medidos por números inteiros, triângulos estes chamados Pitágoricos.
Determinaremos a hipotenusa de um triangulo retângulo com um cateto ܾ ൌ 2‫ ݕݔ‬e outro
‫ ²ݔ‬െ ‫ .²ݕ‬
ܽଶ ൌ ܾ ଶ ൅ ܿ ଶ → ܽଶ ൌ ሺ2‫ݕݔ‬ሻଶ ൅ ሺ‫ ݔ‬ଶ െ ‫ ݕ‬ଶ ሻଶ
ܽଶ ൌ 4‫ ݔ‬ଶ ‫ ݕ‬ଶ ൅ ‫ ݔ‬ସ െ 2‫ ݔ‬ଶ ‫ ݕ‬ଶ ൅ ‫ ݕ‬ସ
ܽଶ ൌ ‫ ݔ‬ସ ൅ 2‫ ݔ‬ଶ ‫ ݕ‬ଶ ൅ ‫ ݕ‬ସ → ܽଶ ൌ ሺ‫ ݔ‬ଶ ൅ ‫ ݕ‬ଶ ሻଶ
ܽ ൌ ‫ݔ‬ଶ ൅ ‫ݕ‬ଶ
Tomando x e y inteiros, primos entre si, um deles sendo par e x maior que y, podemos montar a seguinte
tabela.
Analise um pouco melhor esta
Cateto Cateto Hipotenusa fórmula.
x y x² - y² 2xy x² + y² O que acontece se você atribuir
2 1 3 4 5 para x e y valores ambos pares ou
3 2 5 12 13 ambos impares?
4 1 15 8 17
4 3 7 24 25
5 2 21 20 29 Mostre que se as medidas dos
5 4 9 40 41 catetos de um triângulo retângulo
6 1 35 12 37 são pares, então a hipotenusa nunca
M M M M M será um número impar.

32. Construção de figuras com régua e compasso.
1)De inicio, utilizaremos um segmento de 4 cm de comprimento, para construir um
segmento de 4 2 cm.
Roteiro:
a)Faça um segmento de 4 cm.
b) Construa um quadrado de lado 4cm.
A diagonal deste polígono terá 4 2 cm.
2) Construiremos um triângulo, conhecendo-se os três lados: 4, 5 e 7 cm.
Roteiro:
a) Usando a régua faça um dos lados
b) Com centro em cada extremidade, com aberturas respectivamente iguais aos outros
lados, faz-se o cruzamento dos arcos, determinando o terceiro vértice e definindo a figura.
3) utilizando um segmento de 4cm de comprimento, vamos construir um segmento e
medida 4 3 cm.
Roteiro:
a) Usando a régua faça um dos lados
b) Utilizando a ideia do Roteiro2, construa o triângulo equilátero de lado 4cm.

33. c) Tomado como base um dos lados do triângulo
desenhado, construa outro triangulo equilátero.
d) A figura formada é um losango. Traçando a
diagonal maior temos a união das duas alturas de um
triangulo equilátero. Logo:
Sua vez...
4 3 4 3
+ = 4 3 cm 1) Construa um segmento de comprimento √2 cm.
2) Construa um segmento com a medida de √5 cm.
2 2
3) Construa um segmento de √6 cm
4) Construa um hexágono regular de lado √6.
Representação geométrica dos números irracionais
Nesse momento utilizaremos os conceitos abordados, até o momento para realizarmos a
representação geométrica dos números irracionais.
Os matérias utilizados serão: par de esquadros e um compasso. Esta representação será
realizada no conjunto dos números reais não negativos ሺԹା ሻ
Representando a reta dos (Թା ).
Utilizando o compasso faremos uma circunferência de raio 1 centrada em 1
Utilizando o teorema de Pitágoras, encontramos a medida do comprimento da origem até o
raio da circunferência. Que é de 2 , para projetar está medida na reta basta utilizar o compasso
com a ponta seca na origem e a outra no final do segmento como ilustrado a seguir.
2
Assim encontramos o valor , na reta (Թା ).

34. Utilizando dessa mesma ideia faremos a representação geométrica das outras distâncias.
Observe nas ilustrações a seguir que o raio da circunferência auxiliar tem a medida unitária, esse
raio utilizado é sempre perpendicular a medida determinada anteriormente.
Calculo de 3:
2
Calculo de 4:
Representação na reta.
Sua vez... Faça a representação geométrica de √5, √6 e √7. Em
“http://www.youtube.com/watch?v=DBQkIviCRZc.”Você encontrará um vídeo, que pode ser útil na realização do
exercício.

35. Capitulo 4.
Circunferência .
Os pontos ao lado estão a 2 ܿ݉ do ponto ܲ . Considerando todos os
pontos que estão a 2 ܿ݉ do ponto do ponto ܲ , eles formam uma curva
denominada circunferência.
Assim podemos escrever:
Definição: Circunferência pode ser entendida como o conjunto de todos os
pontos equidistantes a um ponto fixo P , chamado de centro da circunferência. A
distância de um ponto qualquer da circunferência até o ponto ܲ é chamado de raio
da circunferência. O dobro do raio é dito: diâmetro da circunferência.
Corda
Definição: Segmento que possui como extremidades dois pontos
da circunferência. Os segmentos MN e MQ são exemplos de cordas
Diâmetro.
Definição: segmento que possui como extremidades dois pontos da circunferência, passando
pelo cento da mesma. Ou seja, diâmetro é uma corda que passa pelo centro da circunferência. Os
segmentos RS e WT são exemplos de diâmetros.
Posição de ponto e circunferência.
Em uma circunferência de centro ࡼ e raio ࢘ tomado um ponto qualquer ࡭, pertencente ao
mesmo plano da circunferência, temos os seguintes caso:

36. Círculo
Definição: Circulo ou (disco) pode ser entendido como união dos pontos internos de uma
circunferência e a circunferência.
Partes do círculo
Setor Circular:
݅ሻ Setor circular menor ‫ ܤܱܣ‬é o conjunto dos pontos dos raios OA e OB e de todos os
pontos do circulo que estão no interior do ângulo ‫ܣ‬Ô‫.ܤ‬
݅݅ሻ Setor circular maior ‫ ܤܱܣ‬é o conjunto dos pontos dos raios OA e OB e de todos os
pontos do circulo c que estão no exterior do ângulo ‫ܣ‬Ô‫. ܤ‬
Segmento circular:
݅ሻ Segmento circular menor ࡭࡮ e a intersecção do circulo com O semi-plano de origem na
reta AB e que não contem o centro da circunferência.

37. ݅݅ሻ Segmento circular maior ࡭࡮ e a intersecção do circulo com o semi-plano de origem na
reta ࡭࡮ e que contem o centro ܱ.
Semicírculo:
Quando ‫ ܣ‬e ‫ ܤ‬são extremidades de um diâmetro do circulo, semicírculo AB e a intersecção
do circulo com um dos semi-planos de origem na reta. AB
Secante.
Uma reta secante a uma circunferência e uma reta que intercepta a circunferência em dois
pontos distintos. Podemos dizer ainda que a circunferência e a reta são secantes.
Propriedade.
݅ሻ A reta perpendicular à secante, conduzida pelo centro da circunferência, passa pelo ponto
médio da corda.
݅݅ሻ A reta conduzida pelo centro e que passa pelo ponto médio da corda é perpendicular a
secante.

38. Tangente.
Uma reta tangente a uma circunferência é uma reta que intercepta a circunferência em um
único ponto.
Propriedade
݅ሻ Qualquer reta perpendicular a um raio na sua extremidade da circunferência e tangente a
circunferência.
݅݅ሻ Toda tangente a uma circunferência e perpendicular ao raio no ponto da tangencia.
Posições relativas de duas circunferências.
Circunferências tangentes.
Dizemos que duas circunferências, C1 e C2 , são tangentes quando ambas possuem um único
ponto, ܶ, em comum.
Se traçarmos uma reta ‫ ݏ‬passando pelo ponto de tangencia ܶ de duas circunferências
tangentes internas, teremos como consequência:
݅ሻ Que a reta s será tangente a as duas circunferências.

39. ݅݅ሻ Como existe uma única reta perpendicular à reta ‫ ݏ‬que passa pelo ponto ܶ, teremos os
pontos O1 , O2 e ܶ pertencentes a uma única reta.
Circunferências Concêntricas.
Quando uma circunferência, C1 , e interna a C2 de forma que o centro de C1 coincida com o
centro de C2 dizemos que C1 e C2 são concêntricas.
Circunferências secantes.
Duas circunferências são secantes se tem apenas dois pontos, distintos, em comum. Observe
a figura a seguir:
Segmentos Tangentes.
Verificaremos algumas propriedades de segmentos tangentes a uma circunferência. Antes
disse faremos uma breve revisão, observando a ilustração a
seguir.
݅ሻ C e uma circunferência de centro ܱ.
݅݅ሻ O ponto ܲ externo a circunferência ‫.ܥ‬
݅݅݅ሻ Onde PA e PB são tangentes a circunferência ‫, ܥ‬
nos pontos ‫ ܣ‬e ‫.ܤ‬
Propriedades.
Tracejaremos um segmento OP , assim como os raios OA e OB . Teremos então a formação
dos triângulos ܲ‫ ܱܣ‬e ܲ‫.ܱܤ‬
Observando melhor esses triângulos podemos aplicar
um caso especial de congruência de triângulos retângulos
(Cateto-hipotenusa). Logo:

40. OA ≡ OB (raio)


OP Comum os dois triângulos
ˆ ˆ
A = B = 90º

Conclusões:
݅ሻ Se de um ponto ܲ, externo a uma circunferência, traçarmos segmentos PA e PB , onde
ambos tangenciam uma circunferência nos pontos ‫ ܣ‬e ‫ ,ܤ‬então:
PA ≡ PB
݅݅ሻ Observando a congruência dos triângulos ܲ‫ ܱܣ‬e ܲ‫ ,ܱܤ‬verificamos que:
ˆ ˆ
APO ≡ BPO
ˆ ˆ
݅݅݅ሻ A conclusão de que APO ≡ BPO implica que o segmento de reta OP e bissetriz do
ˆ
ângulo APB . Se os lados de um ângulo tangenciam uma circunferência então o cento da mesma
está contido na bissetriz desse ângulo.
Arcos de uma Circunferência.
Observando as ilustrações a seguir, construiremos a ideia de arco.
Na circunferência ‫ , ܥ‬de centro ܱ temos dois de seus pontos ‫ ܣ‬e ‫ ܤ‬que
não são extremidades de um diâmetro. Esses pontos permitem decompor a
circunferência em duas partes chamadas de arcos.
Sempre que se faz referência a um arco , considera-se o arco menor . Onde ‫ ܣ‬e ‫ ܤ‬são
as extremidades do arco.
Ângulo Central.
Definição: É chamado de ângulo central, o ângulo que tem como
vértice o centro, ܱ , de uma circunferência, como mostrado na
ilustração.
- AÔB é um ângulo central.
- é o arco correspondente ao ângulo central.
Medida de um Arco.

41. Para determinarmos a medida de um arco primeiramente é necessário sabermos qual é
unidade de arco. Chamaremos de unidade de arco, o arco correspondente a um ângulo central de 1º.
Como mostra o desenho.
Em ainda em duas circunferências concêntricas, o ângulo central em cada circunferência
será o mesmo, logo o comprimento dos arcos correspondentes será igual.
Medida do ângulo inscrito em uma circunferência.
Definição: Um ângulo será inscrito a uma circunferência quando o
seu vértice pertencer a uma circunferência, e os lados secantes a ela.
Observando melhor a figura podemos escrever:
ˆ
- AVB é um ângulo inscrito.
- ˆ
é o arco correspondente ao ângulo AVB
- AÔB é o ângulo central correspondente ao arco .
Podemos dizer ainda que AÔB é o ângulo central correspondente
ˆ
ao ângulo inscrito AVB , pois ambos determinam o mesmo arco .
Medida do ângulo inscrito.
Podemos classificar de três formas o ângulo inscrito, relacionando-o com o centro, ܱ, da
circunferência.
Faremos algumas abreviações de modo que:
- Ângulo inscrito. AVB = α
ˆ
- Ângulo Central. AÔB = θ , essa medida também será a medida arco .
ˆ
1º Caso: Com o centro, O, pertencente a um dos lados do ângulo interno AVB .
O triangulo OVB é isósceles, pois OB e OV são raios da circunferência. Pela propriedade
ˆ ˆ
do triangulo isósceles, sabemos que V ≡ B , logo a medida do ângulo
V = B =α .
ˆ ˆ

42. O ângulo BÔA = θ , é o ângulo externo do triângulo ܱܸ‫ .ܤ‬Por isso, o ângulo θ é igual à
θ
soma dos ângulos internos não adjacentes a ele, logo: α + α = θ → 2α = θ → α=
2
ˆ
2º Caso: Com o centro, ܱ, externo ao ângulo inscrito AVB .
Tracejando a semirreta VO , que determina o ponto T na circunferência. Temos então dois
ângulos, φ = AVT e β = BVT , como representados na figura.
ˆ ˆ
TA TB
φ= e β=
2 2
Usando a ideia do ૚º࡯ࢇ࢙࢕, temos:
AB θ
α =β−φ → α =β−φ → α = → α=
2 2
ˆ
3º Caso: Com o centro, O, internamente ao ângulo AVB .
α = Tracejando a semirreta VO , que determina o ponto ܶ na circunferência. A semirreta
esta sob a bissetriz do ângulo α , assim ela divide o ângulo α em α1 e α 2 , consequentemente
divide o arco ‫ , ܤܣ‬em ‫ ܶܣ‬e ܶ‫ , ܤ‬de forma análoga, ao 1º caso, podemos escrever:
஻் ஺்
ߙଵ ൌ
ଶ
݁ ߙଶ ൌ
ଶ
Visto que ߙଵ ൅ ߙଶ ൌ ߙ
Logo:
‫ߠ ܤܣ ܤܶ ܶܣ‬
ߙൌ ൅ ൌ →
2 2 2 2
ߠ
ߙൌ
2
Conclusão: O ângulo inscrito a uma circunferência equivale à metade do ângulo central
θ
correspondente. α =
2
Radiano.
Até o momento utilizamos apenas o grau como unidade de medida de ângulos e arcos.
Porém existe outra unidade de medida, que será muito utilizada no estudo de trigonometria, o
radiano.
Definição: radiano é o arco da circunferência cujo comprimento é igual ao raio da
circunferência que o contém. Chama-se 1 radiano e representa-se por 1 ‫ ݀ܽݎ‬de arco.

43. De forma análoga o ângulo central θ corresponde ao arco de 1 ‫ . ݀ܽݎ‬Da definição que a
medida de um arco ‫ ܤܣ‬em radianos é dada por:
Comprimento de AB
Medida em rad do arco AB =
raio
Comprimento da Circunferência.
O comprimento, ‫ , ܥ‬de uma circunferência e dado em função do
raio, ࢘, por meio da relação C = 2.π .r , onde π é um número
irracional, correspondente a razão entre o comprimento da circunferência e o seu diâmetro.
Utilizando essa relação determinaremos a medida d arco de uma volta em radianos:
஼௢௠௣௥௜௠௘௡௧௢஺஻
Medida em ‫ ݀ܽݎ‬do ‫ ܤܣ‬ൌ
௥௔௜௢
2. ߨ. ‫ݎ‬
ൌ 2. ‫݀ܽݎ .ݎ‬
‫ݎ‬
Essa medida de 2. π.rad corresponde ao arco de uma circunferência, ou seja, o arco tem a
medida de 360°, assim a medida de um arco de 180º será equivalente a π.rad .
Quadratura do círculo.
Dentre os muitos problemas que intrigaram os matemáticos de muitas as épocas, nenhum
problema despertou mais fascínio do que aquele de construir um quadrado de área igual à área de
um círculo qualquer, utilizando-se de régua e compasso.
Os Egípcios por volta de 1800 a.C pensavam ter “resolvido” o problema, tomando o lado do
quadrado como 8/9 do diâmetro do círculo. Podemos ainda citar Nicholas de Cusa1 (1401 - 1450)
considerado melhor eclesiástico do que matemático. Na igreja ele subiu ao posto de cardeal, mas no
domínio da matemática era considerado como um desorientado quadrador – de – círculo. Sua
doutrina filosófica da “concordância de contrários” levou-o a acreditar que máximos é mínimos são
relacionados. Ele acreditava que tomando as médias de polígonos inscritos e circunscritos tinha
chegado à quadratura. O seu erro é menos importante que o fato de ser ele um dos primeiros
europeus modernos a atacar um problema que havia fascinado os grandes pensadores da
antiguidade, assim o seu esforço estimularia os seus contemporâneos.
1
(Cusa era o nome latino de uma cidade sobre o Mosela.)

44. O Francês Pierre Laurent Watzel, por volta de 1835, publicou efetivamente a
impossibilidade de se efetuar determinadas construções geométricas utilizando apenas régua e
compasso.
A busca para a solução deste problema esta ligada diretamente ao número π , “pi”, que é a
razão, constante, entre o comprimento da circunferência e o seu diâmetro correspondente.
Representando matematicamente chegamos á seguinte expressão:
C C: Comprimento da
π= ⇒ C = π.D ⇒
D circunferência.
⇒ C = 2.π .r
D: Diâmetro.(dobro do raio).
Porém a área do círculo e dada pelo produto do raio r ² por π , ou seja, AC = π .r ² . Podemos
dizer então que a área de um círculo será tão precisa quanto for a determinação de π . Para entender
melhor essa idéia faremos a analise da seguinte situação: Suponha um o circulo de raio igual a 2
cm, desejamos construir um quadrado de área igual.
Para nossa análise utilizaremos das equações que permitem o calculo das áreas do circulo,
AC , e do quadrado AQ .
AQ = AC
x ² = 4π ⇒ x = 4π
⇒x=2 π
Para que a área do quadrado igual área
AC = π . r ² do círculo, o lado do quadrado deve ter a
AC = π .2² AQ = x ² medida de 2 π cm.
AC = 4π cm²
Concluímos que tomando como unidade de comprimento o raio do circulo dado, 2 cm, o
comprimento do lado do quadrado equivalente será de 2 π . Logo se o problema pudesse ser
resolvido com instrumentos euclidianos seria possível construir um segmento unitário de tamanho
π e a partir desse segmento podemos construir um quadrado de lado 2 π . Porém isso não é
possível como mostrou o matemático alemão Ferdinand Von Lindemann, que demonstrou que π
não é algébrico, ou seja, π não é solução de nenhuma equação polinomial com coeficientes de
números inteiros, consequentemente isso implica que π , também não é algébrico. Isso implica
dizer que não é possível construir segmentos, com régua e compasso, que tenham o tamanho de π, e
π .

45. Capitulo 5.
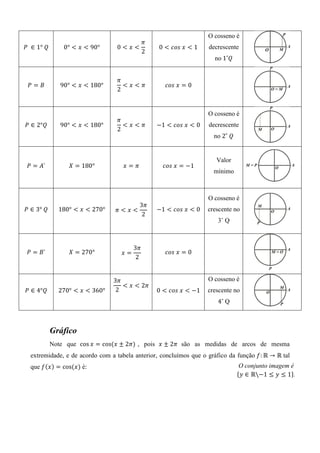
Razões trigonométricas.
Uma das necessidades mais antigas da humanidade é a de medir distâncias algo
extremamente fácil de ser realizado no caso de medidas curtas, ou entre pontos acessíveis. Bastando
verificar quantas vezes uma dada unidade de medida esta contida no comprimento a ser medido.
Essa é a ideia usada nos instrumentos de medida mais comuns para medir comprimentos: trenas,
fitas métricas, réguas, etc.
Se medir distâncias curtas é fácil, como podemos fazer a medida de
distâncias não tão acessíveis?
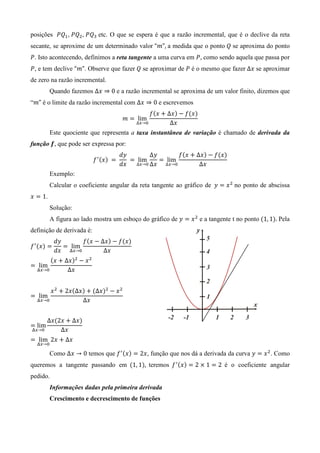
Para obter essas medidas realizaremos algumas
experiências, com medidas conhecidas (acessíveis). Para
isso tomaremos um triângulo retângulo. De medidas
ሺ1,8; 2,4; 3ሻ.Observe a ilustração.
Utilizando a figura tracejaremos retas, auxiliares,
paralelas ao segmento CB.
Observe, com atenção, os novos triângulo formados
AB1C1 , AB2C2 , AB3C3 , ⋯ AB7C7 , todos são semelhantes
entre si e semelhantes ao triângulo ABC . Assim podemos escrever as seguintes razões:
B1C1 B2 C 2 BC BC
[i ] = =L= 7 7 = = 0,75
AB1 AB 2 AB 7 AB
B1C1 B2 C 2 BC BC
[ii ] = =L= 3 3 = = ,08
AC 1 AC 2 AC 3 AC
AB1 AB 2 AB 7 AB
[iii ] = =L= = = 0,6
A1C1 A2 C 2 A7 C 7 AC
Conclusões:
ˆ
Se fixarmos o ângulo A que está presente em todos os demais triângulos, as razões.

46. ˆ ˆ
cateto oposto a A cateto adjacente a A cateto oposto a A ˆ
, ,
hipotenusa hipotenusa cateto adjacente a Aˆ
Não depende do tamanho do triângulo considerado. Em qualquer um dos triângulos, AB1C1 ,
AB2C2 , AB3C3 , L AB7C7 , essas razões valem respectivamente:
‫ ܽ ݋ݐݏ݋݌݋ ݋ݐ݁ݐܽܥ‬Â ‫ ܽ ݁ݐ݆݊݁ܽ݀ܽ ݋ݐ݁ݐܽܥ‬Â ‫ ܽ ݋ݐݏ݋݌݋ ݋ݐ݁ݐܽܥ‬Â
ൌ ൌ
݄݅‫ܽݏݑ݊݁ݐ݋݌‬
ᇣᇧᇧᇧ ᇧᇧᇤᇧᇧᇧ ݄݅‫ܽݏݑ݊݁ݐ݋݌‬
ᇧᇧᇥ ᇣᇧᇧᇧᇧᇧᇧᇤᇧᇧᇧᇧᇧᇧᇥ ᇣᇧᇧᇧ ‫݁ݐ݆݊݁ܿܽ݀ܽ ݋ݐ݁ݐܽܥ‬
ᇧᇧᇤᇧᇧᇧ ᇧᇧᇥ
଴,଼ ଴,଺ ଴,଻ହ
ˆ
Esses números estão diretamente ligados à medida o ângulo A .Se utilizássemos outro
ˆ ˆ
triângulo retângulo qualquer, com medidas diferentes, com um ângulo P diferente de A ,
encontraremos as seguintes razões:
ˆ
cateto oposto a P
= 0,833333333
hipotenusa
ˆ
cateto adjacente a P
= 0,7
hipotenusa
ˆ
cateto adjacente a P
= 1,02041
hipotenusa
መ
Para cada ângulo agudo ሺ‫ܣ‬ሻ, essas três razões que só dependem
መ
da medida do ângulo ሺ‫ܣ‬ሻ, vão agora receber um nome.
መ
Dado um triângulo ‫ ܥܤܣ‬retângulo em ‫ ܤ‬e que tenha ሺ‫ܣ‬ሻ como
um de seus ângulos. Denomina-se:
መ
Seno de um ângulo ‫ܣ‬
෡
Chama-se seno de um ângulo ࡭ a razão entre o cateto oposto ao ângulo e a hipotenusa.
ܾ
መ መ ෡
ܵ݁݊‫ ܣ‬ൌ ൫ܵ݁݊‫݈ ܣ‬ê െ ‫" :݁ݏ‬Seno de A"൯
ܿ
መ
Cosseno de um ângulo ‫ܣ‬
෡
Chama-se seno de um ângulo ࡭ a razão entre o cateto oposto ao ângulo e a hipotenusa.
ܽ
መ መ መ
‫ ܣݏ݋ܥ‬ൌ ሺ‫݈ ܣݏ݋ܥ‬ê െ ‫"ܣ ݁݀ ݋݊݁ݏݏ݋ܥ" :݁ݏ‬ሻ
ܿ
መ
Tangente de um ângulo ‫ܣ‬
መ
Chama-se tangente de um ângulo ‫ ܣ‬a razão entre o cateto oposto ao ângulo e o cateto adjacente.

47. ܾ
መ መ ෢
ܶ݃‫ ܣ‬ൌ ൫‫݈ ܣ݃ݐ‬ê െ ‫:݁ݏ‬tangente de A ൯
ܽ
Razões inversas
As razões inversas das três acima são chamadas respectivamente de cossecante, secante e
ˆ
cotangente de A . Serão expressas abaixo.
Cossecante. (Inverso da razão seno.)
1 ܿ ܿ
መ መ
‫ ݋ܥ‬െ ‫ ܣܿ݁ݏ‬ൌ ܵ݁݊ିଵ ‫ ܣ‬ൌ ൌ መ
→ ‫ ݋ܥ‬െ ‫ ܣܿ݁ݏ‬ൌ
መ
ܵ݁݊‫ܣ‬ ܾ ܾ
Secante. (Inverso da razão cosseno).
1 ܿ ܿ
መ መ
ܵ݁ܿ‫ ܣ‬ൌ ‫ି ݏ݋ܥ‬ଵ ‫ ܣ‬ൌ ൌ መ
→ ܵ݁ܿ‫ ܣ‬ൌ
መ
ܿ‫ܣݏ݋‬ ܾ ܽ
Cotangente. (inverso de tangente)
1 ܿ ܿ
መ መ
‫ ܣݐ݋ܥ‬ൌ ܶܽ݃ିଵ ‫ ܣ‬ൌ ൌ መ
→ ‫ ܣݐ݋ܥ‬ൌ
መ
ܶܽ݃‫ܣ‬ ܾ ܽ
Aplicações.
Exemplo 1.
Ao apoiar uma escada num muro vertical, qual o valor
numérico das razões trigonométricas? Sabendo que o muro é de
4m e o comprimento da escada 5m
4 AC 4
Sen â = , cos â = , tgâ =
5 5 AC
Utilizando o teorema de Pitágoras temo que:
( AC) ² + 4² = 5²
AC = 9 Caso fosse tomado como referência o ângulo ˆ
b , as
AC = 3 razões mudariam? Há algum caso que elas seriam
iguais? Justifique. Qual o valor da medida do ângulo para que isso
4 3 4
Sen â = , cos â = , tgâ = ocorra?
5 5 3
Exemplo 2
Tomemos o seguinte triângulo retângulo. As razões nesse triângulo são as mesmas da
triangulo anterior. Visto que esse triângulo é semelhante ao caso anterior. O
triângulo pertence ao terceiro caso de semelhança de triângulos logo:
3 ‫ݔ‬ 3 ‫ݔ‬
‫ ܽݏ݋ܥ‬ൌ
ො መ
ൌ ‫ ݀ݏ݋ܥ‬ൌ → ൌ →‫ݔ‬ൌ9
5 15 5 15

48. Exemplo 3.
ସ
෠
No triangulo ‫ , ܥܤܣ‬retângulo em ‫ ,ܣ‬de hipotenusa de 15 ܿ݉, sabe-se que ܵ݁݊‫ ܤ‬ൌ
ହ
determine:
a) O valor de ‫ ܥܣ‬e ‫.ܥܤ‬
௫ ସ
෠
ܵ݁݊‫ ܤ‬ൌ ൌ → ‫ ݔ‬ൌ 12ܿ݉.
ଵହ ହ
15ଶ ൌ 12ଶ ൅ ‫ ݕ‬ଶ → ‫ ݕ‬ൌ 9
෠ ෠
b) ‫ ܤݏ݋ܥ‬e ܶ݃‫ܤ‬
9 12
෠
‫ ܤݏ݋ܥ‬ൌ ෠
ܶ݃‫ ܤ‬ൌ
15 9
መ መ መ መ
c) (Sua Vez) ܵ݁݊‫ ܥ‬e ‫ ܥ݃ܶ , ܥݏ݋ܥ‬e ‫. ܥ݃ݐ݋ܥ‬
Relações entre razões trigonométricas.
As razões trigonométricas de um mesmo ângulo têm relações entre si. Observe:
ˆ b ˆ ˆ a
senB = ⇒ c . senB = b cosB = ⇒ c .cosB = a
ˆ
c c
Utilizando o teorema de Pitágoras.
c2 = a 2 + b2 ⇒
ˆ ˆ
c 2 = (c.senB ) 2 + (c.cosB )2
ˆ ˆ
c 2 = c 2.sen2 B + c 2.cos2 B
ˆ ˆ
1 = sen2 B + cos2 B
Logo:
෠ ෠
ܵ݁݊ଶ ‫ ܤ‬൅ ‫ ݏ݋ܥ‬ଶ ‫ ܤ‬ൌ 1
ௌ௘௡஻෠
Calculando o quociente , no mesmo triângulo, temos:
෠
஼௢௦஻
b
ˆ c
senB b c b
= ˆ
= . = = tgB
ˆ a
cosB c a a
c
Logo:
෠
ܵ݁݊‫ܤ‬
෠
ܶ݃‫ ܤ‬ൌ
෠
‫ܤݏ݋ܥ‬

49. ˆ
Estas relações permitem que sejam obtidas todas as razões trigonométricas de um ângulo agudo B ,
uma vez conhecendo qualquer uma delas.
Exemplo 4.
Sabendo que a tangente de um ângulo agudo α , é igual a 2. Calcule sen α e cos α . Como
senα
tgα = = 2, , ou seja, senα = 2 cos α . Substituindo na relação sen 2 α + cos 2 α = 1 , temos:
cos α
(2cosα )2 + cos²α = 1 ⇒ 4cos²α + cos²α = 1 ⇒
1 1
cos²α = ⇒ cosα =
5 5
5 2 5
cosα = → Senα = 2cosα =
5 5
Razões trigonométricas de ângulos fundamentais.
i) Seno, cosseno e tangente do ângulo de 30°.
Para obter o valor das seguintes razões, faremos uso de um triângulo
equilátero de lado ݈ . Ao traçar uma de suas alturas obtemos dois triângulos
௟ ௟√ଷ
retângulos de medidas ݈ , e com ângulos de 30°, 60° e 90°.
ଶ ଷ
Utilizaremos apenas um destes triângulos para realizar as demonstrações.
l
l 1 1 1
sen30° = 2 = . = ⇒ sen30° =
l 2 l 2 2
l 3
l 3 1 1 3 3
cos30° = 2 = . = ⇒ cos30° =
l 2 l 2 2
l
l 2 3 3
tg30° = 2 = . = ⇒ tg30° =
l 3 2 l 3 3 3
2
ii) Seno, cosseno e tangente do ângulo de 45°.
Para obter o valor das seguintes razões, faremos uso de um quadrado
de lado l . Ao traçar uma de suas diagonais obtemos dois triângulos
retângulos de medidas l , l e l 2 com ângulos de 45°, 45° e 90°.
Novamente utilizaremos apenas um destes triângulos para realizar as
demonstrações.

50. l l 2 2 2
sen45° = = . = ⇒ sen30° =
l 2 1 l 2 2 2
2
l l 2 2 2
cos45° = = . = ⇒ sen45° =
l 2 1 l 2 2 2
2
l
Tg45° = 2 = 1 ⇒ tg45° = 1
l
2
iii) Seno, cosseno e tangente do ângulo de 60°.
Para obter o valor destas razões, faremos uso do triângulo já visto em “(i)”, porém tomando como
ângulo referencial o de medida de 60°.
l 3
l 3 1 1 3 3
sen60° = 2 = . = ⇒ sen60° =
l 2 l 2 2
l
l 1 1 1
cos60° 2 = . = ⇒ cos60° =
l 2 l 2 2
l 3
l 3 2
tg60° = 2 = . ⇒ tg60° = 3
l 2 l
2
Agora podemos construir a tabela com o seno, cosseno e a tangente dos principais ângulos
ou ainda dos ângulos fundamentais.
30° 45° 60°
1
senα 2 3
2 2 2
1
cosα 3 2
2 2 2
tg α 3
1 3
3
Seno, cosseno e tangente de ângulos quaisquer.
Para obter uma das razões trigonométricas de um ângulo qualquer incluindo ângulos não
fundamentais, como o de 23°, podemos utilizar o seguinte processo:

51. Com o auxilio de um transferidor, construímos um ângulo de 23°.
Utilizando deste ângulo medido faremos um triangulo retângulo.
Depois de construído medimos os lados deste triângulo e construímos as
devidas razões.
2,12 5 2,12
sen23 = ≅ 0,39 cos23 = ≅ 0,92 tg23 = ≅ 0,424
5,43 5,43 5
Agora podemos utilizar das razões do ângulo de 23° para determinar os lados quaisquer de um
triangulo retângulo, que tenho um de seus ângulos medindo 23°.
3 3 ‫ݔ‬ ‫ݔ‬
‫ °32ݏ݋ܥ‬ൌ → 0,39 ൌ → ࢟ ൌ ૠ, ૟ૢ ܵ݁݊23° ൌ → 0.92 ൌ → ࢞ ൌ ૠ, ૙ૠ
‫ݕ‬ ‫ݕ‬ 7,69 7,69
Aplicações.
As razões trigonométricas são, também, muito utilizadas na resolução de alguns problemas
físicos. Porém para compreender melhor essas soluções, e a utilização dessa ferramenta,
necessitamos alguns conceitos físicos.
Noção de força (F ) .
Força é o resultado da interação entre corpos. Ela pode produzir equilíbrio, variação de
velocidade e deformação. Por exemplo, quando um jogador de futebol da um chute, a força que ele
aplica na bola só aparece no momento em que o pé toca a bola. Essa força produz velocidade.
Assim que a bola se afastar do pé, a força que este aplicou nela deixa de existir – a bola ganhou
velocidade. Dependendo da direção e do sentido que uma força é aplicada, o efeito produzido é
diferente. Logo a força a força requer uma apresentação vetorial. A soma vetorial da ação de
r
varias forças produz o efeito de uma única força denominada resultante ( R) . Se o corpo se
encontra em equilíbrio, concluímos que a resultante é nula.

52. Força-peso (P ) .
A força peso (P ) é uma força de campo, pois ocorre pela ação à distância entre os corpos.
A intensidade de P pode ser expressa matematicamente multiplicando a massa m pela intensidade
r
da aceleração da gravidade ( g ) . P = mg Vetorialmente, temos: P = mg .
Exemplo 1.
A figura ao lado mostra uma partícula, na qual são aplicadas duas
forças de intensidades respectivamente iguais a 12N e 18N. Determinar a
intensidade da resultante.
Para determinar a intensidade da força resultante devemos primeiramente, projetar a
intensidade de F1 e F2 , nos eixos x e y.
Assim temos:
F1 x F1 y
Sen 30° = Cos 30° =
F1 F1
F1 x = F1 Sen30° F1 y = F1 Cos30°
F1 x = 6 N F1 y ≅ 10,4 N
Fy = 15,59 N
2
Repetindo a mesma ideia para F2 , temos:
F2 x = 9 N F2 y = 15,59 N .
O sistema de força é equivalente ao expressado abaixo:
Para determinar a intensidade da força resultante basta utilizar do
teorema de Pitágoras.
2
a 2 = b 2 + c 2 ⇒ R = 15 2 + 5,19 2 ⇒ R = 15,87 N
Exemplo 2.
Dois cabos estão atados em C, mantêm suspensa uma
carga, como mostra a figura. Determine as trações em AC e BC.

53. Para determinarmos as trações em cada cabo primeiramente devemos projetar as trações
em um eixo coordenado relativo, tomando como origem o ponto C,
como mostrado na ilustração.
Para resolução deste exercício devemos notar que o corpo
esta em equilíbrio logo a resultante das forças será igual a zero.
Assim podemos escrever que a soma das forças projetadas
nos eixos respectivos também será igual a zero.
Soma das forças no eixo x. Soma das forças no eixo Y.
∑F x =0 ∑F y =0
Depois de projetadas as forças nos eixos x e y,
teremos a seguinte representação:
Bastando realizar a soma das forças nos
respectivos eixos.
Soma das forças no eixo x. Soma das forças no eixo Y.
∑F x =0 ∑F y =0
− TCA .Cos50º + TCB .Cos30º = 0 TCA .Sen50º + TCB .Sen30º − 400 = 0
0,866 TCB = 0,643TCA TCA .Sen50º + 0,742.Sen30º − 400 = 0
TCB = 0,742TCA TCA = 351,75 N
Logo:
TCA = 351,75 N TCB = 261N

54. Capitulo 6.
Funções trigonométricas.
Introdução:
A história das funções trigonométricas como iremos ver é a evolução de diversos
resultados. Destacam-se os trabalhos de François Viéte (1540 - 1603) e principalmente de
Leonhard Euler (1707 - 1783) em um dos seus mais importantes tratados: Introductio in
analysin infinitorum (1748).
Para definirmos as funções trigonométricas, iremos iniciar com o estudo do ciclo
trigonométrico e as determinações positivas e negativas de um arco. A ideia central é que as
funções trigonométricas serão definidas a partir de outra função que associa a cada numero
real um ponto sobre o ciclo trigonométrico. Feito isso, na seção seguinte, definiremos as
funções seno, cosseno, tangente.
Ciclo trigonométrico – determinações
Ciclo trigonométrico
Chamamos de ciclo trigonométrico a uma circunferência de raio unitário na qual
fixamos um ponto (A) como origem dos arcos e a adotamos o sentido anti-horário como
positivo.
Arco trigonométrico
Chamamos de arco trigonométrico ‫ ܲܣ‬ao conjunto dos infinitos arcos de origem ‫ ܣ‬e
extremidade ܲ . Esses arcos são obtidos, partindo- se da origem ‫ ܣ‬e girando em qualquer
sentido (positivo ou negativo) até a extremidade ܲ, seja na primeira passagem ou após varias
voltas completas no ciclo trigonométrico.
Analogamente, chamamos de ângulo trigonométrico ‫ ܱܲܣ‬ao conjunto dos infinitos
ângulos de lado inicial a ሬሬሬሬሬԦ e lado terminal ሬሬሬሬሬԦ.
ܱ‫ܣ‬ ܱܲ

55. Conjunto das determinações de um arco
Seja P um ponto qualquer de um ciclo trigonométrico de origem A. A medida do arco AP,
de origem A e extremidade P é, por convenção:
Positiva se o sentido do percurso de A para P for o anti-horário.
Negativo se o sentido de percurso de A para P for horário
O ponto P é extremidade de infinitos arcos de origem A e a medida de cada um deles é
chamada determinação. A medida ∝଴ do arco AP, tal que 0 ൑ ∝଴ ൏ 2ߨ é chamada primeira
determinação positiva do arco.
Primeira determinação positiva
Adicionando à primeira medida o numero 2ߨ , que equivale a percorrer uma volta do sentido
anti-horário, obtém-se o numero ∝଴ ൅ 2ߨ que é a segunda determinação positiva de ‫ܲܣ‬
Subtraindo da primeira determinação positiva o número 2ߨ , que equivale a percorrer uma
volta no sentido horário, obtém-se ∝଴ െ 2ߨ que é a primeira determinação negativa do arco ‫. ܲܣ‬

56. Funções Trigonométricas
Consideremos no ciclo trigonométrico de origem ‫ ,ܣ‬um sistema cartesiano ortogonal
ܱܻܺ conforme mostra a figura abaixo. Os pontos ‫ ܣ‬ሺ1, 0ሻ, ‫ܤ‬ሺ0, 1ሻ, ‫’ܣ‬ሺെ1, 0ሻ e ‫’ܤ‬ሺ0, െ1ሻ
dividem o ciclo trigonométrico em quatro quadrantes. Quando dizemos que um arco ‫ܲܣ‬
pertence ao 2˚ quadrante, por exemplo, queremos dizer que a extremidade ܲ pertence ao
segundo quadrante.
Definição da função seno
O seno de um arco trigonométrico ‫ ܲܣ‬de extremidade ܲ é a ordenada do ponto ܲ .
Representa-se: ܵ݁݊ ‫ ܲܣ‬ൌ ܱܰ
A cada numero real ‫ ݔ‬corresponde um único ponto P, extremidade do arco AP de
medida ‫ . ݔ‬A cada ponto P, por sua vez, corresponde uma única ordenada camada seno de ‫. ݔ‬
A função de Թ em Թ que a cada número real associa a ordenada do ponto P é, por definição,
a função seno. Em símbolo ݂: Թ ⟶ Թ ‫݂ ݁ݑݍ ݈ܽݐ‬ሺ‫ݔ‬ሻ ൌ ‫݊݁ݏ‬ሺ‫ݔ‬ሻ ൌ ܱܰ

57. Observação
గ
A definição acima é coerente com aquela no triangulo retângulo. De fato, se 0 ൏ ‫ ݔ‬൏
ଶ
então ܲ߳ ‫ °ܫ‬quadrante e além disso ܱܲ ൌ 1 (raio) e ‫ ܲܯ‬ൌ ܱܰ . Assim no triângulo ܱ‫ܲܯ‬
retângulo em ‫ , ܯ‬termos:
ܿܽ‫݋ݐݏ݋݌݋ .ݐ‬ ‫ܲܯ‬ ‫ܲܯ‬
‫ ݔ ݊݁ݏ‬ൌ ⇔ ‫ ݔ ݊݁ݏ‬ൌ ⇔ ‫ ݔ ݊݁ݏ‬ൌ ⇔ ‫ ݔ ݊݁ݏ‬ൌ ܱܰ
݄݅‫ܽݏݑ݊݁ݐ݋݌‬ ܱܲ 1
Variação da função seno.
Enquanto o ponto P percorre a primeira volta, no sentido anti-horário, o numero real ‫ݔ‬
varia de 0 ܽ 2ߨ e o seno de ‫ ݔ‬varia de െ1 ܽ 1. Observe na tabela abaixo, variações possíveis.
Medida do
Posição do Medida do arco Propriedad No ciclo
arco em Seno de ࢞
ponto P em graus e trigonométrico
radianos
ܲ≡‫ܣ‬ ‫ ݔ‬ൌ 0° ‫ݔ‬ൌ0 ܵ݁݊ ‫ ݔ‬ൌ 0
O seno é
ߨ crescente
ܲ ∈ 1° ܳ 0° ൏ ‫ ݔ‬൏ 90° 0൏‫ݔ‬൏ 0 ൏ ‫ ݔ ݊݁ݏ‬൏ 1
2 no 1°
quadrante
ߨ Valor
ܲൌ‫ܤ‬ 90° ൏ ‫ ݔ‬൏ 180° ൏‫ݔ‬൏ߨ ‫ ݔ ݊݁ݏ‬ൌ 1 Máximo
2

58. ߨ O seno é
ܲ ∈ 2°ܳ 90° ൏ ‫ ݔ‬൏ 180° ൏‫ݔ‬൏ߨ 0 ൏ ‫ ݔ ݊݁ݏ‬൏ 1
2 decrescente
ܲ ൌ ‫`ܣ‬ ܺ ൌ 180° ‫ݔ‬ൌߨ ‫ ݔ ݊݁ݏ‬ൌ 0
3ߨ O seno é
ܲ ∈ 3° ܳ 180° ൏ ‫ ݔ‬൏ 270° ߨ൏‫ݔ‬൏ െ1 ൏ ‫ ݔ ݊݁ݏ‬൏ 0
2 decrescente
3ߨ Valor
ܲ ൌ ‫`ܤ‬ ܺ ൌ 270° ‫ݔ‬ൌ ‫ ݔ ݊݁ݏ‬ൌ െ1
2 mínimo
3ߨ O seno é
ܲ ∈ 4°ܳ 270° ൏ ‫ ݔ‬൏ 360° ൏ ‫ ݔ‬൏ 2ߨ െ1 ൏ ‫ ݔ ݊݁ݏ‬൏ 0
2 crescente
Gráfico
Note que ‫ ݔ ݊݁ݏ‬ൌ ‫ ݊݁ݏ‬ሺ‫ ݔ‬േ 2ߨሻ , pois ‫ ݔ ݁ ݔ‬േ 2ߨ são as medidas de arcos de mesma
extremidade e de acordo com a tabela do item anterior, concluímos que o gráfico da função
݂: Թ → Թ tal que ݂ሺ‫ݔ‬ሻ ൌ ‫ ݔ ݊݁ݏ‬é:
E o conjunto imagem é ሼ‫ ∈ ݕ‬Թ| െ 1 ൑ ‫ ݕ‬൑ 1ሽ
Temos que:

59. Propriedades.
Do que foi apresentado anteriormente podemos concluir que a função seno é:
i) Positiva na 1˚e 2˚ quadrantes; negativo no 3˚ e 4˚ quadrantes.
ii) Crescente nos 1˚ e 4˚ quadrantes e decrescentes nos 2˚ e 3˚ quadrantes.
iii) Impar, pois ‫ ݊݁ݏ‬ሺെ‫ݔ‬ሻ ൌ െ‫ݔ ݊݁ݏ‬
iii) Periódica de período 2ߨ .
Função cosseno
Definição
෢
O cosseno de um arco trigonométrica ‫ ܲܣ‬de extremidade ܲ , é a abscissa do ponto ܲ . É
representada por:

60. ෢
A cada numero real corresponde um único ponto P, extremidade do arco ‫ ܲܣ‬de medida ‫ . ݔ‬A
cada ponto P, por sua vez, corresponde uma única abscissa chamada cosseno de ‫ . ݔ‬A função de Թ
em Թ que a cada numero real ‫ ݔ‬associa a abscissa do ponto P é, por definição, a função co-seno.
Em símbolos
݂: Թ → Թ ‫݂ ݁ݑݍ ݈ܽݐ‬ሺ‫ݔ‬ሻ ൌ ܿ‫ݏ݋‬ሺ‫ݔ‬ሻ ൌ ܱ‫ܯ‬
Obs. A definição dada é coerente com aquela apresentada no triângulo retângulo. Pois
గ
temos, se 0 ൏ ‫ ݔ‬൏ então P pertence ao 1˚ quadrante e além disso ܱܲ ൌ 1 (raio).
ଶ
Assim, no triângulo OMP retângulo em M, temos:
ܿܽ‫݁ݐ݆݊݁ܿܽ݀ܽ .ݐ‬ ܱ‫ܯ‬ ܱ‫ܯ‬
ܿ‫ ݔݏ݋‬ൌ ⟺ ܿ‫ ݔݏ݋‬ൌ ⇔ ܿ‫ ݔݏ݋‬ൌ ⟺ ܿ‫ ݔݏ݋‬ൌ ܱ‫ܯ‬
݄݅‫ܽݏݑ݊݁ݐ݋݌‬ ܱܲ 1
Variação da função cosseno
Enquanto o ponto P percorre a primeira volta no sentido anti-horário, o número real ‫ ݔ‬varia
de 0 a 2ߨ e co-seno de ‫ ݔ‬varia de -1 a 1. Observe, na tabela a seguir as varias situações possíveis.
Posição Medida do
Medida do arco No ciclo
do arco em Cosseno de ࢞ Propriedade
em graus Trigonométrico
Ponto p radianos
Valor
ܲ≡‫ܣ‬ ‫ ݔ‬ൌ 0° ‫ݔ‬ൌ0 ܿ‫ ݔ ݏ݋‬ൌ 1
Máximo

61. O cosseno é
ߨ
ܲ ∈ 1° ܳ 0° ൏ ‫ ݔ‬൏ 90° 0൏‫ݔ‬൏ 0 ൏ ܿ‫ ݔ ݏ݋‬൏ 1 decrescente
2
no 1˚ܳ
ߨ
ܲൌ‫ܤ‬ 90° ൏ ‫ ݔ‬൏ 180° ൏‫ݔ‬൏ߨ ܿ‫ ݔ ݏ݋‬ൌ 0
2
O cosseno é
ߨ
ܲ ∈ 2°ܳ 90° ൏ ‫ ݔ‬൏ 180° ൏‫ݔ‬൏ߨ െ1 ൏ ܿ‫ ݔ ݏ݋‬൏ 0 decrescente
2
no 2˚ ܳ
Valor
ܲ ൌ ‫`ܣ‬ ܺ ൌ 180° ‫ݔ‬ൌߨ ܿ‫ ݔ ݏ݋‬ൌ െ1
mínimo
O cosseno é
3ߨ
ܲ ∈ 3° ܳ 180° ൏ ‫ ݔ‬൏ 270° ߨ൏‫ݔ‬൏ െ1 ൏ ܿ‫ ݔ ݏ݋‬൏ 0 crescente no
2
3˚ Q
3ߨ
ܲ ൌ ‫`ܤ‬ ܺ ൌ 270° ‫ݔ‬ൌ ܿ‫ ݔ ݏ݋‬ൌ 0
2
3ߨ O cosseno é
൏ ‫ ݔ‬൏ 2ߨ
ܲ ∈ 4°ܳ 270° ൏ ‫ ݔ‬൏ 360° 2 0 ൏ ܿ‫ ݔ ݏ݋‬൏ െ1 crescente no
4˚ Q
Gráfico
Note que cos ‫ ݔ‬ൌ cos ‫ ݔ‬േ 2ߨሻ , pois ‫ ݔ‬േ 2ߨ são as medidas de arcos de mesma
ሺ
extremidade, e de acordo com a tabela anterior, concluímos que o gráfico da função ݂: Թ → Թ tal
que ݂ሺ‫ݔ‬ሻ ൌ cos ‫ݔ‬ሻ é:
ሺ O conjunto imagem é
ሼ‫ ∈ ݕ‬Թെ1 ൑ ‫ ݕ‬൑ 1ሽ.

62. Note que:
Propriedades
Do que foi apresentado, podemos concluir que a função cosseno é positiva no primeiro e
quarto quadrantes. Negativa no segundo e terceiro quadrantes.
a) Positiva no primeiro e quarto quadrantes. Decrescente no primeiro e segundo
quadrantes.
b) Par, pois cosሺെ‫ݔ‬ሻ ൌ ‫ݔݏ݋ܥ‬
cosሺെ40°ሻ ൌ cos 40 °
c) Periódica de período 2ߨ
Proposta de exercícios

63. 1) Calcule:
a) ‫˚0 ݏ݋ܥ‬ b) ‫˚03 ݏ݋ܥ‬ c) ‫˚54 ݏ݋ܥ‬ d) ‫ ˚09 ݏ݋ܥ‬
e) ‫˚021 ݏ݋ܥ‬ f) ܵ݁݊ 150˚ g) ܵ݁݊ 180˚ h ) ‫˚087 ݏ݋ܥ‬
Gabarito.
√ଷ √ଶ ଵ √ଷ ଵ
a) 0 b) c) d) 0 e)െ ଶ f) െ g)െ1 h) ଶ
ଶ ଶ ଶ

64. Função tangente
Definição
෢
Consideremos um arco ‫ ܲܣ‬com ܲ ് ‫ ܦ ് ܲ ݁ ܤ‬e seja ܶ a interseção da reta ܱܲ com o eixo
das tangentes ‫.ܶܣ‬
෢
Por definição ‫ ܲܣ ݃ݐ‬ൌ ‫ܶܣ‬
A função tangente é tal que
ߨ
݂: Թ െ ቄ݇ߨ ൅ , ݇ ߳ Ժቅ → Թ
2
‫ ݕ‬ൌ ‫ ݔ݃ݐ‬ൌ ‫ܶܣ‬
Observe que o ponto P, numa volta completa no ciclo trigonométrico, faz o valor da
tangente (AT) tender a ൅∞ (ou a െ∞) quando o ponto P se aproxima de B ou D (onde a tangente
não existe). A cada meia volta, verificamos que todos os valores da tangente se repetem.
Consequências
De definição da função ‫ ݕ‬ൌ ‫ ݔ ݃ݐ‬decorre que:
గ
Domínio ‫ܦ‬ሺ݂ሻ ൌ Թ െ ቄ݇ߨ ൅ ଶ , ݇߳ Ժቅ
Imagem ‫݉ܫ‬ሺ݂ሻ ൌ Թ

65. Gráfico.
Propriedades
O período da função tangente é ߨ.
A função ‫ ݕ‬ൌ ‫ ݔ ݃ݐ‬é impar ‫݃ݐ‬ሺെ‫ݔ‬ሻ ൌ െ‫.ݔ ݃ݐ‬
A função ‫ ݕ‬ൌ ‫ ݔ ݃ݐ‬é crescente no intervalo
ߨ ߨ
݇ߨ െ ൏ ‫ ݔ‬൏ ݇ߨ ൅ , ݇ ߳ Ժ.
2 2

66. Capitulo 7.
Derivada e a reta tangente
Os gregos a reta tangente a um ponto de uma circunferência como sendo a reta que toca a
circunferência neste ponto e é perpendicular ao raio no ponto de tangência. Porém, no caso de uma
curva qualquer a situação é mais delicada e vai exigir o conceito de limite.
Precisamos definir o raio de uma curva qualquer, o que é tão complicado quanto caracterizar
a reta tangente;
Uma teta que passa por um único ponto de uma curva nem sempre é uma reta tangente;
Uma verdadeira tangente pode tocar a curva em mais de um ponto; (݂݅݃‫)1 ܽݎݑ‬
Assim, para uma curva qualquer, foi preciso esperar até o século XVII para se ter uma
definição satisfatória de tangente.
Para resolver a questão vamos considerar a função ‫ ݕ‬ൌ ݂ሺ‫ݔ‬ሻ e seu gráfico representativo
mostrado na ݂݅݃‫.2 ܽݎݑ‬

67. Sejam ‫ ݔ‬e ݂ሺ‫ݔ‬ሻ as coordenadas do ponto ܲ onde desejamos traçar a tangente. Consideremos
outro ponto ܳ de gráfico de ݂, cujas coordenadas são ܳ ൫‫ ݔ‬൅ ∆‫݂ ,ݔ‬ሺ‫ ݔ‬൅ ∆‫ݔ‬ሻ൯. O declive da reta
secante PQ é dado pelo quociente
Δ‫ݕ‬ ݂ሺ‫ ݔ‬൅ ∆‫ݔ‬ሻ െ ݂ሺ‫ݔ‬ሻ
ൌ
Δ‫ݔ‬ ∆‫ݔ‬
Chamado razão incremental, pois ∆‫ ݔ‬é realmente um incremento que damos a abscissa de
ܲ para obtermos a abscissa de ܳ.
୼௬
Ao considerarmos o quociente de dois incrementos ୼௫ , na verdade, o estamos considerando
como uma taxa média variação de ‫ ݕ‬em relação ‫.ݔ‬
Vamos imaginar agora (‫ ,)3 ܽݎݑ݃݅ܨ‬que, enquanto o ponto ܲ permanece fixo, o ponto ܳ
aproxima-se de ܲ, passando por sucessivas posições ܳଵ, ܳଶ , ܳଷ , etc. Logo, a secante ܲܳ assumirá as

68. posições ܲܳଵ, ܲܳଶ, ܲܳଷ etc. O que se espera é que a razão incremental, que é o declive da reta
secante, se aproxime de um determinado valor “݉”, a medida que o ponto ܳ se aproxima do ponto
ܲ. Isto acontecendo, definimos a reta tangente a uma curva em ܲ, como sendo aquela que passa por
ܲ, e tem declive “݉”. Observe que fazer ܳ se aproximar de ܲ é o mesmo que fazer ∆‫ ݔ‬se aproximar
de zero na razão incremental.
Quando fazemos ∆‫ 0 ⇒ ݔ‬e a razão incremental se aproxima de um valor finito, dizemos que
“݉” é o limite da razão incremental com ∆‫ 0 ⇒ ݔ‬e escrevemos
݂ሺ‫ ݔ‬൅ ∆‫ݔ‬ሻ െ ݂ሺ‫ݔ‬ሻ
݉ ൌ lim
∆௫→଴ ∆‫ݔ‬
Este quociente que representa a taxa instantânea de variação é chamado de derivada da
função ࢌ, que pode ser expressa por:
݀‫ݕ‬ Δ‫ݕ‬ ݂ሺ‫ ݔ‬൅ ∆‫ݔ‬ሻ െ ݂ሺ‫ݔ‬ሻ
݂ ᇱ ሺ‫ݔ‬ሻ ൌ ൌ lim ൌ lim
݀‫ݔ‬ ∆௫→଴ Δ‫ݔ‬ ∆௫→଴ ∆‫ݔ‬
Exemplo:
Calcular o coeficiente angular da reta tangente ao gráfico de ‫ ݕ‬ൌ ‫ ݔ‬ଶ no ponto de abscissa
‫ ݔ‬ൌ 1.
Solução:
A figura ao lado mostra um esboço do gráfico de ‫ ݕ‬ൌ ‫ ݔ‬ଶ e a tangente t no ponto ሺ1, 1ሻ. Pela
definição de derivada é:
݀‫ݕ‬ ݂ሺ‫ ݔ‬െ Δ‫ݔ‬ሻ െ ݂ሺ‫ݔ‬ሻ
݂ ᇱ ሺ‫ݔ‬ሻ ൌ ൌ lim
݀‫୼ ݔ‬௫→଴ Δ‫ݔ‬
ሺ‫ ݔ‬൅ Δ‫ݔ‬ሻଶ െ ‫ ݔ‬ଶ
ൌ lim
୼௫→଴ Δ‫ݔ‬
‫ ݔ‬ଶ ൅ 2‫ݔ‬ሺΔ‫ݔ‬ሻ ൅ ሺΔ‫ݔ‬ሻଶ െ ‫ ݔ‬ଶ
ൌ lim
୼௫→଴ Δ‫ݔ‬
Δ‫ݔ‬ሺ2‫ ݔ‬൅ Δ‫ݔ‬ሻ
ൌ lim
୼௫→଴ Δ‫ݔ‬
ൌ lim 2‫ ݔ‬൅ Δ‫ݔ‬
୼௫→଴
Como Δ‫ 0 → ݔ‬temos que ݂ ᇱ ሺ‫ݔ‬ሻ ൌ 2‫ ,ݔ‬função que nos dá a derivada da curva ‫ ݕ‬ൌ ‫ ݔ‬ଶ . Como
queremos a tangente passando em ሺ1, 1ሻ, teremos ݂ ᇱ ሺ‫ݔ‬ሻ ൌ 2 ൈ 1 ൌ 2 é o coeficiente angular
pedido.
Informações dadas pela primeira derivada
Crescimento e decrescimento de funções

69. Muitas vezes se torna importante se determinar se uma função ݂ está aumentando ou
ௗ௬
diminuindo. E a derivada pode ser usada para esse propósito.
ௗ௫
Seja uma função ݂ definida no intervalo I, e ‫ݔ‬ଵ ݁ ‫ݔ‬ଶ pertencentes a I, podemos ter três casos:
1) ݂ é crescente em I se ݂ሺ‫ݔ‬ଵ ሻ ൏ ݂ሺ‫ݔ‬ଶ ሻ quando ‫ݔ‬ଵ ൏ ‫ݔ‬ଶ .
2) ݂ é decrescente em I se ݂ሺ‫ݔ‬ଵ ሻ ൐ ݂ሺ‫ݔ‬ଶ ሻ quando ‫ݔ‬ଵ ൏ ‫ݔ‬ଶ .
3) ݂ é constante em I se ݂ሺ‫ݔ‬ଵ ሻ ൌ ݂ሺ‫ݔ‬ଶ ሻ para todo ‫ݔ‬ଵ , ‫ݔ‬ଶ .
Em outras palavras:
“Critério da primeira derivada serve para determinar se uma função é crescente ou
decrescente”
݂ሺ‫ݔ‬ሻ é crescente nos intervalos que ݂ ᇱ ሺ‫ݔ‬ሻ ൐ 0
݂ሺ‫ݔ‬ሻ é decrescente nos intervalos que ′݂ሺ‫ݔ‬ሻ ൏ 0
Exemplo:
య
Calcula-se que daqui a ‫ ݐ‬meses a população de certa cidade será ܲሺ‫ݐ‬ሻ ൌ 3‫ ݐ‬൅ 5‫ ݐ‬మ ൅ 6000.
Determine os intervalos que a função é crescente ou decrescente.
Solução:
ଵହ
A derivada de ܲሺ‫ݐ‬ሻ é ܲᇱ ሺ‫ݐ‬ሻ ൌ ‫ ݐ‬൅ 3, que é continua para todos os valores de ‫ ݐ‬e se
ଶ
଺
anula em ‫ ݐ‬ൌ െ ଵହ. Portanto, o sinal da derivada permanece constante nos intervalos െ∞ ൏ ‫ ݐ‬൏

70. ଺ ଺
െ ଵହ e െ ଵହ ൏ ‫ ݐ‬൏ ∞. Vamos escolher em cada intervalo um numero de teste “c” e encontrarmos o
sinal de ܲᇱ ሺ‫ݐ‬ሻ.
Intervalo Numero de teste “ࢉ” Sinal de P` Conclusão
6
െ∞ ൏ ‫ ݐ‬൏ െ െ2 ݂´ሺ2ሻ ൏ 0 ܲሺ‫ݐ‬ሻ é decrescente.
5
6
െ ൏‫ݐ‬൏∞ 2 ݂´ሺ2ሻ ൏ 0 ሺ‫ݐ‬ሻ é decrescente.
5
Máximos e mínimos relativos
Dizemos que uma função ݂ possuirá máximo relativo no ponto ‫ ݔ‬ൌ ܿ, se ݂ሺܿሻ ≤ ݂ሺ‫ݔ‬ሻ para
todos os valores de ‫ ݔ‬no intervalo ܽ ൏ ‫ ݔ‬൏ ܾ que contenha o ponto ܿ . Uma função ݂ possuirá
mínimo relativo no ponto ‫ ݔ‬ൌ ܿ, se ݂ሺܿሻ ≥ ݂ሺ‫ݔ‬ሻ, para todos os valores de ‫ ݔ‬no intervalo ܽ ൏ ‫ ݔ‬൏ ܾ
que contenha o ponto ܿ.
Exemplo:
A concentração de um fármaco no sangue, após sua administração por via
intramuscular, em dose única é dada por:
10‫ݐ‬
‫ ݕ‬ൌ ‫ܥ‬ሺ‫ݐ‬ሻ ൌ , ‫0 ≥ ݐ‬
‫ݐ‬ଶ ൅ 2‫ ݐ‬൅ 1
Onde o tempo ‫ ݐ‬é em horas.
a) Determine os intervalos onde a concentração da substância no sangue está
aumentando e onde está diminuindo.
b) Qual o comportamento da função em ‫ ݐ‬ൌ 1?
Solução:
a) Como ሺ‫ ݐ‬൅ 1ሻଶ ൌ ‫ ݐ‬ଶ ൅ 2‫ ݐ‬൅ 1, a função poderá ser escrita como
ଵ଴௧
‫ܥ‬ሺ‫ݐ‬ሻ ൌ ሺ௧ାଵሻమ , ‫0 ≥ ݐ‬
Portanto, sua derivada é
10ሺ‫ ݐ‬൅ 1ሻଶ െ ሺ10‫ݐ‬ሻ2ሺ‫ ݐ‬൅ 1ሻ 10ሺ1 െ ‫ݐ‬ሻ
‫ ܥ‬ᇱ ሺ‫ݐ‬ሻ ൌ ൌ , ‫0≥ݐ‬
ሺ‫ ݐ‬൅ 1ሻସ ሺ‫ ݐ‬൅ 1ሻସ
Podemos concluir que, para ‫ ݐ‬ൌ 1, a derivada ‫ ܥ‬ᇱ ሺ1ሻ ൌ 0 de modo que iremos estudar os
sinais da derivada nos intervalos 0 ൏ ‫ ݐ‬൏ 1 ݁ ‫ ݐ‬൐ 1.
Intervalos Número de teste “c” Sinal de C`(t) Conclusão
0൏‫ݐ‬൏1 1 ‫´ܥ‬ሺ‫ݐ‬ሻ ‫ܥ‬ሺ‫ݐ‬ሻ Crescente
2
t>1 2 C´(2) C(t) decrescente

71. b) Como a concentração cresce para ‫ ݐ‬൏ 1 e decresce para ‫ ݐ‬൐ 1, obviamente no ponto
‫ ݐ‬ൌ 1 ocorre um máximo.
Pontos críticos e números críticos.
Vimos no exemplo anterior a função ݂, aumentando em ݂ ᇱ ൐ 0 ou diminuindo em
݂′ ൏ 0. Chamamos de numero crítico ܿ quando ݂ ᇱ ሺܿሻ ൌ 0 ou quando não existe. O ponto crítico
corresponde ao ponto ሺܿ, ݂ሺܿሻሻ no gráfico de f.
Vejamos alguns exemplos de funções com pontos críticos onde a derivada é nula, de modo
que a reta tangente à curva da função no ponto crítico é horizontal:
Exemplos de funções que não é possível traçar uma reta tangente pelo ponto crítico:
Resumo
Sobre o teste da primeira derivada
Dada ‫ ݕ‬ൌ ݂ሺ‫ݔ‬ሻ
1ሻ Determinar os pontos críticos de ݂ que podem ser pontos de máximo ou de mínimo
relativos.
2ሻ Testar cada um dos pontos críticos encontrados para verificar se ݂ ᇱ ሺ‫ݔ‬ሻ muda de sinal. Se
݂ ᇱ ሺ‫ݔ‬ሻ mudar de sinal teremos:
a) De mais para menos, então ݂ tem um máximo em ‫ ݔ‬ൌ ‫ݔ‬ଵ
b) De menos para mais, então ݂ tem um m ‫ ݔ‬ൌ ‫ݔ‬ଵ
Exemplo:
Um psicólogo constata que a capacidade de aprender ou compreender novos conceitos e
ଷ
ideias depende da idade, e que esta capacidade pode ser representada por ‫ܥ‬ሺ‫ݐ‬ሻ ൌ െ ଶ ‫ ݐ‬ଶ ൅ 60‫ ݐ‬൅
24, após ‫ ݐ‬anos. Com que idade a capacidade de aprendizagem é máxima?
Solução:

72. Derivando ‫ܥ‬ሺ‫ݐ‬ሻ para encontrar os pontos críticos temos: ‫ ܥ‬ᇱ ሺ‫ݐ‬ሻ ൌ െ3‫ ݐ‬൅ 60, cuja raiz é
‫ ݐ‬ൌ 20 que é o único ponto crítico de C. O esquema a seguir mostra as sinais da derivada.
Intervalo Número de teste “࢞” Sinal de ࡯´ሺ࢚ሻ Conclusão
0 ൏ ‫ ݔ‬൏ 20 19 ‫´ܥ‬ሺ19ሻ ൐ 0 ‫ ܥ‬é crescente
‫ ݔ‬൐ 20 21 ‫´ܥ‬ሺ21ሻ ൐ 0 ‫ ܥ‬é decrescente
Como o sinal da derivada muda de mais para menos, temos um máximo relativo em ‫ ݐ‬ൌ 20,
que corresponde a idade de máxima aprendizagem.

73. Progressões.
Em quanto à população humana cresce em progressão geométrica, a
produção de alimentos cresce em produção aritmética.
“Thomas Malthus.”
Na matemática as sequências numéricas são muito importantes, estão associadas aos
processos de contagem e ao desenvolvimento do sistema de numeração. Há registros de problemas
envolvendo diversos tipos de sequências nos principais documentos das civilizações antigas. A
cerca de 2000 A.C., os Babilônios possuíam tábuas de cálculo nas quais se encontram sequências de
quadrados e cubos de números inteiros.
Sequências.
Conjunto de elementos de qualquer natureza organizados ou escritos em uma ordem
determinada. Na maior parte das sequências a ordem em que os elementos estão organizados é
responsável por sua definição.
Exemplos de sequências (S ) .
Sequência dos dias a semana.
S1 = (domingo, segunda-feira, terça-feira, ..., sábado)
Sequência dos dias do mês.
S2 = (1 de abril, 2 de abril, ..., 29 de abri, 30 de abril)
Sequência dos primos.
S3 = (2;3;5;7;11;13;17;19;23....)
Sequência dos números pares.
S4 = (2;4;6;8;10;12...)
Representação de uma sequência.
Para representarmos uma sequência escrevemos os seus termos, ou elementos, entre
parênteses. É importante observar que, caso seja alterado a ordem de um ou mais termos de uma
sequência, consequentemente o significado da sequência é alterado. Logo:
(2; 3; 4; 5) ≠ (3; 2; 5; 4)
Representação genérica de uma sequência.
Para representarmos de forma genérica uma sequência podemos utilizar a seguinte notação:
(a1 ; a2 ; a3 ; a 4 ; L, an , L ) com n ∈ Ν *

74. Observe que os índices associados as letras indicam as posições dos termos na sequência, ou
seja:
a1 Representação do 1° termo da sequência.
a 2 Representação do 2° termo da sequência.
an Representação do enésimo termo da sequência
Ainda podemos representar genericamente três termos consecutivos de uma sequência da
seguinte maneira:
(an −1; an ; an +1 )
Progressão Aritmética
Define-se como progressão aritmética (P.A.) toda sequência dada pela formula de
recorrência:
ܽଵ ୀ ܽ
ܽ௡ ൌ ܽ௡ିଵ ൅ ‫ ∈ ݊ ∀ ,ݎ‬ℕ, ݊ ≥ 2
Onde ܽ e ‫ ݎ‬pertencem aos números reais.
Assim, uma P.A. é uma sequência onde cada termo, a partir do segundo, se da pela soma do
termo anterior com uma constante ‫ ݎ‬dada.
Exemplos:
݂ଵ ൌ ሺ1, 3, 5, 7, 9, … ሻ ‫ܽ ݁݀݊݋‬ଵ ൌ 1 ݁ ‫ ݎ‬ൌ 2
݂ଶ ൌ ሺ0, െ2 , െ4, െ6, െ8, … ሻ ‫ܽ ݁݀݊݋‬ଵ ൌ 0 ݁ ‫ ݎ‬ൌ െ2
݂ଷ ൌ ሺ3, 3, 3, 3, 3, … ሻ ‫ܽ ݁݀݊݋‬ଵ ൌ 3 ݁ ‫ ݎ‬ൌ 0
1 3 5 7 1
݂ସ ൌ ൬ , , , , … ൰ ‫ܽ ݁݀݊݋‬ଵ ൌ ݁ ‫ ݎ‬ൌ 1
2 2 2 2 2
As progressões aritméticas são classificadas em três categorias:
Crescentes são as P.A. onde cada termo é maior que o anterior. Isto ira ocorrer somente se
‫ ݎ‬൐ 0, pois:
ܽ௡ ൐ ܽ௡ିଵ ⟺ ܽ௡ െ ܽ௡ିଵ ൐ 0 ⇔ ‫ ݎ‬൐ 0.
Exemplo: ࢌ૚ ࢋ ࢌ૝
Constantes são as P.A. onde cada termo é igual ao anterior. Isto ocorre quando ‫ ݎ‬ൌ 0, pois:
ܽ௡ ൌ ܽ௡ିଵ ⇔ ܽ௡ െ ܽ௡ିଵ ൌ 0 ⇔ ‫ ݎ‬ൌ 0.
Exemplo: ࢌ૜

75. Decrescente são as P.A. onde cada termo é menor que o anterior. Isto ocorre quando ‫ ݎ‬൏ 0,
pois:
ܽ௡ ൏ ܽ௡ିଵ ⇔ ܽ௡ െ ܽ௡ିଵ ൏ 0 ⇔ ‫ ݎ‬൏ 0.
Exemplo: ࢌ૛
Notações especiais:
Quando queremos uma P.A. com 3 ou 4 ou 5 termos, podemos utilizar a seguinte notação:
i) Para 3 termos: ሺ‫ ݔ ,ݔ‬൅ ‫ ݔ ,ݎ‬൅ 2‫ݎ‬ሻ ‫ ݑ݋‬ሺ‫ ݔ‬െ ‫ ݔ ,ݔ ,ݎ‬൅ ‫ݎ‬ሻ.
ii) Para 4 termos: ሺ‫ ݔ ,ݔ‬൅ ‫ ݔ ,ݎ‬൅ 2‫ ݔ ,ݎ‬൅ 3‫ݎ‬ሻ ‫ ݑ݋‬ሺ‫ ݔ‬െ 3‫ ݔ ,ݕ‬െ ‫ ݔ ,ݕ‬൅ ‫ ݔ ,ݕ‬൅ 3‫ݕ‬ሻ onde
௥
‫ݕ‬ൌ .
ଶ
iii) Para 5 termos: ሺ‫ ݔ ,ݔ‬൅ ‫ ݔ ,ݎ‬൅ 2‫ ݔ ,ݎ‬൅ 3‫ݎ‬ሻ ‫ ݑ݋‬ሺ‫ ݔ‬െ 2‫ ݔ ,ݎ‬െ ‫ ݔ ,ݔ ,ݎ‬൅ ‫ ݔ ,ݎ‬൅ 2‫ݎ‬ሻ.
Exercícios:
1) Determina x de modo que (x, 2x+1, 5x+7) seja uma P.A.
2) Obter uma P.A. de três termos tais que sua soma seja 24 e seu produto seja 440.
Respostas:
1) Devemos ter ܽଶ െ ܽଵ ൌ ܽଷ െ ܽଶ , então:
ሺ2‫ ݔ‬൅ 1ሻ െ ‫ ݔ‬ൌ ሺ5‫ ݔ‬൅ 7ሻ െ ሺ2‫ ݔ‬൅ 1ሻ ⟹ ‫ ݔ‬൅ 1 ൌ 3‫ ݔ‬൅ 6 ⇒
ହ
⇒ ‫ ݔ‬ൌ െଶ
2) Empregando a notação especial ሺ‫ ݔ‬െ ‫ ݔ ,ݔ ,ݎ‬൅ ‫ݎ‬ሻ para a P.A. temos:
i) ሺ‫ ݔ‬െ ‫ݎ‬ሻ ൅ ‫ ݔ‬൅ ሺ‫ ݔ‬൅ ‫ݎ‬ሻ ൌ 24
ii) ሺ‫ ݔ‬െ ‫ݎ‬ሻ ∙ ‫ ∙ ݔ‬ሺ‫ ݔ‬൅ ‫ݎ‬ሻ ൌ 440
De i) obtemos x = 8, substituindo em ii) vem:
ሺ8 െ ‫ݎ‬ሻ ∙ 8 ∙ ሺ8 ൅ ‫ݎ‬ሻ ൌ 440 ⇔ 64 െ ‫ ݎ‬ଶ ൌ 55 ⇔ ‫ ݎ‬ଶ െ 9 ⇔ ‫.3 ± ݎ‬
Assim, a ܲ. ‫ .ܣ‬procurada é:
ሺ5, 8, 11ሻ para ‫ ݔ‬ൌ 8 ݁ ‫ ݎ‬ൌ 3 ou ሺ11, 8, 5ሻ para ‫ ݔ‬െ 8 ݁ ‫ ݎ‬ൌ െ3.
Termo Geral de uma P.A.
Seja uma P.A. ሺܽ௡ ሻ ൌ ሺܽଵ , ܽଶ , ܽଷ , ܽସ , … ሻ. Pela definição de P.A. temos que:
ܽଶ ൌ ܽଵ ൅ ‫ݎ‬

76. ܽ_3 ൌ ܽଶ ൅ ‫ ݎ‬ൌ ܽଵ ൅ ‫ ݎ‬൅ ‫ ݎ‬ൌ ܽଵ ൅ 2‫ ݎ‬
ܽସ ൌ ܽଷ ൅ ‫ ݎ‬ൌ ܽଵ ൅ 2‫ ݎ‬൅ ‫ ݎ‬ൌ ܽଵ ൅ 3‫ݎ‬
ܽ௡ ൌ ܽଵ ൅ ሺ݊ െ 1ሻ‫ݎ‬
Esta expressão traduz o enésimo termo da P.A. em função do primeiro termo e da razão.
Esta formula é conhecida como expressão do termo geral.
Exemplos:
1) Na progressão aritmética ሺࢇ࢔ ሻ ൌ ሺ૜, ૠ, ૚૚ , … ሻ, determine o 10˚ termo.
Solução:
Temos que ܽଵ଴ ൌ ሺ10 െ 1ሻ‫ .ݎ‬Como ܽଵ ൌ 3 ݁ ‫ ݎ‬ൌ 4 obtemos:
ܽଵ଴ ൌ 3 ൅ 9 ∗ 4 ൌ 39.
Logo, concluímos que o 10˚ termo é 39.
2) Se as eleições para presidente continuarem a ocorrer a cada quatro anos, então em que
ano ocorrera a vigésima eleição a partir de 2006?
Solução:
A P.A. (2006, 2010, 2014, . . .) tem como primeiro termo 2006 e razão igual a 4.
Logo:
ܽଶ଴ ൌ ܽଵ ൅ 19 ‫ ݎ‬ൌ 2006 ൅ 19 ൈ 4 ൌ 2082.
Concluímos que a vigésima eleição será no ano de 2082.
3) Obter a razão da P.A. em que o primeiro termo é 8 e o vigésimo é 30.
Solução:
ܽଶ଴ ൌ ܽଵ ൅ 19‫ 03 ⇒ ݎ‬ൌ െ8 ൅ 19 ‫ ݎ ⇒ ݎ‬ൌ 2.
Exercícios
1) Calcular o 17˚ de uma P.A. cujo primeiro termo é 3 e cuja razão é 5.
2) Obter o primeiro termo de uma P.A. de razão 4 cujo 23˚ termo é 86.
3) Calcule a razão de uma P.A. de 23 termos cujos primeiro termo é 8 e o ultimo termo é 74.
4) Qual é o termo igual a 60 na P.A. em que o 2˚ termo é 24 e a razão é 2?
Soma de termos de uma P.A.
Vamos deduzir uma formula para soma Sn dos termos de uma P.A.

77. Teorema 1.
௡ሺ௡ାଵሻ
A soma dos n primeiros inteiros positivos é .
ଶ
Demonstração:
ଵ ሺଵାଵሻ
i) Para n = 1, temos: 1 ൌ (sentença verdadeira).
ଶ
ii) Admitamos a validade da formula para n = p:
‫݌‬ሺ‫ ݌‬൅ 1ሻ
1 ൅ 2 ൅ 3 ൅ ⋯൅ ‫ ݌‬ൌ
2
E provemos para ݊ ൌ ‫ ݌‬൅ 1:
‫݌‬ሺ‫ ݌‬൅ 1ሻ
1 ൅ 2 ൅ 3 ൅ ⋯ ൅ ‫ ݌‬൅ ሺ‫ ݌‬൅ 1ሻ ൌ ൅ ሺ‫ ݌‬൅ 1ሻ ൌ
2
‫݌‬ሺ‫ ݌‬൅ 1ሻ ൅ 2ሺ‫ ݌‬൅ 1ሻ ሺ‫ ݌‬൅ 1ሻሺ‫ ݌‬൅ 2ሻ
ൌ ൌ .
2 2
Então:
݊ሺ݊ ൅ 1ሻ
1 ൅ 2 ൅ 3 ൅ ⋯൅ ݊ ൌ , ∀ ݊ ∈ ℕ∗
2
Exemplo:
A soma dos 50 termos iniciais da sequência dos inteiros positivos é:
50ሺ50 ൅ 1ሻ
1 ൅ 2 ൅ 3 ൅ 4 ൅ ⋯ ൅ 50 ൌ ൌ 25 ൈ 51 ൌ 1275
2
Teorema 2
Em toda P.A. tem-se:
݊ሺ݊ െ 1ሻ
ܵ௡ ൌ ݊ܽଵ ൅ ‫ݎ‬
2
Teorema 3
Em toda P.A. tem-se:
݊ሺܽଵ ൅ ܽ௡ ሻ
ܵ௡ ൌ
2
Demonstração
݊ሺ݊ െ 1ሻ 2݊ܽଵ ൅ ݊ሺ݊ െ 1ሻ‫݊ ݎ‬ሾ2ܽଵ ൅ ሺ݊ െ 1ሻ‫ݎ‬ሿ
ܵ௡ ൌ ݊ܽଵ ൅ ൈ ‫ ݎ‬ൌ ൌ ൌ
2 2 2
݊ሾܽଵ ൅ ܽଵ ൅ ሺ݊ െ 1ሻ‫ݎ‬ሿ ݊ሺܽଵ ൅ ܽ௡ ሻ
ൌ ൌ
2 2
Exemplos:
1) A soma dos 15 termos iniciais da P.A. ሺെ2, 1, 4, 7, . . . ሻé:

78. 15 ൈ 14
ܵଵହ ൌ 15ሺെ2ሻ ൅ ൈ 3 ൌ െ30 ൅ 315 ൌ 285.
2
2) A soma dos múltiplos inteiros de 2 desde 4 ate 100 pode ser calculada notando-se que
ሺ4, 6, 8, . . . , 100ሻ é uma ܲ. ‫ .ܣ‬de 49 termos em que ܽଵ ൌ 4 e ܽସଽ ൌ 100:
49ሺ4 ൅ 100ሻ
ܵସଽ ൌ ൌ 49 ൈ 52 ൌ 2548
2
Progressões Geométricas. (P.G)
Suponha o financiamento de 300 Reais, no qual os juros serão cobrados da seguinte
maneira, expressa pela tabela.
1º Mês 2º Mês 3º Mês
Inicial
(+10% da inicial) (+10% da anterior) (+10% da anterior)
R$ 300,00 R$ 330,00 R$ 363,00 R$ 399,93
Observe que cada nova parcela é obtida pela multiplicação do fator 1,1 na parcela anterior.
Fator 1,1??....
Inicial 300
10  10 
1º Mês 300 + 300 3001 +  300.(1,1) 300.(1,1) R$ 330,00
100  100 
10  10 
2º Mês 330 + 330 3301 +  330.(1,1) 300 . (1,1) ² R$ 363,00
100  100 
10  10 
3º Mês 363 + 363 3631 +  363.(1,1) 300 . (1,1) ³ R$ 399,93
100  100 
10  10 
4º Mês 399,93 + 399,93 399,931 +  399,93.(1,1) 300 . (1,1)
4
R$ 439,923
100  100 
Definição:
Progressão Geométrica ܲ. ‫ ܩ‬é toda sequência numérica de termos, não nulos, em que cada
um, a partir do segundo, é obtido pela multiplicação do termo anterior por um fator fixo não nulo,
a2
uma constante (q ) , denominado razão da ܲ‫ .ܩ‬Para determinarmos a razão q de uma PG basta; .
a1
Para o caso acima, q =1,1.

79. a1 a2 a3 a4 ... a9
⇓ ⇓ ⇓ ⇓ ... ⇓
300 300.(1.1) 300.(1.1).(1,1) =300.(1.1)² 300.(1.1)³ ... 300.(1.1)8
300,00 330,00 363,00 399,93 ... 643,07
Qual o valor que deverá ser pago daqui a um ano e meio?
As Progressões Geométricas (PG) podem ser classificadas em crescentes, decrescentes,
constantes e oscilantes. Essa classificação é feita observando-se os termos em posições ordenadas.
Exemplos:
1) (2, 4, 8, 16, 32, ...) q = 2, crescente.
2) ( 4, 4, 4, ...) q = 1, constante.
1 1 1
3) (16, 8, 4, 2, 1, , ) q= , decrescente.
2 4 2
4) (-1, -3, -9, -27, -81) q = 3, decrescente. Qual a
relação
1 1 1 entre as razões e
5) (-8, -4, -2, -1, - , - ) q= , crescente. a classificação
2 4 2
das Progressões
6) (-1, 3, -9, 27, -81) q = -3, oscilante. Geometricas?
Termo geral de uma PG.
Seja (a1 ; a 2 ; a3 ; a 4 ; L, a n , L ) uma PG, pela definição q ≠ 0 e a1 ≠ 0 . Podemos
escrever:
a2 = a1q
a3 = a2 q
a 4 = a3 q
a5 = a4 q
an = an −1q
Multiplicando estas (n − 1) igualdades membro a membro, obteremos:
a2 ⋅ a3 ⋅ a4 ⋅ L an −1 ⋅ an = (a2 q )⋅ (a2 q )⋅ (a3 q )⋅ (a4 q )⋅ ⋅ L (an −1q )
a2 ⋅ a3 ⋅ a4 ⋅ L an −1 ⋅ an = a2 ⋅ a3 ⋅ a4 ⋅ L an −1 ⋅ q ⋅ q ⋅ q ⋅ L q ⋅ an =
14 4 2 3
( n −1) fatores
a2 ⋅ a3 ⋅ a4 ⋅ L an −1 ⋅ an = a1 ⋅ a2 ⋅ a3 ⋅ a4 ⋅ L an −1 ⋅ q n −1
Logo:
an = a1 ⋅ q n −1

80. Por esta equação matemática podemos calcular qualquer termo de uma ࡼࡳ, conhecendo a1 e
q.
Aplicações:
1
1) Qual a razão da PG. ( ; − 2; 8; − 32; 128)
2
−2 2
Calculo da razão: q = = −2 ⋅ = − 4
1 1
2
3 3 
2) Determinar o 13º termo da PG.  ; ;L
 16 4 
Calculo do 13º.
Calculo da razão:
3) Encontrar a razão da PG em que a1 = 640 e a6 = 20 .
20
a6 = a1 ⋅ q 5 ⇒ 20 = 640 ⋅ q 5 ⇒ = q5
640
1 1 1
q5 = ⇒ q5 = 5 → q=
32 2 2
1
4) Encontrar o número de termos da PG que tem como razão , primeiro termo 6144 e
2
último termo 3.
5) Qual o termo geral da PG (2; 4; 8; ....)
an = 2 ⋅ 2n −1
an = 2n
6) Interpole 8 meios geométricos entre 5 e 2560.
Interpolar ‫ ܖ‬meios geométricos é colocar ‫ ܖ‬números entre extremos, de modo a obter uma
ࡼࡳ com ݊ ൅ 2 termos. Para resolver esta questão podemos utilizar da seguinte ideia.

81. a1 ; __; __; __; __; __; __; __; __;a10
1444442444443
8 meios
5 ; __; __; __; __; __; __; __; __;2560
Para encontrarmos os oito meios, basta encontrarmos a razão da PG.
a10 = a1 ⋅ q 9 ⇒ 2560 = 5 ⋅ q 9
2560
= q 9 ⇒ 512 = q 9
5
q = 9 29 → q = 2
Soma dos termos de uma ࡼࡳ finita.
São muitos os casos de aplicações matemáticas que é necessário calcular a soma de uma
progressão geométrica; um dos mais conhecidos envolve a prestação de financiamento de compra
de um bem qualquer cujas prestações são corrigidas periodicamente segundo uma porcentagem
fixa.
3 3 3 3 3 
Utilizaremos da seguinte PG.  ; ; ; ; 
 2 4 8 16 32 
Vamos realizar a somatória dessa ࡼࡳ, indicada por ࡿ.
3 3 3 3 3
S= + + + +
2 4 8 16 32
Um método que pode ser utilizado para calcular a soma dos termos de uma ܲ‫ ܩ‬finita
consiste em multiplicar toda expressão S pela razão q e, em seguida obter o resultado de ‫ .ܵ – ܵݍ‬
Observe:
3 3 3 3 3 1 1
(݅) S = + + + + . Onde a razão q = assim multiplicaremos a expressão S por q = ,
2 4 8 16 32 2 2
obtendo:
3 3 3 3 3
(݅݅) S ⋅ q = + + + +
4 8 16 32 64
Agora faremos (݅݅) − (݅), ou seja, ‫.ܵ – ܵݍ‬
1 1 3 3 3 3 3  3 3 3 3 3 
qS - S = S - S = - S = . + + + + − + + + + 
2 2  4 8 16 32 64   2 4 8 16 32 
1 3 3 93
- S= − ⇒ S=
2 64 2 32
93
Assim obtemos que o valor da somatória S =
32

82. De forma genérica podemos escrever a soma dos termos de uma ܲ‫ , ܩ‬como:
Vamos reproduzir a ideia anterior, porém de forma genérica. Isso nos conduzirá a uma
formula que permite o cálculo do somatório dos termos de uma ܲ‫. ܩ‬
S = a1 + a2 + a3 + a4 + L + an .
S = a1 + a1q + a1q 2 + a1q 3 + L + a1q n−1 (i )
Agora vamos multiplicar toda a expressão (i ) por q.
Sq = a1q + a1q ² + a1q 3 + a1q 4 + L + a1q n (ii )
Fazendo (ii) − (i) ⇒ Sq − S
a1 ⋅ q n − a1
Sq − S → S(q − 1) = a 1 ⋅ q n − a 1 → S =
q −1
S=
(
a1 ⋅ qn − 1 )
q −1
Assim temos que a soma dos ݊ termos de uma ܲ‫ ܩ‬finita pode ser dada pela expressão:
Sn =
(
a1 ⋅ q n − 1 )
q −1
Aplicações:
n
8
1
1) Qual a valor de S n = ∑ 16 ⋅ 
n=1  2
O significado a expressão acima é a soma dos oito termos desta ࡼࡳ, ‫ ,݆ܽ݁ݏ ݑ݋‬S8 .
n 1 2 3 8
8
1 1 1 1 1
∑ 16 ⋅ 2  = 16 ⋅  2  + 16 ⋅  2  + 16 ⋅  2  + L16 ⋅  2 
n =1          
n
8
1 1 1
∑ 16 ⋅ 2  = 8 + 4 + 2 + 1 + L + 16 q = 2
n =1  
 18 
8 ⋅  − 1
Sn =
(
a1 q − 1
n
)
→ S8 =
2

 255
=
q −1 1 16
−1
2
n
255 8
1 255
S8 =
16
ou ∑ 16 ⋅ 2  = 16
n =1  
2) Quantos termos devem ser somados à ࡼࡳ , finita (૚; ૜; ૢ; ૛ૠ, . . . ) para que o
resultado seja ૜ ૛ૡ૙?

83. a1 = 1 q=3 S n = 3280
Sn =
( )
a1 q n − 1
⇒ 3280 =
(
1 3n − 1)
q −1 3 −1
3n − 1
3280 = ⇒ 6559 = 3n
2
3 = 3n ⇒ n = 8
8
Limite da soma dos termos de uma PG.
É interessante observar que os termos, de algumas progressões geométricas, à medida que a
sequência e desenvolvida mais se aproximam de zero, no entanto sem atingi-lo ou superá-lo.
Exemplo:
 1 1 1 1  1
 8; 4; 2; 1; ; ; ; ; L a20 = 8 ⋅ = 0,000015258
 2 4 8 16  219
Realizando cálculo do a20 desta sequência obteremos um valor muito próximo de zero.
Sequências como esta são convergentes para zero. Para que uma sequência seja convergente
para zero é necessário que a razão esteja compreendida entre 0 e 1, ou entre -1 e 0. (− 1< q < 1) .
Quando numa PG. de termos não nulos com razão maior igual a 1 (1 ≤ q ) , ou menor igual a - 1
(q ≤ −1) , dizemos que a sequência é divergente, uma sequência divergente não possui soma finita.
O interessante é que em uma sequência convergente para zero, soma dos termos da
sequência, por maior que seja nunca ultrapassará certo limite. Vamos considerar uma PG
convergente para zero cuja soma dos termos é calculada aumentando-se o número de termos a cada
passo.
 1 1 1 1 1 1 
 8; 4; 2; 1; ; ; ; ; ; ;L
 2 4 8 16 32 64 
Vamos calcular a soma dos quatro primeiros termos.
1 
8 4 − 1 
Sn = 1
(
a q −1 n
)
→ S4 = 
2  ⇒ S = 15
q −1 1 4
−1
2
Agora, a soma dos 6 primeiros termos:
1 
8 6 − 1 
S6 =
(
a1 q − 1
6
→
) S6 = 
2  = 15,75 ⇒ S = 15,75
6
q −1 1
−1
2
Soma dos 8 primeiros termos:

84. 1 
8 8 − 1 
S8 =
(
a1 q − 1 8
→
) S8 = 
2  = 15,9375 ⇒ S = 15,9375
8
q −1 1
−1
2
Soma dos 10 primeiros termos:
 1 
8 10 − 1 
S10 =
(
a1 q − 1 10
→
) S10 = 
2  =⇒ S = 15,984375
10
q −1 1
−1
2
Seguindo essa ideia, podemos concluir de forma intuitiva que por mais que aumente o
número de termos, o valor da somatória não excederá o valor de 16, ou ainda que o valor limite da
somatória é 16. A representação matemática que expressa essa ideia e a seguinte:
lim S n = 16
n →∞
O significado da expressão e que o limite da soma S n , com n tendendo ao infinito, é cada
vez mais próximo de 16, sem nunca ultrapassá-lo.
Para deduzirmos a expressão algébrica que permite o cálculo do limite da soma de uma
progressão Geométrica convergente para zero, utilizaremos da progressão Geométrica anterior.
 1 1 1 1 1 1 
 8; 4; 2; 1; ; ; ; ; ; ;L
 2 4 8 16 32 64 
A soma do n primeiros termos desta ࡼࡳ

 1  n  
8 ⋅   − 1 n → ∞ (n tende ao infinito )
 2   
Sn =  

1 
−1
 1  → 0   1  tende a zero. 
n n
2   
 2 
   2  
  
Assim a soma expressada em forma de limite pode ser indicada da seguinte maneira:
 1  n 
8 ⋅   − 1
 2   8 ⋅ [0 − 1]
lim Sn =  = = 16
1 1
n →∞
−1 −1
2 2
De forma análoga podemos escrever:
a1
lim S n = , q ≠ 0 e −1 < q < 1
n →∞ 1− q

85. Aplicações:
∞ n
1
1) Cálculo do valor de ∑   .
n =1  2 
Representando o somatório acima termos:
∞ n
1 1 1 1 1 1
∑  2  = 2 + 4 + 8 + 16 + L
n =1  
onde a razão é : q =
2
O somatório mostra uma PG convergente para zero, assim temos:
1
a1
lim Sn = 1 − q = 2 1 = 1
n→∞
1−
2
Por mais que adicionemos termos ao somatório, este jamais ultrapassará o
resulta1, que é o limite dessa somatória.
x x x x
2) Cálculo do valor x tal que: x + + + + +L = 8
2 4 8 16
1
a1 = x q= lim S n =8
2 n→∞
x
8= ⇒x=4
1
1−
2
3) Paradoxo da corrida entre Aquiles e tartaruga, proposto por Zenão, na Grécia
antiga: “Caso seja realizado uma corrida entre Aquiles, considerado o atleta perfeito, e
uma tartaruga que sai 100 metros a frente do atleta, então Aquiles nunca alcançará a
alcançará mesmo correndo a uma velocidade 10 vezes maior que dela”
Veja a ilustração.

86. Intuitivamente podemos interpretar o problema como uma progressão geométrica,
 1 1 
representando os espaços percorridos por Aquiles. 100 ; 10; ; ;L , logo o ponto de encontro
 10 100 
entre Aquiles e a Tartaruga, pode ser encontrado somado às distâncias percorridas por Aquiles.
1 1
Sn = 100 + 10 + + +L
10 100
n
 1
Assim temos um PG convergente para zero, de razão q =   . A soma dos n primeiros
 10 
termos pode ser expressa por:
 1  n 
100 ⋅   − 1
 10 
 

Sn =
1
−1
10
n
 1 
Mais uma vez, aumentando o valor de n, temos que   se torna cada vez menor. Para
 10 
n
1
uma situação limite em que: n → ∞   →0
2
Assim podemos a soma expressa em forma de limite fica:
100 1000
lim S n = =
1 9
n →∞
−1
10
1000
Concluímos que é a distância máxima que Aquiles percorrerá antes de ultrapassar a
9
Tartaruga.

87. Capitulo 9.
Introdução a cônicas.
Parábola.
Considerações.
Seja uma reta e um ponto Marcaremos agora um
que não é pertencente à reta. conjunto de pontos com a mesma
Ambos pertencentes ao mesmo plano. distância do ponto e da reta .
Definição:
Parábola é o conjunto de pontos equidistantes de um ponto dado ‫ , ܨ‬denominado foco, e uma reta
dada d , denominada diretriz.
Elementos da parábola.
Foco da Parábola: O ponto F usado na definição de parábola é
denominado foco da parábola.
Diretriz da parábola: A reta ݀ usada na definição de parábola é
denominada diretriz da parábola.
Parâmetro da parábola (‫ :)݌‬A distância de F até a diretriz d , FD , é
denominada Parâmetro da parábola.
Eixo de simetria da parábola: A reta e que passa por F e é
perpendicular a diretriz d , é denominada eixo de simetria da parábola.

88. Vértice da parábola: O ponto V da parábola é o ponto de intersecção da reta e com a parábola.
Equação da parábola de vértice na origem.
Relacionado o foco F e a diretriz d , podemos chegar à
equação da parábola.
1º Caso
Diretriz paralela ao eixo y, e foco .
Para este caso onde o vértice esta localizado na origem, e a
parábola é simétrica em relação ao eixo ‫ ,ݔ‬a equação desta
parábola pode ser escrita como:
2º Caso.
Diretriz paralela ao eixo y, e foco .
Neste caso o vértice também esta localizado na
origem, e a parábola continua sendo simétrica em relação
ao eixo ‫ , ݔ‬a equação desta parábola pode ser escrita
como:
3º Caso.
Diretriz paralela ao eixo , e foco .
O vértice localizado na origem, a parábola é
simétrica em relação ao eixo , a equação desta
parábola pode ser escrita como:

89. Exemplo 1
Determinaremos a equação da parábola
de foco e diretriz .
Para solução utilizaremos da expressão:
Logo:
Exemplo 2
Determinar o foco e a diretriz da parábola de equação
.
Para solução utilizaremos da expressão:
Logo:
O foco será
A distância do vértice ao foco é e a diretriz é
Gráfico de uma função f (x ) = ax 2 + bx + c, a ≠ 0 f: R → R .
É possível demonstrar, que a representação geométrica da função
1 ∆
f ( x ) = ax 2 + bx + c, a ≠ 0 f : R → R é uma parábola de diretriz d de equações y = − − ,
4 a 4a
reta paralela ao eixo dos x. as coordenas do foco F podem ser encontradas utilizando da seguinte
 b 1 ∆  b ∆
expressão matemática, F =  − ; −  , assim como o vértice V =  − ;−  e o eixo de
 2a 4a 4a   2a 4a 
b
simetria e = − , reta paralela ao eixo dos y.
2a

90. Aplicações.
As propriedades da parabola permitem varias aplicações praticas. Vejamos algumas:
Dentre as mais utilizadas é para captar um conjunto de feixes de ondas eletromagneticas, oriundas
de um satelite artificial. São as chamadas antenas parabolicas. O feixe de raios atinge a antena
que tem o formato parábolico e reflete, todos os feixes passando,exatamente, pelo foco onde estará
instalado um receptor que decodificará e enviará para o receptor televisão, que rezultarão na
programação que você assiste. Os aparelhos de radar operão de forma semelhante às antenas
parabólicas.
Uma outra aplicação e na contrução de lentes parábolicas utilizadas nos instrumentos de
iluminação como farois dos veiculos a lampada fica posta exatamente no foco assim o feixe de
raios é refletido, isso permite direcionar os feixes para iluminar um ponto especifico, mormalmento
para o solo, evitando que a luz ofusque a visão de um motorista que venha em direção oposta.

91. Elipse.
Considerações.
Sejam dois pontos fixos e tal que a
distância entre eles seja .
Marcaremos agora uma serie de pontos,
onde a soma de suas distâncias aos pontos fixos
e , seja uma constante maior que .
Representando algebricamente podemos escrever:
constante, tal que:
Definição:
Uma elipse é um conjunto de pontos do plano
cuja soma das distâncias a dois pontos fixos é
constante e maior do que a distância entre eles
.
Elementos da elipse
Focos da elipse: são os pontos F1 e F2 , a distância
entre eles é denominada distância focal 2c .
Eixo menor da elipse B1 B2 : Cuja distância mede 2b .
Eixo maior da elipse A1 A2 : Cuja distância tem a
medida da constante da definição 2a .
Centro da elipse: Representado pelo ponto O .
c
Excentricidade da elipse (e): Número que representa a razão
a
Uma observação interessante e que
quanto maior a excentricidade, mais achatada
será a elipse.

92. Equação da elipse com centro na origem.
Consideremos uma elipse com as extremidades do eixo maior nos pontos A 1 (− a,0) e
A 2 (a,0) , e do eixo menor B1 (0, b) e B2 (0,−b) . Consideremos um ponto qualquer da elipse P( x,y) .
A equação reduzida da elipse de focos no eixo x ,
e centro O na origem é definida por:
x² y²
+ =1
a² b²
Exemplo 1.
Determine a equação da elipse de focos F1 (3,0) e F2 (0,−3) vértices que são extremidades
do eixo maior, A 1 = (5 , 0) e A 2 = (− 5 , 0) .
Interpretando os dados do problema, os focos estão no eixo dos ‫ .ݔ‬Logo: a = 5 e c = 3 .
a 2 = b2 + c2
25 = b2 + 9
b2 = 16
x² y² x² y²
+ =1 → + =1
a² b² 5² b²
x² y²
+ =1
25 16
Exemplo 2.
Determine a equação da elipse de focos F1 (0,2) e F2 (0,−2)
vértices que são extremidades do eixo maior, A 1 = (0 ,7) e
A 2 = (0 , − 7) .
x² y² x² y²
a 2 = b2 + c 2 + =1 → + =1
7 2 b² 49 b2
49 = b2 + 4
x² y²
b2 = 45 + =1
49 45

93. Exemplo 3.
Uma elipse de focos nos pontos F1 (0,3) e F2 (0,−3) . Se o comprimento do eixo menor da
elipse é 2, qual a equação da elipse?
c = 3 , 2b = 2 → b = 1
a2 = b2 + c2
a2 = 1 + 9 = 10
Observar que neste caso os focos então localizados no eixo dos y. Logo:
x² y² x² y²
+ =1 → + =1
b² a² 1 10
Exemplo 4.
Qual o foco e as extremidades do eixo maior da elipse de equação 5x2 + 20y 2 = 100
5x2 20y 2 x2 y 2
5x + 20y = 100 →
2 2
+ =1 → + =1
100 100 20 5
Como 20 > 5 , o eixo maior é o dos ‫ ,ݔ‬logo:
a2 = 20 → a = 2 5
b2 = 5 →b= 5
a2 = b2 + c2 → 20 = 5 + c2 → c = 15
( ) ( )
Concluímos que os focos são os pontos F1 15 ,0 e F2 − 15 ,0 as extremidades do eixo
( ) (
maior são A1 = 2 5 , 0 e A 2 = − 2 5 ,0 . )
Exemplo 5.
( ) ( )
Sabendo que os focos F1 0, 3 e F2 0,− 3 a excentricidade e =
1
2
. Determine a equação
da elipse.
c 1
c= 3 e= = →a=2 3
a 2
a 2 = b2 + c 2 → 2 3( ) − ( 3)
2 2
= b2 → b2 = 9
x² y² x² y²
+ =1 → + =1
b² a² 9 12
Exemplo 6.

94. O eixo maior de uma elipse são s pontos A1 (6,0) e A2 (− 6,0) . Onde o ponto P(3 , 2) . Qual a
equação da elipse. a = 6
x² y² 3² 2² 16
+ =1 → 2
+ 2 = → b2 =
a² b² 6 b 3
x² y² x 2 3y 2
+ =1 → + =1
6² 16 36 16
3
Exemplo 7.
c x2 y 2
Qual a excentricidade e = da elipse: + =1
a 16 9
a2 = 16 → a = 4 b2 = 4 → b = 2 c2 = a 2 − b2 → c = 2
2
e=
4
Pesquise como pode ser realizado o desenho de uma elipse? Elabore uma explicação como
se estivesse explicando a um colega!
Existe alguma aplicação utilizando a ideia de elipse? Pesquise!

95. Hipérbole.
Considerações
Sejam dois pontos fixos, F1 e F2 , de um plano cuja distância entre eles é 2c.
Marcaremos agora pontos de forma que a diferença
de suas distâncias até os pontos F1 e F2 , em módulo, seja
constante, de valor 2a < 2c , assim temos:
AF1 − AF2 = BF1 − BF2 = CF1 − CF2 = L
= OF1 − OF2 = 2a
é constante, tal que : 2a < 2c
Definição:
Hipérbole é o conjunto dos pontos do plano tal que a
diferença das distâncias a dois pontos fixos, em módulo, é
constante e menor que a distância entre eles.
Elementos da Hipérbole.
Focos da hipérbole: são os pontos F1 e F2 , a distância entre eles e denominado distância focal 2c .
Eixo real ou transverso são os vértices da
hipérbole: A1 e A2 , onde A1 F2 − A1F1 = 2a
Eixo imaginário ou conjugado: segmento
B1 B2 de comprimento 2b .
Centro da hipérbole: e o ponto médio de F1 F2 e
de A1 A2 .
Excentricidade da hipérbole: E a razão
c
representada por: e =
a

96. Equação da Hipérbole com centro na origem
Consideremos uma Hipérbole com os focos, F1 e F2 pertencentes ao eixo x , e o centro é a
origem O(0,0) A equação reduzida da hipérbole, para este caso pode ser escrita como:
x² y²
− =1
a² b²
Onde ܾ é equivalente a b² = c² − a²
Se os focos pertencerem ao eixo ‫ ,ݕ‬à equação reduzida da hipérbole será equivalente a:
y² x²
− =1
a² b²
Exemplo 1.
Seja F1 (5,0) e F2 (− 5,0) os focos de uma hipérbole de vértices A 1 (3,0) e A 2 (− 3,0) . Qual a
equação dessa hipérbole.
c=5
x2 y2
a =3 − =1
9 16
c 2 = a 2 + b2 → b2 = 16

97. Exemplo 2.
3
Seja F1 (6,0) e F2 (− 6,0) os focos de uma hipérbole e de excentricidade igual a
2
c 3 2c
c=6 e= = →a= →a =4
a 2 3
c 2 = a 2 + b2 → 36 = b2 + 16 → b2 = 20
x2 y 2
− =1
16 20
Exemplo 3.
Uma hipérbole com focos F1 (0,6) e F2 (0,−6) com eixo
transversal de comprimento 8. Qual a equação da hipérbole?
c=6
2a = 8 →a =4
36 = b + 16
2
→ b2 = 20
y 2 x2 y 2 x2
− =1 → − =1 → 20y 2 − 16x 2 = 320
OU
a 2 b2 16 20
Exemplo 4.
( )
Uma hipérbole de focos F1 (0,3) e F2 (0,−3) passando pelo ponto P 2, 5 . Qual a equação
da hipérbole? c = 3
c 2 = a 2 + b2 → 32 = a 2 + b2 → 9 − b2 = a 2
2
y 2 x2 y2 x2 5 22
− =1 → − =1 → − =1
a 2 b2 9 − b2 b2 9 − b2 b 2
→
5
−
4
=1 →
5b2 − 4 9 − b2
=1
( )
9 − b2 b2 b2 9 − b2 ( )
5b2 − 36 + 4b2
(
b 9−b
2 2
= 1 → 5b2 − 36 + 4b2 = b2 9 − b2
) ( )
→ 5b2 − 36 + 4b2 = 9b2 − b4
// // // → b2 = 6
9 − 6 = a2 → a2 = 3
y 2 x2
− =1 → 2y 2 − x 2 = 6
OU
3 6

98. Exemplo 5.
Determine os pontos correspondentes aos focos, às coordenas dos vértices e excentricidade
dessa hipérbole, definida pela equação:
(  1 
) x2 y 2 Observando a equação concluímos que os
5x − 3y = 135 → 5x − 3y = 135 × 
2 2 2 2
 → − =1 focos estão no eixo dos x.
 135  27 45
Focos:
a 2 = 27
b2 = 45 e
c 2 = 27 + 45 → c = 6 2
Arestas:
6 2 2 2
e= → e=
27 9 e
Existe alguma aplicação utilizando a ideia de hipérbole? Pesquise!

99. Bibliografia.
SANTIAGO,Genário Sobreira, Matemática para Ciências Biológicas. 1ª ed. RDS 2009
PESCO,Dirce Uesu e ARNAUT,Roberto Geraldo,Matemática Básica. V.Un.,5ª ed. Rio de
Janeiro,CECIERJ, 2005.
LIMA, Elon Lages , CARVALHO, Paulo Cezar Pinto, WAGNER, Eduardo e MORGADO,
Augusto César, Temas e problemas Elementares. Rio de janeiro, 2ªed. SOCIEDADE
BRASILEIRA DE MATEMÁTICA 2005.
LEZZI, Gelson, DOLCE, Osvaldo, DEGENSZAJN, David, PÉRIGO, Roberto e ALMEIDA, Nilze
de. Coleção MATEMÁTICA Ciência e Aplicações. V 3. 2ªed.São Paulo:ATUAL 2004.
LEZZI, Gelson, DOLCE, Osvaldo e MACHADO, Antonio. Matemática realidade. 8 ano, 6ª ed.
São Paulo: ATUAL 2009.
STOCCO SMOLE, Kátia Cristina e DINIZ,Maria Ignez de Souza Viera.MATEMÁTICA
ENSINO MÉDIO V.1,2 e 3. 4ªed. São Paulo:SARAIVA 2004.
DANTE, Luiz Roberto. Tudo é Matemática 8 ano, 3ªed.São Paulo:Ática 2010.
LIMA, Elon Lages , CARVALHO, Paulo Cezar Pinto, WAGNER, Eduardo e MORGADO,
Augusto César, A Matemática do Ensino Médio. V2, 6ªed. Rio de janeiro SOCIEDADE
BRASILEIRA DE MATEMÁTICA 2005.
DOLCE,Osvaldo e POMPEO,José Nicolau, Fundamentos de Matemática Elementar, geometria
espacial.V 10, 2ªed. São Paulo ATUAL.
IEZZI,Gelson e HAZZAN, Samuel FUNDAMENTOS DE MATEMÁTICA ELEMENTAR V. 4
SEQUENCIAS MATRIZES DETERMINANTES. 2ª ed. São Paulo ATUAL 1997.
PARANÁ, Djalma Nunes, FÍSICA. V. un. 6ªed. Ática
LIMA, Elon Lages , CARVALHO, Paulo Cezar Pinto, WAGNER, Eduardo e MORGADO,
Augusto César, Temas e problemas., 2ªed. Rio de janeiro SOCIEDADE BRASILEIRA DE
MATEMÁTICA 2001.
IEZZI,Gelson, FUNDAMENTOS DE MATEMÁTICA ELEMENTAR V. 7 GEOMETRIA
ANALÍTICA. 2ª ed. São Paulo ATUAL 1997.
DANTE, Luiz Roberto. Tudo é Matemática 9 ano, 1ªed.São Paulo:ABDR 2002.
BONJORNO, José Roberto, BONJORNO,Regina Azenha e OLIVARES, Ayrton. MATEMÁTICA
Fazendo a Diferença 7 série. 1ª ed. São Paulo FTD 2006.
IEZZI,Gelson, FUNDAMENTOS DE MATEMÁTICA ELEMENTAR V. 3
TRIGONOMETRIA. 2ª ed. São Paulo ATUAL 1997.
BEZERRA, Manoel Jairo,MATEMÁTICA para o ensino médio V. un. 5ªed.São Paulo Scipione
2004.

100. IEZZI,Gelson, MURAKAMI, Carlos e MACHADO, Nilson José FUNDAMENTOS DE
MATEMÁTICA ELEMENTAR V. 8 LIMITES DERIVADAS NOÇÕES DE INTEGRAL. 3ª
ed. São Paulo ATUAL.
MACHADO, Antonio dos Santos, MATEMÁTICA TEMAS E METAS 2- Trigonometria e
Progressões. São Paulo Atual 1998.
SOUZA, Maria Helena Soares de e SPINELL, Walter, MATEMÁTICA 2˚ grau volume 1. São
Paulo Scipione.