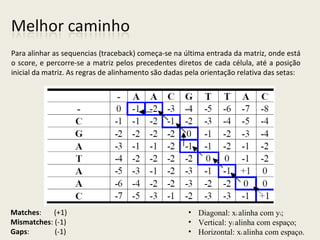
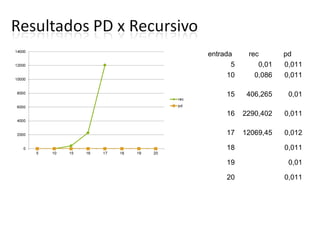
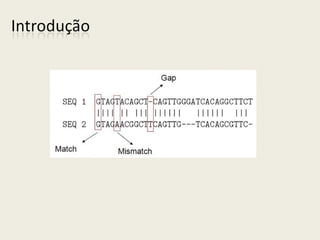
O documento discute alinhamento de sequências e como comparar duas sequências de DNA ou proteínas. Explica que alinhar sequências permite estudar evolução molecular, detectar doenças e mais. Descreve como calcular o score de um alinhamento e apresenta algoritmos recursivo e de programação dinâmica para encontrar o alinhamento ótimo.

2. Comparar sequências
 Recuperação de Informação: dada uma chave, buscar em um
dicionário por palavras que se assemelham à chave.
 Biologia Molecular: dadas duas sequências de DNA, identificar se
são semelhantes.
 Para que serve?

3.  Por que alinhamos sequências ?
Comparar genes de DNA
Estudar a estrutura de proteínas
 Estudar evolução molecular
Detecção de doenças, vírus, etc.

4. Um alinhamento de duas sequências de caracteres α e β é
obtido inserindo-se espaços (gaps) nas sequências e então
colocando-se uma sobre a outra de modo que cada
caractere ou espaço esteja emparelhado a um único
caractere (ou a um espaço) da outra cadeia.
• Exemplo:
• Sequências:
• α = AAACTGCACAATCTTAATGCCCTTTTAT
• β = GCGGATCAACTTATTCCATCTCTT
• Alinhamento:
• α′ = AAACTGCA-CAATCTTAATGCC--CTTTTAT
• β ′ =--GC-GGATCAA-CTT-ATTCCATCTCTT--

6. Ex: match +1 (good)
mismatch -1 (bad)
gap -2 (worse)
G A - C G G A T T A G
G A T C G G A A T A G
score = 9 ·1+ 1·(-1) + 1·(-2) = 6
O score que é a soma dos valores associados a cada posição, de
acordo com o grau de similaridade entre os elementos
correspondentes.
 Cálculo do Score

7. Problema: Alinhamento de duas cadeias de caracteres.
Entrada: Duas cadeias de caracteres
Saída: O alinhamento ideal das cadeias, possivelmente
incluindo as lacunas “gap’s”.

8. 1. Subestrutura Ótima
Sendo assim, há três alternativas possíveis para resolver o problema:
i) (m, n) M∈
ii) a m-ésima posição de X M∉
iii) a n-ésima posiçao de Y M∉
Caso ocorra o caso (i), teremos
OPT(m, n) = αXmYn + OPT(m -1, n -1).
Caso ocorra o caso (ii), teremos que “pagar” o custo de um intervalo desde a m-
ésima posição de X que não foi encontrada e alinhar X1, X2, ..., Xm-1 bem como Y1, Y2,
..., Yn. Deste modo teremos:
OPT(m, n) = δ + OPT(m -1, n).
Caso ocorra o caso (iii), será semelhante ao caso (ii), porém: OPT(m, n) = δ +
OPT(m, n -1).

9. 2. Expressão Recursiva
i *δ se j=0
j *δ se i=0
OPT(i,j)
MAX [αXiYj + OPT(i -1, j -1), δ
+ OPT(i -1, j), δ + OPT(i, j -1)]
δ – gap (custo pelo espaço)
αXiYj – custo de emparelhar Xi e Yj

10. 3. Algoritmo utilizando a força bruta (RECURSIVO)
1. Alinhamento_recursivo(X,m,Y,n)
2. If m = 0
3. then return n*δ
4. If n = 0
5. then return m*δ
6. A = αXiYj + Alinhamento_recursivo(X,m-1,Y,n-1)
7. B = δ + Alinhamento_recursivo(X,m-1,Y,n)
8. C = δ + Alinhamento_recursivo(X,m,Y,n-1)
9. return max (A,B,C)

11. • A complexidade para o algoritmo alinhamento_recursivo(X,i,Y,j) baseado
na expressão recursiva é:
T(m,n) = T(m-1,n-1) + T(m,n-1) + T(m-1,n) + Θ(1)
T(m,n) ≥ 3T(m-1,n-1) + Θ(1)
T(m,n) = Ω(3min(m,n)
)
 Ordem exponencial!
3.1 Análise do algoritmo alinhamento_ recursivo

12. 3.2 Algoritmo Utilizando Programação Dinâmica
1. Alinhamento_PD(X,Y,δ)
2. Initialize A[i,0] = i*δ for i = 0, ..., m
3. Initialize A[0,j] = j*δ for j = 1, ..., n
4. For i = 1, ..., m
5. For j = 1, ..., n
6. A[i,j] = max (αXiYj + A[i -1, j -1], δ + A[i -1, j], δ + A[i, j -1])
7. Endfor
8. Endfor
9. Return A[m,n]

13.  A complexidade para o algoritmo Alinhamento_PD é Θ(m*n), pois é o
tempo de preencher a matriz A.
 Este custo está expresso nas linhas 3 à 5 do algoritmo
Alinhamento_PD(X,Y,δ). As demais linhas têm tempo constante, ou
seja, Θ(1).
 O espaço ocupado é Θ(m*n), pois o tamanho da matriz é (m+1)*(n+1).
 Tempo de execução Θ(m*n)
3.3 Análise do algoritmo Alinhamento_PD(X,Y,δ)

14. 4. Algoritmo para mostrar a solução ótima

15. Matches: (+1)
Mismatches: (-1)
Gaps: (-1)
Para alinhar as sequencias (traceback) começa-se na última entrada da matriz, onde está
o score, e percorre-se a matriz pelos precedentes diretos de cada célula, até a posição
inicial da matriz. As regras de alinhamento são dadas pela orientação relativa das setas:

• Diagonal: xi alinha com yi;
• Vertical: yi alinha com espaço;
• Horizontal: xi alinha com espaço.

17. entrada rec pd
5 0,01 0,011
10 0,086 0,011
15 406,265 0,01
16 2290,402 0,011
17 12069,45 0,012
18 0,011
19 0,01
20 0,011

18. • Diferentes aplicações, diferentes formas de
solução.
• Algoritmo recursivo tem tempo exponencial.
• Programação Dinâmica oferece uma solução
em tempo polinomial.

19. • T. H. Cormen, C. E. Leiserson, and R. L. Rivest, Introduction to algorithms, 1st
ed., The MIT Press, 1990.
• V. Bafna, E. L. Lawler, and P. A. Pevzner, Approximation algorithms for
multiple sequence alignment, Theoretical Computer Science 182 (1997), 233–
244.
• Freitas, Ana T., Alinhamento de Sequências, Guia do 2o Laboratório de
Biologia Computacional, Outubro de 2007.
• P. Bonizzoni and G. D. Vedova, The complexity of multiple sequence
alignment with SP-score that is a metric, Theoretical Computer Science 259
(2001), 63–79.